Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2017 Mar 27;2(3):1163–1171. doi: 10.1021/acsomega.6b00468

Fitting Single-Walled Carbon Nanotube Optical Spectra

Moritz Pfohl †,‡, Daniel D Tune †,§, Arko Graf ∥, Jana Zaumseil ∥, Ralph Krupke †,‡, Benjamin S Flavel †,*
PMCID: PMC5377271  PMID: 28393134

Abstract

graphic file with name ao-2016-004689_0002.jpg

In this work, a comprehensive methodology for the fitting of single-walled carbon nanotube absorption spectra is presented. Different approaches to background subtraction, choice of line profile, and calculation of full width at half-maximum are discussed both in the context of previous literature and the contemporary understanding of carbon nanotube photophysics. The fitting is improved by the inclusion of exciton–phonon sidebands, and new techniques to improve the individualization of overlapped nanotube spectra by exploiting correlations between the first- and second-order optical transitions and the exciton–phonon sidebands are presented. Consideration of metallic nanotubes allows an analysis of the metallic/semiconducting content, and a process of constraining the fit of highly congested spectra of carbon nanotube solid films according to the spectral weights of each (n, m) species in solution is also presented, allowing for more reliable resolution of overlapping peaks into single (n, m) species contributions.

Introduction

Single-walled carbon nanotubes (SWCNTs) are an intensively studied nanomaterial and our fundamental understanding of their unique electronic, physical, chemical, and optical properties has steadily increased over the past 2 decades.1 This has been accompanied by an explosion of applications-based research into SWCNTs in all fields of science from photonics,2−4 telecommunications,5 solar cells,6,7 batteries,8 fuel cells,9 high-frequency transistors,10 biosensors,11 and novel memory devices,12 through to sports equipment and cancer research.7,13−15 Amongst other characteristics, it is their structure-dependent optical properties that make SWCNTs such an interesting material. Optical absorption spectroscopy of SWCNTs reveals sets of diameter-dependent absorption bands in the infrared, visible, and ultraviolet wavelength regimes, corresponding to the discrete energetic transitions of this one-dimensional nanomaterial. These are labeled the first (S11), second (S22), and third (S33) transitions of a (semiconducting) SWCNT and were originally modeled using the single particle approximation.16 However, two-photon excitation experiments have since revealed the excitonic nature of SWCNT optical transitions and theoretical models have been modified to include confined electron–electron interactions and exciton binding energies by solving the Bethe–Salpeter equation.17,18 Distinctions have been made between dissimilar SWCNTs based on their chirality, as indicated by the (n, m) indices, with each semiconducting chirality possessing a unique set of S11, S22, and S33 transition energies, and where small changes in the chiral angle and diameter can cause large changes in the optical and electronic properties of a nanotube. Many different (n, m) species and electronic types of SWCNTs (metallic and semiconducting) are present within as-grown nanotubes, and theoretical calculations, verified by experimental observations, have established databases of the unique optical “fingerprint” associated with each species.19

In the case of semiconducting SWCNTs, photoluminescence (PL) spectroscopy, and the ability to measure two-dimensional PL contour maps, has allowed for further experimental verification of each nanotube’s optical fingerprint and has provided an essential tool in the qualitative determination of the (n, m) distribution of as-grown SWCNT powders.20 However, the insensitivity of PL measurements to metallic SWCNTs, and the strongly varying quantum yield between (n, m) species, especially for zig-zag nanotubes,21−23 has resulted in a PL-based quantitative assessment of the (n, m) distribution remaining elaborate and difficult. Despite this, advances in the physical information that can be obtained with this technique continue to be made and the level of finesse with which PL spectra can be individualized into single (n, m) contributions and analyzed is improving.24−27 Raman spectral mapping may offer an alternative solution in the future but currently suffers from the need for elaborate tunable excitation sources. In addition to that, highly structure-dependent and unknown sensitivity factors exacerbate the interpretation of the measurement data.28 A much newer addition to the toolbox of spectroscopic probes of carbon nanotubes is variance spectroscopy.29 This is a fluorescence-based technique that can provide excellent quantitative information on the (n, m) distribution of a polychiral material, as well as extract single-species spectra from such mixtures, and which will no doubt have a significant research impact as the required equipment and software become more prevalent. However, due in part to its broad applicability beyond the realm of carbon nanotubes, optical absorption spectroscopy will remain the most widely available and easily accessible technique in the near future and is still considered the preferred method for concentration, electronic purity, and (n, m) determination.30

The extraction of physical information from simple optical measurements has allowed for the rapid development of chirality-enriched growth techniques31 and sorting processes, such as gel permeation,32,33 density-gradient ultracentrifugation,34 phase extraction,35 and polymer wrapping.36 All of these sorting techniques have been shown to produce single chirality SWCNTs, in some cases up to milligram quantities, and this new availability of material has in turn led to a further increase in applications-based research with SWCNTs. As single chirality SWCNTs move from being an exotic nanomaterial that is available in only a few research laboratories to something commonly available from commercial suppliers, it is imperative that methods of standardization are developed. Indeed, to this end, the ISO Technical Specification ISO/TS 10868:2011 (currently under revision)37 establishes broad guidelines for the optical characterization of SWCNTs and the US-based National Institute of Standards and Technology (NIST) has released (6, 5) SWCNTs grown from the CoMoCat process and prepared under standardized conditions, as well as a basic “How-To Guide” for near infrared measurements of large diameter, arc discharge SWCNTs.38

Throughout the work in our laboratories, we have repeatedly found the need to reliably decongest the optical absorption spectra of single-/few-chirality, as well as polychiral, SWCNT samples and have, thus endeavored to develop a practical, yet robust, system of doing so. Of course, there are several software packages available for the generic fitting of multipeak spectra, each with a plethora of options for how the peaks should be approximated. However, the resultant fitting output rapidly loses physical significance as the number of peaks and their degree of congestion becomes excessive. Factors such as the type of background subtraction employed and the line shape used to approximate the various peaks are critical in obtaining accurate information from the decongestion process. Naturally, one can generate the “best” fit by simply using the largest number of adjustable parameters; however, each of these parameters should have its origin in real physical processes or the reliability, reproducibility, and usefulness of the obtained information are questionable.

Therefore, in the present work, a significantly improved method for decongesting carbon nanotube optical absorption spectra is provided that is grounded in the underlying physical processes and takes advantage of several unique characteristics of the material to markedly improve the quality and accuracy of the obtained information, particularly in the case of the polychiral and highly overlapped spectra that those in the carbon nanotube research community are routinely faced with, for example, in the development of new sorting or growth processes in which the (n, m) distribution can sometimes be large and unknown.39 The common background subtraction procedures reported in the literature, the various line profiles that have been used, and (n, m) specific absorption databases have been combined with the current state-of-the-art in understanding of carbon nanotube photophysics to develop a comprehensive methodology for the quantitative characterization and (n, m) assignment of SWCNT spectra. Values of interest such as the (n, m) distribution and semiconducting purity can be determined quickly and reproducibly from the spectra of a polychiral material.

In the simplest case, the S11 and/or S22 regions of a spectrum can be fitted independently using one of several methods as previously reported. To this, we add the new ability to also consider the well-established, and in some cases very significant, contribution of the exciton–phonon sideband (EPS) to the spectra. The inclusion of this nanotube-specific, real-world constraint should significantly improve the accuracy and relevance of the output, particularly in the case of polychiral spectra. This work then takes the fitting process a step further by providing the option to fit the entire spectrum simultaneously, including the S11 and S22 peaks, and their respective EPS contributions. Such a heavily constrained fitting is only possible in this case because of the well-defined relationships that exist between the physical processes underlying the features observed in carbon nanotube optical absorption spectra, and the existence of complete databases and formulae of the measured energies/wavelengths, and goes beyond anything that can be achieved using generic multipeak fitting software packages. As a further useful addition, in the common case of a polychiral nanotube suspension being used to prepare a solid film, the initial (n, m) assignment and spectral weight data obtained from a fit of the solution spectrum can be used to constrain the fitting of the film’s much more heavily congested spectrum, for which the real-world relevance of any fitting procedure would otherwise be questionable. Naturally, as with any decongestion and fitting procedure, there are limitations to the minimum degree of uncertainty that can be obtained, as discussed later. Throughout this work, we have attempted to bring together the theoretical framework and understanding underlying carbon nanotube optical absorption spectra into a single, accessible resource for researchers who need to deal with such spectra, as well as to provide a useful, practical, and robust fitting tool for both expert and novice alike. The work is structured such that the article gives an overview of the theory and review of the literature, as well as some important examples, the Supporting Information file provides more detailed and specific descriptions of fitting processes and mathematical derivations, and the MATLAB code and LabVIEW-based graphical user interface allow readers to implement the entire fitting process in their own work.

Results and Discussion

In the decongestion of carbon nanotube absorption spectra into individual (n, m) contributions, and the determination of the spectral weight of each species and metallic content, the analyst is faced with many decisions regarding the appropriate model to best approximate their measured data. These decisions include: determination of the spectral regions associated with metallic or semiconducting nanotubes and their respective (n, m) dependent optical transitions, the spectral line shape, the full width at half-maximum (FWHM) and whether this is a fixed or variable parameter amongst (n, m) species, the appropriate S11 to S22 height or area ratio, consideration of EPS contributions and their proper magnitude relative to the main peaks, and, before any of this can be done, what type of background subtraction, if any, should be applied to the spectra. In the following discussion, we will first address the theoretical basis and implications of these factors and then demonstrate their application and some important considerations in their results.

Background Subtraction

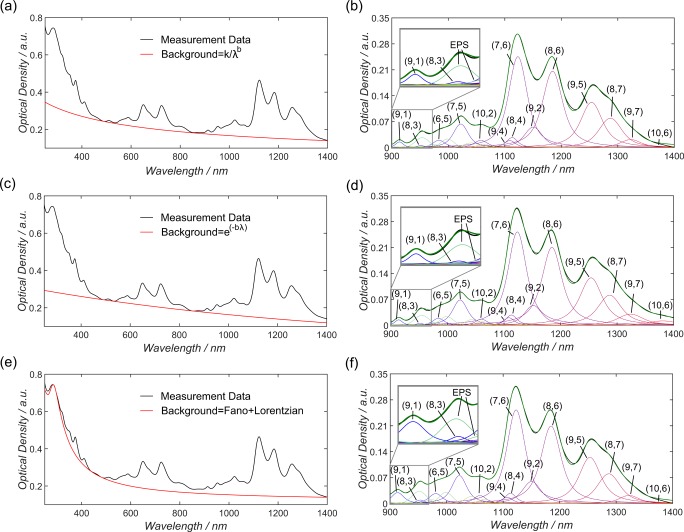
The initial decision regarding background subtraction is extremely important as it affects all of the subsequent steps in the fitting process and can result in markedly different (n, m) distributions being calculated. The background in carbon nanotube absorption spectra emerges from a high-energy component often attributed to a π–plasmon interaction and overall scattering from carbonaceous materials, catalyst particles, and bundled or defected nanotubes.40,41 For aqueous suspensions of SWCNTs, Nair et al.,40 Naumov et al.,41 and Ohmori et al.42 have all presented different approaches to deal with the absorption background. With the aid of sequential centrifugation and difference spectra, Ohmori et al. were able to almost completely remove the contribution from the scattering background in SWCNT spectra and were left with only the high-energy π–plasmon interaction, which they fitted with a Lorentzian.42 Naumov et al. provided additional experimental evidence that the shape of the background is dependent on metallic nanotube content, chemical modification, defect level, and the formation of bundles.41 In their work, a background profile in the form Ae(−bλ) was found to best accommodate this contribution, with A being the Beer Law proportionality constant, which depends linearly on concentration. Alternatively, Nair et al. empirically determined the form k/λb, based on the work of Ryabenko et al.,43 to best approximate their spectra of highly functionalized carbon nanotubes.40 In a recent publication, Tian et al. proposed a new routine for background subtraction of carbon nanotube films based on an overlap of Fano and Lorentzian line shapes.39 The Fano component models the strong coupling of an exciton around the M saddle point of the graphene lattice Brillouin zone (∼4.5 eV) to an underlying free electron–hole pair continuum and is very sensitive to bundling.44 The Lorentzian component models the π-plasmon resonance (∼5.3 eV), as suggested by Landi et al.45 The Fano profile is proportional to (a + ε)2/(1 + ε2) with “a” being a fitting parameter and ε = (E – Eres)/(Γ/2), where E is the energy, Eres the peak position of the Fano profile, and Γ its FWHM.46 To exemplify the critical importance of background subtraction, Figure 1 compares the approaches outlined by (a) Nair, (c) Naumov, and (e) Tian, showing how the corresponding (n, m) distributions subsequently calculated can differ considerably, particularly at the edges of the wavelength region, that is, for the (n, m) species (9, 7) (2.56, 4.22, and 2.36% for the methods based on Nair et al., Naumov et al., and Tian et al., respectively) and (10, 6) (0.08, 1.83, and 0.08% for the methods based on Nair et al., Naumov et al., and Tian et al., respectively) on the long wavelength side, and (9, 1) (0.25, 0.22, and 0.44% for the methods based on Nair et al., Naumov et al., and Tian et al., respectively) on the short wavelength side, as listed in Table S1 in the Supporting Information. The result of these considerations is that irrespective of the background subtraction method employed the degree of uncertainty in any quantitative information obtained for (n, m) species near the edges of the considered wavelength range will always be greater than that for those in the middle of the range. In addition, it must be mentioned that the issue of “correct” background shape and the various parameters contributing to it are still under investigation and debate. The large number of different nanotube preparation methods and media available for their suspension, means that a one size-fits-all approach to background subtraction is unlikely to be possible and the backgrounds found in the literature can only serve as a guide. Therefore, in the included code in the Supporting Information it is possible to not only use the background shapes defined in the literature but also to input any arbitrary reference plot data as the background. We hope that this feature will provide the flexibility to analyze a broad spectrum of different nanotube suspensions and enable the further study of background shapes in the future.

Figure 1.

Figure 1

Open in a new tab

Three different background subtraction methods proposed by Nair et al. (a), Naumov et al. (c), and Tian et al. (e).39−41 The measured absorption spectra are shown in black and the background profiles in red. The different background subtraction techniques result in comparable (n, m) distributions for shorter wavelengths in (b) and (d) but clearly deviate for (f). Above 1300 nm, (b) and (f) are comparable, whereas (d) clearly deviates, e.g., in the contribution of (9, 7) or (10, 6). A representative PL measurement is shown in Figure S1.

Spectral Line Shape

The choice of correct line shape to be used for the individual (n, m) species fitting has varied in the literature. However, it is accepted that a symmetric line shape can be used to fit optical absorption measurements.47 Luo et al.21 and Ohmori et al.42 used Lorentzian line shapes, whereas Nair et al.,40 Naumov et al.,41 and Hagen et al.48 used Voigtian line shapes, and Lolli et al.49 fitted their data using Gaussian line profiles. In theory, the Voigt function is best suited to fully capture the underlying physical processes that give rise to SWCNT absorption spectra, that is, a convolution of a single finite excited state lifetime (Lorentzian)50,51 and a random distribution of transition frequencies from heterogeneous environments (Gaussian), including thermal effects that might play a minor role.52 Or, to put it briefly, the shape is essentially Lorentzian, but with variable Gaussian broadening.52 Detailed descriptions of the Voigt, Lorentz, and Gauss expressions used in this work can be found in the Supporting Information.

FWHM

Following the selection of line shape, the FWHM must be defined. Similar to the choice of line profile, different empirical approaches for estimating the FWHM have been presented in the literature. Nair et al. divided their absorption spectra into three regions: S11, S22, and M11 for metallic SWCNTs,40 and for each region they assumed a fixed FWHM in energy space. A related approach was carried out by Hagen et al., who assumed a fixed FWHM for S11 transitions below 1.4 eV.53 Lolli et al. and Naumov et al. assumed a constant FWHM in wavenumber units.41,49 On the basis of the fitting data provided by Ohmori et al.,42 Tune et al., as well as Liu et al., proposed a linear increase in FWHM with increasing nanotube diameter (in energy space).54,55 Recently, Kadria-Villi et al. suggested a diameter-dependent FWHM in cm–1 for PL measurements.56 In the examples provided in the main text, the FWHM of Lorentzian and Gaussian functions were modeled on the values provided by Nair et al. as they were found to provide the best fit for our particular nanotube suspensions.40 For comparison, Figure S2 shows both the initial and fitted FWHM values for a constant FWHM in eV and in nm,40 or with a diameter dependent,56 or E11 dependence.55 The initial value in energy space was converted into wavelength and allowed to vary between 80% and 130%. These boundary conditions were determined based on numerous absorption spectra of monochiral, (n, m) enriched, and polychiral nanotube dispersions in aqueous and organic solutions. Nevertheless, in the code provided in the Supporting Information, it is possible to change the boundary conditions or use any of the other approaches for FWHM estimation by defining an equation to estimate the start values.

The definition of an initial value for the FWHM of the Voigtian line shape is complicated by the fact that it is a convolution of a Gaussian and Lorentzian line profile. Nevertheless, Olivero et al. provided an analytic expression for the Voigtian FWHM as a function of the Lorentzian and Gaussian FWHM,57 as shown in eq 1 and in eq S21–S26

graphic file with name ao-2016-004689_m001.jpg 1

To calculate Voigtian line profiles, several different approaches have been proposed, including numerical approximations of the Faddeeva, and therefore complex error function (eqs S27 and S28),58−60 Fourier transformations, and weighted sums of Lorentzian and Gaussian line shapes.61−63 In the present work, the procedure outlined by Schreier58 for the rapid approximation of the Faddeeva function was used in combination with the MATLAB implementations from Cherkasov.64 Thus, the Voigtian function was expressed in terms of the complex error function, as shown in the Supporting Information.

Exciton–Phonon Sidebands

Being excitonic in nature, the analysis of the optical properties of carbon nanotubes has revealed sidebands that are assigned to resonances emerging from the absorption of light by a bound exciton–phonon state.65,66 According to the work of Perebeinos et al., an EPS can be assigned to optical nanotube transitions and is located ∼0.2 eV above the peak energy.66 Dynamic effects lead to the transfer of a fraction of the spectral weight from the main nanotube peak to the EPS, and the magnitude of this transfer scales inversely with the diameter, as shown in eq S33.66 It is, therefore, crucial to consider EPS contributions when analyzing absorption spectra, especially for monochiral or chirality-enriched suspensions, as pointed out by Berciaud et al.,67 and demonstrated in Figure S4. For polychiral solutions, it may be reasonable to consider only the EPS of the most intense peaks, as any EPS of smaller peaks will have only a small effect on the overall fit. In analyzing PL spectra, Jones et al. and Rocha et al. proposed fitting the EPS with Lorentzian line profiles with a fixed FWHM of 18 meV (Jones), or twice the FWHM of the S11 peak (Rocha).26,27 With its sharp onset and long tail toward higher energies, the EPS is asymmetric in nature.66 However, in the present study, the EPS contribution was approximated with a symmetric line profile to simplify the computation. The decision was made to fit the sharp onset of the EPS peak with a Gaussian line shape to minimize interference with the modeling of the nanotube absorption, which would occur by fitting the broad tail. In this work the default initial FWHM of the EPS was empirically determined to be 40 nm.

Initial Peak Heights

One of the most crucial factors in obtaining a physically meaningful fit is the choice of the initial starting values of the peak heights of each (n, m) species. In the case of near-monochiral suspensions, the determination of the initial starting value is straightforward as it is given simply by the peak height in the absorption measurement. However, in the case of polychiral mixtures, the determination of starting values is complicated by spectral overlap. Nair et al. proposed a weighting scheme that is reliant on peaks being flanked by a valley to their right and left.40 They provided an automated routine to determine these parameters and also offered the possibility to insert peaks and valleys manually. Tian et al. introduced a different weighting scheme based on the sum of the two-norm of the residuals and the spectral weight multiplied by a prefactor, which was obtained empirically.68 Luo et al. and Wang et al. proposed a combined approach of correlating PL intensities and optical absorption spectra via an assumed log-normal distribution of the SWCNT diameters and an electron–phonon model that provided them with S22 absorption extinction coefficients.21,69 On the basis of these absorption coefficients and the PL intensities, they calculated the peak intensities of each (n, m) species in the optical absorption. The pitfall in their approach is the low PL quantum yield of zig-zag nanotubes that might cause an underrepresentation of these tubes in the optical absorption spectrum and therefore an unphysical fit.22 The approach used in the present study is shown in Figure 2, where the absorption value of the spectrum to be fitted, at the wavelength corresponding to each (n, m) species to be included, is taken as the starting value for the peak height of that species and is allowed to vary between 10 and 90%. This method is useful for broad, congested spectral features from many nanotubes. A further alternative method is shown in Figure S5 and is included as an option in the fitting routine provided.

Figure 2.

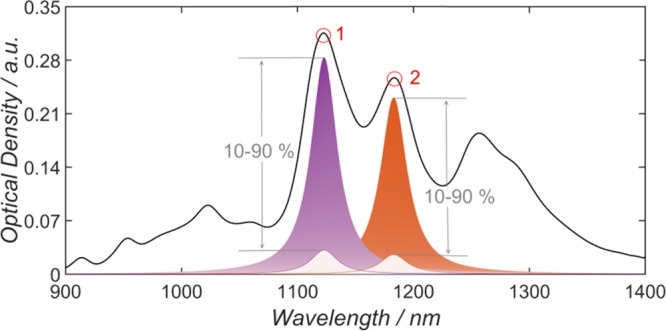
Figure 2

Open in a new tab

Schematic procedure of height assignment for peaks 1 and 2, where the height of the individual (n, m) species is allowed to vary between 10 and 90% of the initial height.

To make a quantitative comparison between fits of a particular spectrum, the quality of the fit can be determined by calculating the normalized sum of squared errors (nSSE), as described in eq 2, where ycalc is the fitted spectrum, ymeas is the absorption measurement, and 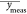Inline graphic is the mean value of the measurement. It is important to mention that the nSSE is equal to 1-R2, where R2(70) is a common measure of goodness of fit in regression analysis in statistics.71 The numerator in eq 2 is equal to the sum of squared residuals or the sum of squared errors of prediction.72 The denominator is the total sum of squares, indicating the deviation from the mean value and causing a normalization of the result. The closer the nSSE is to 0, the better the fit.

graphic file with name ao-2016-004689_m003.jpg 2

A comparison of the different line profiles and their associated nSSE are shown in Figure S6.

Selection of (n, m) Species to Fit

The final, critical, consideration is that of the choice of (n, m) species to be fitted under a given spectrum. It is simply not possible to take a polychiral absorption spectrum and extract the (n, m) abundance by some kind of generic multipeak fitting procedure. However, with a good understanding of the underlying photophysics, and with databases of measured transition energies, combined with information from other characterization techniques such as PL or Raman measurement, it is possible to obtain useful information. In the examples in this work, PL was used to first qualitatively determine the (n, m) species to be included in the fit. The validity of this approach was verified by taking two different solutions enriched in (6, 5) and (7, 5), and mixing them in known ratios of 2:1, 1:1, and 1:2. By comparing the concentrations of (6, 5) and (7, 5) in the starting solutions to the measured and calculated concentrations in the mixtures, a relative error of 10.8 ± 2.5% was obtained, as shown in Figures S7 and S8. These experiments highlight the level of accuracy and internal consistency of the fitting routine used to determine the ratio of (6, 5):(7, 5) as it is reliant upon an accurate, reproducible spectral fit of the range between 900 and 1250 nm consisting of six different (n, m) species and their associated EPS.

Spectral Weight and (n, m) Distribution

Each (n, m) species has a different absorption cross section, and experimentally determined values can be found in the literature.47,55,73 Although a full set of measured values is not yet available, Sanchez et al. provided an empirically derived formula for estimating the absorption cross section and molar absorptivity of different (n, m) species based on their diameter.47 For the calculation of the (n, m) distribution, either the spectral weight (area under an individual peak, divided by the total area under the region of the spectrum considered) or the relative concentration based on the optical density and molar absorptivity (as shown in eq S35) can be employed. An example of the spectral weight and relative concentration calculated in the aforementioned ways is shown in Figure 3. Spectra of the polychiral mixtures that were used to generate these plots are shown for reference in Figure S9.

Figure 3.

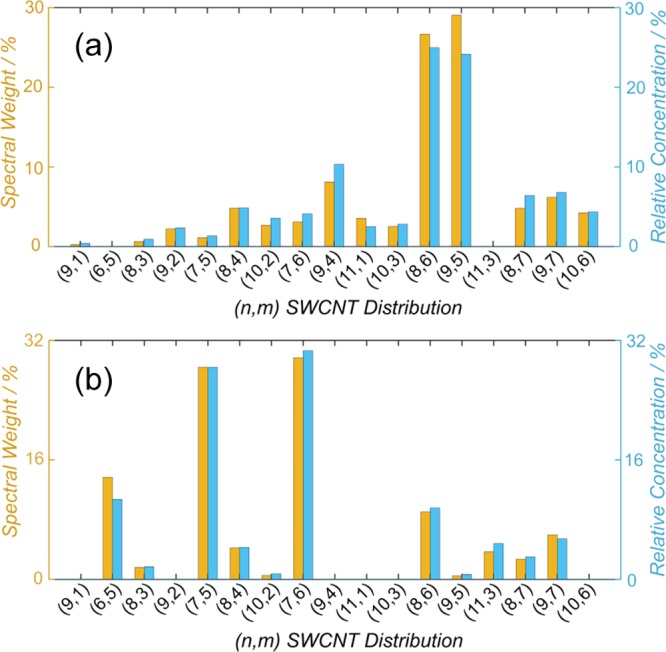
Figure 3

Open in a new tab

Histograms showing the (n, m) abundance of two different polychiral solutions (a) and (b), shown in Figure S9. The data is presented as both spectral weight and relative concentration.

Constrained Fit of Entire Spectrum

A fit of the entire spectrum can be performed by dividing the absorption spectrum into different regions, as proposed by Nair et al.40 However, such piecewise fitting of complete spectra has the potential to lead to nonphysical fits of the experimental data. For example, when a larger (n, m) distribution is required to fit S22 than is necessary for S11, or vice versa. In reality, these spectral regimes are physically coupled and the (n, m) distribution must, therefore, remain the same, independent of the region of consideration. Ohmori et al. reported a ratio of 1.15 for S11/S22, whereas Miyata et al. reported a ratio of 1.2 for the integrated molar absorption coefficients.42,74

These values are overall estimates and a definite ratio could not be provided, neither in terms of intensity nor area, due to the spectral overlap and the assignment of one peak to multiple (n, m) species. Nair et al. reported that, for their fits, 30 out of 39 considered semiconducting SWCNTs had an S11/S22 peak intensity ratio larger than one, thus 9 of the included SWCNTs had a larger peak intensity in S22 than they had in S11.40 In an ideal system without any doping effects, which might reduce S11 intensity, the absorption cross section of the second optical transition is smaller than that of the first one, which should always result in a smaller peak intensity of the S22 absorption.73 Along with constraining the fit of the S22 region to only include those (n, m) species that were fitted in the S11 region, this assumption was used in the present study to also constrain the height of the peak in the S22 region to be a fraction of the S11 height, and the starting value for the fit was initially set to 4 (S11,height/S22,height = 4), and allowed to vary between 1 and 5. All fractions (S11,height/S22,height pair for each (n, m) species) were constrained to be within ±20% to guarantee for a comparable distribution of peak intensities. In this way, an S22 peak was prevented from becoming larger than its S11 counterpart. Additionally, the FWHM of the S22 peak was restricted to be smaller than the FWHM of the S11 counterpart to prevent not only the intensity but also the area of the of the (n, m) species in S11, being smaller than that in S22. An example of such a “constrained” fitting procedure is provided in Figure 4a.

Figure 4.

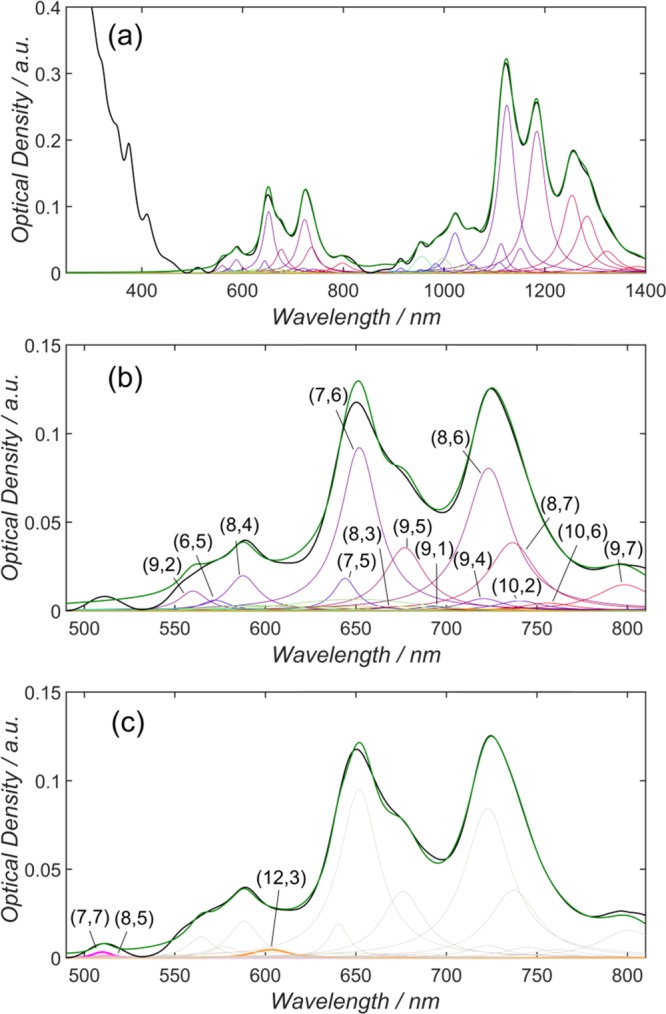
Figure 4

Open in a new tab

(a) Fit of entire spectral region that was background corrected according to Naumov et al.41 The measured absorption spectrum is shown in black, and the calculated spectrum is shown in green. (b) Close-up of fit of S22 region that was constrained by the (n, m) species assigned to the S11 region with an intensity variation of S11/S22 between 1 and 5. It can be seen in the region 500–620 nm that the experimental data has been poorly replicated. (c) Upon inclusion of three metallic species, the fit of the S22 region was significantly improved.

As well as preventing nonphysical fits to the data, the great advantage of fitting the entire spectrum of a polychiral sample under such constrained conditions is that once all of the S22 peaks are removed, what is left in that region is predominantly due to absorption by metallic nanotubes, thereby providing some information about the metallic/semiconducting purity. However, care must be taken to ensure that a poor fit in S22 is not a result of missing (n, m) species in the fit of S11 (as shown in detail in Figure S10). Upon evaluating a close-up of the S22 region in Figure 4a, shown in Figure 4b, it is apparent that the wavelength regime between 500 and 620 nm was not properly fitted. As demonstrated in Figure 4c, by adding four additional metallic nanotubes to the absorption spectrum ((7,7), (8,5) and (12,3)), the quality of the fit is improved (nSSE = 2.87 × 10–3 compared to 3.30 × 10–3). Table S2 summarizes the spectral weights of (n, m) species determined from the fits in Figure 4a,c. The spectral weight of the metallic tubes in solution was calculated to be 0.37% (total area of metallic nanotubes divided by the sum of the area of metallic and semiconducting S11 nanotubes).

Therefore, the semiconducting purity in S11, according to spectral weight, of the solution is 99.63%, which is in good agreement with previously reported values for gel-sorted nanotube solutions.75 However, due to a possible overlap of metallic nanotubes and the S22 phonon sideband, the metallic peak assignment is complicated. Likewise, the overlap of large diameter M11 peaks with smaller diameter S22 peaks makes assignment difficult and means that this method is best suited to fit nanotubes with a narrow diameter distribution.

The results of the solution fit can be used to fit film absorption measurements based on the spectral concentration of each (n, m) species. A detailed discussion on the film-fitting procedure and associated analysis of the effect of different backgrounds and possible fields of application is given in the Supporting Information.

Conclusions

A comprehensive and up-to-date methodology for fitting carbon nanotube absorption spectra was presented. The entire MATLAB code used in this work is provided in the Supporting Information, as well as a straightforward LabVIEW-based graphical user interface to improve accessibility for those less familiar with the MATLAB environment, but who would still like to employ the functionality of the algorithms in their work. The presented methodology provides the possibility of using different backgrounds for different experimental conditions, modeling of exciton–phonon sidebands, evaluation of the semiconducting purity of the sample by inclusion of metallic species, determination of concentration based on the spectral weight and absorption cross section of species, and the fitting of solid film absorption spectra based on the results of solution measurements. Although the processes used in this work, and made available in the MATLAB code and associated graphical user interface, are certainly an improvement over the use of generic peak fitting software for the specialized task of fitting carbon nanotube absorption spectra, the use of complementary techniques such as PL and Raman spectroscopy is still required to obtain physically significant data. In short, absorption spectroscopy alone should not be seen as the kind of “turnkey” solution that other techniques such as variance spectroscopy have the potential to be. However, we expect that the work presented herein will prove to be a useful resource and tool for those in the research community who employ optical absorption spectroscopy in their carbon nanotube work for a quantitative, yet reliable, analysis.

Methods

Preparation of SWCNT Solutions

SWCNT dispersions were prepared from aqueous surfactant wrapped dispersions using sodium dodecylsulfate (SDS, Merck), sodium cholate (SC, ≥99%, Sigma-Aldrich), and co-surfactant mixtures thereof. Detailed experimental details can be found in previous publications.14,32 In brief, small diameter HiPco (NanoIntegris) were suspended in 2 wt % SDS by sonication for 1 h followed by ultracentrifugation for 1 h at 64 206g (SW-40-TI rotor). The SDS concentration was then adjusted to 1.6 wt % SDS, and the sample was added to 40 mL of Sephacryl-S200 gel (Amersham Biosciences). Following the separation at 1.6 wt % SDS, the SDS concentration was gradually lowered in 0.2 wt % steps down to a concentration of 0.8 wt %. The absorption spectra shown in Figures 1, 2, and 4 were taken from SWCNT solutions with a starting concentration of 1 wt % SDS. The respective PL map is shown in Figure S1.

UV and PL Measurements

Optical absorption measurements of nanotube dispersions were performed on a Varian Cary 500 spectrophotometer. For the PLE maps of the SWCNT dispersion, the spectrally separated output of a WhiteLase SC400 supercontinuum laser source (Fianium Ltd.) was used for excitation and spectra were recorded with an Acton SpectraPro SP2358 (grating 150 lines/mm) spectrometer with an OMA-V InGaAs line camera (Princeton Instruments) and corrected for background and wavelength-dependent sensitivity/excitation power.

Acknowledgments

B.S.F. gratefully acknowledges support from the Deutsche Forschungsgemeinschaft (DFG) under grant numbers FL 834/1-1 and FL 834/2-1. R.K. acknowledges funding by the DFG under INST 163/354-1 FUGG. A.G. and J.Z. acknowledge financial support by European Research Council under the European Union’s Seventh Framework Programme (FP/2007-2013)/ERC Grant Agreement No. 306298.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.6b00468.

  • MATLAB-based routines to fit solution and film absorption measurements (PDF)

  • A LabVIEW-based graphical user interface incorporating the MATLAB fitting routines (ZIP) (ZIP)

The authors declare no competing financial interest.

Supplementary Material

ao6b00468_si_001.pdf (3.4MB, pdf)
ao6b00468_si_002.zip (316.5KB, zip)
ao6b00468_si_003.zip (7MB, zip)

References

  1. Jorio A.; Dresselhaus G.; Dresselhaus M. S.. Carbon Nanotubes; Springer: Berlin, 2008. [Google Scholar]
  2. Avouris P.; Freitag M.; Perebeinos V. Carbon-nanotube photonics and optoelectronics. Nat. Photonics 2008, 2, 341–350. 10.1038/nphoton.2008.94. [DOI] [Google Scholar]
  3. Pyatkov F.; Fütterling V.; Khasminskaya S.; Flavel B. S.; Hennrich F.; Kappes M. M.; Krupke R.; Pernice W. H. P. Cavity-enhanced light emission from electrically driven carbon nanotubes. Nat. Photonics 2016, 10, 420–427. 10.1038/nphoton.2016.70. [DOI] [Google Scholar]
  4. Engel M.; Moore K. E.; Alam A.; Dehm S.; Krupke R.; Flavel B. S. Photocurrent Spectroscopy of (n, m) Sorted Solution-Processed Single-Walled Carbon Nanotubes. ACS Nano 2014, 8, 9324–9331. 10.1021/nn503278d. [DOI] [PubMed] [Google Scholar]
  5. Tatsuura S.; Furuki M.; Sato Y.; Iwasa I.; Tian M.; Mitsu H. Semiconductor carbon nanotubes as ultrafast switching materials for optical telecommunications. Adv. Mater. 2003, 15, 534–537. 10.1002/adma.200390125. [DOI] [Google Scholar]
  6. Arnold M. S.; Blackburn J. L.; Crochet J. J.; Doorn S. K.; Duque J. G.; Mohite A.; Telg H. Recent developments in the photophysics of single-walled carbon nanotubes for their use as active and passive material elements in thin film photovoltaics. Phys. Chem. Chem. Phys. 2013, 15, 14896–14918. 10.1039/c3cp52752b. [DOI] [PubMed] [Google Scholar]
  7. Tune D. D.; Hennrich F.; Dehm S.; Klein M. F. G.; Glaser K.; Colsmann A.; Shapter J. G.; Lemmer U.; Kappes M. M.; Krupke R.; Flavel B. S. The Role of Nanotubes in Carbon Nanotube–Silicon Solar Cells. Adv. Energy Mater. 2013, 3, 1091–1097. 10.1002/aenm.201200949. [DOI] [Google Scholar]
  8. Landi B. J.; Ganter M. J.; Cress C. D.; DiLeo R. A.; Raffaelle R. P. Carbon nanotubes for lithium ion batteries. Energy Environ. Sci. 2009, 2, 638–654. 10.1039/b904116h. [DOI] [Google Scholar]
  9. Varga Á.; Pfohl M.; Brunelli N. A.; Schreier M.; Giapis K. P.; Haile S. M. Carbon nanotubes as electronic interconnects in solid acid fuel cell electrodes. Phys. Chem. Chem. Phys. 2013, 15, 15470–15476. 10.1039/c3cp52586d. [DOI] [PubMed] [Google Scholar]
  10. Steiner M.; Engel M.; Lin Y.-M.; Wu Y.; Jenkins K.; Farmer D. B.; Humes J. J.; Yoder N. L.; Seo J.-W. T.; Green A. A.; Hersam M. C.; Krupke R.; Avouris P. High-frequency performance of scaled carbon nanotube array field-effect transistors. Appl. Phys. Lett. 2012, 101, 053123 10.1063/1.4742325. [DOI] [Google Scholar]
  11. Wang J. Carbon-Nanotube Based Electrochemical Biosensors: A Review. Electroanalysis 2005, 17, 7–14. 10.1002/elan.200403113. [DOI] [Google Scholar]
  12. Flavel B. S.; Yu J.; Shapter J. G.; Quinton J. S. Patterned ferrocenemethanol modified carbon nanotube electrodes on silane modified silicon. J. Mater. Chem. 2007, 17, 4757–4761. 10.1039/b716284g. [DOI] [Google Scholar]
  13. Yu X.; Munge B.; Patel V.; Jensen G.; Bhirde A.; Gong J. D.; Kim S. N.; Gillespie J.; Gutkind J. S.; Papadimitrakopoulos F.; Rusling J. F. Carbon Nanotube Amplification Strategies for Highly Sensitive Immunodetection of Cancer Biomarkers. J. Am. Chem. Soc. 2006, 128, 11199–11205. 10.1021/ja062117e. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Pfohl M.; Glaser K.; Ludwig J.; Tune D. D.; Dehm S.; Kayser C.; Colsmann A.; Krupke R.; Flavel B. S. Performance Enhancement of Polymer-Free Carbon Nanotube Solar Cells via Transfer Matrix Modeling. Adv. Energy Mater. 2016, 6, 1501345 10.1002/aenm.201501345. [DOI] [Google Scholar]
  15. Bindl D. J.; Safron N. S.; Arnold M. S. Dissociating Excitons Photogenerated in Semiconducting Carbon Nanotubes at Polymeric Photovoltaic Heterojunction Interfaces. ACS Nano 2010, 4, 5657–5664. 10.1021/nn1012397. [DOI] [PubMed] [Google Scholar]
  16. Reich S.; Thomsen C.; Maultzsch J.. Carbon Nanotubes: Basic Concepts and Physical Properties; John Wiley & Sons, 2008. [Google Scholar]
  17. Maultzsch J.; Pomraenke R.; Reich S.; Chang E.; Prezzi D.; Ruini A.; Molinari E.; Strano M. S.; Thomsen C.; Lienau C. Exciton binding energies in carbon nanotubes from two-photon photoluminescence. Phys. Rev. B 2005, 72, 241402 10.1103/PhysRevB.72.241402. [DOI] [Google Scholar]
  18. Jiang J.; Saito R.; Samsonidze G. G.; Jorio A.; Chou S. G.; Dresselhaus G.; Dresselhaus M. S. Chirality dependence of exciton effects in single-wall carbon nanotubes: Tight-binding model. Phys. Rev. B 2007, 75, 035407 10.1103/PhysRevB.75.035407. [DOI] [Google Scholar]
  19. Kataura H.; Kumazawa Y.; Maniwa Y.; Umezu I.; Suzuki S.; Ohtsuka Y.; Achiba Y. Optical properties of single-wall carbon nanotubes. Synth. Met. 1999, 103, 2555–2558. 10.1016/S0379-6779(98)00278-1. [DOI] [Google Scholar]
  20. Bachilo S. M.; Strano M. S.; Kittrell C.; Hauge R. H.; Smalley R. E.; Weisman R. B. Structure-Assigned Optical Spectra of Single-Walled Carbon Nanotubes. Science 2002, 298, 2361–2366. 10.1126/science.1078727. [DOI] [PubMed] [Google Scholar]
  21. Luo Z.; Pfefferle L. D.; Haller G. L.; Papadimitrakopoulos F. (n,m) Abundance Evaluation of Single-Walled Carbon Nanotubes by Fluorescence and Absorption Spectroscopy. J. Am. Chem. Soc. 2006, 128, 15511–15516. 10.1021/ja0657096. [DOI] [PubMed] [Google Scholar]
  22. Oyama Y.; Saito R.; Sato K.; Jiang J.; Samsonidze G. G.; Grüneis A.; Miyauchi Y.; Maruyama S.; Jorio A.; Dresselhaus G.; Dresselhaus M. S. Photoluminescence intensity of single-wall carbon nanotubes. Carbon 2006, 44, 873–879. 10.1016/j.carbon.2005.10.024. [DOI] [Google Scholar]
  23. Tsyboulski D. A.; Rocha J.-D. R.; Bachilo S. M.; Cognet L.; Weisman R. B. Structure-Dependent Fluorescence Efficiencies of Individual Single-Walled Carbon Nanotubes. Nano Lett. 2007, 7, 3080–3085. 10.1021/nl071561s. [DOI] [PubMed] [Google Scholar]
  24. Cambré S.; Campo J.; Beirnaert C.; Verlackt C.; Cool P.; Wenseleers W. Asymmetric dyes align inside carbon nanotubes to yield a large nonlinear optical response. Nat. Nanotechnol. 2015, 10, 248–252. 10.1038/nnano.2015.1. [DOI] [PubMed] [Google Scholar]
  25. Cambré S.; Santos S. M.; Wenseleers W.; Nugraha A. R. T.; Saito R.; Cognet L.; Lounis B. Luminescence Properties of Individual Empty and Water-Filled Single-Walled Carbon Nanotubes. ACS Nano 2012, 6, 2649–2655. 10.1021/nn300035y. [DOI] [PubMed] [Google Scholar]
  26. Jones M.; Engtrakul C.; Metzger W. K.; Ellingson R. J.; Nozik A. J.; Heben M. J.; Rumbles G. Analysis of photoluminescence from solubilized single-walled carbon nanotubes. Phys. Rev. B: Condens. Matter Mater. Phys. 2005, 71, 115426 10.1103/PhysRevB.71.115426. [DOI] [Google Scholar]
  27. Rocha J.-D. R.; Bachilo S. M.; Ghosh S.; Arepalli S.; Weisman R. B. Efficient Spectrofluorimetric Analysis of Single-Walled Carbon Nanotube Samples. Anal. Chem. 2011, 83, 7431–7437. 10.1021/ac2014788. [DOI] [PubMed] [Google Scholar]
  28. Lebedkin S.; Arnold K.; Kiowski O.; Hennrich F.; Kappes M. M. Raman study of individually dispersed single-walled carbon nanotubes under pressure. Phys. Rev. B: Condens. Matter Mater. Phys. 2006, 73, 094109 10.1103/PhysRevB.73.094109. [DOI] [Google Scholar]
  29. Streit J. K.; Bachilo S. M.; Sanchez S. R.; Lin C.-W.; Weisman R. B. Variance Spectroscopy. J. Phys. Chem. Lett. 2015, 6, 3976–3981. 10.1021/acs.jpclett.5b01835. [DOI] [PubMed] [Google Scholar]
  30. Itkis M. E.; Perea D. E.; Jung R.; Niyogi S.; Haddon R. C. Comparison of Analytical Techniques for Purity Evaluation of Single-Walled Carbon Nanotubes. J. Am. Chem. Soc. 2005, 127, 3439–3448. 10.1021/ja043061w. [DOI] [PubMed] [Google Scholar]
  31. He M.; Jiang H.; Liu B.; Fedotov P. V.; Chernov A. I.; Obraztsova E. D.; Cavalca F.; Wagner J. B.; Hansen T. W.; Anoshkin I. V.; Obraztsova E. A.; Belkin A. V.; Sairanen E.; Nasibulin A. G.; Lehtonen J.; Kauppinen E. I. Chiral-Selective Growth of Single-Walled Carbon Nanotubes on Lattice-Mismatched Epitaxial Cobalt Nanoparticles. Sci. Rep. 2013, 3, 1460 10.1038/srep01460. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Flavel B. S.; Moore K. E.; Pfohl M.; Kappes M. M.; Hennrich F. Separation of Single-Walled Carbon Nanotubes with a Gel Permeation Chromatography System. ACS Nano 2014, 8, 1817–1826. 10.1021/nn4062116. [DOI] [PubMed] [Google Scholar]
  33. Liu H.; Nishide D.; Tanaka T.; Kataura H. Large-scale single-chirality separation of single-wall carbon nanotubes by simple gel chromatography. Nat. Commun. 2011, 2, 309 10.1038/ncomms1313. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Arnold M. S.; Green A. A.; Hulvat J. F.; Stupp S. I.; Hersam M. C. Sorting carbon nanotubes by electronic structure using density differentiation. Nat. Nanotechnol. 2006, 1, 60–65. 10.1038/nnano.2006.52. [DOI] [PubMed] [Google Scholar]
  35. Khripin C. Y.; Fagan J. A.; Zheng M. Spontaneous Partition of Carbon Nanotubes in Polymer-Modified Aqueous Phases. J. Am. Chem. Soc. 2013, 135, 6822–6825. 10.1021/ja402762e. [DOI] [PubMed] [Google Scholar]
  36. Nish A.; Hwang J.-Y.; Doig J.; Nicholas R. J. Highly selective dispersion of single-walled carbon nanotubes using aromatic polymers. Nat. Nanotechnol. 2007, 2, 640–646. 10.1038/nnano.2007.290. [DOI] [PubMed] [Google Scholar]
  37. ISO/TS 10868:2011. Nanotechnologies — Characterization of Single-Wall Carbon Nanotubes Using Ultraviolet-Visible-Near Infrared (UV-vis-NIR) Absorption Spectroscopy; International Organization for Standardization: Switzerland, 2011. [Google Scholar]
  38. Arepalli S.; Freiman S. W.; Hooker S. A.; Migler K. D.. Measurement Issues in Single-Wall Carbon Nanotubes; Special Publication (NIST SP) - 960.19; NIST, 2008. [Google Scholar]
  39. Tian Y.; Jiang H.; Anoshkin I. V.; Kauppinen L. J. I.; Mustonen K.; Nasibulin A. G.; Kauppinen E. I. A reference material of single-walled carbon nanotubes: quantitative chirality assessment using optical absorption spectroscopy. RSC Adv. 2015, 5, 102974–102980. 10.1039/C5RA23326G. [DOI] [Google Scholar]
  40. Nair N.; Usrey M. L.; Kim W.-J.; Braatz R. D.; Strano M. S. Estimation of the (n,m) Concentration Distribution of Single-Walled Carbon Nanotubes from Photoabsorption Spectra. Anal. Chem. 2006, 78, 7689–7696. 10.1021/ac0610917. [DOI] [PubMed] [Google Scholar]
  41. Naumov A. V.; Ghosh S.; Tsyboulski D. A.; Bachilo S. M.; Weisman R. B. Analyzing Absorption Backgrounds in Single-Walled Carbon Nanotube Spectra. ACS Nano 2011, 5, 1639–1648. 10.1021/nn1035922. [DOI] [PubMed] [Google Scholar]
  42. Ohmori S.; Saito T.; Tange M.; Shukla B.; Okazaki T.; Yumura M.; Iijima S. Fundamental Importance of Background Analysis in Precise Characterization of Single-Walled Carbon Nanotubes by Optical Absorption Spectroscopy. J. Phys. Chem. C 2010, 114, 10077–10081. 10.1021/jp9120172. [DOI] [Google Scholar]
  43. Ryabenko A. G.; Dorofeeva T. V.; Zvereva G. I. UV–VIS–NIR spectroscopy study of sensitivity of single-wall carbon nanotubes to chemical processing and Van-der-Waals SWNT/SWNT interaction. Verification of the SWNT content measurements by absorption spectroscopy. Carbon 2004, 42, 1523–1535. 10.1016/j.carbon.2004.02.005. [DOI] [Google Scholar]
  44. Crochet J. J.; Hoseinkhani S.; Lüer L.; Hertel T.; Doorn S. K.; Lanzani G. Free-Carrier Generation in Aggregates of Single-Wall Carbon Nanotubes by Photoexcitation in the Ultraviolet Regime. Phys. Rev. Lett. 2011, 107, 257402 10.1103/PhysRevLett.107.257402. [DOI] [PubMed] [Google Scholar]
  45. Landi B. J.; Ruf H. J.; Evans C. M.; Cress C. D.; Raffaelle R. P. Purity Assessment of Single-Wall Carbon Nanotubes, Using Optical Absorption Spectroscopy. J. Phys. Chem. B 2005, 109, 9952–9965. 10.1021/jp044990c. [DOI] [PubMed] [Google Scholar]
  46. Fano U. Effects of Configuration Interaction on Intensities and Phase Shifts. Phys. Rev. 1961, 124, 1866–1878. 10.1103/PhysRev.124.1866. [DOI] [Google Scholar]
  47. Sanchez S. R.; Bachilo S. M.; Kadria-Vili Y.; Lin C.-W.; Weisman R. B. (n,m)-Specific Absorption Cross Sections of Single-Walled Carbon Nanotubes Measured by Variance Spectroscopy. Nano Lett. 2016, 16, 6903–6909. 10.1021/acs.nanolett.6b02819. [DOI] [PubMed] [Google Scholar]
  48. Hagen A.; Moos G.; Talalaev V.; Hertel T. Electronic structure and dynamics of optically excited single-wall carbon nanotubes. Appl. Phys. A: Mater. Sci. Process. 2004, 78, 1137–1145. 10.1007/s00339-003-2465-1. [DOI] [Google Scholar]
  49. Lolli G.; Zhang L.; Balzano L.; Sakulchaicharoen N.; Tan Y.; Resasco D. E. Tailoring (n,m) Structure of Single-Walled Carbon Nanotubes by Modifying Reaction Conditions and the Nature of the Support of CoMo Catalysts. J. Phys. Chem. B 2006, 110, 2108–2115. 10.1021/jp056095e. [DOI] [PubMed] [Google Scholar]
  50. Hertel V. I.; Schulz C.-P.. Linienbreiten, Multiphotonenprozesse und mehr. In Atome, Moleküle und optische Physik 1: Atomphysik und Grundlagen der Spektroskopie; Springer: Berlin, 2008; pp 157–193. [Google Scholar]
  51. Weisskopf V.; Wigner E. Berechnung der natürlichen Linienbreite auf Grund der Diracschen Lichttheorie. Z. Phys. 1930, 63, 54–73. 10.1007/BF01336768. [DOI] [Google Scholar]
  52. Meier R. J. On art and science in curve-fitting vibrational spectra. Vib. Spectrosc. 2005, 39, 266–269. 10.1016/j.vibspec.2005.03.003. [DOI] [Google Scholar]
  53. Hagen A.; Hertel T. Quantitative Analysis of Optical Spectra from Individual Single-Wall Carbon Nanotubes. Nano Lett. 2003, 3, 383–388. 10.1021/nl020237o. [DOI] [Google Scholar]
  54. Tune D. D.; Shapter J. G. The potential sunlight harvesting efficiency of carbon nanotube solar cells. Energy Environ. Sci. 2013, 6, 2572–2577. 10.1039/c3ee41731j. [DOI] [Google Scholar]
  55. Liu K.; Hong X.; Choi S.; Jin C.; Capaz R. B.; Kim J.; Wang W.; Bai X.; Louie S. G.; Wang E.; Wang F. Systematic determination of absolute absorption cross-section of individual carbon nanotubes. Proc. Natl. Acad. Sci. U.S.A. 2014, 111, 7564–7569. 10.1073/pnas.1318851111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Kadria-Vili Y.; Bachilo S. M.; Blackburn J. L.; Weisman R. B. Photoluminescence Side Band Spectroscopy of Individual Single-Walled Carbon Nanotubes. J. Phys. Chem. C 2016, 120, 23898–23904. 10.1021/acs.jpcc.6b08768. [DOI] [Google Scholar]
  57. Olivero J. J.; Longbothum R. L. Empirical fits to the Voigt line width: A brief review. J. Quant. Spectrosc. Radiat. Transfer 1977, 17, 233–236. 10.1016/0022-4073(77)90161-3. [DOI] [Google Scholar]
  58. Schreier F. Optimized implementations of rational approximations for the Voigt and complex error function. J. Quant. Spectrosc. Radiat. Transfer 2011, 112, 1010–1025. 10.1016/j.jqsrt.2010.12.010. [DOI] [Google Scholar]
  59. Humlíček J. Optimized computation of the voigt and complex probability functions. J. Quant. Spectrosc. Radiat. Transfer 1982, 27, 437–444. 10.1016/0022-4073(82)90078-4. [DOI] [Google Scholar]
  60. Weideman J. A. C. Computation of the Complex Error Function. SIAM J. Numer. Anal. 1994, 31, 1497–1518. 10.1137/0731077. [DOI] [Google Scholar]
  61. Jian H.; Chunmin Z. The accurate calculation of the Fourier transform of the pure Voigt function. J. Opt. A: Pure Appl. Opt. 2005, 7, 613. 10.1088/1464-4258/7/10/014. [DOI] [Google Scholar]
  62. Westberg J.; Wang J.; Axner O. Fast and non-approximate methodology for calculation of wavelength-modulated Voigt lineshape functions suitable for real-time curve fitting. J. Quant. Spectrosc. Radiat. Transfer 2012, 113, 2049–2057. 10.1016/j.jqsrt.2012.05.023. [DOI] [Google Scholar]
  63. Liu Y.; Lin J.; Huang G.; Guo Y.; Duan C. Simple empirical analytical approximation to the Voigt profile. J. Opt. Soc. Am. B 2001, 18, 666–672. 10.1364/JOSAB.18.000666. [DOI] [Google Scholar]
  64. Lukyanov D. B.; Vazhnova T.; Cherkasov N.; Casci J. L.; Birtill J. J. Insights into Brønsted Acid Sites in the Zeolite Mordenite. J. Phys. Chem. C 2014, 118, 23918–23929. 10.1021/jp5086334. [DOI] [Google Scholar]
  65. Dresselhaus M. S.; Dresselhaus G.; Saito R.; Jorio A. Exciton photophysics of carbon nanotubes. Annu. Rev. Phys. Chem. 2007, 58, 719–747. 10.1146/annurev.physchem.58.032806.104628. [DOI] [PubMed] [Google Scholar]
  66. Perebeinos V.; Tersoff J.; Avouris P. Effect of exciton-phonon coupling in the calculated optical absorption of carbon nanotubes. Phys. Rev. Lett. 2005, 94, 027402 10.1103/PhysRevLett.94.027402. [DOI] [PubMed] [Google Scholar]
  67. Berciaud S.; Cognet L.; Poulin P.; Weisman R. B.; Lounis B. Absorption Spectroscopy of Individual Single-Walled Carbon Nanotubes. Nano Lett. 2007, 7, 1203–1207. 10.1021/nl062933k. [DOI] [PubMed] [Google Scholar]
  68. Tian Y.; Jiang H.; Pfaler J. v.; Zhu Z.; Nasibulin A. G.; Nikitin T.; Aitchison B.; Khriachtchev L.; Brown D. P.; Kauppinen E. I. Analysis of the Size Distribution of Single-Walled Carbon Nanotubes Using Optical Absorption Spectroscopy. J. Phys. Chem. Lett. 2010, 1, 1143–1148. 10.1021/jz100161p. [DOI] [Google Scholar]
  69. Wang B.; Poa C. H. P.; Wei L.; Li L.-J.; Yang Y.; Chen Y. (n,m) Selectivity of Single-Walled Carbon Nanotubes by Different Carbon Precursors on Co–Mo Catalysts. J. Am. Chem. Soc. 2007, 129, 9014–9019. 10.1021/ja070808k. [DOI] [PubMed] [Google Scholar]
  70. Hackl P.Einführung in die Ökonometrie; Pearson Deutschland GmbH, 2008; Vol. 7118. [Google Scholar]
  71. Mendenhall W.; Beaver R. J.; Beaver B. M.. Introduction to Probability and Statistics; Cengage Learning, 2012. [Google Scholar]
  72. Tsay R. S.Analysis of Financial Time Series; John Wiley & Sons, 2005; Vol. 543. [Google Scholar]
  73. Streit J. K.; Bachilo S. M.; Ghosh S.; Lin C.-W.; Weisman R. B. Directly Measured Optical Absorption Cross Sections for Structure-Selected Single-Walled Carbon Nanotubes. Nano Lett. 2014, 14, 1530–1536. 10.1021/nl404791y. [DOI] [PubMed] [Google Scholar]
  74. Miyata Y.; Yanagi K.; Maniwa Y.; Kataura H. Optical Evaluation of the Metal-to-Semiconductor Ratio of Single-Wall Carbon Nanotubes. J. Phys. Chem. C 2008, 112, 13187–13191. 10.1021/jp804006f. [DOI] [Google Scholar]
  75. Tulevski G. S.; Franklin A. D.; Afzali A. High Purity Isolation and Quantification of Semiconducting Carbon Nanotubes via Column Chromatography. ACS Nano 2013, 7, 2971–2976. 10.1021/nn400053k. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao6b00468_si_001.pdf (3.4MB, pdf)
ao6b00468_si_002.zip (316.5KB, zip)
ao6b00468_si_003.zip (7MB, zip)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES