Abstract
Dendritic Ca2+ spike endows cortical pyramidal cell with powerful ability of synaptic integration, which is critical for neuronal computation. Here we propose a two-compartment conductance-based model to investigate how the Ca2+ activity of apical dendrite participates in the action potential (AP) initiation to affect the firing properties of pyramidal neurons. We have shown that the apical input with sufficient intensity triggers a dendritic Ca2+ spike, which significantly boosts dendritic inputs as it propagates to soma. Such event instantaneously shifts the limit cycle attractor of the neuron and results in a burst of APs, which makes its firing rate reach a plateau steady-state level. Delivering current to two chambers simultaneously increases the level of neuronal excitability and decreases the threshold of input-output relation. Here the back-propagating APs facilitate the initiation of dendritic Ca2+ spike and evoke BAC firing. These findings indicate that the proposed model is capable of reproducing in vitro experimental observations. By determining spike initiating dynamics, we have provided a fundamental link between dendritic Ca2+ spike and output APs, which could contribute to mechanically interpreting how dendritic Ca2+ activity participates in the simple computations of pyramidal neuron.
Pyramidal neurons are common cell types found in the cerebral cortex and hippocampus of mammalian brain1,2,3. Their structures are characterized by a pyramidal shaped soma and extended apical and basal dendritic trees. This kind of nerve cells have powerful capability of processing information, which could effectively and precisely transform incoming signals into specific patterns of action potential (AP) output. During this procedure, their dendrites play a particularly vital role, since they are the predominant receiving sites for synaptic signals1,4,5,6,7,8. The vast branches of dendritic tree endow a pyramidal cell with distinctive morphological feature, which disperse the primary input locations. It is known that APs usually occur in the initial segment of the axon. Due to such spatial arrangement, the apical dendrites have to deliver input signals to the site of AP initiation. Their function is not solely to receive information from connected input cells and transmit it to the axon. Each dendritic branch is also a basic signalling unit for integrating synaptic inputs4,6,7,8,9,10,11, which determines how the receiving signals propagate to the axon. Such nonlinear integration operated by dendrites has a profound influence on neuronal and cortical computation1,2,4,5,6,7,8,9,10.
The dendrites of pyramidal cells rely on their intrinsic nonlinearities, including voltage-gated channels and complex morphology, to integrate synaptic signals4,5,6,7,8,9,10,11. The active ionic channels in their apical dendrites are particularly important in synaptic integration. A common channel is the voltage-dependent Ca2+ current that flows into the cell1,4,5,6,7,12,13,14. The activation of its conductance could cause a threshold-dependent, all-or-none regenerative response in dendrites, which is often referred to as dendritic Ca2+ spike4,7,11,14,15,16,17. The existence of active Ca2+ channel in apical dendrites make pyramidal neurons operate in either global or two-stage integration mode18,19. For simple global integration mode, input signals directly contribute to AP output by triggering excitatory postsynaptic potentials (EPSPs) that spread to the AP initiation zone. In latter integration mode, the synaptic input directly activates the Ca2+ channel in dendrites and triggers dendritic spikes7,14,15,16,17,20, which propagates forward to the axon where the global integration occurs18,19. Such integration lies at the heart of neural computation, which is tightly related to coincidence detection1,16,21,22, orientation tuning22, binding of synaptic signals from brain areas23, and enhancing stimulus selectivity24. Understanding how it participates in AP output is therefore fundamental to understanding how relevant circuits function in cortical computation of mammalian brain.
Earlier studies have extensively explored the dendritic Ca2+ activities and their effects on neuronal firing behaviors with in vitro approaches. It is found that the synaptic inputs at different sites of dendrite16,17,25, the back-propagating APs17,26,27, and the local NMDA spikes7,28,29 are all important determinants for activating Ca2+ conductance and triggering dendritic Ca2+ spike. This regenerative event at apical dendrites can boost distal synaptic inputs and enhance synaptic efficacy, which is hypothesized as the main biological mechanism for propagating synaptic inputs at the distal tuft to the soma of layer 5 pyramidal neurons15,16,17,28. It is usually characterized by a steep change followed by a plateau in the subthreshold input-output transformations conferred by dendrites. Further, the additional inward current associated with Ca2+ spike provides a strong local depolarization in dendritic membrane, which can enhance the somatic/axonal AP outputs. In particular, it can significantly increase the gain of input-output relation of pyramidal neuron, which triggers a burst of APs in the soma/axon and switches the firing mode of the cell to bursting23,26,30,31,32. However, it is still not well understood how dendritic Ca2+ spike participates in AP initiation to influence the somatic/axonal output.
In addition to above in vitro observations, there are also modeling studies that focus on the dendritic Ca2+ activity21,33,34,35,36,37. Most of them use biophysically realistic neurons that are modeled in NEURON or GENESIS to understand the mechanism underlying the generation and propagation of dendritic Ca2+ spike. Such complex multi-compartment models are not sufficiently simple to allow one to uncover the dynamical or biophysical basis for AP initiation related to dendritic Ca2+ activity. There are also studies that use two compartments to model pyramidal neurons with dendritic Ca2+ channel. Such simple point-neuron models have been adopted to study their firing patterns38,39,40, spike-timing predictions41, spike timing-dependent plasticity42, and spike-frequency adaptation43. However, it has attracted little attention about the somatic/axonal AP initiation associated with dendritic Ca2+ spike. Further, Larkum et al.26 have used a two-compartment integrate-and-fire (IF) model to reproduce the gain modulation of pyramidal cell induced by top-down dendritic Ca2+ spike. However, in IF model an AP is explicitly generated when its membrane voltage reaches a predefined threshold44. That is, the IF model is unable to reproduce how inward and outward ionic currents interact at the subthreshold potentials to initiate AP. Therefore, it is still largely unknown that how dendritic Ca2+ spike affects the AP initiation of individual pyramidal cells.
Here we develop a five-dimensional (5D) two-compartment model (as shown in Fig. 1a) by introducing Ca2+ current into the passive dendrite of a reduced Pinsky-Rinzel (PR) model45,46. Contrary to IF model, the generation of APs in our model implicitly results from the dynamical interactions of inward Na+ and outward K+ currents at the subthreshold voltages45,46,47. With this model, we have systematically investigated the firing behaviors of the pyramidal neuron with passive and active dendrite to the input current injected at different sites of the neuron. The dynamical basis for relevant AP initiation is determined with phase plane and bifurcation analysis. Our simulations indicate that the proposed model here is able to reproduce a variety of in vitro experimental observations of pyramidal neurons, which is also amenable to both dynamical analysis and efficient simulation.
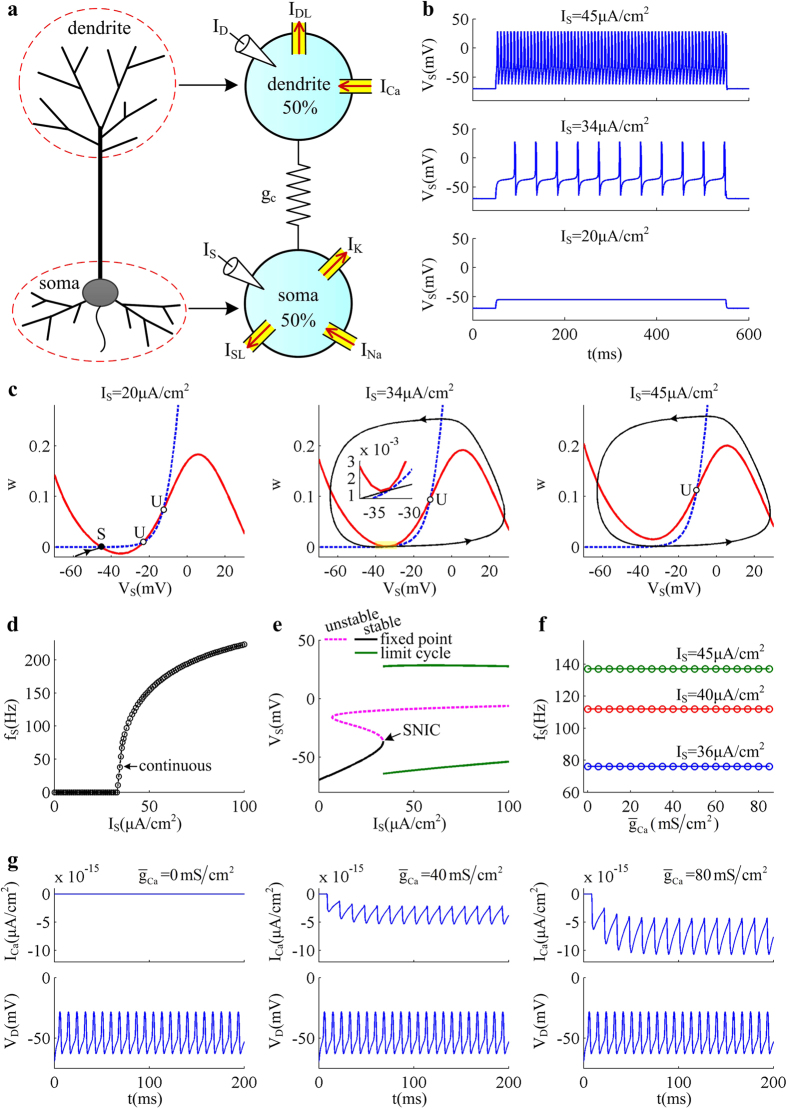
Figure 1. Input-output relation and relevant spike initiating dynamics evoked by somatic input.
(a) 5D two-compartment model of the pyramidal neuron. One chamber represents the basal zone around soma, and the other one is apical dendrite. Two chambers are connected by an internal conductance gc. The stimulus current can be independently injected into soma and dendrite. Red arrows in the right panel indicate the direction of relevant current flow. (b) Sample responses triggered by three values of IS, which is indicated on the top of each panel. (c) Phase portraits in  plane to subthreshold and suprathreshold IS. Blue dotted line represents w-nullcline and red solid line is VS-nullcline. They represent the states where corresponding variable neither increases nor decreases. Black solid line is a sample VS trajectory, where arrows indicate the direction of its motion. ‘S’ indicates the intersection between two nullclines is stable and ‘U’ is unstable. (d) Relation between average firing rate fS and somatic input IS, i.e.,
plane to subthreshold and suprathreshold IS. Blue dotted line represents w-nullcline and red solid line is VS-nullcline. They represent the states where corresponding variable neither increases nor decreases. Black solid line is a sample VS trajectory, where arrows indicate the direction of its motion. ‘S’ indicates the intersection between two nullclines is stable and ‘U’ is unstable. (d) Relation between average firing rate fS and somatic input IS, i.e.,  curve. (e) Bifurcation diagram of the 5D model, here the bifurcation parameter is IS. Vertical axis gives the somatic voltage VS at the fixed point or at the max/min of limit cycle as input IS is increased. (f) Relation between average firing rate fS and Ca2+ conductance
curve. (e) Bifurcation diagram of the 5D model, here the bifurcation parameter is IS. Vertical axis gives the somatic voltage VS at the fixed point or at the max/min of limit cycle as input IS is increased. (f) Relation between average firing rate fS and Ca2+ conductance 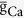 (i.e.,
(i.e., 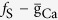 curve) with three values of input IS. (g) Time courses of dendritic Ca2+ current ICa and dendritic voltage VD in the cases of
curve) with three values of input IS. (g) Time courses of dendritic Ca2+ current ICa and dendritic voltage VD in the cases of 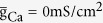 ,
, 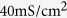 , and
, and 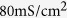 . Corresponding somatic injection is
. Corresponding somatic injection is 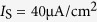 . For (b–g), the dendritic input is
. For (b–g), the dendritic input is 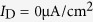 .
.
Results
Somatic input is unable to trigger dendritic Ca2+ spike in the absence of dendritic input
We first investigate the spiking properties of the 5D model neuron to somatic input IS. The current ID injected at dendritic chamber is absent, i.e., 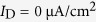 . Figure 1b–e give the input-output relation and corresponding dynamical basis of AP initiation in the case of
. Figure 1b–e give the input-output relation and corresponding dynamical basis of AP initiation in the case of 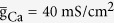 . We find that the neuron is unable to generate APs when
. We find that the neuron is unable to generate APs when 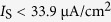 (Fig. 1b and d). At these small values of IS, the neuron exist in quiescent state and its somatic membrane potential VS is eventually stabilized at a subthreshold voltage. With
(Fig. 1b and d). At these small values of IS, the neuron exist in quiescent state and its somatic membrane potential VS is eventually stabilized at a subthreshold voltage. With 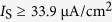 , the neuron generates repetitive APs. In this case, the average firing rate fS increases with input IS from 0 Hz. The relation between fS and IS (i.e., fS − IS curve) is continuous (Fig. 1d).
, the neuron generates repetitive APs. In this case, the average firing rate fS increases with input IS from 0 Hz. The relation between fS and IS (i.e., fS − IS curve) is continuous (Fig. 1d).
Figure 1c illustrates the dynamical basis of AP initiation associated with the observed behaviors shown in Fig. 1b and d. With 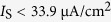 , the VS- and w-nullclines intersect at three points in
, the VS- and w-nullclines intersect at three points in  phase plane (left panel, Fig. 1c). Since the leftmost intersection is a stable node, all of VS trajectories converge to this equilibrium and the neuron does not fire APs. Increasing IS shifts VS-nullcline upwards, while does not alter the position of w-nullcline. In this case, the distance between stable node and unstable saddle decreases. With
phase plane (left panel, Fig. 1c). Since the leftmost intersection is a stable node, all of VS trajectories converge to this equilibrium and the neuron does not fire APs. Increasing IS shifts VS-nullcline upwards, while does not alter the position of w-nullcline. In this case, the distance between stable node and unstable saddle decreases. With 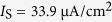 , these two equilibriums coalesce and annihilate each other. At the same time, a stable limit cycle is generated in
, these two equilibriums coalesce and annihilate each other. At the same time, a stable limit cycle is generated in  phase plane (Fig. 1c). Since the stable node corresponding to resting state no longer exists, VS trajectory jumps to the limit cycle attractor and the neuron starts to fire tonic spikes. The transition from resting to repetitive spiking occurs through a saddle-node on invariant circle (SNIC) bifurcation of equilibrium (Fig. 1e), which corresponds to the continuous
phase plane (Fig. 1c). Since the stable node corresponding to resting state no longer exists, VS trajectory jumps to the limit cycle attractor and the neuron starts to fire tonic spikes. The transition from resting to repetitive spiking occurs through a saddle-node on invariant circle (SNIC) bifurcation of equilibrium (Fig. 1e), which corresponds to the continuous  curve.
curve.
In the absence of ID, the firing rate fS of the model evoked by IS does not change with the maximum conductance 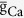 of dendritic Ca2+ current (Fig. 1f). With
of dendritic Ca2+ current (Fig. 1f). With 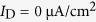 , there is no external driver activating Ca2+ conductance and thus dendritic Ca2+ spike is missing. Here IS only activates the Na+ channel in soma. Although the Na+-APs can be back-propagated to dendrite, such bottom-up input is unable to drive VD to reach the threshold voltage for activating Ca2+ current (Fig. 1g). Under these conditions, increasing
, there is no external driver activating Ca2+ conductance and thus dendritic Ca2+ spike is missing. Here IS only activates the Na+ channel in soma. Although the Na+-APs can be back-propagated to dendrite, such bottom-up input is unable to drive VD to reach the threshold voltage for activating Ca2+ current (Fig. 1g). Under these conditions, increasing 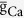 produces no effects on the spiking behaviors of the neuron to somatic input.
produces no effects on the spiking behaviors of the neuron to somatic input.
Apical input activates dendritic Ca2+ current and results in burst of somatic APs
In this section, we investigate how 5D model neuron responds to apical input injected at dendrite. Here somatic input IS is absent, i.e., 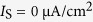 . The firing behaviors of the model is determined with different values of
. The firing behaviors of the model is determined with different values of 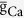 , which are summarized in Fig. 2.
, which are summarized in Fig. 2.
Figure 2. Firing properties evoked by dendritic input.
(a) Sample responses of the 5D model triggered by apical input ID in the cases of 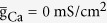 ,
, 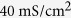 , and
, and 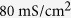 . ID is in
. ID is in 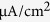 , which is indicated on the left. (b) Instantaneous firing rate finst with three values of
, which is indicated on the left. (b) Instantaneous firing rate finst with three values of 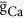 . Corresponding dendritic inputs are
. Corresponding dendritic inputs are 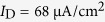 ,
, 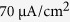 , and
, and 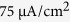 . (c) Relation between average firing rate fS and input ID (i.e.,
. (c) Relation between average firing rate fS and input ID (i.e., 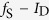 curve) with three values of
curve) with three values of 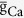 . Somatic injection is
. Somatic injection is 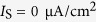 .
.
With 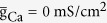 , the dendritic Ca2+ current is blocked and the dendrite becomes passive. In this case, the neuron exists in quiescent state with
, the dendritic Ca2+ current is blocked and the dendrite becomes passive. In this case, the neuron exists in quiescent state with 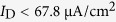 and there are still no APs generated. Once ID exceeds
and there are still no APs generated. Once ID exceeds 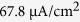 , repetitive APs are initiated in somatic chamber (left panel, Fig. 2a). The threshold of ID here is much larger than that of IS directly injected to soma. This is because the dendritic compartment in the model serves as a current sink allowing only part of the input current to invade the soma. From Fig. 2c, one can find that the fS − ID curve is continuous when blocking dendritic Ca2+ current, which indicates that the neuron is able to fire low-frequency APs to injected current ID. As ID is increased, the slope of fS − ID curve (i.e., input-output gain) is obviously reduced. Further, the evoked spike trains are always repetitive and the instantaneous firing rate finst remains constant with time (top panel, Fig. 2b). The finst in our study is calculated based on the reciprocal of relevant ISI in each spike train.
, repetitive APs are initiated in somatic chamber (left panel, Fig. 2a). The threshold of ID here is much larger than that of IS directly injected to soma. This is because the dendritic compartment in the model serves as a current sink allowing only part of the input current to invade the soma. From Fig. 2c, one can find that the fS − ID curve is continuous when blocking dendritic Ca2+ current, which indicates that the neuron is able to fire low-frequency APs to injected current ID. As ID is increased, the slope of fS − ID curve (i.e., input-output gain) is obviously reduced. Further, the evoked spike trains are always repetitive and the instantaneous firing rate finst remains constant with time (top panel, Fig. 2b). The finst in our study is calculated based on the reciprocal of relevant ISI in each spike train.
With 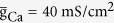 or
or 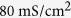 , there is active Ca2+ current in dendritic chamber. We find that the threshold value of ID for triggering somatic APs does not change with
, there is active Ca2+ current in dendritic chamber. We find that the threshold value of ID for triggering somatic APs does not change with 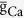 , which is still
, which is still 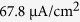 . However, the time course of the spike train is no longer repetitive (center and right panels, Fig. 2a). At the onset of ID, the model generates a burst of high-frequency spikes, which then slowly transits to repetitive spiking with low frequency. From Fig. 2b, one can observe that the instantaneous firing rate finst first quickly increases to a peak value and then slowly decays to a lower plateau level. Under these conditions, the fS − ID curve with
. However, the time course of the spike train is no longer repetitive (center and right panels, Fig. 2a). At the onset of ID, the model generates a burst of high-frequency spikes, which then slowly transits to repetitive spiking with low frequency. From Fig. 2b, one can observe that the instantaneous firing rate finst first quickly increases to a peak value and then slowly decays to a lower plateau level. Under these conditions, the fS − ID curve with 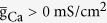 is no longer continuous, and the neuron becomes unable to maintain low-frequency spiking. As shown in Fig. 2c, the average firing rate fS immediately jumps to a high value once ID reaches the threshold for triggering APs. After that, the slope of
is no longer continuous, and the neuron becomes unable to maintain low-frequency spiking. As shown in Fig. 2c, the average firing rate fS immediately jumps to a high value once ID reaches the threshold for triggering APs. After that, the slope of 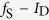 curve (i.e., input-output gain) with
curve (i.e., input-output gain) with 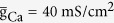 or
or 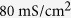 both changes little as ID is increased. These simulations indicate that the activation of dendritic Ca2+ current boosts excitatory input ID and facilitates the generation of somatic APs, i.e., an active dendritic integration occurs.
both changes little as ID is increased. These simulations indicate that the activation of dendritic Ca2+ current boosts excitatory input ID and facilitates the generation of somatic APs, i.e., an active dendritic integration occurs.
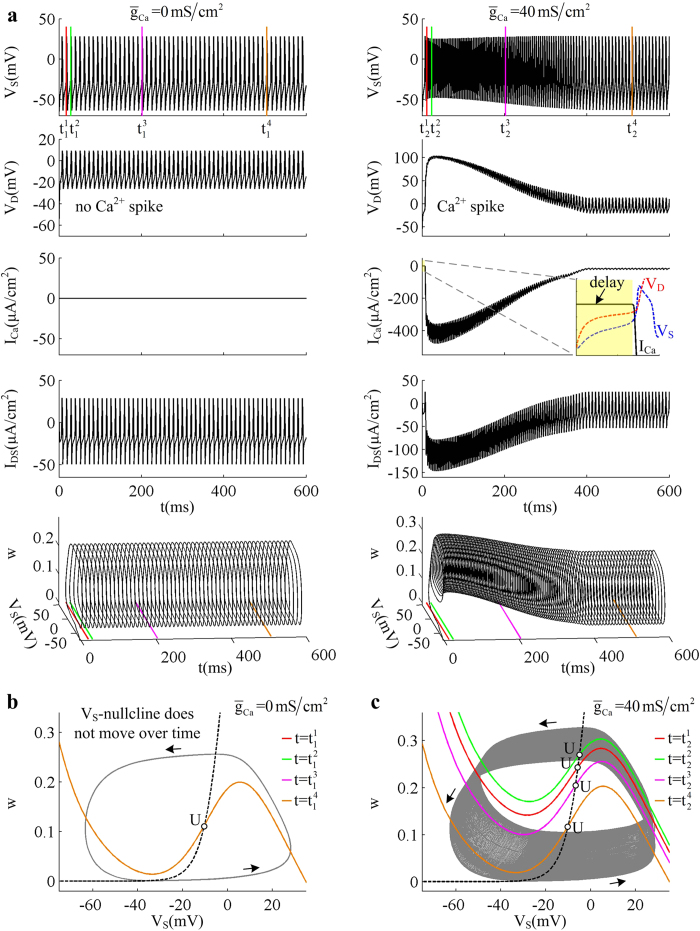
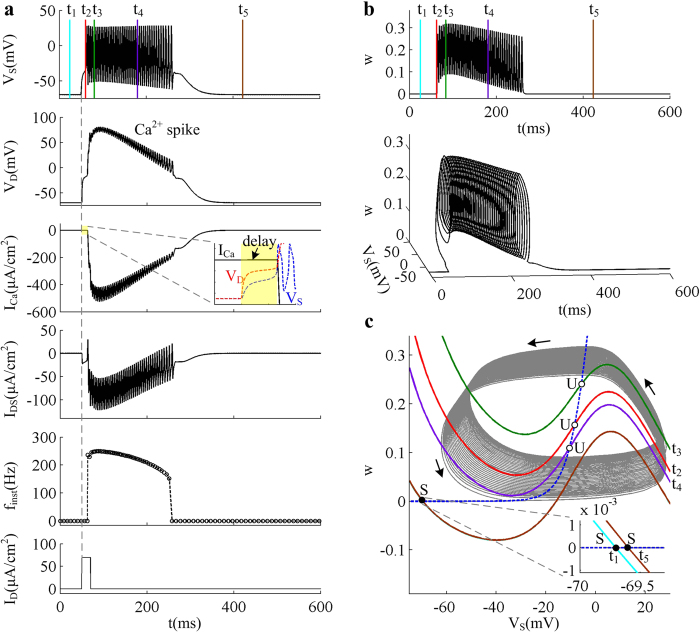
Dynamical basis for the burst of APs associated with dendritic Ca2+ spike
In previous section, we have determined the spiking properties of 5D model neuron stimulated by apical input ID alone. Our next step is to uncover the AP initiating dynamics associated with these behaviors.
When blocking dendritic Ca2+ current (i.e., 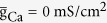 ), the dendrite becomes passive. Its membrane voltage VD only oscillates repetitively along with VS and there are no dendritic spikes evoked (left panels, Fig. 3a). Here the internal current IDS between two chambers is also repetitive, which transmits depolarizing input ID from dendrite to soma. Under these conditions, the intersection between VS- and w-nullclines and corresponding limit cycle attractor both remain unchanged from one AP to the next (Fig. 3b). As a result, the neuron generates repetitive spike trains.
), the dendrite becomes passive. Its membrane voltage VD only oscillates repetitively along with VS and there are no dendritic spikes evoked (left panels, Fig. 3a). Here the internal current IDS between two chambers is also repetitive, which transmits depolarizing input ID from dendrite to soma. Under these conditions, the intersection between VS- and w-nullclines and corresponding limit cycle attractor both remain unchanged from one AP to the next (Fig. 3b). As a result, the neuron generates repetitive spike trains.
Figure 3. Spike initiating dynamics evoked by dendritic input.
(a) Sample responses of the 5D model with 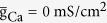 and
and 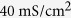 . Somatic voltage VS, dendritic voltage VD, dendritic Ca2+ current ICa, and internal current IDS are plotted against time. The close-up shows that the Ca2+ conductance is activated when dendritic voltage VD exceeds a threshold value. The sample response is also plotted in
. Somatic voltage VS, dendritic voltage VD, dendritic Ca2+ current ICa, and internal current IDS are plotted against time. The close-up shows that the Ca2+ conductance is activated when dendritic voltage VD exceeds a threshold value. The sample response is also plotted in 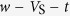 space (bottom panel). Color lines indicate the times at which the nullclines in (b) and (c) are calculated. Here dendritic input is
space (bottom panel). Color lines indicate the times at which the nullclines in (b) and (c) are calculated. Here dendritic input is 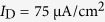 . (b) Two-dimensional phase portraits in
. (b) Two-dimensional phase portraits in  plane for
plane for 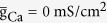 . (c) Phase portraits in
. (c) Phase portraits in  plane for
plane for 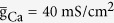 . For (b) and (c), the VS- and w-nullclines are respectively calculated at four time points indicated by colored lines in (a). Black dotted lines represent w-nullclines, which are the same at different time points. The inverted N-shape lines with other colors are the VS-nullcline at the corresponding time point indicated in (a). With
. For (b) and (c), the VS- and w-nullclines are respectively calculated at four time points indicated by colored lines in (a). Black dotted lines represent w-nullclines, which are the same at different time points. The inverted N-shape lines with other colors are the VS-nullcline at the corresponding time point indicated in (a). With 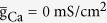 , the VS-nullcline does not move over time. Gray solid line is the sample VS trajectory of the recorded spike trains, and black arrows indicate the direction of its motion. ‘U’ indicates unstable fixed point. Somatic injection is
, the VS-nullcline does not move over time. Gray solid line is the sample VS trajectory of the recorded spike trains, and black arrows indicate the direction of its motion. ‘U’ indicates unstable fixed point. Somatic injection is 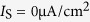 .
.
With 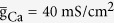 , the onset of apical input ID depolarizes membrane voltage VD and VS. When VD exceeds a threshold value, the Ca2+ conductance is activated and then a broader Ca2+ spike is initiated in the dendrite (right panels, Fig. 3a). When this event occurs, ICa first rapidly falls to a minimum value and then slowly rises to a steady-state plateau level. Note that the negative sign of ICa means this current is inward. Since Ca2+ flows into the dendritic cell, such Ca2+ spike evokes a prolonged obvious depolarization of dendritic membrane voltage. Under these conditions, there is an obviously depolarizing sink in internal current IDS, which coincides with dendritic Ca2+ spike. That is, the presence of dendritic Ca2+ spike boosts apical input as it spreads to soma. Due to such active integration, a constant input of
, the onset of apical input ID depolarizes membrane voltage VD and VS. When VD exceeds a threshold value, the Ca2+ conductance is activated and then a broader Ca2+ spike is initiated in the dendrite (right panels, Fig. 3a). When this event occurs, ICa first rapidly falls to a minimum value and then slowly rises to a steady-state plateau level. Note that the negative sign of ICa means this current is inward. Since Ca2+ flows into the dendritic cell, such Ca2+ spike evokes a prolonged obvious depolarization of dendritic membrane voltage. Under these conditions, there is an obviously depolarizing sink in internal current IDS, which coincides with dendritic Ca2+ spike. That is, the presence of dendritic Ca2+ spike boosts apical input as it spreads to soma. Due to such active integration, a constant input of 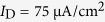 is amplified to a non-periodic current IDS with a maximum intensity around
is amplified to a non-periodic current IDS with a maximum intensity around 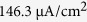 to invade the soma. Such depolarizing internal current shifts VS-nullcline upwards instantaneously in the first rapid phase of Ca2+ spike, and forces two nullclines to interact at an unstable fixed point (Fig. 3c). Then all of the VS trajectories converge to limit cycle attractor, and the neuron generates initial APs. Before ICa reaches peak value, the amplitude of depolarizing IDS continues to increase. It drives unstable fixed point upwards and the limit cycle attractor moves upwards accordingly, which makes firing rate finst further increase. In the second phase of dendritic Ca2+ spike, ICa slowly gets weak and the amplitude of depolarizing IDS becomes to decrease. In this case, the unstable fixed point and relevant limit cycle attractor both moves downwards (Fig. 3c), which leads to a decay of firing rate finst to its steady-state plateau level. Therefore, the model generates a burst of somatic APs when dendritic Ca2+ spike is initiated. Once such local spike is evoked, the amplitude of dendritic voltage VD and internal current IDS with a specific value of
to invade the soma. Such depolarizing internal current shifts VS-nullcline upwards instantaneously in the first rapid phase of Ca2+ spike, and forces two nullclines to interact at an unstable fixed point (Fig. 3c). Then all of the VS trajectories converge to limit cycle attractor, and the neuron generates initial APs. Before ICa reaches peak value, the amplitude of depolarizing IDS continues to increase. It drives unstable fixed point upwards and the limit cycle attractor moves upwards accordingly, which makes firing rate finst further increase. In the second phase of dendritic Ca2+ spike, ICa slowly gets weak and the amplitude of depolarizing IDS becomes to decrease. In this case, the unstable fixed point and relevant limit cycle attractor both moves downwards (Fig. 3c), which leads to a decay of firing rate finst to its steady-state plateau level. Therefore, the model generates a burst of somatic APs when dendritic Ca2+ spike is initiated. Once such local spike is evoked, the amplitude of dendritic voltage VD and internal current IDS with a specific value of 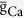 both varies little with apical input ID. Then, the input-output gain with
both varies little with apical input ID. Then, the input-output gain with 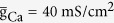 or
or 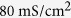 changes little in the observed range of ID.
changes little in the observed range of ID.
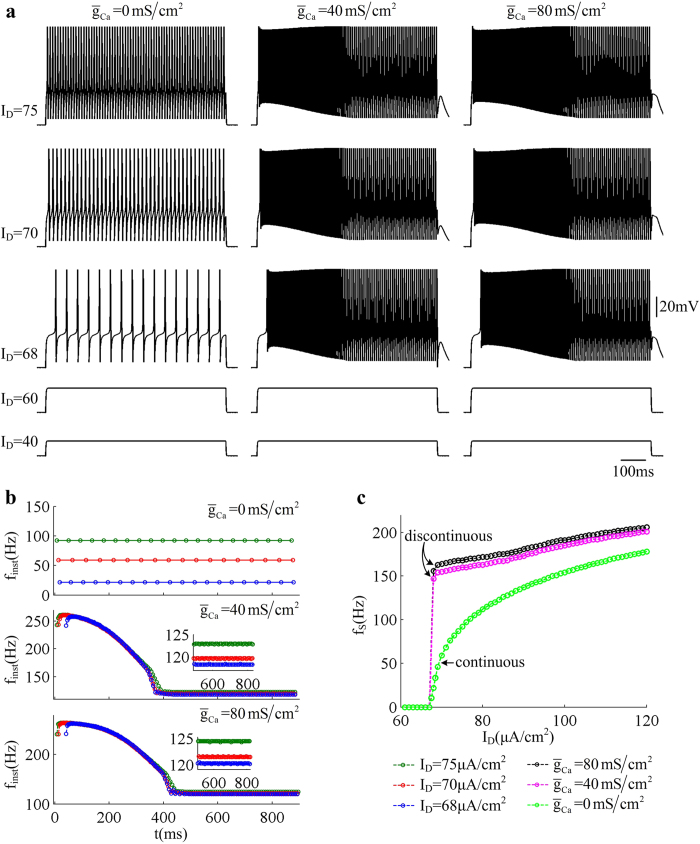
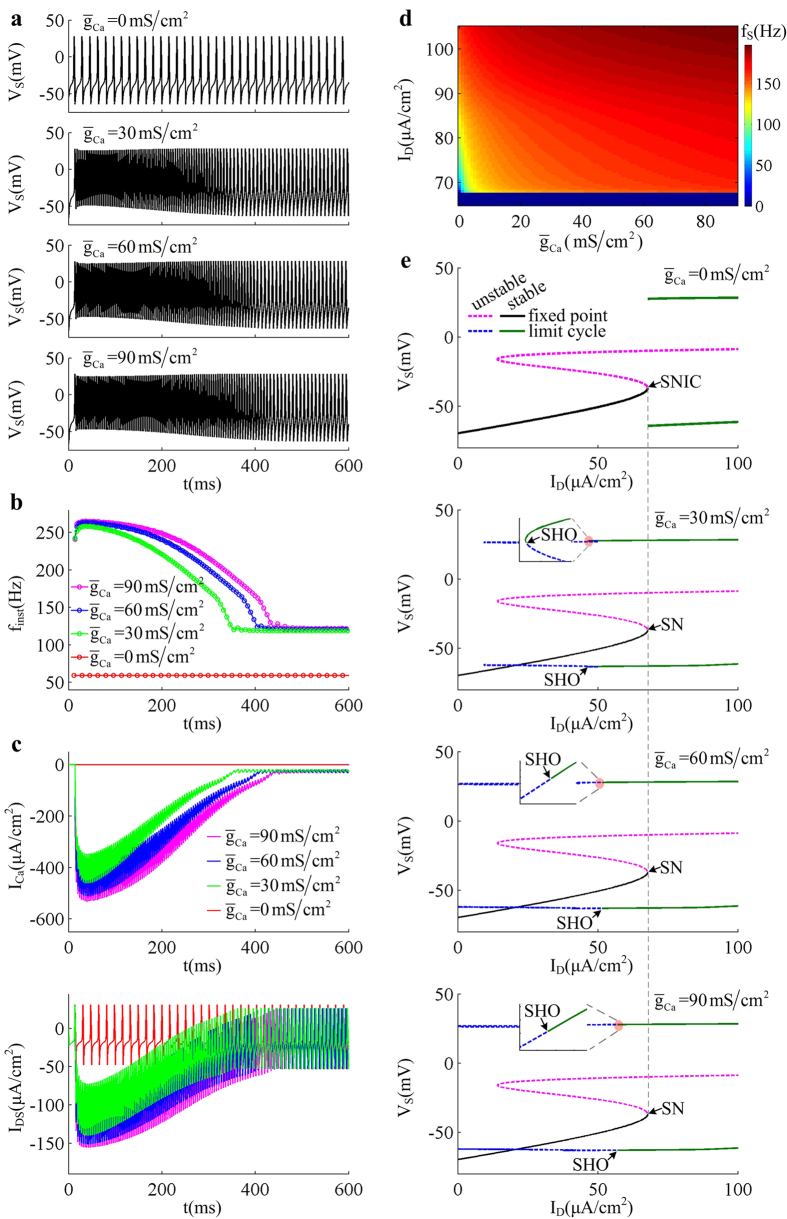
Figure 4 shows the AP initiating dynamics associated with the firing behaviors of the neuron as Ca2+ conductance 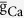 is increased from
is increased from 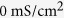 to
to 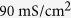 . Increasing
. Increasing 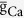 results in more somatic APs during the course of dendritic Ca2+ spike (Fig. 4a and b). It is known that the intensity of ICa is proportional to
results in more somatic APs during the course of dendritic Ca2+ spike (Fig. 4a and b). It is known that the intensity of ICa is proportional to 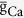 , and increasing its conductance extends the duration of dendritic Ca2+ spike (Fig. 4c). Then, the depolarizing current IDS induced by dendritic spike becomes progressively more prominent with
, and increasing its conductance extends the duration of dendritic Ca2+ spike (Fig. 4c). Then, the depolarizing current IDS induced by dendritic spike becomes progressively more prominent with 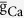 . Such stronger depolarizing current accelerates the spike initiation in somatic chamber, and drives neuron to fire more APs at a given value of ID. Then, the average firing rate fS increases as Ca2+ conductance is increased (Fig. 4d). However, varying
. Such stronger depolarizing current accelerates the spike initiation in somatic chamber, and drives neuron to fire more APs at a given value of ID. Then, the average firing rate fS increases as Ca2+ conductance is increased (Fig. 4d). However, varying 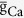 does not alter the kinetics or voltage-dependency of Ca2+ current. Then, the threshold of apical input ID for activating dendritic Ca2+ channel or evoking somatic APs remains unchanged as
does not alter the kinetics or voltage-dependency of Ca2+ current. Then, the threshold of apical input ID for activating dendritic Ca2+ channel or evoking somatic APs remains unchanged as 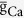 is increased (Fig. 4d). From Fig. 4e, one can find that blocking dendritic Ca2+ current results in a SNIC bifurcation of the equilibrium, which endows the neuron with a continuous
is increased (Fig. 4d). From Fig. 4e, one can find that blocking dendritic Ca2+ current results in a SNIC bifurcation of the equilibrium, which endows the neuron with a continuous 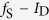 curve (Fig. 2c). Introducing dendritic Ca2+ channel extends the stable limit cycle to the value of ID below the bifurcation point of equilibrium, followed by unstable limit cycle. In this case, the equilibrium loses its stability via a saddle-node (SN) bifurcation, which corresponds to the transitions of resting to tonic spiking. When such kind of bifurcation occurs, the neuron fails to fire low-frequency APs48, and its
curve (Fig. 2c). Introducing dendritic Ca2+ channel extends the stable limit cycle to the value of ID below the bifurcation point of equilibrium, followed by unstable limit cycle. In this case, the equilibrium loses its stability via a saddle-node (SN) bifurcation, which corresponds to the transitions of resting to tonic spiking. When such kind of bifurcation occurs, the neuron fails to fire low-frequency APs48, and its 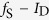 curve becomes discontinuous (Fig. 2c). Unlike equilibrium, the limit cycle transits from unstable to stable via saddle homoclinic orbit (SHO) bifurcation (Fig. 4e). As ID is increased, the unstable limit cycle disappears via a subcritical SHO bifurcation, and the stable limit cycle appears via a supercritical SHO bifurcation. The presence of Ca2+ current in dendrite increases the dimension of the system, and makes the SHO bifurcations of limit cycle attractor occur at the value of ID below SN bifurcation. What’s more, the SHO bifurcation also occurs at different values of apical input as
curve becomes discontinuous (Fig. 2c). Unlike equilibrium, the limit cycle transits from unstable to stable via saddle homoclinic orbit (SHO) bifurcation (Fig. 4e). As ID is increased, the unstable limit cycle disappears via a subcritical SHO bifurcation, and the stable limit cycle appears via a supercritical SHO bifurcation. The presence of Ca2+ current in dendrite increases the dimension of the system, and makes the SHO bifurcations of limit cycle attractor occur at the value of ID below SN bifurcation. What’s more, the SHO bifurcation also occurs at different values of apical input as 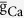 is increased (Fig. 4e). All these modulations of firing behavior and corresponding spike initiating dynamics with
is increased (Fig. 4e). All these modulations of firing behavior and corresponding spike initiating dynamics with 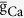 are due to dendritic Ca2+ activity, which endows dendrites with the powerful ability to actively integrate excitatory inputs.
are due to dendritic Ca2+ activity, which endows dendrites with the powerful ability to actively integrate excitatory inputs.
Figure 4. Effects of varying Ca2+ conductance on spike initiating dynamics evoked by dendritic input.
(a) Spike train recorded in the soma of 5D model in the cases of 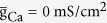 ,
, 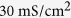 ,
, 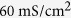 , and
, and 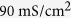 . (b) The instantaneous firing rate finst for each spike train. (c) Time courses of dendritic Ca2+ current ICa and corresponding internal current IDS with each value of
. (b) The instantaneous firing rate finst for each spike train. (c) Time courses of dendritic Ca2+ current ICa and corresponding internal current IDS with each value of 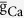 . For (a–c), the corresponding dendritic input is
. For (a–c), the corresponding dendritic input is 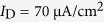 . (d) Average firing rate fS is plotted against ID and
. (d) Average firing rate fS is plotted against ID and 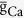 . (e) Bifurcation diagram with different values of
. (e) Bifurcation diagram with different values of 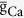 . Here the bifurcation parameter is apical input ID. Type of the bifurcation for equilibrium or limit cycle is indicated on each plot. Somatic input is
. Here the bifurcation parameter is apical input ID. Type of the bifurcation for equilibrium or limit cycle is indicated on each plot. Somatic input is 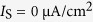 .
.
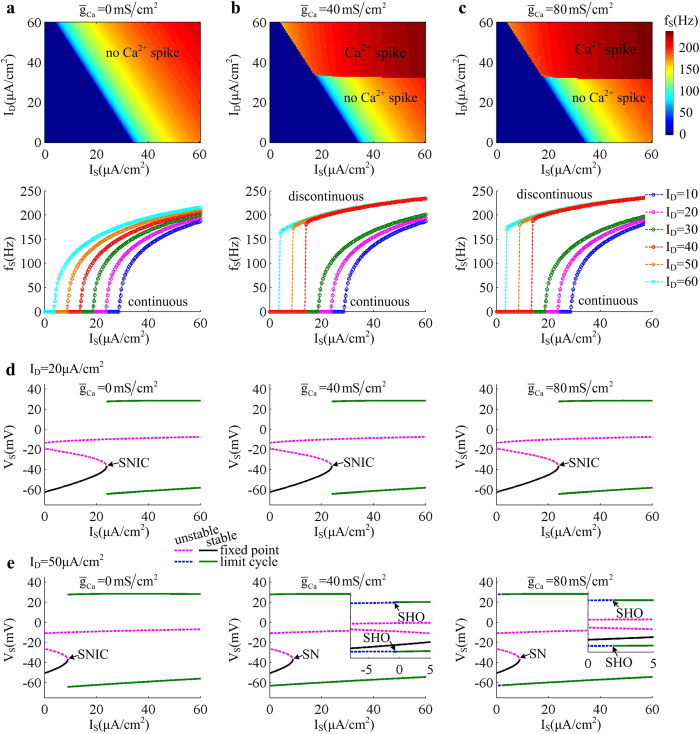
Coincident somatic and dendritic inputs facilitate dendritic Ca2+ spike
Here we determine the firing properties of the 5D model neuron evoked by the stimulation of coincident IS and ID, which are summarized in (IS, ID) parameter space for 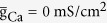 ,
, 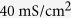 and
and 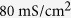 . One can find that the threshold value of input IS for triggering APs in somatic chamber decreases linearly with dendritic input ID (Fig. 5a–c). This is because that introducing positive ID results in a depolarizing current transmitted to somatic chamber. Such current increases the level of neuronal excitability and makes it more prone to generate APs to somatic stimulus. Then, the rheobase of IS decreases with dendritic input ID.
. One can find that the threshold value of input IS for triggering APs in somatic chamber decreases linearly with dendritic input ID (Fig. 5a–c). This is because that introducing positive ID results in a depolarizing current transmitted to somatic chamber. Such current increases the level of neuronal excitability and makes it more prone to generate APs to somatic stimulus. Then, the rheobase of IS decreases with dendritic input ID.
Figure 5. Firing properties evoked by coincident somatic and dendritic inputs.
The firing rate fS of the 5D model is calculated for three values of 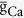 , which are (a)
, which are (a) 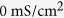 . (b)
. (b) 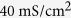 and (c)
and (c) 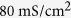 , respectively. For (a–c), top panels give the average firing rate fS plotted against input IS and ID. Bottom panels show the
, respectively. For (a–c), top panels give the average firing rate fS plotted against input IS and ID. Bottom panels show the  curves with different values of ID. The bifurcation diagrams related to coincident inputs at soma and dendrite with each value of
curves with different values of ID. The bifurcation diagrams related to coincident inputs at soma and dendrite with each value of 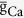 are given in (d) and (e). Here the bifurcation parameter is somatic input IS. We compute one-parameter bifurcation with two values of dendritic input, which are (d)
are given in (d) and (e). Here the bifurcation parameter is somatic input IS. We compute one-parameter bifurcation with two values of dendritic input, which are (d)
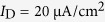 and (e)
and (e) 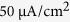 . The lower value of ID is unable to activate dendritic Ca2+ conductance, but the latter could trigger dendritic Ca2+ spike. Type of the bifurcation for equilibrium or limit cycle is indicated on each plot.
. The lower value of ID is unable to activate dendritic Ca2+ conductance, but the latter could trigger dendritic Ca2+ spike. Type of the bifurcation for equilibrium or limit cycle is indicated on each plot.
Varying Ca2+ conductance 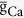 produces no effects on the rheobase of IS in the observed range of ID, which only determines whether there is dendritic Ca2+ spike. When blocking Ca2+ current (i.e.,
produces no effects on the rheobase of IS in the observed range of ID, which only determines whether there is dendritic Ca2+ spike. When blocking Ca2+ current (i.e., 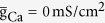 ), the dendrite is passive and there is no dendritic Ca2+ spike in (IS, ID) parameter space. Here the fS−IS curve is always continuous in the range of
), the dendrite is passive and there is no dendritic Ca2+ spike in (IS, ID) parameter space. Here the fS−IS curve is always continuous in the range of 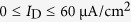 (Fig. 5a), which is generated by a SNIC bifurcation of equilibrium (Fig. 5d). With
(Fig. 5a), which is generated by a SNIC bifurcation of equilibrium (Fig. 5d). With 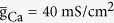 or
or 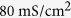 , there is dendritic Ca2+ spike elicited in (IS, ID) parameter space once ID reaches a threshold value. Such event causes firing rate fS quickly to converge to its plateau level at the onset of IS (Fig. 5b and c). Then, the fS − IS curve becomes discontinuous, which is generated via a SN bifurcation of equilibrium (Fig. 5e). Further, introducing dendritic Ca2+ current changes the bifurcation of limit cycle from SNIC to SHO, and makes it occur at another value of IS below the bifurcation of equilibrium. Meanwhile, increasing
, there is dendritic Ca2+ spike elicited in (IS, ID) parameter space once ID reaches a threshold value. Such event causes firing rate fS quickly to converge to its plateau level at the onset of IS (Fig. 5b and c). Then, the fS − IS curve becomes discontinuous, which is generated via a SN bifurcation of equilibrium (Fig. 5e). Further, introducing dendritic Ca2+ current changes the bifurcation of limit cycle from SNIC to SHO, and makes it occur at another value of IS below the bifurcation of equilibrium. Meanwhile, increasing 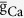 is also able to alter the value of IS for causing the SHO bifurcation of limit cycle (Fig. 5e).
is also able to alter the value of IS for causing the SHO bifurcation of limit cycle (Fig. 5e).
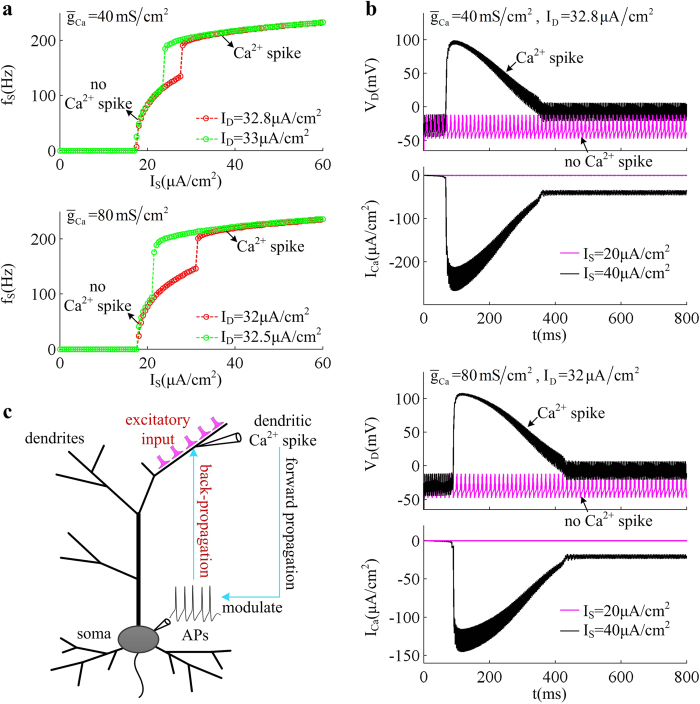
We also find that the threshold values of apical input ID for evoking dendritic Ca2+ spike in (IS, ID) parameter space are significantly lower than those in the absent of IS. This indicates that the bottom-up input is conducive to the initiation of dendritic Ca2+ spike. Particularly, with some moderate values of ID, the Ca2+ current is unable to be activated by IS above and close to the bifurcation point of equilibrium (Fig. 6a). Here only somatic input with sufficient intensity can force VD to reach the threshold for initiating dendritic Ca2+ spike (Fig. 6b). It is known that the firing frequency fS is an increasing function of IS. Thus, the back-propagation of spiking behavior with high frequency contributes to activating Ca2+ spike, which is also referred to as BAC firing17,23,26. These results demonstrate that the dendritic Ca2+ spike is the outcome of the interaction between back-propagated APs and excitatory synaptic inputs (Fig. 6c). Such prolonged regenerative spikes elicited in apical dendrites can be forward propagated to the AP initiation zone to modulate the final output of the neuron.
Figure 6. BAC firing evoked by coincident injections to two chambers.
(a)  curves of 5D model with
curves of 5D model with 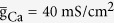 and
and 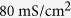 . For
. For 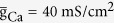 , the value of dendritic input is
, the value of dendritic input is 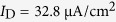 and
and 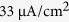 . For
. For 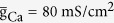 , they are
, they are 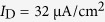 and
and 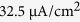 . (b) Dendritic voltage VD and associated Ca2+ current ICa for each value of
. (b) Dendritic voltage VD and associated Ca2+ current ICa for each value of 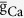 . The value of IS and ID are indicated in each plot. (c) Dendritic Ca2+ spike is evoked by the interactions between the back-propagating APs and the excitatory inputs received by apical dendrites. The Ca2+ spike induced by back-propagating APs is also referred to as BAC firing, which can be propagated to soma to modulate the output APs.
. The value of IS and ID are indicated in each plot. (c) Dendritic Ca2+ spike is evoked by the interactions between the back-propagating APs and the excitatory inputs received by apical dendrites. The Ca2+ spike induced by back-propagating APs is also referred to as BAC firing, which can be propagated to soma to modulate the output APs.
Discussion
Our simulations have shown that injecting current to soma alone makes the 5D model neuron generate continuous input-output relation through a SNIC bifurcation of equilibrium. Here the bottom-up input from soma to dendrite is unable to activate dendritic Ca2+ conductance. Thus, varying Ca2+ conductance produces no effects on the output APs. Injecting current to apical dendrite alone results in a distinct input-output relation. When blocking Ca2+ channel, the input-output relation is still continuous, and the bifurcation structures of equilibrium and limit cycle both remain the same. When there is active Ca2+ channel in dendrite, the apical input with sufficient intensity is able to activate Ca2+ conductance and trigger a prolonged Ca2+ spike. This event boosts depolarized input as it spreads to soma, and facilitates the initiation of somatic APs. Under this condition, the neuron generates a burst of high-frequency APs during the course of dendritic Ca2+ spike. Then, the 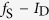 curve becomes discontinuous, and the firing rate quickly reaches a plateau level. These simulations demonstrate that the top-down information received by passive or active dendrite modulates the output APs in a distinct way, which depends critically on the site of synaptic inputs.
curve becomes discontinuous, and the firing rate quickly reaches a plateau level. These simulations demonstrate that the top-down information received by passive or active dendrite modulates the output APs in a distinct way, which depends critically on the site of synaptic inputs.
The firing rate of the 5D model neuron evoked by conjunct inputs to dendrite and soma is summarized in (IS, ID) parameter space. It is shown that simultaneously injecting constant current to two chambers shifts the threshold of  curve to a lower value. When blocking dendritic Ca2+ current, the top-down input arriving at apical dendrite only increases the excitability of the neuron and reduces the rheobase of somatic input, which does not alter the shape of input-output relation. For the dendrite with Ca2+ channel, the top-down input with sufficient intensity triggers Ca2+ spike. This event results in a burst of APs in soma and significantly increases firing frequency, which leads to a discontinuous input-output relation. Here the timing of burst is able to detect whether there are coincident somatic and dendritic inputs. In fact, such burst pattern associated with dendritic Ca2+ spike has been observed in previous experimental26,30,31,32 and modeling35,37,39,40 reports. We have not only reproduced it with a simplified conductance-based model, but also determined the dynamical basis of relevant spike initiation with phase plane analysis. These investigations could contribute to uncovering how the Ca2+ activity in apical dendrites participates in neuronal computation.
curve to a lower value. When blocking dendritic Ca2+ current, the top-down input arriving at apical dendrite only increases the excitability of the neuron and reduces the rheobase of somatic input, which does not alter the shape of input-output relation. For the dendrite with Ca2+ channel, the top-down input with sufficient intensity triggers Ca2+ spike. This event results in a burst of APs in soma and significantly increases firing frequency, which leads to a discontinuous input-output relation. Here the timing of burst is able to detect whether there are coincident somatic and dendritic inputs. In fact, such burst pattern associated with dendritic Ca2+ spike has been observed in previous experimental26,30,31,32 and modeling35,37,39,40 reports. We have not only reproduced it with a simplified conductance-based model, but also determined the dynamical basis of relevant spike initiation with phase plane analysis. These investigations could contribute to uncovering how the Ca2+ activity in apical dendrites participates in neuronal computation.
It is shown that somatic input decreases the threshold value of apical input for triggering dendritic spike. This indicates that the back-propagating APs are conducive to the initiation of dendritic Ca2+ spike, i.e., BAC firing occurs. The simulations with our simple 5D model suggest that the generation of BAC firing arises from the interactions between back-propagating spikes and dendritic excitatory input, which is in accordance with previous predictions17,23,26,27. During this procedure, the back-propagating APs play a crucial role in connecting two zones of spike initiation, which enables the integration of synaptic inputs to be disturbed in space and time. Meanwhile, BAC firing is a common mechanism for pyramidal neuron to associate conjunct somatic and dendritic inputs25. Without BAC firing, the dendritic input has much less effects on the firing behavior than somatic input. Once it occurs, the firing rate and spike timing is dominated by the input received by apical dendrites. Thus, this event completely alters the relative importance of synaptic inputs to the cell. Two-compartment model is the minimum individual unit of the neuron to capture such complex phenomenon. Each chamber has its own mechanism for spike initiation, which enables the neuron to integrate synaptic inputs simultaneously in two separated regions. Thus, it can effectively reproduce the BAC firing. Further, earlier in vitro experiment26 has predicted that the distal dendritic inputs lead to a higher gain and higher variability of the spike train than somatic input. This phenomenon is missing in our simulations, which is because that the injected currents here are all deterministic and do not include noise. Larkum et al.26 have shown that the noisy components in current injection are the dominant factor for relevant gain modulation, since they significantly alter the initial slope of input-output relation.
The dendritic Ca2+ spikes in our simulations are triggered by current steps injected to the dendrite. Its roles are discussed in augmenting the influence of dendritic current flowing from the dendrite to the soma over the Na+-APs. That is, the influences of relevant Ca2+ spike are studied in the presence of background activity. This makes the argument that Ca2+ spike augments dendritic current problematic. To determine how dendritic Ca2+ spike influences somatic APs by itself, we use apical input to generate a brief pulse to trigger a single dendritic Ca2+ spike and repeat above simulations. As expected, the inward current associated with dendritic Ca2+ spike provides a strong local depolarization that boosts apical input. The resulting sustained depolarization spreads to the soma and causes a burst of high-frequency APs (Fig. 7). These modulatory effects are similar to that evoked by current steps. It indicates that a Ca2+ spike in apical dendrites without additional dendritic input influences the initiation of somatic APs just the same as those with dendritic inputs.
Figure 7. Somatic APs and initiating dynamics evoked by pulse injected at dendritic chamber.
(a) Sample responses of the 5D model triggered by pulse input ID in the cases of 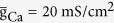 . Somatic voltage VS, dendritic voltage VD, dendritic Ca2+ current ICa, internal current IDS, and instantaneous firing rate finst are plotted against time. The amplitude of ID is
. Somatic voltage VS, dendritic voltage VD, dendritic Ca2+ current ICa, internal current IDS, and instantaneous firing rate finst are plotted against time. The amplitude of ID is 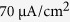 and its duration is 20 ms. (b) Plot of K+ activation variable w against time with
and its duration is 20 ms. (b) Plot of K+ activation variable w against time with 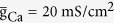 . The spike train recorded in soma is also plotted in
. The spike train recorded in soma is also plotted in 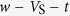 space. Five color lines in panel (a) and (b) indicate the times at which the nullclines are calculated. (c) Two-dimensional phase portraits in
space. Five color lines in panel (a) and (b) indicate the times at which the nullclines are calculated. (c) Two-dimensional phase portraits in  plane. The VS- and w-nullclines are respectively calculated at time point t1 − t5 indicated by colored lines in (a) and (b). Blue dotted line represents w-nullcline, and the inverted N-shape lines are the VS-nullclines at corresponding time point. Gray solid line is the VS trajectory, and black arrows indicate its direction. ‘S’ indicates stable fixed point, and ‘U’ indicates unstable fixed point. Somatic injection is
plane. The VS- and w-nullclines are respectively calculated at time point t1 − t5 indicated by colored lines in (a) and (b). Blue dotted line represents w-nullcline, and the inverted N-shape lines are the VS-nullclines at corresponding time point. Gray solid line is the VS trajectory, and black arrows indicate its direction. ‘S’ indicates stable fixed point, and ‘U’ indicates unstable fixed point. Somatic injection is 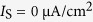 .
.
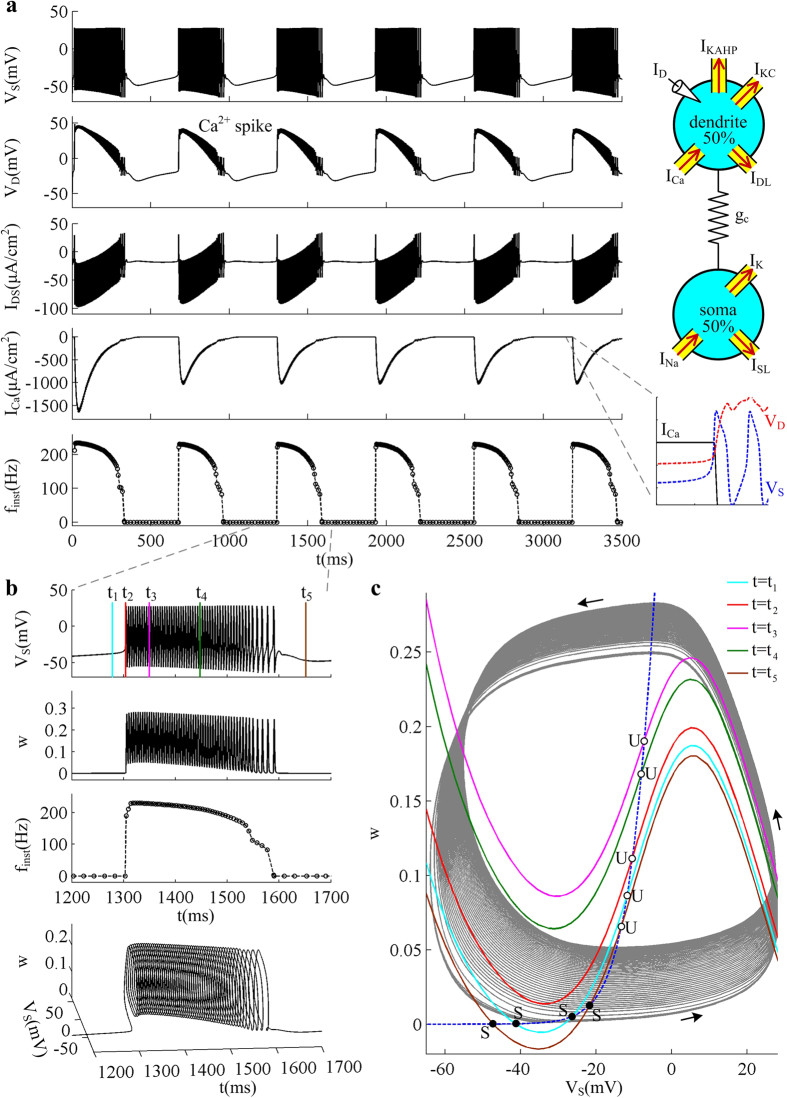
Many Ca2+-models include the dynamics of intracellular Ca2+ concentration 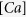 37,38,39,43,49,50,51,52,53, which is tightly related to the Ca2+ influx through voltage-gated channels. It has been used in modeling37,39,40 and experimental15,16 studies to characterize dendritic Ca2+ spike. Here we introduce the dynamics of
37,38,39,43,49,50,51,52,53, which is tightly related to the Ca2+ influx through voltage-gated channels. It has been used in modeling37,39,40 and experimental15,16 studies to characterize dendritic Ca2+ spike. Here we introduce the dynamics of 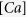 and two types of Ca2+-activated K+ current to the dendrite of our 5D model (see Methods for model specification). By injecting current step to apical dendrite, we repeat the simulations to test whether dendritic Ca2+ spike has effects comparable with those described above. It is shown that the neuron generates periodic bursting behavior to constant apical input after introducing Ca2+ concentration and K+ currents (Fig. 8a), which makes the difference between burst and tonic spiking more distinguishable. As expected, each dendritic Ca2+ spike has similar effects on the initiation of somatic APs in more biophysically realistic model (Fig. 8) and in 5D model (Figs 2 and 7). This suggests that the simplifications inherent in our 5D two-compartment model do not compromise the applicability of our findings to biophysically realistic conditions.
and two types of Ca2+-activated K+ current to the dendrite of our 5D model (see Methods for model specification). By injecting current step to apical dendrite, we repeat the simulations to test whether dendritic Ca2+ spike has effects comparable with those described above. It is shown that the neuron generates periodic bursting behavior to constant apical input after introducing Ca2+ concentration and K+ currents (Fig. 8a), which makes the difference between burst and tonic spiking more distinguishable. As expected, each dendritic Ca2+ spike has similar effects on the initiation of somatic APs in more biophysically realistic model (Fig. 8) and in 5D model (Figs 2 and 7). This suggests that the simplifications inherent in our 5D two-compartment model do not compromise the applicability of our findings to biophysically realistic conditions.
Figure 8. Bursting activities associated with dendritic Ca2+ spike in a more biophysically realistic model.
(a) Schematic of the biophysically realistic model is shown in the top-right panel. The apical input is 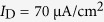 , and somatic input is
, and somatic input is 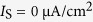 . Left panels show the sample responses recorded in its soma. Somatic voltage VS, dendritic voltage VD, internal current IDS, dendritic Ca2+ current ICa, and instantaneous firing rate finst are plotted against time. The bottom-right close-up shows that the Ca2+ conductance is activated when dendritic voltage VD exceeds a threshold value. (b) Close-up of somatic voltage VS, K+ activation variable w, and firing rate finst. Bottom panel shows the close-up of VS trajectory in
. Left panels show the sample responses recorded in its soma. Somatic voltage VS, dendritic voltage VD, internal current IDS, dendritic Ca2+ current ICa, and instantaneous firing rate finst are plotted against time. The bottom-right close-up shows that the Ca2+ conductance is activated when dendritic voltage VD exceeds a threshold value. (b) Close-up of somatic voltage VS, K+ activation variable w, and firing rate finst. Bottom panel shows the close-up of VS trajectory in 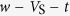 space. Five color lines indicate the times at which the nullclines are calculated. (c) Two-dimensional phase portraits in
space. Five color lines indicate the times at which the nullclines are calculated. (c) Two-dimensional phase portraits in  plane. The VS- and w-nullclines are respectively calculated at time point t1 −t5 indicated by colored lines in (b). Blue dotted line represents w-nullcline, and the inverted N-shape lines are the VS-nullcline at corresponding time point. Gray solid line is the VS trajectory, and black arrows indicate its direction. ‘S’ indicates stable fixed point, and ‘U’ indicates unstable fixed point. The maximum conductance of dendritic Ca2+ current is
plane. The VS- and w-nullclines are respectively calculated at time point t1 −t5 indicated by colored lines in (b). Blue dotted line represents w-nullcline, and the inverted N-shape lines are the VS-nullcline at corresponding time point. Gray solid line is the VS trajectory, and black arrows indicate its direction. ‘S’ indicates stable fixed point, and ‘U’ indicates unstable fixed point. The maximum conductance of dendritic Ca2+ current is 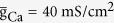 .
.
As a common cell type in mammalian brain, pyramidal neurons have been studied with theoretical approaches that incorporate dendritic Ca2+ channel in multi-compartmental models21,33,34,35,36,37. These complex models may express more than 10 voltage-gated channels, which are non-homegenously distributed along the somato-dendritic axis. Using biophysically realistic, high-dimensional neuron models is reasonably straightforward. But they may fail to provide greater insights into the mechanism underlying AP initiation than the experiments upon which they are based, since they include so many extraneous details. There are also theoretical studies using simple two-compartment models to describe the Ca2+ activity of dendrites for pyramidal cell38,39,40,41,42,43. However, none of them has provided a satisfied interpretation of how dendritic Ca2+ spike participates in the initiating dynamics of somatic/axonal APs. Unlike earlier models, our model starts simple and excludes extraneous details, which is made only as complex as required to reproduce the phenomena of interest. It enables one to perform phase plane and bifurcation analysis on how Ca2+ spikes initiated in apical dendrites affect the global integration of the neuron. With our simple model, one can visualize and interpret how two-stage integration mode occurs in pyramidal cells. Even so, our predictions and corresponding interpretations require validation with complex models and experiments.
In summary, the current study addresses the importance of Ca2+ spike of apical dendrites in affecting the firing behaviors of two-compartment neurons during different sites of current injection. Our simulations provide a deep and interpretable insight into the connection between dendritic Ca2+ spike and firing pattern by relating them to somatic AP initiation. Determining how dendritic Ca2+ activities and input locations modulate the cellular responses is a pivotal first step toward uncovering how the Ca2+ activity of active dendrite participates in neuronal computation. The simplified two-compartment model proposed here is able to capture the complex phenomena of pyramidal neurons in experiments, which could be used to obtain a mechanistic understanding about how relevant circuits participate in cortical computation.
Methods
Simulations are based on the two-compartmental models of cortical pyramidal neuron, which are the reduced version of PR model. One compartment represents the apical dendritic zone, and the other one represents the basal integration zone around the soma plus axonal initial segment. From apical integration zone, the input signals transmitted to soma can be processed via dendritic Ca2+ spike. Two-compartment neuron is the simplest structure to capture such spatial inputs.
Our starting model is derived by introducing a voltage-dependent Ca2+ current to the passive dendrite of a simple two-compartment model proposed in our earlier studies45,46. The right panel of Fig. 1a shows the schematic representation of the two-compartment neuron, which is a 5D model. There are three ionic currents in somatic compartment, which are inward Na+ current (INa), outward K+ current (Ik), and passive leak current (ISL). Here two active currents, i.e., INa and Ik, are responsible for generating APs. For dendritic chamber, there are two ionic currents, which are inward Ca2+ current (ICa) and passive leak current (IDL). The somatic and dendritic chambers are connected by an internal coupling conductance 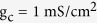 . The dynamics of their membrane potential VS and VD are governed by the following current-balance equations
. The dynamics of their membrane potential VS and VD are governed by the following current-balance equations
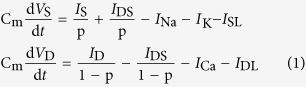 |
where 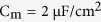 is the membrane capacitance,
is the membrane capacitance, 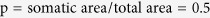 is a morphological parameter.
is a morphological parameter. 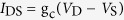 is the internal current that flows through conductance gc and connects two chambers. IS and ID are two input currents respectively injected at soma and dendrite, which are used to stimulate the neuron.
is the internal current that flows through conductance gc and connects two chambers. IS and ID are two input currents respectively injected at soma and dendrite, which are used to stimulate the neuron.
Three voltage-dependent currents included in somatic chamber are
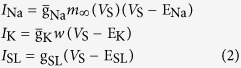 |
where 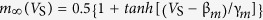 is the steady-state activation function for inward Na+ channel. w is the activation variable for slow K+ current, which is governed by the following differential equation
is the steady-state activation function for inward Na+ channel. w is the activation variable for slow K+ current, which is governed by the following differential equation
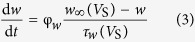 |
Here 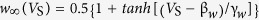 and
and 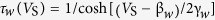 are respectively the steady-state activation function and time constant of this slow current.
are respectively the steady-state activation function and time constant of this slow current. 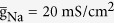 ,
,  ,
, 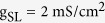 are the maximum conductances associated with the currents, and
are the maximum conductances associated with the currents, and 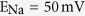 ,
, 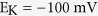 ,
, 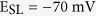 are their relevant reversal potentials. Unless otherwise stated,
are their relevant reversal potentials. Unless otherwise stated, 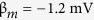 ,
, 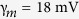 ,
, 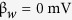 ,
, 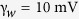 , and
, and 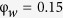 .
.
Two voltage-dependent currents used in dendrite are
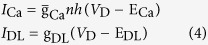 |
where 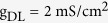 ,
,  ,
, 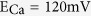 , and Ca2+ maximum conductance
, and Ca2+ maximum conductance 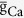 is varied as explained in Results. The dynamics of Ca2+ current is governed by an activation variable n and an inactivation variable h, which are characterized by the following equations
is varied as explained in Results. The dynamics of Ca2+ current is governed by an activation variable n and an inactivation variable h, which are characterized by the following equations
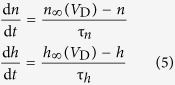 |
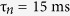 and
and 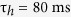 are the time constant of the first-order kinetics for variable n and h. Their steady-state functions are
are the time constant of the first-order kinetics for variable n and h. Their steady-state functions are
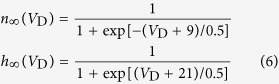 |
The kinetics of dendritic Ca2+ channel here is the same as that described by Larkum et al.26. Unless otherwise stated, our stimulations are all based on this 5D model.
To make above 5D two-compartment model more biophysically realistic, we introduce the dynamics of intracellular Ca2+ concentration 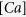 and two types of Ca2+-activated K+ current to its dendrite (see Fig. 8). The K+ channels include short-duration Ca2+-dependent K+ current (IKC) and long-duration Ca2+-dependent K+ current (IKAHP), which are commonly distributed in the dendrites of pyramidal cells37,39,40. Their activations are both related to the dynamics of
and two types of Ca2+-activated K+ current to its dendrite (see Fig. 8). The K+ channels include short-duration Ca2+-dependent K+ current (IKC) and long-duration Ca2+-dependent K+ current (IKAHP), which are commonly distributed in the dendrites of pyramidal cells37,39,40. Their activations are both related to the dynamics of 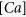 . After introducing IKC and IKAHP, the membrane equation for dendritic voltage VD becomes
. After introducing IKC and IKAHP, the membrane equation for dendritic voltage VD becomes
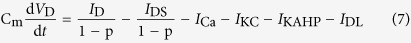 |
The details of IKC and IKAHP follow the descriptions by Pinsky and Rinzel39, which are 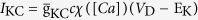 , and
, and  . Values of the maximum conductance are
. Values of the maximum conductance are 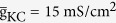 and
and 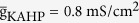 . The kinetics of their activation variable c and q obeys
. The kinetics of their activation variable c and q obeys
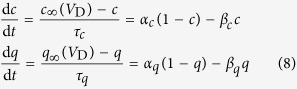 |
where
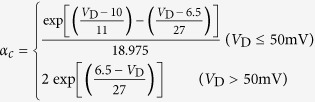 |
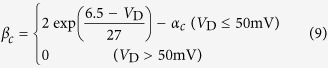 |
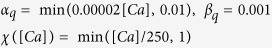 |
The kinetics for intracellular Ca2+ concentration [Ca] follows
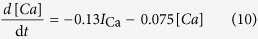 |
That is, the [Ca] is increased proportionally to Ca2+ influx ICa37,39. All other parameters in this more biophysically realistic model are the same as in the 5D model.
Note that the dynamics of [Ca] is not considered in the simple 5D model. As mentioned in Introduction, dendritic Ca2+ spike is the voltage transient caused by the activation of dendritic Ca2+ conductance5,6,7,11,23. It is a local regenerative response involving the positive feedback loop between dendritic voltage and Ca2+ influx6,7. Using a voltage-dependent current ICa is sufficient to reproduce such regenerative dendritic response and its dependence on Ca2+ dynamics26. By excluding the extraneous details, we propose a biophysical model complex enough to reproduce dendritic Ca2+ spike yet simple enough for characterizing its effects on the initiating dynamics of somatic APs. Further, the results in Fig. 8 show that ignoring the dynamics of Ca2+ concentration [Ca] does not alter our predictions about how dendritic spike affects the initiating dynamics of somatic APs.
Finally, the two-compartment models are integrated in MATLAB using numerical integrator ode23, with a time resolution of 0.01 ms. The phase plane and bifurcation analyses are performed with the publicly available software package XPPAUT54.
Additional Information
How to cite this article: Yi, G. et al. Action potential initiation in a two-compartment model of pyramidal neuron mediated by dendritic Ca2+ spike. Sci. Rep. 7, 45684; doi: 10.1038/srep45684 (2017).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Acknowledgments
This work was supported by grants from the National Natural Science Foundation of China (Nos. 61372010, 61471265 and 61601320), the China Postdoctoral Science Foundation (No. 2015M580202), and the Specialized Research Fund for the Doctoral Program of Higher Education (No. 20130032110065).
Footnotes
The authors declare no competing financial interests.
Author Contributions G.S.Y., J.W. and X.L.W. conceived and designed the research, G.S.Y. and J.W. performed the simulations, G.S.Y., J.W. and X.L.W. wrote the paper. All authors reviewed the manuscript.
References
- Spruston N. Pyramidal neurons: dendritic structure and synaptic integration. Nat. Rev. Neurosci. 9, 206–221 (2008). [DOI] [PubMed] [Google Scholar]
- Elston G. N. Cortex, cognition and the cell: new insights into the pyramidal neuron and prefrontal function. Cereb. Cortex 13, 1124–1138 (2003). [DOI] [PubMed] [Google Scholar]
- Ramon y Cajal S. Histology of the nervous system of man and vertebrates(Oxford University Press, Oxford, 1995). [Google Scholar]
- Palmer L. M. Dendritic integration in pyramidal neurons during network activity and disease. Brain Res. Bull. 103, 2–10 (2014). [DOI] [PubMed] [Google Scholar]
- Grienberger C., Chen X. & Konnerth A. Dendritic function in vivo. Trends Neurosci. 38, 45–54 (2015). [DOI] [PubMed] [Google Scholar]
- Stuart G. J. & Spruston N. Dendritic integration: 60 years of progress. Nat. Neurosci. 18, 1713–21 (2015). [DOI] [PubMed] [Google Scholar]
- Major G., Larkum M. E. & Schiller J. Active properties of neocortical pyramidal neuron dendrites. Annu. Rev. Neurosci. 36, 1–24 (2013). [DOI] [PubMed] [Google Scholar]
- Branco T. & Häusser M. The single dendritic branch as a fundamental functional unit in the nervous system. Curr. Opin. Neurobiol. 20, 494–502 (2010). [DOI] [PubMed] [Google Scholar]
- Branco T. & Häusser M. Synaptic integration gradients in single cortical pyramidal cell dendrites. Neuron. 69, 885–92 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vetter P., Roth A. & Häusser M. Propagation of action potentials in dendrites depends on dendritic morphology. J. Neurophysiol. 85, 926–37 (2001). [DOI] [PubMed] [Google Scholar]
- Tran-Van-Minh A. et al. Contribution of sublinear and supralinear dendritic integration to neuronal computations. Front. Cell. Neurosci. 9, 67 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kitamura K. & Häusser M. Dendritic calcium signaling triggered by spontaneous and sensory-evoked climbing fiber input to cerebellar Purkinje cells in vivo. J. Neurosci. 31, 10847–58 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Branco T., Clark B. A. & Häusser M. Dendritic discrimination of temporal input sequences in cortical neurons. Science 329, 1671–5 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larkum M. E. & Nevian T. Synaptic clustering by dendritic signalling mechanisms. Curr. Opin. Neurobiol. 18, 321–331 (2008). [DOI] [PubMed] [Google Scholar]
- Schiller J., Schiller Y., Stuart G. & Sakmann B. Calcium action potentials restricted to distal apical dendrites of rat neocortical pyramidal neurons. J. Physiol. 505, 605–616 (1997). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larkum M. E., Kaiser K. M. M. & Sakmann B. Calcium electrogenesis in distal apical dendrites of layer 5 pyramidal cells at a critical frequency of back-propagating action potentials. Proc. Natl. Acad. Sci. USA 96, 14600–14604 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larkum M. E., Zhu J. J. & Sakmann B. A new cellular mechanism for coupling inputs arriving at different cortical layers. Nature 398, 338–341 (1999). [DOI] [PubMed] [Google Scholar]
- Katz Y. et al. Synapse distribution suggests a two-stage model of dendritic integration in CA1 pyramidal neurons. Neuron 63, 171–7 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gasparini S. & Magee J. C. State-dependent dendritic computation in hippocampal CA1 pyramidal neurons. J. Neurosci. 26, 2088–2100 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gasparini S., Migliore M. & Magee J. C. On the initiation and propagation of dendritic spikes in CA1 pyramidal neurons. J. Neurosci. 24, 11046–11056 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chua Y. & Morrison A. Effects of calcium spikes in the layer 5 pyramidal neuron on coincidence detection and activity propagation. Front. Comput. Neurosci. 10, 76 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shai A., Anastassiou C., Larkum M. & Koch C. Physiology of layer 5 pyramidal neurons in mouse primary visual cortex: coincidence detection through bursting. PLoS Comput. Biol. 11, e1004090 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larkum M. A cellular mechanism for cortical associations: an organizing principle for the cerebral cortex. Trends Neurosci. 36, 141–151 (2013). [DOI] [PubMed] [Google Scholar]
- Grienberger C., Chen X. & Konnerth A. NMDA receptor-dependent multidendrite Ca2+ spikes required for hippocampal burst firing in vivo. Neuron 81, 1274–81 (2014). [DOI] [PubMed] [Google Scholar]
- Larkum M. E., Zhu J. J. & Sakmann B. Dendritic mechanisms underlying the coupling of the dendritic with the axonal action potential initiation zone of adult rat layer 5 pyramidal neurons. J. Physiol. 533, 447–466 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larkum M. E., Senn W. & Lüscher H. R. Top-down dendritic input increases the gain of layer 5 pyramidal neurons. Cereb. Cortex 14, 1059–1070 (2004). [DOI] [PubMed] [Google Scholar]
- Hage T. A. & Khaliq Z. M. Tonic firing rate controls dendritic Ca2+ signaling and synaptic gain in substantia nigra dopamine neurons. J. Neurosci. 35, 5823–36 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larkum M. E., Nevian T., Sandler M., Polsky A. & Schiller J. Synaptic integration in tuft dendrites of layer 5 pyramidal neurons: a new unifying principle. Science 325, 756–60 (2009). [DOI] [PubMed] [Google Scholar]
- Polsky A., Mel B. W. & Schiller J. Computational subunits in thin dendrites of pyramidal cells. Nat. Neurosci. 7, 621–627 (2004). [DOI] [PubMed] [Google Scholar]
- Palmer L. M. et al. The cellular basis of GABA(B)-mediated interhemispheric inhibition. Science 335, 989–93 (2012). [DOI] [PubMed] [Google Scholar]
- Larkum M. E. & Zhu J. J. Signaling of layer 1 and whisker evoked Ca2+ and Na+ action potentials in distal and terminal dendrites of rat neocortical pyramidal neurons in vitro and in vivo. J. Neurosci. 22, 6991–7005 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams S. R. & Stuart G. J. Mechanisms and consequences of action potential burst firing in rat neocortical pyramidal neurons. J. Physiol. 521, 467–482 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hay E. & Segev I. Dendritic excitability and gain control in recurrent cortical microcircuits. Cereb. Cortex 25, 3561–71 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zomorrodi R., Kröger H. & Timofeev I. Modeling thalamocortical cell: impact of Ca2+ channel distribution and cell geometry on firing pattern. Front. Comput. Neurosci. 2, 5 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siegel M., Körding K. P. & König P. Integrating top-down and bottom-up sensory processing by somato-dendritic interactions. J. Comput. Neurosci. 8, 161–73 (2000). [DOI] [PubMed] [Google Scholar]
- Miyasho T. et al. Low-threshold potassium channels and a low-threshold calcium channel regulate Ca spike firing in the dendrites of cerebellar Purkinje neurons: a modeling study. Brain Res. 891, 106–15 (2001). [DOI] [PubMed] [Google Scholar]
- Traub R. D., Wong R. K., Miles R. & Michelson H. A model of a CA3 hippocampal pyramidal neuron incorporating voltage-clamp data on intrinsic conductances. J. Neurophysiol. 66, 635–50 (1991). [DOI] [PubMed] [Google Scholar]
- Ferguson K. A. & Campbell S. A. A two compartment model of a CA1 pyramidal neuron. Canadian Applied Mathematics Quarterly 17, 293–307 (2009). [Google Scholar]
- Pinsky P. F. & Rinzel J. Intrinsic and network rhythmogenesis in a reduced Traub model for CA3 neurons. J. Comput. Neurosci. 1, 39–60 (1994). [DOI] [PubMed] [Google Scholar]
- Mainen Z. F. & Sejnowski T. J. Influence of dendritic structure on firing pattern in model neocortical neurons. Nature 382, 363–6 (1996). [DOI] [PubMed] [Google Scholar]
- Naud R., Bathellier B. & Gerstner W. Spike-timing prediction in cortical neurons with active dendrites. Front. Comput. Neurosci. 8, 90 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ilan L. B., Gidon A. & Segev I. Interregional synaptic competition in neurons with multiple STDP-inducing signals. J. Neurophysiol. 105, 989–98 (2011). [DOI] [PubMed] [Google Scholar]
- Wang X. J. Calcium coding and adaptive temporal computation in cortical pyramidal neurons. J. Neurophysiol. 79, 1549–66 (1998). [DOI] [PubMed] [Google Scholar]
- Brette R. What is the most realistic single-compartment model of spike initiation? PLoS Comput. Biol. 11, e1004114 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yi G. S. et al. Exploring how extracellular electric field modulates neuron activity through dynamical analysis of a two-compartment neuron model. J. Comput. Neurosci. 36, 383–99 (2014). [DOI] [PubMed] [Google Scholar]
- Yi G. S. et al. Neuronal spike initiation modulated by extracellular electric fields. PLoS One 9, e97481 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yi G. S. et al. Spike-frequency adaptation of a two-compartment neuron modulated by extracellular electric fields. Biol. Cybern. 109, 287–306 (2015). [DOI] [PubMed] [Google Scholar]
- Izhikevich E. M. Dynamical systems in neuroscience: the geometry of excitability and bursting(The MIT Press, London, 2007). [Google Scholar]
- Nadkarni S. & Jung P. Dressed neurons: modeling neural-glial interactions. Phys. Biol. 1, 35–41 (2004). [DOI] [PubMed] [Google Scholar]
- Ma J. & Tang J. A review for dynamics of collective behaviors of network of neurons. Sci. China Technol. Sci. 58, 2038–20045 (2015). [Google Scholar]
- Goldberg M., De Pittà M., Volman V., Berry H. & Ben-Jacob E. Nonlinear gap junctions enable long-distance propagation of pulsating calcium waves in astrocyte networks. PLoS Comput. Biol. 6, e1000909 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li J. et al. Dynamic transition of neuronal firing induced by abnormal astrocytic glutamate oscillation. Sci. Rep. 6, 32343 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dayan P. & Abbott L. F. Theoretical neuroscience: computational and mathematical modeling of neural systems(The MIT Press, London, 2005). [Google Scholar]
- Ermentrout B. Simulating, analyzing, and animating dynamical systems: a guide to Xppaut for researchers and students(SIAM, Philadelphia, 2002). [Google Scholar]