A Model for Designing Adaptive Laboratory Evolution Experiments

ABSTRACT

The occurrence of mutations is a cornerstone of the evolutionary theory of adaptation, capitalizing on the rare chance that a mutation confers a fitness benefit. Natural selection is increasingly being leveraged in laboratory settings for industrial and basic science applications. Despite increasing deployment, there are no standardized procedures available for designing and performing adaptive laboratory evolution (ALE) experiments. Thus, there is a need to optimize the experimental design, specifically for determining when to consider an experiment complete and for balancing outcomes with available resources (i.e., laboratory supplies, personnel, and time). To design and to better understand ALE experiments, a simulator, ALEsim, was developed, validated, and applied to the optimization of ALE experiments. The effects of various passage sizes were experimentally determined and subsequently evaluated with ALEsim, to explain differences in experimental outcomes. Furthermore, a beneficial mutation rate of 10^−6.9 to 10^−8.4 mutations per cell division was derived. A retrospective analysis of ALE experiments revealed that passage sizes typically employed in serial passage batch culture ALE experiments led to inefficient production and fixation of beneficial mutations. ALEsim and the results described here will aid in the design of ALE experiments to fit the exact needs of a project while taking into account the resources required and will lower the barriers to entry for this experimental technique.

IMPORTANCE ALE is a widely used scientific technique to increase scientific understanding, as well as to create industrially relevant organisms. The manner in which ALE experiments are conducted is highly manual and uniform, with little optimization for efficiency. Such inefficiencies result in suboptimal experiments that can take multiple months to complete. With the availability of automation and computer simulations, we can now perform these experiments in an optimized fashion and can design experiments to generate greater fitness in an accelerated time frame, thereby pushing the limits of what adaptive laboratory evolution can achieve.

INTRODUCTION

Adaptive laboratory evolution (ALE) has been performed in vitro for decades, and the field is expanding. ALE involves subjecting a population of organisms to a given environment, in the laboratory, and allowing natural selection to increase the overall fitness of the population. In laboratory settings, this is typically performed with organisms possessing short generation times. The basic principles governing ALE experiments are easily understood across a breadth of disciplines, which has led to its adoption in many laboratories (1, 2). The recent growth in the use of ALE can be attributed to the ease of access and decreasing costs of genome sequencing (3–5). Decreasing sequencing costs have led to increased investigation of genomic, transcriptomic, and additional data types over the course of evolution (5). While the analysis of ALE experiments has grown, the manner in which ALE experiments themselves are performed has remained relatively ad hoc. The most commonly employed techniques are chemostat adaptation and serially passaged batch culture adaptation, with batch culture adaptation being more popular because it is easily expanded and does not require complex machinery (3, 6).

A primary attribute of any ALE experiment is the selection pressure imposed on the culture. The selection pressure (i.e., exponential growth, biomass yield, stationary phase, or lag phase) is responsible for the outcome of the evolution study (4, 7–10). For example, in a 24-h serially passaged batch culture ALE experiment with fast-growing bacteria, the culture is subjected to alternating environments of feast and famine. There are excess nutrients at the beginning of each batch but, inevitably, the nutrients are consumed within 24 h and a stationary phase is reached. Because of these alternating environmental conditions, the selection pressure is complex and fitness is achieved through various methods (e.g., stationary-phase fitness, lag phase duration, and growth rate all contribute) (9). This complexity often confounds the analysis, depending on the application. To decrease the complexity, the cells can be kept in one phase (e.g., the exponential phase) to mitigate most of the alternating selection and to focus selection specifically on fitness gains through growth rates. In such cases, fitness can be treated as interchangeable with the growth rate. The desired outcome of the experiment would dictate the ideal selection pressure to be imposed and thereby the experimental design, but the difference between the two designs is nontrivial.

There are several parameters that affect the outcome of a serially passaged batch culture ALE experiment. A primary parameter involved is the passage size (11–13). Specifically, passage size determines how much of the population is allowed to propagate to each subsequent batch culture. If a beneficial mutation occurs but is lost when the bottleneck is imposed, then the rate of evolution can be slowed or even halted. Since smaller passage sizes can decrease the rate of evolution, it is often easier to perform a serially passaged batch culture ALE under alternating environments of feast and famine when a change in passage size affects only the duration of the growth and stationary phases. If the application requires exponential-phase passaging, however, a change in passage size also changes the time when the culture must be passaged. Because of this, the passage size is often dictated by an individual's schedule. Typically, the time between passaging can be no shorter than ∼12 h. Consequently, as the culture adapts and begins to grow more quickly, the passage size must be decreased. As an example, a previous study adapting Escherichia coli to glycerol in 250-ml batches started with a passage size of approximately 100 μl and was using a passage size of less than 0.1 μl by the end of the experiment (14). A more in-depth retrospective analysis revealed similar trends when passage amounts were significantly decreased (14–18). In those studies, the reduction in the population size, or bottleneck (i.e., passage size), became so significant that the calculated number of cells being passaged was on the order of 10 or even occasionally 1. The chance of capturing a beneficial mutation in a reasonable time frame when passaging only tens of cells from a culture of millions is practically null; at that point, continuing the experiment is futile. The question then becomes, at what point is the passage size too low?

The passage size can have a large impact on the trajectory of an ALE experiment. This can be seen in a comparison of two studies that evolved wild-type E. coli K-12 MG1655 on M9 glucose minimal medium (7, 18). One study (7) used a consistent passage size of 800 μl from 25-ml batches on an automated platform. The second study (18) was performed “by hand” and had widely varying passage sizes that were considerably smaller than those in the automated study. The outcomes of the ALE experiments were quite distinct. The final growth rates achieved were 1.00 ± 0.24 h⁻¹ and 0.79 ± 0.01 h⁻¹ in the consistent- and variable-passage-size studies, respectively. The apparent lack of fitness achieved in the variable-passage study was due not to a lack of available beneficial mutations (as the same strains and culture conditions were used) but rather to an experimental design that was insufficient to find and to fix the mutations in a reasonable amount of time. Understanding why these two outcomes differed is imperative for the efficient design of ALE experiments.

Theoretical studies have looked at the effect of passage size on serially passaged batch culture adaptation and have resulted in various predictions of an ideal passage size, depending on the model used (19, 20). The ideal passage sizes calculated are ideal from a mathematical standpoint. This essentially gives the best chance for various mutations of different selective advantages to fix in a population. The ideal passage sizes calculated in these studies are relatively large (13.5% and 20%) (19, 20). As mentioned previously, a larger passage size necessitates an increase in resources. More specifically, the resources required increase exponentially with passage size, while the gains slowly diminish. This work thus focuses on examining the diminishing returns in the context of the desired result and the resources available. We set out to examine the impact of the key ALE parameter, namely, passage size. To address this, we created an in silico evolutionary model that simulates the dynamics of capturing and fixing beneficial mutations in the context of an exponentially passaged batch culture ALE experiment. After building the model, we parameterized it by using a combination of 30 independent ALE experiments with E. coli on glycerol minimal medium across five different passage sizes (i.e., 10%, 1%, 0.1%, 0.01%, and 0.001%). Using the parameterized model, we investigated the biological consequences of changing passage sizes and the closeness to optimal conditions of a given experiment. With this knowledge, an experiment can be designed to fit the desired outcome, giving consideration to the resources required to achieve it and the feasibility of performing such an experiment.

RESULTS

Modeling of the ALE process.

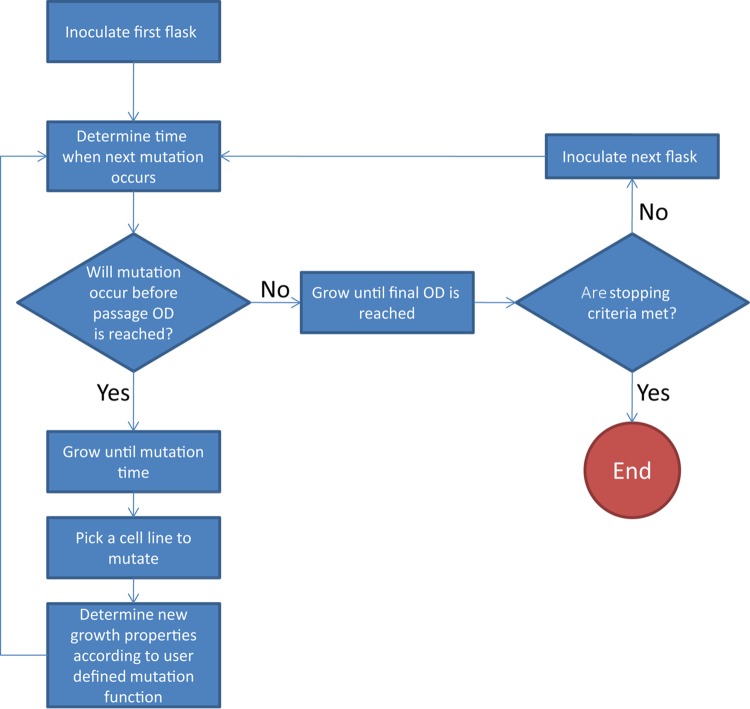
ALEsim is a model built on the basic principles of exponential growth, in order to understand the dynamics of ALE. The scope of ALEsim is to predict the observed growth rate for each batch culture of an ALE experiment while allowing individual cells to change their growth rates when dividing (i.e., a proxy for receiving a beneficial mutation). This preferentially finds only beneficial mutations that are fixed. It is likely that other beneficially mutations are not observed, due to clonal interference. The observed population growth rate is different from a clonal growth rate, in that each batch culture of an ALE experiment involves a population of multiple clones with different growth rates. Figure 1 provides the workflow of the modeling process, and the full details for ALEsim are provided in the supplemental material. Each in silico experiment begins with clonal inoculation of a strain with a given growth rate. A population of mixed phenotypes can be used in this framework, but here the starting population is assumed to be isogenic, with the same phenotypic behavior. The organism is allowed to replicate according to an exponential growth function. During each cell division event, there is a probability that the organism will mutate and start a new lineage with a mutated growth rate. This new lineage is allowed to grow alongside the parent strain according to an exponential growth function but with its mutated growth rate. The new lineage is allowed to continue mutating in the simulation.

FIG 1.

ALEsim flow chart. A workflow outlining the logical steps the simulator takes when performing a single simulated ALE experiment is presented. Due to the stochastic nature of ALE experiments (in vivo and in silico), multiple experiments are averaged together to identify general trends.

Mutated growth rates in ALEsim must be constrained to remain biologically meaningful, i.e., growth rates that are of magnitudes that remain plausible. These rates are determined empirically by the user, as performed here from the parameterization experiment (see below). The growth rates can be constrained to allow various types of epistasis. For example, if two distinct growth rates are allowed, then there is a possibility that a single cell line could mutate twice and receive both mutations. ALEsim employs the flexibility to define the type of epistasis between the two mutations, if any epistasis at all is to occur. Similarly, an order for the accumulated mutations can be set, as certain mutations can be beneficial only in the presence of a preexisting mutation (i.e., epistasis can be modeled). As the population of cells continues to replicate and to mutate, the total cell count naturally increases. When the cell count reaches a given threshold, a simple random sample of cells is used to inoculate the next batch culture. The threshold corresponds to a target cell count at which to passage the cells to the next batch culture. The number of cells taken is determined by the passage size, which is a percentage of the total culture volume. After this sample is computed, a new batch culture is started with the chosen cells and corresponding growth rates. Figure 2 provides the key parameters of the model.

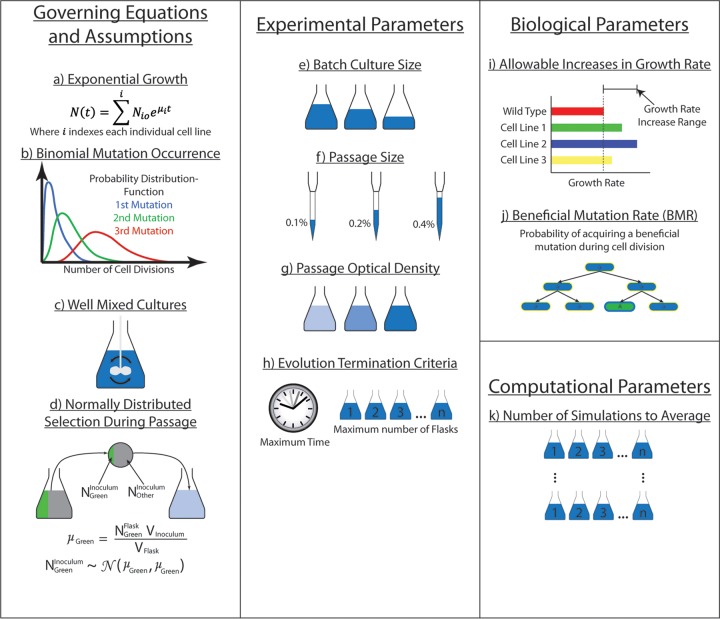
FIG 2.

Governing equations, assumptions, and parameters for ALEsim. (a) Microbe growth occurs according to an exponential growth curve, where μ is the growth rate, t is the time elapsed, N₀ is the initial cell count at t = 0, and N(t) is the cell count at the given time t. No lag phase or stationary phase is modeled. The total cell count, N(t), is determined by summation of exponential growth curves for all individual cell lines. (b) Favorable mutations occur during cell growth according to a binomial distribution, where each cell division represents one Bernoulli trial with a probability of success equal to the beneficial mutation rate (BMR). (c) Each flask is modeled as a completely homogeneous culture. (d) The number of cells represented for each cell line in each inoculum (N_Green^Inoculum and N_Other^Inoculum) is randomly chosen according to a normal distribution with a mean and variance equal to the number of cells represented in the flask (N_Green^Flask) times the ratio of the flask volume (V_flask) to the inoculum volume (V_inoculum). (e to g) The volume of medium per flask (e), the inoculum volume (f), and the passage optical density (g) can be altered. (h) The simulated ALE experiment can be stopped after a specified amount of time or a maximum number of flasks. (i) Based on the relative growth rate increases seen in ALE experiments, a range of allowable growth rate increases is determined. (j) Based on matching the evolution trajectory (plot of growth rate versus flask number) with various beneficial mutation rates (BMRs), the probability of a favorable mutation is obtained. (k) Since each ALE is based on randomly generated mutations, multiple ALE simulations are averaged together to obtain repeatable results from the same parameters. The number of simulations is controlled by the user.

With the use of the basic principles of microbial growth and a brute force computational approach, many of the fundamental attributes of natural selection are intrinsically contained in the simulation, including clonal interference, which is pervasive in asexual evolution. ALEsim can be used to model a system in which two local maxima are possible but the greater maximum can be found only by first acquiring a mutation that is initially suboptimal, compared to other possible single beneficial mutations (21). How to achieve this is shown in the model documentation (see the supplemental material). The experimental parameters can be modulated to potentially find an experiment design that would find the desired optimum or both optima.

Given the stochastic nature of many steps in the model, the results are nondeterministic. Stochasticity is incorporated into the model in three ways, i.e., (i) when a cell mutates its growth rate, (ii) to what growth rate a cell mutates, and (iii) what cell sample is propagated to a subsequent batch culture. The simulation is then run multiple times, to capture the dynamics of the stochasticity (22).

For a simulation using the developed model to be biologically meaningful, three types of parameter sets must be determined. The first set of parameters is experimental, i.e., batch culture size, passage size, passage optical density (OD) (or cell count), and experiment length. These parameters can be set on the basis of the desired experimental setup (23). The second set of parameters is statistical, i.e., random number seed and number of identical experiments to run. The random number seed is set by the native random number generator. The number of parallel simulations to run is determined by the statistical power needed. Depending on the magnitudes and complexities of the parameters set, the numbers of simulations can vary drastically. For the results shown here, 500 simulations were computed unless otherwise stated. It was found that, after 500 simulations, there was no appreciable difference in the means or spread of the distribution of results calculated, when combined with another set of 500. The third set of parameters is biological, i.e., beneficial mutation rate (BMR) and allowed increases in growth rate. These parameters are defined in the models and can be constrained by any method that can be expressed programmatically, whether they are randomly decided within a meaningful range or set to distinct values. This set of parameters must be derived experimentally. Intuitively, these parameters can be different for different strains and conditions and can even change during the course of a single experiment (24, 25). As long as the values determined are biologically meaningful, generalizations about the ALE process can be concluded.

Alternative models of evolution and adaption have been developed to understand the dynamics of evolution. These types of mathematical models capture various aspects of adaptation, including selection, drift, and clonal interference (26–28). Classically, this has been a target of the field of population genetics (29–31). An expansion of the Fisher model was developed by Wahl and Zhu and conceptually relates to ALEsim in that it targets the question of passage sizes (32). However, ALEsim deviates from the classic mathematical approach and uses an in silico organism that can replicate, mutate, and evolve. Simulations here are carried out by brute force, with the cells being allowed to grow under the conditions laid out by the user. The advantage of such a method is that the experimental and biological parameters can be strictly controlled over the course of an experiment. The resulting simulation is able to more closely mimic the conditions of an actual laboratory evolution experiment in its entirety, where parameters are not always constant throughout. This approach differs from the use of a digital organism in that it is an attempt to model specific biology instead of general evolutionary dynamics, which allows for direct modeling of the ALE experiment as it would be performed in a laboratory (33).

Parameterization of ALEsim by evolving E. coli on glycerol minimal medium.

The two biological parameters, i.e., the beneficial mutation rate and allowed increases in growth rate, were determined by using 30 independent cultures of Escherichia coli K-12 MG1655 evolved in 15 ml of 0.2% glycerol M9 minimal medium until a stable growth rate was observed in most experiments (38 days). One experiment lasted only 23 days after it was restarted, due to contamination. The 30 experiments were separated into five groups of six passage sizes, and each group was evolved under identical conditions except for the passage size. The passage sizes used were 10%, 1%, 0.1%, 0.01%, and 0.001% of the culture size (15 ml). The growth rate in each experiment was monitored over the course of the experiment by using optical density measurements as a proxy for cell counts (Fig. 3). Fitness-related details can be found in the supplemental material.

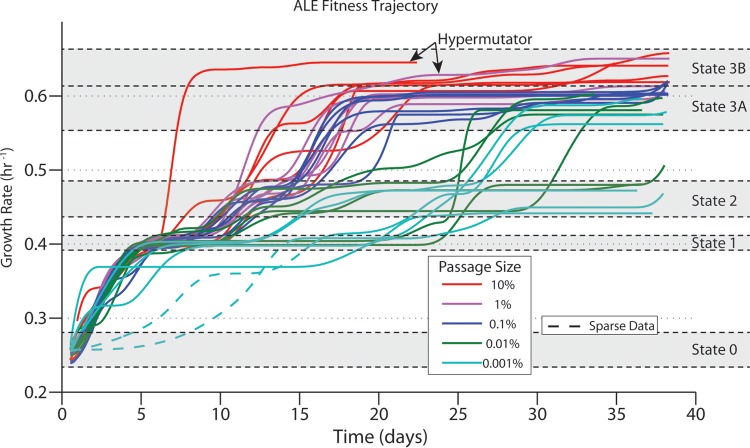
FIG 3.

Fitness trajectories of E. coli evolved on glycerol. The absolute growth rates of independently evolved cultures of E. coli, as fitted by a cubic spline for all ALE experiments, are indicated for different passage sizes. Dashed lines represent regions where the spline fit is based on sparse data and therefore is not considered accurate. The small upturn in growth rates at the endpoint is an artifact of the spline interpolation and is ignored in determinations of endpoint growth rates. All except five ALE experiments reached fitness state 3. The rates at which the final growth rate was achieved varied. The hypermutating strain with a passage size of 10% reached state 3 significantly faster than all others (it possessed a mutation in mutY). The purple hypermutating strain was identified as a potential hypermutating strain based on the number of mutations fixed (P = 0.003; false discovery rate, 0.087) and the presence of a frameshift insertion in mutL.

Allowed increases in growth rates were determined by identifying jumps in growth rates from the fitness trajectories. A spline was fit to the growth rate of each experiment, and significant increases in growth rates were identified as discussed previously (7). The resulting jumps in growth rates showed that the plateaus in growth occurred at specific values (Fig. 3 and 4); these plateaus were identified as states 1, 2, 3A, and 3B. State 3 was split into two substates since there was a significant difference between state 3A and state 3B (Wilcoxon rank test, P < 0.01); however, there was no identifiable increase in growth rate or gap between the states that would characterize this transition. The gap was most likely obscured, since the difference between the growth rates was fairly small and noise in the measurements could bleed into any gap that might exist. Figure 4 groups the jumps in fitness observed by the transition between states. Contrary to the conclusion of other ALE experiments, the jumps in fitness did not occur in order of the largest magnitude to the smallest. This study yielded an allowed increase in growth rates that could be used to constrain ALEsim. In simulations run here, the allowed growth rates were set to the mean of the range of each state.

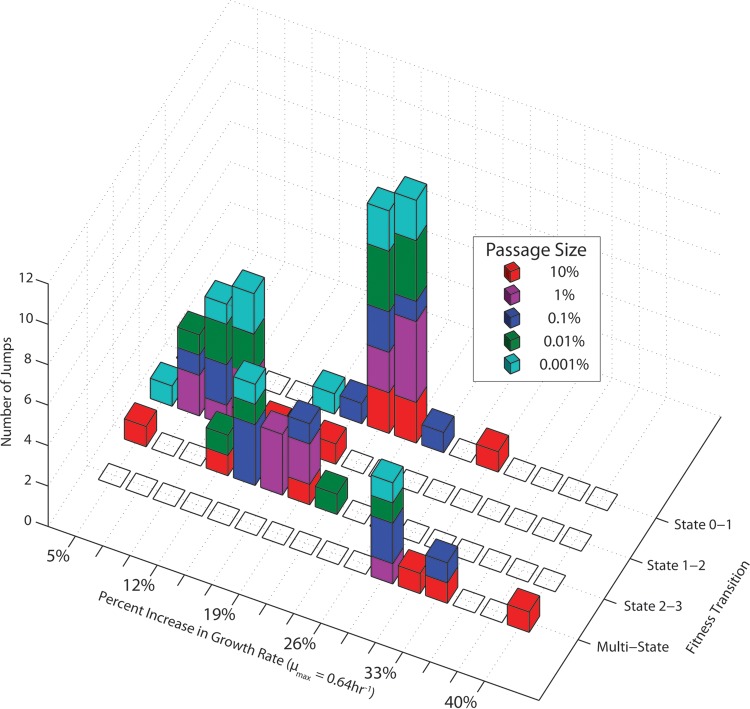
FIG 4.

Distribution of fitness increases in glycerol ALE experiments. A histogram of the normalized increases in growth rate (μ_max = 0.64 h⁻¹) attributed to each jump for the different experiments is presented. The fitness increases were categorized according to which state transition was made. The different passage sizes (indicated by different colors) did not show any significant variance in the ability to fix distinct increases in growth rates. A few small jumps not shown were small observed increases in fitness that did not jump between any of the identified states.

The BMR can be calculated by fitting ALEsim to the distribution of the end states. Passage sizes of 10% to 0.1% did not show any appreciable variation between states; therefore, only the experiments with passage sizes of 0.01% and 0.001% were used for fitting. ALEsim was fit by performing simulations that allowed only single jumps from one state to another. Multistate jumps and two sequential jumps were not allowed. This simplification skews the BMR calculations to include only beneficial mutations that were fixed in the population. There is a potential that other beneficial mutations are possible but were not observed due to either clonal interference or genetic drift (34). As observed in the fitness trajectories for passage sizes of 0.01% and 0.001%, not all experiments were able to make jumps to occupy all of the states. For instance, with a passage size of 0.01%, only 4 of 6 experiments were able to make the transition from state 2 to state 3 by the end of the experiment. In simulations, the same distribution among the various end states is observed. The distribution observed in simulations is highly dependent on the supply of beneficial mutations captured by the BMR parameter. Thus, the BMR can be fit to yield the same distribution across states as observed experimentally. The BMR was computed using transitions both from state 2 to state 3 and from state 1 to state 2. Since all experiments made the transition from state 1 to state 2, the distribution was used at the day 20 time when a distribution existed. The 95% confidence interval for the BMR was calculated by fitting the BMR to the 95% confidence interval of the experimental distribution of states. The results yielded a BMR of 10^−6.9 to 10^−8.4 mutations per cell division. The confidence interval was determined by a maximum likelihood estimate, as implemented in the binofit function in MATLAB.

Retrospective validation of ALEsim.

ALEsim and the derived parameters (beneficial mutation rate and allowed increases in growth rate) were analyzed by using two previously performed ALE experiments on glucose (7, 18) and a legacy experiment on glycerol (14). The two glucose experiments yielded disparate final growth rates despite identical strains and media (E. coli K-12 MG1655 in M9 glucose minimal medium), i.e., 0.79 ± 0.01 with 3 replicates and 1.00 ± 0.02 with 6 replicates in the studies by Charusanti et al. (18) and LaCroix et al. (7), respectively. The only differences between the experiments were three experimental parameters, namely, batch culture volumes (250 ml versus 25 ml), ODs when passaged (variable OD versus OD at 600 nm [OD₆₀₀] of 1.2), and passage sizes (variable versus 800 μl). ALEsim was constrained to allow only the jumps in growth rates observed in those studies, and then it simulated the expected fitness trajectories for the two experimental parameters. The only differences explicitly defined in ALEsim were the different batch culture volumes, passage ODs, and passage volumes. The results showed that the difference in the final growth rates achieved could be sufficiently explained by the differences in those parameters alone (Fig. 5). Furthermore, when a legacy data set for evolving E. coli on glycerol minimal medium was simulated, ALEsim was able to successfully predict that all experiments (n = 4) should reach fitness state 3 for the given experimental parameters, as reported in the original study (14). The largely different outcomes in fitness (i.e., no fitness jumps versus a significant increase) on glucose and the consistent prediction of fitness with a legacy glycerol data set further highlight the importance of properly designing an experiment and validate ALEsim and its parameterization.

FIG 5.

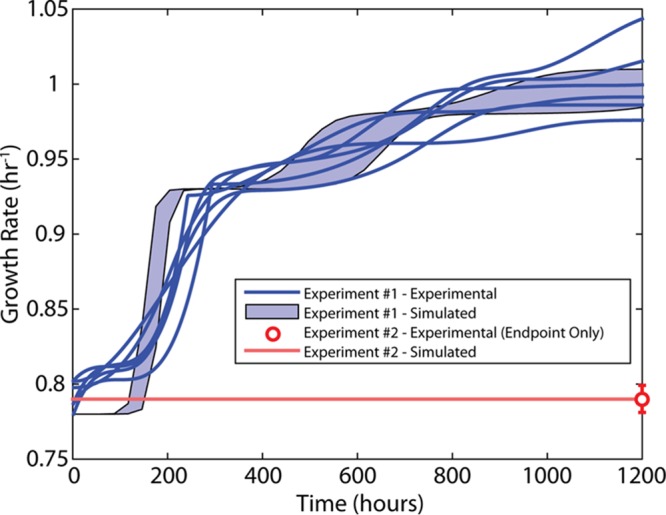
Simulated versus experimental results with large and small passage sizes. Two ALE experiments with E. coli MG1655 in M9 glucose minimal medium were simulated using ALEsim. The strain and medium conditions were identical in the two experiments. The only differences were in the culture volume (25 ml versus 250 ml), the optical density when passaged (variable versus OD₆₀₀ of 1.2), and the passage volume (variable versus 800 μl) (experiment 1 had the 25-ml culture volume, OD₆₀₀ of 1.2, and 800-μl passage volume, while experiment 2 had the 250-ml culture volume, variable OD₆₀₀, and variable passage volume). The variable nature of the optical density when passaged and the passage size in the latter experiment was a consequence of manually passaging the culture each day. The former experiment employed an automated system for monitoring and passaging the culture, to maintain consistency. Although the same strain and conditions were used, the final fitness levels achieved in the two experiments were quite different. ALEsim was used to simulate these experiments, with the only differences being the three aforementioned parameters. The ALEsim results showed that the differences in these parameters were sufficient to explain why the final growth rates achieved were different, further highlighting the importance of choosing the parameters properly. The simulated results are represented by a 95% confidence interval. The confidence interval for experiment 2 is too small to be visible.

ALEsim applications.

Simulations of ALE experiments with the derived beneficial mutation rate and fitness states can enable statements to be made about optimality. The time required to see a given increase in fitness was simulated for a range of increases in growth rates over a range of passage sizes (Fig. 6). The results show the average time needed to see a measurable change in growth rate due to a beneficial mutation for a range of passage sizes. Figure 6 was derived for growth rate increases that occurred from a single mutational event. Based on the passage size and length of time with no increase in growth rate, a conclusion can be drawn about how close a population is to reaching another state of increased fitness. For example, if a given evolution experiment has achieved a certain growth rate, μ, and has not shown an increase in growth rate for 13 days with a passage size of 0.1%, then there is no likely increase in growth rate available that is greater than 0.10 h⁻¹ from a single mutational event.

FIG 6.

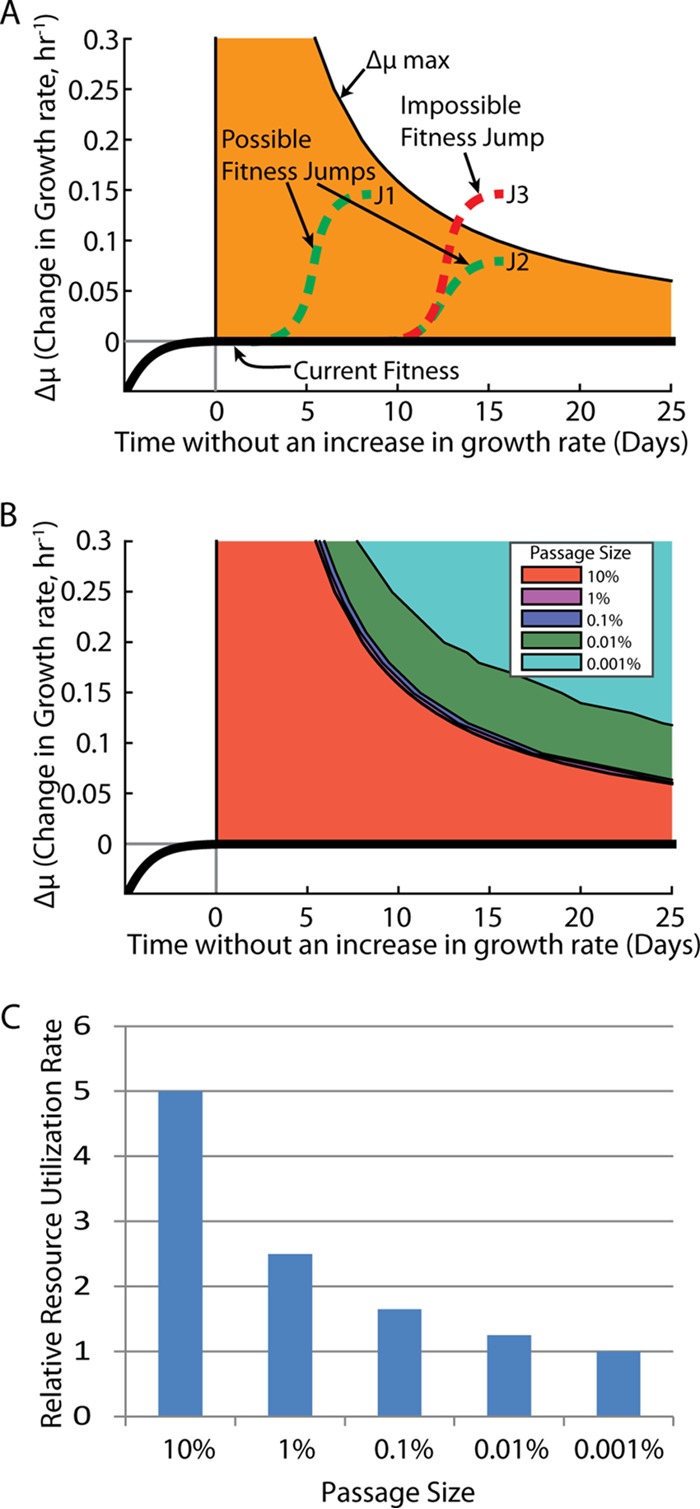
Upper bound on possible jumps in growth rates. (A) Upper bounds on possible jumps in growth rates are shown. At a given point in time, a jump that reaches above the upper bound from a single mutation is statistically infeasible (95% confidence limit), whereas jumps that stay below the line are possible. (B) The upper bounds on jumps for different passage sizes are shown. These experiments were simulated with parameters that matched the experimental parameters used. Increasing the passage size can have a significant impact on the upper bound. Consequently, the time required to eliminate jumps of certain magnitudes can be much longer. As the passage size increases, however, there comes a point at which the returns begin to diminish, such that passage sizes between 0.1% and 10% do not show a large difference in the time required to find a given jump. (C) Relative amounts of resources needed to perform an ALE experiment were normalized to the smallest passage size. As the passage size is increased, the resource usage begins to increase greatly.

Increasing the passage size increases the probability of capturing a beneficial mutation; however, this also leads to an increase in the resources needed to sustain the experiment (Fig. 6). For example, if an ALE experiment with a passage size of 0.1% were being passaged twice a day (every 12 h), then the same experiment with a passage size of 10% would need to be passaged 6 times a day (every 4 h). The magnitude of resources needed to maintain an experiment tends to scale with each batch. Thus, the more batches that need to be processed, the more medium, pipette tips, culture vessels, and labor costs are required. A single person can feasibly perform an experiment with passaging every 12 h, whereas passaging every 4 h would require coordinated efforts by multiple persons or an automated platform. Therefore, understanding what is gained with the larger passage size is important before committing to such a large expenditure of resources. ALEsim can quantify the gains or losses achievable with different passage sizes, to help identify the ideal experimental setup (Fig. 6).

Mutation frequency analysis by passage size.

Clones from the endpoint populations of each independent experiment were isolated and resequenced. Two clones showed hypermutating tendencies, which were identified by the number of mutations (P < 0.01) and the presence of a mutation in mutY or mutL. Experiments with larger passage sizes demonstrated increases in the number of mutations found. Therefore, mutated alleles were grouped by passage size. Clones isolated from experiments with larger passage sizes, on average, had more alleles being selected (Fig. 7). Of all mutations identified, those in glpK were specifically tracked. Mutations in glpK were shown previously to be causal (with a significant impact on fitness) and ubiquitous, with this allele mutating more than any other alleles under glycerol growth conditions (14). Thus, glpK is a good indicator of how effective the various passage sizes are at fixing beneficial mutations, and there is a positive relationship between the fixing of glpK mutations and the passage size until saturation is reached. With the passage size decreased to the lowest value (0.001%), the observed fraction that was fixed was only 0.33 (2/6 experiments).

FIG 7.

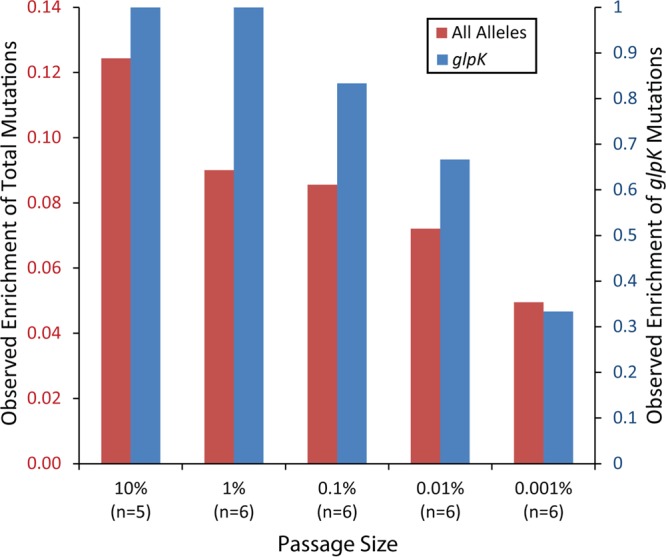
Genetic analysis by passage size. The bar chart presents the observed fraction of mutations at a given passage volume. As a general trend, the larger the passage size is, the greater the probability is of a mutation in a given allele being fixed in the population. Data for a key mutation in the glpK gene and for all mutations are indicated. The ordinal rank of passage size was compared to the observed fraction of mutations using a Wilcoxon rank test, which resulted in P values of 0.008 and 0.024 for all mutations and glpK mutations, respectively.

DISCUSSION

The conceptual purpose of an ALE experiment is to move an organism toward a more optimal (fit) state in the presence of selection pressure. Absolute optimality is difficult to define, if that is even possible. It has been shown that, even for laboratory evolution, there is still room for evolution after 50,000 generations (35). The continual ability of organisms to evolve and to innovate makes it difficult to analyze the results of an ALE experiment in the context of optimality. What is immediately apparent is that there are diminishing returns. As an ALE experiment progresses, the increase in growth rate or fitness tends to decrease in magnitude (1, 36–40). The smaller increases take longer times to occur and to become fixed in the population (see the supplemental material). Given this property and the desire to understand and to leverage the ALE process, ALEsim was built and validated by performing a control experiment. ALEsim was first parameterized with a set of control experiments using different passage sizes. Parameterization revealed a beneficial mutation rate of 10^−6.9 to 10^−8.4 mutations per cell division, consistent with previously reported values and distinct fitness states (24, 25). Validation was then carried out using additional legacy experiments, and ALEsim proved sufficient to explain the differences in observed experimental outcomes (i.e., growth rates) based on the parameters employed in each study (i.e., passage size, passage OD, and culture volume) (Fig. 5). Lastly, ALEsim was applied to quantify tradeoffs in experimental design considerations for desired outcomes and was used to demonstrate how it can be leveraged for determination of the key aspect of experiment termination.

The ability to design and to optimize ALE experiments is available with the ALEsim computational framework. Given a certain amount of resources, ALEsim can calculate how best to deploy them at different stages of an experiment to shorten project timelines and to achieve desired outputs. For example, near the beginning of the ALE experiments, the increases in growth rates found are typically quite large. Because of this, a large passage size does not have an additional benefit. This was evident in the experiment performed here, in that passage sizes of 0.1%, 1%, and 10% mostly reached states 1, 2, and 3A at about the same time (Fig. 3). For planning future ALE experiments, the added resource usage needed to maintain an experiment with a 10% passage size does not appear to be justified. However, the added benefits become apparent when the transition from state 3A to state 3B is examined. It could then be suggested that, if the goal is to get as close to the absolute optimal state as reasonably possible, then the added resources needed for an experiment with a 10% passage size would need to be maintained only after initial large increases in growth rates or fitness are found. This would not eliminate the difficulty of maintaining such an experiment but would at least reduce the time during which the experiment would need to be run with such a high resource “burn” rate. With ALEsim, these types of resource/fitness trade-off analyses can be calculated and should be leveraged in experimental design. The approach of dynamic resource allocation allows project optimization typical of engineering process design.

Knowing the distance to optimality can aid in determining when to terminate an ALE experiment. The typical method of determining when to stop an ALE experiment is to determine subjectively that no more increases in fitness are being observed. However, this approach of waiting to observe a plateau in fitness can be artificial with small passage sizes. An example of how this approach can be misleading is the observation that passage sizes of 0.1% and 1% showed no increases in growth rates for at least 15 days after reaching state 3A (Fig. 3). However, given that slight increases in growth rates beyond state 3A to state 3B with a passage size of 10% were observed, it can be concluded that state 3A is not the optimal state. Thus, if only a 1% passage size was used, then the experiment could be terminated before finding state 3B. Furthermore, it would be incorrect to compare experiments with a 10% passage size versus a 1% passage size without understanding the context of the effects of the different passage sizes. Perhaps the best example of this is provided through the analysis of legacy ALE experiments (Fig. 5). Two experiments with the same strain and medium conditions yielded vastly different fitness outcomes. This difference is explainable within the scope of ALEsim. Therefore, having access to a computational framework such as ALEsim can enable researchers to make informed decisions about when to terminate an experiment, given the capacity and resources of the experimental setup and the desired or acceptable outcome. This type of termination analysis is laid out in Fig. 6 and can be calculated de novo for any experiment, given the current growth rate and passage size. It should be noted that this type of analysis could result in a standard for the ALE community, as one could state the ALEsim-generated Δμ at the time of termination.

The ability to design and to carry out complicated and high-resource-burn ALE experiments is likely possible only though automation of the ALE process. Automation was utilized here and in previous studies (4, 7, 41). Manual processes are often hampered by researcher availability, whereas machines can measure and passage cells around the clock; for example, approximately 5 to 7 passages per day were performed in automated studies (4, 7, 41), compared to 1 or 2 passages per day in manual studies (14, 15, 18). Thus, the ability to automate and to optimize ALE studies is likely to accelerate adoption of the ALE experimental technique and to broaden the application areas. Furthermore, the ALEsim framework and output can be used as a basis for modeling much of the legacy data currently available for ALE experiments, including lag, exponential, stationary, and stressed phases. Because the selection pressure in such experiments is more complex and growth is defined by more than the growth rate parameter (such as lag-phase duration, stationary-phase mutation rate, or growth phase transitions), ALEsim would have to be expanded from its current format. Nonetheless, the analysis of ALEsim and its parameterization presented here demonstrates the utility of using simulated design in the ALE process and establishes a portable code base.

The field of adaptive laboratory evolution is expanding, largely due to lower costs of next-generation sequencing. Innovative applications are appearing and are being applied to a range of organisms (1, 3). This growth in ALE use has occurred without a standard operating procedure for performing and quantifying these experiments, which leads to ill-defined experimental endpoints and the inefficient use of resources. The ALEsim computational platform developed here provides a means to quantify experiments and to facilitate their design, matching the desired outcome with the resources available.

MATERIALS AND METHODS

Adaptive laboratory evolution.

Adaptive laboratory evolutions were started from wild-type E. coli strain MG1655 (ATCC 47076) glycerol frozen stock, and cells were grown overnight in 15 ml of magnetically stirred 0.2% glycerol M9 minimal medium supplemented with trace elements. The magnetic stirring was performed at 1,150 rpm, sufficient for completely aerobic growth. Thirty experiments were started from 150-μl aliquots from the overnight preculture. The experiments were performed with vessels and medium identical to those used for the preculture. The optical density at 600 nm (OD₆₀₀) of the culture was monitored over the course of each batch culture. When the culture reached an OD₆₀₀ of 0.300 (±10%), as measured by a plate reader with a 100-μl sample volume in a 96-well flat-bottom microplate, an aliquot was taken and passaged to a new batch culture with sterile medium. An OD₆₀₀ of 0.300 was chosen to preclude reaching the stationary phase in any of the cultures and ensured that the OD₆₀₀ measurements had not begun to saturate. Growth rates for each culture were determined using OD₆₀₀ measurements taken over the lifetime of each batch culture.

Medium.

All cultures were grown in 0.2% glycerol M9 minimal medium. The medium consisted of 0.2% glycerol (by volume), 0.1 mM CaCl₂, 2.0 mM MgSO₄, trace element solution, and M9 salts. The 4,000× trace element solution consisted of 27 g/liter FeCl₃·6H₂O, 2 g/liter ZnCl₂·4H₂O, 2 g/liter CoCl₂·6H₂O, 2 g/liter NaMoO₄·2H₂O, 1 g/liter CaCl₂·H₂O, 1.3 g/liter CuCl₂·6H₂O, 0.5 g/liter H₃BO₃, and concentrated HCl, dissolved in double-distilled water and sterile filtered. The 10× M9 salt solution consisted of 68 g/liter anhydrous Na₂HPO₄, 30 g/liter KH₂PO₄, 5 g/liter NaCl, and 10 g/liter NH₄Cl, dissolved in double-distilled water and autoclaved. Final concentrations in the medium were 1×.

DNA sequencing.

Genomic DNA was isolated using a Macherey-Nagel NucleoSpin Tissue kit. The quality of DNA was assessed with UV absorbance ratios, using a NanoDrop spectrophotometer. DNA was quantified using a Qubit double-stranded DNA high-sensitivity assay. Paired-end resequencing libraries were generated using an Illumina Nextera XT kit, with a total of 700 pg of input DNA. Sequences were obtained using an Illumina MiSeq sequencer with a MiSeq 600-cycle reagent kit v3; breseq pipeline v0.23 with bowtie2 was used to map sequencing reads and to identify mutations relative to the E. coli K-12 MG1655 genome (NCBI accession no. NC_000913.2) (42). All samples had an average mapped coverage of at least 25-fold.

Computer modeling.

Modeling of simulations was performed using MATLAB 2015b, on a Windows 7 professional platform. Detailed descriptions are found as comments in the supplemental material. The beneficial mutation rate was computed by maximum likelihood estimation, calculated for making a transition from state 1 to state 2 and from state 2 to state 3, with passage sizes of 0.01% and 0.001%. These passage sizes were chosen because they were the only ones that showed a distribution of states achieved. The transition from state 1 to state 2 was capped at 20 days, to give a maximally distributed data set. The transition from state 2 to state 3 was started by assuming that state 2 had already been achieved. Thus, the simulated time was started based on when state 2 was achieved, which varied for different experiments.

A value of 1.55 × 10¹² cells · liter⁻¹ · OD₆₀₀⁻¹ was used to estimate the number of cells in a culture for a given OD₆₀₀, with a 1-cm-path-length cuvette, for the purposes of ALEsim. A standard curve relating the OD₆₀₀ measured by the plate reader with a 100-μl sample volume, in a 96-well flat-bottom microplate, to the OD₆₀₀ measured with a 1-cm cuvette yielded a ratio of 3.15 for equivalent measurements for the two values. The biomass (grams of dry weight) per OD₆₀₀ per volume was calculated by filtering known volumes of cultures at specific OD₆₀₀ values though 0.22-μm filters. The filters were weighed before and after filtering and drying, to obtain the total dry weight of the culture. The differences in those values were used to calculate a value of 0.45 g of dry weight · liter⁻¹ · OD₆₀₀⁻¹. The dry mass per cell was reported previously as 2.9 × 10⁻¹³g of dry weight · cell⁻¹ (43). The quotient of these two values gives the final conversion factor of 1.55 × 10¹² cells · liter⁻¹ · OD⁻¹, to estimate the cell counts of cultures at various OD values and volumes. For E. coli, the dry mass per cell can vary over a range of growth rates (23). Using a variable such as OD to cell count factor as a function of growth rate is possible with ALEsim but incurs a marked increase in simulation time. Thus, identical simulations were performed using only the highest and lowest dry mass per cell values expected for the growth rates observed (i.e., the extremes). Only a 10% difference between the two extremes in the distribution of simulated endpoint growth rates was observed (see Fig. S1 in the supplemental material). Therefore, use of a constant average value for dry mass per cell over the range of growth rates expected was determined to be sufficient, considering the benefits in computation time.

Although possible with ALEsim, deleterious and neutral mutations were not considered during this study. A deleterious mutation rate of 1 in 5,000 was computed previously (44). In the application demonstrated here, the population sizes were sufficiently large (10⁵ to 10⁹ cells) that the effects of deleterious and neutral mutations would be negligible. With smaller population sizes (e.g., several orders of magnitude smaller than the population sizes modeled here), the effects of these mutations would become more pronounced and should not be ignored.