Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Aug 14;4:6071. doi: 10.1038/srep06071

Radiative efficiency of lead iodide based perovskite solar cells

Kristofer Tvingstedt 1,a, Olga Malinkiewicz 2, Andreas Baumann 3, Carsten Deibel 1, Henry J Snaith 4, Vladimir Dyakonov 1,3, Henk J Bolink 2
PMCID: PMC5377528  PMID: 25317958

Abstract

The maximum efficiency of any solar cell can be evaluated in terms of its corresponding ability to emit light. We herein determine the important figure of merit of radiative efficiency for Methylammonium Lead Iodide perovskite solar cells and, to put in context, relate it to an organic photovoltaic (OPV) model device. We evaluate the reciprocity relation between electroluminescence and photovoltaic quantum efficiency and conclude that the emission from the perovskite devices is dominated by a sharp band-to-band transition that has a radiative efficiency much higher than that of an average OPV device. As a consequence, the perovskite have the benefit of retaining an open circuit voltage ~0.14 V closer to its radiative limit than the OPV cell. Additionally, and in contrast to OPVs, we show that the photoluminescence of the perovskite solar cell is substantially quenched under short circuit conditions in accordance with how an ideal photovoltaic cell should operate.

The ability of a solar cell to emit light is intuitively not an essential property that first comes to mind in striving for high power conversion efficiencies. “–A solar cell should deliver current and not light” is a statement that most would probably agree with directly. However, one needs to recognize that a solar cell in fact should do both, just depending on where it is operating in the current-voltage (I–V) curve. At short circuit (Jsc), a solar cell should indeed emit as little light as possible, as all absorbed photons should effectively be converted to free charges that can flow in the external circuit. Hence, at Jsc one of course desires to have as little recombination as possible, and the discussion of what type of recombination, radiative or non-radiative, gets almost irrelevant as it should not be there at all in the first place. Negligible recombination at Jsc has in fact also already been achieved for many promising photovoltaic materials found in both OPVs and dye sensitized solar cells (DSSC).

But, as a solar cell at Jsc is not producing any power we must also consider what happens as we expose our device to a load. With an infinite load our device ends up at open circuit (VOC) conditions and no external current is allowed to flow. Hence, all free charges generated must also recombine, simply because it is the only option. At any other point in the 4th power generating quadrant of the I–V curve, we will observe a transition from no (or weak) recombination at Jsc to 100% recombination at VOC. How this transition occurs depends in fact very much on the ability of the solar cell to emit light. The best solar cell, generating the highest VOC, will be the one where the absorbed photon flux equals the emitted flux under open circuit conditions. Such a solar cell, ideal to be pursued for highest efficiency, is also said to be in “the radiative limit”. The reason good solar cells should only have radiative transitions available for recombination lies in the fact that these pathways are directly related to the necessary transitions that also gives rise to absorption. Therefore, even for an ideal solar cell, radiative recombination pathways cannot be avoided whereas the non-radiative pathways, unrelated to the states involved in absorption, have no such justification. These pathways are not needed and should therefore be minimized, a task that is generally not so easy.

The approach of optical reciprocity between absorption and emission – first introduced by Kirchhoff1, refined by Planck2 for black body (BB) radiation and extended to non-equilibrium conditions by Würfel3 – was adapted to parameters directly relevant to photovoltaics by Rau quite recently4. The optical reciprocity theorem states that the emission spectra of thermal radiation from any (grey) body in thermal equilibrium with its surrounding is equal to the product of the black body radiation of the surrounding (earth at 300 K) and the absorptance spectra of the grey body. Würfel extended the postulate to conditions out of thermal equilibrium by concluding that when increasing the chemical potential of the grey body radiator (by for example applying a voltage) the spectral shape of emission remains the same as the thermal emission, but its intensity will increase exponentially with the applied chemical potential. This was also experimentally verified for a GaAs LED in Würfels paper “The chemical potential of radiation” in 19823. By the assumptions made by Rau4, the reciprocity relation was extended to hold also between Electroluminescence (EL) and EQEPV(E). Rau's reciprocity relation (R.R.R.) therefore directly connects photovoltaic quantum efficiency and EL efficiency. Conditions for the validity of and limitations to the R.R.R. are outlined by Kirchartz et. al.5,6 and Wang et. al.7. As the quantities involved in R.R.R. are accessible by standard, yet sensitive, characterization techniques, it has been proposed8 that different PV technologies should be evaluated and compared by the property of “Radiative efficiency”, as this key figure of merit provides information on how far the technology is from its own upper limit.

Thin film photovoltaics have lately attracted much attention as a promising energy alternative to reduce the dependency of fossil and nuclear non-renewable fuels9. Organic polymer/fullerene solar cells (OPV) have the advantage of possible large scale fast manufacturing due to its excellent solution process ability. Recently, methylammonium lead iodide perovskites (MAPI) have emerged as a very interesting class of semiconductor materials that have led to very efficient solar cells. From the first report by Miyasaki et al.10 in 2009, tremendous progress in the performance of MAPI based solar cells has been achieved11,12,13,14,15,16, with power conversion efficiencies (PCE) exceeding 15%11,12,13.

An alternative inverted device layout for perovskite solar cells, without employing a metal oxide hole blocking layer, has recently been described17,18,19. and PCEs in excess of 15% have also been obtained. In this layout, similar to a standard OPV device architecture, the MAPI is sandwiched in between two organic charge transporting layers that effectively block holes and electrons18.

In this work we describe how the radiative efficiency of such a well performing “inverted” MAPI solar cell compares to a solution processed OPV cell based on a well-studied bulk heterojunction Poly[2-methoxy-5-(3′,7′-dimethyloctyloxy)-1,4-phenylenevinylene]:[6,6]-Phenyl-C61-butyric-acid-methyl-ester (MDMO-PPV:PCBM) system20 and investigate how close the open circuit voltage is to the “possible” open circuit voltage of the two respective semiconductors. The similar device configuration allows for a direct comparison of a new and an older thin film photovoltaic technology. As both of these technologies have the potential to change the way energy is utilized in today's society, we pinpoint here a fundamental characteristic, that represents an important leap forward for potentially cheap thin film PVs, as we find that the efficiency of emission of the perovskite solar cell is orders of magnitude higher than for the OPV device. This certifies the smaller number of loss channels present in the former type of devices.

Results and discussion

Optoelectronic reciprocity relation

Rau's reciprocity relation is here expressed in terms of the dark saturation current J0 and the absolute quantum efficiency of electroluminescence EQEEL:

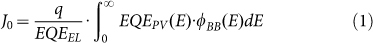graphic file with name srep06071-m1.jpg

where φBB is the photon flux of the environment. A solar cell in its radiative limit (where all recombination is indeed radiative) will have an EQEEL of unity and hence a low dark saturation current:

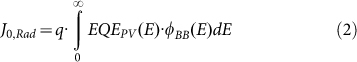graphic file with name srep06071-m2.jpg

The photocurrent at short circuit of an illuminated solar cell is instead given by the product of EQEPV(E) and the solar photon flux hitting the device:

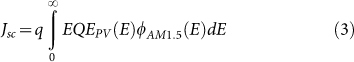graphic file with name srep06071-m3.jpg

To best visualize the constituents of these two important PV integrals, Figure 1 depicts the spectral distribution of the absolute photon fluxes of the two black bodies involved in photovoltaic conversion; that is the sun and the 300 K black body environment (the earth).

Figure 1. Spectral energy distribution of the two photon fluxes governing photovoltaic energy conversion on earth.

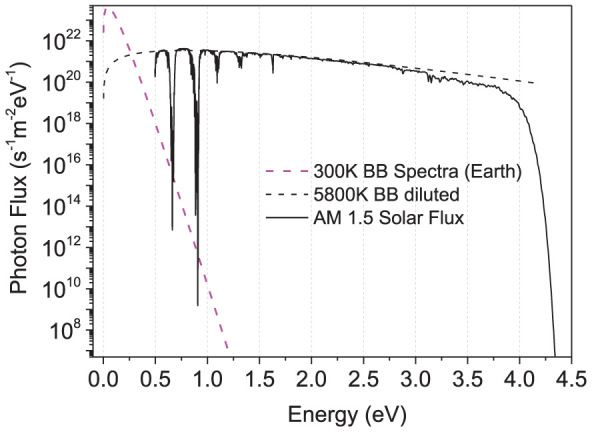
Figure 1

Open in a new tab

The sun flux, closely originating from a distance diluted 5800 K blackbody source (dashed black line) filtered by the earth atmosphere (solid black line) determines the short circuit current. The earth environment 300 K blackbody flux governs instead the dark saturation current (Magenta dashed line). Note the very large range of absolute values on the Y-axis.

As the open circuit voltage of any type of solar cell is determined by the ratio of the two corresponding currents

graphic file with name srep06071-m4.jpg

a low dark saturation current and a high solar photocurrent should of course always be strived for. Both of these currents are however largely determined by the same parameter: namely the EQEPV(E). (Apart from the spectral shape of EQEPV(E) it is in fact only the radiative efficiency EQEEL that determines the open circuit voltage.) From Figure 1 and Equations 1–3 it becomes obvious that the best solar cells must have a high EQEPV(E) in the energy region where the solar flux dominates the spectra and simultaneously an as low as possible EQEPV(E) in the energy region where the earth BB flux dominates. This condition is satisfied by a solar cell with a sharp stepwise EQEPV(E) function, being 100% above the band gap and being zero below. This shape of the EQEPV(E) was indeed assumed by Shockley and Queisser in their detailed balance paper21 on determining the upper limits to photovoltaic energy conversion. It should perhaps be noted that the stepwise EQEPV(E) is no prerequisite for detailed balance per se; it is merely the sought-after spectral shape to reach the upper limit.

The open circuit voltage hence, is determined by:

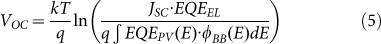graphic file with name srep06071-m5.jpg

The first option to increase VOC is to lower J0,Rad (denominator in Eqn. 5) by changing the spectral shape of the EQEPV(E), the sharper the step shape the higher the VOC. The only other, and more potent, option to increase the VOC is instead to increase the EQEEL towards unity by minimizing the non-radiative recombination pathways, bringing VOC closer to the radiative limit. The radiative efficiency hence relates to the offset between band gap and open circuit voltage defined by: Woc ≡ (Egap/q) – Voc.

A highly relevant figure of merit to compare different PV technologies is therefore to determine how far they are from their respective radiative upper limits8 and hence also what we focus on here. This can be determined in two separate ways: A) One basically measures the EQEEL of the cell in absolute terms. This is performed by injecting a small forward current, as close as possible to the short circuit photocurrent (determined under solar illumination) and then measure how many photons are emitted from the device. The procedure is hence analog to measuring the efficiency of a LED close to the very onset of emission. With the EQEEL determined and the device dark saturation current (J0), obtained from Eqn. 4, one can calculate the dark saturation current in the radiative limit (J0,Rad) via their simple relation

graphic file with name srep06071-m6.jpg

and then also the corresponding open circuit voltage in the radiative limit (VOC,Rad). B) The second method to determine radiative efficiency relies on measuring the EQEPV(E) at the band edge and then calculate J0,Rad via Eqn. 2. Since J0,Rad calculated this way is fully determined by the shape of the EQEPV(E) at very low energies and the earth blackbody spectrum is such a strongly decreasing exponential function, it is essential to measure the spectral shape of EQEPV(E) very accurately with high sensitivity to minimize measurement noise in the lowest energy regime. By rearranging Eqn. 5 one obtains:

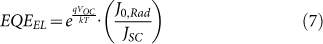graphic file with name srep06071-m7.jpg

so that with a reliable value of J0,Rad available, one can instead calculate the radiative efficiency. Hence two methods are available and here we have pursued both methods to verify their accuracy in determining the radiative efficiency and as such we assess if the R.R.R. is valid for the new perovskite based solar cells.

Devices

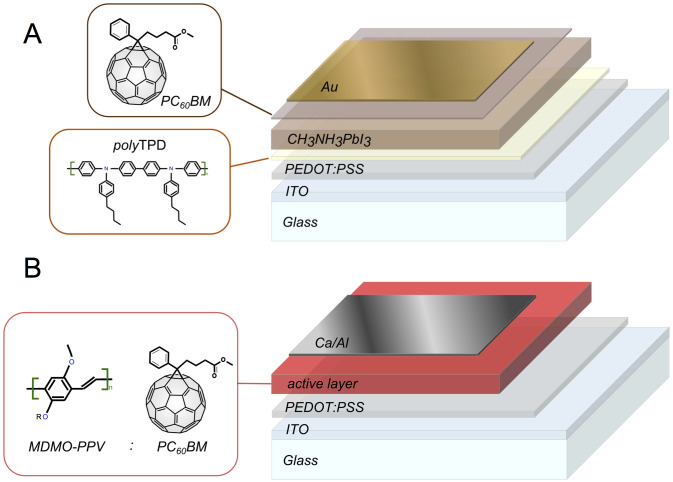
The device structures of the two types of solar cells used in this study are shown schematically in Figure 2. We first emphasize that the I–V characteristics of the fresh MAPI cells showed negligible hysteresis, meaning that concerns related to voltage sweep direction and time dependence, could be safely disregarded22. Such dependencies would likely affect the illuminated and dark I–V sweeps differently, and may therefore also invalidate the superposition assumption in the R.R.R. A short circuit current of 189 A/m2, an open circuit voltage of 1080 mV and a fill factor (FF) of 55% were obtained for the MAPI cell. The OPV showed, as expected, substantially worse performance with a JSC limited to only 32 A/m2, a VOC of 830 mV and a FF of 51%.

Figure 2. Device layout of the studied solar cells.

Figure 2

Open in a new tab

(A) Perovskite (MAPI) and (B) Organic (MDMO-PPV:PCBM) cells.

Quantum efficiency of radiative recombination

The observed peak position of electroluminescence from the MAPI cell is similar to that detected earlier by photoluminescence23 and is located at 760 nm or 1.61 eV (Figure 3A) and the shape is independent of the injection current density. The very sharp peak with a full-width-at-half-maximum of only 81 meV indicates that the emission comes from a narrow distribution of states likely located at the band edge of this perovskite semiconductor24. The peak of the EL coincides with the location of the steep slope of the EQEPV(E) spectra, highlighting the complete absence of any Stokes shift in the MAPI material. Hence, the assumption that this MAPI structure is a direct band gap semiconductor with its band gap energy located at the peak of EL emission is highly justified, but actually somewhat in disagreement with recent published values18,25,26 of the band gap of MAPI cells. Those were obtained from diffuse reflectance spectroscopy or UPS, and reported to be 1.50–1.57 eV. This implies that either the earlier band gap determination is not fully justified, or the here observed radiative recombination does not occur over the band gap, but from higher lying electronic states, which we deem less likely to occur. It must be pointed out that the absorptance and corresponding EQEPV(E) spectra actually do extend to slightly lower energies than the peak position of the EL spectra, indicating that absorption does indeed occur slightly below the here determined band gap from EL, also in our device.

Figure 3. Radiative efficiency of the MAPI cell.

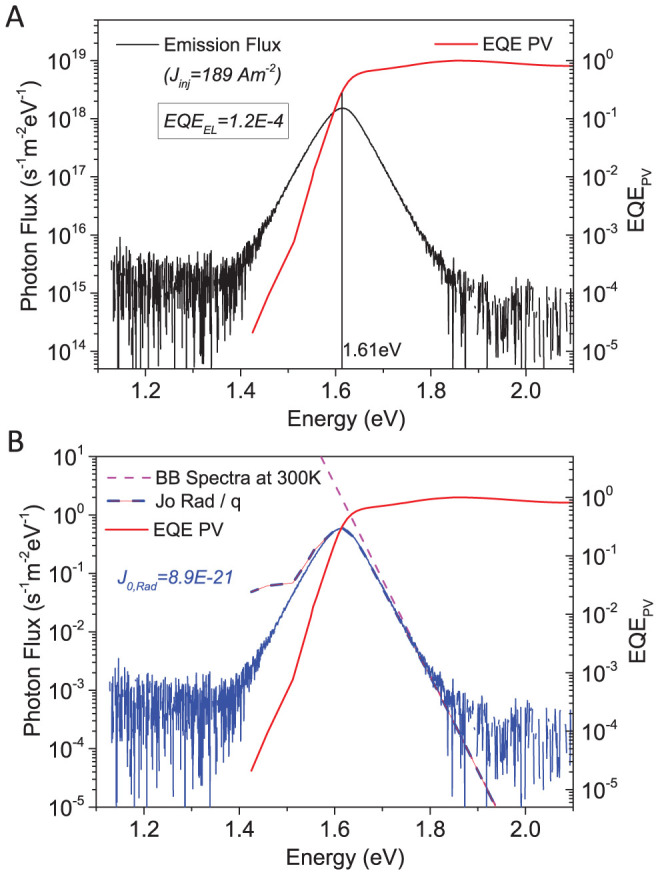
Figure 3

Open in a new tab

(A) EQEPV (red) and the spectral emission flux (black) at a current injection condition corresponding to Jsc at 1 sun. The vertical line at the peak of EL marks the direct band gap energy at 1.61 eV. The ratio between the total emitted number of photons and the injected current equals the EQEEL. (B) The 300 K BB spectra (dashed magenta) multiplied with the EQEPV provides the photon flux distribution (thick dashed blue line) which, when integrated, corresponds to the dark saturation current in its radiative limit. The identical shape of the spectra, with ~18 magnitudes lower emission flux compared to in (A), certifies the reciprocity relation.

A typical EL spectrum obtained by driving the perovskite cells at a current density similar to its JSC is depicted in Figure 3A, showing the measured photon flux distribution (in eV) (black line). When this flux distribution is integrated over all energies the total EL flux is obtained, which when divided with the injected current provides the value of the radiative efficiency EQEEL under solar flux charge carrier density.

Figure 3B shows the measured EQEPV(E) spectra, the spectral distribution of the 300 K BB environment radiation, and the sought-after product of these two spectra. This spectrum, in accordance with the R.R.R. of Eqn. 2 represents the radiative recombination flux of our MAPI cell in the dark, in the case that everything that is absorbed is also reemitted. The dashed blue line hence embodies the radiative spectral distribution of the dark saturation current in its radiative limit. Integrated over all energies we obtain the actual dark saturation current in its radiative limit (J0,Rad). We point out that it is in general not sufficient to get the full value of the J0,Rad by just integrating the EQEPV:BB spectra product, as we cannot accurately enough measure the EQEPV at the required lowest energies. Incomplete determination of EQE at the band edge will therefore inevitably lead to an underestimation of the correct value of J0,Rad, which also seems to be the case for several of the spectra presented in ref.8. The curve presented in our Figure 3B is also dominated by noise at energies just slightly below the peak. However, the electroluminescence flux spectra obtained under conditions of much higher applied chemical potentials (Figure 3A), do nicely provide the needed full spectral shape of the product, provided that the R.R.R. does hold. The thin blue line is hence the measured EL flux spectra basically fitted to the absolute values of the thick dashed line. The error made by not using the electroluminescence spectral shape would, however, be less than a factor of two, as at least half of the curve shape was already correctly determined without the emission study. The similarity in shape of the calculated J0,Rad spectra and the measured emission distribution and, more importantly, their direct relation to J0 via Eqn.6 confirms the validity of using the R.R.R.

For the reference MDMO-PPV:PCBM solar cell, depicted in Figure 4, the electroluminescence peak originates from recombination via the interfacial charge transfer (CT) state27. The energy of the CT state relates to the difference between the LUMO level of the PCBM and the HOMO level of the MDMO-PPV. However, the very large impact of reorganization energy present in soft materials leads to a pronounced Stokes shift and electroluminescence peaks can no longer directly be used as a reliable estimation of the actual band gap energy. To account for the influence of reorganization energy, we have instead followed the proposal in Ref.28 that a better representation of band gap energy is identified by the crossing of the reduced EQEPV and the EL emission spectra. Hence, the correct band gap energy in the OPV device is ~0.2 eV higher than the peak position of electroluminescence. (Our concerns with the MAPI band gap are converse, such that the published values are lower than the peak EL position) The band gap determination for the reorganizing polymer-fullerene blend is here identified in this device at 1.46 eV.

Figure 4. Radiative efficiency of the reference OPV cell.

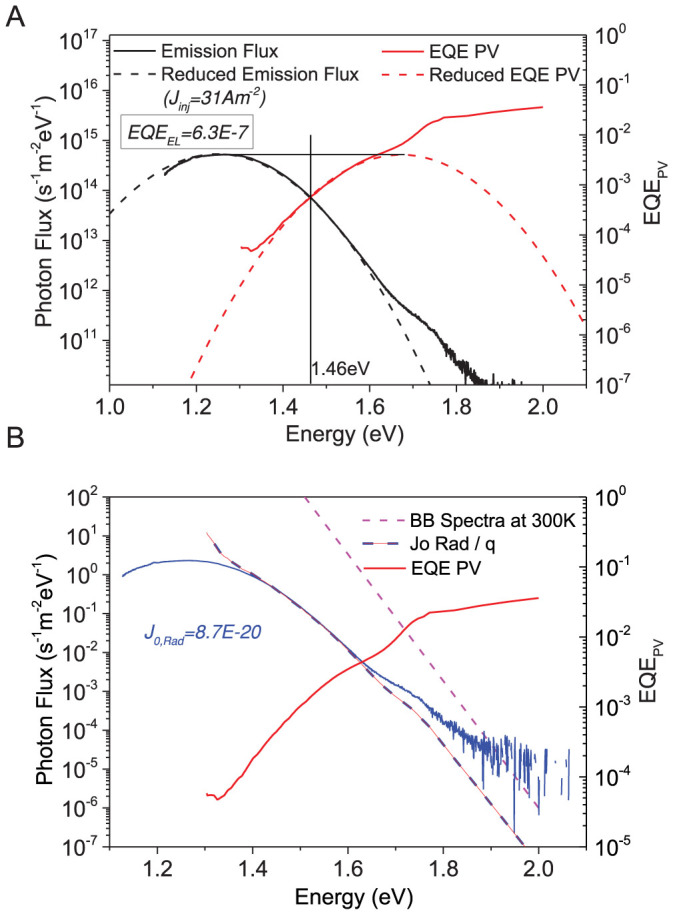
Figure 4

Open in a new tab

(A) EQEPV and spectral emission flux at a current injection condition corresponding to Jsc at 1 sun. The EQEEL is identified substantially lower for this reference material. The vertical black line, corresponding now to the crossing of the reduced spectra28, marks the band gap energy at 1.46 eV. (B) The 300 K BB spectra multiplied with the EQEPV provides again the photon flux distribution corresponding to the dark saturation current in its radiative limit. The obtained J0,Rad is just one magnitude higher than for the MAPI cell.

An accurate determination of the band gap is of course essential to be able to make a useful notion regarding the offset value Woc.

The large Stokes shift and limited EQEPV sensitivity of our setup also do limit the spectral range over which we can confirm the measured spectral emission shape and the calculated shape (dashed) for the organic solar cell in Figure 4B. It is however in close accordance with earlier published spectral fits where peak positions were slightly better covered28. For these types of materials the emission study is therefore more important to get a better coverage of the J0,Rad energy distribution, to allow a better determination of its integrated value.

We herein hence chose to determine J0,Rad for the two devices via the integrated fitted spectra (thin blue lines in 3B and 4B) and subsequently J0 via eqn.6 for both studied solar cells. This allows us to calculate VOC,Rad and the real VOC, both via Eqn. 4. This calculated real VOC is in very good agreement with the measured VOC under AM 1.5 simulated solar spectra illumination (Table 1).

Table 1. Summary of the photovoltaic key parameters for the two types of PV devices studied.

  MAPI MDMO-PPV:PCBM
Eg (eV) 1.61 ± 0.01 1.46 ± 0.02
Jsc (A/m2) 189 (±0.5) 32 (±0.5)
J0 (A/m2) 7.4 (±4.6) E-17 1.4 (±0.7) E-13
J0,Rad (A/m2) 8.9 (±0.6) E-21 8.7 (±0.6) E-20
Rad. efficiency (measured EQEEL) 1.2 (±0.1) E-4 6.3 (±0.1) E-7
Voc,Rad (V) 1.33 ± 0.02 1.22 ± 0.02
Voc (V) kTln(Jsc/Jo) 1.09 ± 0.02 0.85 ± 0.02
Voc (V) measured 1.08 ± 0.01 0.83 ± 0.01
Δ Voc, Non-Rad 0.23 ± 0.02 0.37 ± 0.02
WOC (eV) 0.53 ± 0.03 0.63 ± 0.03
Open in a new tab

We see that the MAPI cell has a substantial advantage over the OPV cell. The offset (ΔVOC, Non-Rad) between actual open circuit voltage and open circuit voltage in the radiative limit of only ~0.23 V for the perovskite considerably outperforms the OPV cell which has an offset as high as ~0.37 V. The fact that the MAPI cell has a radiative efficiency ~190 times higher hence leads to an open circuit voltage being ~0.14 V closer to its radiative limit than the MDMO-PPV:PCBM cell. Our band gap assignment furthermore designates that the VOC is ~0.1 V closer to the band gap than that observed for the OPV cell.

A radiative efficiency of ~1E-4 puts the perovskite solar cell in a good position, when compared to other earlier generation photovoltaic technologies. Numbers of radiative efficiency, taken from Green's compiled list8, ranges from 0.225 for a GaAs cell to 2.7E-9 for an undisclosed OPV cell from Konarka. The here studied MAPI cell substantially outperforms both DSSC (7.2E-8), amorphous Si (5.3E-8) as well as CdTe cells (1E-6) and is just slightly behind Cu(In,Ga)Se2 with a there stated radiative efficiency of 5.7E-4. We again note that some of the lowest values listed therein are however likely underestimations.

Photoluminescence quenching

In addition to the noteworthy radiative efficiency of the MAPI cell, we also like to point out the strikingly different feature of photoluminescence (PL) quenching behavior for the two devices, when evaluated simply at different external loading conditions. It is still widely argued within several emerging PV technology communities that a good photovoltaic material combination (donor-acceptor or with interfacial layers) should display strong PL quenching of the main absorber due to beneficial induced charge transfer. It is for example frequently highlighted that in donor-acceptor bulk heterojunctions, the PL quenching of the donor material induced by the (fullerene) acceptor presence is a sought-after feature. Likewise, in DSSC, the choice of electrode interfacial layers is frequently based on their ability to quench the emission of the absorber dye. This is, however, in general only a good signature and suited figure of merit for obtaining high yield of photo induced charge transfer to obtain a higher photocurrent generation, but not at all a good figure of merit for simultaneously achieving a high open circuit voltage. In fact, it is quite the opposite. Frequently, these PL quenching studies are performed on neat films without the presence of electrodes. Hence the sample under study is actually closer to the condition of a solar cell at open circuit rather than short circuit. Therefore, as argued above, substantial non-radiative recombination pathways must have been introduced if the sample has a reduced photoluminescence. Therefore, we here point out that a much better “quenching figure of merit” for photovoltaics, that allows for achieving both a high photo current and photo voltage, is if the photoluminescence of a completed device is quenched only when the device is going from open circuit to short circuit conditions.

For both the MAPI and the OPV cells, the photoluminescence of the dominant absorber is also reduced by the mere presence of another charge accepting material in the device. However, some residual photoluminescence, of different magnitude, still remains for both devices. The PL and EL spectra of the two types of cells are plotted in Figure 5 (no longer in absolute flux). In the OPV cell, the emission, when excited with a 405 nm continuous wave laser, is dominated by radiative recombination of Frenkel excitons within pure phases of the PCBM acceptor (Figure 5A). Some PL also arises from pure phases of polymer. In the OPV, the presence of radiative interfacial charge transfer state (CT) recombination is almost completely masked by the low energy tail of the photoluminescence of the pure phases. The electroluminescence is on the other hand completely dominated by CT recombination, as expected. Only at very high injection conditions do we see a hint of pure phase population.

Figure 5. Device PL quenching.

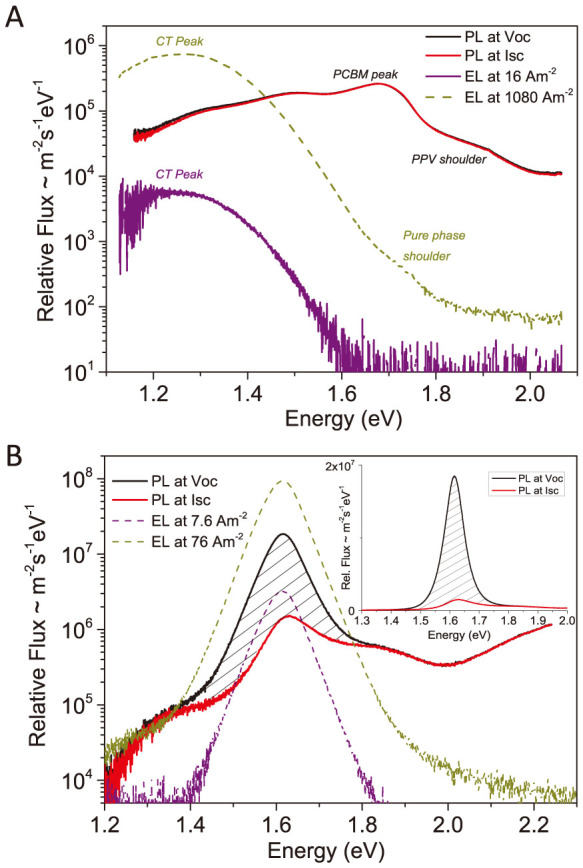
Figure 5

Open in a new tab

(A) PL of the MDMO-PPV:PCBM at open (black line) and short circuit (red line) conditions highlighting the negligible loading dependence. (B) The MAPI cell displays in contrary substantially different PL quenching behavior under device open (black line) and short circuit (red line) conditions. Inset shows the same data on a linear scale. EL spectra are further included in both graphs to emphasize their spectral position related to PL as well as their spectral shape independence on injection conditions. The units on the Y-axis are no longer absolute, but still correspond to m−2s−1eV−1.

There is, however, no influence at all of the device contact condition on the PL intensity. That is the PL intensity is the same at open circuit and at short circuit conditions. This is in fact an almost universal feature of all organic solar cells. This feature, the independence of luminescence to external loading, is caused by the two main shortcomings of OPV devices; namely, the very strong binding energy of the photogenerated Frenkel excitons and the very low radiative efficiency of the free carrier recombination. Hence, if photo induced charge transfer, expected to be required to generate a decent photocurrent from excitonic materials, is always associated with the introduction of non-radiative recombination pathways, then organic photovoltaics may be in quite a dilemma29.

However, for the MAPI cell in Figure 5B the story is very different. As the PL emission is located at the very same energetic position as EL, the assumption that the strong PL emission originates from the recombination of the same type of charge pairs as in EL, namely free charge carriers, is justified. Then, its intensity should also very much depend on whether the device is at open or short circuit conditions. Indeed, both on a linear (inset) and log scale, the effect of simply allowing the photogenerated charges to take another path (external cables) than recombining within the film, substantially affects the luminescence intensity. This then fully confirms that the PL emission originates from completely free charges that are just waiting to get out of the device and produce current.

Conclusions

The emission from the MAPI perovskite solar cells are dominated by sharp band-to-band transitions and have a radiative efficiency almost a factor 200 higher than that of a model organic solar cell. This leads to the benefit of retaining an open circuit voltage significantly closer to the maximum open circuit voltage wherein all recombination events lead to the emission of photons. The figure of merit of a radiative efficiency above 10−4 put these solar cells above amorphous Silicon, DSSC, and CdTe but slightly below that of Cu(In,Ga)Se2 solar cells. We have herein also highlighted that the perovskite photoluminescence is rather strong at open circuit conditions, and substantially quenched at short circuit, showing that the primary excited states are free carriers without significant binding energy, similar to other solar cells with high radiative efficiency in the list of ref.8. Perovskites have already reached impressive power conversion efficiencies, and one of the main reasons for this is found in its high photovoltage which relates directly to its comparatively high ability to emit light.

Methods

The perovskite solar cells studied herein were prepared by sandwiching the methylammonium lead iodide (MAPI) between two electron and hole selective layers. First, a 75 nm thick film of poly(3,4-ethylenedioxythiophene):poly (styrenesulfonic acid) (PEDOT:PSS) CLEVIOS P VP Al 4083 from Hereaus was spin-coated on an ITO covered glass substrate. After annealing for 15 minutes at 150°C, a thin layer of the electron blocking material poly[N,N0-bis(4-butylphenyl)-N,N0-bis(phenyl)benzidine] (polyTPD) from ADS was deposited (30 nm) from a chlorobenzene solution (7 mg ml−1) and then annealed at 180°C during 30 minutes. To ensure a high purity and a high control of the thickness, the CH3NH3PbI3 layers were prepared by the co-evaporation of the two starting materials PbI2 and CH3NH3I in a high vacuum chamber as described previously18,30. A MAPI layer thickness of 250 nm was used for the present study. Subsequently, a thin layer (20 nm) of the hole blocking material [6,6]-phenyl C61-butyric acid methylester (PCBM60) Solenne BV was deposited from a chlorobenzene solution (10 mg ml−1) using meniscus coating31. The device was completed by the thermal sublimation of the top metal (Au) electrode to a thickness of 100 nm. The solar cells (active area of 6.5 mm2) were then encapsulated with a glass cover using a UV curable epoxy sealant (Ossila E131 Encapsulation Epoxy), with a UV exposure time of 5 min.

The reference MDMO-PPV:PCBM OPV cell (active area of 9.2 mm2) was manufactured by spin coating a 110 nm thick layer of the active material in a stoichiometric ratio of 1:4 from a chlorobenzene solution. The PPV (CAS 177716-59-5) was obtained from Sigma Aldrich and the fullerene from Solenne BV. The bottom electrode comprised again ITO but with a 40 nm hole selective PEDOT:PSS (Al 4083) film. The top electron selective electrode comprised a sublimated Ca(3 nm)/Al(110 nm) combination.

I–V characterization was performed under inert atmosphere using an Oriel 1160 AM 1.5 G solar simulator. The EQEPV(λ) was determined with a home built setup comprising an Oriel Halogen lamp, a light chopper coupled to an Oriel monochromator, a Hamamatsu K3413-02 Si reference cell and two lock-in amplifiers to measure the corresponding photocurrents. Electroluminescence spectra were determined by an Acton SpectraPro SP2560 monochromator coupled to a N2 cooled Spec10LN Si CCD camera from Princeton Instruments.

The light was coupled from the cell to the monochromator entrance via an Oriel liquid light guide (5 mm diameter) placed very close to the front of the cells. The entire spectral system was photon flux calibrated with a reference Halogen lamp mounted in a LMS-100 integrating sphere from Labsphere. The absolute photon flux determination was performed by placing the cell at a set known distance of 18.3 mm from a 1 cm2 area Hamamatsu S2281 Si photo detector. The solar cell was forward biased via an Agilent 4155C parameter analyzer in sourced current mode, and the Si photodiode current was collected by the same. Knowledge about the spectral distribution of the cell emission, the spectral response of the Si-photo detector, and the assumption of a point source emitting uniformly into a half sphere, allows determination of the weak absolute EL photon flux from the solar cell. The dominant error in radiative efficiency determination via any of the outlined methods is in general found in the temperature uncertainty in any of the J0 calculations. All measurements were conducted at ambient room temperature but the samples are likely to heat up by some degrees both during the solar simulator illuminated VOC determination and likely also due to the injection current during the emission efficiency determination. A temperature error margin of ±3 K has hence been assumed in the J0 calculations of table 1. Errors in areas of the cells are neglected as we here only deal with the ratio between Jsc and J0. The uncertainties in measured EL efficiency are expected to be governed by the small distance imprecision between the cell and the photo detector. The ability of reproducing the measured VOC with decent accuracy via combining the two methods also attests that our measurements inaccuracy is well within the acceptable boundaries.

Acknowledgments

K.T. and C.D. acknowledges the People Programme (Marie Curie Actions) of the European Union's Seventh Framework Programme FP7 under the REA grant agreement PIEF-GA-2012-327199. A.B. was financed by the Bavarian Ministry of Economic Affairs and Media, Energy and Technology. V.D. acknowledges the financial support from the Bavarian State Ministry of Education and Culture, Science and Arts within the Collaborative Research Network “Solar Technologies go Hybrid”. H.J.S. is supported by the UK Engineering and Physical Sciences Research Council. The work conducted by O.M. and H.J.B. was supported by the Spanish Ministry of Economy and Competitiveness (MINECO) (MAT2011-24594), the Generalitat Valenciana (Prometeo/2012/053).

Footnotes

The authors declare no competing financial interests.

Author Contributions K.T. and A.B. manufactured and characterized I–V of the OPV cells in Würzburg. O.M. manufactured and characterized I–V and EQE of the MAPI cells in Valencia. K.T. measured EL, PL and EQE of all cells in Würzburg. K.T. wrote the paper. O.M., A.B., C.D., H.J.S., V.D. and H.J.B. all contributed with discussion, feedback and comments on the manuscript. V.D. and H.J.B. supervised the research.

References

  1. Kirchhoff G. Ueber das Verhältniss zwischen dem Emissionsvermögen und dem Absorptionsvermögen der Körper für Wärme und Licht. Annalen der Physik und Chemie 109, 275–301 (1860). [Google Scholar]
  2. Planck M. Theorie der Wärmestrahlung. (Barth, Leipzig, 1906). [Google Scholar]
  3. Würfel P. The chemical potential of radiation. J. Phys. C Sol. Stat. 15, 3967–3985 (1982). [Google Scholar]
  4. Rau U. Reciprocity relation between photovoltaic quantum efficiency and electroluminescent emission of solar cells. Phys. Rev. B 76, 085303 (2007). [Google Scholar]
  5. Kirchartz T. & Rau U. Detailed balance and reciprocity in solar cells. Phys. Stat. Sol. (a) 205, 2737–2751 (2008). [Google Scholar]
  6. Kirchartz T., Matteis J. & Rau U. Detailed balance theory of excitonic and bulk heterojunction solar cells. Phys. Rev. B 78, 235320 (2008). [Google Scholar]
  7. Wang X. & Lundstrom M. S. On the use of Rau's reciprocity to deduce external radiative efficiency in solar cells. IEEE J. Photovoltaics 3, 1348–1353 (2013). [Google Scholar]
  8. Green M. A. Radiative efficiency of state-of-the-art photovoltaic cells. Prog. Photovoltaics 20, 472–476 (2012). [Google Scholar]
  9. Darling S. B. & You F. The case for organic photovoltaics. RSC Advances 3, 17633–17648 (2013). [Google Scholar]
  10. Kojima A., Teshima K., Shirai Y. & Miyasaka T. Organometal halide perovskites as visible-light sensitizers for photovoltaic cells. J. Am. Chem. Soc. 131, 6050–6051 (2009). [DOI] [PubMed] [Google Scholar]
  11. Wang J. T.-W. et al. Low-temperature processed electron collection layers of graphene/TiO2 nanocomposites in thin film perovskite solar cells. Nano Lett. 14, 724–730 (2014). [DOI] [PubMed] [Google Scholar]
  12. Liu D. & Kelly T. L. Perovskite solar cells with a planar heterojunction structure prepared using room-temperature solution processing techniques. Nat. Photon. 8, 133–138 (2014). [Google Scholar]
  13. Liu M., Johnston M. B. & Snaith H. J. Efficient planar heterojunction perovskite solar cells by vapour deposition. Nature 501, 395–398 (2013). [DOI] [PubMed] [Google Scholar]
  14. Burschka J. et al. Sequential deposition as a route to high-performance perovskite-sensitized solar cells. Nature 499, 316–319 (2013). [DOI] [PubMed] [Google Scholar]
  15. Ball J. M., Lee M. M., Hey A. & Snaith H. J. Low-temperature processed meso-superstructured to thin-film perovskite solar cells. En. & Environ. Sci. 6, 1739–1743 (2013). [Google Scholar]
  16. Lee M. M., Teuscher J., Miyasaka T., Murakami T. N. & Snaith H. J. Efficient hybrid solar cells based on meso-superstructured organometal halide perovskites. Science 338, 643–647 (2012). [DOI] [PubMed] [Google Scholar]
  17. Sun S. Y. et al. The origin of high efficiency in low-temperature solution-processable bilayer organometal halide hybrid solar cells. En. & Environ. Sci. 7, 399–407 (2014). [Google Scholar]
  18. Malinkiewicz O. et al. Perovskite solar cells employing organic charge transport layers. Nat. Photon. 8, 128–133 (2014). [Google Scholar]
  19. Jeng J-Y. et al. CH3NH3PbI3 Perovskite/fullerene planar-heterojunction hybrid solar cells. Adv. Mat. 25, 3727–3732 (2013). [DOI] [PubMed] [Google Scholar]
  20. Koster L. J. A., Smits E., Mihailetchi V. & Blom P. Device model for the operation of polymer/fullerene bulk heterojunction solar cells. Phys. Rev. B 72, 085205 (2005). [Google Scholar]
  21. Shockley W. & Queisser H. J. Detailed balance limit of efficiency of p-n junction solar cells. J. Appl. Phys. 32, 510 (1961). [Google Scholar]
  22. Snaith H. J. et al. Anomalous hysteresis in perovskite solar cells. J. Phys. Chem. Lett. 5, 1511–1515 (2014). [DOI] [PubMed] [Google Scholar]
  23. Sun S. et al. The origin of high efficiency in low-temperature solution-processable bilayer organometal halide hybrid solar cells. En. & Environ. Sci. 7, 399–407 (2014). [Google Scholar]
  24. Deschler F. et al. High photoluminescence efficiency and optically pumped lasing in solution-processed mixed halide perovskite semiconductors. J. Phys. Chem. Lett. 5, 1421–1426 (2014). [DOI] [PubMed] [Google Scholar]
  25. Kim H. S. et al. Lead iodide perovskite sensitized all-solid-state submicron thin film mesoscopic solar cell with efficiency exceeding 9%. Sci. rep. 2, 591 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Eperon G. E. et al. Formamidinium lead trihalide: a broadly tunable perovskite for efficient planar heterojunction solar cells. En. & Enviro. Sci. 7, 982 (2014). [Google Scholar]
  27. Tvingstedt K. et al. Electroluminescence from charge transfer states in polymer solar cells. J. Am. Chem. Soc. 131, 11819–11824 (2009). [DOI] [PubMed] [Google Scholar]
  28. Vandewal K., Tvingstedt K., Gadisa A., Inganäs O. & Manca J. V. Relating the open-circuit voltage to interface molecular properties of donor:acceptor bulk heterojunction solar cells. Phys. Rev. B 81, 125204 (2010). [Google Scholar]
  29. Kirchartz T., Taretto K. & Rau U. Efficiency limits of organic bulk heterojunction solar cells. J. Phys. Chem. C. 113, 17958–17966 (2009). [Google Scholar]
  30. Roldan-Carmona C. et al. Flexible high efficiency perovskite solar cells. En. & Environ. Sci. 7, 994–997 (2014). [Google Scholar]
  31. Malinkiewicz O., Lenes M., Brine H. & Bolink H. J. Meniscus coated high open-circuit voltage bi-layer solar cells. Rsc Adv. 2, 3335–3339 (2012). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES