Abstract
We study the evolution of male and female mating strategies and mate choice for female fecundity and male fertilization ability in a system where both sexes can mate with multiple partners, and where there is variation in individual quality (i.e. in the availability of resources individuals can allocate to matings, mate choice and production of gametes). We find that when the cost of mating differs between sexes, the sex with higher cost of mating is reluctant to accept matings and is often also choosy, while the other sex accepts all matings. With equal mating costs, the evolution of mating strategies depends on the strength of female sperm limitation, so that when sperm limitation is strong, males are often reluctant and choosy, whereas females tend to accept available matings. Male reluctance evolves because a male's benefit per mating diminishes rapidly as he mates too often, hence losing out in the process of sperm competition as he spends much of his resources on mating costs rather than ejaculate production. When sperm limitation is weaker, females become more reluctant and males are more eager to mate. The model thus suggests that reversed sex roles are plausible outcomes of polyandry and limited sperm production. Implications for empirical studies of mate choice are discussed.
Keywords: sperm competition, multiple mating, sexual selection, sex roles, polyandry
1. Introduction
Mate choice is an important aspect of sexual selection, but also a topic that has been vigorously debated ever since Darwin [1] introduced the theory of sexual selection (e.g. [2–5]). Mate choice can evolve when the availability of partners exceeds an individual's optimal mating frequency, and when an individual can accrue some sort of benefit by choosing between the available partners. For a very long time, studies and theory of mate choice concentrated almost exclusively on female mate choice (e.g. [2]), which is easy to understand as the theory of sexual selection was originally proposed to explain the evolution of exaggerated male secondary sexual characters that do not confer a survival advantage [1]. However, mate choice is not restricted to females but is a more general phenomenon, as males are also expected to exert mate choice in realistic biological circumstances [6,7]. A growing number of empirical studies have found evidence for male mate choice, including systems where males compete for mating opportunities, do not provide parental care and possess exaggerated secondary sexual characters (e.g. [6,8–11]).
The benefits of mate choice have been traditionally divided into ‘indirect’ benefits that influence the genetic quality of offspring (e.g. ‘good’ or ‘compatible’ genes [12], or increased attractiveness of sons [13]) and ‘direct’ benefits that increase the number of produced offspring (e.g. fecundity and fertility of potential mates, parenting quality [14]). For the past few decades, most theoretical and empirical work has focused on the difficult problem of mate choice for indirect benefits, whereas evolution of mate choice for direct benefits has received much less attention. However, mate choice for direct benefits is perhaps a more general biological phenomenon than choice for genetic benefits [3], and can possibly underlie choice also in systems where only indirect benefits have been traditionally considered [15].
Benefits of mate choice can also be divided into ‘fixed’ and ‘dilutable’ benefits [16]. Fixed benefits are those that do not depend on the preferred individual's number of mating partners, such as ‘good genes’ benefits. Dilutable benefits are those that are diminished in proportion to the number of partners mating with the same preferred mate. It is likely that most direct benefits of mate choice are dilutable. For example, males should prefer females with high fecundity as mating partners. However, if females mate multiply, the expected number of offspring per male decreases rapidly with the number of female matings, potentially eroding the benefit of choosing more fecund females altogether. Similarly, females should prefer males with good fertilization ability (large ejaculates), but if a male mates with several females, his ejaculates will be smaller and the fertilization ability correspondingly lower [17–19]. Thus, while mate choice for dilutable benefits is a biologically realistic scenario, it is complicated by the negative effects of choice on the magnitude of benefits of choice.
In this paper, we study the evolution of male and female mating strategies and mate choice for dilutable direct benefits—female fecundity and male fertilization ability—in a polyandrous system where both males and females can mate with multiple partners. Polyandry, where females mate with several males, is ubiquitous across the animal kingdom [20]. Multiple mating often increases the reproductive success of females (e.g. [21–27]). However, female multiple mating decreases the expected fitness gain per mating for males [28], and is expected to influence the evolution of male ejaculate sizes and male mating rates [29–31]. In addition, female mating rates and male ejaculate characteristics are also expected to exhibit coevolutionary dynamics [32,33].
For females, a male's ability to fertilize her eggs is a critical aspect of male quality. In many studies, female fertility has been shown to increase with increasing numbers of received sperm, and females have been found to prefer males that produce ejaculates with more sperm [18,34–38]. Although the cost of a single sperm is usually negligible in comparison with the cost of an egg, ejaculates often contain millions of sperm. Costs of producing ejaculates with sufficient numbers of sperm can set a limit to the number of successful copulations a male can perform [17,39,40]. Male mating capacity is thus not without limits, and this can lead to evolution of prudent male mating strategies, including male mate choice and strategic sperm allocation [10,39].
The feedbacks between male and female mating strategies and the expected payoffs per mating for both males and females make it very difficult to predict the types of mating strategies that will evolve in a population. The complexity of the feedbacks is probably the main reason why there are no models for coevolution of male and female mating strategies in polyandrous systems, despite the obvious biological relevance of such models compared with ones that look at evolution of reproductive strategies in one sex only. Here, we present a model for the evolution of male and female mating strategies and mate choice in a system where mating rates, female sperm limitation, the degree of sperm competition and male ejaculate sizes are all emergent properties of coevolving mating strategies.
2. Model description
We study the evolution of male and female mating strategies and mate choice in a system where both males and females vary in quality (i.e. in the amount of resources individuals can allocate to production of gametes, to direct mating costs and to mate choice). For simplicity, we assume the population consists of five equally frequent quality types of each sex. Variation in quality is assumed to be non-heritable, caused by, for example, variation in environmental conditions. Individuals express quality-dependent mating strategies that evolve to maximize their fitness, given the quality of the focal individual and the mating strategies of all other individuals in the population. Many empirical studies have found individuals to adjust their mating strategies depending on their condition [41–46]. We ran separate analyses for populations differing in (i) strength of sperm limitation (figure 1), (ii) sex-specific mating costs, (iii) cost of mate choice and (iv) population density, in order to assess the effects of these variables on the evolution of preference functions (table 1).
Figure 1.
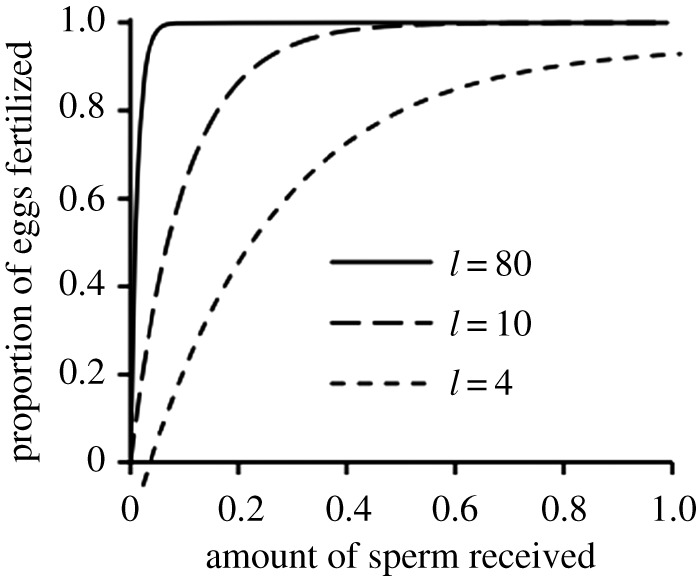
Female fertility functions mapping the proportion of eggs fertilized to the amount of sperm received. Weak sperm limitation l = 80, intermediate sperm limitation l = 10 and strong sperm limitation l = 4.
Table 1.
Model parameters and functions.
| variables and parameters | description | range, values |
|---|---|---|
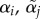 |
Elevation (intercept) of mate preference function for type i females and type j males. (Throughout, male variables are labelled with a tilde ∼, which is easy to remember by its resemblance to the tail of a sperm.) The intercept evolves independently for each type of male and female. | 0 ≤ α ≤ 1 |
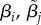 |
Slope of mate preference function for type i females and type j males. The slope evolves independently for each type of male and female. | −∞ < β < ∞ |
| e | Expected number of mate encounters (proxy for population density). Assuming an even sex ratio, this is the same for both sexes. | [10,20] |
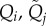 |
Quality of type i female and type j male. Corresponds to the amount of resources available to invest in choosiness, mating, and gamete production. For both sexes, we model five different types. | [0.5, 0.625, 0.75, 0.875, 1] |
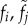 |
Frequency of type i females and type j males. We assume all types are equally frequent. | 0.2 |
| cch | Cost of choosiness. | [0.01, 0.1] |
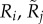 |
Resources available to type i females and type j males for gamete production and mating. We assume the ability to discriminate between mates requires time and/or sensory and neural resources that could otherwise be used for finding food. Thus, for an individual of given Q and β, we let R = Q(1 − βcch) be the amount of resources available for gamete production and mating. We assume that R is reflected in visible traits (e.g. body size and nutritional state), and is therefore the aspect of quality that is observable by potential mates. | |
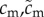 |
Cost of mating for females and males. To make no a priori assumption about multiple mating being intrinsically more beneficial for either low- or high-quality individuals, we assume that all individuals of the same sex suffer the same proportional resource loss per additional mating. (For an alternative formulation with absolute rather than proportional mating costs for males, see the electronic supplementary material.) | [0.01, 0.1] |
| l | Saturation coefficient of the female fertility function g (see below). | [4, 10, 80] |
| s | The total amount of sperm a female receives from all her matings. | |
| g | Female fertility function; maps female fertility to the amount of sperm received s. g = 1 − exp(−l · s) | |
| pij |
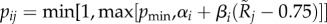 . Probability that a type i female accepts a type j male. The mid-point (0.75) of the considered quality range is used as a reference point at which mate acceptance takes its baseline value αi. . Probability that a type i female accepts a type j male. The mid-point (0.75) of the considered quality range is used as a reference point at which mate acceptance takes its baseline value αi. |
|
 |
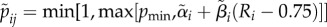 . Probability that a type j male accepts a type i female. . Probability that a type j male accepts a type i female. |
|
| pmin | Minimum mate acceptance probability that can be implemented by a strategy. pmin > 0 avoids convergence problems that arise when behaviour towards certain classes becomes selectively neutral if those classes always reject the focal class. | 0.001 |
In our model, each type of male and female is characterized by a mate preference function with two evolving parameters: α, the probability of accepting an average-quality individual of the opposite sex as a mating partner, and β, the slope of the acceptance probability on the quality of the opposite sex individuals. Non-zero slope of the preference function indicates choosiness [4]. Choosiness is assumed to be costly, so that an individual with a steeper slope allocates a larger proportion of available resources to discriminating between potential mates, and respectively, a smaller proportion to other reproductive functions (gamete production and direct mating costs).
We further assume that each mating carries a cost, the magnitude of which is controlled by a sex-specific parameter. In order to focus on key differences between males and females (males strive to maximize the number of sired offspring while females strive to maximize the number of fertilized eggs), we model the cost of mating similarly for both males and females. Specifically, we assume that the cost of mating is proportional to the amount of resources of an individual, so that individuals with fewer resources pay a smaller absolute cost per mating. This assumption is made in order not to make matings relatively more costly for lower-quality individuals, which would a priori prevent low-quality individuals from expressing high mating rates. However, alternatively, we have also modelled a system where the absolute cost of mating is the same for all males, regardless of quality and the results are largely unchanged (see the electronic supplementary material, figures S2–S3). The cost of mating may reflect energetic or time costs associated with obtaining and performing a mating (e.g. costs of courtship or copulation behaviour), or risk of losing a proportion of future reproductive success through damage incurred during copulation (e.g. [47,48]).
In the model, female fitness is the number of fertilized eggs produced, and male fitness is the number of eggs the male fertilizes. Female fitness depends on the amount of resources allocated to production of eggs, and the rate at which those eggs are fertilized. Female fertilization rate is modelled as a saturating function of sperm intake, so if the female receives few sperm she can only fertilize a small proportion of her eggs, but if she receives many sperm, fertilization rate asymptotically approaches 100%. Male fitness is the sum of all the eggs a male fertilizes from the females he mates with. If a female mates with more than one male, the focal male's share of paternity is given by his share of total sperm the female received from all the males she mated with (i.e. we assume fair raffle sperm competition [49]).
Male ejaculate size is modelled as the amount of resources allocated to gamete production divided by the expected number of matings for the male. For simplicity, all ejaculates of a male are of equal size (i.e. a male does not adjust ejaculate size to different female types). A male has the same ejaculate size in every mating (i.e. males do not run out of sperm). This may be either because actual matings match expected matings, or because males store sperm over sufficient timespans so that stochastic deficits and surpluses in mating success average out over time. Each mating costs a proportion of the male's resources. What remains (if anything) of these resources after subtracting these costs is interpreted as total ejaculate, which is divided evenly between matings.
The technical procedure to calculate the fitness of resident and mutant strategies for each male and female type, and to find the evolutionary equilibrium, is as follows. For a type j resident male with mate acceptance probabilities 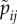 , the expected number of matings with type i females is
, the expected number of matings with type i females is 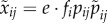 . Here, e is the expected number of females encountered, fi is the proportion of type i females among all potential females and pij is a type i female's probability of accepting by a type j male. (Throughout, we mark male variables with a tilde: ∼. And in double-indexed variables, we denote female type by the first index and male type by the second index.) Similarly, for a mutant male with behaviour
. Here, e is the expected number of females encountered, fi is the proportion of type i females among all potential females and pij is a type i female's probability of accepting by a type j male. (Throughout, we mark male variables with a tilde: ∼. And in double-indexed variables, we denote female type by the first index and male type by the second index.) Similarly, for a mutant male with behaviour 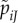 (reflecting mutated baseline acceptance
(reflecting mutated baseline acceptance 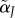 and/or choosiness
and/or choosiness 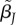 ), the expected number of matings with type i females is
), the expected number of matings with type i females is 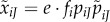 . We use the capitalized index J for mutants because later we need to keep track of both mutant and resident types in the same equation.
. We use the capitalized index J for mutants because later we need to keep track of both mutant and resident types in the same equation.
The expected total number of matings is 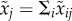 for resident males and
for resident males and 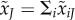 for mutant males.
for mutant males.
The ejaculate size of a type J mutant is given by 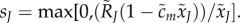 Here, the maximum is taken to prevent negative ejaculate sizes when males mate more than they can ‘afford’. If male behaviour is near its optimum, however, maximization is unnecessary because males avoid mating too often.
Here, the maximum is taken to prevent negative ejaculate sizes when males mate more than they can ‘afford’. If male behaviour is near its optimum, however, maximization is unnecessary because males avoid mating too often.
For a type i female, the expected number of matings with type j males is 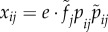 .
.
We model sperm limitation using the function g[s] = 1 − exp[−l s], which maps female fertility to sperm intake s in a saturating manner. Saturation is faster (i.e. sperm limitation is weaker) if the saturation coefficient l is large (figure 1).
Female reproduction in a given reproductive cycle is a function of resources Ri, number of matings x, and sperm intake s:
Here, the expression Ri(1 − xcm) can be interpreted as fecundity (i.e. the number of eggs produced per cycle). This formulation implies that females who mate more than xmax = ceil[1/cm] times will not produce any offspring in the cycle in question. Such mating histories without offspring production can be left out of the fitness calculations.
Fitness of a mutant type J male is given by
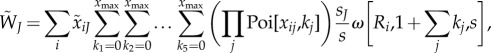 |
where Poi[x,k] is the Poisson probability of mating k times when the expected number is x, and s = sJ + ∑jkjsj is the total sperm intake from a mating history that includes 1+ ∑jkj matings in total. In the calculation of 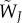 , the first summation is over female types that may mate with the focal male (an expected number of
, the first summation is over female types that may mate with the focal male (an expected number of 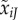 times). Within each female type, we need to account for sperm competition faced by the focal male. Hence the subsequent summations go through possible numbers of matings with male type after male type, jointly covering all possible female mating histories with resident males. The multiplication gives the female's probability of mating k1 times with type 1 males and k2 times with type 2 males, etc. The term sJ/s is the focal male's paternity share, reflecting his ejaculate size relative to the female's total sperm intake. The last term ω represents the offspring produced by type i females under any given mating history.
times). Within each female type, we need to account for sperm competition faced by the focal male. Hence the subsequent summations go through possible numbers of matings with male type after male type, jointly covering all possible female mating histories with resident males. The multiplication gives the female's probability of mating k1 times with type 1 males and k2 times with type 2 males, etc. The term sJ/s is the focal male's paternity share, reflecting his ejaculate size relative to the female's total sperm intake. The last term ω represents the offspring produced by type i females under any given mating history.
Mutant male fitness 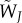 can be expressed as a function of the underlying mutant behavioural parameters
can be expressed as a function of the underlying mutant behavioural parameters 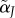 and
and 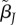 , and at equilibrium should be at a local maximum with respect to both of these.
, and at equilibrium should be at a local maximum with respect to both of these.
Similarly, fitness of a mutant type I female is given by
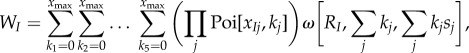 |
and can be expressed as a function of the underlying mutant behavioural parameters αI and βI.
To increase computational efficiency, we neglect a small proportion of females with extreme mating histories, by replacing xmax with the lowest integer that accounts for at least 99.99% of female mating histories.
We found equilibria iteratively as follows. In each time step, for each type of each sex, we calculated mutant fitnesses for the 3 × 3 = 9 strategies that can be created by independently increasing (by a small amount δ), decreasing or leaving unchanged each of the two behavioural parameters (baseline acceptance and choosiness) of the resident strategy. If any mutant strategy had higher fitness than the resident strategy, we used the best mutant strategy as the resident strategy of the next time step. We successively used δ = 0.001, δ = 0.0001 and δ = 0.00001 for 5000 iterations each. For each parameter combination, we used two alternative starting points, corresponding to initial strategies with low (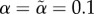 ) or high (
) or high (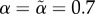 ) baseline acceptance, and zero choosiness (
) baseline acceptance, and zero choosiness (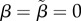 ). Convergence between the simulations was practically perfect for all cases except the case depicted in the seventh column in the electronic supplementary material, figure S3, and even there the deviance was minor (not shown).
). Convergence between the simulations was practically perfect for all cases except the case depicted in the seventh column in the electronic supplementary material, figure S3, and even there the deviance was minor (not shown).
3. Results
The equilibrium mate preference functions for different sex-specific mating costs and for different strengths of sperm limitation (assuming cheap mate choice and low population density) are shown in figure 2. In the electronic supplementary material, we present results for expensive mate choice at low population and for both cheap and expensive mate choice at higher population density (electronic supplementary material, figure S1; all cases presented in electronic supplementary material assume strong sperm limitation). At higher population density, the patterns are qualitatively similar to the patterns at low population density, except that mate acceptance probabilities are lower for the more reluctant sex; this can be understood as a strategy to avoid excessive mating costs at high population density. For ease of discussion, we mainly focus on the results for low population density.
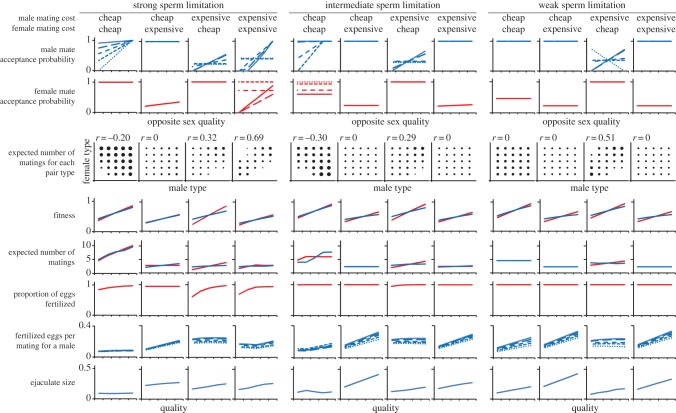
Figure 2.
Evolutionarily stable outcomes for strong, intermediate and weak sperm limitation at low density (e = 10) and with cheap mate choice (cch = 0.01). For each sperm limitation scenario, the columns represent cases with different combinations of sex-specific mating costs. The first row of panels shows mate acceptance probabilities for different types of males (solid line indicates highest quality males and the dotted line lowest quality males), with female quality on the x-axis. The second row shows the corresponding mate acceptance probabilities for females. The third row shows the expected number of matings for each pair type, with dot size indicating frequency. The correlation coefficient is calculated by weighting each pair with the expected frequency of matings. The fourth row shows the fitness for each type of male and female (connected by a line: blue for males and red for females). The fifth row shows the expected number of matings for each type of male and female. The sixth row shows the proportion of fertilized eggs for each female type. The seventh row shows the amount of eggs each male type will fertilize by mating with a female of given type. The bottom row shows the ejaculate size for each male type.
We find that when the cost of mating differs between the sexes (being cheap for one sex and expensive for the other), mating strategies of the two sexes evolve to be highly divergent. The sex for which matings are cheap evolves to accept all mating opportunities, while the sex for which matings are expensive evolves to be reluctant, and sometimes also choosy (figure 2). The reason for the divergence in mating strategies is that the sex for which matings are more expensive restricts the number of matings in the population to a level which is optimal for that sex. At this point, members of the other sex would still benefit from increased number of matings, and this sex consequently evolves to accept all mating opportunities (of course, if population density was extremely low so that reproduction of both sexes would be limited by availability of mating partners, both sexes should evolve eagerness to mate). Our results show that when the costs of mating differ substantially between the two sexes, evolution should result in highly divergent sex roles in eagerness to mate.
The evolution of mating strategies also depends on the strength of sperm limitation. With strong sperm limitation and cheap matings for both sexes (figure 2, column 1), females evolve to accept all matings and (especially the lower-quality) males evolve to be choosy, preferring high-quality females. With intermediate sperm limitation and cheap matings for both sexes (figure 2, column 5), lower-quality males again prefer high-quality females, but female mating strategies diverge, with high-quality females refusing a fraction of mating opportunities and lowest quality females accepting all mating opportunities. The difference in female strategies is explained by male choosiness: low-quality females are discriminated against by low-quality males and thus need to accept all mating opportunities to achieve high fertilization success, whereas high-quality females, being accepted by all males, need to limit their mating rate to avoid superfluous mating costs. With weak sperm limitation and cheap matings for both sexes (figure 2, column 9), all males are eager to mate and all females show low mate acceptance rate without choosiness. It is easy to understand why females are eager to mate when sperm limitation strong: in these conditions, it is difficult for females to obtain enough sperm for fertilizing all their eggs. On the other hand, when sperm limitation is weak, females can easily get enough sperm for fertilization, and extra matings would only result in higher mating costs without increasing fertility.
When matings are expensive for either one or both of the sexes, we observe a variety of mating strategies evolving, especially for males. In contrast to the cases discussed above, here we often observe the highest-quality males being most choosy (see figure 2, columns 3, 4, 7 and 11). Why males display so much condition-dependent choosiness is not intuitively obvious, but the following mechanisms may play a role. Before the evolution of choosiness in either sex, all males experience the same mating frequency, with high-quality males having larger ejaculates than low-quality males. As paternity is a saturating function of ejaculate size, high-quality males experience lower marginal paternity gains; in other words, their paternity does not change much if they slightly reduce their ejaculate size. This creates an incentive for high-quality males to re-allocate resources from ejaculate size to either choosiness or mating frequency (or both). Which option they choose appears to depend on the magnitude of male mating costs: if male mating is expensive, high-quality males invest in choosiness (figure 2, columns 3, 4, 7 and 11). By contrast, if male mating is cheap, high-quality males invest in mating frequency (figure 2, columns 1 and 5). Low-quality males may then become the choosy ones, since their lower mating frequency (lower elevation of mate preference function) makes choice more economical for them. This is because the same level of choosiness (same slope of the mate preference function) has a greater effect on relative mating rates when the elevation of the mate preference function is low than when it is high. For example, the difference between 1% and 2% mate acceptance probability means that the more preferred type is mated twice as often as the less preferred type. By contrast, the difference between 99% and 100% mate acceptance probability has only negligible effect on mating rates between the less and more preferred types. In one particularly intriguing case (figure 2, column 11), we see the lowest-quality males preferring low-quality females while higher-quality males prefer higher-quality females. This may arise because low-quality males (whose ejaculates are small) avoid females presenting a high level of sperm competition.
We observe that female choice evolves only when choice is cheap, whereas male choice evolves also when choice is expensive (see the electronic supplementary material, figures S1–S3). In our model, female choice can only yield benefits if males differ in their ejaculate sizes (and thus in their capability to increase the fertilization rate of female eggs). In some circumstances (e.g. first column in figure 2), male mating strategies evolve in a way that equalizes the ejaculate sizes for all males, removing any possible benefits of female choice. Also, if a female is strongly sperm limited, for example due to male discrimination (see the low-quality females in the fourth column in figure 2), she should accept all mating opportunities and not be choosy. On the other hand, if a female has more mating opportunities than she needs to achieve high fertilization rate (e.g. due to males preferring this type of female), it may benefit her to limit the number of matings and to choose males that provide the largest ejaculates (see the fourth column in figure 2).
The benefits of choice for a male can be visualized by calculating the number of eggs a male expects to fertilize by mating with each type of female. If female types differ in this respect, then it may be possible for a male to increase his fitness by biasing his mating efforts towards females that provide higher fitness returns per mating. Interestingly, comparing the cheap and expensive mate choice scenarios when matings are cheap for both sexes (compare the first column in figure 2 and electronic supplementary material, figure S1), we see that while male mate choice only evolves when choice is cheap, the benefits of choice appear to be larger in the expensive mate choice scenario than in the cheap mate choice scenario (the slopes in the panel ‘fertilized eggs per mating for a male’ are steeper). The reason for this is that the benefits of choice are dilutable: male choice for females that provide higher fitness returns increases the number of matings for these females, which consequently lowers the fitness benefits these females provide. When choice is cheap, minor benefits of choosiness are sufficient to maintain choice in the population. However, when choosiness is expensive, it may not pay for males to choose even when there are clear differences in fitness returns among different female types. At evolutionary equilibrium, the feedbacks between choosiness and the benefits of choice result in the surprising pattern that choosiness is highest in populations where the benefits of choice appear smallest. And vice versa, the benefits of choice appear to be largest in populations where choosiness is absent.
These considerations, and the underlying results, highlight the complexity of models that allow for interactions among different strategies—as the strategy of each type in both sexes affects the optimal strategies of each other type in both sexes, the system can become so complex that interpretations are difficult. This teaches us an important lesson: if we know that the system has complex interactions, we should be very cautious when formulating hypotheses about patterns we expect to see in nature. A case in point is the degree of assortative mating we observe in our simulations. Depending on the costs of mating, the correlation between mating partner qualities can be anything from slightly negative to strongly positive (see the correlations in the panel ‘expected number of matings for each pair type’ in figure 2). Yet all these patterns arise from the same mechanism, but under different values for sex-specific mating costs.
Our model also reveals that information about mating patterns does not constitute direct evidence about mate choice by the opposite sex. For example, we sometimes observe that higher-quality males mate much more often than lower-quality males (see first and fifth column in figure 2). Such a pattern would be expected if females preferred higher-quality males as mating partners, in line with the classic view of sex roles and sexual selection. However, in our model, this is not the case. Instead, lower-quality males mate less because they have lower mate acceptance rates and they are more choosy than higher-quality males. Thus, a pattern that a naive observer could take as evidence of female preference for high-quality males is actually caused by reluctance and choosiness of the lowest-quality males. The important take-home message here is that it is not possible to infer female choice (or male choice) from mating frequencies alone. Instead, choosiness must be measured directly by quantifying the mate preferences.
4. Discussion
We analysed the evolution of male and female mate preference functions in a system where mating rates, female sperm limitation, degree of sperm competition and male ejaculate sizes are all emergent properties of evolving male and female mating strategies. While many previous models have considered interactions between two or more of these factors [16,29,30,32,33,50,51], no previous study has considered a dynamic system where all these critical factors can evolve in response to each other. Härdling et al. [52] analysed a model that is conceptually similar to ours, but their model did not allow for sperm competition, direct mating costs or costly mate preferences, and differed in many assumptions (e.g. having only two types of males and females). As far as we are aware, our model is the first to consider the evolution of mutual mate choice in polyandrous systems, despite the repeated calls for models that explicitly incorporate the dynamic feedbacks between evolving male and female reproductive strategies and allow for female multiple mating (e.g. [50,53]).
Our model produced a number of results that are relevant for understanding variation in male and female sex roles observed in nature. Perhaps the most important result is that female sperm limitation can select for evolution of female eagerness and multiple mating, which diminishes the expected benefit from each mating for males and results in male reluctance and choosiness. Male choosiness causes non-preferred females to become even more sperm limited, which then further selects for eagerness in these females. The results of our model are in line with mounting empirical evidence for feedbacks among sperm limitation, female competition and male choice in polyandrous systems [8–10,17,25,54,55].
The results of our model also suggest the traditional idea of eager males and choosy females does not necessarily hold when polyandry is considered. The ‘Darwin–Bateman paradigm’ [56] of traditional sex roles was developed with the implicit assumption of female monandry and unlimited male mating capacity, which would give rise to a steep and linear relationship between mating and reproductive success in males. However, when female multiple mating and a trade-off between male mating rate and sperm competitive ability are considered, the relationship between mating rate and reproductive success can in fact be stronger in females than in males, resulting in reversed sex roles [57]. In our simulations, we often observe reversed sex roles, with males being reluctant and choosy, and females being eager and non-choosy, especially when sperm limitation is strong. Our results thus add to understanding the complexity of interactions that underlie variation in sex roles observed in natural systems.
Our model considers mate choice for dilutable benefits (female fecundity and male fertilization ability). Such benefits are expected to decrease with the evolution of mate choice: as preferred individuals mate more, the benefit of mating with them is diluted as it is shared among their partners. Nevertheless, mate choice does exist at evolutionary equilibrium in our simulations, and it is more common when mate choice is cheap than when it is costly. The feedback between mate choice and the magnitude of benefits of choice results in the interesting pattern that when mate choice evolves (when choice is cheap), the benefits of choice seem to be almost undetectable. By contrast, when mate choice does not evolve (when choice is expensive), there would seem to be appreciable benefits of mate choice. We conclude from this that, to detect dilutable benefits of mate choice in empirical studies, it is necessary to use experimental designs that hold constant the mating frequency of the chosen sex.
The model also exposes a problem for inferring the cause of differential mating success from observational data. Say, for example, that a researcher was measuring some aspect of male quality and correlating it with male mating rate, and finding that higher-quality males mate more often than lower-quality males. Such a pattern might easily (but erroneously) be taken as evidence for female choice, or for male–male competition for mating opportunities. In our simulations, we often observe higher-quality males mating more than lower-quality males. However, this pattern most often arises from the lowest-quality males being more reluctant, more choosy or both than higher-quality males, not from female choice or male–male competition. To infer the cause of biases in mating rates, it is thus not sufficient to record mating rates, but it is necessary to study the underlying mechanisms directly. Higher choosiness of low-quality males was also predicted in the model of Härdling et al. [52]. There is very little empirical research on male quality and choosiness, but observations of increased choosiness in sperm-depleted Drosophila melanogaster males [46] suggest that at least temporary variation in male quality influences choosiness in the manner these models predict. Further empirical tests on the association between male quality and choosiness will be needed to assess the generality of the pattern.
While our model reveals how feedbacks between sperm limitation and sperm competition can influence the evolution of mating strategies and mate choice, the model does not consider factors like mate guarding, strategic ejaculations or heritable variation in individual quality. In our model, female sperm limitation is the factor driving female multiple mating. However, similar dynamics and mating strategies may evolve also in systems where females mate multiply to increase the genetic diversity of offspring, to protect against infanticide by paternity confusion, to safeguard against infertile matings or to gain access to nuptial gifts [28,58]. In particular, we argue that male reluctance and choosiness are plausible outcomes of sperm competition and female multiple mating.
Supplementary Material
Acknowledgements
We thank Piret Avila and Petri Rautiala for helpful discussions, and two anonymous reviewers for comments that improved the manuscript.
Data accessibility
Matlab codes for the simulations are publicly available on the Dryad Digital Repository (http://dx.doi.org/10.5061/dryad.1vc8g) [59].
Authors' contributions
M.P. conceived the study and drew the figures; L.F. and M.P. developed the model, analysed the data and wrote the manuscript; L.F. coded the simulations.
Competing interests
We have no competing interests.
Funding
The work was supported by the Academy of Finland (grant no. 258386 for M.P. and grant no. 283486 for L.F.).
References
- 1.Darwin C. 1871. The descent of man and selection in relation to sex. London, UK: John Murray. [Google Scholar]
- 2.Kokko H, Brooks R, Jennions MD, Morley J. 2003. The evolution of mate choice and mating biases. Proc. R. Soc. Lond. B 270, 653–664. ( 10.1098/rspb.2002.2235) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kotiaho JS, Puurtinen M. 2007. Mate choice for indirect genetic benefits: scrutiny of the current paradigm. Funct. Ecol. 21, 638–644. ( 10.1111/j.1365-2435.2007.01286.x) [DOI] [Google Scholar]
- 4.Edward DA. 2015. The description of mate choice. Behav. Ecol. 26, 301–310. ( 10.1093/beheco/aru142) [DOI] [Google Scholar]
- 5.Bateson P. 1983. Mate choice. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 6.Edward DA, Chapman T. 2011. The evolution and significance of male mate choice. Trends Ecol. Evol. 26, 647–654. ( 10.1016/j.tree.2011.07.012) [DOI] [PubMed] [Google Scholar]
- 7.Bonduriansky R. 2001. The evolution of male mate choice in insects: a synthesis of ideas and evidence. Biol. Rev. 76, 305–339. ( 10.1017/S1464793101005693) [DOI] [PubMed] [Google Scholar]
- 8.Preston BT, Stevenson IR, Pemberton JM, Coltman DW, Wilson K. 2005. Male mate choice influences female promiscuity in Soay sheep. Proc. R. Soc. B 272, 365–373. ( 10.1098/rspb.2004.2977) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sæther SA, Fiske P, Kålås JA. 2001. Male mate choice, sexual conflict and strategic allocation of copulations in a lekking bird. Proc. R. Soc. Lond. B 268, 2097–2102. ( 10.1098/rspb.2001.1745) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bro-Jorgensen J. 2007. Reversed sexual conflict in a promiscuous antelope. Curr. Biol. 17, 2157–2161. ( 10.1016/j.cub.2007.11.026) [DOI] [PubMed] [Google Scholar]
- 11.Cotton AJ, Cotton S, Small J, Pomiankowski A. 2014. Male mate preference for female eyespan and fecundity in the stalk-eyed fly, Teleopsis dalmanni. Behav. Ecol. 26, 376–385. ( 10.1093/beheco/aru192) [DOI] [Google Scholar]
- 12.Puurtinen M, Ketola T, Kotiaho J. 2009. The good-genes and compatible-genes benefits of mate choice. Am. Nat. 174, 741–752. ( 10.1086/606024) [DOI] [PubMed] [Google Scholar]
- 13.Kokko H, Booksmythe I, Jennions MD. 2015. Mate-sampling costs and sexy sons. J. Evol. Biol. 28, 259–266. ( 10.1111/jeb.12532) [DOI] [PubMed] [Google Scholar]
- 14.Kirkpatrick M, Ryan MJ. 1991. The evolution of mating preferences and the paradox of the lek. Nature 350, 33–38. ( 10.1038/350033a0) [DOI] [Google Scholar]
- 15.Sheldon BC. 1994. Male phenotype, fertility, and the pursuit of extra-pair copulations by female birds. Proc. R. Soc. Lond. B 257, 25–30. ( 10.1098/rspb.1994.0089) [DOI] [Google Scholar]
- 16.Tazzyman SJ, Seymour RM, Pomiankowski A. 2012. Fixed and dilutable benefits: female choice for good genes or fertility. Proc. R. Soc. B 279, 334–340. ( 10.1098/rspb.2011.0633) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Preston BT, Stevenson IR, Pemberton JM, Wilson K. 2001. Dominant rams lose out by sperm depletion. Nature 409, 681–682. ( 10.1038/35055617) [DOI] [PubMed] [Google Scholar]
- 18.Nakatsuru K, Kramer DL. 1982. Is sperm cheap? Limited male fertility and female choice in the lemon tetra (Pisces, Characidae). Science 216, 753–755. ( 10.1126/science.216.4547.753) [DOI] [PubMed] [Google Scholar]
- 19.Warner RR, Shapiro DY, Marcanato A, Petersen CW. 1995. Sexual conflict: males with highest mating success convey the lowest fertilization benefits to females. Proc. R. Soc. Lond. B 262, 135–139. ( 10.1098/rspb.1995.0187) [DOI] [PubMed] [Google Scholar]
- 20.Taylor ML, Price TAR, Wedell N. 2014. Polyandry in nature: a global analysis. Trends Ecol. Evol. 29, 376–383. ( 10.1016/j.tree.2014.04.005) [DOI] [PubMed] [Google Scholar]
- 21.Arnqvist G, Nilsson T. 2000. The evolution of polyandry: multiple mating and female fitness in insects. Anim. Behav. 60, 145–164. ( 10.1006/anbe.2000.1446) [DOI] [PubMed] [Google Scholar]
- 22.Caspers BA, Krause ET, Hendrix R, Kopp M, Rupp O, Rosentreter K, Steinfartz S. 2014. The more the better: polyandry and genetic similarity are positively linked to reproductive success in a natural population of terrestrial salamanders (Salamandra salamandra). Mol. Ecol. 23, 239–250. ( 10.1111/mec.12577) [DOI] [PubMed] [Google Scholar]
- 23.Noble DWA, Keogh JS, Whiting MJ. 2013. Multiple mating in a lizard increases fecundity but provides no evidence for genetic benefits. Behav. Ecol. 24, 1128–1137. ( 10.1093/beheco/art040) [DOI] [Google Scholar]
- 24.Okada K, Archer CR, Katsuki M, Suzaki Y, Sharma MD, House CM, Hosken DJ. 2015. Polyandry and fitness in female horned flour beetles, Gnatocerus cornutus. Anim. Behav. 106, 11–16. ( 10.1016/j.anbehav.2015.05.008) [DOI] [Google Scholar]
- 25.Baker RH, Ashwell RI, Richards TA, Fowler K, Chapman T, Pomiankowski A. 2001. Effects of multiple mating and male eye span on female reproductive output in the stalk-eyed fly, Cyrtodiopsis dalmanni. Behav. Ecol. 12, 732–739. ( 10.1093/beheco/12.6.732) [DOI] [Google Scholar]
- 26.Byrne PG, Whiting MJ. 2008. Simultaneous polyandry increases fertilization success in an African foam-nesting treefrog. Anim. Behav. 76, 1157–1164. ( 10.1016/j.anbehav.2008.05.019) [DOI] [Google Scholar]
- 27.Taylor ML, Wigmore C, Hodgson DJ, Wedell N, Hosken DJ. 2008. Multiple mating increases female fitness in Drosophila simulans. Anim. Behav. 76, 963–970. ( 10.1016/j.anbehav.2008.05.015) [DOI] [Google Scholar]
- 28.Parker GA, Birkhead TR. 2013. Polyandry: the history of a revolution. Phil. Trans. R. Soc. B 368, 20120335 ( 10.1098/rstb.2012.0335) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Williams PD, Day T, Cameron E. 2005. The evolution of sperm-allocation strategies and the degree of sperm competition. Evolution 59, 492–499. ( 10.1554/04-668.1.s1) [DOI] [PubMed] [Google Scholar]
- 30.Fromhage L, McNamara JM, Houston AI. 2008. Sperm allocation strategies and female resistance: a unifying perspective. Am. Nat. 172, 25–33. ( 10.1086/587806) [DOI] [PubMed] [Google Scholar]
- 31.Parker GA, Pizzari T. 2010. Sperm competition and ejaculate economics. Biol. Rev. 85, 897–934. ( 10.1111/j.1469-185X.2010.00140.x) [DOI] [PubMed] [Google Scholar]
- 32.Abe J, Kamimura Y. 2015. Sperm economy between female mating frequency and male ejaculate allocation. Am. Nat. 185, 406–416. ( 10.1086/679586) [DOI] [PubMed] [Google Scholar]
- 33.Bocedi G, Reid JM. 2016. Coevolutionary feedbacks between female mating interval and male allocation to competing sperm traits can drive evolution of costly polyandry. Am. Nat. 187, 334–350. ( 10.1086/684746) [DOI] [PubMed] [Google Scholar]
- 34.Markow TA, Quaid M, Kerr S. 1978. Male mating experience and competitive courtship success in Drosophila melanogaster. Nature 276, 821–822. ( 10.1038/276821a0) [DOI] [Google Scholar]
- 35.Harris WE, Moore PJ. 2005. Female mate preference and sexual conflict: females prefer males that have had fewer consorts. Am. Nat. 165, S64–S71. ( 10.1086/429352) [DOI] [PubMed] [Google Scholar]
- 36.Scarponi V, Chowdhury D, Godin J-GJ. 2015. Male mating history influences female mate choice in the Trinidadian guppy (Poecilia reticulata). Ethology 121, 1091–1103. ( 10.1111/eth.12427) [DOI] [Google Scholar]
- 37.Smith C, Reichard M. 2005. Females solicit sneakers to improve fertilization success in the bitterling fish (Rhodeus sericeus). Proc. R. Soc. B 272, 1683–1688. ( 10.1098/rspb.2005.3140) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Stockley P, Bro-Jorgensen J. 2011. Female competition and its evolutionary consequences in mammals. Biol. Rev. 86, 341–366. ( 10.1111/j.1469-185X.2010.00149.x) [DOI] [PubMed] [Google Scholar]
- 39.Wedell N, Gage MJG, Parker GA. 2002. Sperm competition, male prudence and sperm-limited females. Trends Ecol. Evol. 17, 313–320. ( 10.1016/S0169-5347(02)02533-8) [DOI] [Google Scholar]
- 40.Dewsbury DA. 1982. Ejaculate cost and male choice. Am. Nat. 119, 601–610. ( 10.1086/283938) [DOI] [Google Scholar]
- 41.Basolo AL. 2004. Variation between and within the sexes in body size preferences. Anim. Behav. 68, 75–82. ( 10.1016/j.anbehav.2003.07.019) [DOI] [Google Scholar]
- 42.Holveck MJ, Riebel K. 2010. Low-quality females prefer low-quality males when choosing a mate. Proc. R. Soc. B 277, 153–160. ( 10.1098/rspb.2009.1222) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Cotton S, Small J, Pomiankowski A. 2006. Sexual selection and condition-dependent mate preferences. Curr. Biol. 16, R755–R765. ( 10.1016/j.cub.2006.08.022) [DOI] [PubMed] [Google Scholar]
- 44.Candolin U, Salesto T. 2009. Does competition allow male mate choosiness in threespine sticklebacks? Am. Nat. 173, 273–277. ( 10.1086/595753) [DOI] [PubMed] [Google Scholar]
- 45.Bel-Venner MC, Dray S, Allaine D, Menu F, Venner S. 2008. Unexpected male choosiness for mates in a spider. Proc. R. Soc. B 275, 77–82. ( 10.1098/rspb.2007.1278) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Byrne PG, Rice WR. 2006. Evidence for adaptive male mate choice in the fruit fly Drosophila melanogaster. Proc. R. Soc. B 273, 917–922. ( 10.1098/rspb.2005.3372) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Edvardsson M, Tregenza T. 2005. Why do male Callosobruchus maculatus harm their mates? Behav. Ecol. 16, 788–793. ( 10.1093/beheco/ari055) [DOI] [Google Scholar]
- 48.Stockley P. 1997. Sexual conflict resulting from adaptations to sperm competition. Trends Ecol. Evol. 12, 154–159. ( 10.1016/S0169-5347(97)01000-8) [DOI] [PubMed] [Google Scholar]
- 49.Parker GA. 1982. Why are there so many tiny sperm? Sperm competition and the maintenance of two sexes. J. Theor. Biol. 96, 281–294. ( 10.1016/0022-5193(82)90225-9) [DOI] [PubMed] [Google Scholar]
- 50.Tazzyman SJ, Pizzari T, Seymour RM, Pomiankowski A. 2009. The evolution of continuous variation in ejaculate expenditure strategy. Am. Nat. 174, E71–E82. ( 10.1086/603612) [DOI] [PubMed] [Google Scholar]
- 51.Alonzo SH, Pizzari T. 2013. Selection on female remating interval is influenced by male sperm competition strategies and ejaculate characteristics. Phil. Trans. R. Soc. B 368, 20120044 ( 10.1098/rstb.2012.0044) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Härdling R, Gosden T, Aguilee R. 2008. Male mating constraints affect mutual mate choice: prudent male courting and sperm-limited females. Am. Nat. 172, 259–271. ( 10.1086/589452) [DOI] [PubMed] [Google Scholar]
- 53.Galvani A, Johnstone R. 1998. Sperm allocation in an uncertain world. Behav. Ecol. Sociobiol. 44, 161–168. ( 10.1007/s002650050528) [DOI] [Google Scholar]
- 54.Schwagmeyer PL, Parker GA. 1990. Male mate choice as predicted by sperm competition in thirteen-lined ground squirrels. Nature 348, 62–64. ( 10.1038/348062a0) [DOI] [Google Scholar]
- 55.Charlat S, Reuter M, Dyson EA, Hornett EA, Duplouy A, Davies N, Roderick GK, Wedell N, Hurst GD. 2007. Male-killing bacteria trigger a cycle of increasing male fatigue and female promiscuity. Curr. Biol. 17, 273–277. ( 10.1016/j.cub.2006.11.068) [DOI] [PubMed] [Google Scholar]
- 56.Dewsbury DA. 2005. The Darwin–Bateman paradigm in historical context. Integr. Comp. Biol. 45, 831–837. ( 10.1093/icb/45.5.831) [DOI] [PubMed] [Google Scholar]
- 57.Lorch PD. 2002. Understanding reversals in the relative strength of sexual selection on males and females: a role for sperm competition? Am. Nat. 159, 645–657. ( 10.1086/339992) [DOI] [PubMed] [Google Scholar]
- 58.Kvarnemo C, Simmons LW. 2013. Polyandry as a mediator of sexual selection before and after mating. Phil. Trans. R. Soc. B 368, 20120042 ( 10.1098/Rstb.2012.0042) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Puurtinen M, Fromhage L. 2017. Simulation code for: Evolution of male and female choice in polyandrous systems. Dryad Digital Repository. ( 10.5061/dryad.1vc8g) [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- Puurtinen M, Fromhage L. 2017. Simulation code for: Evolution of male and female choice in polyandrous systems. Dryad Digital Repository. ( 10.5061/dryad.1vc8g) [DOI] [PMC free article] [PubMed]
Supplementary Materials
Data Availability Statement
Matlab codes for the simulations are publicly available on the Dryad Digital Repository (http://dx.doi.org/10.5061/dryad.1vc8g) [59].