Allometric growth in reef-building corals

Abstract

Predicting demographic rates is a critical part of forecasting the future of ecosystems under global change. Here, we test if growth rates can be predicted from morphological traits for a highly diverse group of colonial symbiotic organisms: scleractinian corals. We ask whether growth is isometric or allometric among corals, and whether most variation in coral growth rates occurs at the level of the species or morphological group. We estimate growth as change in planar area for 11 species, across five morphological groups and over 5 years. We show that coral growth rates are best predicted from colony size and morphology rather than species. Coral size follows a power scaling law with a constant exponent of 0.91. Despite being colonial organisms, corals have consistent allometric scaling in growth. This consistency simplifies the task of projecting community responses to disturbance and climate change.

1. Introduction

Predicting variation in life history is an essential element of ecology and evolution. Combined demographic rates determine fitness, and therefore the effects of selection and adaptation. Demographic rates are also critical to link population, community and ecosystem ecology. Thus, developing robust predictors of demographic rates across entire assemblages is a critical component of forecasting how global change, through its effects on species diversity and composition, affects ecosystem function. For instance, how communities recover from low densities following extreme disturbances, such as forest fires [1] or extreme weather events [2], depends on differential growth rates among survivors and new recruits. Here, we determine the best morphological predictors of growth rates of reef-building coral colonies, the ecosystem engineers of one of the most threatened ecosystems on the planet [3].

Growth is a key demographic rate. From an organismal point of view, it measures energetic and resource investment into somatic extension [4]. From a population perspective, growth measures change in size, which in turn mediates changes in other demographic rates (such as mortality and fecundity) [5]. From an ecosystem perspective, growth leads to biomass production and creates habitat structure, and hence the contribution of the population to multiple ecosystem functions [6]. Accurate predictions of growth rates are therefore useful across ecological scales.

Most of what we know about growth comes from unitary organisms, which typically have size-dependent growth rates because of geometric and energetic constraints. In the most extreme cases, somatic growth ceases once reproductive maturity is reached, a phenomenon known as determinate growth [7]. In contrast, species with indeterminate growth partition energy and resources between reproduction and growth throughout their life. There are energetic reasons to expect growth to be size-dependent even for species with indeterminate growth. For most organisms, metabolic rate scales with body mass [8]. Hence, the amount of energy available for growth follows scaling laws, which have been hypothesized to arise out of physical constraints associated with the fractal networks that distribute resources within organisms [9]. Although the exact value of the scaling exponent and its consistency across organisms have been hotly debated for nearly a century, it is always less than 1 (e.g. [10,11]), indicating that growth slows down as organisms get bigger.

For colonial organisms, both the relationship between size and age [12], and the size-dependent allometric constraints that drive growth scaling laws, do not necessarily apply. In fact, whether ‘body size’ applies to the entire colony, or to the modules from which it is composed, depends on the physiological process and on the level of integration among modules. For example, among social insects metabolic rate scales allometrically as a power law of colony size, but isometrically among isolated worker groups that lack the social integration of a colony [13]. Hence, allometric variation seems to be an indicator of integration among modules in colonial organisms.

Among corals, growth is a function of the addition of modules to the colony and loss of modules through partial mortality. Early work suggested that rates of linear extension are independent of colony size [14,15]. For circular colonies, constant radial extension results in a curvilinear relationship between sizes at different times, asymptotically approaching the no-growth line as the ratio of perimeter to area decreases with size. Moreover, there is also evidence for complex allometries in energy acquisition, which affect the energy available for growth. On the one hand, resource acquisition is predicted to scale allometrically with body size in corals as resource availability to interior modules is reduced because of active depletion or passive deflection by modules on the exterior—similar to a self-shading effect [16,17]. On the other hand, process-based models of the effect of irradiance and gas diffusion on photosynthesis and respiration predict that large colonies have a positive energy balance over a broader range of flow and light conditions than small colonies [18,19]. These predictions are supported by positive correlations between predicted energy acquisition, tissue biomass and reproductive output [18]. Clearly, more work is needed to test alternative hypotheses regarding growth in reef corals. Here, we contrast support for the hypotheses that scleractinian corals have isometric versus allometric growth across a range of colony morphologies.

Partial mortality has the potential to decouple colonies' metabolic capacity for growth from their realized growth [12,15]. In particular, the probability of injury increases in direct proportion to colony size [12,20], and hence larger colonies exhibit lower rates of net colony growth [14,21]. Moreover, the high frequency and stochasticity of disturbances on coral reefs might mean that temporal variation in demographic rates can overwhelm any other signal [22]. Hence, we compare temporal variation in growth rates with inter-species and inter-morphological group variation.

Trait-based ecology is a promising approach to understanding the drivers of variation in demographic rates across ecological assemblages [23]. Rather than focusing on taxonomic identity as a driver of variation, this approach aims to identify traits associated with variation in response to environmental gradients, or in demographic rates. This approach is particularly pertinent to the goal of estimating demographic rates in diverse assemblages [24]. Estimating demographic rates individually for each species is logistically impossible for any but the simplest assemblages, due to the number of parameters that require estimation, and the large number of rare species [25], for which sufficient replication is difficult to obtain. Trait-based demography is potentially an efficient solution to this problem if easily measured traits can be identified as proxies of demographic rates. However, the success of this approach depends on the proportion of variation in demographic rates associated with traits versus idiosyncratic variation among and within species.

Trait variation across species is not independent, as it is the result of evolution. Hence, some combinations of traits occur far more frequently than others, so that species (and individuals) are typically organized in trait space into groups of similar traits and function [26]. Assessing how much of the variation in demographic rates is explained by these trait-functional groups is a parsimonious way of identifying whether predictive traits are likely to be included in the group classification. It is also an efficient way to be able to scale from ecological neighbourhoods to ecosystem functions and predict how such functions respond to global change [27]. This is an urgent task for coral reefs in particular, given the level of threat to this ecosystem. Predicting growth rates across entire coral assemblages is critical to being able to forecast recovery from disturbances.

Reef-building corals can be classified into morphological groups according to the general shape of their colonies. Typical groups include massive, encrusting, foliacious, and multiple types of branching forms that vary in the length, width and organization of branches. These morphological groups are known to differ functionally in terms of contribution to reef accretion [16] and habitat provision [28]. Hence, being able to predict production rates for different morphological groups is critical to forecasting changes in these different ecosystem functions. The groups also differ in demographic rates, such as size-specific mortality schedules (e.g. [29]) and fecundity (e.g. [30]). Finally, colony morphologies differ markedly in the degree of three-dimensionality, tissue penetration in skeleton and surface-to-volume ratio, all of which have been hypothesized to affect growth rates [16]. In accordance with a trait-based approach, we hypothesize that most variation in demographic rates occurs between morphological groups rather than between species of the same morphology.

Here, we ask how best to predict growth of reef corals. Specifically, we ask: (i) whether growth scales isometrically or allometrically with colony size; (ii) whether scaling is similar for all species, can be predicted from morphology or is species-specific; and (iii) how interspecific variation in growth rate compares to temporal intra-specific variation. Answers to these questions are essential for predicting variation in growth rates across entire coral assemblages, and hence for projecting recovery from disturbances, such as the 2016 mass bleaching event.

2. Material and methods

(a). Field data

Coral growth can be quantified in different ways. We focus on quantifying change in cover (or horizontal planar area), which is a metric of live coral used for example in global biodiversity assessments [31]. Space and access to light are the main limiting resources for which corals compete. Change in planar area is thus the most appropriate metric from a coral demography perspective [32]. Three-dimensional surface area and volume are also important metrics of size, as they correspond, respectively, to live tissue biomass and deposited skeleton. These metrics are far more difficult to estimate in situ, especially non-destructively. However, tight morphotype-specific scaling relationships between these metrics of size [33] suggest that planar area can serve as an effective proxy for three-dimensional colony growth.

We estimated growth as the change in planar area for 11 species of scleractinian corals, across five morphological groups: tabular (Acropora cytherea and A. hyacinthus), arborescent (A. intermedia and A. robusta), corymbose (A. spathulata, A. millepora and A. nasuta), digitate (A. cf digitifera and A. humilis) and massive (Goniastrea pectinata and G. retiformis). We tagged 30 colonies of each species with numbered cattle tags, or with metal tags hammered into the substrate in the vicinity of the colonies. All colonies are distributed along a 500 × 10 m area on the reef crest at Trimodal reef, between South and Palfrey islands (14.699839° S, 145.448674° E), Lizard Island, Australia.

Each tagged colony was photographed from above with a two-dimensional scale plate placed level with the surface of the colony. The angle of the camera was horizontal, and the distance from the colony was such that the entire colony was visible in the photograph. Colonies were photographed yearly in November 2009, 2010, 2011, 2012 and 2013. The images were corrected for barrel distortion, and the scale and outline of each colony were digitized in ImageJ for estimation of planar area. Every year, dead or missing colonies were replaced in order to maintain approximately 30 colonies per species. To minimize the effect of observation error caused by slight differences in angle, the distance from the camera or positioning of the scale, 60% to 90% of the colonies were photographed twice to three times independently every year, all photographs were digitized twice independently and estimates of area were averaged. In total we had 980 estimates of colony planar area, which are the average of 2 to 9 replicate estimates for each of the 330 colonies (30 colonies × 11 species) each year.

(b). Analysis

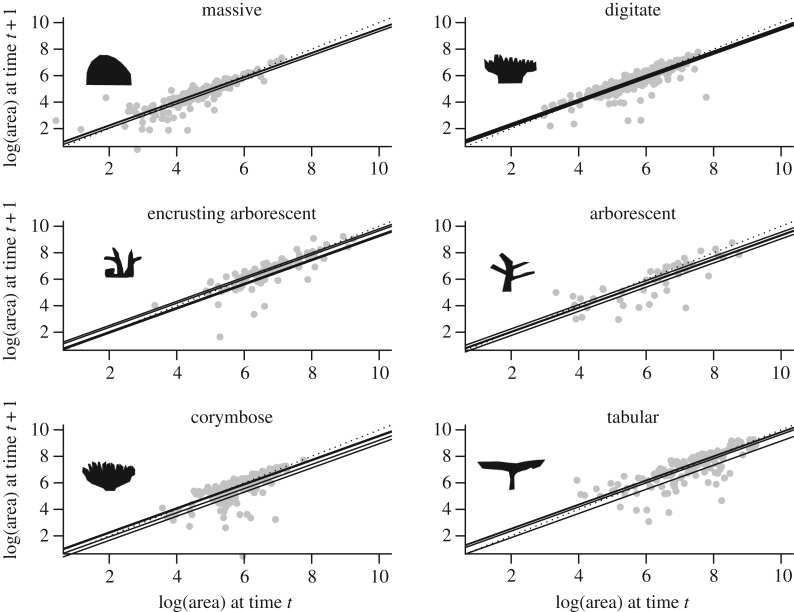
We used ordinary least squares to fit linear models to estimates of planar area at one point in time as a function of its planar area the year before, species, morphological group, year and combinations of the above as outlined below. On a log–log plot of area at time t as a function of area at time t − 1, a line with a slope of 1 and an intercept of 0 corresponds to no change in area. Colonies above this no-growth line increase in size, and colonies below it decrease in size between time points. A line of slope 1 and non-zero intercept indicates isometric growth: colonies grow or shrink by a fixed proportion of their current colony size. A slope of more than 1 indicates accelerating growth, and a slope of less than 1 decelerating growth. For lines with slope less than 1 (and positive intercepts) once the line intercepts the unity line, colonies start shrinking on average. Model selection was done using Akaike's information criterion (AICc). Analyses were conducted using the ‘lm’ and ‘lmer’ [34] functions in the statistical programing language R [35].

Our main goal was to find a model that best predicts change in planar area, and hence we compare the fit of different combinations of predictor variables. Specifically, to test whether growth rates change as a function of colony size, we fitted models with size the previous year as a predictor variable, and as an offset. We also compared models with and without morphological group or species to determine which level of differences best predicts change in planar area. Because our sampling design included repeated measurements of the same colonies, we also compared models with and without colony as a random effect (electronic supplementary material). We assessed the robustness of our results to group classification (see electronic supplementary material).

Change in planar area integrates colony growth with partial mortality. To attempt to disentangle ability to grow from ability to withstand such conditions, we used quantile models using the rq function in the package quantreg [36]. Specifically, we hypothesize that the 95th quantile function reflects the limits of how much colonies can grow, and the 5th quantile of the susceptibility to partial mortality. We fitted quantile regressions through the median as well, to check the robustness of inferences from the OLS regression to skew and heterogeneity of variances in the residual variation.

Also, we considered temporal variation by comparing models that included year and all possible interactions with morphological group and species. We asked how between-group variation in change in planar area compares with between-year variation, and whether temporal variation affects all groups similarly or differently.

3. Results

A model that includes size the previous year as a predictor of size in the current year was always selected regardless of other variables included (table 1). All models fitted, with the exception of the quantile regression for the 0.05 quantile, had a positive slope of less than one, and positive intercepts (table 2). That is, irrespective of which model is fitted, growth as a proportion of colony size decreases with increasing size, and at some point intercepts the unity line so that, on average, colonies stop growing (figure 1).

Table 1.

Model selection for the effect of time, species and morphological group. Italics indicate the model with the lowest AICc value.

model	d.f.	AICc	adjusted R2
log(areat+1) ∼ offset(log(areat))	2	1971.377
log(areat+1) ∼ offset(log(areat)) + group	7	1964.730	0.7985
log(areat+1) ∼ offset(log(areat)) + year	5	1950.108	0.8081
log(areat+1) ∼ offset(log(areat)) + species	12	1971.011	0.7976
log(areat+1) ∼ log(areat)	3	1955.052	0.7807
log(areat+1) ∼ log(areat) + group	8	1946.720	0.7837
log(areat+1) ∼ log(areat) + log(areat):group	8	1947.799	0.7833
log(areat+1) ∼ log(areat) × group	13	1955.384	0.7833
log(areat+1) ∼ log(areat) + species	13	1952.889	0.7835
log(areat+1) ∼ log(areat) + log(areat):species	13	1953.215	0.7833
log(areat+1) ∼ log(areat) × species	23	1957.555	0.7846
log(areat+1) ∼ log(areat) + year	6	1927.974	0.7895
log(areat+1) ∼ log(areat) + log(areat):year	6	1919.232	0.7911
log(areat+1) ∼ log(areat) × year	9	1914.654	0.7915
log(areat+1) ∼ log(areat) + year + group	11	1917.721	0.7927
log(areat+1) ∼ log(areat) + year × group	26	1908.040	0.7986
log(areat+1) ∼ log(areat) × group × year	49	1910.305	0.7921
log(areat+1) ∼ log(areat) + year + species	16	1923.726	0.7926
log(areat+1) ∼ log(areat) + year × species	46	1924.281	0.7997
log(areat+1) ∼ log(areat) × species × year	89	1929.261	0.8074

Table 2.

Parameter estimates (mean intercepts across years) for the OLS and quantile regression models' 95th, 50th and 5th quantile regressions of planar area at time t as a function of planar area at time t − 1 and morphological group.

	OLS	95th	50th	5th
α	0.913	0.851	0.944	1.111
βarborescent	0.375	1.368	0.308	−2.121
βencrusting arborescent	0.181	1.559	0.232	−2.952
βcorymbose	0.207	1.298	0.218	−2.611
βdigitate	0.431	1.272	0.352	−1.619
βmassive	0.361	1.163	0.305	−1.388
βtabular	0.503	1.756	0.467	−2.231

Figure 1.

Size at time t + 1 as a function of size at t for each morphological group as per panel label. Circles represent data, full lines the best fitted model as per table 1 (one line for each year) and dotted line the no-growth line (when size is unchanged between 1 year and the next).

In a comparison among models where parameters vary as a function of species, morphological group, year and combinations of these predictor variables, the model with the lowest AICc has a common slope but different intercepts for the interaction of each morphological group and year (table 1). This result is robust to using colony as a random effect in the models (electronic supplementary material).

A comparison of R² values between models with species or with morphological groups as predictors shows that variation between species within morphological groups is minimal (e.g. best OLS model with equivalent species-level model has a 0.11% difference; table 1). The distribution of residuals for this model (figure 1) indicates that negative residuals are more spread than positive residuals, and further justifies the quantile regression analysis. The residuals also identify three potential outliers, hence all analyses were repeated after removing these outliers with no effect on the results.

The ranking in growth rate for the different morphological groups (which is a function of the intercept in these models, because the slope is constant) changed between quantiles (figure 2). For the 95th quantile, the ranking from lowest to highest is massive, digitate, corymbose, arborescent, encrusting arborescent and tabular. For the median quantile, representing a trade-off between positive and negative change in size, the ranking becomes corymbose, encrusting arborescent, arborescent, massive, digitate and tabular. For the 5th quantile, the ranking is encrusting arborescent, corymbose, tabular, arborescent, digitate and massive. Parameter estimates for these three models are presented in table 2.

Figure 2.

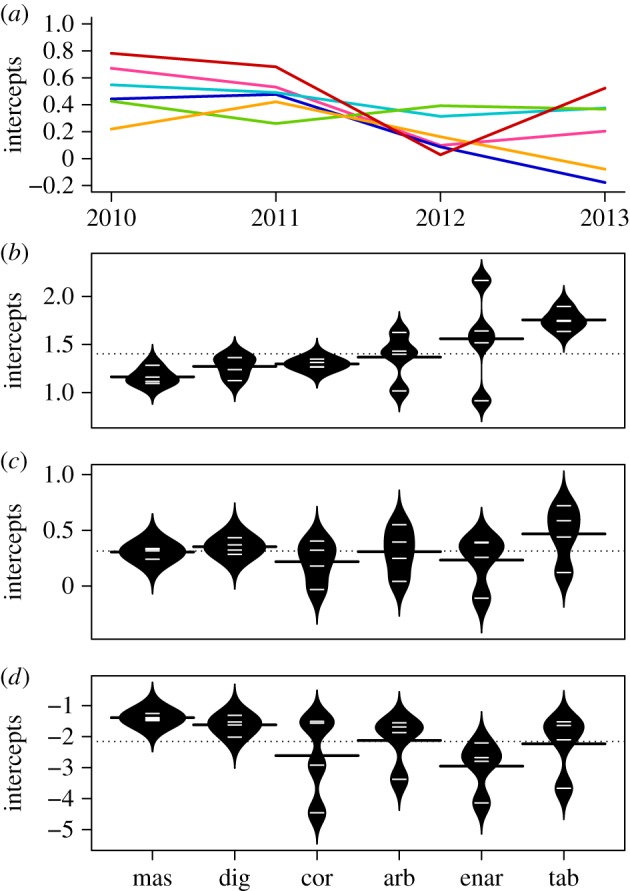
Comparison of temporal variation in mean, maximum, median and minimum growth. (a) OLS estimates of intercepts for the best model as per table 1, for each year and each morphological group. The red line represents tabular colonies, orange arborescent, green massive, turquoise digitate, blue corymbose and pink encrusting arborescent. (b–d) Intercepts across years for the (b) 95th, (c) 50th and (d) 5th quantile regressions of size at time t as a function of size at time t − 1 and morphological group (as per the best model in table 1). Estimates are plotted as white lines in the centre of each black polygon, which represents a normal density curve around the estimates and is intercepted by a black line representing the mean for each morphological group. The dotted line represents the mean across all morphological groups. mas, massive; dig, digitate; cor, corymbose; arb, arborescent; enar, encrusting arborescent; tab, tabular.

There are also clear differences in inter-annual variability among morphological groups. All groups, with the exception of massive colonies, had a decrease in both the ability to grow and median growth within the study period (table 2). Massive colonies had very low inter-annual variability in both the OLS and the three quantile regression models (figures 1 and 2). All groups, with the exception of encrusting arborescents, also had increasing reductions in size over the study period. Encrusting arborescents decreased their losses, but were also the group with the highest losses overall (table 2 and figure 2).

4. Discussion

Coral growth rates scale with size according to a power law with constant slope across all species. This result is clearly indicative of allometric growth among corals: if growth were isometric, size in successive years would be proportional to size in previous years, yielding a slope of one in log–log space. Allometric growth is consistent with the hypothesis of colony-level integration among modules. Integration can take the form of energy or nutrient sharing among modules, and/or it can be a consequence of geometric constraints associated with colony morphology. The identical estimated slope across morphological groups implies that constraints placed by size on growth are highly consistent across these morphological groups in reef-building corals. For all species in our study, colonies increase in size up to a point when, on average, they stop growing.

Colonial organisms can theoretically grow indefinitely by adding modules to their colony, but in practice there are geometric and structural constraints to how modules are added. Proportional growth rates are expected to decrease with size because of geometric constraints in how corals add cover [32,37]. Corals increase in planar area by adding area at the periphery of the colony. Because the ratio of perimeter to area decreases with size, unless radial increments increase with size, the proportional growth rate necessarily decreases with size. Perimeter increases with area according to functions that depend on the shape of the colony, but that, typically, asymptotically approach the line of zero growth. Constant radial increment thus corresponds to allometric growth.

Net growth is a function not only of the ability to grow, but also of partial mortality. This trade-off is reflected in the changed rankings observed in the median quantile regression, where most morphological groups have similar growth rates, and the lowest quantile regression, where the rankings are largely reversed. While exponent estimates for maximum, median and mean growth are all indicative of allometric scaling, the exponent estimate for the approximate lower bound of net (negative) growth (5th percentile) is not significantly different from one. This indicates that partial mortality is a fixed fraction of colony area, independent of colony size, a finding that is consistent with previous reports that the probability of injury increases proportionately with colony size [12,20]. Because growth decreases with colony size and partial mortality is isometric, it follows that, at a threshold colony size, partial mortality will cancel growth, and colonies above this threshold will tend to shrink, on average.

In addition to the geometric constraints, there are also energetic colony-level constraints to growth in corals. Energy acquisition is predicted to scale allometrically in corals [17]. Additionally, larger colonies may invest a disproportionate portion of available energy to maintenance or reproduction, reducing energy available for growth [38–41]. Similarly to unitary organisms, both geometric and energetic constraints are probably involved in determining growth rates in colonial organisms and are indicative of integration among the modules of the colony. Specifically, the geometric constraints we discuss arise out of partitioning of tasks among modules, a key characteristic of colony integration, with growing modules situated at the periphery of the colony. Colony-level energetic constraints are indicative of energy partitioning among modules.

We found that variation in size-dependent growth is best predicted by morphological group rather than species. This is consistent with previous studies showing that colony morphology is associated with coral adaptive strategies [42]. In addition, there is an extensive literature reporting marked differences in life-history rates among different morphological groups of coral reef invertebrates [29,43–45]. For example, Gladfelter et al. [37] reported a 20-fold difference in growth rates between branching and massive corals, and Morgan & Kench [46] reported a 30-fold difference in skeletal extension among branching versus encrusting colonies. Nonetheless, at some scale phylogeny is likely to be important. For example, family in addition to morphology was an important predictor of growth rates across the order Scleractinia [24]. Future studies increasing the taxonomic breadth of growth estimates will be critical to further test the generality of our common scaling exponent.

Finally, it is interesting to note that inter-annual variation was generally greater than inter-group variation, but that the degree of these discrepancies differed among the groups. Specifically, robust slow-growing morphologies such as massive and digitate had the least temporal variation, whereas the more fragile fast-growing morphologies such as tables and arborescent had the highest (figures 1 and 2). The shifts in rankings between good and bad years for fast and slow growers highlight the long recognized need for long-term studies for robust estimates of coral growth rates. In combination, the shifts in rankings for different quantiles of growth and the patterns of temporal variation support the existence of a trade-off in robustness and ability to grow in corals. The morphological groups most likely to be able to withstand disturbances are also the slowest to grow. If disturbances become too frequent or too extreme in magnitude, the ability of reefs to recover will be compromised.

Tight scaling relationships between two-dimensional and three-dimensional metrics of size [33] suggest that it is possible to convert growth across different metrics. Thus our estimates of growth rates, coupled with morphotype-specific scaling relationships between volume, planar and surface area [33], allow estimating not only how coral cover changes, but also reef production. Both mortality [29] and fecundity [30] are best modelled at the morphological group level. Therefore, combining geometric conversions with assemblage size structure information will allow for a range of estimates about reef-scale functional processes, such as reef production (growth), erosion (mortality) and the reproductive output (fecundity) for meta-population models.

The importance of colony size as a predictor of growth has implications for monitoring reef coral communities and predicting their responses to global change. Modelling of demographic change in coral populations and communities should incorporate allometric scaling of size. Current results suggest a constant scaling exponent of 0.91, but this value and its generality may be revised as more data accumulate. Both mortality [29] and fecundity [30] are also size-dependent, which is consistent with the classical approach of size-dependent demography for corals [47]. An important implication of this result is that constant growth underestimates rapid growth of small colonies, typical of early successional stages following a disturbance, and overestimates growth of large colonies. As global change increases the frequency and intensity of episodic disturbances, size structures will shift downwards [48], and this will alter how fast remaining individuals are able to regrow.

The most commonly reported metric of reef health is coral cover, but in isolation it does not allow forecasting change in ecosystem function or recovery. Size distributions and morphological group abundances emerge as two essential variables that are easy to quantify, and should be prioritized in coral reef monitoring. In combination these variables also allow predicting habitat function changes in the reef, as habitat complexity is determined by which coral morphotypes are present, and fish communities reflect habitat complexity. Projections of how coral cover will respond to environmental change often use coral cover as a state variable and assume that growth is a fixed proportion of existing cover (i.e. that it is isometric) [49,50]. The allometry of growth that we documented here means that shifts in size structure will lead to systematic changes in the proportional growth in cover of population, which such models will not capture. Predictions about community shifts under global change will need to consider differences in susceptibility, recovery potential and their interaction.

Data accessibility

Data used in this manuscript are included as electronic supplementary material.

Authors' contributions

All authors designed the study and collected the data. M.D. analysed the data and wrote the first draft. All authors contributed substantially to revisions.

Competing interests

We have no competing interests.

Funding

We thank the ARC Centre of Excellence for Coral Reef Studies and the Australian Research Council for fellowship and research support. We are also grateful to the Scottish Funding Council (MASTS, grant reference HR09011) and to the ERC project bioTIME (grant number 250189).