The impact of temperature changes on vector-borne disease transmission: Culicoides midges and bluetongue virus

Abstract

It is a long recognized fact that climatic variations, especially temperature, affect the life history of biting insects. This is particularly important when considering vector-borne diseases, especially in temperate regions where climatic fluctuations are large. In general, it has been found that most biological processes occur at a faster rate at higher temperatures, although not all processes change in the same manner. This differential response to temperature, often considered as a trade-off between onward transmission and vector life expectancy, leads to the total transmission potential of an infected vector being maximized at intermediate temperatures. Here we go beyond the concept of a static optimal temperature, and mathematically model how realistic temperature variation impacts transmission dynamics. We use bluetongue virus (BTV), under UK temperatures and transmitted by Culicoides midges, as a well-studied example where temperature fluctuations play a major role. We first consider an optimal temperature profile that maximizes transmission, and show that this is characterized by a warm day to maximize biting followed by cooler weather to maximize vector life expectancy. This understanding can then be related to recorded representative temperature patterns for England, the UK region which has experienced BTV cases, allowing us to infer historical transmissibility of BTV, as well as using forecasts of climate change to predict future transmissibility. Our results show that when BTV first invaded northern Europe in 2006 the cumulative transmission intensity was higher than any point in the last 50 years, although with climate change such high risks are the expected norm by 2050. Such predictions would indicate that regular BTV epizootics should be expected in the UK in the future.

1. Introduction

Biting midges of genus Culicoides transmit a number of arboviruses causing several livestock diseases of veterinary and economic importance, for example African horse sickness virus (AHSV), epizootic haemorrhagic disease virus (EHDV) and bluetongue virus (BTV) [1] as well as the recently discovered Schmallenberg virus (SBV) where Culicoides midges have been confirmed as the vector [2]. In this work, we focus on modelling BTV transmission in the UK due to its economic importance to the livestock industry given the costs associated with livestock losses, movement restrictions and vaccination. In 2006, an outbreak of BTV (serotype 8) detected initially in Maastricht, The Netherlands, but probably initially introduced in Belgium [3], demonstrated that the virus had the potential both to invade previously disease-free areas, shifting northwards from its traditional European range within the Mediterranean basin [4], and to overwinter within its new range, with cases being detected as far north as Sweden [5]. Widespread vaccination campaigns and movement restrictions had controlled the disease in northern European countries after 2006; see Zientara & Sánchez-Vizcaíno [6] for a review of vaccination effectiveness by European region and against specific BTV serotypes. However, BTV continued to circulate in southern Europe, especially in Italy (serotypes 2, 4, 16), and invaded southeastern Europe for the first time in 2014 (serotype 4); see Kyriakis et al. [7] for a review of European outbreaks of BTV up to 2014 by country and serotype. Recently, BTV serotype 8 has re-emerged in France [8]. The difficulty in eradicating BTV in Europe is echoed by the persistence of both enzootic and epizootic patterns across large regions of the USA [9].

Integrating climate data into transmission models has been identified as a key methodological challenge for vector-borne disease (VBD) prediction in general [10,11], and climate-driven modelling in particular has become increasingly popular for malaria [12–16]. The effect of climatic conditions, in particular temperature but also rainfall, wind velocity and other factors, on the activity and abundance of midges has long been recognized [17]. Long-term temperature averages have been seen as a determining factor for regions within which BTV becomes enzootic [18] and short-term temperature fluctuations (as well as wind direction/velocity) were seen as important to understanding the early epizootic outbreak of BTV in 2006 around Maastricht [19,20]. A change in climate can alter BTV transmission by midges in two main ways: first, a change in climatic conditions could create a more or less suitable environment for the vector population, consequentially climate change could alter the numbers of vectors available to transmit the VBD between vertebrate hosts; second, the bionomics of midges and the rate at which BTV incubates within infected midges depend upon climatic conditions, most notably temperature, which may have different typical values and ranges in the future compared with the present; see Wittmann & Baylis [21] and Elbers et al. [22] for excellent overviews of climatic factors in midge-borne transmission.

Modelling the population dynamics of midges, and therefore their response to climate change, is a significant challenge. There are large uncertainties and knowledge gaps in the understanding of immature Culicoides ecology [23] that make mechanistic modelling of the full population dynamics highly unreliable. This partly explains why modelling studies on midge population dynamics have chosen statistical approaches in preference to a mechanistic one. In response to the expanded range of BTV transmission, there has been an increasing number of European studies investigating the statistical predictors of various aspects of Culicoides abundance, measured via trapping capture. The emerging picture is highly complex, involving multiple climatic and topographical predictors even when only one country and one species is considered and temporal variation is excluded by fitting to maximum capture sizes over a year, e.g. Culicoides imicola in Spain [24]. When seasonal variation in midge activity is also considered, for example by imputing the duration and peak timing of the midge season, additional climatic predictors become important, such as mean temperature during spring [25]. Different midge species and midge species groups have been reported as having significantly different responses to climatic variables [26,27]. This differential response to climate continues even when distinguishing between morphologically similar species within a single Culicoides species group [28]. Moreover, there is evidence of adaptation of insect populations to changing climate [29] and, therefore, it is not clear whether statistical models for midge population dynamics informed by current capture data will remain predictive in the future.

While for midges the interaction between climate and population ecology is highly complex, and depends upon a range of factors, the bionomics of individual midges have been observed to most strongly depend upon temperature; for midges higher temperatures imply a faster mortality rate and shorter periods between bloodmeals [30]. The functional dependence of biting frequency [31] and life expectancy [32] upon temperature has been quantified for Culicoides sonorensis. Although these functional relations are derived for only one midge species, in part because of serious technical challenges in the laboratory colonization of midge species [33], they are widely used in the recent BTV mechanistic modelling literature [34–38]. BTV develops within infected midges more rapidly at higher temperatures and therefore the extrinsic incubation period (EIP) between the bite that infected a midge and when subsequent midge bites are infectious is shorter at higher temperatures. The distribution of EIP duration has been imputed for a range of midge species and BTV strain combinations [39].

To address the challenge of including daily varying temperature time series in predictions of BTV transmission intensity, we have developed a novel mechanistic and temperature-driven model for infectious biting by midges. Mathematical expressions relating the intensity of VBD transmission to entomological and epidemiological parameters have existed in the literature since the seminal work of MacDonald [40] (who defined the VBD basic reproductive ratio R₀; i.e. the expected number of secondary cases among host vertebrates per primary infected host) and Garrett-Jones [41] (who defined vectorial capacity C; i.e. the contribution to R₀ due to 1 day of biting upon the primary infected host). At constant temperature, R₀ can be determined from the rates of midge life processes at that temperature. This approach has been used to define temperature-dependent R₀ values for BTV in the non-spatial context [34], the spatial context [42] and in order to assess the possible impact of climate change [43]. However, strong daily fluctuations in temperature, as are commonly observed in northern Europe, challenge the validity of this approach for BTV. The viraemic period of a vertebrate host is typically several days, and it is unclear which daily temperatures are most relevant to R₀. Moreover, midges infected by biting an infectious host will continue to be sensitive to changing temperature for their entire life span. Within the model framework, we consider the joint probabilities of vector infection, surviving its EIP and making infectious bites at each daily (dawn or dusk) activity period.

It is very common in the general VBD modelling literature to either assume that there is no variation between infected vectors' EIP duration if they experience the same temperatures (e.g. [12]) or implicitly assume that the EIP duration for each infected vector is exponentially distributed around an average duration (e.g. [42,43]). In fact, experimental observation of cohorts of BTV-infected midges disagrees with both of these common assumptions; there is observed variation between the EIP durations of midges infected with BTV but not as much variation as implied by the exponential distributed assumption [39]. Although these distinctions may seem pedantic, the variation between midge EIP durations has been identified as a contributing factor to BTV transmission at constant temperature [44]. That an interplay exists between EIP variance and varying temperature can be understood intuitively. The exponential model for EIP allows infected, but latent, midges to become infectious at any time the temperature is above the critical development temperature for BTV, irrespective of any previous temperature encountered by the midge; therefore short isolated periods of warm weather will be expected to amplify transmission. On the other hand, a deterministic model similar to that described by Paaijmans et al. [12] assumes that a fixed amount of accumulated degree-days must be ‘felt’ by a BTV-infected midge before transmission is possible, an assumption that assigns relatively higher transmission intensity to sustained periods of warmer weather. We model EIP using a random threshold model which generalizes the two common EIP assumptions mentioned above as special cases and can also be parametrized to reflect laboratory-observed midge EIP durations.

We present two transmission metrics that can be calculated from our model which explicitly incorporate the full temperature sequence encountered during transmission and the seasonal pattern of midge activity: vectorial capacity per midge (Ĉ), i.e. the expected number of secondary cases due to a single midge able to feed on the primary infectious host per day, and a seasonal reproductive ratio (R(t)), i.e. the expected number of secondary cases due to a primary infectious host that became infectious on day t, which can be thought of as a time-varying generalization of the standard MacDonald concept of R₀ [40] or the livestock-to-livestock case reproductive ratio as defined by Fraser [45]. As mentioned above, mechanistic modelling of the midge population dynamics, and therefore estimating the rate at which susceptible midges bite infectious livestock, is not currently feasible due to fundamental knowledge gaps [23]. We model the biting rate of susceptible midges using a statistical model for daily flight activity of midges already extant in the literature as a proxy for biting rate per livestock host [46]. The Sanders et al. [46] model was chosen because it was parametrized using captures of midges in the UK to make daily predictions of flight activity with temperature as a predictor; therefore, it agrees with both the location of this study and the daily time scale of the model developed here, and is informed by temperature. We find the pattern of temperature that gives the maximum possible Ĉ and show that the maximizing pattern implies significantly more day-to-future transmission risk than any constant temperature. Turning to historic temperatures, we use the central England temperature (CET) time series [47] to calculate R(t) for each day of 2006 (the BTV invasion year and an outlier hot year in northern Europe) and demonstrate that static approaches to temperature under-estimate transmission risk at the beginning of the vector season and over-estimate at the end of the season. Finally, we use the United Kingdom climate projector (UKCP09) [48] to extend the historic CET time series with an ensemble of future projections of temperatures in England. We calculate cumulative R(t) (R_cum(year)) for years since 1950 and project into the future using the extend temperature dataset. This reveals that the year of BTV invasion into northern Europe (2006) was also the peak year of cumulative BTV transmission intensity in the UK on record, with the general trend being year-on-year increase in cumulative BTV transmission risk.

2. Material and methods

2.1. Temperature-dependent transmission model formulation

Environmental temperature has been observed to strongly affect midge life histories and thus transmission intensity estimates. Higher temperature implies faster virus development for infected latent midges (σ), more frequent biting (α) and more rapid mortality (μ). We use temperature-dependent rates derived from both field and laboratory experimentation on Culicoides genus midges (figure 1a–c):

2.1

Predictions for the efficacy of each of four links in the transmission cycle (1, vector population biting activity; 2, vector competence; 3, the chance of an infected vector surviving its EIP; and 4, its subsequent number of potentially infectious bites upon hosts) can be extrapolated from knowing the three key temperature-dependent rates given in equation (2.1). Essentially, we consider the probability that a midge makes an infectious bite at each daily dawn/dusk active period after its initial infection. These probabilities, combined with an estimate of the biting from susceptible midges, provide two quantitative estimates of transmission risk which depend on the calendar day t: (i) the vectorial capacity per vector (Ĉ(t)) and (ii) a seasonal reproductive ratio (R(t)). The vectorial capacity per vector, Ĉ(t), measures the total subsequent expected cases among hosts due to a single susceptible vector in the vicinity of an infected host at the start of day t, assuming all other hosts are susceptible; as such Ĉ(t) provides a quantification of disease risk solely due to daily temperatures on day t and afterwards (we denote subsequent days using τ) without other seasonal effects. The seasonal reproductive ratio R(t) is defined as the expected number of secondary hosts infected due to all vectors infected by biting a host that itself became infected on day t in a totally susceptible population. For simplicity, we consider only cattle hosts for BTV, in agreement with the predominant host species in the northern European outbreaks spread by Culicoides obsoletus group midges. This assumption slightly amplifies predictions of transmission compared with an alternative scenario where sheep receive a portion of the bites from the midge population, due to sheep having a shorter BTV viraemic period but equal susceptibility to that of cattle; see Turner et al. [49] for modelling with two midge and livestock host species. Unlike the capacity per vector, R(t) requires an estimate of the number of midges biting per host, which is known to have strong seasonal variation in the UK (and elsewhere) and therefore cannot be simply computed from a constant temperature and will vary from day to day. In summary, we combine two models in order to generate climate-driven VBD transmission risk predictions:

• —A novel mechanistic model for the stochastic life events for midge vectors post-infection (e.g. biting, dying, completing EIP), which is based on the cumulative development of three biological processes for the midge: the biting rate (α), the pathogen incubation rate (σ) and the mortality rate (μ) under varying ambient temperature. This model accounts for both day-to-day variation in temperature and individual-level (stochastic) variation between vectors and allows us to calculate Ĉ(t) for each day included in a times series of daily temperatures.
• —An existing statistical model for UK midge flight activity which includes temperature and day of the year as predictor variables [46]. We use the flight activity as a proxy for the (stochastic) number of bites experienced per infected cattle per day. From the statistical model, we can derive the expected number of susceptible midges per cattle actively seeking a bloodmeal on any given day of the year and temperature on that day. Combined with Ĉ values over the possible viraemic period of the host cattle this allows us to calculate R for each day included in a times series of daily temperatures.

Figure 1.

Temperature-dependent rates and capacity per vector. Temperature-dependent rates for midges: biting rate per day (a), mortality rate per day (b), rate of BTV incubation within the midge vector per day (c). (d) Vectorial capacity per vector at static constant temperatures for the three EIP models. The saw-tooth pattern for deterministic (fixed duration) EIP is due to modelling bites at discrete daily activity periods rather than assuming that midges can bite continuously. For each EIP model, transmission was maximized by a static temperature of 19.2–19.6°C; the intensity of transmission was greater for models where variance in EIP is larger.

Most processes (e.g. biting and death) are considered Markovian (i.e. they are expected to occur at a Poisson rate depending only on the temperature that day). However, the EIP is modelled so that the chance of the midge becoming infectious on any day can depend on the full sequence of temperatures post-infection. When temperature varies, such that the temperature today and going forward daily in time is 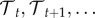, the probability of biting on a given day τ is defined by the current temperature,

2.2

the probability that the midge has survived from the beginning of day t until the activity period at the end of day τ is calculated from a cumulative sum over all temperature-dependent death rates from to ,

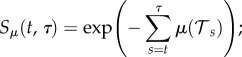2.3

and the probability that the midge has completed its EIP and transitioned to infectiousness between the activity period at the end of day t and the activity period at the end of day τ again depends on a cumulative sum,

2.4

where F_k is the cumulative distribution function of a gamma distribution with mean 1 and shape k. The accumulated rate in the survival probability (2.3) includes the infection day t because the midge has to survive that day, which depends on the temperature on day t, whereas the incubation probability (2.4) does not include day t; this is because we assume that any infected vector is infected at the end of day t and, therefore, its EIP only depends on temperatures starting on day t + 1.

By combining probabilities (2.2)–(2.4), we can specify the capacity per vector mathematically,

2.5

where V is the vector competence (the product of the probabilities per bite of transmission from host to vector and vector to host) which we point estimate as V = 0.045 [34,39]. Using the above definition of 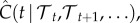we define the daily reproductive ratio as

2.6

where P_H(τ, t) is the probability that a host infected on day t is infectious on day τ. In this work, we focus on cattle hosts, which are estimated to have a gamma-distributed infectiousness duration with mean 23.6 days and shape parameter 5 [34]. We assume that the estimated average midge flight activity measure by one trap each day τ derived from Sanders et al. [46] is a measure of biting activity per host M(τ); that is, the numbers of midges attracted per trap were similar to those seeking a host at dusk/dawn. Therefore, in combining Ĉ with the daily reproductive ratio R we re-scale M(τ) by 1 / [P_α(τ)S_μ(τ, τ)] because is the expected infections among cattle due to a single midge alive at the beginning of day τ, whereas, by assumption, M(τ) measures only the sub-population that both survives and is ready to bite on day τ.

2.2. Extrinsic incubation period as a random threshold model

The EIP model (2.4) is equivalent to a stochastic threshold model: at the infecting bite each midge can be thought of as having an independent random threshold quantity X ∼ Γ(k, k) (i.e. the threshold is gamma distributed with mean 1 and shape k) and a zero accumulated incubation rate. The accumulated incubation rate increases by on each day s after infection (this can be directly extended to any period or even continuous time) and the midge becomes infectious on the first day that its accumulated incubation is greater than X. This choice of model for the EIP is motivated by three useful properties of the gamma distribution which give greater modelling flexibility than previous EIP models extant in the literature,

• —. k = 1 recovers the popular Markovian model for vector EIP (e.g. [50]).
• —F_∞(x) = 1 if x > 1 and F_∞(x) = 0 if x ≤ 1. k = ∞ recovers the deterministic rate model used by Paaijmans et al. [12].
• —If the temperature is constant , then where X is gamma distributed with mean 1 and shape k. By the scaling property of gamma random variables this implies that at constant temperature the EIP duration is gamma distributed with mean days and shape k.

The scaling property is highly useful for fitting our temperature dynamic model to laboratory experiments, because the shape parameter k is invariant to scaling in the mean EIP duration. Experimentally EIP durations of BTV-infected midges kept at constant temperature have been fitted to a gamma distribution; see Carpenter et al. [39], who found general agreement across combinations of BTV serotype and midge species for the critical development temperature (posterior median estimates: 11.4–13.3°C) and virus replication rate per degree (posterior median estimates: 0.016–0.019) but not the shape statistic k for the gamma distribution (posterior median estimates: 7.7–116.2). The statistics of EIP duration for C. obsoletus group midges infected with BTV serotype 8 were not tested. We use the smallest posterior median estimate k = 7.7 derived from data on Culicoides bolitinos infected with BTV serotype 1 [51] as our BTV fitted model in order to see the greatest difference in prediction from both the Markov EIP assumption (k = 1) and the deterministic EIP assumption (k = ∞).

2.3. Model for biting from susceptible midge population

We use a midge flight activity model from Sanders et al. [46] which was calibrated using data from a wide range of British midge capture sites as an estimate for the number of midges ready to bite per host per day (the expected number of bites per cattle on day t is denoted M(t)). We are assuming that the attractiveness of a single trap was comparable to the attractiveness of a single host and that midge flight activity is a reasonable proxy for successful host seeking. The flight activity of the midge population is generated according to a generalized linear mixed-effects model with Poisson distributed capture data and a log-link function for the mean number of trapped midges on a day. Climatic predictor variables (temperature, wind and precipitation) are introduced as normally distributed random effects in the linear predictor term. Precipitation was found to have only a weak effect, which echoes other findings on midge activity (e.g. [17]) and is not included in this work. We also neglect wind effects in this work to focus on temperature-driven processes. Other predictor variables included were seasonality (a day of year effect was introduced via trigonometric functions), an over-dispersion parameter and an auto-regressive process, to capture temporal auto-correlation between flight activity.

We use the expected number of bites from susceptible midges per host on day t (M(t)) in calculating R(t); this is an average over both the intrinsic randomness in midges per host and also the unexplained variation between capture locations implied by the mixed-effects model,

2.7

where x(t) are the predictor variables on day t (temperature and seasonality), 〈β〉 is the posterior mean of the regression coefficients, Σ_β is their posterior covariance matrix and σ²_d is the posterior over-dispersion parameter variance. The final term is due to the additional variance in the linear predictor caused by the auto-regressive process. We used parameter values fitted for all females of the C. obsoletus species group, the main group of northern European vector species for BTV from the supporting information of Sanders et al. [46].

2.4. Maximization of capacity per vector over temperature sequences

We maximized Ĉ over the high-dimensional input space of possible 50 day temperature profiles by constructing sequentially improved estimates starting from an initial guess that the optimal temperature profile was the constant maximizing temperature (≈20°C) on each day. At each step, the previous estimate was used as the initial guess for the next optimizing algorithm: alternatively using a quasi-Newton method with Broyden–Fletcher–Goldfarb–Shanno (BFGS) Hessian updates (e.g. [52]) implemented by the MATLAB fminunc function and the Nelder–Mead simplex method (e.g. [53]) implemented by the MATLAB fminsearch function. Alternation between optimization algorithms was repeated until no further improvement could be made.

2.5. Temperature data sources

In this work, we use both historical temperature records and forecasted temperature projections for England (other parts of the UK are likely to be colder and less at risk of BTV transmission). We use the CET dataset as our historic time series of UK temperatures; this is the longest instrumental record of temperature in the world with a daily data series beginning in 1772. The representative mean temperatures for England are estimated by aggregation over a large number separate measurements [47]. The CET dataset can be freely downloaded from www.metoffice.gov.uk/hadobs/hadcet/data/download.html. For our projections of temperatures in England in the future, we use the UKCP09 climate projector [48]. UKCP09 gives an ensemble of climatic time series to represent uncertainty in any forecast, each realization being generated by an estimate of climatic change relative to the baseline climatology at the chosen location during 1961–1990 [48]. We use 100 realizations of the hourly temperatures at the geographical centre of England to generate 100 mean daily temperature time-series realizations, which in turn imply 100 realizations of the BTV R(t) time series whenever these are projected into the future. Uncertainty in our forecast of BTV risk in England is measured as the variation between these time-series realizations. Access to UKCP09 climate projections is free for non-commercial use from ukclimateprojections.metoffice.gov.uk.

3. Results

The transmission model used in this work is general enough to allow a spectrum of distinct assumptions for the duration of the vector EIP. However, for clarity we give results for three important examples:

• (1) A deterministic EIP duration model.

• (2) A Markov (or memoryless) EIP duration model.

• (3) An intermediate EIP duration model which more closely matches BTV observations.

The three different forms for the EIP correspond to distinct assumptions about the variation in EIP between infected midge vectors. The deterministic model assumes that the EIP duration is solely due to an accumulated incubation rate above a critical temperature for BTV. Under this assumption, infected midges experiencing the same temperature pattern have identical EIPs with no random variation between midges. The Markovian model assumes that each infected midge has a chance of completing its EIP before its latest biting activity period due only to the temperature felt since the previous activity period. The intermediate model at constant temperature predicts a gamma-distributed EIP duration and can therefore be parametrized to match the observation of midge cohorts, as described in the Material and methods. When temperatures vary the BTV-fitted EIP model is dependent on both total accumulated incubation since infection and chance variation between midges that experience identical temperatures.

3.1. Maximal vectorial capacity per vector

One approach to modelling the effect of climate on transmission intensity is to consider a ‘typical’ static temperature which governs the rate of each temperature-dependent process in the transmission cycle. In this case, it is relatively straightforward to compute the effects of a static temperature on each process, and hence the temperature that maximizes the total transmission (figure 1d). The concept of a static temperature (especially in temperate climates) is however rather simplistic, and does not reflect the dynamics and sequential nature of the process rates. In particular, different elements of the transmission process are important at different times, and the temperature which maximizes the efficacy of each link in BTV transmission differs. For example, the temperature at which the lifetime biting activity of the vector is maximized will be different from the temperature most conducive to midges surviving their EIP. Within the wider context of the reproductive ratio modelling literature, using a static temperature is equivalent to the instantaneous reproductive ratio of cattle-to-cattle transmission of BTV, whereas we focus on the case reproductive ratio (see Fraser [45] for a discussion on the differences between the two reproductive ratios).

If a static temperature is assumed, it is relatively straightforward (and computationally achievable) to sweep through all feasible temperatures and hence find the maximum for static temperature Ĉ_static. Figure 1d shows that the per vector capacity Ĉ_static is maximized by intermediate temperatures, which strike a balance between frequency of feeding and the vector mortality rate. For all three EIP models, the capacity per vector is maximized by a static temperature of , with the maximum value being secondary cattle infections per initial cattle case per midge, depending on the variance of the EIP duration (figure 1d). As expected, highly variable EIP durations (e.g. Markovian) lead to the largest values of Ĉ, as there is the greatest chance of vectors surviving this period and therefore able to infect new hosts [44]. We note that the saw-tooth behaviour of the deterministic length EIP assumption occurs due to the EIP passing an integer number of days such that the vector must survive an extra day before it can feed and infect at dusk. The optimal static temperature is slightly lower for our model than the 20–25°C reported by Gubbins et al. [34]. This is because they follow the common modelling assumption that the vectors bite according to a Poisson process, which allows for multiple successful bites per midge per day and therefore favours rapid biting at higher temperatures more than our model, which only allows for at most a single successful bite per midge per day.

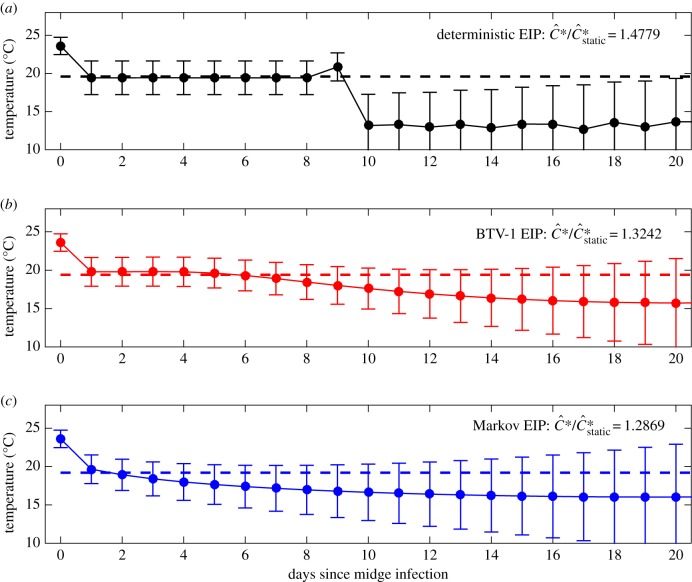
Turning to the situation where the temperature varies, sweeping over all possible temperature combinations is unfeasible; instead we treat the profile of daily temperatures over the next 50 days as an input vector and optimize to find the maximum value of Ĉ over possible inputs (see Material and methods). To gain some understanding of the robustness of this optimal temperature series, we consider the impact on Ĉ of changing each day's temperature independently. In particular, we find the range of daily temperature changes that lead to a 1% change in the total value of Ĉ (estimated from the Hessian at the optimum point). Figure 2 shows the temperature profiles that maximize Ĉ assuming different EIP distributions. For each form of EIP distribution, a high initial temperature is preferred (23.6°C), as this maximizes the probability of a bite on the infection day; following this, cooler temperatures are optimal (decreasing from 19–20°C to 12.5–15°C), increasing the probability that the vector will survive to generate secondary cases in cattle. As expected, the temperatures at later times (many days after the initial infecting bite) play a reduced role (as shown by the temperature ranges that generate a 1% reduction in Ĉ); many of the vectors will fail to survive for this length of time, hence even large shifts in temperature have a minimal effect on the total value of Ĉ. For each EIP model, the maximal per vector capacity Ĉ* over temperature profiles was substantially greater than its maximum over static temperatures Ĉ*_static with the greatest difference for the deterministic model (48% greater than the static maximum) compared with the EIP models with higher variance: the BTV-1 parametrized model (32% greater than the static maximum) and the Markov EIP model (28% greater than the static maximum). The maximizing temperature profiles can be understood with reference to the static temperatures that optimize different aspects of BTV transmission. The single temperature that maximizes the chance of a midge surviving a single day and taking a bloodmeal is 23.6°C; however, the static temperature which maximizes the chance of a BTV-infected midge vector surviving its EIP is 19.6°C (for all EIP distributions), while the static temperature which gives the greatest expected number of lifetime midge bites is much cooler: 12.9°C. Therefore, a profile of cooling temperatures can imply greater risk of transmission originating from an initially hot day than any single static temperature, since it is possible for each aspect of transmission to be maximized by the changing temperature. In fact, the maximizing temperature profile for Ĉ using the deterministic EIP model essentially progresses via sharp transitions between the optimal temperatures for midge infection probability (day 0), surviving EIP (days 1–9) and subsequent lifetime biting (days 10+). The abrupt transitions in this temperature profile are optimal for the deterministic EIP model because any surviving infected midge is either definitely latent throughout post-infection days 1–8 or definitely infectious throughout days 10+ (figure 2). By contrast, the stochastic EIP models always include the possibility that a surviving midge infected on day 0 may be latent or infectious. The temperature profile that maximizes the average number of bites post-infection reflects the underlying chance that the midge has completed its EIP, which favours maximizing temperature sequences with smoother transition from high to low temperature (figure 2).

Figure 2.

First 20 days of maximizing temperature sequences for Ĉ. The daily sequence of temperatures that imply maximal vectorial capacity per vector (Ĉ*) for each of the three EIP models: deterministic (a), fitted to BTV EIP in midges (b) and Markovian (c). The bars indicate how much the temperature would need to vary on that day to reduce Ĉ by 1% compared with Ĉ*. The dashed lines show the optimal static temperature for Ĉ*_static.

3.2. Seasonally varying reproductive ratio in 2006

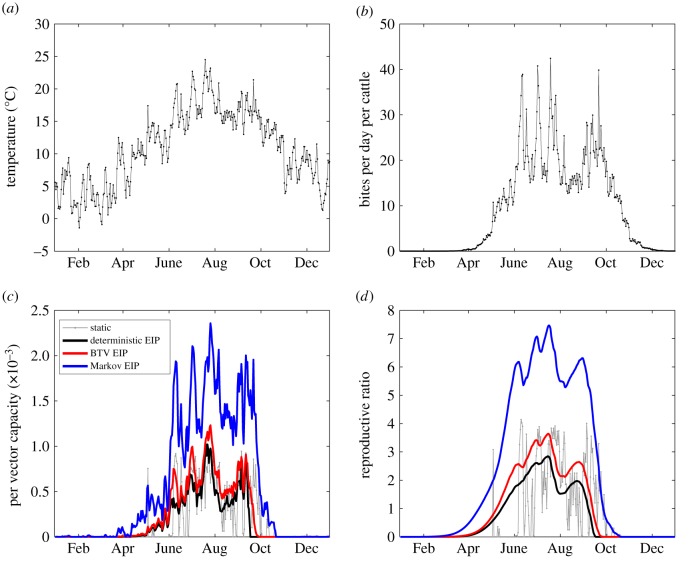
Given the interaction between day of the year and temperature, it makes less sense to optimize R(t); for example, the optimum would be potentially different for each day, t. Instead, we link our model findings to observed temperature time series in order to trace patterns of transmission intensity during and between years. The historic CET data, and the UKCP09 predictions forward, can be used to calculate the capacity per vector Ĉ in a similar manner to what is achieved in figure 2. We also calculate the time series of expected biting from susceptible midges per host on each day (M(t)) that is implied by the historic sequence of temperatures and their days of the year. We initially focus on the year 2006, when temperatures were high and BTV made its first recorded invasion into northern Europe. The daily temperature shows marked stochastic fluctuations about their seasonal profile (figure 3a), which induce even more pronounced fluctuations in M(t) (figure 3b). Both the static version of the capacity per vector (Ĉ_static) and the associated daily reproductive ratio (R_static(t); grey curve shows values for the deterministic EIP model) mimic this fluctuating behaviour (figure 3c,d). By contrast, the values calculated using temperature profiles from 2006 are somewhat smoother (figure 3c,d). Peak Ĉ occurred around mid- to late July for each EIP model, which coincided with a number of days of high mean temperature (20–25°C) followed by a dip in temperature; thus approximately matching the temperature sequence identified as maximal above.

Figure 3.

Daily temperatures, expected midge biting and BTV risk for 2006. (a) The daily mean temperature for 2006 (CET dataset). (b) Expected number of midge bites per cattle host for each day in 2006 from the susceptible midge population. (c) The vectorial capacity per vector on each day (Ĉ(t)) of 2006 for deterministic EIP (black curve), BTV-fitted EIP (red curve) and Markov EIP (blue curve). Static temperature capacity per vector with deterministic EIP also given (grey curve). (d) The seasonal reproductive ratio on each day (R(t)) of 2006 for deterministic EIP (black curve), BTV-fitted EIP (red curve) and Markov EIP (blue curve). Static temperature reproductive ratio (R_static(t)) per vector with deterministic EIP also given (grey curve).

Three features are apparent from a comparison of R(t) with R_static(t) for 2006 (figure 3d): (i) early in the vector season (late April–May) R(t) generally predicts greater BTV transmission intensity than R_static(t), (ii) late in the vector season (September) R(t) generally predicts lesser BTV transmission intensity than R_static(t), and (iii) the EIP model is a substantial factor in BTV transmission prediction. The seasonal discrepancy of BTV transmission prediction between using a temperature profile and using a static temperature can be explained by considering at which temperatures BTV can develop within the midge vector. During the early season, bites during an infectious cow's viraemic period infect midge vectors at temperatures below the development threshold temperature for BTV of 13.4°C [39]; therefore R_static(t) = 0. However, the R(t) transmission metric identifies that a proportion of midges infected in the early season will survive until warmer temperatures arrive (June) and therefore potentially cause secondary cases in cattle. The opposite effect also holds: in the late season bites on infectious cattle will infect midges at temperatures above the BTV development threshold, implying relatively high values of R_static(t). However, because the temperature drops during autumn/winter midges infected during the late season are unlikely to complete their EIP and contribute to BTV transmission, which implies relatively low values of R(t) at the end of the season. Both the deterministic EIP model (figure 3d; black curve) and the BTV-fitted EIP model (red curve) predict a similar pattern for R(t) in 2006, although with different scaling: peak transmissibility was predicted in mid-July with a secondary peak in early September due to an unseasonably warm month. It is notable that these two main peaks in R(t) correspond to double peaks in the first clinical appearance of BTV in 2006 derived from a retrospective study of the epizootic outbreak in northern Europe for both cattle and sheep with a delay of a few weeks [3]. During the core vector season (May–August) assuming a Markov EIP (blue curve) gave R(t) values 2–2.75 times greater than using the EIP model fitted to BTV, which reflects the greater probability a midge has of surviving its EIP under this assumption. At the beginning and end of the midge season, the multiplier in transmission prediction associated with the Markov EIP assumption was enormous. This is due to the fundamental, but unrealistic, assumption of the Markov EIP model that even a single day with temperature above the development threshold can allow completion of the midge EIP.

3.3. Historic and future bluetongue virus transmissibility

The continuous temperature approach can be extended to historical data and future predictions of temperature. We calculate time series for R(t) and a yearly cumulative time series, , for 1950–2015 using the CET times series. These time series are projected into the future (2016–2049) using the UKCP09 climate projector [48] for future temperature predictions at the geographical centre of England. Before estimating future VBD transmission risk associated with climate change, it is necessary to assess a baseline transmission risk [11]. UKCP09 uses 1961–1990 as a climate baseline for prediction; therefore, it is natural that we present our results relative to this baseline. In line with our previous analysis, we find that assuming a Markov EIP implies the greatest baseline BTV transmission risk (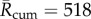 mean over the 1961–1990 baseline) and assuming deterministic EIP implies substantially less baseline BTV transmission risk (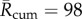) with the BTV-fitted EIP model between these two extremes () (figure 4).

Figure 4.

Trends in yearly cumulative risk and average R(t) profiles. (a,c,e) The cumulative reproductive ratio R_cum for each historical year from 1950 to 2015 (bars) and UKCP09-derived realizations for 2016–2049 (dots) using the deterministic (a,b), BTV fitted (c,d) and Markov (e,f) EIP models. Three periods are highlighted: baseline 1961–1990 years (green), recent years 2000–2015 (purple) and midterm future years 2035–2049 (orange). Other years are given in grey. The 10 year running averages are shown (dashed curves). (b,d,f) Daily averages for reproductive ratio (〈R(t)〉) for baseline (green), recent (purple) and future (orange) for each EIP model. Future years were also averaged over UKCP09 realizations for each year. Individual year R(t) profiles are shown as thinner curves. The length of the epidemic season is when R(t) > 1 (black dashed line).

We observe substantial year-to-year variation in R_cum(year) during both the baseline years 1961–1990 (green bars and curves) and the recent past 2000–2015 (purple bars and curves) relative to a 10 year running average (dashed lines). Projecting into the future the uncertainty between R_cum(year) realizations is also large with values lower than any seen since the 1950s still being feasible in 2034–2049 (orange dots and curves; figure 4). However, on average the trend is towards greater mean cumulative values (), greater mean peak values (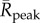) in the year and longer durations when a BTV outbreak is expected to multiply (average number of days per year that R(t) > 1) (figure 4). Each of these mean transmission risk measures increases substantially both between the baseline years compared with the most recent 16 years (2000–2015) and between the recent years and the 16 years in our forecast furtherest in the future (2034–2049) (see table 1 for absolute values and relative changes).

Table 1.

Mean R_cum, R_peak and transmission season duration (when R(t) > 1) in the past, recent years and the near future.

	deterministic EIP			BTV EIP			Markov EIP
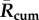			duration			duration		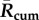	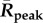duration
Baseline (1961–1990)	98	1.35	39.8	154	1.9	63.4	518	4.86	137.1
Recent (2000–2015)	140	1.76	60.4	207	2.3	88.0	622	5.44	148.3
Future (2034–2049)	234	2.45	106.8	324	3.2	123.2	830	6.65	167.1
B →R % change	+42.9%	+30.3%	+51.8%	+34.4%	+21.1%	+38.8%	+20.0%	+11.9%	+8.2 %
R →F % change	+67.1%	+39.2%	+76.8%	+56.5%	+39.1%	+40.0%	+33.4%	+22.2%	+12.7%

The prediction that BTV transmission risk is increased in the UK compared with 1961–1990 is robust to the choice of EIP model; both the deterministic and Markov EIP assumptions lead to qualitatively similar results to those derived from the BTV-fitted EIP model (figure 4). However, the relative increase in BTV transmissibility implied by using the deterministic or BTV-fitted EIP models/distributions is consistently much higher than the increases derived using the Markov EIP model. The average duration over which a BTV epizootic is expected to multiply in the UK grows faster than the peak transmission intensity over the year () for the first two EIP models. This is due to longer sustained periods above the critical temperature being observed recently (2000–2015) and being predicted in the future (2034–2049). By contrast, using the Markov EIP model to predict BTV transmission risk suggests that BTV epizootic risk was higher in the past, is currently higher and will be higher in the future than predicted by the other two EIP models but that the relative change in transmission risk is much less pronounced (table 1).

4. Discussion and conclusion

We have investigated the effect of temperature variation on the transmission intensity of BTV at three time scales: (i) day-to-future transmission captured by the capacity per vector Ĉ, (ii) infectious generation-to-future transmission captured by the seasonal reproductive ratio R(t) (t denoting the first day a host is infected), and (iii) year-on-year transmission captured by the cumulative reproductive ratio over a year R_cum. For each measure of transmission intensity, we compared results between three distinct assumptions for the EIP: a deterministic model (which is identical to the EIP model presented in [12] albeit with a development rate appropriate for BTV spread by Culicoides genus midges rather than Plasmodium falciparum spread by Anopheles genus mosquitoes), a Markovian model (which assumes that vector EIP can be modelled as a one-stage Markov process, e.g. [50]) and a novel intermediate EIP model that predicts a gamma-distributed EIP at static temperatures and can therefore be fitted to laboratory studies of midge EIP duration.

The per vector capacity Ĉ could be substantially greater with a changing pattern of temperatures than is possible with a static temperature. From the perspective of a single midge infected due to biting on a single day a changing pattern of temperature gives the opportunity for the temperature to segue between the optimal temperatures for each process involved in transmission (infection, surviving the EIP, inflicting infectious bites post-EIP). Although the maximizing temperature profile was broadly similar for each EIP model (initially high and then falling) the details and predicted transmission intensity were sensitive to the EIP model (despite each model predicting identical average EIP durations). The deterministic model for EIP suggests that a sequence of daily temperatures could maximize each transmission process as the midge transits from latent infection to infectiousness. The EIP models with random variability cannot be optimized in this manner because of the uncertainty of disease state at each future biting period. The stochastic models both imply on average greater transmission because the chance of midges surviving their EIP is greater than for the deterministic model [44] and are optimized by a smoother transition to lower temperatures where expected lifetime bites are maximized.

The historic and projected temperatures associated with particular times of year allowed us to extend the calculation to evaluate the daily reproductive ratio R(t)—the expected number of secondary hosts (cattle) that a single host infected on day t will produce in a totally susceptible population—or the cumulative sum of this quantity over the entire year R_cum. We are able to make this transition from per vector capacity to reproductive ratio because the day of year and temperature profile allow us to estimate the number of midges biting per host, using a daily flight activity model calibrated for seasonal variation in English midges as a proxy for the expected biting rate of susceptible midges on infectious cattle per day [46]. Four short-comings of the biting model (M(t)) used in this work should be noted: (i) the capture experiments used to parametrize M(t) were not performed on farms and therefore do not include the likely amplification in midge abundance due to the presence of livestock hosts [26,27]; (ii) the parameters used were specifically targeted for C. obsoletus group female midges ignoring other midge species also likely to play a role in BTV transmission in the UK, e.g. Culicoides pulicaris; (iii) the length of the midge season depends upon climatic trends, such as mean spring temperature [25,28], hence sustained climate change could lead to a longer midge season and more generations of midges per year [22] which is not captured by the statistical model used in this work; and (iv) relating midge capture experiments to the actual animal biting rate is difficult. In this work, we use a model derived from an elevated passive suction trap aimed at capturing midges in flight [46] but attractive trap types could be used as a different proxy for biting, for example traps that attract using UV (blacklight) light. However, UV traps report a significantly lower rate of midge capture than pootering from livestock when directly, and simultaneously, compared [54]. Therefore, interpreting the capture results for UV light traps as a proxy biting rate has its own challenges; see Mullens et al. [23] for a general discussion on this point. Because of the passive trapping mechanism used to inform the biting model, the results in this paper are probably a lower estimate for the absolute BTV transmission risk among cattle herds in England. Much greater understanding of the population dynamics and host preferences of midge species, and therefore their biting rate on livestock, is required. Nonetheless, despite the conservative estimate for transmission intensity many of the R(t) values calculated are large, indicating that sustained transmission for at least one season is highly likely if BTV is established among naive cattle herds in England. Moreover, even if the model for expected biting from the susceptible midge population underestimates the true biting rate by some factor then, so long as the predicted relative response of flying activity to temperature change robustly reflects relative changes in the true biting rate, the percentage change in R_cum still gives a reliable estimate of changing BTV transmission intensity.

We have focused on the impact of the historical and predicted temperature profile on the reproductive ratio of BTV in the England. England provides an interesting test-case as it possesses large variations in climate (both day to day and over the year) and is considered to be at the edge of sustainable transmission. BTV first invaded northern Europe in 2006. This was a particularly warm year in England with the highest total R_cum values calculated from the historic CET record. Nonetheless, England and the rest of the UK had no detected incidence of BTV until August 2007 [55]. Validating reproductive ratio models directly from incidence data can be challenging when the timing of the initial outbreak and the levels of population susceptibility are not known; see Fraser [45] for a discussion on fitting time-varying reproductive ratio values to incidence data. However, we note an interesting concordance between the double-wave pattern of clinical signs of BTV among naive cattle and sheep populations in Belgium in 2006, where BTV serotype 8 probably first invaded in the spring of that year [3], and the double-peak pattern of R(t) as we have calculated using CET data from England for that year. Belgium has a similar climate to the UK and the invasion of BTV-8 occurred early in 2006 among naive livestock herds; therefore, one might expect a close association between R(t) and incidence. By contrast, BTV-8 successfully invaded the UK in August 2007 [55], which is late in the ‘at-risk’ period for BTV transmission. In the years subsequent to 2006 in northern Europe, and in all enzootic regions of southern Europe, a comparison between incidence and R(t) must take into account local temperatures, the seasonality of the local midge populations and the background level of susceptibility of the livestock population to each circulating serotype. This is a promising avenue for future work. Moreover, the R(t) values calculated in this work refer to transmission within a closed spatial environment (e.g. a single farm) with no dispersal of vectors. In practice, large-scale outbreaks require both transmission within the farm and transmission across the farming landscape. Fully quantifying this aspect is complex, depending on the local farming environment. However, it is clear that the within farm R(t) is a key quantity in this process; having R(t) > 1 for sustained periods is obviously a prerequisite for a large-scale spatial outbreak.

Clearly, environmental temperature is not the only factor that determines the changing risk of outbreaks. Climate change is expected to increase the range of the important BTV transmitting midge species in Europe, such as C. imicola [56], and there is evidence that this is already occurring [57]. Climate change is likely to change the range of other potential vector species; equally climate will also affect the profitability of different farming practices, potentially leading to changes in host abundance. Similarly, the risk of an outbreak is often linked to long-range movement of infection-carrying organisms; see Carpenter et al. [58] for a discussion of potential introduction mechanisms of midge-borne pathogens. One such movement is the long-range dispersal of insect vectors, such as that which precipitated the 2007 outbreak of BTV in England/UK, which is often associated with prevailing wind conditions. Another example is the world-wide trade of animals, which can introduce novel diseases to livestock herds across vast distances (see Fèvre et al. [59] for a review of a number of examples); therefore, increased international trade could increase the number of importations of infectious animals and/or midges. However, both of these are difficult to quantify (see Jacquet et al. [57] for a discussion of the difficulties of quantifying midge introduction via globalized transport), and may be influenced by many factors in addition to climate change. Moreover, it is possible that VBDs are introduced into naive regions in Europe more frequently than generally supposed, albeit cryptically, but outbreaks are not observed due to introductions not coinciding with optimal climate conditions, as is suspected for Rift Valley fever virus [60]. By focusing in this paper on BTV transmission intensity (as captured by the reproductive ratio, R) we are able to quantify the potential scale of an outbreak should the disease invade, assessing how this crucial epidemiological value is affected by recent (and predicted) changes in temperature. Although we focus solely on BTV spread by Culicoides midges in this work our modelling approach is directly applicable to any VBD spread by insects that bite once per gonotrophic cycle and have a distinct daily activity period, for example malaria spread by Anopheles genus mosquitoes. The necessary ingredients are estimates of temperature dependence in biting rate, incubation rate and mortality rate for the vector–pathogen system in question, as well as an estimate of vector population density over the season. Other vectors that bite more than once in their gonotrophic cycle can be incorporated with minor adjustment to the underlying mechanism: moving from a discrete-time to continuous-time framework. This would allow the framework to be applied to the many diseases spread by Aedes aegypti (which is known to bite frequently during its gonotrophic cycle [61]), such as yellow fever, chikungunya, dengue and Zika virus.

We found that although 2006 was an outlier year for BTV transmission intensity nonetheless the trend is of a steady (but fluctuating) increase in the cumulative R_cum (summed over a year) over the past 60 years, and that UKCP09 climate projection predicts this trend to continue over the next decades, although the rate of increase depends on the underlying assumption on the midge EIP variability. In particular, assuming a Markov model for the EIP distribution probably overestimates the absolute transmissibility of BTV by a significant factor whilst also underestimating how rapidly the relative transmission intensity of BTV is increasing. However, despite these high R_cum values in England in 2006 this potential was never realized, as the infection did not reach the UK in this year—this highlights the underlying stochastic nature of such opportunistic invasions. It was not until 2007 that the UK experienced its first BTV cases. We expect that the peak R_cum value in 2006 will be commonly exceeded in future years, suggesting that widespread outbreaks of BTV may become more common and a policy of annual vaccinations may be necessary to protect UK livestock. Whether BTV becomes enzootic in the UK or whether we experience stochastic invasions from warmer regions depends largely on the ability of the virus to overwinter. BTV probably cannot be sustained in its mammalian hosts over winter when biting vectors are close to absent, and given that there is no evidence of vertical transmission (females to offspring) in the midge vectors, a number of alternative mechanisms have been proposed [62]. The survival of infected midges over the winter season is one possible overwintering mechanism with recent evidence implicating overwintering in long-lived midges, albeit in California [63]. Whatever the precise mechanism(s) for overwintering the predicted future temperature patterns of the UK climate suggest that, first, invasive BTV will be more likely to establish itself in the UK due to higher values of R(t) and, second, the length of the BTV transmission period in the UK will increase due to longer periods when R(t) > 1, making overwintering more likely. In any case, even if other contributing factors to BTV risk in the UK were to remain unchanged, such as the length of the midge-free period or rate of infectious introductions from abroad, BTV is likely to become a more persistent feature of the UK livestock industry in the future.

Authors' contributions

S.P.C.B. gathered the UK climate data and formulated the transmission model. Both S.P.C.B. and M.J.K. analysed transmission results and prepared the manuscript.

Competing interests

We have no competing interests.

Funding

This research was funded by the ERA-NET project LiveEpi.

Disclaimer

These organizations give no warranties, express or implied, as to the accuracy of the UKCP09 and do not accept any liability for loss or damage, which may arise from reliance upon the UKCP09 and any use of the UKCP09 is undertaken entirely at the user's risk.