Computational optical palpation: a finite-element approach to micro-scale tactile imaging using a compliant sensor

Abstract

High-resolution tactile imaging, superior to the sense of touch, has potential for future biomedical applications such as robotic surgery. In this paper, we propose a tactile imaging method, termed computational optical palpation, based on measuring the change in thickness of a thin, compliant layer with optical coherence tomography and calculating tactile stress using finite-element analysis. We demonstrate our method on test targets and on freshly excised human breast fibroadenoma, demonstrating a resolution of up to 15–25 µm and a field of view of up to 7 mm. Our method is open source and readily adaptable to other imaging modalities, such as ultrasonography and confocal microscopy.

1. Introduction

The sense of touch is essential to our capacity to manipulate objects and to feel their size, shape, texture and stiffness. However, there is a limit to the sensitivity and resolution of natural human tactile capacity [1]. Many advances have been made that improve on human tactile capacity by employing artificial sensors in robotics applications [2], such as manufacturing and prosthetics, thereby, extending this capacity to automated machines [3]. Artificial tactile sensing is increasingly being considered in clinical settings, for instance, for robot-assisted minimally invasive surgery. When performing surgery through small-footprint incisions, robotic assistance can provide enhanced vision and dextrous capacity to the surgeon, but is accompanied by a loss of tactile function [4]. The presence of tactile feedback in such surgery has been identified as a critical factor in improving patient outcomes [5]. More generally, both inside and outside the operating theatre, physicians routinely use the sense of touch to identify tissue types and diagnose pathologies, such as cancer, edema, infection, scarring and inflammation. This diagnostic method is referred to as palpation and its utility stems from the fact that many diseases change the mechanical properties and structure of tissue [6]. For instance, lobular and ductal carcinoma of the breast have been reported to be up to 14 times stiffer than surrounding healthy tissue [7].

Artificial tactile sensors have the capacity to provide, in a robotic setting, better resolution, sensitivity and objectivity than conventional palpation. Commercial systems have been developed that do so by spatially mapping the stress applied to a tissue surface [2]. Maps of tactile stress can be displayed as an image, in principle, enabling the physician to exploit the contrast and texture observed in the stress maps for diagnosis. This is termed tactile imaging and has been demonstrated in vaginal and pelvic floor assessment, and prostate and breast cancer diagnosis, with the potential to achieve sensitivity and specificity values comparable to current non-invasive diagnostic methods, such as magnetic resonance imaging (MRI), at a fraction of the cost [2]. These tactile imaging systems often employ arrays of piezoelectric or capacitive sensors. Their resolution is determined by the spacing of the sensor elements, termed taxels or sensels, which is typically more than 1 mm [2]. Recently, nanowire tactile sensors have been fabricated, achieving a taxel resolution of 2.7 µm [8]. To be effective in clinical applications, a challenge for these high-resolutions sensors is to extend the field of view to beyond the demonstrated 100–200 µm [8]. In addition, the rigid nature of many of these devices poses challenges for use on tissue with uneven surface topography.

In this paper, we present a new alternative termed computational optical palpation. In this method, a thin, compliant and transparent layer of mechanically uniform material is compressed against an object, and the layer thickness is measured using the volumetric optical imaging technique, optical coherence tomography (OCT). Using finite-element analysis (FEA), the imparted tactile stress can be accurately estimated solely from the measured thickness of the layer and its known mechanical properties. This method has the distinctive feature of avoiding the use of discrete sensor arrays in favour of use of an imaging system. The spatial resolution is related to the resolution of the imaging system, rather than to the spacing of individual sensors, making it readily capable of micro-scale resolution. Furthermore, the compliant layer readily conforms to the sample surface, which is an important characteristic for probing samples with uneven surface topography [3]. An added benefit of using an imaging system is that corresponding images of sample structure are provided alongside tactile stress maps.

We have previously demonstrated the combination of a compliant, transparent layer with OCT, termed optical palpation, showing the ability to delineate mechanical features, in both ex vivo and in vivo scenarios [9,10]. In these demonstrations, layer strain was measured and used to determine stress from a look-up table obtained by calibration, which is similar, in principle, to taxel array methods [8,9]. However, as we demonstrate in this paper, the mechanically coupled and continuous nature of the compliant layer necessitates the use of a more sophisticated three-dimensional mechanical model. Only by the use of such a model can tactile stress imparted to mechanically and structurally heterogeneous objects be imaged with high resolution and accuracy. We demonstrate stress maps with accuracy to within 5% of the expected value in the typical regime of operation, and a resolution of 15–25 µm, which is close to the resolution of the underlying imaging system, over 5–7 mm fields of view. Such performance is a valuable step towards the translation of tactile sensing to clinical applications, such as diagnosis and monitoring [2,4]. An additional benefit is that our method is directly adaptable to other imaging modalities, from confocal microscopy on the sub-micrometre scale, to ultrasonography on a more macro-scale. Furthermore, it could be combined with optical elastography to quantify stiffness in a volume with higher accuracy than has been demonstrated [11]. We further aim to facilitate implementation by making the method open source, as described in the Data accessibility.

2. Computational optical palpation

Figure 1 shows our method diagrammatically, from acquisition to meshing. In figure 1a, a thin, compliant, transparent layer of uniform material (we use silicone rubber), henceforth referred to as the compliant layer, is shown positioned against a transparent glass window, which is part of the OCT imaging system [12,13]. The compliant layer is compressed against a sample, deforming based on the sample's mechanical properties and surface topography. OCT volume images of the layer are captured in its unloaded and loaded states. Descriptions of the layer fabrication, and of the OCT imaging system and acquisition method, are provided in the electronic supplementary material. Figure 1b shows representative cross-sectional images that clearly delineate the compliant layer; the sample is a silicone test target, as described in §6.3. From such recorded images, it is straightforward to extract the thickness of the compliant layer before and after compression; for this purpose, we employ a Canny edge detector developed previously [9]. The last panel in the figure is described in §3.

Figure 1.

Computational optical palpation. (a) Diagram of the experimental sample set-up and incident optical beam, and (b) representative OCT cross-sectional images, in the (i) unloaded and (ii) loaded states, showing the compliant layer CL being compressed against the sample S on a rigid substrate (oblique dashed); W: window, CL: compliant layer, S: sample. In (b), CL and S are marked by false colour, and the intensity image captured by OCT is shown; L₀(x,y) and L₁(x,y) represent compliant layer thickness in the unloaded and loaded states. (c) Cross section of the meshed FEA assembly used in the (i) unloaded and (ii) loaded states. CL boundaries are, respectively, modelled by WCB: window contact body, and SCB: sample contact body. The SCB geometry reflects the lower CL boundary, marked by the dashed line in (b). Scale bar, 500 µm. (Online version in colour.)

There exists a relationship between the deformation (here, boundary displacement) of the layer, its intrinsic mechanical properties and stress. It is, indeed, sufficient to know two of these parameters in order to estimate the third. We have knowledge of the bulk mechanical properties of the compliant layer from standardized mechanical testing. We can also estimate boundary displacement from the compliant layer thickness observed in the unloaded and loaded OCT volumes. The change in thickness from compression, however, does not itself quantify displacement; rather, it has to be converted to a vectorial form, described in §3. The main remaining difficulty in attaining accurate measurements of tactile stress, however, lies in defining an accurate mechanical model, which we describe in the next section.

In our previous demonstrations of optical palpation [9,10], the mechanical model is based upon the assumption that, when applied to a sample, the stress field within the compliant layer is uniform and uniaxial [14]. This assumption only holds true for samples possessing no significant mechanical heterogeneity and with a flat surface geometry. Furthermore, it assumes that there is no friction present at the boundaries of the compliant layer. The inferior results obtained from this overly simplified method are included alongside the method advanced here in §§5–7 to emphasize the consequences of making such assumptions and to justify the need for our more computationally demanding numerical approach.

In §3, we describe the more complex mechanical model used in computational optical palpation, and compare it to our previous method. In §4, we quantify friction and its effect on our method.

3. Mechanical model

Tactile stress is calculated using FEA solely by modelling the deformation of the layer and its contact boundaries. Figure 1c shows the FEA assembly. Deformation in the compliant layer body is dictated by the equation of dynamic equilibrium, which, omitting body forces (such as the negligible effect of gravity), is given as

where σ is the Cauchy stress tensor and u is the displacement ( is acceleration). (Although the measurement is made quasi-statically, a dynamic model is preferred over a static model for reasons discussed in the electronic supplementary material.) The compliant layer is hyperelastic [15] and modelled using the Mooney–Rivlin material model [16,17], which, for an incompressible material, is given as

where B is the left Cauchy–Green deformation tensor, I₁ and I₂ are its first and second invariants, respectively, and I is the identity. C₁ and C₂ are the Mooney–Rivlin material coefficients of the silicone rubber used for the compliant layer, which were found from uniaxial test data (Instron, Norwood, MA, USA) to be 2.23 [±0.04] and 0.70 [±0.03] kPa [95% CI], respectively.

Regarding the boundary conditions of the simulation, we have access to the uncompressed and compressed compliant layer thickness from the experimental data. However, we cannot directly estimate from these data the three-dimensional vectors describing the displacement of the boundary that are required for FEA. To overcome this, we employ separate bodies to model the contact of the compliant layer with the window and with the sample, as shown in figure 1c. By displacing the sample contact body (SCB) to match the final thickness observed in the compressed OCT image, we aim to mimic the boundary behaviour of the compliant layer. Notably, the SCB is not representative of the sample, but only its interface with the compliant layer. Lateral boundaries not in contact with the window or the sample are specified to be stress free. Solving this assembly using FEA yields the full three-dimensional stress field within the compliant layer, allowing us to extract the stress at the bottom interface, i.e. tactile stress. A detailed description of the FEA is given in the electronic supplementary material. Stress, inherently, is a three-dimensional tensor; however, we extract the axial, or z-normal, component, which we use as a quantification of axial tactile stress, corresponding to what would be typically measured by many discrete tactile arrays. It is also trivial to extract stress that is normal to the compliant layer surface or, alternatively, the traction force vectors, if motivated by a particular application.

To evaluate the proposed method, and provide a justification for the necessity of numerical computation, we compare our method to the calibration approach (optical palpation) employed previously [9]. In that approach, numerical computation is avoided by finding a closed-form solution to the deformation of the compliant layer. This is a common approach employed in image-based mechanical characterization techniques [18]. This is done by assuming that the layer is linear-elastic, isotropic and homogeneous, as described by a constitutive equation, given as

where δ_ij is the Kronecker delta, λ and μ are the Lamé parameters, σ_ij is the stress tensor and ɛ_ij is the strain tensor. Under uniaxial compression, the equation reduces to Hooke's law, i.e. E = σ/ɛ, where E is Young's modulus (E = 3μ). The compliant layer is hyperelastic [15], meaning that as it is compressed further, the apparent Young's modulus increases. Therefore, Young's modulus is adjusted based on the measured axial strain. Tactile stress for each spatial location (x, y) is considered independent, and can be trivially calculated as

where strain ɛ(x,y) = (L₁(x,y) − L₀(x,y))/L₀(x,y), with L₀(x,y) and L₁(x,y) being the layer thickness before and after loading, respectively, at each lateral coordinate observed from OCT images, figure 1b; and E[ɛ(x,y)] is the strain-adjusted Young's modulus. Hereon, we refer to this approach as the algebraic method. The assumptions implicit in this method are unrealistic; however, they enable a rapid and direct solution, often the highest priority in a clinical setting.

4. Friction

Taking account of friction at the interfaces of the compliant layer is necessary to determine stress at the sample surface accurately. We have estimated friction for various lubrication and loading force experimental conditions by relating experimental data to an FEA-generated calibration. The so-determined coefficients of friction were used as a ‘best guess’ a priori estimate for the interface between the compliant layer and the window in subsequent measurements, and were used to generate the computational results presented in §§5 and 6. The friction at the interface with the sample is not included in our method; we provide a rationale for this omission later in the section.

There are numerous ways to estimate friction [19]. We used a novel method based on phase-sensitive OCT [20,21] (described in the electronic supplementary material). Briefly, we reconstruct the axial displacement depth profile in the compliant layer, from the window to the sample interface. The interface between the compliant layer and the window is used as the reference reflector in the OCT system. This interferometer configuration is termed common path and signifies that the interface corresponds to zero relative axial displacement [22]. During compression, the magnitude of the accumulated displacement will continuously increase with depth, reaching its highest value at the interface with the sample. If the compliant layer is uniformly compressed, and there is no friction, then the displacement depth profile will be strictly linear. However, if friction is present, it will distort the displacement gradients close to the boundaries. This characteristic is presented in figure 2a, which shows FEA-simulated profiles (solid black curves) of displacement with a varying coefficient of friction at the interface with the window. The friction contact model is described in the electronic supplementary material.

Figure 2.

Friction. (a) Friction calibration curves: normalized local displacement with respect to depth. Black solid curves show simulated data with coefficients of friction of 0.1, 0.2, 0.3 and 0.4. Dashed black line shows the ideal case of no friction. Experimental data shown in colour as labelled. A local region is magnified in the inset. (b) Mean reconstructed stress at each friction condition using the algebraic and computational method validated against independently measured (expected) stress. Error bars represent the deviation in stress that results from ±0.05 variation in estimated friction. (Online version in colour.)

We imaged the displacement profile in the compliant layer under different lubrication and load conditions to probe the range of friction likely to be encountered under real experimental conditions. Prior to compression, poly(dimethylsiloxane) (PDMS) oil (AK50, Wacker, Germany) was used to lubricate the compliant layer–window and the compliant layer–sample interfaces thereby minimizing friction. Three different quantities of lubricating PDMS oil were used to vary friction, denoted as low (covered with oil), medium (wiped with oil) and high (no oil). While this description of the lubrication conditions is subjective, it is likely to be similarly subjective in practical applications. Thus, a conservative ±0.05 variation in the coefficient of friction is considered for evaluating the error of the proposed technique in the following sections. For each friction condition, a flat load cell (LSB200, FUTEK, CA) with a brushed aluminium surface was used to provide a gross force directly onto the compliant layer of 0.5 N, which was then increased to 1.5 N. At each load force, additional micro-scale compression was then applied by a piezoelectric transducer, additionally compressing the compliant layer by less than 1 µm. The resulting displacement profiles versus depth in the layer were measured by phase-sensitive OCT [20]. Profiles for each trial were scaled to have the same displacement value at the sample-side interface, and overlayed on the FEA characteristic curves for different friction conditions (figure 2a).

In figure 2a, in the case of high friction, where no oil was used, the measured displacement profile closely matched that of a modelled coefficient of friction of 0.30, for both 0.5 and 1.5 N preload. At 0.5 N, low and medium friction corresponded to friction coefficients of around 0.12 and 0.15, respectively; however, as the preload was increased, friction increased to around 0.20 and 0.24. Such behaviour demonstrates that friction is force-dependent in our experiments, which may have arisen from oil being exuded from the interface at higher preload forces. This is not seen in the high-friction condition, supporting this theory, as no oil was used in that case.

As stated above, we only model the friction at the interface with the window. This is because the window is sufficiently rigid that we can assume it undergoes no lateral displacement; however, a soft sample may deform with the compliant layer, and as we have no estimate of its lateral displacement, we cannot model friction at this interface effectively. Particularly, we cannot reconcile the lateral displacement of the true sample with that of the SCB. Although this presents a complication, the cause—namely, the sample deforming laterally along with the compliant layer—will, in fact, reduce the error caused by an incomplete friction model. In such a case, the shear forces at the compliant layer–sample interface will be much smaller than in the case of a rigid boundary, and their modulation, through varying friction, will have a proportionately smaller effect on overall stress. This is an important consideration: if a sample is sufficiently stiff, friction can be modelled, having a significant effect on obtaining accurate stress; and if a sample is sufficiently soft, friction cannot be modelled, however, the effect will be somewhat diminished. In the next section, we describe how we estimate the error associated with this uncertainty.

5. Tactile sensing

We validate the accuracy of our method by employing the data obtained from the friction experiments as follows. For each of the six experiments (three friction levels and two force values), we know the change in thickness of the layer from OCT images, and we have estimates of friction, constituting the necessary inputs for optical palpation. Using the computational method, we can extract surface stress. By integrating the stress across the surface, we estimate the total stress experienced by the compliant layer, which we then compare to an independent measure of stress obtained as the ratio of applied force (0.5 or 1.5 N, as determined by the load cell) over the compliant layer's surface area observed in OCT (expected stress). We further evaluate the performance of our technique by comparing it to the algebraic method.

Figure 2b shows total stress calculated by the algebraic and computational methods, compared to the expected stress. Beyond the case of low friction at 0.5 N, the accuracy of the algebraic method degrades with added friction and force. This is expected, as the model does not account for friction. The computational method is significantly more accurate. For every value of the coefficient of friction, including a nominal friction of 0.1 assigned to the compliant layer–SCB boundary, additional simulations were run at values of ±0.05, and the error bars represent its effect on the final stress. This variation in the coefficient of friction was chosen as a conservative value based on the repeatability observed in previous friction experiments with similar layer sizes and loading conditions. This shows the extent that a conservative error in estimating friction can have on tactile stress. Our method is accurate (to within 5% for 0.5 N and 15% for 1.5 N) except for the case of 1.5 N and high friction, which represents a compression beyond 50%. Coupled with high friction, which in practice would be mitigated by using lubricating oil, this case is well beyond the worst-case scenario for most practical applications of optical palpation. Furthermore, in this scenario, the mechanical state of the compliant layer is in a heavily nonlinear regime, at which point our model breaks down. By contrast, at 0.5 N, the compliant layer underwent roughly 10–20% compression, which represents its typical range of operation in the experiments described in §6. Thus, we conclude that we are able to effectively account for friction over the range of scenarios relevant to tissues, and probed in this paper. We note, for higher force sensing of materials stiffer than typical soft tissues, a stiffer compliant layer material can be used.

6. Tactile imaging

In this section, we investigate the accuracy of both versions of optical palpation in reconstructing spatially varying maps of tactile stress. However, there are no tractable means of simultaneously and independently measuring spatially resolved tactile stress with the fields of view and resolution scales provided by optical palpation. For an initial validation, we model the entire optical palpation experiment in FEA. Unlike in previous sections, the FEA now models the mechanics and geometry of both the compliant layer and the sample. From this FEA model, we extract the unloaded and loaded thickness of the compliant layer, as would otherwise be available from experimental data. We also extract the surface tactile stress, which is compared to the values estimated with our methods. The model is described in detail in the electronic supplementary material. Two sample mechanical models were tested, in order to evaluate the effects of surface structure in a mechanically homogeneous sample and mechanical heterogeneity in the bulk. An actual silicone test target was also tested experimentally and compared with a full FEA simulation.

6.1. Structural heterogeneity simulation

Tactile imaging was simulated on a sample with a sinusoidal surface topography and the same mechanical properties as the compliant layer. The sample was 5 by 5 mm in width and 2 mm in depth, on average. The surface in contact with the compliant layer had a sinusoidal profile in x, and was invariant in y. The sample is illustrated in figure 3a, with five peaks distributed across the 5 mm lateral extent, and an amplitude of 0.25 mm. The sample was compressed by 0.5 mm towards the window, which resulted in less than 15% strain for the assembly. To demonstrate the capacity of our technique, a coefficient of friction of 0.3 was used for the compliant layer interface with the window and 0.1 for the interface with the sample. A mesh size of 50 µm was used.

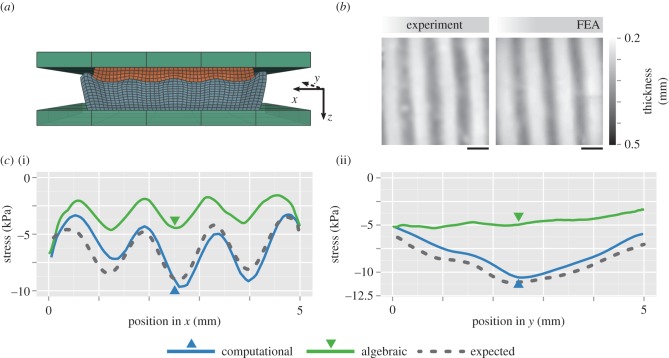
Figure 3.

Comparison of simulated computational and algebraic optical palpation against full FEA simulation. (a,c) FEA assembly of a simulated experiment, showing: (a) the stress layer (orange) compressed against a sample (blue) with a sinusoidal surface topography; (c) the stress layer compressed against a sample with adjoining columns of soft and stiff material. (b,d) Modelled central cross-sectional profiles of stress along the x (i) and y (ii) directions, corresponding to (a) and (c), comparing the algebraic and computational methods against expected stress. Arrows denote the location of the corresponding x and y orthogonal cross sections. (Online version in colour.)

Figure 3b shows the central cross-sectional profile of tactile stress along the x- and y-directions, estimated using computational optical palpation applied to the simulation data. The profiles of stress closely correspond to the profiles of expected stress, extracted from the full FEA simulation. This is particularly evident when compared to the estimate provided by the algebraic method. This demonstration clearly emphasizes the importance of combining optical palpation with a comprehensive and three-dimensional mechanical model for the case of uneven sample surface topography.

6.2. Mechanical heterogeneity simulation

Tactile imaging was simulated on a sample with adjacent equal-sized columns of soft and stiff material, 5 by 5 mm in width and 2 mm in depth, figure 3c. The soft material had the same properties as the compliant layer, and the stiff material was roughly three times stiffer. The sample was again compressed by 0.5 mm toward the window. A coefficient of friction of 0.3 was used for the compliant layer interface with the window and 0.1 for the interface with the sample.

Figure 3d shows the central cross-sectional profiles of tactile stress along the x- and y-directions, respectively, estimated using the computational technique. A mesh size of 50 µm was used. Again, the profiles of stress closely correspond to the profiles of expected stress, extracted from the full FEA model. Similar to figure 3b, the estimates provided by the algebraic method are far less accurate.

6.3. Experimental demonstration

To demonstrate computational optical palpation experimentally, we fabricated a sample with a sinusoidal surface geometry closely approximating that used in the FEA simulation. The sample surface profile was created using a three-dimensional printer (Replicator 2X, MakerBot, NY) to print a mould for casting silicone rubber. The samples were then imaged in their unloaded state using OCT, and their real geometry was reconstructed in FEA (figure 4a) to account for inaccuracies introduced by the fabrication process. The sample was compressed against the compliant layer with a flat aluminium plate. The unloaded assembly thickness was approximately 2.75 mm, which was compressed by 0.7 mm, corresponding to an average of 25% strain. FEA was used to fully model the real experiment, based on the imaged geometry, known mechanical properties and aforementioned boundary conditions.

Figure 4.

Experimental demonstration. (a) FEA assembly of the simulation with exact sample geometry generated from OCT. (b) En face maps of the compressed stress layer thickness obtained from the experiment and FEA simulation. Scale bar, 1 mm. (c) Central cross-sectional profiles of stress along the x (i) and y (ii) directions, reconstructed from experimental data using the algebraic and computational methods, and compared against expected stress from simulation. Arrows denote the location of the corresponding x and y orthogonal cross sections. (Online version in colour.)

Figure 4b shows the loaded thickness of the compliant layer in both the experiment and the FEA simulation. The loaded thicknesses match closely, suggesting that the FEA simulation faithfully represents the experiment and that the tactile stress extracted from the full simulation is likely to be close to the tactile stress determined through the experiment. We perform computational optical palpation using only the experimentally measured thickness, and an estimate of friction (0.15), which corresponds to the closest matching experimental condition from figure 2. The estimate of tactile stress using both the algebraic and computational approaches applied to the measured data is presented in figure 4c, again as a cross-sectional profile along the x- and y-directions. The computational optical palpation approach compares very closely to the expected stress from the full FEA model. This result contrasts with the substantial inaccuracy of the algebraic method. The small differences introduced between computational optical palpation and the purely FEA-simulated data likely arise from a number of experimental factors that could not easily be incorporated into the simulation, such as the slight tilting of the flat compression plate with respect to the window and non-uniform friction.

7. Resolution

In this section, we present estimations of the resolution of computational optical palpation. To evaluate the experimental resolution, we mapped the stress applied to a 500 µm wide cube fabricated from stiff silicone resting directly on a rigid back-plate. Tactile stress was reconstructed using both the algebraic (figure 5a) and the computational (figure 5b) methods. In the computational method, a 10 µm mesh size was used to match the OCT transverse resolution. Qualitatively, one observes in figure 5 a significant improvement in resolution using the computational method, in particular evidenced by sharper feature boundaries. Uneven surface features become particularly visible in computational optical palpation images; the structural OCT cross section is provided in figure 5c, showing the existence of surface perturbations within the sample (7 µm RMS roughness); the cross-correlation of perturbations in the layer thickness and stress was 0.85, which provides supporting evidence that the spatial variation seen in tactile stress is likely representative of true sample features.

Figure 5.

Maps of axial stress produced by a stiff silicone cube, reconstructed using the (a) algebraic and (b) computational method. (c) Cross-sectional OCT image of the sample; arrow shows micro-scale surface perturbations. (a–c) Scale bar, 300 µm. (d,e) Cross-sectional plots of stress along the x-direction (horizontal; through the centre of (a,b)), (d) simulated, and (e) experimental; reconstructed using the algebraic and computational approaches, respectively. (f) Demonstration of computational optical palpation on a 5-cent Australian coin, 19 mm in diameter (i); map of tactile stress (ii). Scale bar, 1 mm. (Online version in colour.)

To quantify resolution, we measured the 10–90% spatial response across the feature edge. Figure 5d,e shows the cross-sectional plot of stress along the x-direction. Figure 5d was generated using simulated data, by modelling uniform compression of a 500 µm wide square area across the stress sensor. Figure 5e is experimental data, as shown in figure 5a,b. The measured resolution for the algebraic method was 180 µm and 250 µm, in the simulation and experimental data, respectively. A 180 µm resolution was also measured in our previous work [9]. Using the computational method, the resolution improved to 15 µm and 20 µm, in the simulation and experimental data, respectively. This represents over an order of magnitude improvement.

To demonstrate its capacity further, computational optical palpation was performed on a 5-cent Australian coin. A 5 by 5 mm region was probed from the 19 mm diameter coin, as visualized in figure 5f. A mesh size of 10 µm was used, producing a tactile stress map with clearly delineated features. The resolution for the coin was comparable; below 25 µm for selected sharp boundaries.

Towards a clinical application of optical palpation, we imaged tactile stress produced on a freshly excised fibroadenoma of the human breast. The mesh size was 50 µm over a 7 mm field of view. OCT data were derived from [11], which describes the ethical approval and method for tissue handling. Briefly, breast tissue was surgically removed and a 2 × 2 × 1 cm region of interest was excised, such that the fibroadenoma was present on the widest edge of the sample. The compliant layer was compressed against that edge, with the sample held by a rigid plate. Fibroadenoma is a benign tumour characterized by the growth of fibrous nodules within fibrous and glandular breast tissue. OCT structure, as a maximum intensity projection, and haematoxylin and eosin histology, are presented in figure 6c,d, respectively. The image presents a region comprising individual fibrous nodes, and a region enclosed by a dense fibrous cap. In the corresponding histology, figure 6d, nodules are emphasized by purple epithelial cells, which circumscribe individual nodes. With computational optical palpation, figure 6b, we can pick out distinct textural differences in stress in these regions. Individual fibrous nodules are particularly evident. The dense fibrous cap is significantly smoother. These features are poorly distinguishable in the image produced by the algebraic method (figure 6a). Feature contrast (as tactile stress to local noise ratio) was enhanced roughly twofold in the nodules marked in figure 6.

Figure 6.

Map of axial stress produced by fibroadenoma of the breast, reconstructed using the (a) algebraic and (b) computational approach. (c) Maximum intensity projection of the OCT volume in z; intensity normalized. (d) Corresponding haematoxylin and eosin histology. Arrows: individual fibrous nodules (in (d), representative, not corresponding, nodules are marked); stars: region enclosed by a dense fibrous cap; white triangles: artefacts in layer thickness detection. Scale bar, 1 mm. (Online version in colour.)

8. Discussion

Computational optical palpation has several advantages over methods employing taxel arrays. Primarily, the stress-sensing element is only required to consist of a readily disposable uniform and transparent material, which is simpler to fabricate for applications requiring high resolution and flexibility of the sensor. However, the requirement of an imaging system is added; but brings the benefit of providing corresponding structural information. Structural images may be used to recognize features in the palpated object, and may provide information on the quality of contact with the stress sensor. For instance, for the experimental results reported here, live structural images were used to confirm complete contact between the compliant layer and the sample. In practice, it would be currently challenging to adapt imaging systems, such as OCT, to applications such as prosthetics, humanoid robotics and automation, although much progress has been made in miniaturizing OCT systems [23]. In medicine, however, imaging systems are routinely used and available. Optical palpation can be employed as a standalone system [2,24], or adapted to other existing imaging tools, such as ultrasonography and confocal microscopy, likely with little or no required changes to hardware. The computational method is open source, accessible at https://github.com/philipwijesinghe/computational-optical-palpation, as described in the Data accessibility.

The distinct advantages posed by optical palpation, to date, have been undermined by the effects of mechanical coupling, which exists between all parts of the stress sensor. This coupling arises because the compliant layer is continuous and nearly incompressible. In such materials, tactile stress applied to a local area elicits stress and strain in adjacent areas. Thus, to calculate tactile stress accurately, one must consider the stress and strain state in all parts of the layer, as we do with computation, rather than independently, as is done in the algebraic method.

The largest contribution of computation is seen in spatial resolution, improving it by more than an order of magnitude, from 180–250 µm to 15–25 µm. In theory, the resolution limit for computational optical palpation is set by the resolution of the imaging system and the meshing density of the FEA model. The lateral resolution of the OCT imaging system used to generate the results presented in this paper is 11 µm; however, OCT systems have been demonstrated with sub 2 µm resolution [25,26]. Application of the computational method to confocal microscopy opens up the possibility of performing computational optical palpation at resolutions well below 1 µm.

The ultimate challenge in reconstructing high-resolution tactile images is the potentially high computation time. The required time to extract tactile stress using FEA is closely related to the total number of elements in the model, implying a trade-off between field of view and resolution, which can be tailored to individual applications. For the results shown in figures 2–4, approximately 100 k elements were used, resulting in a mesh resolution of approximately 50 µm over a 5 by 5 mm field of view, and a computation time of under 30 min when performed on a personal computer, and under 15 min on a workstation (details in Data accessibility). This can be greatly improved with more powerful hardware, and parallelization [27]. For the results shown in figures 5 and 6, with over 200 k elements, computation time was over 2 h, presenting a challenge for clinical applications. The time can be reduced by evaluating smaller fields of view or by employing adaptive meshing, dynamically refining the mesh close to sharp stress features.

A further limitation of computational optical palpation is the requirement for the accurate modelling of friction. Despite the attraction of the calibration approach to estimating friction presented here, friction remains an unknown in the strict sense, and further, may vary across the surface of the compliant layer. Direct measurement of three-dimensional boundary displacement in the layer would remove the need to know friction entirely, and could be achieved with digital volume correlation (DVC) [28]; however, it is likely that structural features will have to be introduced to the compliant layer to make DVC possible.

The algebraic method described here is, in principle, similar to the method used in taxel array techniques [8,9]. Fundamentally, stress applied to a region of a stress sensor, or a sensing element, results in its deformation or strain. In the case of optical palpation, this strain is measured directly, while in taxel array methods, the strain in each sensor element produces a change in its electrical properties, such as capacitance or resistance [2,3]. With calibration, stress can be extracted from any of these measured properties. In these applications, each taxel, element or region of the compliant layer is considered mechanically independent. As taxel array methods are developed to be more compact with higher sensor density, mechanical crosstalk may become prominent, particularly in sensors fabricated from continuous, nearly incompressible materials [2,3,29]. Therefore, similar computational approaches may well have application in improving the accuracy of these sensors.

It is important to consider the effect of the compliant layer design on the performance of optical palpation. As with other tactile imaging techniques, optical palpation maps the force per unit area on the sample surface. For a uniform applied force at the distal surface of the layer, the force at the sample surface will be modulated by the stiffness of the sample and its surface topography, as well as by the stiffness, displacement and thickness of the compliant layer. For instance, a soft layer will comply with the sample topography and produce more uniform tactile images, while a stiff layer will contact only the superficial ridges of the sample surface and produce sharp boundaries in tactile stress. Areas not in contact with the compliant layer will not confer force, thus no tactile contrast will be formed. For diagnostic applications, where contrast is of interest for the entire surface area, complete contact is desirable. The displacement and thickness of the layer should be kept higher than the amplitude of the surface topography of tissue to ensure contact. For highly irregular tissues, this may be problematic as the layer thickness requirements may exceed that observable with OCT (approx. 2–3 mm). Ultimately, the layer design and applied displacement should be evaluated and optimized based on the intended application.

An important application of computational optical palpation is in disease diagnosis. Optical palpation has already been demonstrated in assessing both malignant breast tissue [9] and skin lesions [10]. Palpation-like imaging has been employed and is now commercially available, for breast (SureTouch, Medical Tactile Imaging), and prostate, vaginal and pelvic floor (PTI/VTI, Advanced Tactile Imaging) analysis [2]. In the current configuration, illustrated in [10], computational optical palpation may be directly applied to superficially accessible tissue, such as the above skin, breast, prostate and pelvic floor applications. In-cavity or small-footprint probe configurations are possible, and are already being demonstrated for OCT imaging through needle-based [30] and endoscopic [31] formats. However, further development is required to implement a compliant layer within a compact probe-based form factor.

In the closely related field of elastography, techniques have been developed to map tissue mechanical properties into two- or three-dimensional images, termed elastograms. Elastography systems based on MRI, ultrasound and OCT have been developed [18,22,32]. OCT-based elastography methods have been demonstrated using compression [22], air-puff [33] and acoustic radiation force [34,35] loading, among others [32]. A common challenge in these techniques is their capacity to estimate an intrinsic mechanical property (e.g. Young's modulus). Recently, our group has demonstrated an OCT-based elastography method [11], which incorporates the optical palpation method [9] to reconstruct high-resolution images of tissue stiffness. This method combines tactile surface stress maps with tissue volume strain maps to form volume images of estimates of Young's modulus [11]. Recently, in a similar vein, computational inverse methods have been applied to OCT-based elastography, estimating Young's modulus using a three-dimensional model of tissue mechanics [36]. In this demonstration, tissue is preloaded with the compliant layer (as in this paper), and then phase-sensitive OCT is used to extract local tissue displacement over a volume. Young's modulus is estimated only from this local displacement, with no computational capacity to consider friction effects and the layer's nonlinear state. Integrating our method with the inverse method will likely improve the quality of tissue elasticity images, which could lead to more accurate disease diagnosis.

Furthermore, on a cellular scale, accurate quantification of tactile stress has been invaluable in understanding cellular mechanical processes [6,37], facilitated by stress measurement techniques such as atomic force microscopy [38] and traction force microscopy [39]. The high resolution provided by computational optical palpation, particularly if translated to high-resolution OCT [25], may provide a novel tool to study cellular-scale forces [40] and for characterizing biomaterials [41].

Authors' contributions

P.W. developed the methodology and carried out the work. P.W., D.S. and B.K. designed the experiments, analysed and interpreted the results and drafted the manuscript. All authors gave final approval for publication.

Competing interests

We declare we have no competing interests.

Funding

This research was supported, in part, by grants and fellowships from the Australian Research Council, the National Health and Medical Research Council (Australia), the National Breast Cancer Foundation (Australia) and the Department of Health, Western Australia.