Frequency tuning and directional sensitivity of tympanal vibrations in the field cricket Gryllus bimaculatus

Abstract

Female field crickets use phonotaxis to locate males by their calling song. Male song production and female behavioural sensitivity form a pair of matched frequency filters, which in Gryllus bimaculatus are tuned to a frequency of about 4.7 kHz. Directional sensitivity is supported by an elaborate system of acoustic tracheae, which make the ears function as pressure difference receivers. As a result, phase differences between left and right sound inputs are transformed into vibration amplitude differences. Here we critically tested the hypothesis that acoustic properties of internal transmissions play a major role in tuning directional sensitivity to the calling song frequency, by measuring tympanal vibrations as a function of sound direction and frequency. Rather than sharp frequency tuning of directional sensitivity corresponding to the calling song, we found broad frequency tuning, with optima shifted to higher frequencies. These findings agree with predictions from a vector summation model for combining external and internal sounds. We show that the model provides robust directional sensitivity that is, however, broadly tuned with an optimum well above the calling song frequency. We therefore advocate that additional filtering, e.g. at a higher (neuronal) level, significantly contributes to frequency tuning of directional sensitivity.

1. Introduction

In field crickets, directional hearing is crucially important for females to find a suitable mate. Male crickets produce the typical calling song by means of stridulation [1,2] and females locate the males by phonotaxis [3–6]. In the field cricket Gryllus bimaculatus, female phonotaxis is narrowly tuned to a frequency of about 4.7 kHz [7–10], which matches the carrier frequency of the male's calling song [10]. Auditory frequency tuning has been observed behaviourally [11–13], for central neurons involved in phonotaxis [14,15], and in peripheral neurons encoding unilateral sound intensity [16–18]. Phonotaxis is highly accurate; females may show re-orientation responses to directions deviating as little as one degree from the midline [19]. Auditory nerve measurements and laser vibrometer measurements of the tympanal membranes suggest that the physiological basis for behavioural sensitivity can be traced back to tympanal membrane oscillations. This implies an important role for the mechanical properties of the hearing system in boosting directional sensitivity [20–23].

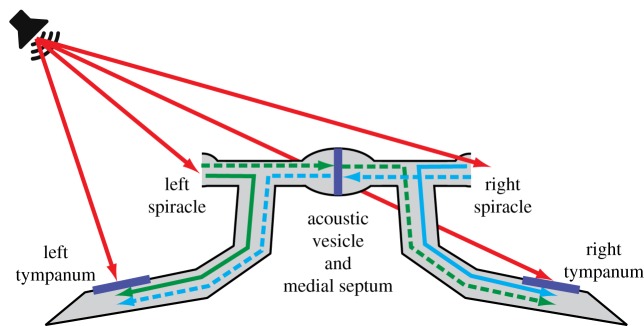
To achieve their remarkable directional sensitivity crickets, like many other small animals with good directional hearing, have evolved specialized internal air-filled pathways between the left and right tympanal membranes [24–26]. Cricket ears are located on the proximal part of their prothoracic tibias. They function as pressure difference receivers: sounds can reach the large posterior tympanal membrane both directly from the outside and indirectly from the inside, through a system of large acoustic tracheae (figure 1). The acoustic tracheae link each tympanum to the ipsilateral spiracle, and via a transverse acoustic trachea with an enlargement, the acoustic vesicle and a medial septum to the contralateral spiracle. These internal connections thus allow for three additional, potential sound inputs to the tympanal membrane, two originating from the acoustic spiracles, located on the thorax and a third from the contralateral tympanal membrane. Superposition of ipsilateral and contralateral sounds at the level of the tympana transforms phase shifts between the different sound inputs into amplitude differences, improving directional sensitivity already at the peripheral level, without the need to neuronally encode and process sound phases [21,23,24,27].

Figure 1.

Sound interactions in the cricket auditory system. The tympana are located on the tibia of the prothoracic legs. Sound from different inputs may propagate through air-filled tracheae and act on the interior tympanum surface by linear superposition. Red arrows indicate direct, external sounds at the four inputs. Internal transmissions from spiracles to ipsi- and contralateral tympana are given in green and blue; solid lines for ipsilateral transmissions and dashed lines for contralateral transmissions. Internal propagation from the contralateral tympanum is presumably negligible [23] and omitted in the diagram. Contralateral transmissions include the action of the medial septum, located centrally in the transverse acoustic vesicle.

It has been suggested, furthermore, that the acoustical properties of the internal connections play a major role in frequency tuning of directional sensitivity [21]. In this view, amplitudes and phase shifts for the internal transmissions are optimized to provide peak sensitivity at the calling song frequency, thus boosting directional sensitivity [23,28]. Similar modulations of amplitude and phase for sounds transmitted in the acoustic trachea have been shown for bush crickets [29]. Transmission from the contralateral spiracles involves an additional phase shift due to the medial septum [30,31], which varies steeply with sound frequency [9,32]. This supposedly contributes to a sharp peak in directional selectivity at about the calling song carrier frequency and suggests a critical role for acoustical interactions in frequency tuning [21,27].

Experimental support for mechanical tuning as the primary factor defining frequency tuning of directionality is, however, limited. Few experiments addressed the interaction between frequency tuning and directional sensitivity, and typically, showed high interindividual variability. Moreover, Kostarakos et al. [10] indicated a mismatch between the carrier frequency of the calling song and peripheral sensitivity tuning. In tree crickets, mechanical tuning was found to be broader than behavioural tuning, indicating additional filtering, presumably to account for temperature effects on sensitivity [33]. This raises the question to what extent directional sensitivity is determined by mechanical tuning in the acoustic tracheae, and how field crickets achieve robust directional sensitivity despite variations in mechanical tuning properties.

Variability of tuning properties may partly relate to the definition used for directional sensitivity. Previous studies mostly quantified directional sensitivity based on response ratios for different directions, expressed in dB on a logarithmic scale. Obviously, a ratio is highly sensitive to small values of the denominator and therefore emphasizes minor variations in the low-amplitude range, whereas larger variations at high amplitudes are less consequential. For the animal, it may be more advantageous to balance increments and decrements from opposite sides. This could be achieved by using the difference in left and right vibration amplitudes rather than in their ratio.

By taking the difference between left and right ear, vibration increments and decrements get equal weight. This, however, is directly in conflict with sharp mechanical tuning to the calling song frequency. In this case, amplitude and phase changes in the internal paths should simultaneously support optimal summation on one side and optimal cancellation on the opposite side. We show through simple model simulations that, for the field cricket, these are actually conflicting requirements in the frequency range near the calling song. Rather than sharp tuning at the calling song frequency, one should expect broader tuning shifted to higher frequencies. Both the diversity in previously published results and theoretical boundary conditions therefore challenge the hypothesis that mechanical properties of the acoustic trachea and associated membranes limit sensitivity to the calling song frequency.

Here, we critically tested the hypothesis of peripheral, acoustical tuning to the calling song frequency, by measuring the responsiveness of the tympanum as a function of sound direction and sound frequency. The vibrations of the tympanum were recorded using a laser Doppler vibrometer (LDV), for animals with both acoustic spiracles open, allowing for interactions between internal and external forces. Under the assumption that for sounds from sources located far away the directional responses of the left and right tympanum are mirror images, we can quantify directional sensitivity as the difference in vibration amplitudes for sounds originating from the left and from the right-hand side, measured for a single tympanum. Our results show that a difference measure provides more robust tuning than a ratio measure, and supports good directional sensitivity at the calling song frequency. Left–right amplitude differences, however, increase with sound frequency beyond the calling song frequency. We furthermore show that these results are in line with a vector summation model for the different sound inputs as proposed previously by Michelsen et al. [23].

We argue that tympanal vibrations do not provide sharp tuning centred at the calling song frequency, but relatively broad tuning, which is, on average, shifted to higher frequencies. Matching frequency tuning of auditory behavioural sensitivity to the frequency of the male calling song therefore probably involves additional filtering, for example in transforming vibrations into neural excitations.

2. Methods

2.1. Model simulations

To study the requirements for optimal directional sensitivity at the calling song frequency, we used the vector summation model as proposed by Michelsen et al. [23]. It assumes linear superposition of sounds that reach the tympanum directly at the external side and indirectly at the internal side by means of internal transmissions originating from the ipsilateral and contralateral spiracles. The internal transmissions affect both amplitude and phase of the sounds reaching the tympanum, depending on the path taken. Each tympanum acts as a pressure difference receiver as illustrated in figure 1. Internal sounds act on the inside of the tympanum, which is therefore sensitive to the difference between internal and external sounds. Optimal summation occurs when the external and internal sound inputs are 180° out of phase, i.e. when external ‘pushing’ is synchronized with internal ‘pulling’. Optimal cancellation occurs when the internal and external inputs are exactly in-phase. In accordance with Michelsen et al. [23], we assume that contributions from the contralateral tympanum are negligible, making each tympanum functionally a triple-input sensor.

For each sound direction and sound frequency, one can calculate left and right vibration amplitudes from (i) amplitude and phase of the sound at each external input and (ii) the change of amplitude and phase in the internal paths. We assumed equal sound amplitudes at each external input, ignoring any diffraction effects. The latter is allowed, at least for frequencies near the calling song frequency, for which amplitude variations owing to diffraction are negligible [23]. In the calculations, spiracles were positioned at a distance of 4 mm from the animal's midline, corresponding to a thorax width of 8 mm and tympana at a distance of 12 mm. Spiracles and tympana were positioned at equal distance and equal height relative to a point straight ahead at large distance. Phase shifts at the external inputs were calculated based on distance to the sound source, which was located at 93 cm (equivalent to the distance in the experiments). The relative gains for the internal transmissions, defined as a multiplication factor relative to the direct, external sound amplitude at the tympanum, were chosen equal to the values reported by Michelsen et al. [23] at the calling song frequency of 4.7 kHz (0.55 and 1.48 for contralateral and ipsilateral transmissions, respectively). In the model simulations, we show how vibration amplitudes and hence directional sensitivity (hypothetically) vary as a function of phase for both ipsilateral and contralateral internal transmissions.

2.2. Animals

For laser vibrometer experiments, we used adult, two-spotted field crickets (Gryllus bimaculatus (De Geer)) obtained from a commercial supplier (Kreca, The Netherlands). Crickets were kept in terraria (18 × 32 × 21 cm) at room temperature and a 12 L : 12 D cycle. Water and food (ground-up pet food, seeds, apples or vegetables) were available ad libitum.

To prepare animals for recordings, they were immobilized with an abdominal injection of 0.1 ml neurotoxin (Vapona, The Netherlands), containing permethrin (0.25%) and tetramethrin (0.05%). After the animal stopped moving, a similar amount of fluid was extracted from the abdomen to counteract pressure effects. If an animal was not completely immobilized, we repeated the treatment with a smaller dose. Immobilized animals were mounted on a cork platform (r = 23 mm) placed in the recording set-up with the help of Plasticine. Both acoustic spiracles were opened by removing the spiracle flaps, while carefully preventing any bleeding of haemolymph that might have obstructed the acoustic tracheae.

2.3. Recording set-up

Experiments were performed in an anechoic box (2 × 2 × 2 m) completely covered with acoustic foam (SH002 aixFOAM, Germany). The box was placed in a climate-controlled room; measurements were done at room temperature (21°C). The cricket was placed in the centre of the room, 100 ± 1 cm above the floor. The loudspeaker (cone tweeter, VISATON TW 6 NG, frequency response 1–30 kHz) was placed on a movable arm, suspended from the ceiling, at a distance of 93 ± 1 cm from the cricket, at the same height as the cricket. Rotation of the movable arm around the cricket was computer-controlled by means of a JVL integrated servomotor (MAC00-B1). Sound directions are defined relative to the animal's midline (figure 2a), with straight ahead corresponding to 0°. Loudspeaker position was varied in 30° steps, from +30° to the right of the animal's midline to −180° to the left. Loudspeaker positions between +60° and +180° ipsilateral (same side as the recorded tympanum) were omitted owing to the presence of the LDV. Positioning of the loudspeaker was accurate to about 1°. To account for the non-flat frequency response of the loudspeaker, we recorded both the input to the loudspeaker and the resulting sound pressures. Sounds were recorded by a one-fourth inch free-field microphone in combination with a conditioning amplifier (Brüel & Kjær (B&K), Nærum, Denmark, Nexus 2670, microphone 4939). It was positioned vertically, pointing downward, at 25 mm above the pronotum of the animal. To compensate for the free-field effect in the orthogonal configuration in our set-up, we calibrated the microphone against a one-eighth inch sound pressure microphone (B&K, type 5935 and type 2839 amplifier).

Figure 2.

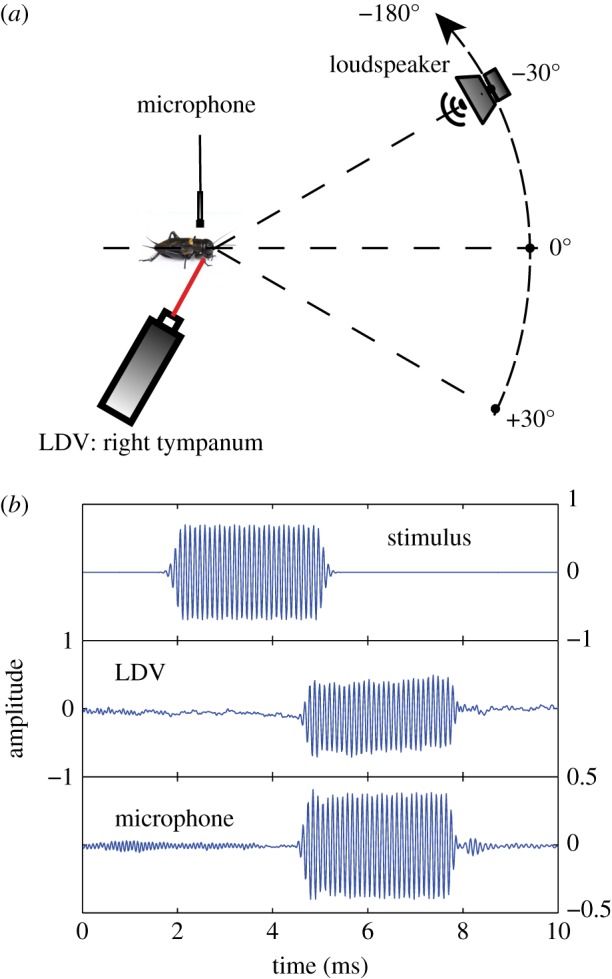
Laser Doppler vibrometer (LDV) and microphone measurements. (a) Schematic of the experimental set-up: the LDV measured vibrations of the right posterior tympanum, for sounds varying from +30° to −180° relative to straight ahead (0°). Sound pressure amplitudes were recorded with a microphone located 25 mm above the centre of the pronotum. (b) Example of the recorded stimulus, LDV and microphone responses. Amplitudes are given in arbitrary units; we were merely interested in normalized gains, measured in the linear range (see electronic supplementary material, figure S1). Because the order of stimuli was randomized, reflections from preceding stimuli (e.g. below the label ‘microphone’) hardly affected the measurements. (Online version in colour.)

Vibrations of the posterior tympanum on the cricket's right-hand (ipsilateral) side were recorded with a Polytec LDV, consisting of an OFV-353 sensor head in combination with an OFV-3001 controller (Polytec, Waldbronn, Germany). The laser beam was carefully focused and positioned on the central part of the tympanum. LDV signals were filtered (1 kHz high-pass, 40 kHz low-pass) and amplified (20 dB) by a Krohn-Hite filter (Brockton, MA, model 3362). The animal's prothoracic leg was positioned in the laser's first optimal standoff distance of 23.5 cm. The animal platform and laser were rigidly mounted on a metal frame to prevent any relative movement. All exposed parts of the frame, and laser were covered with acoustic foam to minimize sound reflections. Recording equipment, except the laser and the microphone, was placed outside the anechoic room.

LDV signals, microphone signals and the stimulus signals going to the loudspeaker were recorded with a National Instruments DAQ board (NI PCIe-6251) at a frequency of 80 k samples s⁻¹. The same NI board was used to generate sound signals at a sample frequency of 160 k samples s⁻¹. Sound generation, positioning of the loudspeaker and signal recordings were controlled by custom-built software in Matlab® (R2013b, The MathWorks™ Inc., Natick, MA).

2.4. Stimuli

Stimuli were pure sinusoidal tones of 4 ms duration, presented with 6 ms interpulse intervals. To minimize transients and spurious high-frequency components, we used a (single-sided) Gaussian-shaped envelope (width 0.2 ms at 1 s.d.) at the start and end of the 4 ms tone (figure 2b). The Gaussian envelope was truncated at 3 s.d., resulting in a time interval of 0.6 ms in which the signal was attenuated, both at the start and end of the stimulus.

A set of multiple stimuli was grouped in a single trial of about 1 s duration. Depending on the type of measurement, the set consisted of combinations of different stimulus amplitudes and frequencies. Stimuli within a trial were presented in randomized order. To synchronize AD and DA signal conversions by the NI board, each trial started with five brief pulses followed by 50 ms of silence. In the main frequency tuning experiments, a trial consisted of 100 frequencies ranging from 2 to 20 kHz in steps of 180 Hz, at fixed stimulus amplitude. Each trial was repeated 20 times for a given direction. A complete set of measurements was obtained in less than 1 h.

In addition to pure sinusoids, we also used sinusoidal frequency sweeps, similar to those used by Michelsen et al. [23], to measure full frequency transfer properties in a single stimulus presentation. Sweeps contained a linear increase in sound frequency, from 0 to 25 kHz in a time interval of 4 ms. Stimulation trials with sweeps contained 30 sweeps at three different amplitudes and were repeated 20 times.

2.5. Data analysis

Measurements consisted of three signals: the stimulus signal (input to the loudspeaker), the LDV signal and the microphone signal (figure 2b). Raw LDV measurements corresponded to velocities of the tympanum. These were converted into displacements, by means of temporal integration. To find the exact time interval with the response to a sound stimulus, we cross-correlated the stimulus channel with the LDV signal and with the microphone signal. The peak of the cross-correlation provided an accurate estimate of the lag between stimulus and response signals. Amplitudes for the 4 ms response intervals were determined using a discrete fast Fourier transfer function. To increase the resolution in the frequency domain, we padded the responses with zeros to a length of 4096 samples, and we selected the frequency that most closely matched the stimulus frequency. As a result, our measurements were, to a large extent, insensitive to noise at other frequencies.

The variations of stimulus amplitude resulting from the (non-flat) frequency characteristic of the speaker were taken into account by calculating the gain for tympanum vibrations as the ratio of LDV displacement amplitude and sound pressure amplitude obtained with the microphone. To discount differences in overall gain values between animals, and to focus on variations as a function of frequency and direction, we normalized the gains for each animal to the mean gain measured for all directions and all frequencies (per animal). This quantification of normalized gain assumes linearity of responses, which we checked in an extensive control experiment (see §3.2.1).

3. Results

3.1. Model simulations

3.1.1. Optimal internal phase shifts for ipsilateral and contralateral sounds

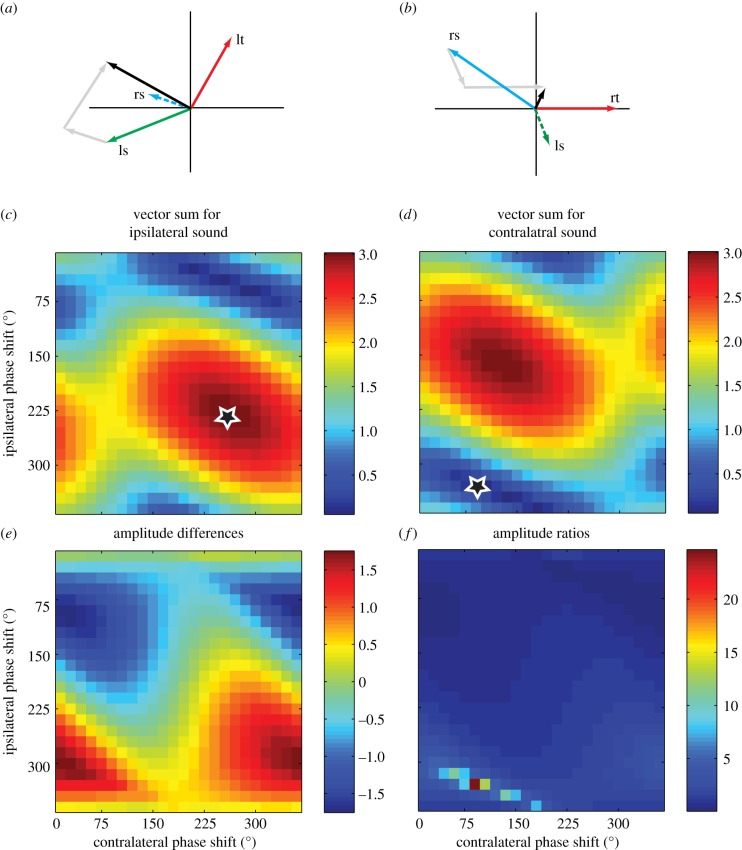
We used model simulations of internally coupled pressure difference receivers to investigate the requirements for optimal directional sensitivity. It has previously been argued that the phase shifts of the internal transmissions are tuned to provide optimal directional sensitivity at the calling song frequency. To address this hypothesis, we calculated the vector sums for external and internal sounds, for all different combinations of phase shifts (0–360°) in the internal paths. Figure 3a,b shows an example of individual contributions to the vector sum, from the three different inputs for a sound coming either from the ipsilateral side (figure 3a) or the contralateral side (figure 3b). Vector lengths correspond to the amplitude, and directions to the phase (all relative to the sound at the ‘rt’ in figure 3b). Labelling of the vectors corresponds to the paths indicated in figure 1. The resulting amplitude (in black) corresponds to the vector length for the sum of the three inputs. Figure 3c,d shows how these amplitudes vary as a function of internal phase shifts. Along the vertical axis, we varied the phase shift in the ipsilateral path, i.e. from the ipsilateral spiracle to the tympanum, and along the horizontal axis the phase shift in the contralateral path. The latter path includes the medial septum, supposedly adding additional phase shifts. For the example in figure 3, we used sound directions at ±60° relative to the straight-ahead direction. Differences in external sound phases are therefore close to the maximum differences that may be relevant for phonotaxis.

Figure 3.

Model results for the effects of internal phase shifts on directional sensitivity. Panels (a,b) show examples of the vector sum (black arrows) of direct, external sounds at the tympanum (lt and rt: left and right tympanum, respectively), and the internally transmitted sounds from the two spiracles (rs and ls: right and left spiracle, respectively). Grey arrows indicate vector summation. The examples show results for ipsilateral (a) and contralateral (b) sounds of 4.7 kHz with the loudspeaker located at +60° and −60°. Panels (c,d) show the amplitudes of the vector sum for all possible (0–360°, in steps of 15°) combinations of ipsilateral and contralateral, internal phase shifts. Optimal directional sensitivity requires high amplitude for ipsilateral sounds (star in panel (c)), and low amplitude for contralateral sounds (star in panel (d)). Panels (e,f) show directional sensitivity, quantified either as a difference (e) or as a ratio (f) for ipsi- and contralateral vibration amplitudes. All scaling is relative to the amplitude of external sounds at the rt, which was defined as unity (see Methods).

It can be seen that maximal vibration amplitudes at the ipsilateral side (figure 3c) are rather broadly tuned for phase shifts. The star indicates maximum summation, but amplitudes decline minimally for small variations in either ipsilateral or contralateral internal phase shifts. Cancellation for a contralateral sound (figure 3b), however, sets different demands. In this case, we look for optimal cancellation (star), which displays high sensitivity to especially the ipsilateral internal phase shift. Most importantly, the optimal combination of phase shifts differs substantially for ipsilateral summation (figure 3c) and for contralateral cancellation (figure 3d). In such a model, a single choice of phase shifts for the two internal paths, therefore, cannot simultaneously optimize summation on one side and cancellation on the other side. For optimal summation, direct external sounds at the tympanum and sounds reaching the tympanum through the ipsilateral spiracle (solid green line on left-hand side in figure 1) should differ by 180° (i.e. when the outside sound ‘pushes’ the inside sound should ‘pull’). The internal phase shift should therefore be 180° minus the difference in external phase shifts. Optimal cancellation for a sound at the contralateral side would require a phase shift in the internal path (solid blue line in right-hand side of figure 1) of 360° minus the external phase difference. Because external phase shifts at the calling song frequency are well below 180°, these are conflicting demands that cannot be met for a single value of the internal phase shift between spiracle and tympanum. A similar conflict holds for the required phase shift in the internal path linking the spiracles, through the transverse acoustic trachea to the contralateral tympana.

For the example in figure 3 we used gains similar to those reported by Michelsen et al. [23] for the different sound paths (see Methods). The choice of amplitudes is, however, not critical and minimally affects the optimal phase shifts required for either summation or cancellation. For sound directions smaller than the ones used in figure 3 (±60°), the discrepancy in optimal phase shifts would be even larger.

3.1.2. Combining conflicting demands for optimal phase shifts

Conflicting demands for the size of internal phase shifts imply that phase differences must be a compromise between optimal summation on the one side and optimal cancellation on the opposite side. This can be illustrated by exploring the effects of internal phase shifts on directional sensitivity. In figure 3e,f, we show the effects of internal phase shifts for two different definitions of directional sensitivity. If we calculate directional sensitivity as the difference between ipsilateral and contralateral amplitudes (figure 3e), the optimal combination of phase shifts is a compromise that is relatively insensitive to the exact choice of phase shifts. If, on the other hand, we calculate directional sensitivity as the ratio between left and right amplitudes, then optimal phase shifts are sharply defined and primarily determined by the minimal response for contralateral sounds (figure 3f). This would require very precise tuning of both ipsilateral and contralateral internal phase shifts.

Different sensitivities to variations in internal phase shifts, as shown in figure 3e,f, also indicate that frequency tuning of directional sensitivity may strongly depend on the definition of directional sensitivity. When taking the difference between left and right responses, ipsilateral increments and contralateral decrements have equal weight, resulting in considerable tolerance for variations in phase shift. For a measure based on a ratio, tuning is primarily determined by the deepest null, leading to large variations with changes in phase.

For left–right amplitude differences, these simulations would also predict an increase of directional sensitivity for higher frequencies, because external phase shifts increase (i.e. a given delay constitutes a progressively larger fraction of the wavelength). This resolves the conflict in phase requirements and, therefore, leads to both optimal summation on the one side and optimal cancellation on the other side. This, of course, only holds if variations in phase shift are not counteracted by variations in amplitude. Data from Michelsen et al. [23], however, show that internal gains increase rather than decrease above the calling song frequency. Phase shift requirements and changes in internal gains therefore predict an increase in directional sensitivity with frequency rather than in optimal tuning at the calling song frequency.

3.2. Experimental results

3.2.1. Control measurements

Recordings of sound pressure amplitudes showed considerable effects of sound frequency, owing to variations in loudspeaker responsiveness (electronic supplementary material, figure S1). These properties of the loudspeaker were taken into account by measuring gains rather than amplitudes. Hereto, we divided the amplitudes of tympanal displacements by the actual sound pressure amplitudes measured with the microphone positioned just above the animal.

The choice of stimulus amplitude for the final experiments was based on an extensive pilot experiment in which we varied sound intensity in small steps, for three frequencies (5, 12 and 15 kHz; roughly corresponding to the calling song frequency, a frequency in the mid-range, and a frequency on the high-frequency slope, respectively). In all cases, the gains (tympanal displacement amplitudes divided by sound pressure amplitudes) were nearly constant over the full range tested (electronic supplementary material, figure S2). Stimulus amplitudes for all subsequent measurements were chosen in the middle of this range, corresponding to a sound pressure level of 78 dB (at 5 kHz). Stimulus amplitudes were, therefore, well within the linear range of the tympanal hearing system, and measured gains for tympanal displacements were independent of sound pressure amplitude.

Previous experiments often used frequency sweeps rather than pure tones. To control for possible differences owing to different stimulus types, we also performed all experiments with frequency sweeps. This yielded nearly identical results to those obtained with pure tones (electronic supplementary material, figure S3). Although frequency tuning curves, especially in the high-frequency range, may vary considerably between animals and between directions, these variations were similar for pure tones and for sweeps. Equality of results for pure tones and for sweeps further supports linearity of response properties, and suggests that our data were not strongly affected by inhomogeneities in the sound field owing to, for example, sound reflections. In the remainder, we show only data for pure tones.

Similarity of results for pure tones and for frequency sweeps also suggests that measurements were quite reproducible, despite individual variation in frequency tuning curves. This is further supported in electronic supplementary material, figure S4, showing an example of 20 repeated measurements of gain (i.e. displacement amplitude divided by sound pressure amplitude) as a function of sound frequency, for all directions. Repeated measurements gave almost identical results. Standard deviations (electronic supplementary material, figure S4b) were generally well below 5% of the mean, except for directions of −90° and −120° and at frequencies above 12 kHz, for which gains of tympanal vibrations were very low.

Finally, we checked the fidelity of the measurements by analysing the magnitude-squared coherence between microphone signals and LDV signals (electronic supplementary material, figure S5). The results show that, on average, coherence values were well above 0.85, and in most cases close to 1.0. Coherence values only dropped below 0.85 for low LDV amplitudes, i.e. for high frequencies in the −90° and −120° directions. Excluding low-coherence data points did not significantly alter the frequency tuning curves. Because we analysed only displacement amplitudes, and not phases (that are more sensitive to low-coherence values), we refrained from excluding any data based on coherences.

3.2.2. Frequency tuning and directional sensitivity

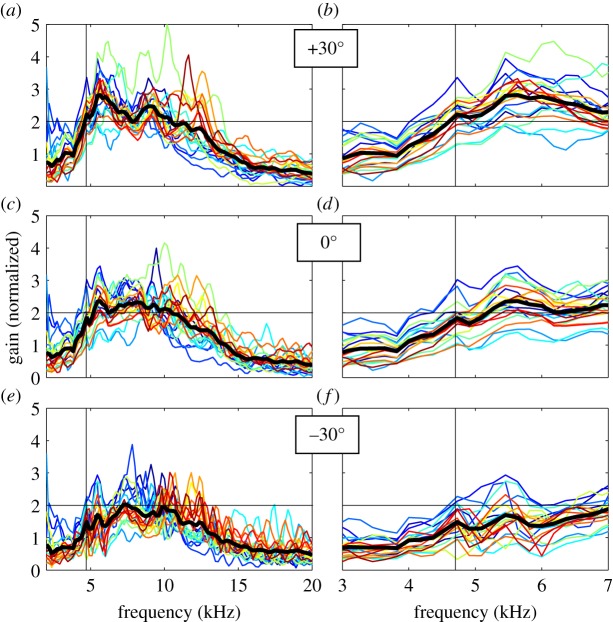
To compare results across individuals, we normalized the data to the mean gain for all frequencies and directions per animal. This removes individual differences in overall sensitivity. Figure 4 shows normalized frequency curves for 20 individuals (eight males, 12 females), for sound directions of 30°, 0° and −30°. Especially in the high-frequency range, above about 8 kHz, data are quite variable between animals. Many animals show narrow, frequency-specific peaks, but the location of these local peaks is highly variable across animals. It should be noted that these variations do not reflect noise in the recordings. Nearly identical variations were seen for repeated measurements (electronic supplementary material, figure S4b), for pure tones and for sinusoidal sweeps (electronic supplementary material, figure S3) and for repeating an experiment after re-mounting an animal (not shown). We found no consistent differences between males and females.

Figure 4.

Frequency tuning curves for 20 crickets, for sound directions of +30°, 0° and −30°. Gains express amplitudes of displacement vibrations divided by sound pressure amplitudes, normalized to the mean value across directions and frequencies for each cricket. Each curve shows the mean for 20 repetitions. Thick, black lines correspond to the mean value for all animals. Panels (b,d,f) show the results for frequencies ranging from 3 to 7 kHz in more detail. Vertical, black lines indicate the 4.7 kHz calling song frequency. A horizontal grid line at a gain of 2 is added for visual guidance.

Despite individual differences in local variations, the global shapes of the tuning curves were comparable. For all sound directions we found broad frequency tuning, with maxima in the mid-frequency range, around 6–8 kHz. In the low-frequency range that is relevant for phonotaxis, the data show a consistent pattern (figure 4b,d,f). Responsiveness was low below about 4 kHz and increased with frequency up to about 5.5 kHz. The calling song frequency (approx. 4.7 kHz) is typically located on the rising slopes of the frequency tuning curves. In some individuals, responsiveness showed a local subpeak at the calling song frequency for the ipsilateral direction (figure 4b), but this did not correspond to a consistent dip for the contralateral direction (figure 4f).

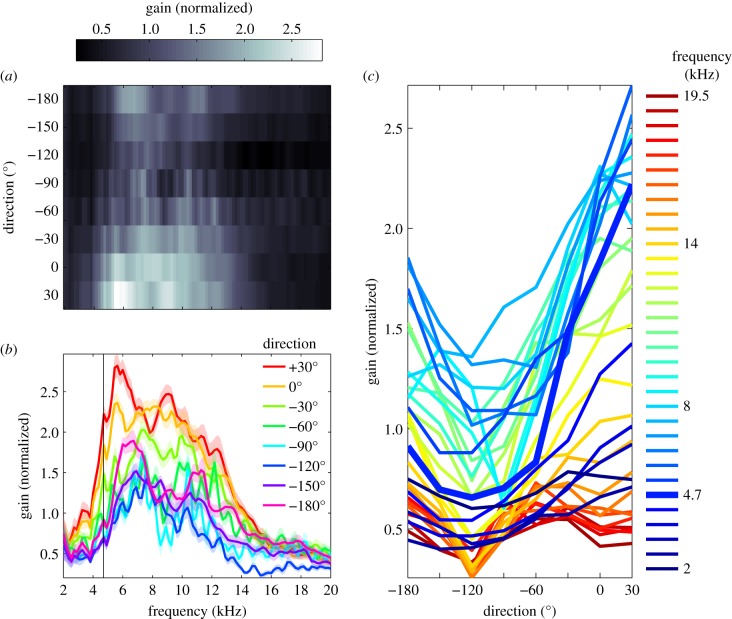
To study the interaction between frequency tuning and directional sensitivity in more detail, we averaged the data for all crickets (thick, black lines in figure 4). This emphasizes general tuning properties that all animals have in common, ignoring most of the idiosyncrasies that are prominent at high frequencies. Averaged, normalized gains for all frequencies and directions are shown in figure 5. The surface plot in figure 5a shows the combined effects of sound direction and frequency. The corresponding frequency and direction tuning curves are shown in figure 5b,c, respectively. Mean response gains for tympanal vibrations are low below about 4 kHz and above 15 kHz. Gains are highest for the 30° direction and decline to a minimum in the −90° or −120° direction. Gain variations with direction are largest in the 4−6 kHz range, but extend up to frequencies of about 14 kHz. Frequency and direction clearly interact in modulating response gains of tympanal vibrations. For ipsilateral sounds (30°) the frequency curves peak on average at about 6 kHz, whereas for contralateral directions the peak shifts to higher frequencies. Figure 5a,b shows that, on average, there is no sharp peak in the frequency curve at the calling song frequency for the ipsilateral direction, nor a clear dip in the contralateral directions.

Figure 5.

Average gains of tympanum displacements as a function of sound direction and sound frequency. Gains quantify displacement amplitudes divided by sound pressure amplitudes, normalized to the mean value for each cricket, and averaged for 20 individuals. (a) Average gains as a function of sound frequency and sound direction. (b) Average gains as a function of frequency for different sound directions (as indicated in the legend). Confidence intervals represent standard errors of the means for 20 crickets. (c) Same gain data as in (a) and (b), plotted as a function of sound direction, with frequency in kHz indicated in the legend. The calling song frequency is about 4.7 kHz, corresponding to the bold, blue line.

Figure 5c shows direction tuning for the different sound frequencies. At low frequencies, between 2 and 3 kHz, sensitivities were low and only weakly modulated by direction. With an increase in frequency, we see a sharp increase in LDV gain, which is most pronounced for the 0° and 30° directions. The increase in gain for these directions continues up to a frequency of about 6 kHz and generates a steep gradient in the direction tuning curves around the straight-ahead direction (0°). At frequencies above about 6 kHz, the peak of the direction tuning curves broadens owing to a relatively strong increase of LDV gain in the −60° direction, and a decrease in the 30° direction. This results in a lower slope of direction tuning curves around the straight-ahead direction.

As a final step, we would like to quantify directional sensitivity as a function of frequency, for directions that are relevant in phonotaxis. During phonotaxis, the animal presumably compares vibration amplitudes from left and right ear, adjusting its direction of movement so as to minimize the differences. The range of directions that is relevant for this behaviour is largely determined by the animals' directional sensitivity and steering behaviour. To assess directional information for different ranges of directions, we therefore compare in figure 6 gain differences relative to the straight-ahead direction (0°). For the 30° direction, we see a peak in directional sensitivity at a frequency of about 6 kHz. For the −30° direction, there is a similar, but slightly larger reduction in gain relative to the straight-ahead direction. The reduction in gain grows with a larger difference in sound directions, but this effect quickly levels off for directional differences larger than 60°. Irrespective of the directions compared, directional sensitivity of tympanal vibrations is not sharply tuned to the calling song frequency. We do observe a local peak in the ipsilateral direction at 5 kHz, and a local dip for contralateral directions beyond −30°, but for all directions the optimum is between 5.5 and 6 kHz. There is a small shift in optimal frequency with a change of direction. At +30°, sensitivity peaks at about 6 kHz. This shifts to slightly lower frequencies for contralateral directions (towards −180°).

Figure 6.

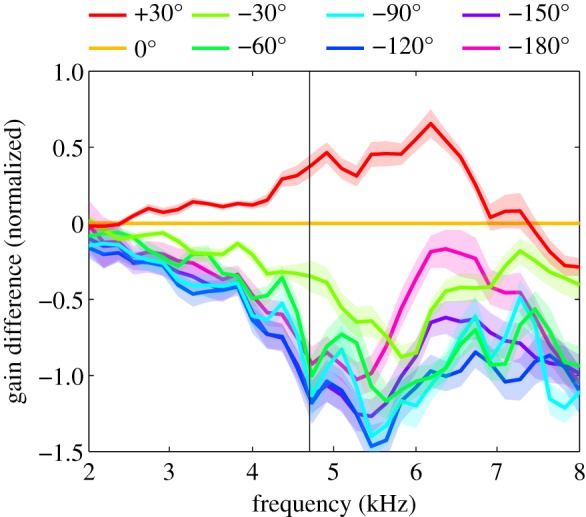
Directional sensitivity. Differences in gain of vibration amplitudes relative to the straight-ahead direction (0°) are plotted as a function of sound frequency. Confidence intervals represent ± 1 s.e.m. for 20 individuals.

4. Discussion

The model that we used is similar to the one proposed by Michelsen et al. [23]. They measured transfer functions for the internal sound transmissions using localized sound stimuli at the two spiracles, and showed how directional sensitivity resulted from the linear combination of sounds arriving at the tympanum from the three dominant inputs (figure 1). Internal transmissions are subjected to frequency-dependent gain modulations and phase shifts that may boost or cancel direct, external inputs. Michelsen et al. [23] showed that especially the input from the contralateral spiracle has a very steep phase–frequency curve, suggesting that proper tuning could only be obtained in a narrow frequency range around the calling song frequency. Michelsen & Löhe [22] confirmed this hypothesis, showing that directional differences of tympanal vibrations were indeed sharply tuned to a frequency of about 4.5 kHz. Moreover, piercing the central membrane in the transverse acoustic trachea completely abolished frequency tuning, suggesting a critical role for contralateral transmissions in generating frequency tuning that properly matches the male calling song [34]. Other findings [9,21–23,35] supported the notion that tuning properties of the acoustical, internal sound pathways provided optimal tuning at the calling song frequency. How can we reconcile our results with these seemingly contradictive findings?

Our calculations for the vector summation model showed that such a model does not necessarily predict sharp frequency tuning for directional sensitivity. Sharp tuning is only expected when using a ratio measure for directional sensitivity in which case directional sensitivity is highly sensitive to internal phase shifts, and therefore to sound frequency. If, on the other hand, we define directional sensitivity as the difference in ipsilateral versus contralateral responsiveness, taking both increments and decrements equally into account, then we obtain more robust directional tuning that is less sensitive to variations in internal phase shifts. Model calculations also showed that internal phase shifts cannot simultaneously provide optimal cancellation on one side and optimal enhancement on the other side, because it would require different phase shifts in comparable pathways. Based on the model, and on the increase in gain of internal transmissions with frequency [23], we might therefore expect an increase in directional sensitivity with frequency above the calling song frequency.

Our experimental results showed that left–right amplitude differences of tympanal vibrations support good directional sensitivity at the calling song frequency, despite minimal differences in the external sound field. Model simulations for internally coupled ears in vertebrates [36,37] have shown a similar functionality of internally connected ears, where coupling may enhance amplitude differences in the high-frequency range. We found that for the field cricket, directional sensitivity was not limited to the calling song frequency, but was rather broadly tuned, similar to observations in a tree cricket [33]. In our data, the calling song frequency was located on the rising slope of the frequency tuning function, which peaked at a frequency of about 6 kHz for directions in the range of ±30° (figure 6).

A second difference between our and previous results relates to the nature of LDV measurements. Michelsen et al. [22,23] used raw LDV measurements, corresponding to tympanal membrane velocities. We integrated the LDV velocity measurements to obtain displacements. Although the choice is fairly arbitrary, we think displacements may be more relevant, because mechanoreceptors are probably amplitude-limited but not necessarily affected by time-resolved speed. It should be noted that velocity measurements relatively overestimate high-frequency responses, compared with displacement measurements. We found frequency tuning of directionality to be shifted towards frequencies higher than the calling song frequency, which would be further accentuated when analysing vibration velocities.

Our model simulations indicated that it is critical how one defines directional sensitivity. We used the difference in gains for different sound directions (figure 6), which for a symmetrical system is equivalent to the difference in left ear and right ear for a particular direction of sound. Michelsen et al. [22,23] also analysed directional differences, but quantified velocity amplitudes relative to the amplitude in the 0° direction, in decibels. Their directional difference is, therefore, a difference of log-transformed ratios, which overemphasizes small values (reductions) relative to large values (increments). As a result, cancellation for contralateral sound directions dominates the difference, whereas summation for ipsilateral sounds is less consequential. This may explain their finding that directionality primarily resulted from contralateral cancellations, with minimal enhancement in the ipsilateral direction. In our measurements, using a difference rather than a ratio, we found cancellations and enhancements of equal magnitude. In addition to underestimating the contribution from ipsilateral enhancements, ratio measurements are also more sensitive to noise in low-amplitude responses, and inflate directional sensitivities in the low-frequency range. Comparing these two measures of directional sensitivity for our experimental data (electronic supplementary material, figure S6) shows higher variability in the low-frequency range (2–4 kHz) for ratios, and for six out of 20 animals a shift of the optimal frequency to a lower value (electronic supplementary material, figure S6c).

In agreement with previous findings [9,10,23], both measures show rather large differences between individuals: optimal frequencies (electronic supplementary material, figure S3c) range from about 4.5 to 7 kHz for amplitude differences, and from 2.2 to 7 kHz for amplitude ratios. Irrespective of the definition adopted, directional sensitivity was not sharply tuned to the calling song frequency. Our data instead suggest that directional sensitivity is more broadly tuned and that the calling song frequency is located on the rising slope of the tuning curve.

Despite the mismatch in frequency tuning, left–right differences in gain of tympanal vibrations support robust directional sensitivity at the calling song frequency. Model calculations suggest that small changes in phase shift hardly affect the amplitude of the vector sum (figure 3c). At higher frequencies, however, directional sensitivity becomes inherently unstable owing to the very steep phase–frequency curve for contralateral internal sounds [23]. It has been suggested that evolutionary optimization of the cricket calling song frequency might depend on conflicting demands based on (i) a reduction of directional information due to scattering effects for high-frequency sounds in cluttered environments and (ii) an increase of directional information owing to larger differences in external phase shifts for higher frequencies [22,38]. Our measurements and analyses suggest that robustness of directional sensitivity may also favour a relatively low calling song frequency.

Despite the variations in mechanical, acoustic tuning properties, female behavioural sensitivity and for example neuronal sensitivity at the level of the AN1 neuron in the prothoracic ganglia show frequency tuning that properly matches the male calling song [39]. This suggests that the match of female tuning to the male calling song frequency may arise beyond the level of tympanal membrane oscillations. This may involve frequency selective coupling of mechanoreceptors in the chordotonal organ similar to frequency tuning in the human cochlea or in bush crickets [40]. Moreover, coupling of tympanal sound pressure differences to actual mechanotransduction may involve several nonlinear, and frequency-dependent steps [41–44]. Such uncoupling of mechanical and neuronal sensitivity allows for robust directional sensitivity and broad auditory frequency tuning in general.

Ethics

All experiments were conducted according to the standards of the ethical committee of Wageningen University.

Data accessibility

Data supporting this article are deposited in the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.td022 [45].

Authors' contributions

J.L. and O.L. initiated the work described in this study. All authors participated in the design of the study. U.C. carried out all measurements. M.L. and U.C. built the experimental set-up and developed the software for data analysis. M.L. drafted the manuscript. All authors provided comments on drafts of the manuscript and gave final approval for publication.

Competing interests

We declare we have no competing interests.

Funding

This study received no funding from grants.