Population genetics of immune-related multilocus copy number variation in Native Americans

Abstract

While multiallelic copy number variation (mCNV) loci are a major component of genomic variation, quantifying the individual copy number of a locus and defining genotypes is challenging. Few methods exist to study how mCNV genetic diversity is apportioned within and between populations (i.e. to define the population genetic structure of mCNV). These inferences are critical in populations with a small effective size, such as Amerindians, that may not fit the Hardy–Weinberg model due to inbreeding, assortative mating, population subdivision, natural selection or a combination of these evolutionary factors. We propose a likelihood-based method that simultaneously infers mCNV allele frequencies and the population structure parameter f, which quantifies the departure of homozygosity from the Hardy–Weinberg expectation. This method is implemented in the freely available software CNVice, which also infers individual genotypes using information from both the population and from trios, if available. We studied the population genetics of five immune-related mCNV loci associated with complex diseases (beta-defensins, CCL3L1/CCL4L1, FCGR3A, FCGR3B and FCGR2C) in 12 traditional Native American populations and found that the population structure parameters inferred for these mCNVs are comparable to but lower than those for single nucleotide polymorphisms studied in the same populations.

1. Introduction

Multiallelic copy number variation (mCNV) is an underappreciated and complex component of genetic variation that has been challenging to detect for two reasons. First, they are not effectively tagged by flanking single nucleotide polymorphisms (SNPs). Second, direct measurements of hybridization intensity from SNP or comparative genome hybridization arrays are often noisy. Techniques based on polymerase chain reaction (PCR) such as the paralogue ratio test (PRT) [1] and, more recently, sequence read depth analysis from short-read second-generation sequencing have begun to allow analysis of mCNV across different human populations [2–5]. However, the number of human populations studied remains low and has focused mainly on Europeans.

Complex mCNV involves genes that are of biological and medical interest. For example, the immune system proteins beta-defensins (DEFB), macrophage inflammatory protein 1α (MIP-1α) and Fcγ receptors (FCGRs) are encoded by mCNV loci that modulate susceptibility to infectious and autoimmune diseases. DEFB are small cationic peptides with a role in innate immunity that interact with pathogens by depolarizing and rendering their cellular membrane permeable. Increases in copy number (CN) of DEFB are associated with psoriasis [6], as well as an increase in HIV load and impaired immune reconstitution following the initiation of highly active antiretroviral therapy [7].

MIP-1α, also known as the chemokine ligand 3-like 1 (encoded by CCL3L1), binds the CC chemokine receptors CCR1, CCR3 and CCR5, and their CNV has been inconsistently associated with clinical parameters of HIV infection [8,9].

A cluster of Fc gamma receptors with low affinities for IgG shows mCNV (FCGR3A, FCGR3B and FCGR2C), and there is some evidence of association with disease. Low FCGR3B CN is associated with glomerulonephritis, systemic lupus erythematosus and rheumatoid arthritis [10,11], and the non-synonymous FCGR2C mutation rs10917661 results in an activated FcRIIc protein with cytotoxic effects [12].

The study of mCNV is challenging due to difficulties in quantifying the number of copies of a locus in an individual [13] and, consequently, quantifying how genetic diversity is apportioned between individuals and populations. Typing methods do not reveal true genotypes for CNV loci, as is the case of SNPs; rather, quantitative information about total copy numbers of a locus in both chromosomes (diploid CN) is produced. Therefore, in the absence of information from segregation in pedigrees or physical information from molecular methods such as fibre-FISH, the true CN genotype that identifies the allele carried by each chromosome can only be probabilistically inferred from the distribution of observed diploid copy numbers in a population. This limits the application of population genetics models developed for diploid genotypes, and indeed, specific methods have been proposed to (i) infer combined SNPs/CNV haplotypes [14]; (ii) quantify population differentiation by the F_ST-like V_ST statistic in which quantitative intensity ratios are directly obtained from the genotyping signals [15]; and (iii) infer CN allele frequencies assuming Hardy–Weinberg equilibrium [16]. However, some natural populations do not fit the Hardy–Weinberg model, due to inbreeding, assortative mating, population subdivision, natural selection or a combination of these evolutionary forces.

This article has two goals. The first is to propose a method (focused on mCNVs) to study the genetic structure of populations (i.e. the departure from the Hardy–Weinberg model due to the apportioning of genetic diversity within and between populations). To achieve that aim, we generalize the Gaunt et al. [16] algorithm, allowing for deviations from Hardy–Weinberg equilibrium. We implemented our more general approach in the R software CNVice, an acronym for inbreeding coefficients estimation for CNV data, freely available at https://github.com/mairarodrigues/cnvice. Although CNVice measures the departure from Hardy–Weinberg equilibrium in general, and not only that due to recent identity by descent (i.e. inbreeding), the name of the software is reminiscent of the classical inbreeding studies of Wright [17].

We implement a method in CNVice that simultaneously infers for a population (i) the CNV allele frequencies and (ii) a multiallelic f, the most classical and widely used population genetics parameter [17,18]. f quantifies the departure of homozygosity from Hardy–Weinberg expectations, summarizing the genetic structure of natural populations. Formally, the probability of a homozygous genotype (h_k, h_k) for the allele k is 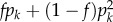and of a heterozygous genotype (h_k, h_q) for the alleles k and q is (1 − f)2p_kp_q [19], where p_k and p_q are the frequencies of k and q alleles in the population. The Hardy–Weinberg equilibrium corresponds to the specific case of f = 0. Moreover, our method infers individual genotype probabilities for CNV loci, based on the observed individual diploid CN, the population allele frequency distribution, the inferred f parameter, as well as information on inheritance patterns from trios, if available.

The second goal of our article is to determine the population genetics and genetic structure of three immune-related mCNV loci in Native American populations, which have been rather neglected in human genome diversity studies. We studied 12 traditional villages from three ethnic South American native groups (figure 1a) whose genetic structure has probably been affected by evolutionary factors, such as strong genetic drift and inbreeding, that are more relevant in small populations and that render methods assuming Hardy–Weinberg equilibrium suboptimal.

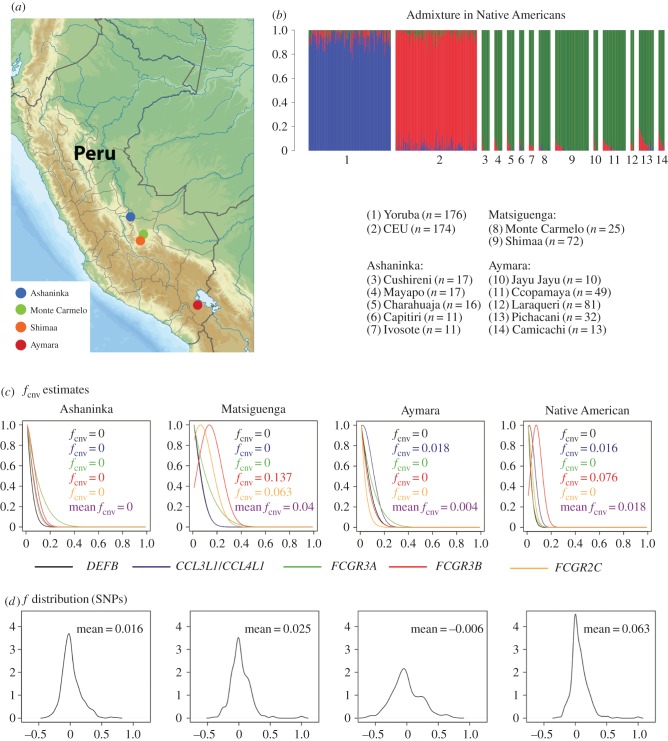
Figure 1.

(a) Geographical location of the three studied ethnic groups (Ashaninka, Matsiguenga and Aymara). (b) Barplot of individual continental ancestry for the populations included in this study and for parental populations from public databases: (1) Yoruba (HapMap YRI, n = 176); (2) European ancestry individuals (HapMap CEU, n = 174); and the Peruvian populations from the present study. Ashaninka villages: (3) Cushireni, n = 17; (4) Mayapo, n = 17; (5) Charahuaja, n = 16; (6) Capitiri, n = 11; (7) Ivosote, n = 11. Matsiguenga villages: (8) Monte Carmelo, n = 25; (9) Shimaa, n = 72. Aymara villages: (10) Jayu Jayu, n = 10; (11) Ccopamaya, n = 49; (12) Laraqueri, n = 8; (13) Pichacani, n = 32; (14) Camicachi, n = 13. Ancestry colours: blue: African; red: European; green: Native American. This analysis used 103 ancestry informative markers [19] and was performed with Admixture v. 1.2 software. (c) Profiled-likelihood and maximum-likelihood estimation of the population structure parameter f_CNV for each multilocus CNV locus. The vertical axis of each locus is standardized according to its maximum likelihood. Native American squares correspond to the entire set of studied individuals from the three ethnic groups. (d) Empirical distribution of the f parameters estimated for 695 unlinked SNPs for each ethnic group.

Using CNVice, we inferred CN genotypes at the beta-defensin (DEFB) locus, the CCL3L1/CCL4L1 locus and the low affinity Fc gamma receptor cluster locus (FCGR). mCNV at the FCGR locus can be further subdivided into CNV of the individual genes, namely FCGR2C, FCGR3A and FCGR3B. All mCNV loci studied show a high level of CN diversity.

2. Results and discussion

2.1. Assessing population structure with CNVice

We tested CNVice and compared it with CoNVEM [16], which also estimates mCNV allele frequencies using the expectation maximization (EM) algorithm but assumes Hardy–Weinberg equilibrium. For this, we used simulated data representing different levels of diversity at a mCNV locus (measured by expected heterozygosity H under Hardy–Weinberg equilibrium, and by the number of alleles, electronic supplementary material, table S1). The ranges of parameters were consistent with those previously observed at the mCNV loci analysed in this study. Both CoNVEM and our new CNVice software estimate allele frequencies for mCNV loci. Electronic supplementary material, figure S1, compares allele frequencies estimated with CoNVEM and CNVice, under different levels of population diversity. In general, CoNVEM and CNVice produce similar allele frequency estimates. However, in some instances, CNVice estimates are more accurate than CoNVEM as the departure from Hardy–Weinberg equilibrium increases (electronic supplementary material, figure S1a and table S2).

Table 1 and electronic supplementary material, table S2, show CNVice inferences of allele frequencies and f_CNV on simulated data. In all cases, CNVice 95% CIs of allele frequencies contain the true allele frequencies. Moreover, CNVice estimations of allele frequencies become less accurate when the allele frequency spectrum is dominated by a very common allele (more than 0.60). In this case, the frequency of the most common allele is underestimated and the frequencies of rare alleles are overestimated.

Table 1.

Estimation of the population structure parameter f by CNVice. Monte Carlo simulations (1000 replications) were performed sampling from populations with different levels of diversity, assuming a sample size of 100 individuals and different values of the f parameter: 0.05, 0.10 and 0.20. Estimated f_CNV values correspond to the mean of the 1000 replications. Allele frequencies and diversity parameters for the six simulated populations are in electronic supplementary material, table S1. Allele frequencies estimated by CNVice together with f_CNV are listed in electronic supplementary material, table S3.

			observed f = 0.05		f = 0.10		f = 0.20
pop	alleles	genetic diversity	estimated fCNV	[CI 95%]	estimated fCNV	[CI 95%]	estimated fCNV	[CI 95%]
1	3	0.66	0.07150	[0.00000;0.23972]	0.10221	[0.00000;0.29497]	0.17170	[0.00000;0.40610]
2	4	0.38	0.03901	[0.00000;0.21126]	0.06026	[0.00000;0.27732]	0.10469	[0.00000;0.39309]
3	3	0.56	0.04858	[0.00000;0.16891]	0.08628	[0.00000;0.23701]	0.17951	[0.00000;0.37278]
4	9	0.88	0.05316	[0.00000;0.20805]	0.08369	[0.00000;0.27313]	0.17085	[0.00000;0.41368]
5	9	0.19	0.17217	[0.00000;0.69289]	0.18816	[0.00000;0.72492]	0.23368	[0.00000;0.81062]
6	7	0.61	0.03502	[0.00000;0.19410]	0.05859	[0.00000;0.26130]	0.12928	[0.00000;0.42511]

CNVice is novel in its estimation of the population structure parameter f from mCNV data. The estimator f_CNV captures the population structure for most mCNV loci when there is departure from Hardy–Weinberg equilibrium (table 1; electronic supplementary material, table S2), but, as in the case of allele frequency estimations, f is underestimated when there is a very common allele. When the mCNV locus diversity is very low, due to the presence of a predominant allele (frequency > 0.80 in electronic supplementary material, table S2), CNVice estimators have a large bias, a problem shared by most estimators of f statistics in scenarios of low genetic diversity [20].

2.2. The genetic structure of Native American populations for immune-related multiallelic copy number variation loci

The very low European or African admixture of the studied populations indicates that they are reasonable representatives of autochthonous Native American traditional populations (figure 1b, average individual non-Native American ancestry: 2%). Previous studies of the genetic structure and evolution of mCNV have focused on the global level [3,15,21,22]. This is the first population genetics study that assesses the level of population structure of mCNV loci (in this case, immune-related) in a set of autochthonous and traditional villages from different linguistic groups, residing in different environments (the Andean highlands and the Amazon Yunga forest) (figure 1a). In this case, the 12 studied populations are scattered in an area of nearly 25 000 km² (similar to the size of Sardinia) that was peopled at least 10 000 years ago [23]. Therefore, our study is informative about how inbreeding, genetic drift, gene flow and probable selective pressures (associated with different environments) shape the genetic structure of traditional populations for mCNV loci.

Figure 1c,d and electronic supplementary material, tables S3–S7, show the observed diploid CN distributions, the inferred allele frequencies and f_CNV for the studied mCNV loci. Estimated f_CNV values are within the range of f estimates observed for unlinked SNPs in the same populations (figure 1d). CNVice allows assessment of the uncertainty of the inference by examining the estimated f_CNV-likelihood profile (figure 1c). On the other hand, it has the limitation that it only allows positive values of f_CNV.

The five immune-related mCNV loci studied here have a level of population structure (mean f_CNV = 0.018) that is lower than the mean f = 0.136 observed for 695 unlinked SNPs. The two Matsiguenga villages, which are separated by nearly 80 km in the same Amazon Yunga valley, show the highest level of population structure (figure 1c, mean f_CNV = 0.04).

DEFB mCNV [21] and FCGR mCNV [22] have low levels of genetic structure worldwide when compared with genome-wide estimates for CNV loci [15]. When we used CNVice to estimate allele frequencies and f_CNV based on published DEFB [21] and FCGR3B data [22], we confirmed the low level of worldwide genetic structure previously observed (electronic supplementary material, tables S8 and S9 and figure S3). By contrast, the genetic structure of CCL3L1/CCL4L1 is higher worldwide [3]. The estimated f_CNV values for Native Americans studied here are partially consistent with the patterns of population structure observed for FCGR mCNV and CCL3L1/CCL4L1 mCNV worldwide. Indeed, despite local variation in the f_CNV statistics between the 12 Native American populations, the inferred f_CNV values across the populations are 0 for DEFB, FCGR3A and FCGR2C and higher (0.016) for CCL3L1/CCL4L1 (electronic supplementary material, tables S3–S7). FCGR3B had the highest observed f_CNV (0.076).

The following features of the genetic structure of the immune-related mCNVs in Peruvian Native Americans are noteworthy:

• (i) For DEFB (electronic supplementary material, table S3), the Shimaa population exhibited an elevated frequency of a diploid CN of 7 (11.4% versus 1.7% globally [21]). Considering that the two-copy allele is most common worldwide, the Shimaa result probably derives from being the only studied population in which the five-copy allele is common (frequency of 9% versus less than 0.4% elsewhere), which may reflect the action of genetic drift.

• (ii) For CCL3L1/CCL4L1 (electronic supplementary material, table S4), our Native American populations share modal diploid copy numbers (3–4 copies) with West African Yoruba [9] and differ from Europeans (modal diploid CN: 2 [24]). This is because Native Americans show two-copy alleles as modal. Native Americans are more diverse than Europeans [24] but less diverse than Africans [9].

• (iii) Both the CCL3L1/CCL4L1 genes occur in a single CNV block in most populations (although they are separate in a small number of Ethiopian samples) [9]. The high correlation (Pearson R² > 0.91, p < 0.001) between the normalized CN values across the pairs of the three amplified loci (CCL3C, CCL4A and LTR61A; figure 2) in Native American populations suggests that, in these populations, the region encompassing the CCL3L1 and CCL4L1 genes is on the same repeat unit.

• (iv) For FCGR3B, the Amazonian Yunga populations have the highest known frequency of gene deletion, probably due to genetic drift with frequencies of homozygosity for this deletion of 2.4% and 11.6% in Ashaninkas and Matsiguengas, respectively, versus less than 0.31% in the worldwide Human Genome Diversity Panel (HGDP) populations [22]. This trend is also seen, although less strikingly, for FCGR2C gene deletions (electronic supplementary material, tables S6–S7).

• (v) Q57X is a relevant substitution in FCGR2C (rs10917661, electronic supplementary material, table S10). While the frequency of this sequence variant in South and Central Native American samples from the HGDP is similar to that in many other global populations (0.24) [22], our samples from Western South Amerindians have the lowest frequency (0.07) of this allele (electronic supplementary material, table S10); only that in East Asians is lower (0.05).

Figure 2.

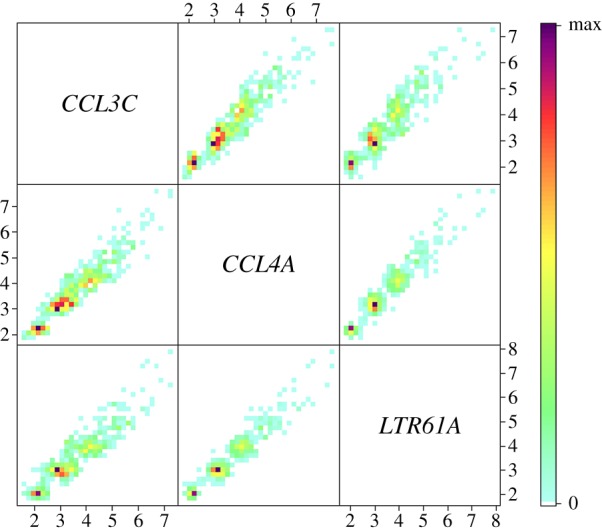
Correlation of copy numbers for the three markers used to infer copy number of the CCL3L1/CCL4L1 region. Dispersion matrix of the normalized copy number values for CCL3C, CCL4A and LTR61A markers for 522 Native American individuals genotyped for the regions CCL3L1/CCL4L1. Colours correspond to point density. The high correlation (Pearson R² > 0.91, p < 0.001) between the normalized CN values across the pairs of the three amplified loci suggests that in these populations, the region encompassing the CCL3L1 and CCL4L1 genes belongs to the same repeat unit.

2.3. Inferring copy number variation genotypes using trios

Defining individual CN genotypes for mCNV may be challenging, but it is important, for example, to identify carriers of specific alleles to be re-sequenced to study their associated nucleotide diversity and genomic organization. This information may be particularly relevant in neglected populations with few studied individuals such as Native Americans, to compare the nucleotide diversity and genomic organization of CNV alleles with other well-studied populations. As an example of how CNVice uses both population diploid CN frequencies and trio diploid copy numbers to infer individual mCNV genotypes, we consider data from an Ashaninka trio for the DEFB cluster (a mother with 2 copies, a father with 4 copies and an offspring with 4 copies) (figure 3). In this population, the DEFB diploid CN varies from 0 to 9 with the following respective absolute frequencies: (0, 0, 7, 45, 51, 23, 10, 5, 1, 1) for 143 individuals (i.e. 0 individuals with 0 copy, 0 individuals with 1 copy, eight individuals with 2 copies and so forth) (electronic supplementary material, table S11, line 6, column Diplotype frequencies (CN)). The possible genotypes for the offspring ASH064, as for all individuals with 4 copies in the population, are (0, 4), (1, 3) or (2, 2). First, CNVice estimates f_CNV = 0 and the vector of allele frequencies for the population, P = (0, 0.25, 0.56, 0.12, 0.04, 0.02, 0, 0.002, 0, 0) for alleles from 0 to 7 copies, using the observed CN distribution above (figure 3a). Based on this information and following equation (3.1) in §3.2, the probabilities of each of the three genotypes are 0.839 for (2, 2), 0.161 for (1, 3) and 0 for (0, 4). Note that these genotype probabilities apply to all individuals with diploid CN equal to 4 (figure 3b).

Figure 3.

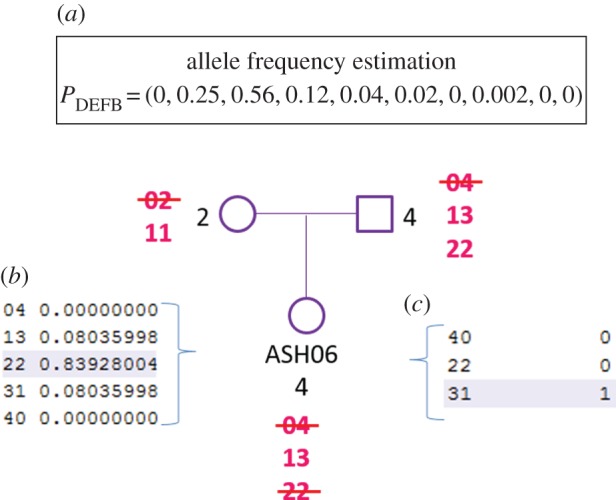
Improving individual CNV genotype estimation with trio information. (a) Vector of allele frequencies for the locus DEFB in the Ashaninka population; (b) individual genotype probabilities for ASH06 without using trio information but conditioning on observed diploid copy number, inferred allele frequencies and f_CNV; (c) individual genotype posterior probabilities for ASH06 (i.e. considering parental CNV information). (Online version in colour.)

Equation (3.1) (§3.2) estimates a prior probability of a genotype, given population genetics information. If trio information is available, CNVice uses the parents' diploid CN information applying the Bayes theorem, to estimate a posterior probability of a genotype, considering the prior probability estimated by equation (3.1) and also diploid CN information from the parents. As shown in figure 3c, for individual ASH06, with information of the parents' diploid CN, CNVice infers that this individual carries the (1, 3) genotype and not the (2, 2) genotype for DEFB. This calculation takes into account the population allele frequencies, the individual's genotype frequencies and the parents' genotype frequencies. As figure 3 shows, because there is no allele 0 in the population, the genotypes (0, 4) for individual ASH06, (0, 2) for the individual's mother and (0, 4) for the individual's father are eliminated from the calculation. As the only possible allele the mother can pass on to her offspring is 1, the only possible genotype for ASH06 is (1, 3). This reasoning is formalized in equation (3.2) of §3.2.

We tested this functionality of CNVice in 53 trios with unique diploid CN combinations for DEFB, CCL3L1/CCL4L1, FCGR3A, FCGR3B and FCGR2C, and found that the inferences of offspring genotypes improve in 49% of cases, with the posterior probability of the most likely genotype increasing on average from 0.74 to 0.83 (electronic supplementary material, table S11 and figure S2). This means that, in general, the information about the diploid CN of the parents reduces the uncertainty about the individual genotype. However, a decrease in the probability of the most likely genotype, or an increase in the uncertainty of the individual genotype (as seen in 7.6% of cases in electronic supplementary material, figure S2), is still an optimized result and indicates that there was as overestimation in the prior probability. Because trio information limits the possible genotypes of an individual, by imposing additional constraints on its calculation, trio information corrects such over- or underestimates of prior probabilities.

3. Material and methods

In this section, we outline the material and methods; further details are given in the electronic supplementary material section.

3.1. Populations, samples and genotyping

We analysed between 324 and 375 individuals (depending on the locus) hierarchically sampled from 12 populations (hereafter called villages), belonging to three Peruvian ethnic groups (figure 1a; electronic supplementary material, table S12): (i) 143 Ashaninka from five villages along the Junin River (central Peru); (ii) 113 Matsiguenga living in the villages of Monte Carmelo (n = 24) and Shimaa (n = 89), in southern Peru; and (iii) 120 Aymara highlanders from the Andean region, living in five villages near Titicaca Lake (southern Peru). The Ashaninkas and Matsiguengas are settled in the Amazon Yunga tropical forest environment, and their languages belong to the Arawak linguistic family, while the highlanders' language, Aymara, belongs to the Andean linguistic family. For population genetics analyses, we avoided genotyping parents, offspring or siblings for CNVs, except for the Ashaninkas. For the latter, 69 families composed of two parents and their offspring were further genotyped for 277 individuals, which include the 143 unrelated individuals considered for the main analyses (electronic supplementary material, table S12). The Institutional Review Boards of the participant institutions approved this study.

We used 103 ancestry informative marker SNPs [25] to estimate African, European and Native American ancestry in these villages, using the software Admixture v. 1.2 [26].

To compare the genetic structure based on mCNVs with that based on SNP genotypes, we used 695 SNPs that were unlinked between them as well as with respect to the mCNV loci. These SNPs were genotyped in 124 individuals from the same studied populations. The 695 SNP genotypes are the intersection of two datasets obtained using different technologies: 1442 gene-centric and cancer-associated SNPs from an Illumina Golden Gate Oligonucleotide Pool Assay (genotyped by Dr Stephen J Chanock's group at the National Cancer Institute), and 2.3M SNPs genotyped with the Illumina's HumanOmni2.5-8v1 array. We used the hierfstat R package [27] to estimate the f statistics for each SNP.

We measured diploid CN in the DEFB region, CCL3L1/CCL4L1 and for the FCGR3A, FCGR3B and FCGR2C genes, using the PRT approach, described previously for each locus [1,28,29]. The latter technique is a development of quantitative PCR that uses a single primer pair to simultaneously amplify both a test locus and a reference locus, allowing an accurate CN determination [1].

After amplification, the ratio of the amounts of amplification products (i.e. the corresponding areas under their capillary electrophoresis peaks) between the reference and test locus is calculated. Reference samples with known CN (electronic supplementary material, table S13) are then used to convert these ratios in an expected CN estimation, which is a continuous number. Next, a probabilistic model is used to obtain a maximum-likelihood estimation of the discrete CN, combining information from different primers [28]. The relative proportions of each allele for SNPs on the promoter of DEFB103 (rs2737902), FCGR3A/FCGR3B genes (rs1042207 C > T, Arg234X), FCGR3B HNA1a/1b allelotype (rs76714703 C > T, Asn468Ser) and FCGR2C null variation (rs10917661 C > T, Glu57X) were determined using multiplex restriction enzyme digest variant ratio (REDVR) [21,22].

The combined use of multiplex REDVR with PRT allows the determination of CN, the relative proportion of each allele for SNPs and paralogue genes, which adds an additional layer of complexity. For instance, in contrast with the CCL3L1/CCL4L1 and beta-defensin CNs, which gene products are identical between copies, or almost so (and are very likely to have the same function), we can distinguish between deletions in FCGR3A or in FCGR3B. Considering their importance as functionally distinct genes, they are separately included in the analysis. This strategy also implies that FCGR regions are analysed at a higher resolution respect to the other studied mCNVs loci.

3.2. Algorithm

CNVice performs four analyses. First, it estimates allele frequencies for a given population assuming Hardy–Weinberg equilibrium, using the EM algorithm as implemented in CoNVEM [16], conditioned on the observed diploid CN frequencies.

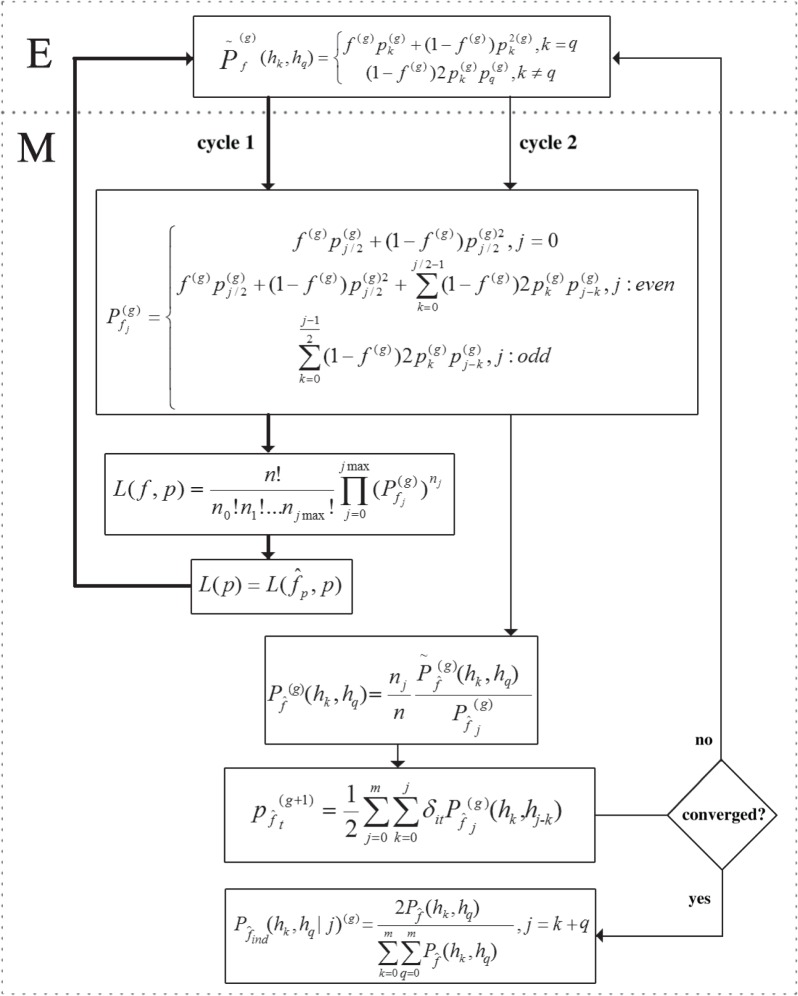
Second, CNVice implements a more general approach to study population structure by jointly estimating f_CNV (i.e. the population structure parameter f) and allele frequencies. For this, a profiled likelihood function and EM algorithm is used [30,31], where the set of allele frequencies is the main parameter and f_CNV is the perturbation parameter. The perturbation parameter is replaced by a maximum-likelihood estimate in the original likelihood while maintaining fixed values for allele frequencies. The analytical derivation and CNVice algorithm are detailed in the electronic supplementary material, and in figure 4, respectively.

Figure 4.

CNVice algorithm. h_k and h_q are alleles, where k and q represent the number of copies of a gene in each chromosome. The observed diploid copy number, or the total copy number, is denoted by j, where j = k + q, k and q being natural numbers. The population structure parameter is f (or f_CNV), and the probability of an allele to be k is p_k. For example, an individual with genotype (h₃, h₁) for a locus L has 3 copies of the allele in one chromosome, 1 copy on the other, and diploid copy number 4; the probability of the allele to be h₃ in the population is given by p₃ and of the allele h₁ is given by p₁. n is the total number of individuals in the sample, and g is the number of iterations. δ_it is a binary variable that indicates whether the t allele is present in genotype i = (h_k, h_q). Steps: E, expectation; M, maximization.

Third, CNVice calculates individual genotype probabilities given a diploid CN and estimates population genotype frequencies, based on both the observed diploid CN distribution and the estimated f_CNV and allele frequencies, using the expression

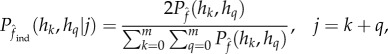3.1

where 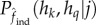is the expected genotypic proportion given the estimated f_CNV.

Finally, CNVice uses trio information, if available, to improve the inference of mCNV genotype by considering diploid copy numbers of the parents and using Bayes theorem. The offspring genotype probability given the diploid CN and genotypic probability of the parents is

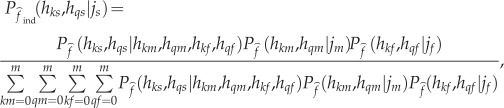3.2

where h_ks and h_qs denote the offspring's alleles; h_km and h_qm denote the mother's alleles; h_kf and h_qf denote the father's alleles; j_m denotes the mother's diploid CN; and j_f denotes the father's diploid CN. It is required that

• (1) k_s + q_s = j_s;

• (2) (h_ks = h_km) or (h_ks = h_qm) or (h_ks = h_kf) or (h_ks = h_qf); and

• (3) (h_qs = h_km) or (h_qs = h_qm) or (h_qs = h_kf) or (h_qs = h_qf).

For the Native American data, we estimated allele frequencies and f_CNV using CNVice. We also used CNVice to assess trios from the Ashaninka population and to infer individual genotypes using information about their parents' diploid CN.

4. Conclusion

We present a novel likelihood approach, implemented in the CNVice software, which allows for the study of the genetic structure of natural populations using the classical f statistic framework. Using Monte Carlo simulations, we show that our method improves (i) the estimation of allele frequencies when departure from Hardy–Weinberg equilibrium increases and (ii) the estimation of individual genotypes in comparison with existing methods, in particular when trio information is available. Using our approach, we observed a low level of genetic structure for three immune-related mCNV loci in a set of traditional Native American populations, settled for at least 10 000 years in the different Andean and Amazon Yunga environments. Our method, used here to infer the genetic structure of traditional Native American populations, is also applicable to the most diverse diploid species of animals and plants, where departure from the Hardy–Weinberg model due to drift, assortative mating or natural selection may be stronger and more frequent than in human populations.

Data accessibility

Details of the statistical methods presented here are in the electronic supplementary material. CNVice is implemented in R, and the source code can be found at https://github.com/mairarodrigues/cnvice. The article's supporting data are also available as electronic supplementary material. The software run time depends mostly on the number of alleles and the sample size that form the distribution of observed diplotype frequencies given as input. For example, an input containing the distribution of eight alleles in a sample size of 120 individuals takes 7.42 min to run in a computer with 12 GB of RAM, while the same allele distribution in a sample size of 30 individuals takes almost seven times less (that is, 1 min). Similarly, an input with four alleles and sample size of 120 takes only 13 s. CNVice also works for larger CN ranges (it has been tested for distributions with up to diploid CN = 20).

Authors' contributions

L.W.Z. performed the CN genotyping and sequence analysis; S.S. and D.D. developed the statistical methods and S.S. carried out experiments with simulated data and Monte Carlo simulations; L.W.Z., E.J.H., R.J.H., L.R.M., H.B., G.B.S.-S., M.H.G., F.R.-S. and M.M. carried out data analysis; D.E.B., R.Z. and R.H.G. participated in sample collection; D.L.T. implemented the software; M.R.R. participated in algorithm development and software implementation; E.T.-S. conceived the work; E.J.H., E.T.-S., D.D. and M.R.R. supervised the work; L.W.Z., S.S., D.D., D.E.B., E.J.H., E.T.-S. and M.R.R. participated in the draft of the manuscript. All authors gave final approval for publication.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by the European Molecular Biology Organization (EMBO) travel grant, Brazilian Ministry of Education (CAPES Agency) and the Brazilian National Research Council (CNPq).