History dependence and the continuum approximation breakdown: the impact of domain growth on Turing’s instability

Abstract

A diffusively driven instability has been hypothesized as a mechanism to drive spatial self-organization in biological systems since the seminal work of Turing. Such systems are often considered on a growing domain, but traditional theoretical studies have only treated the domain size as a bifurcation parameter, neglecting the system non-autonomy. More recently, the conditions for a diffusively driven instability on a growing domain have been determined under stringent conditions, including slow growth, a restriction on the temporal interval over which the prospect of an instability can be considered and a neglect of the impact that time evolution has on the stability properties of the homogeneous reference state from which heterogeneity emerges. Here, we firstly relax this latter assumption and observe that the conditions for the Turing instability are much more complex and depend on the history of the system in general. We proceed to relax all the above constraints, making analytical progress by focusing on specific examples. With faster growth, instabilities can grow transiently and decay, making the prediction of a prospective Turing instability much more difficult. In addition, arbitrarily high spatial frequencies can destabilize, in which case the continuum approximation is predicted to break down.

1. Introduction

Emergent self-organization has long been considered as a mechanism for generating complexity without fine grained control. Hence it has attracted attention in numerous areas of theoretical developmental biology, for instance avian feather bud formation [1] and vertebrate limb development [2,3], as a prospective mechanism for initiating and amplifying heterogeneity on larger lengthscales than the cellular level of genetic regulation. In particular, the classic example is the diffusion driven instability (DDI) of Turing [4], whereby the incorporation of diffusion within an otherwise stable dynamical system induces an instability which drives spatial organization. The interaction is between morphogens, which are traditionally understood to be biochemical gene products, with potential candidates, including Nodal and Lefty [5,6]. Nonetheless, the prospect of more generalized Turing interactions, for instance between cells, has also been considered in fish-skin markings [7].

It has long been recognized that the two species Turing mechanism requires short-range self-activation and long-range self-inhibition [8–10]. This summarizes the results from linear stability analyses which demonstrate that spatially heterogeneous self-organization requires a morphogen that autocatalyses its own production but does not spread extensively, in contrast to a second morphogen that inhibits its own production but spreads much more extensively [8,11]. However, it is also clear that such simplicity need only be limited to two species models, as illustrated by the study of specific systems (e.g. [12,13]) before, very recently, a systematic study by Marcon et al. [14].

Physical examples of Turing’s instability mechanism via short-range self-activation and long-range self-inhibition have been observed in chemically reacting systems [15,16], but confirmation of this mechanism or Turing’s instability more generally in developmental biology has remained elusive, especially with regard to molecular details. Further difficulties concerning the relevance of the Turing instability for developmental biology are associated with its sensitivity to domain geometry, initial conditions and cell-scale details such as gene expression dynamics [17–20]. Despite such difficulties its ability to provide simple explanations not only for spontaneous spatial organization, but also for the extensive amplification of small spatial perturbations [5,6,21,22] and for subtle and non-trivial behaviours, such as stripe splitting in fish markings, entail that the mechanism is still an intensive area of study more than 60 years after its inception.

In particular, numerous studies have investigated how the difficulties with the mechanism may be reduced by considering additional biological detail. This has allowed, for instance, the relaxation of the constraint of different morphogen diffusivities [13] and the amelioration of initial condition sensitivity, by considering Turing’s mechanism on a growing domain [23–27]. The classical means for mathematically studying the latter systems is to treat the domain length as a bifurcation parameter, which we refer to as the adiabatic approximation in that it assumes domain growth is arbitrarily slow compared with any other timescale of the system. As the domain size is then effectively a parameter in the standard linear analysis of the Turing instability, one can readily explore the impact of domain growth and deduce the existence of a critical domain size and spontaneous spatial organization occurs once this domain size is exceeded [11,25]. Within the context of the adiabatic approximation, one also retains the classical understanding that the two-species Turing mechanism requires short-range self-activation and long-range self-inhibition and, more generally, stability conditions can be inferred simply from the analysis of the fixed domain.

However, the accuracy of the adiabatic approximation has recently been considered and Madzvamuseet al. [28] have shown that self-organization can occur without short-range self-activation and long-range self-inhibition. This provides a proof of principle that the adiabatic approximation can oversimplify the dynamics of Turing systems on growing domains and more generally that the Turing system is more complex than previously anticipated.

Nonetheless, the analysis presented by Madzvamuse et al. [28] is subject to numerous stringent constraints. Thus, in turn, the dynamics of Turing systems on growing domains may yet be richer still. In particular, a very slow growth regime was assumed, whereby domain growth was asymptotically slow, compared with the other timescales, and thus only the leading asymptotic correction to the adiabatic approximation is determined. This is also under a further restrictive constraint that a single mid-point approximation is assumed sufficient to track the system evolution between the start time and the time when the prospect of self-organization is assessed. A final simplification is that the prospect of an instability at any given time within the region of validity of the mid-point approximation does not account for the previous stability properties of the system, which evolve with time and should be accommodated.

Hetzer et al. [29] also relaxed these conditions presenting stability analyses in terms of Lyapunov exponents. Given the absence of finite time blow up, the definitions of stability used in this study is dictated by the long time behaviour of the system and, as such is in the context of quasi-asymptotic stability rather than Lyapunov stability [30]. Thus, the prospect of a large deviation from the near-homogeneous state at finite time is not considered. However, developmental self-organization is highly orchestrated temporally as well as spatially. For example, the prospective Turing pair of Nodal and Lefty gene products in the mouse amplify left–right asymmetry around D7.5 of mouse development [31,32], when the embryo is about 400 μm in size (EMAP eMouse Atlas Project, [33]) and long before growth saturates, mitigating against the use of quasi-asymptotic stability as opposed to Lyapunov stability.

Thus, our objective in this paper is to further investigate the impact of domain growth, based on Lyapunov stability, which captures large deviations from the reference state at finite time before growth saturates. In particular, we account for the time evolution of the system stability properties, thereby generalizing Madzvamuse et al.’s framework, with a view to exploring whether this leads to even richer instability dynamics. We will also proceed to relax the further assumptions of Madzvamuse et al. and consider faster growth without the mid-point approximation for Turing systems using specific analytical examples, in particular to examine the impact of a faster growth rate and how this alters the prospect for self-organization.

Hence, in summary, we examine how domain growth impacts the Turing mechanism for self-organization beyond both the adiabatic approximation and the stringent restrictions of Madzvamuse et al. [28].

2. The two species Turing model with asymptotically slow growth

(a). Preliminaries: model definition

As we shall explore the impact of domain evolution on the diffusively driven instability (DDI), we consider a two species Turing reaction diffusion system for time t on a one-dimensional spatial domain¹ with x∈Ω:=[0,L(t)], where L(t)>0 and $\dot{L}(t)\ge 0$ is assumed unless stated otherwise. In particular, the dimensional model is given by

$$\begin{array}{rl}{\mathrm{\partial }}_{t}u+{\mathrm{\nabla }}_x.(\mathbf{\text{a}}u)& =D_u{\mathrm{\nabla }}_x^{2}u+f(u,v)\\ \mathrm{and}{\mathrm{\partial }}_{t}v+{\mathrm{\nabla }}_x.(\mathbf{\text{a}}v)& =D_v{\mathrm{\nabla }}_x^{2}v+g(u,v),\end{array}$$

where u, v are morphogen concentrations and a is the velocity vector induced by domain growth [25]. These equations are supplemented by zero-flux boundary conditions at the boundary ∂Ω(t), representing a physically isolated growing one-dimensional domain. Finally, D_u is the diffusion coefficient of the u morphogen and, without loss, d=D_v/D_u≥1 is the ratio of two diffusion coefficients.

Typically below, we shall consider Schnakenberg kinetics [34], whereby

$$f(u,v)=a-k_{1}u+k_{2}u{v}^2\mathrm{and}g(u,v)=b-k_{2}u{v}^2,$$ 2.1

with a, b dimensional production rates and k₁,k₂ dimensional decay and reaction rates, respectively. In addition to self-upregulation of the short-range activator, whose concentration is u, and the self-inhibition of a long-range inhibitor of concentration v, we also have that the activator upregulates the inhibitor and the inhibitor downregulates the activator. This is referred to as cross kinetics and the Schnakenberg model is a popular example.

There is another possibility, where the activator downregulates the inhibitor, which in turn upregulates the activator. This is referred to as pure kinetics. In the adiabatic analysis of the effect of domain growth, such choices of the kinetics do not alter the pattern forming potential of the morphogen dynamics [11], though this need not be the case more generally. Hence we also consider a paradigm of pure kinetics, named after Gierer & Meinhardt [8], with activator concentration u and inhibitor concentration v, and kinetic functions given by

$$f(u,v)={\rho }_1\frac{u^2}{v}-{\mu }_{u}u+{\rho }_2\mathrm{and}g(u,v)={\rho }_3{u}^2-{\mu }_{v}v,$$ 2.2

where ρ₁,ρ₂,ρ₃,μ_u and μ_v are positive, dimensional parameters.

For convenience, a vector notation will often be adopted, with u=(u,v), F(u)=( f(u),g(u))=U₀ωF_*(u), where U₀ is a representative concentration scale and ω is a representative rate of the kinetics. Considering the simple but illustrative case of uniform growth for a one-dimensional domain in the x-direction, we have a=h(t)xe_x with $h(t)=\dot{L}(t)/L(t)$ the expansion (or contraction) rate of the domain, and a normalized Lagrangian coordinate is given by ξ=x/L(t).

Then non-dimensionalizing via (i) the concentration scale U₀, (ii) the time scale $t=L_0^2/D_u\tau$, with L₀=L(0) the initial domain length, and (iii) the lengthscale L₀, the equations can be reduced to [28]

$${\mathrm{\partial }}_{\tau }\widetilde{\mathbf{\text{u}}}+\tilde{h}(\tau )\widetilde{\mathbf{\text{u}}}=\frac{1}{{\phi }^2(\tau )}\mathbf{\text{D}}{\mathrm{\Delta }}_{\xi }\widetilde{\mathbf{\text{u}}}+\gamma {\widetilde{\mathbf{\text{F}}}}_{\ast }(\widetilde{\mathbf{\text{u}}}).$$ 2.3

Here $\tilde{h}(\tau )=[1/L]\mathrm{\partial }L/\mathrm{\partial }\tau$ is the non-dimensional expansion (or contraction) rate of the domain and

$$\phi (\tau )=\exp {\int }_0^{\tau }\tilde{h}(q)\mathrm{d}q=\frac{L(L_0^2/D_u\tau )}{L_0},\mathbf{\text{D}}=\text{diag}(1,d),\gamma =\frac{\omega L_0^2}{D_u}.$$

Finally, zero flux boundary conditions are inherited. Thus, φ is the non-dimensional domain length, while $\tilde{h}(\tau )\widetilde{\mathbf{\text{u}}}$ represents dilution or concentration of the morphogen due to domain size changes and there is now also a time dependence in the effective diffusion coefficients via 1/φ²(τ). In the adiabatic approximation, one treats L as a bifurcation parameter, and thus $\tilde{h}$ is zero and φ is unity, with the resulting equations having no time dependence. Hence one can analyse the transition from stability to instability as L is varied to assess the impact of domain growth.

For example, Schnakenberg kinetics (2.1) can be rewritten in a dimensionless form ${\tilde{f}}_{\ast }(\tilde{u},\tilde{v})=\tilde{a}-\tilde{u}+\tilde{u}{\tilde{v}}^2$, ${\tilde{g}}_{\ast }(\tilde{u},\tilde{v})=\tilde{b}-\tilde{u}{\tilde{v}}^2$ with $\tilde{a}=a/(k_1{U}_0)=a/(k_2{U}_0{V}_0^2)$, $\tilde{b}=(b/a)\tilde{a}$ and $\omega =k_2{V}_0^2=k_1$. This system has a two dimensional parameter space ($\tilde{a},\tilde{b}$), with $\tilde{a},\tilde{b}>0$, and a closed form homogeneous stationary solution in the adiabatic approximation (or for exponential growth noting equation (2.3)).

Finally, note below that we drop tildes and use t rather than τ to also represent the non-dimensional model to simplify notation.

(b). The reference state for stability analysis

Apart from uniform exponential growth, where h(t) is constant, the non-autonomous system (2.3) does not possess a homogeneous steady state. This is in distinct contrast to the adiabatic approximation. Given the Turing instability is a mechanism to generate spatial organization, in the non-autonomous case, one therefore considers the stability of the time-dependent reference homogeneous solution, u_s, which satisfies [28]

$${\mathrm{\partial }}_t{\mathbf{\text{u}}}_s+h(t){\mathbf{\text{u}}}_s=\gamma \hspace{0.17em}{\mathbf{\text{F}}}_{\ast }({\mathbf{\text{u}}}_s),{\mathbf{\text{u}}}_s(0)={\mathbf{\text{u}}}_s^0.$$ 2.4

Consequently, the choice of initial condition ${\mathbf{\text{u}}}_s^0$ needs care as it determines the reference state u_s, and thus the prospect of a diffusively driven instability to spatial heterogeneity.

The selection of the initial condition ${\mathbf{\text{u}}}_s^0$ is not uniquely determined and any choice would be plausible, in principle, yielding a different reference state in each instance. Nonetheless for the purpose of instability analysis, we consider perturbations about the long-time asymptote of the system assuming no instability. If there was no self-organization this is the solution that would emerge and hence we are looking for instability around this particular reference state. Thus, the initial condition is, to within a possible small random perturbation, given by u* the root of

$$h(\mathrm{\infty }){\mathbf{\text{u}}}^{\ast }=\gamma {\mathbf{\text{F}}}_{\ast }({\mathbf{\text{u}}}^{\ast }).$$

It is implicitly assumed a unique such root exists, noting that an analogous assumption in the absence of growth (h=0) is typically stipulated in studying Turing systems. With linear growth, for instance, where $h(\mathrm{\infty })=0$, one has ${\mathbf{\text{u}}}_s^0={\mathbf{\text{u}}}^{\ast }$ or a tiny perturbation thereof, with u* is the root of F(u*)=0. For exponential growth, however, h(t)=r for all time and hence the suitable choice for initial condition is u*, or a small perturbation thereof, with ru*=γF_*(u*). Note that these choices of initial condition for both linear and exponential growth were used in the original study [28].

(c). The assumption of slow growth

An initial study of (2.3) for asymptotically slow growth was pursued by Madzvamuse et al. [28], albeit subject to the validity of a mid-point approximation. In particular, to characterize slow growth, define ϵ=T_dyn/T_gr where T_dyn is the timescale of the dynamics associated with the kinetics and T_gr is the timescale of growth for the non-dimensional model. In particular, it is convenient to define T_gr as the infimum of the duration required for the domain size to increase by a factor of e during the range of time that is of interest. Thus, it is straightforward to give T_gr in terms of the growth functions; for instance, given linear growth, φ(t)=1+rt, with t non-dimensional time and r a dimensionless characterization of the domain growth expansion rate, we have T_gr=(e−1)/r≈2/r.

Similarly, the characteristic time for the kinetics in the model, denoted T_dyn, can be related to the eigenvalue of largest real part, λ*, of the Jacobian ∂F/∂u, evaluated at the initial condition to ensure that the timescale of at least the initial dynamics is captured. This gives

$$T_{\mathrm{dyn}}=\frac{1}{\gamma |\mathrm{\Re }{\mathrm{\lambda }}^{\ast }|}.$$

Thus, the slow growth constraint requires

$$ϵ=\frac{T_{\mathrm{dyn}}}{T_{\mathrm{gr}}}=\frac{1}{T_{\mathrm{gr}}\gamma |\mathrm{\Re }{\mathrm{\lambda }}^{\ast }|}\ll 1$$

is sufficiently small. With exponential growth for instance, we require that

$$ϵ=\frac{1}{T_{\mathrm{gr}}\gamma |\mathrm{\Re }{\mathrm{\lambda }}^{\ast }|}=\frac{r}{\gamma |\mathrm{\Re }{\mathrm{\lambda }}^{\ast }|}\ll 1$$

and for the linear case ϵ is approximately half of this expression.

In particular, the analysis in Madzvamuse et al. [28] was asymptotic in the ratio ϵ and we bring the dynamical and growth timescales closer in the later sections of this paper.

(d). The notion of stability and instability in a non-autonomous system

The reference state u_s is defined to be unstable in the time interval [t₀,t₁] if and only if [28]

$$\frac{\parallel {\mathbf{\text{u}}}_s(t_1)\parallel }{\parallel {\mathbf{\text{u}}}_s(t_0)\parallel }>1$$ 2.5

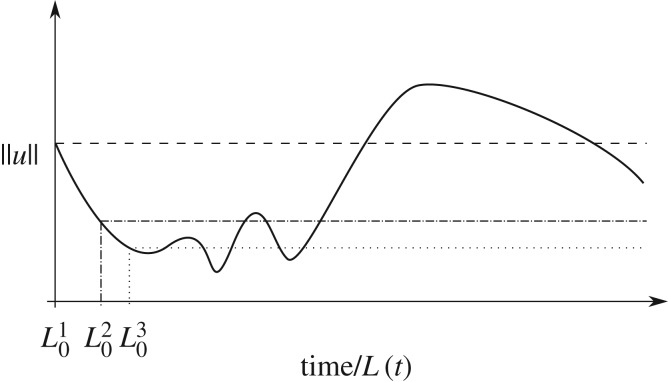
given a norm and is tightly linked to the chosen time interval and the initial time. The impact of such details on the linear stability of a Turing system in the adiabatic case are much simpler [11], whereby the Turing instability occurs providing at least one unstable linear mode is compatible with the boundary conditions. Here, however, the question of instability directly depends on the start time t₀, and the final time t₁, when stability is considered as schematically indicated in figure 1. However, such complexity is extensively removed both in this section and the next, as well as in Madzvamuse et al. [28], due to the mid-point approximation, which requires t₁−t₀∼T_dyn or less; nonetheless the prospect of an instability clearly still possesses a dependence on time and the initial, dimensional domain length. The latter in particular emphasizes that it is necessary to state the scaling used, and thus give parameter values for L₀ and γ or D_u, whenever the Turing space is plotted below.

Figure 1.

An illustration of how instability for the non-autonomous case can be contingent on the interval over which stability is considered, with L₀ referring to initial (dimensional) domain lengths and the horizontal axis denoting time, or equivalently subsequent domain length. The dashed, dotted and dot-dashed lines highlight the boundary between stable and unstable time intervals for given choices of initial lengths $L_0^j$, or equivalently different choices of start time. The norm ∥u∥ represents the time evolution of the norm of the perturbation initiated at the initial time length $L_0^j$.

(e). The Turing space for slowly growing domains

A point in parameter space is in the Turing space if and only if a Turing instability is possible, during the time period considered and for suitable initial conditions. Thus, a point in parametric space, which is also in the Turing space, is typically understood to be such that the reference state is stable in the absence of diffusion but unstable in the presence of diffusion. Conditions for the system to be in the Turing space under the standard constraint of linear theory and also the mid-point approximation, the neglect of homogeneous state evolution and asymptotically slow growth are given by Madzvamuse et al. [28]

$$\begin{array}{rl}& \begin{array}{rl}& -\gamma \hspace{0.17em}\mathrm{tr}\hspace{0.17em}{\mathbf{\text{J}}}_{{\mathbf{\text{u}}}_s(t_{\ast })}+2\hspace{0.17em}h(t_{\ast })>0\\ & -h(t_{\ast })\gamma \hspace{0.17em}\mathrm{tr}\hspace{0.17em}{\mathbf{\text{J}}}_{{\mathbf{\text{u}}}_s(t_{\ast })}+{\gamma }^{2}det\hspace{0.17em}{\mathbf{\text{J}}}_{{\mathbf{\text{u}}}_s(t_{\ast })}>0\end{array}\}\mathcal{S}(t_0,t_1),\\ & \begin{array}{rl}& -\gamma [d{f}_u+g_v]+h(t_{\ast })(1+d)<0\\ & {[h(t_{\ast })(1+d)-\gamma (d{f}_u+g_v)]}^2-4d[{\gamma }^{2}det{\mathbf{\text{J}}}_{{\mathbf{\text{u}}}_s(t_{\ast })}-\gamma h(t_{\ast })\hspace{0.17em}\mathrm{tr}\hspace{0.17em}{\mathbf{\text{J}}}_{{\mathbf{\text{u}}}_s(t_{\ast })}]>0\end{array}\}\mathcal{U}(t_0,t_1).\end{array}$$

Here the Jacobian components f_u,f_v,g_u,g_v are evaluated at u_s(t_*), with t_* the mid-point of the interval [t₀,t₁], with t₁−t₀∼T_dyn or less. In addition, setting h(t_*)=0 gives the adiabatic conditions and the dependence on time is also removed as the homogeneous solution u_s(t_*) collapses to the homogeneous steady state, u*. One can clearly see from this limit that conditions $\mathcal{S}(t_0,t_1)$ arise from stability of the homogeneous state in the absence of diffusion, while conditions $\mathcal{U}(t_0,t_1)$ enforce the presence of instability once diffusion is introduced, as required for Turing’s diffusively driven instability. One can also observe that with these conditions in general the parameter values which will be in the Turing space evolve in time since, for instance, the reference state evolves with time.

This has implications. For instance, consider the parameters within $\mathcal{S}\cap \mathcal{U}$. If these change with increasing time, such as to enter a parameter space region where the reference state was previously unstable to homogeneous perturbations, then these parameters should be excluded from the Turing space. This is because a system starting with these parameter values would not remain near the homogeneous steady state to be ready to be primed for a Turing instability at a later time. Analogous comments also apply as points leave $\mathcal{S}\cap \mathcal{U}$ with increasing time in that parameter values that are in the Turing space at earlier time will have had the opportunity to induce an instability at an earlier time; the fact this is no longer the case for intervals at larger times does not prevent an instability. Hence, the conditions for a parameter space point to be in the Turing space are in fact relatively complex, but still can be determined. In particular, a Turing instability occurs for the first time, at t=t₁>t₀ on

$$\{\underset{\begin{array}{c}\text{stability w.r.t. homogeneous}\\ \text{perturbations always}\end{array}}{\underbrace{\left[\bigcap _{t\in [t_0,t_1]}\overline{\mathcal{S}(t_0,t)}\right]}}\cap [\underset{\begin{array}{c}\text{instability}\\ \text{at time }{t}_1\end{array}}{\underbrace{\overline{\mathcal{U}(t_0,t_1)}}}\setminus \underset{\begin{array}{c}\text{but not unstable}\\ \text{at any earlier time }\\ t>t_0\end{array}}{\underbrace{\bigcup _{t\in (t_0,t_1)}\mathcal{U}(t_0,t)}}]\}\backslash \underset{\begin{array}{c}\text{assuming not}\\ \text{destabilized via}\\ \text{DDI at }{t}_1=t_0\end{array}}{\underbrace{[\overline{\mathcal{S}(t_0,t_0)}\cup \overline{\mathcal{U}(t_0,t_0)}]}}.$$

Hence the Turing space is given by ${\mathcal{T}}^{\mathrm{o}}(t_0,t_1)$, defined to be the opening of the set

$$\mathcal{T}(t_0,t_1):=\underset{\begin{array}{c}\text{DDI occurs at }t=t_0\end{array}}{\underbrace{[\overline{\mathcal{S}(t_0,t_0)}\cap \overline{\mathcal{U}(t_0,t_0)}]}}\cup \left\{\bigcup _{s\in (t_0,t_1]}\underset{\begin{array}{c}\text{Turing instability for first time at }t=s\\ \text{neglecting the subset where in fact DDI occurs at }t=t_0\end{array}}{\underbrace{[\left(\bigcap _{t\in [t_0,s]}\overline{\mathcal{S}(t_0,t)}\right)\cap \left(\overline{\mathcal{U}(t_0,s)}\backslash \hspace{0.17em}\bigcup _{t\in [t_0,s]}\mathcal{U}(t_0,t)\right)]}}\right\}.$$ 2.6

Note that the above expression may simplify extensively; for instance, when the history dependence of $\mathcal{S}$ is such that $\mathcal{S}(t_0,t_1)$ only ever accumulates points as t₁ increases, then $\bigcap _{t\in (0,t_1)}\overline{\mathcal{S}(t_0,t)}=\overline{\mathcal{S}(t_0,t_0)}$. An even greater simplification occurs if the history of $\mathcal{U}$ is such that $\mathcal{U}(t_0,t_1)$ only ever loses points as time increases, with its boundary never unchanged but always shrinking. Then

$$\overline{\mathcal{U}(t_0,s)}\backslash \hspace{0.17em}\bigcup _{t\in [t_0,s]}\mathcal{U}(t_0,t)$$

is empty and the Turing space simplifies to the initial Turing space,

$$\mathcal{S}(t_0,t_0)\cap \mathcal{U}(t_0,t_0).$$ 2.7

More generally, by accommodating the history of the system within the stability conditions, one sees that the instability conditions are fundamentally more complex than originally presented by Madzvamuse et al. [28], highlighting that the impact of domain growth may be more complicated than previously thought.

3. Results I: slowly growing domains

(a). Schnakenberg kinetics

First of all, consider figure 2 where there are plots of the Turing space for the Schnakenberg system, as given by the non-dimensionalization of equations (2.1) and (2.3). In more detail, the figure shows the set of non-dimensional Schnakenberg kinetic parameters (a,b) for which the Turing instability is possible during the time period considered given. Note that use of the initial conditions stipulated in §2b (and also given in section 4.2.1 of Madzvamuse et al. [28]) is implicitly assumed.

Figure 2.

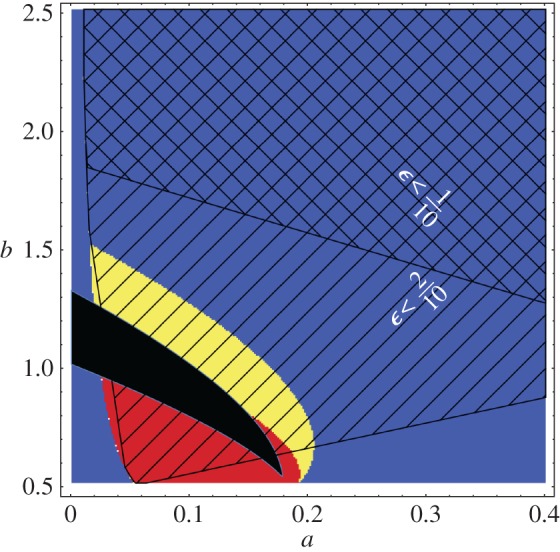
A reconstruction of fig. 1 from [28] for the Schnakenberg model, though for a one-dimensional domain rather than a two-dimensional domain, with zero flux boundary conditions. All non-dimensional kinetic parameters are unity apart from the non-dimensional production rates a,b, which are varied along the axes. In addition, we have taken d=10 and γ=1 (with the latter consistent with multicellular scales L₀=5×10⁻³ cm and $L_0^2/D_u=250\hspace{0.17em}\mathrm{s}$). The initial conditions for these plots are specified in §2b, as also used in Madzvamuse et al. [28]. In black, is a plot of the adiabatic Turing space that is the set of (a,b) parameter values for which a diffusively driven Turing instability can occur, given the adiabatic approximation, whereby the domain length is treated as constant and here equal to 5×10⁻³ cm. The Turing space for an exponentially growing domain φ(t)=e^rt, where r=0.08, and with the same parameter values for d,L₀,γ as in the adiabatic case, is plotted in yellow, according the Turing conditions presented in [28]. Note that $\mathcal{S}(t_0,t)$ (plotted in blue and yellow), $\mathcal{U}(t_0,t)$ (plotted in red and yellow) are time independent for the exponential case. Hence the Turing space, ${\mathcal{T}}^{\mathrm{o}}(t_0,t_1)=\mathcal{S}(t_0,t_1)\cap \mathcal{U}(t_0,t_1)$, is also the same for all t₀,t₁, and given by the yellow region above. We highlight (i) the region of small $ϵ=T_{\mathrm{dyn}}/T_{\mathrm{gr}}<\frac{1}{10}$ using black diagonal lines with negative gradient and (ii) the region of $ϵ=T_{\mathrm{dyn}}/T_{\mathrm{gr}}<\frac{2}{10}$ using black diagonal lines with positive gradient as indicated with the white text. Note that the region of validity of the estimates used [28] requires ϵ≪1 so that the prediction of the location of the Turing space in this example also relies on applying the analysis of [28] in regions where the asymptotic accuracy of the results are breaking down. Yellow online is white in print, red is grey and black remains black. (Online version in colour.)

The adiabatic approximation for the Turing space is plotted in black, and the Turing space for exponential growth with φ(t)=e^rt and r=T⁻¹_gr=0.08 is given in yellow, according to the conditions derived in [28]. There are also different patterns of black diagonal lines demarking regions where ϵ is bounded by 0.1,0.2; in particular, since T_dyn depends on the kinetics, the timescale ratio ϵ varies with (a,b). One can also clearly observe that the requirement of slow growth is relatively constraining even though the growth rate is nominally small. Hence, caution is required with regard to whether the slow growth constraint is satisfied in general, though all results below do ensure this constraint is satisfied or highlight where it is invalid.

For the Schnakenberg model, we proceed to explicitly illustrate the non-trivial dependence of $\mathcal{U}(t_0,t_1)$, and hence the Turing space, on the final time at which stability is considered, t₁, and the start time, t₀ or equivalently, the initial domain length L₀. Hence, here only, time is non-dimensionalized using [5×10⁻³ cm]²/D_u rather than $L_0^2/D_u$ and length is non-dimensionalized by 5×10⁻³ cm rather than L₀ so that physical time and length correspond to the same non-dimensional time and length on comparing results with different initial domain lengths.

Then figure 3 illustrates whether the system is stable or unstable according to criterion (2.5) for variations in the final time and initial domain length, with further parameter values fixed, as detailed in the figure legend. In short, the initial domain size L₀ enters the conditions on the Turing space via the rescaling of model parameters as indicated above. One can clearly see the non-trivial behaviour of the stability region. For instance, this is illustrated by the switching between instability and stability, and then back again, on increasing the final time t₁ for an initial domain size of L₀=7×10⁻³ cm. In particular, this may be understood via figure 1, and explicitly highlights the increase in complexity in understanding the Turing instability in the absence of the adiabatic approximation and also for increases in the time interval over which stability is considered.

Figure 3.

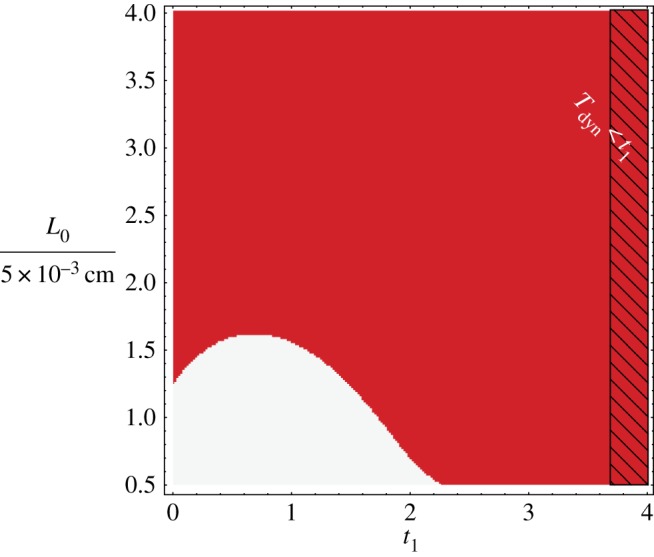
Times for this figure are always non-dimensionalized using (5× 10⁻³ cm)²/D_u, with D_u=10⁻⁷ cm² s⁻¹. The figure illustrates the non-trivial dependence of the instability set $\mathcal{U}(t_0,t_1)$ and hence the Turing space on the non-dimensional final time, t₁, and initial domain length L₀ for the Schnakenberg model, as given by the non-dimensionalization of equations (2.3) and (2.1) on a one-dimensional spatial domain. Domain growth is linear, with φ=1+rt and $r=\frac{1}{40}$, while other non-dimensional parameter values are $a=\frac{24}{100},b=\frac{8}{10}$, d=20,γ=1. In particular, the system is unstable according to criterion (2.5) for values of t₁ and L₀ which are plotted in red and stable otherwise. However, the analysis also requires (i) ϵ=T_dyn/T_gr≪1, which is always satisfied in the plotted range, with ϵ≈0.05, and (ii) t₁<T_dyn=1/[γ|ℜλ*|] and where this is not satisfied is highlighted using black diagonal lines with negative gradient as indicated with the white text. Hence the plotted results are generally within regions where the system satisfies the constraints required for the accuracy of the DDI conditions from Madzvamuse et al. [28]. Note that as domain growth is linear, one needs to solve the ODE system (2.4) to obtain u_s(t). The initial condition is the root of the kinetics ${\mathbf{\text{u}}}_s^0={\mathbf{\text{u}}}^{\ast }$, which is dependent on the parameter values and hence varying throughout the parameter space. Further details can be found in §2b and §4b(ii) of [28]. Red online is black in print and white is light grey. (Online version in colour.)

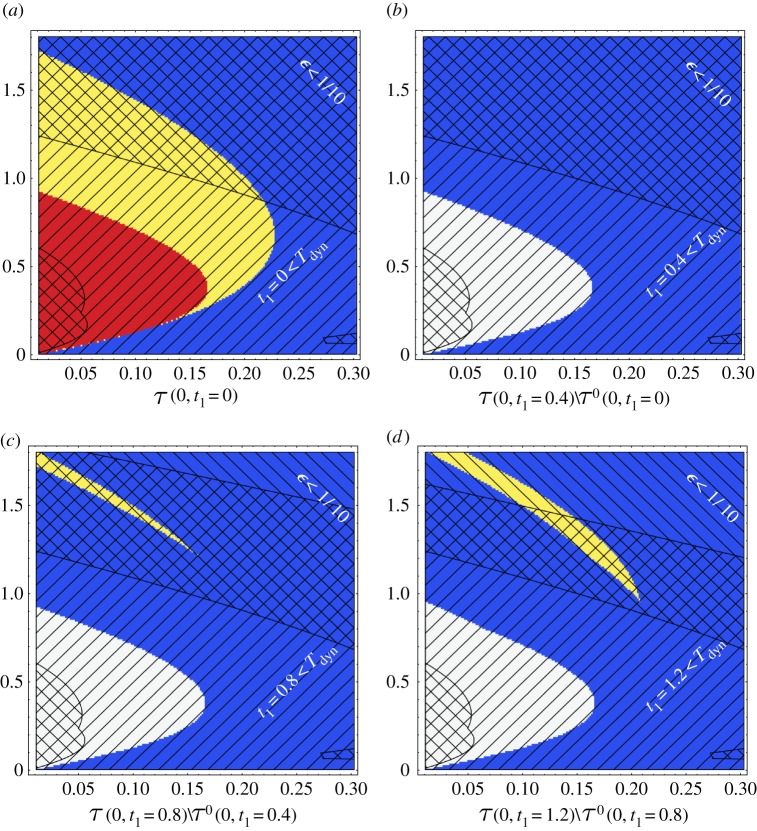
In figure 4, the evolution of the Turing space is considered in detail with an initial time of t₀=0 and a number of final times t₁∈{0,0.4,0.8,1.2} given linear growth, with other parameters given in the figure legend.

Figure 4.

The Turing space for the Schnakenberg model, given by the non-dimensionalization of equations (2.1) and (2.3). All non-dimensional kinetic parameters are unity apart from the non-dimensional production rates a,b which are varied along the axes. In addition, we have taken d=20 and γ=1 (with the latter consistent with multicellular scales L₀=5×10⁻³ cm and $L_0^2/D_u=250\hspace{0.17em}\mathrm{s}$). The initial condition is given by u_s(0)=u* and linear growth, φ(t)=1+rt is imposed, with $r=\frac{1}{20}$ and hence the same procedure for obtaining the reference state u_s(t) is used as described in caption of figure 3. In all plots, the horizontal and vertical axes, respectively, give values for a, b. We also have t₀=0, t₁=0.4n and n=0,1,2,3 for plot (a)–(d), respectively, and again as before the blue and yellow region in each plot gives $\mathcal{S}(t_0,t_1=0.4n)$. (a) Additionally, $\mathcal{U}(t_0,t_0)$ is given in red and yellow. Hence the intersection $\mathcal{S}(t_0,t_0)\cap \mathcal{U}(t_0,t_0)$ is yellow and this is also the initial Turing space. (b)–(d) By contrast, here the yellow region is defined to be (the closure of) the set difference of the instability regions $\mathcal{U}(t_0,t_1=0.4n)\setminus \mathcal{U}(t_0,t_1=0.4(n-1))$. Hence the yellow region is the set difference of the Turing regions $\mathcal{T}(t_0,t_1=0.4n)\setminus {\mathcal{T}}^{\mathrm{o}}(t_0,t_1=0.4(n-1))$, noting equation (2.6). The white regions in these plots are the exclusion of the blue and yellow regions. By standard set manipulations, and with a final set opening, the Turing space at time t₁=0.4n is the union of the initial Turing space with all the prior set differences of Turing regions up to, and including t₁=0.4n. To consider the region of validity for $\mathcal{S},\mathcal{U}$ we highlight (i) the region of small ϵ=T_dyn/T_gr using black diagonal lines with negative gradient and (ii) the region of validity for the mid-point approximation, where t₁<T_dyn, using black diagonal lines with positive gradient as indicated with the white text. Therefore, the analytical insight will be within its region of validity in the intersection of these two regions, which is hashed in the plots. Red online is dark grey in print (R), yellow is light grey (Y), blue is black (B) and white remains white (W). (Online version in colour.)

Firstly, in figure 4a, the blue and yellow regions are defined to be $\mathcal{S}(t_0,t_1)$ with t₁=t₀=0 and thus is where the homogeneous solution is initially stable in the absence of diffusion. Analogously, the region where the homogeneous solution is initially unstable in the presence of diffusion, $\mathcal{U}(t_0,t_0)$, is plotted in red and yellow with the overlap of these regions in yellow. Thus up to a final set opening, the yellow region is the initial Turing space, ${\mathcal{T}}^{\mathrm{o}}(t_0,t_0)$.

With n=1,2,3 for plots (b),(c),(d), respectively, the blue and yellow regions in these plots corresponds to $\mathcal{S}(t_0,t_0+0.4n)$. By contrast though, the yellow region in these plots is the closure of the incremental instability space

$$\mathcal{U}(t_0,t_0+0.4n)\setminus \mathcal{U}(t_0,t_0+0.4(n-1)),$$

with the exclusion of these blue and yellow regions given by white. In particular, the yellow region is thus the incremental Turing space,

$$\mathcal{T}(t_0,t_0+0.4n)\setminus {\mathcal{T}}^{\mathrm{o}}(t_0,t_0+0.4(n-1)).$$

Hence ${\mathcal{T}}^{\mathrm{o}}(t_0=0,t_1=1.2)$, the Turing space at t₁=1.2, is given by the opening of $\mathcal{T}(t_0=0,t_1=1.2)$, in turn given by the union of $\mathcal{T}(t_0,t_0)$ with the union of all incremental Turing spaces,

$$\bigcup _{n=1,2,3}\mathcal{T}(t_0,t_0+0.4n)\setminus {\mathcal{T}}^{\mathrm{o}}(t_0,t_0+0.4(n-1)),$$

that is the union of yellow regions in plots (a)–(d). Analogous remarks also apply for t₁=0.4,0.8. However, the region of validity of the stability analysis within parameter space is also restricted by the constraints required to ensure the accuracy of the expressions for $\mathcal{S}(t_0,t_1)$ and $\mathcal{U}(t_0,t_1)$ in §2e, as highlighted by the black diagonal lines in figure 4.

Nonetheless, one can still clearly observe that for earlier times, t₁≤0.4, there is no change in the Turing space. This is because $\mathcal{U}(t_0,0.4)\subset \mathcal{U}(t_0,t_0)$ and hence no point that corresponds to a stable dynamical system at initial time subsequently destabilizes to spatially heterogeneous perturbations. However, for subsequent times the Turing space expands even if one is restricted to the hashed region to ensure the accuracy of $\mathcal{S}(t_0,t_1)$ and $\mathcal{U}(t_0,t_1)$. These observations illustrate the complexity of Turing space evolution, which cannot be estimated either from the adiabatic approach or from the DDI conditions identified by Madzvamuse et al. [28] applied at single point in time. Finally, the changes in the stability and instability regions, which determine the temporal evolution of the Turing space, occur between t₁=0 and t₁=1.2; this corresponds to only a 6% increase in domain size, so that the history dependence should be considered to understand the prospect of a Turing instability even for small changes in the domain.

(b). Gierer–Meinhardt kinetics

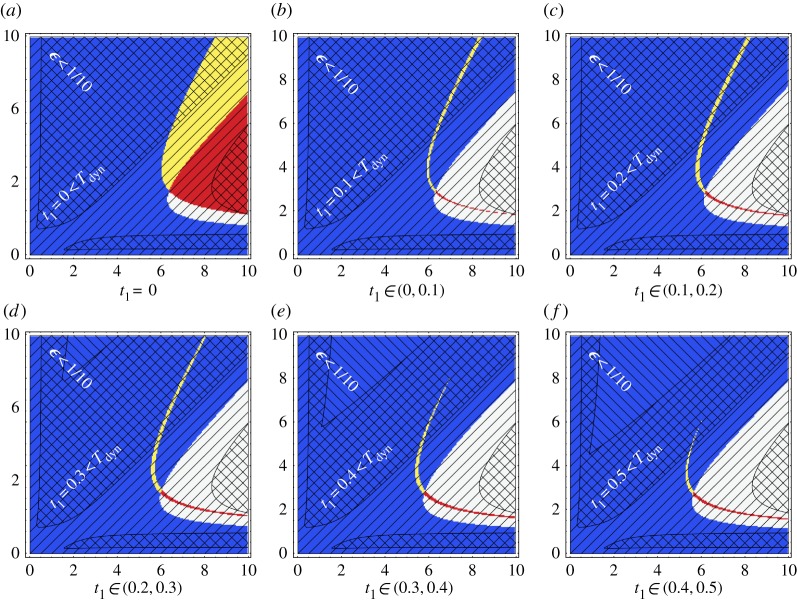
We proceed to examine a set of pure kinetics, via the non-dimensionalization of the Gierer–Meinhardt model given by equations (2.2) and (2.3), considering again linear growth with $r=\frac{1}{10}$. The resulting Turing spaces for Gierer–Meinhardt kinetics are illustrated in figure 5 for ρ₁=ρ₂=ρ₃=1, d=10, γ=1, which are consistent with the physical scales $L_0^2/D_u=250\hspace{0.17em}\mathrm{s}$, L₀=5×10⁻³ cm, and the non-dimensional parameters μ_u and μ_v are varied extensively along the axes.

Figure 5.

Stability regions for the Gierer–Meinhardt model, as defined by the non-dimensionalization of equations (2.2) and (2.3), with parameter values d=10,ρ₁=ρ₂=ρ₃=γ=1, which are consistent with the physical scales $\hspace{0.17em}{L}_0^2/D_u=250s,\hspace{0.17em}{L}_0=5\times {10}^{-3}\hspace{0.17em}\mathrm{cm}$. Once more we have the initial condition is given by u_s(0)=u* with linear growth, φ(t)=1+rt where $r=\frac{1}{10}$. Finally, the horizontal axis in the above plots gives values of the non-dimensional kinetic parameter μ_u and similarly μ_v is given on the vertical axis. The meaning of the black diagonal lines is the same as in figure 4, as indicated by the text in white and thus the region of analytical validity is hashed. The red, white, blue and yellow regions for plot (a) are defined in exactly the same way, in terms of the stability region, $\mathcal{S}(t_0,t_0)$ and the instability region $\mathcal{U}(t_0,t_0)$, as the coloured regions in figure 4a. For plots (b) onwards the colours are analogous, but with the yellow and red regions corresponding to the set difference of the instability regions $\mathcal{U}(t_0,t_1=0.4n)\setminus \mathcal{U}(t_0,t_1=0.4(n-1))$. The yellow contribution intersects the stability region $\mathcal{S}(t_0,t_1=0.4n)$, whereas the red contribution is excluded from the stability region—the red region was an empty set in figure 4. Finally, white is the exclusion of all the other coloured regions. Note that n=1,2,3,4,5, respectively, for plots (b)–(f), with t₁=0.1n, in this figure. Thus, for instance, one can observe the evolution of Turing space for the Gierer–Meinhardt model via the yellow set differences of Turing regions in plots (b)–(f). Red online is dark grey in print (R), yellow is light grey (Y), blue is black (B) and white remains white (W). (Online version in colour.)

In plot figure 5a, we have the region of (μ_u,μ_v) parameter space associated with the stability region, $\mathcal{S}(t_0,t_0)$, plotted in blue and yellow, while the instability region, $\mathcal{U}(t_0,t_0)$, is plotted in red and yellow, with the intersection in yellow and corresponding to the initial Turing space. Analogously, the exclusion is in white. In contrast in later plots (b)–(f), and analogously to figure 4, the yellow region in each plot denotes the incremental Turing space,

$$\mathcal{T}(t_0,t_0+0.1n)\setminus {\mathcal{T}}^{\mathrm{o}}(t_0,t_0+0.1(n-1)),$$

where n=1 for plot (b), n=2 for plot (c) and similarly for plots (d)–(f).

Thus, for instance, ${\mathcal{T}}^{\mathrm{o}}(t_0=0,t_1=0.5)$, the Turing space at t₁=0.5, is given by the opening of $\mathcal{T}(t_0=0,t_1=0.5)$, in turn given by the union of yellow regions in figure 5a–f. Note however that the region of validity is restricted to the hashing in figure 5, analogously to figure 4. Once more, there is a clear history dependence complexity to the Turing space.

4. Results II: examples of the two species Turing model with faster domain growth

We proceed to relax the requirement of slow growth, and do not consider a mid-point approximation, so that the above analysis no longer applies.² The resulting dynamics is more complex again and to facilitate analytical understanding we restrict ourselves to specific linear kinetics and uniform exponential domain growth at a rate r so that h(t)=r is const. In particular, this removes the temporal drift of the stability and instability regions. Thus, in non-dimensional Lagrangian coordinates (2.3), and with D=dD_v=D_u/μ² we consider

$$\begin{array}{rl}{\mathrm{\partial }}_t\left(\begin{array}{c}u\\ v\end{array}\right)+r\left(\begin{array}{c}u\\ v\end{array}\right)& =e^{-2rt}D\left(\begin{array}{cc}{\mu }^2& 0\\ 0& 1\end{array}\right){\mathrm{\partial }}_{xx}\left(\begin{array}{c}u\\ v\end{array}\right)+\left(\begin{array}{c}{c}_u\\ c_v\end{array}\right)+\mathbf{\text{J}}\left(\begin{array}{c}u\\ v\end{array}\right)\text{for}\hspace{0.17em}x\in (0,1),\\ {\mathrm{\partial }}_x\left(\begin{array}{c}u\\ v\end{array}\right)& =\left(\begin{array}{c}0\\ 0\end{array}\right)\text{at }x=0,1,\end{array}$$

where c_u and c_v are constants and the Eulerian domain length stretches in time as φ(t)=e^rt.

With J invertible, so that a steady state exists in the absence of growth, the solution of the homogeneous case for the initial condition (u₀,v₀)^T is given by

$${\mathbf{\text{u}}}_s=\left(\begin{array}{c}{u}_s\\ v_s\end{array}\right)={\mathbf{\text{J}}}_r^{-1}\left(\begin{array}{c}{c}_u\\ c_v\end{array}\right)+\exp ({\mathbf{\text{J}}}_{r}t).[\left(\begin{array}{c}{u}_0\\ v_0\end{array}\right)-{\mathbf{\text{J}}}_r^{-1}\left(\begin{array}{c}{c}_u\\ c_v\end{array}\right)],$$

where J_r=J−rI. Furthermore, J is also chosen so that the homogeneous solution u_s=(u_s,v_s)^T does not blow up with time; as the system is linear this also automatically ensures that u_s, the reference state about which we perturb, is stable with respect to homogeneous perturbations.

To study the time evolution of inhomogeneous perturbations, let us consider each mode separately

$$\left(\begin{array}{c}P\\ Q\end{array}\right)=\left(\begin{array}{c}p(t)\\ q(t)\end{array}\right)\cos (kx),\text{where }k=n\pi ,\text{as }{\mathrm{\partial }}_x\left(\begin{array}{c}P\\ Q\end{array}\right)=\left(\begin{array}{c}0\\ 0\end{array}\right)\text{at }x=0,1,$$

due to the existence of orthogonal basis consisting of the eigenfunctions of the diffusion operator with Neumann boundary conditions. Hence we may focus on the amplitude equations for each mode

$${\mathrm{\partial }}_t\left(\begin{array}{c}p\\ q\end{array}\right)=e^{-2rt}\mathbf{\text{M}}\left(\begin{array}{c}p\\ q\end{array}\right)+{\mathbf{\text{J}}}_r\left(\begin{array}{c}p\\ q\end{array}\right)\text{with}\hspace{0.17em}\mathbf{\text{M}}=\left(\begin{array}{cc}-{\mu }^2{k}^{2}D& 0\\ 0& -k^{2}D\end{array}\right).$$

Defining $F(t)={\int }_0^t\mathrm{d}s{(\phi (s))}^{-2}=(1/2r)(1-e^{-2rt})$, let

$$\left(\begin{array}{c}a\\ b\end{array}\right)=\exp [-F(t)\mathbf{\text{M}}]\left(\begin{array}{c}p\\ q\end{array}\right).$$

As, component-wise,

$$\left(\begin{array}{c}a\\ b\end{array}\right)\ge \left(\begin{array}{c}p\\ q\end{array}\right)\ge \left(\begin{array}{cc}\exp (-{\mu }^2{k}^{2}D\frac{1}{2r})& 0\\ 0& \exp (-k^{2}D\frac{1}{2r})\end{array}\right).\left(\begin{array}{c}a\\ b\end{array}\right)$$

we have that (p,q)^T decays if and only if (a,b)^T decays. Further, the evolution equation for (a,b) is

$$\begin{array}{rl}{\mathrm{\partial }}_t\left(\begin{array}{c}a\\ b\end{array}\right)& =\exp [-F(t)\mathbf{\text{M}}].{\mathbf{\text{J}}}_r.\exp [F(t)\mathbf{\text{M}}].\left(\begin{array}{c}a\\ b\end{array}\right)\\ & =\left(\begin{array}{cc}{J}_{11}-r& J_{12}\exp [({\mu }^2-1){\kappa }^2(t))]\\ J_{21}\exp [(1-{\mu }^2){\kappa }^2(t))]& J_{22}-r\end{array}\right).\left(\begin{array}{c}a\\ b\end{array}\right),\end{array}$$ 4.1

where κ²(t)=k²DF(t) and J₁₁,J₁₂,J₂₁,J₂₂ are the components of J. This coupled system of the first-order linear differential equations with two initial conditions can be equivalently rewritten as a second-order uncoupled equation for a via

$${\mathrm{\partial }}_t^{2}a=(\hspace{0.17em}{J}_{11}-r){\mathrm{\partial }}_{t}a+J_{12}{J}_{21}a[({\mu }^2-1)k^{2}D{(\phi (t))}^{-2}+(\hspace{0.17em}{J}_{22}-r)]({\mathrm{\partial }}_{t}a-(\hspace{0.17em}{J}_{11}-r)a),$$ 4.2

with b given in terms of a and its time derivative, using the first equation of (4.1).

Instead of using special functions to express the general solution, we use the reduction of order form

$$a(t)=a_0(t)(C_1+{\int }_0^t\mathrm{d}sv(s))\mathrm{and}v(t)=C_2\frac{1}{a_0{(t)}^2}\exp (-{\int }_0^t\mathrm{d}s{(\phi (s))}^{-2}),$$ 4.3

where a₀(t) is a particular solution of the second-order equation (4.2) and C₁,C₂ are integration constants. In turn, these can be identified by a particular choice of initial data. We choose C₁=1/a₀(0) so that perturbations initiate from 1.

First note that both the trace and determinant of the matrix governing the time evolution of a,b, via equation (4.1), are constant and equal to the trace and determinant of J_r. Hence, as we required above that the reference state u_s is stable with respect to homogeneous perturbations, we have that for large enough time, t, perturbations (a,b)^T decay. In the classical autonomous case, this would be sufficient to imply the solution decayed for all previous times but we shall show that in the non-autonomous case the instability can instead be triggered at earlier times.

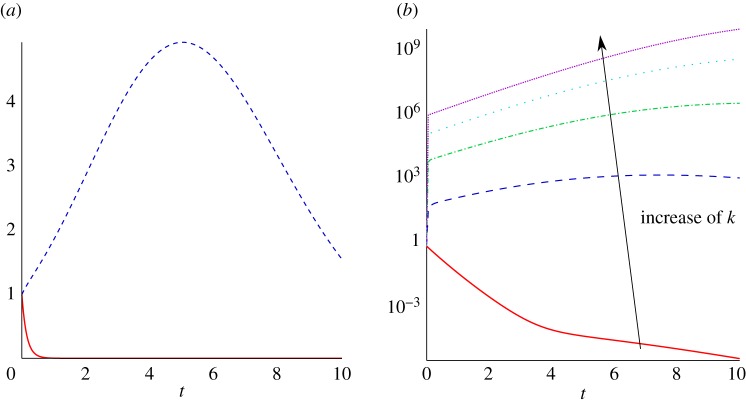
Consider the particular choice of $r=\frac{1}{2},\hspace{0.17em}\mu =\frac{1}{10}$, $D=\frac{100}{99}$ and

$$\mathbf{\text{J}}=\left(\begin{array}{cc}\frac{3}{2}& -2\\ 3& -\frac{7}{2}\end{array}\right),$$

and hence ϵ=T_dyn/T_gr=1. Then a particular solution is

$$a_0(t)=\exp [-3t+e^{-t}{k}^2]k^2+2\exp [-2t+e^{-t}{k}^2]$$

and the general solution reads

$$a(t)=a_0(t)(\frac{e^{-k^2}}{k^2+2}+C_2{\int }_0^t\mathrm{d}s\frac{\exp (-k^2{e}^{-s}+s)}{k^2{(k^2{e}^{-s}+2)}^2}).$$

It is instructive to expand the solution about t=0

$$a(t)\approx 1+t\frac{C_2-k^6-5k^4-4k^2}{(k^2+2)k^2}+O(t^2)$$

to see that first few modes of the perturbations grow initially even though they later decay. The actual solution for C₂=0 (solid line) and C₂=10³ with k=2 (dashed line) is shown in figure 6. Since the prospect of growth at intermediate time depends on the value of C₂, transient growth can be both very large or absent, depending on the initial data. Hence the initiation of an instability can take place in this example even though the large time behaviour would suggest stability. Furthermore, the prospect of an instability is sensitive to the initial noise and, if this system was an approximation to one with additional nonlinear terms that were small near the reference state, there may be sensitivity to the size of the nonlinear terms as these would determine whether the transient growth initiated further nonlinear dynamics.

Figure 6.

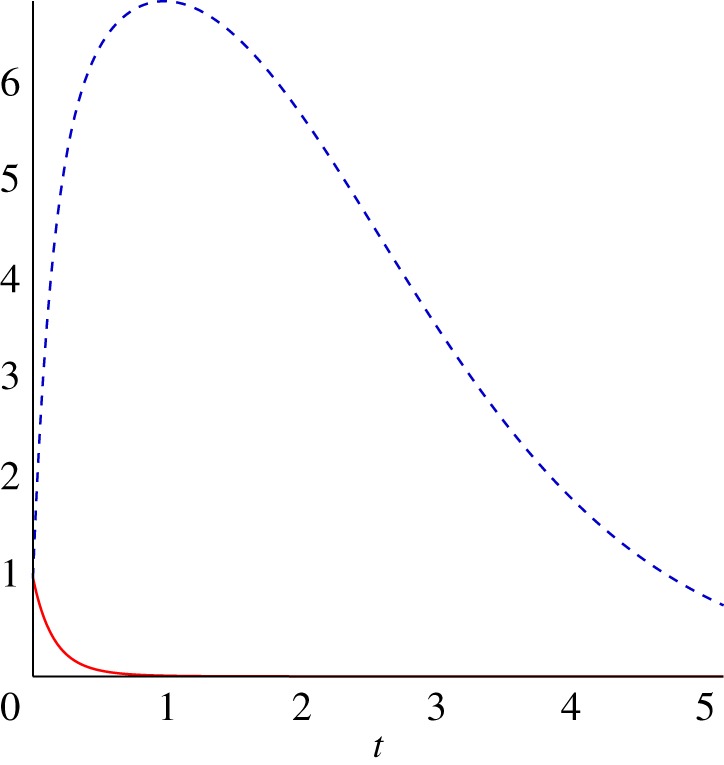
Two solutions of the linear kinetics system with $r=\frac{1}{2},\mu =\frac{1}{10}$, $D=\frac{100}{99}$ with C₂=0 (solid line) and C₂=10³ with k=2 (dashed line). (Online version in colour.)

Finally, let us consider the same system except now with a growth rate $r=\frac{1}{6}$ and, as a result, $ϵ=\frac{1}{3}$. A particular solution is

$$\begin{array}{rl}{a}_0(t)& =\exp [3k^2{e}^{-(1/3)t}](81k^{10}{e}^{-(10/3)t}+1080k^8{e}^{-3t}\\ & +5040k^6{e}^{-(8/3)t}+10080k^4{e}^{-(7/3)t}+8400k^2{e}^{-2t}+2240e^{-(5/3)t}),\end{array}$$

and the general solution reads

$$\begin{array}{rl}a(t)& =a_0(t)(\frac{1}{a_0(0)}\\ & +C_2{\int }_0^t\mathrm{d}s\frac{{81}^2{k}^{20}\exp [-3k^2{e}^{-(1/3)s}]e^s}{{(81k^{10}{e}^{-(5/3)s}+1080k^8{e}^{-(4/3)s}+5040k^6{e}^{-s}+10080k^4{e}^{-(2/3)s}+8400k^2{e}^{-(1/3)s}+2240)}^2}),\end{array}$$

For t∼O(1) or less and k≫1 sufficiently large, we have $a_0(t)\approx 81k^{10}{e}^{-(10/3)t}\exp [3k^2{e}^{-(1/3)t}]$ and hence the term proportional to C₂, denoted C_*, is approximately

$$\begin{array}{rl}{C}_{\ast }& \approx 81C_2{k}^{10}{e}^{-(10/3)t}\exp [3k^2{e}^{-(1/3)t}]{\int }_0^t\mathrm{d}s\exp [-3k^2{e}^{-(1/3)s}]e^{(13/3)s}\\ & =81C_2{k}^{10}{e}^{-(10/3)t}{e}^{(1/\delta )g(t)}{\int }_0^t\mathrm{d}s{e}^{-(1/\delta )g(s)}{e}^{(13/3)s}\end{array}$$

with δ=1/[3k²]≪1 and g(t)=e^−t/3 and higher order corrections down by O(δ). Once t≫δ one can apply Laplace’s method to the integral on the right and thus, except for very small time, we have to leading order in δ for t up to order unity that

$$C_{\ast }\approx 81C_2{k}^{10}{e}^t{e}^{t{g}^{\prime }(t)/\delta }{\int }_0^t\mathrm{d}s{e}^{-s{g}^{\prime }(t)/\delta }\approx 81C_2{k}^8{e}^{4t/3}.$$

From this leading order approximation, one can nonetheless observe modes with C₂≠0 will grow for order unity time, at least providing the wavenumber is large enough to ensure asymptotic corrections are insignificant in the above. This is indicated in figure 7a,b which also highlights that the transient growth becomes more extensive as k increases. Hence, there is a total breakdown of the continuum description for general initial conditions as modes of arbitrarily high wavenumber modes are excited, leading to the growth of fluctuations on smaller scales than that of an individual and thus a loss of self-consistency of the modelling assumptions.³

Figure 7.

(a) Two solutions of the linear kinetics system with $r=\frac{1}{6}$ with C₂=0 (red solid) and C₂=10⁻³ with k=2 (blue dashed). (b) Three solutions of the linear kinetics system with $r=\frac{1}{6}$ and C₂=10⁻³ for k=1 (red solid), k=3 (dark blue dashed), k=5 (green dashed-dotted), k=7 (light blue dotted) and k=9 (purple densely dotted). (Online version in colour.)

5. Discussion and conclusion

We have further explored the impact of domain growth on the conditions for a diffusively driven instability in traditional Turing models. In particular, the common-place adiabatic approximation, whereby the impact of domain growth is considered only as a bifurcation parameter, rather than an explicitly non-autonomous contribution to the dynamics, yields only incomplete and sometimes misleading information about the conditions for a diffusively driven instability in traditional Turing models. This has been previously highlighted in the asymptotically slow growth limit study of Madzvamuse et al. [28].

This previous study’s analysis however relied on stringent constraints, for instance, a mid-point approximation for the system evolution between the initial time, t₀, and the time when the prospect of stability was considered t₁. Implicitly this requires t₁−t₀∼T_dyn or less, where T_dyn is the timescale of the kinetics. Hence there is only a linear temporal evolution, noting that a slow growth timescale is also enforced. In addition, Madzvamuse et al. [28] did not account for the history of the stability behaviour, which has the potential to induce significantly different approximations even within the confines of slow growth and the validity of the mid-point approximation.

Here, in contrast, within the restrictions of slow growth and the mid-point approximation, we have demonstrated firstly a complex dependence on the initial domain length, as highlighted in figure 3. Furthermore, the history of the stability behaviour needs to be considered and we have given a relatively simple expression for the region of parameter space where a Turing instability occurs, which can be evaluated numerically. This highlights very different predictions for the system behaviour in general, as especially seen in figure 4 for Schnakenberg kinetics. In particular, while the stability behaviour for Gierer–Meinhardt model displayed a full history dependence in the conditions for a Turing instability, the Schnakenberg model shows even more complex behaviour when Turing space is initially not evolving with time only to show the full history dependence at later times.

Hence conditions for the prospect of a Turing instability are much more complicated, differing from both the predictions of the adiabatic approximation and those of the framework developed by Madzvamuse et al. [28]. In particular, a linearization of the system at one point in time is sufficient to deduce the stability conditions for either the adiabatic approximation or the framework of Madzvamuse et al. [28]; instead the history of the system stability is required to predict whether self-organization via the Turing mechanism occurs.

On relaxing the slow growth constraint and the mid-point approximation, one must consider different ways of analysing a Turing system. We proceed by considering special cases for a proof of principle demonstration that the dynamics becomes even more complex, and prediction even more difficult and potentially out of reach in general. In particular, intrinsic growth modes can first substantially grow prior to decay. Hence quasi-asymptotic stability may not be appropriate for studying Turing instabilities for such systems compared to Lyapunov stability. In addition, this growth mode behaviour entails that the prospect of a Turing instability is highly dependent on initial conditions, noise and nonlinear interactions, thus making predictions essentially impossible in general. Furthermore, we have also highlighted that the continuum description itself can be lost since modes of arbitrarily high wavenumber become excited, emphasizing the complexity of the dynamics and the loss of biologically relevant behaviour at higher growth rates. Finally, note that such results emerge from equations that are linear; hence nonlinear terms will not remove this system behaviour as it will be inherited by the linearization of the nonlinear system.

From such observations, it is clear that there is a hierarchy, increasing in system behaviour complexity with increases in the ratio of the growth to kinetic timescales, ϵ=T_gr/T_dyn. There is essentially no doubt that the adiabatic approximation is reasonable for ϵ sufficiently small. For instance, this is numerically illustrated in Crampin et al. [25], which also reported numerical observations of a breakdown of adiabatic behaviours for the Schnakenberg model with growth rates approaching two orders of magnitude of the scale of the kinetic rates. However as ϵ increases, non-adiabatic effects do manifest as shown by Madzvamuse et al. [28]. The non-adiabatic conditions for a Turing instability presented in the latter study are refined here to accommodate the evolution of the system stability properties, which can change on the dynamic timescale. Hence changes in the system stability properties can have a significant impact on predictions for a Turing instability even over the course of a relatively small increase in domain size due to growth, as we have observed. However, this framework, including the midpoint approximation, relies on the neglect of O(ϵ²) terms [28] and thus eventually breaks down as ϵ is increased. This stage is referred to as faster growth in the text and new phenomena emerge. These include the breakdown of the continuum approximation, which can be observed once T_gr is within an order of magnitude of T_dyn in the presented cases. However, the quantitative and model-dependent details of the values of ϵ where this hierarchy of behaviours transitions with increasing ϵ is beyond the scope of this proof of principle study, though merits further investigation in assessing the validity of the adiabatic approximation in any specific application.

In terms of interpreting these results in the context of development, note that for domain growth driven by cell proliferation the growth timescale, T_gr, corresponds to the cell doubling time of 24 h or more [35]. Furthermore, studies showing mRNA via in situ hybridization for candidate Turing systems [36] emphasizes that the timescale of transcription and translation should be used for the dynamics. For small proteins, this gives $T_{\mathrm{dyn}}\sim 10\hspace{0.17em}min$ [37] and hence ϵ<0.01. This suggests the validity of the adiabatic approximation for the Schnakenberg model under such circumstances, noting the above-mentioned observations of Crampin [25]. However, for larger proteins, T_dyn can be up to a few hours due to protein production timescales [37] and non-adiabatic corrections may become apparent. Furthermore, during epiboly in developmental gastrulation, local cell velocities of about 1μm min⁻¹, or one cell length every 20 min, are reported [38]. This constitutes a domain rearrangement timescale of about 20 min, and thus one has the parameter regime where any putative Turing mechanism would be plagued by extensive non-adiabatic dynamics or may not be feasible. In turn, this suggests that the Turing mechanism may not be sufficiently robust to be present concomitantly with the magnitude of the domain velocity fields arising during developmental events such as gastrulation.

In summary, we have demonstrated that the conditions for stability or instability of Turing systems on growing domains are more complex than predicted by adiabatic approximations and even the first correction in the slow growth approximation. In particular, this study has emphasized the history dependence of the stability conditions and the transient nature of the unstable modes with faster growth. Thus, we have illustrated the limitations in using the adiabatic approximation and even slow growth asymptotics and, in particular, that there is a much richer dynamics in the transition to self-organization in Turing systems for slowly growing systems. Furthermore on faster growing domains, there can be a complete breakdown, with even the continuum approximation failing, highlighting the complex behaviour associated with the interaction of domain growth with reaction and diffusion dynamics.

Data accessibility

The data in this paper are available from https://doi.org/10.5287/bodleian:o1D411kEO.

Authors' contributions

Both authors equally contributed to the analysis and drafted the manuscript. Both authors gave final approval for publication.

Competing interests

We declare we have no competing interests.

Funding

V.K. would like to thank the Isaac Newton Institute for Mathematical Sciences for its hospitality during the programme Coupling Geometric PDEs with Physics for Cell Morphology, Motility and Pattern Formation supported by EPSRC grant no. EP/K032208/1.