Confidence and certainty: distinct probabilistic quantities for different goals

Abstract

When facing uncertainty, adaptive behavioral strategies demand that the brain performs probabilistic computations. In this probabilistic framework, the notion of certainty and confidence would appear to be closely related, so much so that it is tempting to conclude that these two concepts are one and the same. We argue that there are computational reasons to distinguish between these two concepts. Specifically, we propose that confidence should be defined as the probability that a decision or a proposition, overt or covert, is correct given the evidence, a critical quantity in complex sequential decisions. We suggest that the term certainty should be reserved to refer to the encoding of all other probability distributions over sensory and cognitive variables. We also discuss strategies for studying the neural codes for confidence and certainty and argue that clear definitions of neural codes are essential to understanding the relative contributions of various cortical areas to decision making.

Introduction

William James famously wrote, “Everyone knows what attention is”. Yet cognitive scientists are still struggling to come up with a clear definition of attention. The same might be said of confidence. Just like attention, we all know at least intuitively what confidence is. For instance, when we take an exam, we can feel more of less confident depending on the degree of preparation and prior knowledge, modulated by our personality. But what is this sense of confidence? There have been multiple attempts at defining confidence more precisely, but we still lack a consensual mathematical definition. Such a definition is essential for deepening our understanding of the different types of probabilistic computations underlying behavior and for guiding our search for a neural basis of confidence.

We argue here confidence corresponds to the belief that a choice (for example, choosing the riper of two avocadoes) or a proposition (for example, Nigeria is the most populous country in Africa) is correct based on the available evidence. In most cases, this is indeed the required quantity for solving behavioral tasks that have been designed to probe the level of confidence in humans and animals. Given that confidence is defined as a belief, or probability, over a random variable that can take two values, correct or incorrect, it is a form of certainty. However, this does not mean that certainty reduces to confidence in general. The brain also needs to represent certainty in a decision-independent, but domain-specific, way to enable different estimates of certainty elicited by the same latent variable, such as separate visual and auditory certainties corresponding to the position of the same object. As we will discuss, this domain-specific notion of certainty and the notion of confidence might correspond to different stages of statistical inference in the brain, each with their own computational role in the CNS architecture.

Our focus is on computational principles grounded in probability theory. We do not present an exhaustive review of the literature on confidence, as such reviews are widely available (see refs. 1–3) or discuss algorithmic models based on psychological or neurobiological considerations^4–7. Rather, our goal is to offer a computational and neural coding perspective on confidence in an attempt to clarify what this concept is about and how it differs from the other probabilistic quantities.

The many kinds of uncertainties

Imagine that you are driving your car at night. There are no street lights on the road and your car’s front lights are dim. As you are trying to keep the car on the road you need to determine which direction you and the other traffic are moving. This can be achieved by processing two distinct sensory inputs: the visual flow field created on the retina by your own motion and the vestibular stimulation, which measures acceleration. If the car in front of you suddenly brakes, you have to make a quick decision, based on these sensory inputs, about whether it is better to veer left or right (we are assuming that there are no additional obstacles or cars on either side, in which case the only important question is how to avoid a collision with the car ahead). The best decision requires determining whether your current heading is to the left or right side of the braking car and then to veer in that direction. The noise in the vestibular system as well as the glare of lights and random movement of cars creates uncertainty and, given these sources of stochasticity, you, or rather your brain, cannot know for sure the precise direction of heading.

As this example illustrates, to perform well, the brain needs to be effective at dealing with a daunting array of uncertainties. Some originate in the external world, such as sensory or motor variability, whereas others are internal to the brain and are associated with cognitive variables, timing or abstract states. When dealing with these uncertainties, it is useful to represent current knowledge with probability distributions and update these on the basis of the rules of probabilistic inference—namely Bayes’ theorem⁸. Notably, there is ample experimental evidence that humans and other animals can indeed estimate and employ uncertainty to perform probabilistic inference about sensory, cognitive and motor variables (see ref. ⁹ for a review). In fact, in the particular case of heading direction, humans and animals have been shown to perform near optimally given the uncertainty inherent to the visual and vestibular information^10,11. There is also emerging evidence about how brains implement these uncertainty-based computations in neural circuits⁹.

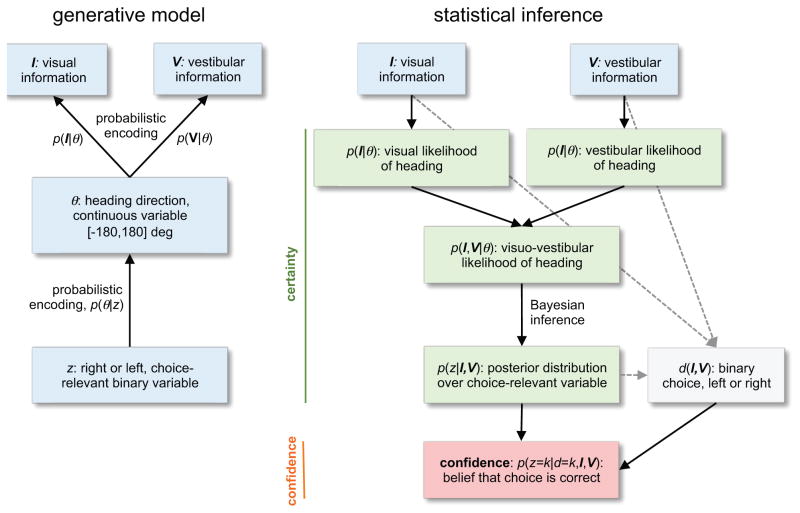
Uncertainty is an intrinsic part of neural computation and there are many varieties of it. However, probability theory, although being the calculus of reasoning with uncertainty data, does not provide us with a clear language for different uncertainty types. Consider, for instance, the multiple forms of uncertainty present in the above example (Fig. 1). To avoid crashing into the car in front of us, the nervous system might infer the current heading direction, denoted by θ, based on the visual information received by the retina, denoted Image. Because of the stochastic and ambiguous nature of visual information, there is not a single value of θ, but an entire distribution p(θ|Image), called the posterior distribution over heading, that is compatible with this information to different degrees (see Box 1 for how these posteriors relate to the likelihoods in Fig. 1). Similarly, we can infer the current heading based on vestibular information, leading to p(θ|Vestib). The width of these posterior distributions specifies the uncertainty associated with inferring the heading direction.

Figure 1.

Confidence and certainty in a visuo-vestibular task. As described in the main text, assume that we are driving in dense traffic and that – based on visual cues, I, and vestibular cues about self-motion, V – we have to decide between veering to the left or right to avoid hitting a car braking in front of us. We determine the best course of action by inverting the generative model (left), which specifies how the choice-relevant latent variable z is assumed to have generated the observations I and V. In our case, z is either right or left, indicating the better direction to veer toward. This z is assumed to stochastically generate a heading direction θ relative to the braking car and compatible with z. The relative heading direction in turn generates the visual and vestibular observations. The generative model is inverted (right) to determine the probability of z = right or z = left given these observations, leading to the posterior distribution p(z|I, V). This posterior can in turn be used to determine the choice d(I, V), which, as the posterior, is a function of the observations. All probability distributions leading up to this choice determine the certainties about various variables involved in the decision-making process. The confidence in this choice, in contrast, is the probability that the choice itself is correct, that is, that the latent state z indeed corresponds to this choice, p(z = k, d = k, I, V). For more details, see Box 1.

Box 1. Computing confidence and certainty in a visuo-vestibular task.

Consider the visuo-vestibular task in which we aim to avoid hitting a car braking ahead of us by veering to the left or right. As illustrated in Figure 1, this problem is approached statistically by inverting a generative model that specifies how likely it is to observe a particular piece of evidence given some choice-related latent state of the world. In our example, the observed evidences are visual and vestibular cues, Iand V, telling us about the location of the braking car and heading direction. The latent state z determines whether it is better to veer to the right or the left of the car given the current heading direction. The generative model links these variables in two steps. First, z is assumed to stochastically generate some heading direction θ relative to the braking car, according to the probability distribution p (θ|z), which conforms to θ < 0° if z = right and θ < 0° otherwise, to enforce consistency between z and θ. Second, the chosen relative heading direction θ generates the visual and vestibular observations, I and V, according to probability distribution p (I|θ) and p (V|θ). These mappings are again stochastic, as many different visual and vestibular observations are, to different degrees, compatible with a given relative heading direction. Together, these distributions fully specify the generative model linking the latent state to the observations. In the main text, we discuss the posteriors, p (θ|I) and p (θ|V), instead of the above likelihoods. According to Bayes rule, these posteriors are proportional to the likelihood multiplied by the prior, p (θ). In this particular instance, the distinction between likelihood and posterior is not critical for the argument.

To infer the latent state z given these observations, I and V, we need to invert the generative model. This inversion is based on the likelihoods of the visual and vestibular information given relative heading, p (I|θ) and p (V|θ). If these likelihoods are independent when conditional on θ, they can be combined into the joint likelihood

$$p(\mathit{I},\mathit{V}\mid \theta )=p(\mathit{I}\mid \theta )p(\mathit{V}\mid \theta )$$

indicating for each θ how likely it is to observe I and V. We can invert this probability by Bayes’ rule

$$p(\theta \mid \mathit{I},\mathit{V})\propto p(\mathit{I},\mathit{V}\mid \theta )p(\theta )$$

returning how likely each relative heading direction is, given the observed evidence. This posterior probability can in turn be used to compute the posterior probability for each latent state z

$$p(z=\text{left}\mid \mathit{I},\mathit{V})=\underset{0°}{\overset{180°}{\int }}p(\theta \mid \mathit{I},\mathit{V})d\theta$$

where we have used the fact that z = left for all θ values from 0° to 180°. An analogous expression returns p (z = right|I, V). This posterior probability is independent of the choice, but can be used to determine the choice. For either choice d, the confidence is the probability that this choice is indeed correct, that is, that choice corresponds to the latent state z. Thus, confidence in our example is the probability p (z = k|d = k, I, V), where k is either left or right, depending on the choice.

To make a decision about whether to veer left or right, we need an intermediate variable, let us call it z, that can take on the values left or right and that corresponds to an abstract state of the world—in this case whether it is best to head right or left of straight ahead to avoid the braking car (Fig. 1). Inferring the likelihood of different values of z requires probabilistic inference to evaluate uncertainty about the state of the world given all sensory evidence, p(z|Image|Vestib). Note that Image and Vestib represent the percept of the sensory evidence, the internal variable available to the decision maker, and not the external data directly. On the basis of this posterior distribution over z, the brain needs to pick a choice that is effectively a function of the visual and vestibular information, d = choice (Image, Vestib). Assuming all other things are equal, the best choice corresponds to the value of z that is more likely in light of the evidence.

Once a choice has been made, overtly or covertly, one can compute the probability that this choice is correct, p(z = k|d = k, Image, Vestib), that is, that z = k if choice d = k is considered (here we could have just as well written p(z = k|Image, Vestib), where k is the current choice, hence our conditioning on d = k, which makes this point more explicit). This last probability distribution is defined over a variable that can take two values, correct (z = k and d = k) or incorrect (z = j and z = k, for all j ≠ k), in reference to a particular, overt or covert, choice d. Thus, it represents the probability that a single hypothesis, H_k, will turn out to be correct, based on the available evidence, p(H_k is correct|choice = H_k, evidence). This stands in contrast to p(z|Image, Vestib), which is a distribution over all possible choices, irrespective of their correctness. The distinction between these two functions is particularly clear for decisions involving more than two choices. For instance, if there are four choices, the variable z can take four possible values and the posterior over z is a function specifying four different probabilities, whereas the probability of being correct given a choice is still defined over two possible states, correct or incorrect. Thus, these two distributions are conceptually and mathematically distinct, a property that will become important once we consider the computational role for either of them.

As just illustrated, these types of decisions involve a number of distinct probability distributions, leading to potential confusion in terminology. Not only is it unclear which of these quantities should be called confidence, but it is just as unclear whether the notions of certainty and confidence are different concepts. In fact, they are often used interchangeably in the literature.

Confidence: definition and computations

We propose that confidence should be used to refer to the probability that a choice is correct, which we denote p(z = k|d = k, Image, Vestib). This definition has a long history in psychophysics^7,12,13 and has been recently used in several studies^14–20. This is also what many authors call confidence^21–27, even if they don’t always formally define it as such. This definition not only applies to decisions, but also to confidence in propositions, or potentially even to aspects of self-confidence. For example, suppose you are asked to express your confidence in the following proposition: “Nigeria is the most populous African country”. This amounts to asking your confidence in choosing this proposition versus “Nigeria is not the most populous African country”. Thus, as for decision confidence, the confidence in this proposition can be defined as the probability that the decision, “Nigeria is the most populous African country”, is correct. The same applies to some aspects of self-confidence. Lionel Messi is presumably highly self-confident in his ability to score in soccer games because the probability that the proposition “I will score” (as opposed to “I will not score”) is correct tends to be high. The concept that unifies all of these seemingly different types of confidence is that they are about a choice being correct, even if only hypothetically, such that confidence can be expressed probabilistically by p(z = k|d = k, evidence). Here we focus mostly on confidence about decisions, but our conclusions apply just as well to propositions.

When compared to the posterior p(z|Image, Vestib) over all possible choices, confidence is the probability mass of this posterior for one particular (overt or covert) choice. But does it ever make sense to maintain a separate measure of confidence rather than continuing to use the full posterior? In other words, why would you use a limited summary, confidence, when the entire posterior distribution is available?

This is because confidence is in fact the only quantity that is needed in a wide variety of tasks. It is particularly important in sequential decisions, when subsequent choices depend on previous decisions^21,28–30. One example of such a task is a post-decision wager, in which subjects are asked to place a bet on whether their decision was correct^28,31,32. The optimal size of the wager, the investment, depends on the degree of belief that the initial choice was correct, with a higher wager when confidence is high³². These types of post-decision wagers can be studied in the laboratory, even in animals¹. One example is a time investment task, initially introduced to study confidence in rats, that requires the decision maker to first gather evidence about which of several choice options is rewarded³³. After a choice is made, the reward is delayed for a randomized interval and it is up to the decision maker to choose how long to wait for this reward. To not wait in vain, it only makes sense to wait extended periods if the decision maker is confident of their choice. In fact, it can be shown that there is no need to store the posterior distribution over the choices for this kind of task: the probabilities associated with the choices that the subject did not select are irrelevant, the only required quantity is the probability that the selected choice is correct. Confidence can also be important for learning from feedback (Box 2) and group decision-making³⁴.

Box 2. The role of confidence when learning from feedback.

Confidence is important when learning from feedback (for example, see ref. 74,). In our heading example, subjects must learn how to map the image of the motion flow field onto adequate responses, which is to say, they need to learn the parameters, such as synaptic weights, W, of the neural network that maps the images onto a sensory representation of the response. Independent of the complexity of these networks, their weights can be adjusted on every trial from the observation of three variables: the sensory (here, visual) input, Image, the choice k made by the subject, d = k, and feedback about the correct choice, z. In reinforcement learning, the feedback about z typically indicates whether the choice is correct (z = k) or not (z ≠ k). Given these variables, the best the brain can do is to learn the posterior distribution over the weights, which is obtained via a simple application of Bayes rule. In the case of a correct choice, we obtain

$$p(\mathit{W}\mid z=k,d=k,\mathit{Image})\propto p(z=k\mid d=k,\mathit{Image},\mathit{W})p(\mathit{W})$$

For incorrect choices, in which case z ≠ k, the weight update is instead

$$\begin{array}{l}p(\mathit{W}\mid z\ne k,d=k,\mathit{Image})\propto p(z\ne k\mid d=k,\mathit{Image},\mathit{W})p(\mathit{W})\\ =\left(1-p(z=k\mid d=k,\mathit{Image},\mathit{W})\right)p(\mathit{W})\end{array}$$

In both cases, the first term on the right hand side of the equation is precisely what we have called confidence. Our definition of confidence in the main text did not include the variable W, but this variable is implicit, as this function is necessarily parameterized in the brain. Counterfactual reasoning emerges as an additional feature of the above learning rule, as for incorrect choices the relevant probability is the belief about the correctness of the un-chosen options, or “what would have happened had I chosen otherwise?”

However, confidence is not always the appropriate measure to use, even in sequential decisions. For instance, if a subject receives further information relevant to a previously taken choice, then the entire posterior distribution over the latent variable z, p (z|Image, Vestib), needs to be updated in the face of new evidence. Even in this situation, confidence may be a computationally efficient summary statistic to use instead of the full posterior distribution. Consider, for example, complex environments in which the posterior distribution might require an inordinate amount of data to learn, involve extremely complex inference to compute or require large neuronal resource to store. As a result, the posterior distributions computed will only be a rough approximation of the true posterior³⁵. Using confidence in these situations as an approximation to the full posterior can be the computationally appropriate strategy that beats other solutions that were optimal if more information were available (for example, see refs. 36,37). Although these ideas are speculative at present, as the field begins to study more complex behavioral questions, we are likely to find that the complexity of the computations faced by the brain strongly constrains what it can compute and store.

Thus far we have defined confidence for discrete choices, but it is possible to extend this definition to continuous variables. In experiments testing confidence for continuous variables, subjects are commonly asked to commit to an estimate and assess the confidence in that estimate (for example, ref. 38). For instance, in the heading task, we could ask subjects to directly estimate their heading direction, and then to report their confidence in that estimate. Thus, confidence is once again a choice-dependent variable: it relates to the accuracy of the choice or a commitment to a particular value. However, we can no longer define confidence as the probability of the current choice being correct because this probability, that is, the probability that the chosen estimate matches the true value, equals zero for continuous variables. Instead, we can define an interval over the chosen estimate that contains the true value with a fixed probability, say 95%. In terms of heading estimation, such an interval is closely related to the variance of the posterior distribution over heading (for example, see ref. 39), illustrating that, when working with continuous variables, it is particularly easy to confuse certainty and confidence. Nevertheless, there is a fundamental difference: although certainty is about the posterior distribution over any latent variables that may be relevant to the task, confidence exists only in the context of a choice that the decision maker has committed to (independent of whether this commitment is overt or covert).

Certainty: definition and computations

Given that we defined confidence with respect to a particular posterior distribution over a binary random variable, correct or incorrect, it is therefore a form of certainty. However, not all forms of certainty can be reduced to confidence according to the definition we propose. Confidence is distinct from all other posterior distributions that might be involved in decision-making because it is related only to the current choice d, which, in our opinion, is the key property of confidence. In contrast, the certainty about direction of motion in the heading task is determined by the posterior distribution p(θ|Image, Vestib), just like the certainty about whether one is moving rightward or leftward is determined by distribution p(z|Image, Vestib), two notions that are independent of whether we have made a choice (Fig. 1). Note that both of these distributions are required to compute the confidence, but they are distinct statistical quantities.

Given our definition of confidence as the probability that the current choice is correct, we suggest that the term certainty is best reserved for all distributions that are choice independent. For example, certainty could refer to the inverse variance of these distributions in the case of continuous variables, such as θ, and to the inverse entropy of the distributions in the case of discrete variables or non-Gaussian distributions. According to this definition, certainty is decision independent because it is not conditioned on a choice. Furthermore, it is domain specific because the degree of certainty has to be specific to each of the variables involved in the inference. For instance, in our heading task above, we need to be able to specify the certainty associated with heading based on vision alone, vestibular information alone or both (Fig. 1). We also need to represent the certainty associated with the binary variable z given all the evidence. These are distinct forms of certainty that might be represented in the brain by distinct neuronal populations. Confidence can also be domain specific, as one could ask a subject to base their decision on a single modality and then ask the confidence in this decision. However, the brain needs to encode only one confidence, the one corresponding to the current decision (assuming that humans and animals can only consider one decision at any given time), whereas it is essential to encode multiple certainties simultaneously.

These definitions have implications for the possible neural implementations of these quantities. We can search for areas specifically involved in the representation of confidence, but not of the posterior distribution over choices, for example, p(z|Image, Vestib). For instance, Lak et al.³³ found that inactivating the orbitofrontal cortex (OFC) selectively impaired rats’ ability to wait in proportion to their confidence level, but preserved their olfactory discrimination performance. Indeed, given that confidence is a choice-dependent quantity, it should involve associative areas such as frontal and prefrontal areas, such as the OFC²¹ or rostro lateral prefrontal cortex (rlPFC)⁴⁰, and it could recruit global signals, such as neuromodulators. Several groups have in fact proposed such a centralized system for confidence estimation^41,42, and that confidence may serve as common currency across tasks⁴³. Certainty, on the other hand, cannot employ similarly global signals since we need to be able to encode distinct levels of certainty for each of the variables involved. Each cortical area has to be able to encode posterior distributions (or likelihood; Fig. 1 and Box 2) specific to the variables encoded in that area. This is a critical feature, without which cortical circuits could not perform optimal probabilistic inference such as cue integration^44–47 or optimal accumulation of evidence over time^48,49. Note that our definition of certainty does not directly address the origins of uncertainty, for instance, whether it is a result of incomplete evidence, incorrect internal model or noisy processing (for example, see refs. 50,51).

Looking for confidence in neural codes

How can we establish that a particular neuron or neural population encodes confidence, certainty or some other cognitive variable? The usual strategy involves recording neuronal activity, with electrodes or its correlates with functional magnetic resonance imaging (fMRI), while manipulating the variable of interest. However, in the case of a variable such as confidence, which is not just a property of the stimulus, but a subjective internal variable, it is not immediately clear how to obtain a precise measurement of the variable in question. The most straightforward approach is to simply ask subjects to report their confidence in their choice, for instance, on a scale of 1 to 5, and then show that a neuron’s firing is correlated with this confidence report. Although straightforward, this method suffers from a few limitations. First, it is difficult to design a version of this task that could work with animals. Second, and more importantly, without specifying what is meant by confidence, it is unclear what subjects are actually reporting. For instance, the behavioral expression of confidence may be dependent on a number of factors: context, bias and other framing effects that are difficult to control. Thus, even if one observes a correlation between neural activity and confidence report, it needs to be established that the correlation is not a result of an unidentified underlying factor contributing to the confidence report.

To go beyond this behavioral correlation approach and establish that neural activity represents confidence, it is important adopt a computational approach and ask what the simplest computations that could generate the neural activity in question are. For instance, for post-decision wagering tasks, the wager must reflect the expected reward, that is, the product of the probability of being correct (confidence) with the reward associated with the choice. By developing a computational model of this task, a subject’s estimate of being correct can be inferred without an explicit report of this probability. Regressing this model-based estimate against neural activity avoids the problem of corruption by other variables, such as anxiety, and provides a rigorous computational estimate of confidence. Other caveats remain, however; for example, the decision maker might compute confidence differently from the model, in which case the model-based approach does not guarantee finding neural representations even if they exist. With these caveats in mind, we next discuss two different computational approaches for how such neural representations could be identified.

Neural coding: the encoding and decoding approaches

The simplest approach to reveal a neural code, and the most widely used, consists of plotting the activity of single neurons as a function of the variable of interest, usually obtained from a model, to generate what is known as a tuning curve. We refer to this as the encoding approach. Using this approach, a significant fraction of neurons in the orbitofrontal cortex of rats have been found to have monotonic tuning curves to confidence²¹. Similarly, neurons with monotonic tuning curves to confidence have been reported in the dorsal pulvinar of rhesus monkeys²⁷ and in the amygdala and hippocampus of human patients⁵².

Human fMRI studies also suggest that the ventral medial prefrontal cortex (vmPFC) and rlPFC encode confidence in humans⁵³. Just like the single-cell studies mentioned above, this analysis is effectively looking for neural responses (or their fMRI proxy, voxel BOLD activation) that are monotonic functions of confidence. This is indeed a simple test that, if positive, suggests that the neurons or brain regions in question encode confidence. Linear regression, however, is limited in the type of codes it can reveal. It works when the neuronal responses are monotonic functions of confidence, but it can fail for some non-monotonic functions that are quite ubiquitous in the brain^54–57.

Another approach, which does not rely on monotonic tuning curves, is to regress the encoded variable not simply against the raw neural activity, but against a feature of the neural tuning curves that may encode it (Fig. 2)^58,59. Although more general, this approach also suffers from a general problem of the encoding approach: it eludes the critical question of what is known about the encoded variable given the neural pattern of activity^44,60–62. This is the relevant question for downstream neurons that have to rely on the activity of upstream neurons to perform computation over the encoded variable. This question can only be answered by adopting a decoding perspective.

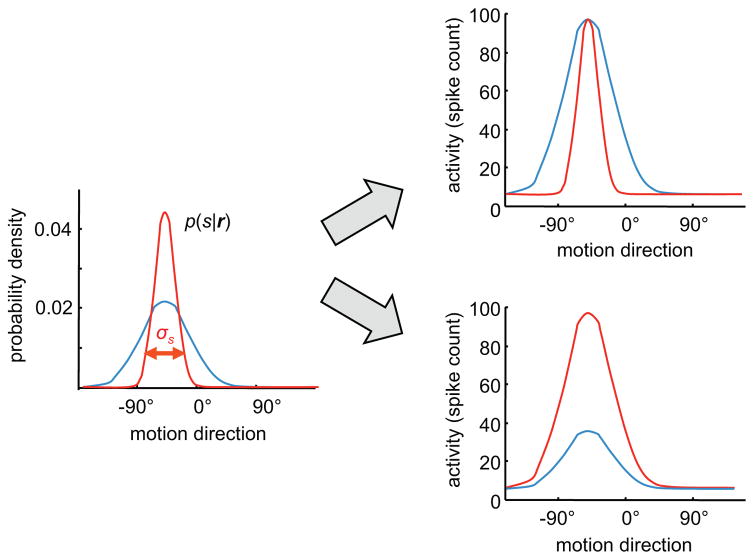
Figure 2.

Two distinct codes for certainty. Left, the encoded probability distribution, p(s|r), illustrated here for direction of motion s given the activity r of a neural population (in all panels, blue curve indicates low certainty and red curve indicates high certainty). Right, tuning curves of an individual neuron for two hypothetical neural codes. Top right, the width of the tuning curves is inversely proportional to certainty ( $1/{\sigma }_s^2$) about the stimulus. Bottom right, the amplitude of the tuning curve is proportional to certainty. Such code can be detected by regressing the variance of the posterior distribution against the width or amplitude of the tuning curves. Unfortunately, finding a significant correlation between certainty and some features of the tuning curves does not guarantee that this feature encodes certainty. It is instead preferable to use a decoding approach, as explained in the main text and Figure 4.

The decoding approach requires switching to the question of read out and asking how one could recover, or decode, some variable x of interest from a set of responses across a population of neurons. Specifically, several authors have suggested defining neural representations as patterns of neural activity from which linear and nonlinear functions, f(x), of the variable of interest can be decoded linearly^63–66.

Note that this definition implies that the variable itself could be decoded linearly, as this corresponds to decoding a particular function of x, namely, the identity function f(x) = x. However, most computations performed by the brain involve much more complex functions (Box 3). For instance, the expected value of a decision is the product of confidence and the reward size, which is a nonlinear function of these two variables (linear functions only allow weighted sums, whereas we need a product in this case). One of the goals of neural computation should be to produce neural representations that simplify the computation and learning of such nonlinear functions. This is precisely what motivates our definition of a neural representation: a set of responses that reduce nonlinear functions to simpler linear operations. Such representations also simplify learning: neurally plausible local learning rules such as the delta rule (a supervised version of Hebb rule⁶⁷) are sufficient to learn optimal linear decoders of nonlinear functions.

Box 3. From probabilistic population codes to monotonic confidence encoding.

The transformation from probabilistic population codes (PPCs) to a monotonic representation of confidence is just a nonlinear transformation and, as such, it can be implemented in basis function networks. To illustrate this, let us consider the example from Box 1, in which a posterior over motion heading p (θ|I, V) is turned into a choice d and an associated confidence, p (z = k|d = k,I, V). Assume that this posterior is encoded in population activity r_θ by a linear PPC, that is, p (θ|I, V) = Z (r_θ)⁻¹ exp (h (θ)^Tr_θ), where Z (r_θ) = ∫ exp(h (θ)^Tr_θ)dθ is the normalization constant, and h (θ) is the locally linear decoder as a function of⁴⁴ θ. Even though the exact location of where the posterior over θ is encoded is not important for the argument, r_θ might, for example, be the activity of area MSTd, which seems to encoded information about self-motion. From this posterior we can compute the posterior over latent states, z, by

$$\begin{array}{l}p(z=\text{left}\mid \mathit{I},\mathit{V})={\int }_{0°}^{180°}p(\theta \mid \mathit{I},\mathit{V})\mathrm{d}\theta =Z{({\mathbf{r}}_{\theta })}^{-1}{\int }_{0°}^{180°}exp(\mathbf{h}{(\theta )}^{\mathrm{T}}{\mathbf{r}}_{\theta })\mathrm{d}\theta \\ =f({\mathbf{r}}_{\theta }),\end{array}$$

which is a nonlinear function f (r_θ) of r_θ. This posterior can consecutively be encoded in a PPC, p (z|I, V) = p (z;r_z) = Z (r_z)⁻¹exp(h (z))^Tr_z), where r_z is a nonlinear function of r_θ such that p (z;r_z) = p (z = left/I, V) as given above holds, and Z (r_z) is again a normalization constant. The basis function networks described in the main text readily implement such nonlinear functions. They can do so efficiently despite the high-dimensional input r_θ, as the distributions encoded by this input can be described by few parameters. See ref. 75 for examples of PPCs that compute marginalizations similar to the above with only quadratic nonlinearities and divisive normalization.

Next we compute confidence from the above posterior over z. Formally, confidence is given by p (z = k|d = k, I, V), such that

$$p(z=k\mid d=k,\mathit{I},\mathit{V})=Z{({\mathbf{r}}_z)}^{-1}\{\begin{array}{cc}exp(\mathbf{h}{(z=\text{left})}^{\mathrm{T}}{\mathbf{r}}_z)& \text{if}d=\text{left},\\ exp(\mathbf{h}{(z=\text{right})}^{\mathrm{T}}{\mathbf{r}}_z)& \text{otherwise}\end{array}$$

The above is again a nonlinear function of r_z and choice d. Thus, independent of how exactly d is encoded in neural population activity, a basis function network can compute the confidence. Assuming linear encoding would yield neural activity that monotonically increases with confidence, similar to many neurons in OFC²¹.

On the other hand, it is equally possible to implement a network in which neural activity directly represents a basis function network of confidence. Furthermore, we do not need to represent the posterior over z with a PPC, as confidence could be directly computed as a nonlinear function of r_θ and d. We only included r_z to make each of the processing steps explicit. This illustrates that, due to the power of basis function networks to perform nonlinear transformations, it becomes possible to move from uncertainties encoded by linear PPCs to a linear or nonlinear encoding of confidence. Critically, however, all steps in the inference require nonlinear transformations, implying that confidence can be neither linearly decoded from r_θ nor from r_z.

Representations that make nonlinear computations linearly decodable are known as basis function representations (see ref. 68 for a review). They require neurons with nonlinear tuning—for example, sigmoidal or bell-shaped tuning curves—to all the variables of interest (for example, confidence and reward; Fig. 3). It is important to realize that, in such basis function representations, the neurons are not guaranteed to exhibit the signature of confidence encoding that most studies have been looking for so far, namely, a monotonic tuning to confidence. Nonetheless, the responses of a set of basis function neurons would provide a perfectly sensible representation of confidence from the point of view of downstream computation (Box 3).

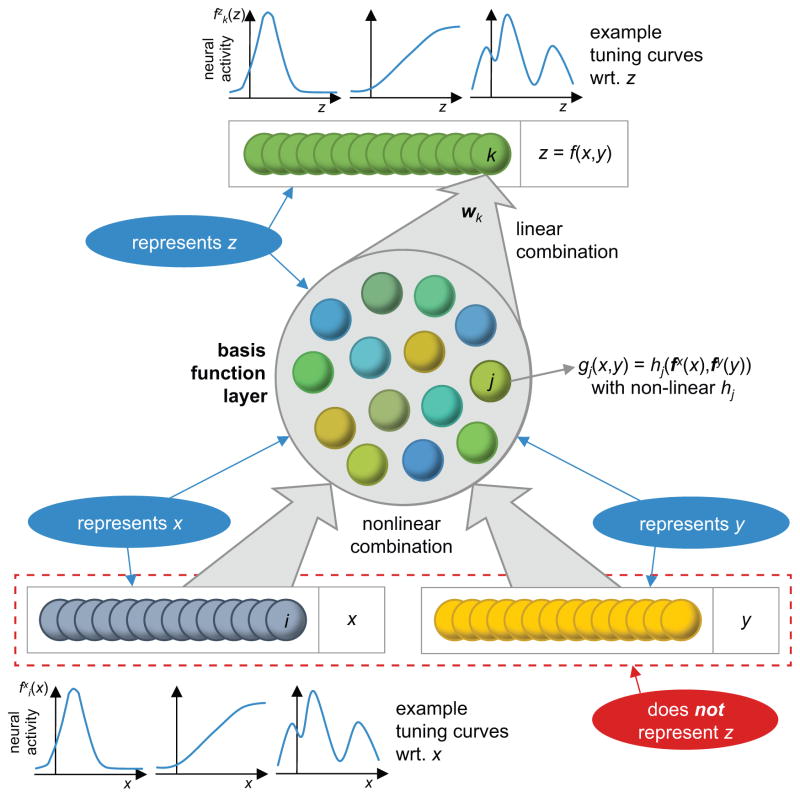
Figure 3.

Nonlinear neural computations by neural populations that linearly represent variables. We say that a neural population represents a variable x if linear and nonlinear functions of x can be estimated linearly from the neural activity. This requires that the neurons have nonlinear tuning curves to x, such as the ones shown in the inset below population x. The network implements the nonlinear function z = (x, y) by first transforming the activity of the neural populations representing x and y (bottom, blue and yellow) into a basis function layer (central circle) whose neurons feature activities g_j (x, y) that are nonlinear combinations of the activities of the two input populations. Second, neurons in the population representing z (top, green) combine the activities of the basis function neurons linearly, as illustrated by weights w_k for neuron k. This population again represents z in a linearly decodable way by featuring nonlinear tuning curves with respect to z. Such a network can compute almost arbitrary nonlinear functions as long as the set of basis functions is sufficiently rich. The bottom neurons representing x and y together contain all the information to compute z, however do not represent z, as z can only be decoded with a nonlinear decoder from these neurons. The central neurons in the basis function layer represent x and y, as their activities can be used to compute f (x, y) = x and f (x, y) = y, which implies that both x and y are linearly decodable from this population. They also represent z, as the activities of neurons in the population z is only a linear transformation of the activity of neurons in the basis function network, making z linearly decodable from this network. Note that both input populations as well as the output population can be part of upstream and downstream basis function networks performing further computations. They are here shown as distinct entities only for the sake of illustration.

Implicit versus explicit representations of confidence and certainty

Given the definition of a representation we have just considered, which brain regions are involved in representing confidence? Single-unit recordings have yielded candidates such as the OFC²¹, pulvinar²⁷ and the supplementary eye field³⁰, whereas vmPFC and rlPFC have been implicated using fMRI^40,53. In addition, given that activity of neurons in the lateral intraparietal cortex (area LIP) reflects the accumulation of sensory evidence for decision-making⁶⁹, it could provide a representation of confidence, perhaps not explicitly, but at least implicitly²². Furthermore, all sensory cortical areas contain information to support decisions and therefore might also contain an implicit representation of confidence. To clarify these issues, we first need to define what we mean by a representation being ‘implicit’ and ‘explicit’.

Let us start with explicit representations. As discussed in the previous section, we consider that an area represents a variable of interest as long as this variable is linearly decodable. Although we do not encourage calling this representation explicit in general, we will do so here solely to distinguish it from implicit representations. Considering this, what does the neural activity in parietal cortex area LIP represent explicitly? One possibility is that it is involved in representing the distribution over choices given the sensory evidence, p(z|sensory evidence). To establish that this is the case, we need to first define what constitutes an explicit neural representation of such probability distributions. Fortunately, we can follow the same logic as for scalar variables: an explicit neural representation of a probability distribution is a set of responses from which one can recover the probability distribution through a linear combination of neuronal responses (Fig. 4). Codes in which this linear combination corresponds to the log of the encoded probability are known a linear probabilistic population codes⁴⁴. Following earlier work from Gold and Shadlen⁴⁸, Beck et al.⁴⁹ used linear PPCs to show that activity in LIP is consistent with the idea that it encodes the log of the posterior distributions over choices, p(z|sensory evidence). Thus, it might explicitly represent the logarithm of this distribution.

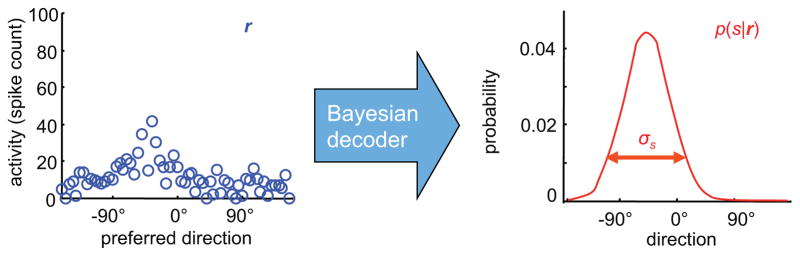
Figure 4.

A Bayesian decoder provides a normative way to relate population activity (left) to the certainty (right). Left, activity of a population of motion selective neurons in response to one particular moving object. Right, corresponding posterior distribution over direction given the vector of activity r, obtained via an application of Bayes rule. Certainty corresponds to the s.d. of the posterior distribution. In some cases, the mapping from the neural activity to the log of the posterior distributions is linear in neural activity. This is what is known as a linear probabilistic population codes.

In addition to representing this posterior distribution, does LIP activity also represent confidence explicitly? To our knowledge, neither confidence nor any function thereof is linearly decodable from LIP activity alone. Nonetheless, if LIP encodes the posterior distributions over choices, it is possible for a nonlinear decoder to yield an estimate of confidence, as is clear from the work of Kiani and Shadlen²². This could therefore constitute an implicit representation of confidence. The problem with calling such a representation implicit is that it can be applied to almost any area. Consider, for instance, area MSTd, which explicitly represents the posterior distribution over heading directions in the sense that a probability distribution over heading could be linearly decoded from MTSd⁴⁷. However, as any decision about heading is likely based on MSTd activity, we could claim that MSTd also contains an implicit representation of confidence. We could even estimate confidence from MSTd activity with a complex nonlinear decoder. Taking this argument a step further would lead us to claim that even the retina contains an implicit representation of visual confidence, which seems to render the concept of implicit representations useless.

To summarize, we propose a definition of confidence representation based on linear decodability that allows us to assign specific and distinct computational roles to cortical areas: early sensory areas represent the posterior distribution over sensory variables (for example, posterior distribution over heading in MSTd), areas such as LIP and the frontal eye fields (FEF) represent the posterior distribution over choices given the sensory evidence, whereas confidence is represented by other frontal areas such as OFC and vmPFC (Box 3). Our current understanding of what these areas represent may be incorrect, but we nevertheless hope that our criteria and hypotheses can guide future research. In contrast, if we were to broaden our definition to include implicit representations or distributional confidence (a related concept, see ref. 2) that apply to any area containing information about confidence in some form, then any area along the visual processing pathway, including the retina, could be said to represent visual confidence.

Conclusion

We suggest defining confidence as the probability that the current choice, over or covert, is correct while reserving the terms certainty and uncertainty to refer to all other kinds of probabilistic representations in neural circuits. The key property of confidence is that it is choice dependent; there is no notion of confidence without a choice, although the choice need not be actualized and can remain covert. In this respect, it is different from the posterior distributions over choices given the sensory evidence, which is independent of whether a choice is even possible.

Although we have eluded this issue thus far, we should be clear is that when we write ‘the probability of being correct’, we actually mean the probability of being correct as estimated by the subject, as opposed to the true probability of being correct, as estimated by an ideal observer with complete knowledge of the world (for example, a generative probabilistic model that has produced the sensory evidence; Fig. 1)¹⁶. This generative model is specific to each task and subjects may not be able to learn this model perfectly well, particularly in complex tasks, and may therefore resort to approximations. This would imply that confidence reports deviate from the actual probability of being correct. Indeed, confidence miscalibration of this type is often reported^24,70–73. Similarly, if confidence estimates obtained by decoding a cortical area strongly deviate from the one observed behaviorally, it does not indicate that the area does not encode confidence, but instead simply reflects a suboptimal step in downstream computation. Finally, it is possible that subjects use more than one representation of confidence and that these representations use distinct approximations to obtain their estimates.

We emphasize that our definitions of confidence, certainty and their neural representations are not entirely new. Other groups have made similar proposals, but we hope that this perspective helps to clarify these definitions by providing clear mathematical foundations. These mathematical definitions may ultimately fail to capture all of the subtleties of these concepts, but, at the very least, they can be used to dissect the computational contributions of various cortical areas to the process of decision-making by providing a clear-cut and testable demarcation between the concepts of confidence and certainty.