Evidence of Systematic Attenuation in the Measurement of Cognitive Deficits in Schizophrenia

Abstract

Cognitive tasks that are too hard or too easy produce imprecise measurements of ability, which, in turn, attenuates group differences and can lead to inaccurate conclusions in clinical research. We aimed to illustrate this problem using a popular experimental measure of working memory—the N-back task—and to suggest corrective strategies for measuring working memory and other cognitive deficits in schizophrenia. Samples of undergraduates (n = 42), community controls (n = 25), outpatients with schizophrenia (n = 33), and inpatients with schizophrenia (n = 17) completed the N-back. Predictors of task difficulty—including load, number of word syllables, and presentation time—were experimentally manipulated. Using a methodology that combined techniques from signal detection theory and item response theory, we examined predictors of difficulty and precision on the N-back task. Load and item type were the two strongest predictors of difficulty. Measurement precision was associated with ability, and ability varied by group; as a result, patients were measured more precisely than controls. Although difficulty was well matched to the ability levels of impaired examinees, most task conditions were too easy for non-impaired participants. In a simulation study, N-back tasks primarily consisting of 1- and 2-back load conditions were unreliable, and attenuated effect size (Cohen’s d) by as much as 50%. The results suggest that N-back tasks, as commonly designed, may underestimate patients’ cognitive deficits due to non-optimized measurement properties. Overall, this cautionary study provides a template for identifying and correcting measurement problems in clinical studies of abnormal cognition.

Cognitive tasks that are too hard or easy produce imprecise measurements (Lord, 1980), confound studies of differential deficit (Chapman & Chapman, 1973), and complicate translational research (Callicott et al., 2000; Manoach et al., 1999). Researchers have explicitly recommended that task difficulty be a main criterion used to select neurobehavioral probes (Gur, Erwin, & Gur, 1992), and problems associated with using tests with non-optimized item properties have been known for many years (Lord & Novick, 1968). Despite this, the relative match, or mismatch, between ability and difficulty is rarely discussed in applied research, likely because there have been few demonstrations of its practical consequences. In this paper, we illustrate these problems using a popular experimental measure of working memory—the N-back task—and suggest strategies for precisely measuring working memory and other cognitive deficits in schizophrenia. The methodology applied is general, and can inform future studies of abnormal cognition in schizophrenia and other neurocognitive disorders.

Item Difficulty and Measurement Error

Ability estimates are most precise when item difficulty is closely matched to ability (Embretson, 1996; Lord, 1980). To understand why, it is important to distinguish between classic and modern conceptualizations of measurement error. Classical test theory defines measurement error as the square root of one minus the ratio of true score variance to observed score variance: standard error of measurement. As such, measurement error in classical test theory is a constant. Modern psychometrics—particularly item response theory (IRT; Lord, 1980)—on the other hand, defines measurement error as the standard deviation of the estimate of ability: standard error of estimate. As such, estimates of measurement error in IRT may vary over scores within a population (Embretson, 1996); specifically, error is often a “U”-shaped function of ability. Although unequal precision is not a desirable property, it is, unfortunately, a real and everpresent one that may go unnoticed by researchers using classical methods (e.g., split-half reliability or coefficient alpha). This problem occurs because items that are too hard or too easy produce little systematic variation in observed test scores (Lord, 1980); in extreme cases, tests may show “floor” or “ceiling” effects (i.e., when all examinees within a particular range of the ability distribution receive the same score; Haynes, Smith, & Hunsley, 2011).

There are practical consequences of administering tests with item difficulties that are poorly matched to ability. It is an axiom of psychometric theory that associations between variables are attenuated to the extent that measures of those variables are unreliable (Haynes et al., 2011; Spearman, 1904). Moreover, because reliability is a function of the standard errors associated with individual estimates of ability obtained within a sample (Embretson, 1996; Lord, 1955), and because, as noted above, error often varies with ability, samples with different mean abilities—such as patients and healthy controls—can be measured with unequal reliability. As a result, associations between ability and outcome, as well as changes in ability, can appear relatively smaller in one group when compared to the other purely due to a measurement confound.

IRT can be used to identify and correct these problems (Thomas, 2011). Unfortunately, the approach is rarely used in neuropsychological test development, and the formal use of IRT in small-scale neurocognitive research is unprecedented. As Strauss (2001, p. 12) noted, IRT’s large sample requirements—usually several hundred to thousand participants—implies that the “… method does not seem practical for testing specific, theoretically based hypotheses...” However, with the use of alternative, less statistically demanding measurement models, it is possible to utilize certain applications from IRT in small-scale research (e.g., Thomas, Brown, Thompson, et al., 2013). We describe one such model next.

Measurement Approach

A limiting factor in the application of IRT to measures of abnormal cognition has been the disconnect between measurement models that are popular in item response theory and measurement models that are popular in cognitive assessment. In particular, most applications of item response theory rely on unidimensional measurement models (i.e., models in which a single person variable is thought to influence item responses), with only a small portion of studies using multidimensional approaches (i.e., models in which multiple person variables are thought to influence item responses) (Thomas, 2011). Applications of the latter that have been published are generally exploratory (e.g., Thomas, Brown, Gur, et al., 2013). Measurement models used in cognitive assessment, in contrast, are often multidimensional, theory-based, and rely heavily on experimental cognitive research.

A prime example is the equal variance signal detection theory (SDT; Snodgrass & Corwin, 1988) model, which is commonly used to score data from recognition memory tasks (e.g., Kane, Conway, Miura, & Colflesh, 2007; Ragland et al., 2002). The SDT model, shown in Figure 1, distinguishes between two classes of items: targets and foils. Targets are repeated (or old) items that the examinee is expected to remember. Foils are non-repeated (or new) items that the examinee is not expected to remember. The SDT model assumes that the presentation of target or foil items during testing invokes a sense of familiarity that can be represented as unimodal, symmetric probability distributions with identical variances but different means. The distance between distributions is a measure of discriminability (d′), and is often the primary outcome score of interest. d′ can reflect perceptual, memory, or other types of sensitivity to the detection of signal against a backdrop of noise (Witt, Taylor, Sugovic, & Wixted, 2015). However, because the familiarity distributions of targets and foils often overlap, the SDT model assumes that examinees must establish a criterion, or level of familiarity, beyond which items will be classified as targets. It is useful to define a measure of bias as the value of the criterion relative to the midpoint between target and foil distributions (C_center). C_center can reflect both perceptual and response biases (Witt et al., 2015). The primary advantage of using the SDT measurement model in studies of abnormal cognition is the ability to disentangle sensitivity from bias.

Figure 1.

Equal variance, signal detection theory model. μ_T = mean of the distribution of familiarity for targets; μ_F = mean of the distribution of familiarity for foils; d′ = μ_T minus μ_F (discrimination); C = criterion; C_center = value of the criterion relative the midpoint between μ_T and μ_F (bias).

Previous work has shown that the SDT model can be formulated as a generalized linear model with coefficients representing examinee ability and item difficulty (DeCarlo, 1998, 2011). In other work (Thomas et al., 2016), and in the Appendix, we show that this model is also equivalent to a multidimensional IRT model, thus linking a valuable body of psychometric research and technical literature to the measurement of a general class of cognitive constructs. Moreover, because this framework assumes certain item properties based on theory, and allows others to be estimated as a function of task properties, sample size demands are greatly reduced. Researchers can use the approach to investigate standard error of ability estimates, even in relatively small samples, provided that the cognitive tasks used are scored using the SDT framework.

The application of modern psychometric ideas to SDT scoring of test data in experimental studies of abnormal cognition would provide tangible evidence of the problems associated with administering items and tests that poorly match difficulty to ability. Next, we describe one domain of assessment that is ripe for the application of these ideas: the assessment of working memory deficits in schizophrenia.

Working Memory Deficits in Schizophrenia

Decreased brain volume, altered morphology, and impaired functioning in brain regions associated with complex cognitive processes (e.g., prefrontal cortex, limbic and paralimbic structures, and temporal lobe) are common in patients diagnosed with schizophrenia (Brown & Thompson, 2010; Levitt, Bobrow, Lucia, & Srinivasan, 2010), and are linked to a host of cognitive deficits, including impaired attention, language, executive functioning, processing speed, and memory (Bilder et al., 2000; Kalkstein, Hurford, & Gur, 2010; Reichenberg & Harvey, 2007). Cognitive deficits are core, treatment-refractory, even endophenotypic traits that might prove useful in identifying targets for the next generation of psychological and pharmacological therapies (Brown et al., 2007; Gur et al., 2007; Hyman & Fenton, 2003; Insel, 2012; Lee et al., 2015).

Working memory is a core deficit in patients diagnosed with schizophrenia (Barch & Smith, 2008; Kalkstein et al., 2010; Lee & Park, 2005). Although the construct has been characterized by several evolving theories (Atkinson & Shiffrin, 1968; Baddeley & Hitch, 1974; Cowan, 1988), it can generally be defined as, “those mechanisms or processes that are involved in the control, regulation and active maintenance of task-relevant information in the service of complex cognition…” (Miyake & Shah, 1999, p. 450). The construct has been intensively studied in cognitive psychology (Baddeley, 1992; Cowan, 1988), neuroscience (Owen, McMillan, Laird, & Bullmore, 2005), and clinical neuropsychology (Lezak, Howieson, Bigler, & Tranel, 2012). Deficits in working memory also occur in several other neurological and psychiatric disorders including attention-deficit/hyperactivity disorder (Engelhardt, Nigg, Carr, & Ferreira, 2008), autism (Williams, Goldstein, Carpenter, & Minshew, 2005), dementia (Salmon & Bondi, 2009), depression (Christopher & MacDonald, 2005), traumatic brain injury (Vallat-Azouvi, Weber, Legrand, & Azouvi, 2007), and post-traumatic stress disorder (Shaw et al., 2009).

The N-back task, where examinees are asked to monitor a continuous stream of stimuli and respond each time an item is repeated from N items before, is one popular measure of working memory deficits in schizophrenia. N-back tasks were introduced to study serial learning and short-term retention of rapidly changing information (Kirchner, 1958; Mackworth, 1959; Welford, 1952). Figure 2 shows an example of a 2-back task (i.e., load or N = 2) using words as stimuli. Examinees are asked to respond to targets but not to foils or lures (i.e., items that have been repeated from some lag other than N [e.g., a 3-back item presented during a 2-back condition; see Figure 2] and thus should not be responded to). The N-back task gained popularity as an experimental working memory paradigm in the 1990s (Cohen & Servanschreiber, 1992; Gevins & Cutillo, 1993; Gevins et al., 1990; Jonides et al., 1997), and has since been widely adapted, using stimuli varying across modality, including letters, digits, words, shapes, pictures, faces, locations, auditory tones, and even odors (Owen et al., 2005). These diverse versions of the N-back task have been shown to require both stimulus-specific processes as well as recruit common brain regions (Nystrom et al., 2000; Owen et al., 2005; Ragland et al., 2002). Although experimental versions of the N-back task are popular in schizophrenia and neuroimaging research—to the point of being considered a “gold standard” paradigm (Glahn et al., 2005; Kane & Engle, 2002; Owen et al., 2005), and have even shown efficacy for use in cognitive remediation (Jaeggi, Buschkuehl, Jonides, & Perrig, 2008)—questions nevertheless remain about the psychometric properties of these tasks (e.g., Jaeggi, Buschkuehl, Perrig, & Meier, 2010).

Figure 2.

Example of a 2-back run from the N-back task. Examinees are asked to respond whenever a word is repeated from 2 words before. Items repeated from 2-back are targets, items that are repeated, but not from 2-back are referred to as lures, and non-repeated items are referred to as foils.

Several investigators have reported only moderate, weak, and even non-significant associations between N-back performance and performance on prototypical working memory paradigms such as measures of simple and complex span (e.g., Jacola et al., 2014; Jaeggi et al., 2010; Kane & Engle, 2002; Miller, Price, Okun, Montijo, & Bowers, 2009; Shamosh et al., 2008; Shelton, Elliott, Matthews, Hill, & Gouvier, 2010). One possible cause for the N-back’s poor validity is poor reliability. Reliability estimates reported in the literature have ranged from poor to good (e.g., Jaeggi et al., 2010; Kane et al., 2007; Salthouse, Atkinson, & Berish, 2003; Shelton et al., 2010) and appear to depend on N-back load condition and stimulus modality (e.g., Jaeggi et al., 2010; Salthouse et al., 2003). Indeed, in a study examining the split-half reliability of the N-back task under different load manipulations, Jaeggi et al. (2010) concluded that, “the N-back task does not seem to be a useful measure of individual differences in working memory [capacity], due to its low reliability.” However, the N-back’s poor, or at least inconsistent, reliability may be a function of poorly matched examinee ability and item difficulty.

Current Study

In this study our first aim was to determine how task manipulations influence difficulty and precision on the N-back. This was accomplished by using techniques from IRT to quantify measurement error for estimates of d′ and C_center produced by a SDT measurement model. As noted above, measurement error varies when item difficulty is not well matched to the full range of ability within a sample. Because the N-back appears to have a restricted range of difficulty (i.e., few load conditions), and because reliability estimates reported in the literature have varied substantially from sample to sample, we hypothesized that error in empirical estimates of d′ and C_center would vary as a function of ability. Our second aim was to use this information to explore the potential impact of imprecision on observed group differences in clinical studies of working memory deficits in schizophrenia. We hypothesized that mismatched ability and difficulty would lead to attenuated precision and effect size. That is, if item difficulty on the N-back is well matched to the abilities of healthy controls or patients, but not both, this should result in unequal precision between groups. Furthermore, because mismatched ability and difficulty increases measurement error, and because measurement error attenuates effect size, we also assumed that restricted range of item difficulty would result in lower effect size for one group when compared to the other.

Method

Participants

We sought to study a heterogeneous sample in order to maximize variance in working memory ability. The sample comprised two cognitively healthy groups—undergraduates (N = 42) and community controls (N = 25)—and two groups of patients diagnosed with either schizophrenia or schizoaffective disorder—outpatients (N = 33) and inpatients (N = 17). Undergraduates were recruited from an experimental subject pool, outpatients and community controls were recruited from the general community, and inpatients were recruited from a locked long-term care facility. Demographic characteristics of the samples are reported in Table 1. Written consent was obtained from all participants. Patients were assessed on their capacity to provide informed consent. When relevant, consent was obtained from court-ordered conservators. Research procedures were reviewed and approved by the UC San Diego Human Subjects Protection Program (protocol numbers 071831, 080435, 101497, and 130874).

Table 1.

Demographic and Clinical Characteristics

	Undergraduates	Community Controls	Outpatients	Inpatients
N	42	25	33	17
Age (SD)	21.07 (2.11)	38.24 (12.39)	44.94 (11.63)	37.88 (11.13)
Male	16 (38%)	10 (40%)	19 (58%)	9 (53%)
Female	26 (62%)	15 (60%)	14 (42%)	8 (47%)
Hispanic	12 (29%)	2 (8%)	9 (27%)	4 (24%)
Race
White	13 (32%)	13 (52%)	16 (48%)	12 (71%)
Black	0 (0%)	4 (16%)	4 (12%)	0 (0%)
Asian	18 (45%)	4 (16%)	0 (0%)	2 (12%)
American Indian	0 (0%)	0 (0%)	0 (0%)	1 (6%)
Multiracial	2 (5%)	4 (16%)	13 (39%)	2 (12%)
Other	7 (18%)	0 (0%)	0 (0%)	0 (0%)
Education (SD)	15 (1.18)	15.12 (2.15)	12.09 (2.26)	11.47 (2.03)
Parental Education (SD)a	--	13.88 (1.81)	12.46 (2.52)	14.10 (2.16)
Std. WRAT	--	106.38 (8.06)	93.53 (12.38)	93.5 (13.49)
Age of Onset	--	--	22.06 (7.2)	19.62 (5.32)
Hospitalizationsb	--	--	9.62 (10.18)	16.71 (9.52)
GAF	--	--	41.34 (4.23)	28.24 (4.98)
SAPS Total	--	--	6.34 (3.73)	6.44 (5.19)
SANS Total	--	--	14.66 (4.12)	5.88 (3.54) c

Note: Two undergraduates declined to report their race.

SAPS = Scale for the Assessment of Positive Symptoms; SANS = Scale for the Assessment of Negative Symptoms.

^aBased on average of mother and father.

^bBased on self-report.

^cAvolition-Apathy and Anhedonia-Asociality Scores for inpatients were based on work, social, and recreational participation within the inpatient facility, and thus are likely smaller (better) than would be observed in the community.

“--” implies that data were not collected.

Diagnoses (or lack thereof) were verified using the patient and non-patient editions of the Structured Clinical Interview for DSM-IV-TR (First, Spitzer, Gibbon, & Williams, 2002a; First, Spitzer, Gibbon, & Williams, 2002b) for both patient groups and community controls, respectively, and by using a self-report questionnaire for the undergraduates. Exclusion criteria included inability to understand consent and self-reported non-fluent English speaker, previous significant head injury (i.e., loss of consciousness > 30 minutes, residual neurological symptoms, or abnormal neuroimaging finding), neurological illness, and severe systemic illness. Patients and community controls were excluded if they had a history of alcohol or substance abuse or dependence within the preceding one month, or had a positive illicit drug toxicology screen at the time of testing. Patients were also excluded if they did not meet diagnostic criteria for schizophrenia or schizoaffective disorder, or if they reported current mania. Undergraduates and community controls were also excluded if they reported any history of psychosis, current Cluster A personality disorder, current Axis I mood disorder, history of psychosis in a first degree family member, or current treatment with any antipsychotic or other psychoactive medication.

Cognitive Task

An N-back task using words as stimuli designed specifically for the purposes of this study was administered to all participants. We generated a list of words using an online word pool database (Wilson, 1988), saved each word’s letter, syllable, and frequency count, and then removed any offensive words and personal names. This left us with a stimulus pool of 32,236 English words taken from all parts of speech. Next, we generated one hundred 40-word lists containing 32 foil and 8 target or lure item types, so that 1 out of every 5 words presented, on average, was either a target or a lure. Words were randomly selected from the word pool.¹ To prevent examinees from guessing the order and rate at which targets and lures were presented, a script written in R (R Core Team, 2013) was used to pseudo-randomize the order of stimulus presentation (although the order was held constant over examinees).

We experimentally manipulated three crossed factors: N-back load (3-levels: 1, 2, or 3), number of word syllables (3-levels: 1, 2, or 3), and presentation time (3-levels: 500ms, 1,500ms, or 2,500ms followed by a blank screen to attain a fixed presentation rate of one word every 3,000ms).² We did not include a 0-back load condition (i.e., where examinees are asked to respond anytime a key word is shown) because we felt that the condition may differ not just quantitatively, but also qualitatively from load conditions that require both active maintenance and continuous updating of newly encoded information. Although load manipulations are common, syllable length and presentation time are generally fixed over items on N-back tasks; however, we reasoned that—because these manipulations can increase pressure on encoding and maintenance processes—they might produce a wider range of item difficulty for the N-back task which could benefit measurement precision overall.

We generated unique 40-word lists for each combination of factors. In addition to the experimentally manipulated factors, word frequency and item count within runs were included in all analyses. At an administration time of two minutes per list, we could not administer all unique combinations of factor levels to each participant. Therefore, we used incomplete counterbalancing of conditions. Participants were administered nine lists each with the requirement that they should receive all levels of each factor. A short set of instructions followed by a practice trial with feedback preceded each new N-back load condition. Participants were encouraged to take short breaks after each run. The task was administered online using a web application designed and programmed for neurocognitive task administration and lasted approximately 25 to 30 minutes per participant. Words were presented in large black font on a light grey background with minimal screen distraction. The protocol was the same for all participants except inpatients, who were administered only six N-back lists (three 1-back followed by three 2-back) due to time and fatigue constraints.

Analyses

Model

All analyses were conducted within the context of SDT. In equal variance SDT models, the probability of responding to stimuli can be expressed using the following general linear model (see DeCarlo, 1998 Appendix A):

$${\mathrm{\Phi }}^{-1}\left(\mathrm{P}\right(U_{ij}=1\left)\right)=-C_{\text{center},i}+Z_j\frac{d_i^{\prime }}{2},$$ (1)

where Φ⁻¹ is the inverse cumulative distribution function for the normal distribution; P(U_ij = 1) is the probability that individual i responds positively (presses the button) to item j; Z_j is a binary variable equal to 1 if item j is a target and −1 if it is a foil or lure; d′_i is the ability of individual i to discriminate between target and foil or lure items; and C_center,i represents individual i’s bias. In order to be consistent with IRT, the SDT model can be modified to express the probability of correct answers (as opposed to the probability of responding) and to include the notion of item difficulty (see Appendix):

$${\mathrm{\Phi }}^{-1}\left(\mathrm{P}\right(X_{ij}=1\left)\right)={\mathrm{\rho }}_j-Z_j{C}_{\text{center},i}+\frac{d_i^{\prime }}{2},$$ (2)

where P(X_ij = 1) is the probability of a correct answer for individual i on item j, and ρ_j represents the easiness of item j.

Task difficulty

ρ_j, d′_i, and C_center,i vary over items and examinees and can be specified as random effects in a mixed effects model. Accordingly, we analyzed the item accuracy data using generalized linear mixed modeling (GLMM; see Hox, 2010 for a review of multilevel or mixed-effects models) and the lme4 package for R (Bates, Maechler, Bolker, & Walker, 2014). To investigate predictors of task difficulty within an SDT scoring framework, we added fixed effect predictors of item accuracy to Equation 2. The predictors of interest included N-back load, number of word syllables, presentation time, and item count within each run (all centered). The effect of item type was also explored, although the effects are complex to dissociate. In the SDT model, values of d′, and C_center determine the difficulty of targets and foils; item difficulty is negatively associated with d′ for both targets and foils, and negatively associated with C_center for foils but positively associated with C_center for targets (see Equation 2). In the current approach, the means of the random effects determined the difficulty of targets and foils. Lure difficulty was determined the same as foil difficulty, except for a dummy-coded “Lure” variable that captured added difficulty due to the complexity of lures. Centered and log-transformed word frequency was included as a covariate. The combined model had the form:

$${\mathrm{\Phi }}^{-1}\left(\mathrm{P}\right(X_{ij}=1\left)\right)={\mathrm{\rho }}_j-Z_j{C}_{\text{center},i}+\frac{d{\text{'}}_i}{2}+\mathrm{N}-{\text{back}}_j\times b_3+{\text{Word Syllables}}_j\times b_4+{\text{Presentation Time}}_j\times b_5+{\text{Word Freguency}}_j\times b_6+{\text{Lure}}_j\times b_7,$$ (3)

where ρ_j, d′_i, and C_center,i were all treated as random effects, and all other terms were fixed effects with values varying depending on item j. The model does not have an intercept term so as to allow the means of d′_i and C_center,i to be non-zero (as they should be).

Measurement precision

In the GLMM approach d′ and C_center are modeled as random effects, which are equivalent to latent abilities in IRT (de Boeck et al., 2011). Individual values of d′ and C_center for all examinees were derived using maximum a posteriori (MAP) estimates. To quantify measurement error for these estimates, we extracted their posterior standard deviations (PSDs). Both MAPs and PSDs are produced by the lme4 R package. PSD, which is interpreted similarly to standard error of estimate, provides an index of measurement (im)precision based on the observed data. Measurement precision based on the model and fitted parameter estimates was quantified using information functions for multidimensional item response theory models (Reckase, 2009). Information, the inverse of squared standard error, is a statistic that reflects precision in ability estimates. We produced information functions for all combinations of item type by N-back factor levels focusing only on d′ while holding C_center to the mean value in the sample.

Effect size

Finally, we simulated data that would allow us to obtain estimates of the expected attenuation in group difference effect size (Cohen’s d) given different combinations of N-back load conditions. This consisted of the following steps: Step 1) we simulated normally distributed d′ and C_center values hypothetically obtained from samples of non-impaired and impaired individuals with d′ means fixed to 0.0 and 0.8 SDs below the overall sample mean in the current study respectively (i.e., corresponding to a Cohen’s d value of 0.8 [large effect]); Step 2) we created a pool of N-back items based on specific combinations of task difficulty factors (see below); Step 3) we calculated d′ for each participant in the simulated data using conventional formulas (Snodgrass & Corwin, 1988); Step 4) we calculated Spearman-Brown-corrected split-half reliability (Rel._S.B.) and Cohen’s d statistics; and Step 5) repeated Steps 2 through 4 for the following N-back load conditions: all 1-back, all 2-back, all 3-back, mix of 1-and 2-back, mix of 1- and 3-back, mix of 2- and 3-back, and mix of 1-, 2-, and 3-back. Importantly, the same total number of item responses were assumed in each simulation (240) hypothetically corresponding to 12 minutes of testing. To improve efficiency, each run had a distribution of 60% foils, 20% targets, and 20% lures. The mean for the non-impaired simulation group was fixed to the unweighted grand mean of the sample, as opposed to the sample mean of controls, in order to account for any demographic mismatch between outpatients and community controls in the current study (see below). We used the Spearman-Brown-corrected split-half reliability so that our results would be consistent with studies of N-back reliability reported in the literature (e.g., Jaeggi et al., 2010). The simulation was programmed in R.

Results Demographic Characteristics

We compared the samples on key characteristics to determine demographic similarity. Because undergraduates are not expected to be demographically similar to patients or community controls, comparisons were restricted only to the latter groups. The samples did not significantly differ with respect to age (F(2,72) = 3.12, ns, η² =.08) or gender (χ²(2; N = 75) = 1.80; ns; φ_c = .16). Moreover, although the groups differed in terms of education (F(2,72) = 19.01, p < .001, η² = .35), they did not significantly differ in terms of mean level of parent education (F(2,46) = 2.79, ns, η² = .11).

Descriptive Accuracy Results

Figure 3 shows mean accuracy results (i.e., the proportion of correct answers) broken down by N-back load, item type, and group. It is notable that accuracies were generally well over 50% and many were above 75%. Undergraduates generally performed better than community controls, followed by outpatients, and then inpatients. Foils were the easiest item type, and lures were the most difficult. Items became consistently harder as N-back load increased.

Figure 3.

Item accuracy by group, item type, and N-back. n refers to the number of observed item responses.

Ability and Task Difficulty

GLMM parameter estimates are reported in Table 2. The mean empirical estimate of discriminability (d′) was 4.20 in the sample, suggesting that the N-back task was moderately easy overall. The mean empirical estimate of bias (C_center) was 0.78, suggesting that foils were much easier—more often responded to correctly—than targets. The lure effect was significantly negative, indicating that lures were much more difficult than foils. Increasing N-back load, word syllables, and item count, as well as decreasing presentation time all predicted significantly worse accuracy. The effect of word frequency was not statistically significant. Interestingly, the standard deviation of empirically estimated item easiness (ρ) was small, suggesting that N-back difficulty was dominated by task rather than individual item features.

Table 2.

Generalized Linear Mixed Model Parameter Estimates

MAP Est. Random Effects	M	S2
Discriminability (d′)	4.20	1.03
Bias (Ccenter)	0.78	0.09
Item Easiness (ρ)	0.01	0.02
Fixed Effects	b	SE	CI95%	exp(b)	rxy.z	p
N-back Load	−0.552	0.028	[−0.607, −0.497]	0.58	0.24	< .001
Word Syllables	−0.094	0.027	[−0.146, −0.042]	0.91	0.04	< .001
Presentation Time	−0.062	0.025	[−0.111, −0.013]	0.94	0.02	0.014
Item Count	−0.009	0.002	[−0.013, −0.006]	0.99	0.06	< .001
Word Frequency	−0.023	0.012	[−0.048, 0.001]	0.98	0.02	0.059
Lure	−2.228	0.068	[−2.362, −2.094]	0.11	0.40	< .001

Note: MAP = maximum a posteriori; b = estimate of regression coefficient; SE = standard error of estimate; CI_95% = 95% confidence interval; exp(b) = coefficients scaled in log-odds; r_xy.z = partial correlation coefficients.

Measurement precision

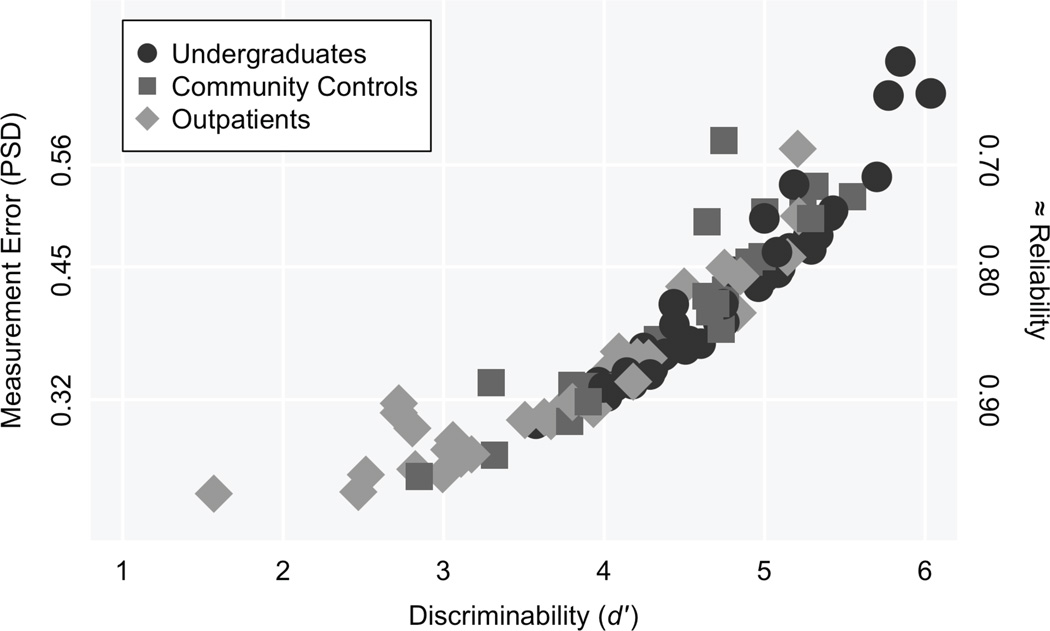
Table 3 reports mean estimates (MAPs) of d′ and C_center as well as measurement errors (PSDs) within each sample. (Note that these results do not attempt to control for demographic covariates.) Ability and measurement precision varied over populations. Figure 4 shows estimates of d′ plotted against the errors of those estimates for undergraduates, community controls, and outpatients (inpatients were omitted from the figure because, due to being administered fewer items [see methods], PSDs associated with inpatients’ ability estimates are higher than other groups). The figure also shows approximate values of reliability corresponding to each PSD level.³ Error appears to be a nonlinear function of ability level; PSDs were generally lower for examinees with low versus high values of d′. The PSDs generally suggest good or even excellent measurement precision in the sample; this is mainly due to the high number of N-back runs administered.

Table 3.

Mean Estimates and Error for Discriminability (d′) and Bias (C_center) by Group

	Undergraduates	Community Controls	Outpatients	Inpatients
Discriminability (d′)
Estimate	4.78	4.61	3.72	3.14
Error (PSD)	0.44	0.45	0.34	0.48
Bias (Ccenter)
Estimate	0.71	0.86	0.72	0.94
Error (PSD)	0.20	0.20	0.16	0.21

Note: PSD = posterior standard deviation.

Figure 4.

Estimates of discriminability (d′) against the measurement error (PSD) of each estimate. PSD = posterior standard deviation. Data for inpatients were omitted because, due to being administered fewer items by design (see methods), PSDs associated with inpatients’ ability estimates are higher than other groups

To further explore measurement precision we created information functions for combinations of N-back load and item type, holding all other task factors at their median values. The results are shown in Figure 5. For interpretability, the information functions (represented by solid, dashed, and dotted lines corresponding to 1, 2, and 3-back loads, respectively) are superimposed over the implied distributions of d′ for undergraduates, community controls, outpatients, and inpatients. As can be seen, the information functions generally peak at d′ values that are lower than the mean of each distribution of ability; this is particularly true of foils and all 1-back conditions. The results suggest that the N-back task was too easy to provide precise, or at least efficient, estimates of d′ for participants with average to above average ability. Moreover, foils provided almost no useful information about ability. Targets at 3-back and lures at 2 and 3-back were the most informative across all groups.

Figure 5.

Information functions for all combinations of N-back load by item type holding all other task factors at their median values. For interpretability, the information functions (represented by solid, dashed, and dotted lines corresponding to 1, 2, and 3-back loads) are superimposed over the implied distributions of discriminability (d′) in undergraduates, community controls, outpatients, and inpatients.

Effect Size

Results of the effect size simulation are reported in Table 4. Reliability was consistently worse for the non-impaired group. Reliability overall was closely tied to N-back difficulty. The simulations that used all 1-back conditions and a combination of both 1- and 2-back conditions both produced unacceptably low reliabilities, and Cohen’s d effect size values were severely attenuated for these simulations dropping by 0.37 (46%) and 0.30 (37%) respectively (i.e., from large to small and medium effects). The two best performing simulations were those that used all 3-back conditions and a mix of 2- and 3-back conditions. Both produced moderate reliabilities (0.75 and 0.70 respectively), and the simulated attenuations in Cohen’s d were 0.18 (22%) and 0.21 (26%) respectively.

Table 4.

Simulation Results

N-back Load	All Rel.S.B.	Non-Impaired Rel.S.B.s	Impaired Rel.S.B.	Simulated Cohen’s d	Measured Cohen’s d	Attenuation in Cohen’s d
All 1-back	0.41	0.30	0.42	0.80	0.43	0.37
All 2-back	0.61	0.50	0.62	0.80	0.54	0.26
All 3-back	0.75	0.68	0.75	0.80	0.62	0.18
Mix of 1- & 2-back	0.53	0.42	0.54	0.80	0.50	0.30
Mix of 1- & 3-back	0.64	0.55	0.64	0.80	0.58	0.22
Mix of 2- & 3-back	0.70	0.61	0.70	0.80	0.59	0.21
Mix of 1-, 2-, & 3-back	0.64	0.53	0.64	0.80	0.56	0.24

Note: Rel._S.B. = Spearman-Brown corrected split-half reliability.

Discussion

The results of this study demonstrate that reliability and measured group differences are both attenuated when cognitive tasks are not well matched to ability within the samples under investigation. These problems were demonstrated using a task commonly used to study working memory deficits in schizophrenia: the N-back task. We found that N-back load and item type were the two primary determinants of task difficulty. Difficulty increased along with N-back load, and lures and targets were both much harder than foils. Task conditions were maximally informative within the low average to highly impaired spectrum of ability. In a simulation study, we found that N-back tasks composed entirely of low load conditions (i.e., 1- and 2-back) were highly unreliable, and may reduce the observed effect size by half.

Strengths and Limitations

Strengths of the study include its novel statistical methodology, the heterogeneous sample, and the use of an experimental design to study task features on the N-back. However, results should be interpreted in light of several limitations. First, our sample and design did not provide data that would be sufficient to examine the dimensionality and construct validity of the N-back task. This topic is discussed in detail below. Second, it is common in psychometrics to examine detailed fit statistics in order to determine how well the theoretical model matches the observed data (Swaminathan, Hambleton, & Rogers, 2007). Although general markers of model fit were good (see supplemental material), we lacked appropriate data to examine item-level fit statistics (i.e., too few responses per item). Third, although common in the literature, we did not include a 0-back load condition, which is sometimes used to form contrast measures which, in theory, control for variance that is irrelevant to the target construct (e.g., attention and motivation). This was because we felt that the 0-back condition—where examinees are typically asked to respond anytime a key word is shown—may differ not just quantitatively, but also qualitatively from load conditions that require both active maintenance and continuous updating of newly encoded information. Fourth, although patients and community controls did not significantly differ in terms of age and gender, controls reported higher education. The difference in education is a common finding that almost certain reflects, at least in part, a consequence of mental illness. The groups were, however, matched on parental education, which may be a better indicator of premorbid demographic similarity. Nonetheless, to the extent that demographic factors exaggerated differences in working memory between groups, unequal reliability as well as attenuation in effect size between groups may have been overestimated. Finally, although our goal was to illustrate a general measurement concern, some results may be specific to characteristics of the current study. However, we purposely collected data from four separate populations and chose a variety of task manipulations in order to increase the range of ability and difficulty under investigation. As a practical guide, researchers may wish to compare their samples’ accuracy statistics to our results (Figure 3).

Significance and Implications

An N-back task with an appropriate number of items, that also includes 2- and 3-back conditions, as well as targets, lures, and foils, is expected to provide reliable, moderately efficient estimates of working memory ability in chronic patients with schizophrenia; the same task, however, is expected to provide less reliable estimates of ability in healthy controls. Because validity coefficients are attenuated by unreliability, associations between N-back scores and outcomes (or predictors) of cognitive impairment can appear weaker in healthy controls when compared to patients with schizophrenia simply due to this measurement artifact. Moreover, the dependence of reliability upon ability has been shown to bring potential confounds in studies of differential deficit (i.e., differences in cognitive abilities between groups; Chapman & Chapman, 1973; Strauss, 2001).

Within the framework of IRT, precision is maximized when predictable variance is maximized. Item information is greatest when the probability of a correct response is 0.50 for dichotomous item responses with no guessing. The common use of SDT to score N-back data in the literature implicitly assumes that examinees do not guess, but rather that response behavior is driven entirely by discriminability (d′) and bias (C_center). Thus, the simple observation that the majority of examinees performed far better than 50% on most N-back items (see Figure 3) suggests that the test does not produce optimally precise or efficient estimates of ability.

The pattern of measurement error (Figure 4) was consistent across samples, suggesting that measurement error was a function of ability but not population. It is reasonable to ask, then, how N-back task manipulations might be altered in such a way to improve the match between ability in difficulty across groups. Our results suggest that researchers should consider using more difficult versions of the N-back task in cognitive studies meant to precisely measure a wide range of individual differences in working memory ability. This is especially true in clinical studies that include healthy controls as a comparison group, or in studies meant to evaluate change over time. Considering the samples as a whole, our results (e.g., Figure 5) suggest that some examinees with below average ability, most examinees with average ability, and nearly all examinees with above average ability might be measured more efficiently and precisely with additional 4- and possibly even 5-back load conditions. Alternative possibilities for increasing item difficulty without increasing N-back load should also be considered. This might include the use of non-word stimuli, a greater proportion of lures, or dual N-back tasks (Jaeggi et al., 2003). The use of pseudowords (pronounceable word-like letter strings) has particular appeal given that pseudowords tend to have a more pronounced word syllable effect (Valdois et al., 2006) and produce higher false-alarm rates (Greene, 2004) relative to words.

There are, however, two major cautions to consider when evaluating these recommendations. First, efficient measurement, as is expected to result from administering more difficult items, could come at the cost of tolerability. Parenthetically, we have observed that participants’ reports of mental workload during the N-back task tend to be high even when performance is very good. Four- and especially 5-back runs may cause participants to prematurely discontinue testing, and thus tolerability must be weighed against the benefits of efficient measurement. Second, and perhaps more challenging, manipulating stimulus factors, especially factors other than N-back load, might fundamentally change the task in a way that threatens construct validity.

Indeed, there is a longstanding debate regarding the relative merits of manipulating task difficulty in order to improve the precision of cognitive measures (see Strauss, 2001). Changing task difficulty to improve reliability could come at the expense of validity. There are likely several overlapping cognitive processes engaged by the N-back: (1) processes meant to maintain goal and task relevant information without passive/external support – e.g., encoding, storage, and rehearsal; (2) processes meant to manipulate information so as to meet task demands – e.g., updating, ordering, and matching; and (3) processes involved in response execution – e.g., bias and inhibition (Cohen et al., 1994; Cohen et al., 1997; Jonides et al., 1997; Kane et al., 2007; Lezak et al., 2012; Oberauer, 2005; Wager & Smith, 2003). Because N-back scores likely reflect a weighted composite of these processes, and because manipulating task difficulty could upset this weighting, the dimensionality of observed scores might vary over conditions (but see Reise, Moore, & Haviland, 2010). From this perspective, it might be argued that task difficulty should only be manipulated if the dimensionality and construct validity of measures can be preserved across conditions.

Researchers interested in investigating, and dissociating, specific deficits using experimental cognitive approaches (see MacDonald & Carter, 2002), may prefer to compare performance scores produced by task conditions that are thought to isolate specific cognitive processes (e.g., Ragland et al., 2002). Unfortunately, under such circumstances—where difficulty is held constant within, but might differ between, experimental conditions—the amount of non-error or informative variance in test scores that is directly related to impaired neurocognitive processes might vary over conditions, thus leading to the presently detailed reliability and effect size confounds. As noted by MacDonald and Carter (2002, pp. 880–81), “The challenge for researchers from the experimental cognitive approach is to ensure that their measures of cognitive processes produce an adequate amount of variance so that they are sensitive to the presence of an impairment…”

There are two general solutions to this problem. First, researchers can explicitly seek to create process-pure or process-isolating tasks that nonetheless have a wide range of difficulty. Second, researchers can develop mathematical cognitive and psychometric measurement models that link manipulations of item difficulty to specific cognitive processes (e.g., Brown, Patt, Sawyer, & Thomas, 2016; Brown, Turner, Mano, Bolden, & Thomas, 2013; Embretson, 1984), thereby allowing for the optimization of measurement precision through difficulty manipulations while also accounting for the changing dimensionality of observed test scores. To this end, further work is needed to determine how best to manipulate task difficulty and model response processes on the N-back and other experimental cognitive measures being used in studies of abnormal cognition in schizophrenia (e.g., Barch & Smith, 2008).

Conclusion

This study has demonstrated how task difficulty affects both reliability and effect size measures of group differences. Although concerns related to mismatched ability and difficulty have been known in the psychometric literature for many years—and acknowledged using classical psychometric methods in schizophrenia research (Chapman & Chapman, 1973)—this study is among the first to show the practical, negative consequences of mismatched ability and difficulty using modern psychometric methods. The problems can be overcome, in part, by administering tasks that include a wide range of difficulty in order to avoid psychometric floor and ceiling effects. However, researchers must also consider how changes to task difficulty affect tolerability as well as both the dimensionality and the construct validity of measures.

General Scientific Summary.

Patients’ cognitive deficits can appear smaller than they truly are due to measurement artifacts. This study suggests that a measure commonly used to assess working memory deficits in schizophrenia can produce unreliable and attenuated estimates of ability because most items are too easy. The methodology presented is general, and can be used by investigators to determine whether cognitive tasks used in research are appropriately calibrated for the samples under investigation.

Appendix

This appendix provides the derivations of the general linear model used in all analyses. Equal variance SDT (DeCarlo, 1998; Snodgrass & Corwin, 1988) first assumes that the distributions of familiarity for targets and foils (or lures) can modeled by two normal distributions (mean μ_T and μ_F, respectively) with equal variance (see Figure 2). The discrimination parameter d′ represents the distance between the two distributions:

$$d´={\mathrm{\mu }}_{\mathrm{T}}-{\mathrm{\mu }}_{\mathrm{F}}.$$ (1)

The decision criterion, C, represents the threshold at which individuals may judge that an item looks familiar enough to respond. C can be centered with respect to the mid-point between the two distributions:

$$C_{\text{center}}=C-\frac{{\mathrm{\mu }}_{\mathrm{T}}+{\mathrm{\mu }}_{\mathrm{F}}}{2}.$$ (2)

The probability of responding given that a target was presented, P(U = 1|Target), corresponds mathematically to the area under the target distribution that is to the right of the criterion:

$${\mathrm{\Phi }}^{-1}\left(\mathrm{P}\right(U=1\left|\text{Target}\right))={\mathrm{\mu }}_{\mathrm{T}}-C,$$ (3)

where Φ⁻¹ is the inverse cumulative distribution function for the normal distribution. Similarly, the probability of responding given that a foil (or lure) was presented, P(U = 1|Foil), corresponds mathematically to the area under the foil distribution that is to the right of the criterion:

$${\mathrm{\Phi }}^{-1}\left(\mathrm{P}\right(U=1\left|\text{Foil}\right))={\mathrm{\mu }}_{\mathrm{F}}-C.$$ (4)

Using binary variable Z = 1 if the test item is a target and Z = −1 if the test item is a foil (or lure), Equations 3 and 4 can be combined into the formula that appears in Appendix A of DeCarlo (1998):

$${\mathrm{\Phi }}^{-1}\left(P\right(U=1\left|Z\right))=({\mathrm{\mu }}_{\mathrm{F}}-C)(\frac{1-Z}{2})+({\mathrm{\mu }}_{\mathrm{T}}-C)(\frac{Z+1}{2})=-C_{\text{center}}+\frac{d\prime }{2}Z.$$ (5)

In order to align the approach with IRT, the model can also be formulated to predict the probably of a correct response. A new binary variable X was thus introduced so that X = 1 for a correct response and X = 0 for an incorrect response. Using the property that Φ⁻¹(1-P) = -Φ⁻¹(P), and knowing that responding is correct when a target is presented whereas non-responding is correct when a foil is presented, Equation 5 yielded

$$\{\begin{array}{c}{\mathrm{\Phi }}^{-1}\left(\mathrm{P}\right(X=1\left|\text{Target}\right))={\mathrm{\Phi }}^{-1}(\mathrm{P}(U=1|\mathrm{Z}=1\left)\right)=-C_{\text{center}}+\frac{d\text{'}}{2}\hfill \\ {\mathrm{\Phi }}^{-1}\left(\mathrm{P}\right(X=1\left|\text{Foil}\right))={\mathrm{\Phi }}^{-1}(1-\mathrm{P}(U=1|\mathrm{Z}=-1\left)\right)=C_{\text{center}}+\frac{d\text{'}}{2}\hfill \end{array}.$$ (6)

These equations were combined, leading to:

$${\mathrm{\Phi }}^{-1}\left(\mathrm{P}\right(X=1\left|Z\right))=-Z{C}_{\text{center}}+\frac{d\prime }{2}.$$ (7)

To account for item differences in easiness (over j of J items) and person differences in ability (over i of N people), as in IRT, we added the term ρ as well as subscripts to each parameter to arrive at our final equation:

$${\mathrm{\Phi }}^{-1}\left(P\right(X_{ij}=1\left)\right)={\mathrm{\rho }}_j-Z_j{C}_{\text{center},i}+\frac{d_i^{\prime }}{2}.$$ (8)

In this form, the model is functionally equivalent to a multidimensional IRT model, but appears superficially distinct due to the use of notation this is common in SDT but not IRT (see Thomas et al., 2016).