Matching weights to simultaneously compare three treatment groups: Comparison to three-way matching

Abstract

BACKGROUND

Propensity score matching is a commonly used tool. However, its use in settings with more than two treatment groups has been less frequent. We examined the performance of a recently developed propensity score weighting method in the three treatment group setting.

METHODS

The matching weight method is an extension of inverse probability of treatment weighting (IPTW) that reweights both exposed and unexposed groups to emulate a propensity score matched population. Matching weights can generalize to multiple treatment groups. The performance of matching weights in the three-group setting was compared via simulation to three-way 1:1:1 propensity score matching and IPTW. We also applied these methods to an empirical example that compared the safety of three analgesics.

RESULTS

Matching weights had similar bias, but better mean squared error (MSE) compared to three-way matching in all scenarios. The benefits were more pronounced in scenarios with a rare outcome, unequally sized treatment groups, or poor covariate overlap. IPTW’s performance was highly dependent on covariate overlap. In the empirical example, matching weights achieved the best balance for 24 out of 35 covariates. Hazard ratios were numerically similar to matching. However, the confidence intervals were narrower for matching weights.

CONCLUSIONS

Matching weights demonstrated improved performance over three-way matching in terms of MSE, particularly in simulation scenarios where finding matched subjects was difficult. Given its natural extension to settings with even more than three groups, we recommend matching weights for comparing outcomes across multiple treatment groups, particularly in settings with rare outcomes or unequal exposure distributions.

INTRODUCTION

The emergence of multiple treatment options makes the availability of comparative effectiveness/safety evidence more important. However, head-to-head clinical trials are not common, let alone trials of multiple active treatment options. Observational studies can play an important role in filling this gap; however, confounding by indication¹ is a challenge.

Initially proposed in 1983, the propensity score² has become a commonly used tool to address confounding in the scientific literature. However, its use in multiple group settings has not received as much attention^3–5. Rassen et al³ explored an extension of propensity score matching to the three-group setting, developing a three-way simultaneous nearest neighbor matching algorithm (three-way matching). However, simultaneous matching in multiple dimensions is computationally burdensome and often leads to many patients being excluded because appropriate matches are unavailable. Therefore, the extension of this approach to four or more groups has not been achieved.

Li and Greene recently proposed a weighting analogue to pairwise 1:1 matching⁶ (matching weights), and demonstrated that its estimand is asymptotically equivalent to the estimand of exact pairwise matching on the propensity score, given common support of the propensity score between treatment groups. As compared to matching, efficiency gains were seen in simulations. Therefore, we hypothesized that matching weights generalized to the setting of three treatment groups would outperform three-way matching.

In the current paper, we generalize matching weights to the setting of three or more treatment groups and present a simulation study that compares the validity and precision of matching weights, three-way matching, and inverse probability of treatment weights. Finally, we use empirical data to demonstrate its performance in a real-life dataset.

METHODS

Matching weights

Li and Greene’s proposed weight is defined as follows for the i-th subject⁶:

$$\text{Matching}\text{weight}=\frac{min(e_i,1-e_i)}{Z_i{e}_i+(1-Z_i)(1-e_i)}$$

where

• e_i is the propensity score

• Z_i is the binary treatment indicator

The denominator is identical to that of inverse probability of treatment weights (IPTW)⁷, the probability of the assigned treatment given covariates. The numerator is the smallest of the propensity score or its complement, which can be thought of as a combination of the numerator for the average treatment effect on the treated weight (“treated weight”)^8,9 and that for the average treatment effect on the untreated weight (“untreated weight”)⁹. These weights' close relationships can be appreciated if they are expressed in the same notation as shown below.

$$\begin{array}{l}\mathit{IPTW}=\frac{1}{Z_i{e}_i+(1-Z_i)(1-e_i)}\\ \text{Treated}\text{weight}=\frac{e_i}{Z_i{e}_i+(1-Z_i)(1-e_i)}\\ \text{Untreated}\text{weight}=\frac{1-e_i}{Z_i{e}_i+(1-Z_i)(1-e_i)}\end{array}$$

Matching weights reduce to the treated weights for those with propensity scores < 0.5, untreated weights for those with propensity scores > 0.5, and at propensity scores = 0.5, matching weights agree with both.

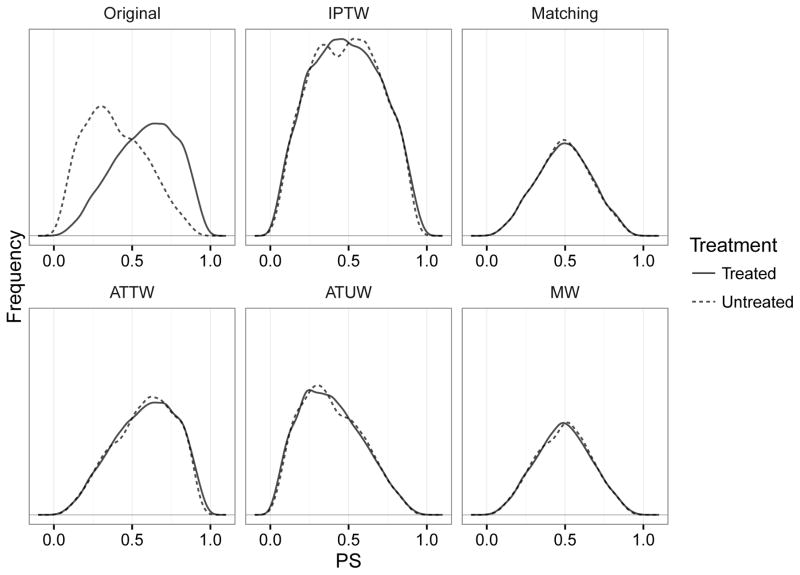
A simulated dataset may help intuitive understanding (Figure 1). Compared to the inverse probability of treatment weights method, which up-weights subjects to balance the distributions of the propensity score, matching weights instead down-weight subjects to achieve balance. In this example, the treated group is as large as the untreated group, making the target of matching weights and 1:1 matching depart from the treated group. If there is a large reservoir of untreated¹⁰, however, most observations fall below propensity score <0.5, making both matching weights and 1:1 matching approximate the treated group similarly well (eFigure 1). Matching weights confer numerical stability compared to inverse probability of treatment weighting, which can suffer from very high weights, by focusing on treatment effects in patients with good overlap on the propensity score.⁶ Compared to matching, matching weights are more efficient because they use all of the original data.

Figure 1.

Illustration of pre- and post-weighting or post-matching distributions of propensity score when the treatment prevalence is 50%. The solid line is the distribution of the propensity scores in the treated, and the dashed line is the distribution in the untreated. Matching and matching weight cohorts have a similar propensity score distribution, indicating that their estimands are similar. However, their distributions are substantially different from the original treated group, indicating their departure from the average treatment effect in the treated.

Abbreviations: IPTW: inverse probability of treatment weights; ATTW: average treatment effect on the treated weights; ATUW: average treatment effect on the untreated weights; MW: matching weights.

Generalization of matching weights

Unlike matching, weighting methods can naturally generalize to a non-dichotomous treatment variable, including three or more treatment groups. For matching weights under K treatment groups, the weight can be generalized as follows.

$$\text{Matching}\text{weight}=\frac{min(e_{1i},\dots ,e_{Ki})}{{\sum }_{k=1}^{K}I(Z_i=k)e_{ki}}$$

where

• e_ki is the generalized propensity score for the kth treatment

  • (i.e., probability of receiving the k-th treatment)

    • Z_i ∈ {1, … K} is a categorical treatment

  • I(·) is an indicator variable (1 if true and 0 if false)

The denominator is the probability of receiving the treatment actually received given covariates. The numerator considers probabilities for all treatment levels and selects the smallest value. For a given individual, the sum of all propensity scores must add up to 1, meaning that a single model must be fit to the data to estimate all of the propensity scores (e.g., multinomial logistic regression).⁴ Again the estimand of this generalized weighting method is asymptotically equivalent to the estimand of exact matching across all treatment groups if common support (i.e., positivity) holds for all treatment levels (proofs in eAppendix page 1–9).

Simulation study

We compared matching weights⁶, stabilized inverse probability treatment weighting¹³, and the three-way matching method developed by Rassen et al³ in simulated datasets (details in eAppendix pages 10–14).

Data Generation

The data generation mechanism followed Franklin et al.¹⁴ The outcome was binary, and the treatment took on three values. There were ten confounders (binary and continuous). Levels of covariate overlap, treatment prevalence, baseline outcome risk, treatment effects, and treatment effect modification were varied. Each dataset had 6,000 subjects. Treatment assignment (T_i ∈ {0, 1, 2}) was generated as a multinomial random variable based on true propensity scores. We generated all combinations of exposure prevalence {33:33:33, 10:45:45, 10:10:80} and weak (near-random treatment assignment; good covariate overlap) and strong (non-random treatment assignment; poor covariate overlap) covariate-treatment associations.

All covariates and treatment jointly determined the true probability of disease for each subject. The counterfactual probability of disease under each treatment was also recorded. To avoid non-collapsibility issues^15,16, a log-probability model was used.

$$log(\mathrm{P}(Y_i=1\mid T_i=t_i,{\mathit{X}}_{\mathit{i}}={\mathit{x}}_{\mathit{i}}))={\beta }_0+{\mathit{x}}_i^T{\mathit{\beta }}_{\mathit{X}}+{\beta }_{T1}I(t_i=1)+{\beta }_{T2}I(t_i=2)+{\beta }_{T1X_4}I(t_i=1)x_{4i}+{\beta }_{T2X_4}I(t_i=2)x_{4i}$$

The bold β_X represents main effects of covariates. Treatment has two main effect terms. The last two terms are treatment-X₄ interactions. Treatment 0 served as the baseline for comparison, and treatments 1 and 2 had no effects or protective effects. The intercept β₀ was manipulated to achieve the baseline disease risk of 5% or 20%. We controlled treatment effect heterogeneity by setting the coefficients of the interaction terms to either zeros (no heterogeneity) or negative (additional protective effect for individuals with x_4i = 1). Combining these simulation parameters, we constructed 48 simulation scenarios (eAppendix page 13). Each scenario was run 1,000 times.

Propensity score estimation

For each simulated dataset, the propensity score model including all covariates was fit by multinomial logistic regression¹⁷. For each subject, three propensity scores (e_0i, e_1i, and e_2i) were estimated.

Matching weight procedure

Weights were estimated from three propensity scores. Subsequent analyses, including balance metrics and risk regression (modified Poisson regression¹⁸), were conducted as weighted analyses^19,20. The treatment variable was the only predictor in the outcome model. We conducted the estimation using the stabilized inverse probability treatment weighting, similarly substituting the weights. Reproducible example R code is provided in eAppendix (pages 15–21).

Three-way matching procedure

Using non-redundant propensity scores to define a two-dimensional propensity score space, we conducted three-way matching without replacement³. The Pharmacoepidemiology Toolbox version 2.4.15 (http://www.drugepi.org) was used. The caliper width was based on the perimeter of the triangle formed by three individuals in a proposed matched trio.³ The maximum allowed perimeter was:

$$0.6\times \sqrt{\frac{{\tau }_0^2+{\tau }_1^2+{\tau }_2^2}{3}}$$

where

$${\tau }_k^2=\frac{\text{Var}(e_{0i}\mid T=k)+\text{Var}(e_{1\mathrm{i}}\mid T=k)}{2}$$

We conducted modified Poisson regression¹⁸ without stratifying on matched trios to maintain the unconditional estimand comparable to that of matching weights.

Performance assessment metrics

We used several assessment metrics to examine validity and efficiency: weighted or matched sample size, covariate balance measured by absolute standardized mean differences,^21,22 bias in risk ratios, simulation variance, estimated variance, mean squared errors (MSE), false positive rates in null scenarios, and coverage probability of confidence intervals. Bias and covariate balance, which measures the potential for confounding bias, are measures of validity, whereas variance is a measure of efficiency.

We calculated standardized mean differences for three pairwise contrasts and averaged them for each covariate. We standardized by dividing the mean difference by the square root of the pooled within-group variance (its definition for binary variables is explained in references).^21,22

We defined bias for an effect estimate as the average risk ratio estimate divided by the true risk ratio. The true risk ratio (estimand) was calculated as the contrast of the marginal counterfactual outcomes (average of the counterfactual probabilities of disease across individuals under each treatment). We calculated this true risk ratio in the unadjusted cohort (for the average treatment effect), matching weight cohort, three-way matched cohort, and inverse probability treatment weight cohort (this should agree with the average treatment effect) to obtain their respective estimands. These adjusted cohorts were newly constructed using the true propensity scores to avoid the influence of the propensity score estimation model performance. The estimands themselves were also compared for their agreement under treatment effect heterogeneity.

The simulation variance is the variance of the estimator across simulation iterations, and represents the true variance of the estimator, whereas the estimated variance was calculated within each iteration and average across all iterations. The bootstrap variance was calculated for matching weights only due to computational burden. The full sequence of propensity score modeling and outcome modeling was bootstrapped¹². For each one of 1,000 iterations of a given scenario, 1,000 bootstrap iterations were conducted. MSE combines bias and true variance (variance + bias²). False positive rates were examined in the null scenarios where there was no treatment effect and no treatment effect heterogeneity. The confidence intervals created from the estimated variance were examined for their coverage of the aforementioned true risk ratios to see whether these intervals are conservative in nature by ignoring uncertainty in the estimated propensity score^6,11.

Empirical study

We re-analyzed Medicare data from a previously published study comparing new users of opioids, COX-2 selective inhibitors (coxibs), and non-selective non-steroidal anti-inflammatory drugs (NSAIDs)^3,23 for various safety outcomes. The empirical analysis was approved by the Partners Healthcare Institutional Review Board. There were 35 covariates including five continuous variables. The propensity score model was pre-specified as a model with squared terms for the continuous variables without any interaction terms. All-cause mortality, any fracture, upper or lower gastrointestinal bleeding, and any cardiovascular events were examined.

The baseline covariates for each treatment group before and after weighting (or matching) were examined. Average standardized mean difference across all three pairwise contrasts was calculated for each variable. For the outcome analyses using Cox models, hazard ratios with corresponding 95% confidence intervals were calculated and compared between methods for each outcome event.

Computing

All analyses were conducted in R (http://cran.r-project.org) versions 3. All code for the simulation study is available online (https://github.com/kaz-yos/mw).

RESULTS

Simulation study

Sample sizes

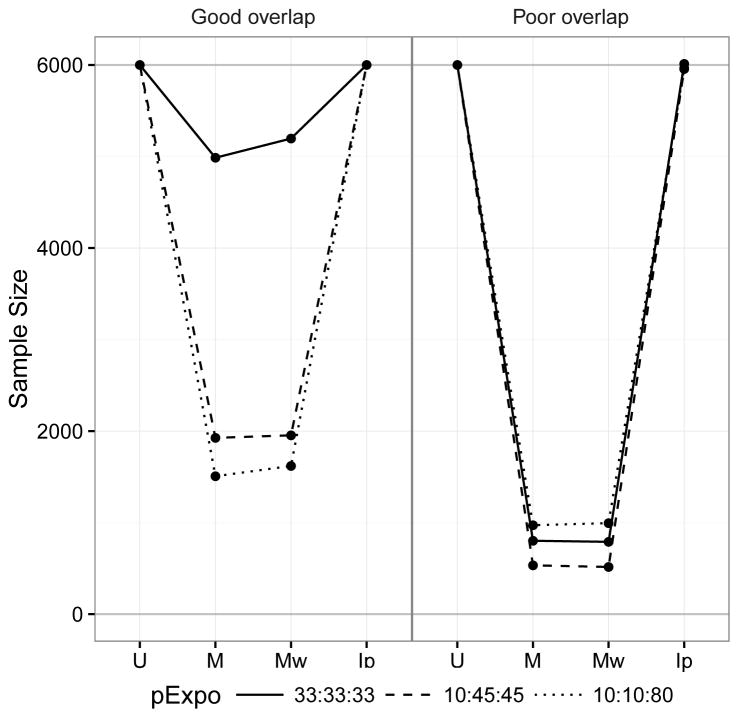
Sample size comparison is presented in Figure 2. The matching weight sample sizes and the matched sample sizes were similar given Rassen et al.’s caliper configuration. They were influenced by both the treatment prevalence and covariate overlap because the size of the common support and number of 1:1:1 matches are influenced by these factors. This means their estimands are similarly affected by the characteristics of the dataset. The unmatched sample size and the stabilized inverse probability treatment weight sample size coincide regardless of the treatment prevalence and covariate overlap. This agrees with the fact that the stabilized inverse probability treatment weight estimates the effect in the entire cohort rather than a subset as in matching weights and matching.

Figure 2.

Comparison of weighted and matched sample sizes under different levels of covariate overlap. IPTW shows a weighted sample size identical to the original cohort. Matching weights and matching are similarly affected by exposure prevalence and poor covariate overlap, indicating shifts in the target population.

Abbreviations: U: Unmatched cohort, M: Matched cohort; Mw: matching weight cohort; Ip: Inverse probability of treatment weight cohort; pExpo: Exposure prevalence

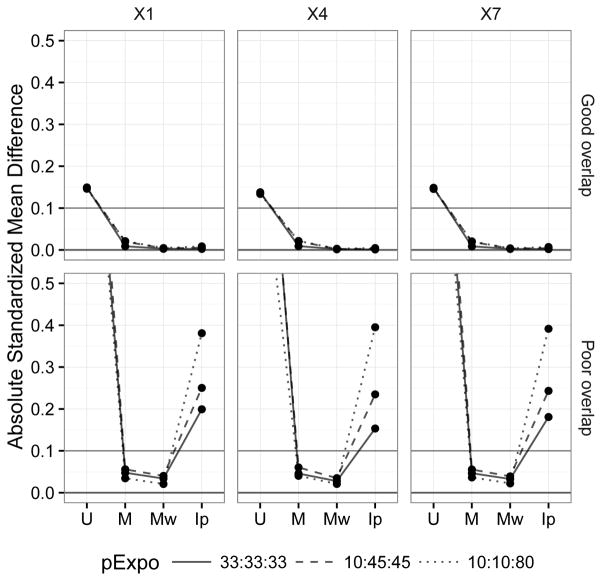
Covariate balance

Figure 3 shows the covariate balance before and after balancing by the different methods. In the good covariate overlap setting where there was a minor imbalance to start with, all methods did well, making all standardized mean differences well below the conventional 0.10 threshold²¹. Among the three methods, matching weights achieved the best balance with near-zero standardized mean differences for all covariates followed by inverse probability treatment weights. In the poor covariate overlap setting, i.e., a setting with positivity violation (some subjects exist outside the common support), inverse probability treatment weights broke down, indicating that the entire cohort estimand is likely not estimable in this setting. In comparison, both matching weights and matching performed reasonably well, likely because of their emphasis on the effect in the common support.

Figure 3.

Comparison of covariate balance before and after matching or weighting by average standardized mean differences under different covariate overlap (selected covariates: X1, X4, and X7). MW performs best in both settings, whereas IPTW only works in the good covariate setting. The other covariates showed similar patterns.

Abbreviations: U: Unmatched cohort, M: Matched cohort; Mw: matching weight cohort; Ip: Inverse probability of treatment weight cohort; pExpo: Exposure prevalence

Bias of estimators

eFigure 2 shows the biases of these methods with respect to their corresponding estimands (1.0 means unbiased). The biases were similarly small for all methods in the good covariate overlap settings. In the poor covariate overlap settings, however, their performance differed. Most noticeably inverse probability treatment weights sometimes gave more biased results than the unadjusted analyses, confirming the difficulty of estimating the effect in the entire cohort in such settings. Both matching weights and three-way matching performed reasonably well in all settings, although in the rare outcome setting, matching weights tended to perform better.

Comparison of estimands

eFigure 3 shows the estimands (true risk ratios to be estimated) of these methods in different settings. In the absence of effect modification (left half of the figure), their estimands numerically agree. In the presence of effect modification, they may differ substantially. Inverse probability treatment weighting by definition has the entire cohort as its target of inference (thus, the agreement between U and Ip in the figure). The estimands of matching weights and three-way matching agreed as expected, but they differed from the inverse probability treatment weights estimand particularly in the unbalanced exposure settings. On the other hand, their estimands were close to each other with good covariate overlap and the 33:33:33 exposure distribution (i.e., a setting in which the matching weight or matched sample sizes are close to the entire cohort).

Variance and MSE of estimators

The matching weight estimator had smaller true variance than the three-way matching estimator, particularly in poor covariate overlap settings (eFigure 4). In these settings, matching yields a small matched cohort, whereas matching weights do leverage data from all subjects although the weighted cohort is similarly small. The difference was most striking in the poor covariate overlap, rare disease, 10:45:45 treatment distribution scenario. This difference was caused by lack of any observed events in treatment group 2 in the matched cohort in some datasets. The estimated variance (eFigure 5) showed a similar pattern but was sometimes anti-conservative for all methods in poor overlap scenarios. The bootstrap variance for matching weights was less often anti-conservative (eFigure 6). Since the bias was small, MSE (eFigure 7) also showed a similar pattern. Importantly, matching weight MSE was always smaller than matching MSE across all scenarios.

False positive rates and coverage

Matching weights had false positive rates > 0.05 for 6 scenarios whereas three-way matching had them for five scenarios (eFigure 8). Undercoverage (coverage < 0.94) was observed in seven scenarios for matching weights and three scenarios for three-way matching (eFigure 9). For matching weights, undercoverage occurred in poor covariate overlap scenarios only, whereas two of the undercoverage scenarios for three-way matching were in good overlap scenarios.

Empirical study

In the three-group analgesic example, there were 23,647 potentially eligible patients before weighting or matching. After matching weights, the weighted sample size was 13,887.9, which was similar to the three-way matched sample size of 13,833, whereas inverse probability treatment weights resulted in a weighted sample size of 23,699.4, which was similar to the original cohort size. Individuals’ assigned weights ranged from 0.0003 to 1 with a median of 0.577 [interquartile range: 0.318–0.897] for matching weights, and 0.241–12.938 with a median of 0.939 [interquartile range: 0.809–1.126] for stabilized inverse probability treatment weights. As seen in eFigure 10, matching weights achieved the best covariate balance most consistently (24 of the 35 covariates) compared to three-way matching (six covariates) and inverse probability treatment weights (five covariates). Thanks to the active comparator design²⁴, the covariate overlap was relatively good (relatively small standardized mean difference in the unmatched cohort), and inverse probability treatment weighting did not break down.

The characteristics of the matching weights cohort and the matched cohorts for selected variables with most imbalances were very similar (eTable 1), again confirming the notion that matching weights are a weighting analogue to matching. As expected from the definition of the common support (overlap area of all three groups), these cohorts are most similar to the smallest group, i.e., the NSAIDs group in the unmatched cohort. The inverse probability treatment weights cohort had somewhat different characteristics with higher morbidity levels, most closely resembling the largest group, i.e., the opioids group.

The outcome model results are shown in Table 1. The hazard ratios were similar using matching weights and three-way matching, but inverse probability treatment weights sometimes differed. Between matching weights and three-way matching, the most noticeable difference was in the opioids-vs-non-selective NSAIDs comparison for the gastrointestinal bleeding outcome, which was the rarest outcome among the four considered in the current study. The standard errors were smaller for matching weights than for three-way matching or inverse probability treatment weighting for all estimates, as reflected by the somewhat narrower confidence intervals.

Table 1.

Comparison of hazard ratios for coxibs and opioids (nonselective NSAIDs as the reference) by different methods and outcomes.

	Coxibs vs nsNSAIDs	Opioids vs nsNSAIDs
	HR [95% CI]	HR [95% CI]
Death
Unmatched	1.70 [1.29, 2.24]	2.82 [2.19, 3.64]
Matched	1.42 [1.06, 1.89]	2.00 [1.49, 2.67]
MW	1.39 [1.06, 1.84]	1.97 [1.52, 2.57]
IPTW	1.38 [1.02, 1.87]	1.96 [1.48, 2.60]
Fracture
Unmatched	1.18 [0.80, 1.75]	5.82 [4.19, 8.09]
Matched	0.95 [0.62, 1.45]	4.71 [3.31, 6.70]
MW	1.01 [0.68, 1.50]	4.73 [3.40, 6.60]
IPTW	0.89 [0.58, 1.36]	4.07 [2.81, 5.88]
GI bleed
Unmatched	0.93 [0.60, 1.44]	1.53 [1.03, 2.26]
Matched	0.93 [0.59, 1.48]	1.00 [0.61, 1.64]
MW	0.86 [0.55, 1.33]	1.11 [0.74, 1.67]
IPTW	0.92 [0.58, 1.46]	1.20 [0.79, 1.80]
Cardiovascular
Unmatched	1.60 [1.30, 1.98]	2.29 [1.88, 2.80]
Matched	1.42 [1.13, 1.78]	1.59 [1.25, 2.00]
MW	1.36 [1.10, 1.67]	1.63 [1.33, 2.00]
IPTW	1.27 [0.98, 1.64]	1.44 [1.12, 1.86]

Abbreviations: MW: matching weights; IPTW: inverse probability of treatment weights; Matched: three-way matching; Coxibs: COX-2 selective inhibitors; nsNSAIDs: non-selective non-steroidal anti-inflammatory drugs; HR: hazard ratio; CI: confidence interval.

DISCUSSION

We examined the usefulness of a recently proposed weighting method⁶ in multiple treatment arm settings, comparing it to the previously described three-way matching method³ as well as inverse probability treatment weighting²⁵ in both simulated data and a reanalysis of a previously published empirical study.²³ Overall, matching weights provided smaller MSE than three-way matching in the scenarios studied mainly due to smaller variance. Better MSE was more pronounced in settings where matching performed poorly, such as with rare disease and poor covariate overlap. Compared to inverse probability treatment weighting, matching weights demonstrated robustness to poor covariate overlap. The false positive rate and coverage rate for matching weights were somewhat less ideal than three-way matching, indicating the need for the bootstrap variance. In the empirical data analysis, matching weights gave similar point estimates compared to three-way matching, but with better covariate balance and narrower confidence intervals.

The strengths of matching weights are the combination of the strengths of matching and weighting. The estimand of the matching weight estimator is asymptotically equivalent to that of 1:1 exact matching. We confirmed that this approximately holds in finite datasets using nearest-neighbor matching (eFigure 3). Those who are nearly equally likely to receive all treatment choices are most represented (Figure 1). Matching weights avoid inflating weights for a small number of subjects in the extremes of the propensity score distribution treated contrary to the norm, which is a major disadvantage of typical inverse probability treatment weighting approaches.

From weighting, matching weights inherit the maximum use of the data, i.e., no one in the dataset is left out, but subjects contribute differing amounts of information depending on their weights. The efficient use of data resulted in lower variance of estimators in our simulation and narrower confidence intervals in our empirical study. As with other weighting methods, matching weights can naturally generalize to multiple treatment group settings, which we demonstrated in this paper. Currently, there appears to be no software available for 4+ group simultaneous matching, which matching weights can easily accommodate.

Matching weights outperformed inverse probability treatment weights in scenarios with poor covariate overlap; however, choice of a method should carefully consider both the clinical question and the data (Table 2). Although matching weights are an extension of inverse probability treatment weights, their targets of inference are different as illustrated in Figure 1. Their estimands (true risk ratios to be estimated) numerically agree if no treatment effect heterogeneity exists (left half of eFigure 3), and they nearly coincide if covariate overlap is good (first and third rows of eFigure 3). However, their estimands are not directly comparable in settings with treatment effect heterogeneity as demonstrated in the right half of eFigure 3, particularly if covariate overlap is poor (second and fourth rows). When making a decision about which propensity score method to employ, the estimand should be decided first based on the clinical question. If it is the causal effect in the entire population, inverse probability treatment weighting is the method of choice.

Table 2.

Characteristic of methods examined in this paper.

	MW	Three-way matching	IPTW
Estimand	Average treatment effect in a subset.a	Average treatment effect in a subset.a	Average treatment effect in the entire cohort.
Robustness to common support violation	Robust within our simulation scenarios.	Robust within our simulation scenarios.	Not robust. Biased in poor covarite overlap settings.
Computation	Simple	Intensive in large datasets.	Simple
Tuning parameter	PS model	PS model. Distance metric and scale. Caliper size. Matching algorithm.	PS model
Analysis	Weighted analysis	Regular analysis	Weighted analysis
Variance	Small in all settings. Estimate using bootstrapping.	Large in poor covariate overlap with rare events.	Small if covariate overlap is substantial. Large if poor.
Diagnostics	SMD after weighting. Weighted sample size in comparison to the full cohort.	SMD after matching. Matched sample size in comparison to the full cohort.	SMD after weighting. Average weight (should be close to 1 if stabilized).

^aThe estimand can be close to the effect in the entire cohort if group sizes are balanced and covariate overlap is substantial. If one of the groups is small and covariate overlap is substantial, the estimand can be close to the effect in the smallest group. If covariate overlap is poor, the estimand is the effect in a small subset that may not be representative of any of the groups.

Abbreviations: MW: matching weights; IPTW: inverse probability of treatment weights; PS: Propensity score; SMD: Standardized mean difference.

Nonetheless, as seen in the poor covariate overlap simulation scenarios, the performance of inverse probability treatment weighting degrades when positivity violations²⁶ exist because the effect in the entire cohort is not estimable. The inverse probability treatment weighting cohort can be “trimmed” to drop subjects who violate positivity, but this will also reduce the effective sample size and modify the target of inference (detailed discussions of propensity score trimming in the two-group setting are in Crump et al²⁷ and Stürmer et al²⁸). Matching weights and matching approach this problem by focusing on the patients with “empirical equipoise”²⁹ --i.e., patients for whom all treatment options under study are appropriate. This subset is not easily definable; however, in the setting of 3+ active treatment groups, the average treatment effect on the treated is not uniquely defined, justifying focusing on this feasible subset. This subset is also where comparative effectiveness evidence may be most useful for decision-making. In practice, the matching weight cohort, as well as the original cohort, should be presented in the baseline table to clarify the subset of the population for which inference was made.

Another potential approach given three or more groups is to match two groups at a time, resulting in three matched cohorts with different pairs of treatment arms (i.e., to separately target the populations for whom those two treatments are equally possible). These three cohorts are not directly comparable to the one cohort given by matching weights or three-way matching. Whether the former is a more appropriate method depends on the clinical question and situation. The mean matching weight (ranges 0 to 1) in the group that had the smallest unweighted sample size may be used to assess the simultaneous common support. This quantity is roughly interpretable as the fraction of the smallest treatment group in clinical equipoise with the other groups. If this fraction is close to 1, the treatment groups have reasonable overlap and the factor constraining the weighted sample size is the number of subjects in the smallest group. On the other hand, if the fraction is close to 0, it is the lack of sufficient common support that is constraining the weighted sample size. In the latter setting, the more meaningful questions may be answered by pairwise comparison. If the problem persists with pairwise matching weights, it means not enough common support exists in the data to enable comparative effectiveness research.

There are potential limitations in the current study. We employed the caliper configuration for three-way matching used in the paper by Rassen et al.³ Currently, no known standard exists for caliper definitions (raw propensity score or logit of propensity score) or caliper widths for three-way matching. In the 4 or more group settings, even the distance metric is hard to define. Matching weights, on the other hand, completely avoids the use of an arbitrary caliper parameter. Investigators can instead focus on the structure of the propensity score model.

Matching methods, including three-way matching, are, by definition, protected against common support (positivity) violations at least with narrow matching calipers. Subjects with propensity scores that are not present in other treatment groups cannot match, and are excluded. This is not true for matching weights, as everybody, even those without exactly comparable subjects in other groups, contributes to the weighted analyses. This is why the theoretical asymptotic equivalence of the estimands of matching weights and matching requires perfect common support in addition to exact matching.⁶ However, poor covariate overlap did not adversely affect matching weights in comparison to inverse probability treatment weights, which did not perform well in poor covariate overlap scenarios.

There have been debates about whether to account for the uncertainty in the estimated propensity score¹¹, which are estimates of the true underlying propensity score. Li and Greene found that not accounting for the uncertainty (using estimated propensity scores as if they were known constants) results in conservative variance estimates⁶, whereas simultaneous estimation of the propensity score and outcome model parameters gave correct variance estimates. We did not pursue this method, as the generalization to multiple treatment group settings and binary outcomes was unclear. They suggested bootstrapping as an alternative that is easier to implement. In our simulation study in the three-group setting with a binary outcome, matching weight variance estimates were somewhat anti-conservative (smaller than the true variance) in poor covariate overlap scenarios. Bootstrap variance performed more accurately and was less often anti-conservative.

In conclusion, matching weights are a viable alternative to matching, especially with three or more treatment groups. Matching weights demonstrated improved performance over three-way matching in terms of MSE. With good covariate overlap, matching weight estimates were similar to inverse probability treatment weight estimates, although, in such settings, the latter may be preferable due to its clearer target of inference. Given its natural extension to settings with more than three groups, we recommend matching weights for comparing outcomes across multiple treatment groups when covariate overlap is relatively limited, outcomes are rare, or exposure distributions are unequal. For variance estimation, use of bootstrapping is preferred.