A Rapid and Robust Gradient Measurement Technique Using Dynamic Single Point Imaging

Abstract

Purpose

We propose a new gradient measurement technique based on dynamic single point imaging (SPI), which allows simple, rapid, and robust measurement of k-space trajectory.

Methods

To enable gradient measurement, we utilize the variable field of view (FOV) property of dynamic SPI which is dependent on gradient shape. First, 1D dynamic SPI data are acquired from a targeted gradient axis, and then relative FOV scaling factors between 1D images or k-spaces at varying encoding times are found. These relative scaling factors are the relative k-space position that can be used for image reconstruction. The gradient measurement technique can also be used to estimate the gradient impulse response function for reproducible gradient estimation as a linear-time invariant system.

Result

The proposed measurement technique was used to improve reconstructed image quality in 3D ultra-short echo, 2D spiral, and multi-echo bipolar gradient echo Cartesian imaging. In multi-echo bipolar gradient echo imaging, measurement of the k-space trajectory allowed the use of a ramp-sampled trajectory for improved acquisition speed (approximately 30%) and more accurate quantitative fat and water separation in a phantom.

Conclusion

The proposed dynamic SPI-based method allows fast k-space trajectory measurement with a simple implementation and no additional hardware for improved image quality.

INTRODUCTION

The gradient system is an essential component in modern clinical MR imaging. It performs temporal-spatial encoding of transverse magnetization through a spatially varying magnetic field. Gradient waveforms can be synthesized to perform a range of image encoding strategies including conventional Cartesian image encoding, as well as non-Cartesian acquisitions such as radial(1) and spiral(2) imaging. Unfortunately, there still exist many factors that inevitably cause distortions in the realized gradient magnetic field: eddy currents(3–6), imperfection induced by the power amplifier, and mechanical/thermal vibrations(7,8). Due to these undesired distortions, it is challenging in practice to realize the actual gradient field exactly as prescribed, which, if the prescribed gradient is assumed during reconstruction, can result in image artifacts (e.g., blurring, ringing, or phase error). This can be a critical issue in non-Cartesian acquisitions, and is further exacerbated in acquisition schemes with a long readout duration such as spiral or echo planar imaging (EPI)(9,10). In these cases, the k-space trajectory is prone to deviate from that prescribed due to accumulated error in the phase evolution resulting from the distorted gradient.

Methods to estimate the actual gradient shape and the resultant k-space trajectory have been previously presented in the MR literature, and can be classified as follows: Imaging based gradient measurement (IGM) and magnetic field monitoring (MFM). In IGM, a (typically) 1D imaging technique based on a specialized pulse sequence is exploited to measure the gradient shape. In MFM, several NMR-based field probes are placed inside the magnet bore and used to record field characteristics temporally and spatially (11–14). While this provides the most direct measurement of the gradient field, the use of additional external hardware adds complication and expense.

According to the methodology of data acquisition, IGM methods can be further classified into two categories: frequency encoding based gradient measurement (FGM) and phase encoding based gradient measurement (PGM). In FGM(15), off-centered selection of a thin slice is performed to the avoid signal dephasing effect caused by gradient, followed by measurement of the phase evolution over encoding time in the manner of frequency encoding. Although the efficacy of this measurement scheme has been verified in many critical studies(16,17), there still exist limitations such as the dependency on slice selection and T₂* decay. Alternatively, in previously proposed PGM methods(18–21), the phase evolution is measured at a constant (and single) echo time after a RF pulse, which is advantageous in terms of reducing the impact of T₂* decay. However, a series of RF pulses must be applied to measure the whole gradient, which requires extensive measurement times.

Once the gradient has been characterized, it can be used directly in image reconstruction to improve image quality. However, such a measurement is specific to the characterized gradient and pulse sequence parameters and is not typically generalizable to other acquisitions. To enable more accurate output waveforms, it is routine in current generation MR systems to perform pre-emphasis correction by inputting a filtered (or intentionally distorted) waveform into the gradient subsystem(22). Such methods rely on the assumption that gradient systems are generally characterizable as linear time invariant (LTI) systems(23). Unfortunately, these system-level corrections do not realize sufficiently accurate waveforms, which may necessitate the further use of the gradient measurement techniques described above. Thus, a more generalizable approach to gradient measurement is to utilize these techniques and the LTI concept to compute a gradient impulse response function (GIRF). This approach allows estimation of the distorted gradient shape instead of directly measuring the realized gradient. By acquiring a comprehensive measurement of the gradient (e.g., obtained from one of the methods described above), the GIRF can be determined as a unique finite impulse response filter, and then any gradient shape realized in the same gradient system can be analytically predicted by convolving an estimated GIRF with the prescribed gradient (24–26).

In this study, we have developed a new gradient measurement method utilizing 1D dynamic single point imaging (SPI)(27) performed across a range of phase encoding time delays, which does not require slice selection, additional equipment, or knowledge about the imaged subject. The field of view (FOV) in SPI changes over phase encoding time delay, exhibiting a variable FOV property under an applied gradient. In the proposed gradient measurement method, 1D SPI encoding is implemented in each gradient axis by linearly scaling the amplitude of a tested gradient with each TR (i.e., from −1x to +1x to implement phase encoding). Then, the FOV scaling factors between different phase encoding time delays are estimated by using k-space or image domain representations of the 1D SPI data. The FOV scaling factors represent relative encoding positions in k-space between two phase encoding time delays, and the 1^st derivative of FOV scaling factors represents relative amplitude in the measured gradient. This measured k-space trajectory can then be utilized in reconstruction to improve image quality.

Three gradient-intensive sequences (ultrashort time echo (UTE) (1), spiral, and multi-echo bipolar gradient echo (GRE)) were tested to evaluate the efficacy of the new SPI-based gradient measurement scheme. In UTE, a center-out radial acquisition is used to minimize the achievable echo time and enable contrast for species with ultrashort T₂*’s. In spiral imaging, the gradient waveforms are simultaneously designed to operate within the peak gradient slew rate and peak gradient amplitude limits. Finally, multi-echo bipolar GRE with ramp sampling for more robust reconstruction in quantitative fat-water imaging is demonstrated. GIRFs were also estimated using the proposed method, and applied to obtain an estimated k-space trajectory in UTE, spiral, and multi-echo bipolar GRE imaging.

METHODS

Theory

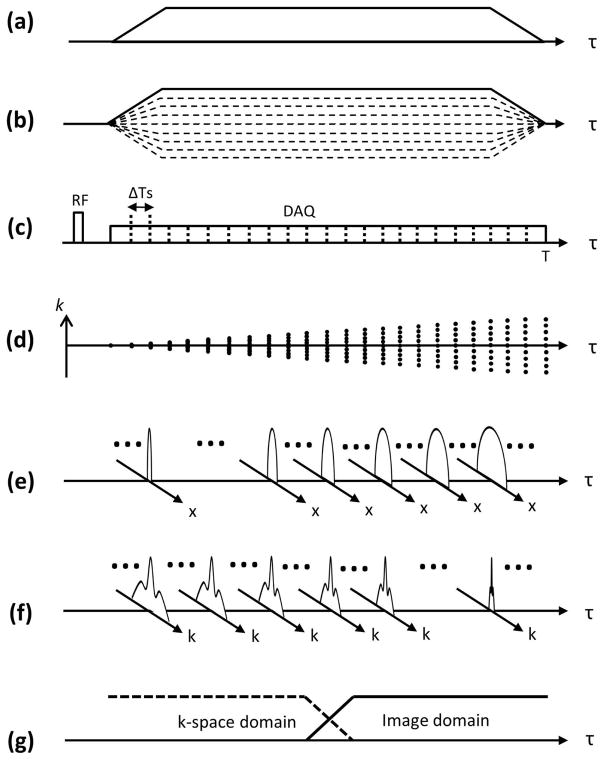
The proposed method is based on assumption that gradient distortion is a LTI function of the gradient input (23). In the proposed technique, 1D dynamic SPI is performed by linearly scaling with N_p steps (−1x to 1x) the entire gradient waveform along a single axis to obtain N_px1 data. Note that dynamic SPI differs from conventional SPI approaches where multiple k-spaces are continuously acquired with a prescribed sampling rate while phase encoding gradients are on.(28–30) Figure 1-a shows an example of a trapezoidal readout gradient to be measured, and Figure 1-b shows the corresponding dynamic SPI encoding gradient used for the proposed calibration technique. The FOV at phase encoding time delay (t_p, the elapsed time after RF excitation) in dynamic SPI is determined by the following equation(28,31,32):

$$\mathit{FOV}(t_p)=\frac{\pi N_p}{\gamma {\int }_0^{t_p}G(\tau )d\tau },$$ (1)

where N_p is the number of phase encoding steps, γ is a gyromagnetic ratio, and G(τ) is an amplitude of maximum phase encoding gradient at time delay τ, for example, which is the trapezoidal gradient with solid line in Figure 1-b. Figure 1-c shows the RF pulse and data acquisition window. Note that in dynamic SPI, multiple images can be acquired at every ΔTs (sampling interval) which improves sampling efficiency over conventional SPI approaches. Figure 1-d shows how the SPI sampling trajectory changes, exhibiting a time-decreasing FOV. The minimum N_p can be determined by the required FOV (typically larger than the diameter of imaged subject to avoid aliasing), fov_R, and gradient amplitude, G(τ), as in the following equation:

$$N_p=\lceil \frac{1}{\pi }{\mathit{fov}}_R\gamma max\left({\int }_0^{t}G(t)d\tau \right)\rceil ,\mathit{where}0\le t<T,$$ (2)

where T is the end of readout. Data is acquired using the same acquisition window as desired for imaging, and numerous k-spaces over encoding time can be obtained depending on the sampling rate.

Figure 1.

1D dynamic SPI acquisition for gradient measurement. An example of (a) targeted gradient, (b) the corresponding SPI encoding gradient, (c) RF transmission and data acquisition, (d) k-space trajectory, (e) image domain SPI data, (f) k-space domain SPI data, and (g) merging filter. 1D SPI sampling can be implemented by simple linear scaling the gradient amplitude with each TR. Note that the FOV change directly reflects the gradient shape. The image or k-space domain data can be adaptively used for FOV scaling search, according to the FOV at encoding time.

FOV scaling search

For gradient measurement, a reference point at a certain encoding time is first selected among the SPI encoded data. Then, the relative FOV scaling factor directly reflects the relative k-space trajectory with respect to the k-space coordinate at reference encoding time, t_r, as following equation shows:

$$\mathit{FOVscale}(t)=\frac{\mathit{FOV}(t_r)}{\mathit{FOV}(t)}=\frac{\pi \gamma {\int }_0^{t}G(\tau )d\tau }{\pi \gamma {\int }_0^{t_r}G(\tau )d\tau }=\frac{k(t)}{k(t_r)},$$ (3)

where t denotes a phase encoding time delay, and k(t) is a k-space position in the unit of cycle m⁻¹ at encoding time, t. Note that any data point can be used for the reference encoding time, t_r, however data acquired around the encoding time at which the SPI image has one-half of the required FOV (fov_R) may be desired such that both k-space and image domain 1D profiles contain enough information (or resolution) for reliable estimation of FOV scaling factors. Two possible approaches to estimate the relative FOV scaling factor exist: a k-space domain or an image domain approach, which can be formulated as a minimization problem. k-Space based optimization is shown in the following equation:

$$\mathit{FOVscale}(t)=\frac{\mathit{FOV}(t_r)}{\mathit{FOV}(t)}={\mathit{argmin}}_s{E}_K(K(t,sk),K(t_r,k)),$$ (4)

where K(t,k) denotes the magnitude of k-space encoded at phase encoding time t in 1D SPI, s is a real number that is local FOV scaling factor, and E_K is an error function between two k-spaces. In practice since a finite number of data (N_p) is acquired, data interpolation is used to synthesize the scaled k-space K(t,sk) from original k-space K(t,k). Image domain optimization is performed as follows:

$$\mathit{FOVscale}(t)=\frac{\mathit{FOV}(t_r)}{\mathit{FOV}(t)}={\mathit{argmin}}_s{E}_I(I(t,x/s),I(t_r,x)),$$ (5)

where I(t,x) denotes the magnitude of 1D image at encoding time t, and E_I is an error function between two images. As in k-space domain, interpolation is applied to synthesize the scaled image I(t,x/s).

The 1D profile in the image domain has more resolution (more information that can be used in FOV scaling search) when the FOV is small (Figure 1-e), while the k-space profile shows a broader line-shape when the FOV is large (Figure 1-f). To exploit this property, the two estimates may be combined using a simple merging filter as shown in Figure 1-g.

Absolute k-space trajectory

As shown in equation 3 above, the estimated FOV scaling factor, FOVscale(t), represents the relative k-space position at encoding time t with respect to the k-space position at the reference encoding time t_r. The absolute k-space trajectory, which allows reconstruction of the image at the prescribed FOV, can be calculated by simply scaling the relative k-space trajectory. Most trivially, this is done by scaling the unitless measured gradient waveform to match the prescribed gradient amplitude (e.g., in units of mTm⁻¹). Note that potentially more accurate scaling could utilize the GIRF-distorted gradient waveform or consider only the plateaus of trapezoidal gradients. Alternatively, a phantom of known dimension could be scanned to obtain this calibration if the system gradient amplitude is inaccurate or unknown. If the targeted gradient system is well calibrated, the DC component at 0 Hz in Fourier transform of the measured and prescribed gradient can be used to obtain the scaling factor.

GIRF

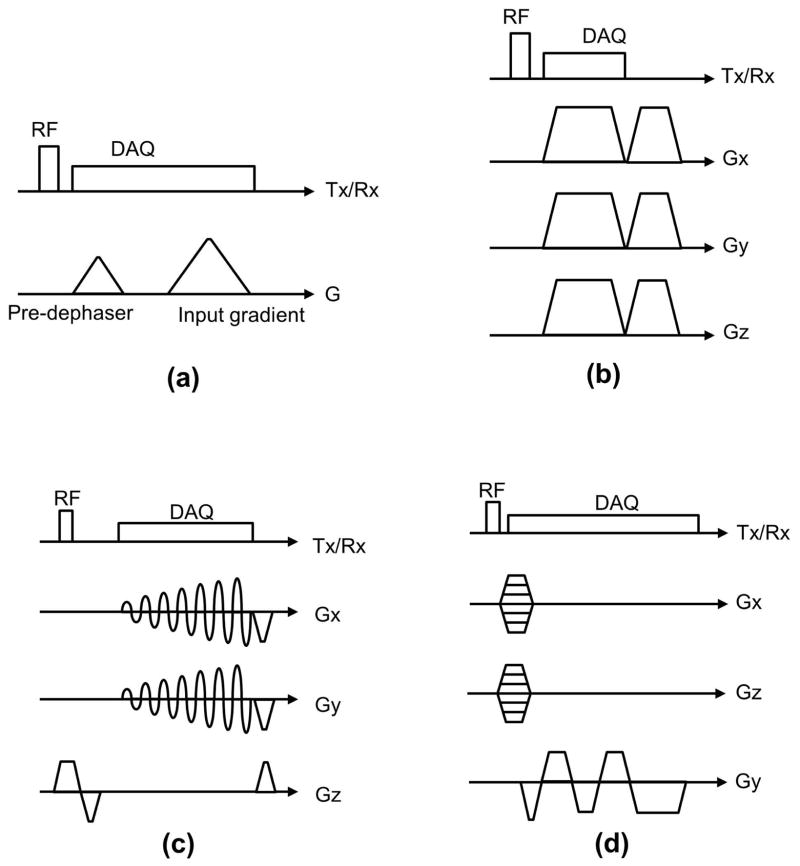
We have utilized the SPI-based gradient measurement technique herein to estimate GIRF, using multiple triangular input gradients using methodology analogous to (24). Figure 2-a shows the pulse sequence diagram depicting the input gradients used for GIRF measurement. Note that a “pre-dephasing” gradient is prescribed before the input gradient to remove ambiguity in FOV scaling estimation due to the large FOV when SPI data is acquired near the center of k-space. We performed estimation of GIRF in the frequency domain (i.e., the transfer function) by dividing the measured output gradient by the prescribed input gradient after discrete Fourier transform to calculate a transfer function of the LTI system. The estimated transfer function is low-pass filtered to cut off unreliable, high frequency components using a reduced cosine filter.

Figure 2.

Pulse sequence diagrams. (a) GIRF estimation, (b) Ultra-short echo (UTE) imaging, (c) spiral imaging, and (d) multi-echo bipolar GRE imaging. Note that in (d) a gradient spoiler is implemented by stretching the readout gradient.

Experimental setup

The imaging parameters for GIRF measurement, dynamic SPI based gradient measurement, and imaging experiments performed on three different scanners are shown in Table 1. For GIRF measurement of a 3T MR750 scanner (S1) (GE Healthcare, Waukesha, WI, USA) utilized 21 triangular gradients with amplitude between 7 mTm⁻¹ and 33 mTm⁻¹, and a slew rate = 200 mTm⁻¹ms⁻¹ were used. A pre-dephasing gradient with amplitude 21.7 mTm⁻¹ was placed with 464 μs spacing before the largest input gradient. To measure the GIRF of a 1.5T Signa HDxt scanner (S2) (GE Healthcare, Waukesha, WI, USA), 15 triangular gradients with amplitudes equally spaced between 6.7 mTm⁻¹ and 20 mTm⁻¹ were prescribed. A pre-dephasing gradient with amplitude 11.4 mTm⁻¹ was prescribed with 476 μs spacing before the largest input gradient. Slew rate = 118 mTm⁻¹ms⁻¹ was used for all triangular gradients. To measure the GIRF of a 3T Signa PET/MR scanner (S3) (GE Healthcare, Waukesha, WI, USA), 21 triangular gradients with amplitude between 10 mTm⁻¹ and 30 mTm⁻¹, and a slew rate = 118 mTm⁻¹ms⁻¹ were used. A pre-dephasing gradient with amplitude 21 mTm⁻¹ was placed with 588 μs spacing before the largest input gradient. GIRFs for all scanners were measured with vender provided pre-emphasis correction turned on. A GE Healthcare 8-channel receive-only head coil was used, and a manufacturer-provided 15 cm spherical phantom (with no internal structure) was imaged. Total scan time to measure GIRF on each of the 3 scanners was 106 sec for S1, 75 sec for S2, and 106 sec for S3.

Table 1.

Imaging parameters. The proposed method was tested on three different clinical scanners.

		GE MR750 (S1)	GE Signa HDxt (S2)	GE Signa PET/MR (S3)
GIRF measurement	RF pulse	24μs hardpulse	24μs hardpulse	24μs hardpulse
	Np	401	401	401
	Flip angle (degree)	6	6	6
	Slew rate (mTm−1ms−1)	200	118	118
	# of input gradient	21	15	21
	Pre-dephaser (mTm−1)	21.7	11.4	21.0
	Input gradients (mTm−1)	7~31	6.7~20	10~30
	Spacing (μs)	464	476	588
	TR(ms)	4.4	4.4	4.4
	Sampling rate (kHz)	500	250	500
	# of data points	988	378	982
	RF Coil	8-ch receive only head coil
	Scan time (sec)	106	75	106
		3D UTE	2D Spiral	3D Ramp sampling
Imaging experiment	RF pulse	24μs hardpulse	Sinc pulse	24μs hardpulse
	Flip angle (degree)	6	30	6
	TE (ms)	0.09	2.42	Cartesian: 1.06, 1.97, 2.87, 3.77 Ramp sampling: 0.85, 1.49, 2.13, 2.77
	TR (ms)	3.3	13	Cartesian: 5.2 Ramp sampling: 3.7
	Sampling rate (kHz)	500	250	500
	# of data points	415	512	Cartesian: 1234 Ramp sampling: 1830
	# of TR	80000	48	101×31
	RF coil	8-ch receive only head coil	Single CH T/R coil	8-ch receive only head coil
	Scan time	4min 28 sec	0.6 sec	Cartesian: 16.3 sec Ramp sampling: 11.6 sec
SPI-based gradient measurement	Np	401	401	401
	TR (ms)	3.3	13	3.7
	Reference time, tr (ms)	0.29	2.94 for x-axis 3.18 for y-axis	21
	Sampling rate (kHz)	500	250	500
	# of data points	415	512	1830
	RF coil	8-ch receive only head coil
	Scan time	4sec	quick: 42sec extensive: 385sec	1.5sec

3D radial UTE imaging was performed on system S1 using a GE Healthcare 8 channel receive-only head coil. k-Space was encoded using a center-out half radial trajectory, using the pulse sequence shown in Figure 2-b. After RF excitation using a 24μs hard pulse, 80,000 spokes were scanned at TE=90 μs (after RF coil deadtime) with an encoding duration of 588 μs. The maximum amplitude of readout gradient was 35 mTm⁻¹, slew rate was 118 mTm⁻¹ms⁻¹, flip angle was 6 degrees, sampling bandwidth was 500 kHz, and TR was 3.3 ms. SPI-based gradient measurement was performed in the x, y, and z directions with Np = 401 using the same scan parameters. An image was reconstructed at FOV = 24×24×24 cm and 1×1×1 mm resolution using gridding. The brain of a human volunteer was scanned under approval from our institutions IRB, and a 15 cm spherical phantom was used for gradient measurement as in GIRF measurement. The scan time for UTE imaging was 4 min 28 sec, and the scan time to perform gradient measurement for all three gradient axes was 4 seconds in total.

2D spiral imaging was performed on GE Signa HDxt scanner (S2) using the pulse sequence in Figure 2-c. A single channel GE Healthcare transmit/receive head coil was used for imaging. A sinc pulse was used to achieve 30 degree flip angle, and a single axial slice at iso-center was obtained. 48 spiral arms with 512 readout points in an arm was encoded with a sampling bandwidth of 250 kHz. FOV was 12×12 cm, slice thickness was 8 mm, and spatial resolution was 1.04×1.04 mm. TR was 13 ms, and TE was 2.42 ms. SPI gradient measurement with Np = 401 was performed in two different ways for comparison: extensive and quick. All 48 different pairs of x and y gradients were measured with the extensive gradient measurement (385 seconds), while 2 pairs of x and y gradients were measured and reproduced to estimate trajectories for all 48 arms using a linear combination in the quick gradient measurement (42 seconds). In the quick measurement, the readout gradients in x and y-axis in the arm with rotational angle θ, gx(θ,t) and gy(θ,t), can be estimated by the following equation.

$$\begin{array}{l}gx(\theta ,t)=\mathit{cos}\theta \ast gx(0,t)-\mathit{sin}\theta \ast gy(\frac{3\pi }{2},t)\\ gy(\theta ,t)=\mathit{sin}\theta \ast gx\left(\frac{\pi }{2},t\right)+\mathit{cos}\theta \ast gy(0,t).\end{array}$$ (6)

Note that gx(0,t), $gx\left(\frac{\pi }{2},t\right)$, gy(0,t), and $gy\left(\frac{3\pi }{2},t\right)$ are measured gradient shapes, where $gx\left(\frac{\pi }{2},t\right)$ can be interpreted as a x-gradient waveform realized in physical y-gradient, and $gy\left(\frac{3\pi }{2},t\right)$ is y-gradient waveform realized in physical x-gradient. A 15 cm spherical phantom was used for gradient measurement as for the GIRF measurement, and a manufacturer-provided resolution phantom was scanned and reconstructed with the nominal and measured (extensively and quickly) k-space trajectory.

In the experiment for multi-echo bipolar GRE imaging, non-selective 3D GRE imaging was performed on GE Signa PET/MR scanner (S3) using an GE Healthcare 8 channel receive-only head coil, with 2 mm spatial resolution and FOV = 6×26×20 cm. Phase encoding was performed in x and z direction with 61 and 201 phase encoding steps, respectively, and frequency encoding was performed in y direction. 8 vials containing 0%, 5%, 10%, 15%, 20%, 30%, 40%, and 50% fat with a T₁ shortening agent were used for the experiment. Two different pulse sequences using the bipolar gradients shown in Figure 2-d were used to acquire 4 gradient echoes, where the readout gradients with a longer and shorter plateau were used for the conventional Cartesian sampling and ramp sampling, respectively. TE was 1061, 1965, 2869, and 3773 μs for Cartesian sampling and 847, 1487, 2127, and 2767 μs for ramp sampling. The maximum amplitude of the readout gradient for Cartesian or ramp sampling acquisition was respectively 22.6 mTm⁻¹ or 33.0 mTm⁻¹. Note that a gradient spoiler was applied in the readout direction by stretching the trapezoidal gradient at the end of the pulse sequence. The minimum TR was 5.2 ms for Cartesian sampling and 3.7 ms for ramp sampling (a 29% reduction), where scan time was 16.3 sec for Cartesian and 11.6 sec for ramp sampling. A 24 μs hard pulse with a 6 degree flip angle was used, and the sampling rate was 250 kHz and 500 kHz bandwidth for Cartesian and ramp sampling acquisitions respectively. SPI-based gradient measurement was performed for ramp sampling in the readout direction (y-axis) with Np = 401. The acquisition time for gradient measurement was 1.5 sec. A 15 cm spherical phantom was used for gradient measurement.

Data processing

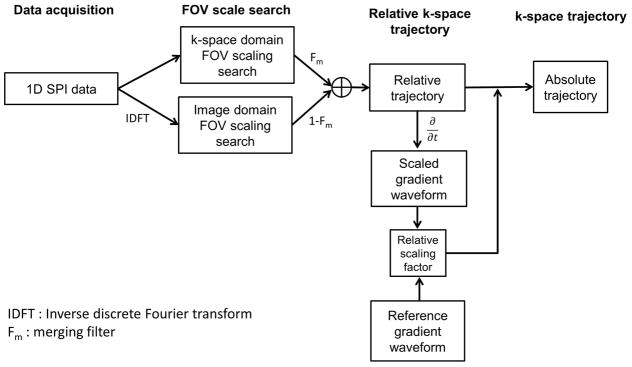
Figure 3 shows a block diagram delineating the steps in the proposed method. The acquired data were processed in MATLAB (The Mathworks Inc, Natick, MA, USA). In the FOV scaling factor search stage, the reference encoding time, t_r, is selected by referring to the nominal trajectory. Once the FOV scaling factors are estimated in k-space and image domain, they are combined using a merging filter. The merging filter was designed to have a linear slope in transition, where the width of transition was prescribed to cover five data points. Then, the absolute k-space trajectory is computed by scaling the relative k-space trajectory to physical gradient units. After estimating trajectories for the sampled k-space data, a convolution gridding reconstruction (33–36) was performed with oversampling ratio = 1.5 and a gridding kernel width = 5 pixels.

Figure 3.

Block diagram. This process is independently performed to obtain the k-space trajectory in each gradient axis.

Note that any non-linear optimization method can be used to solve equation 4 and 5. In GIRF estimation, UTE imaging, and ramp sampling experiments, simple unconstrained optimization based on Nelder-Mead simplex (fminsearch in MATLAB) was used to estimate the FOV scaling factors. In the spiral imaging experiment, bounded nonlinear function optimization based on golden section search and parabolic interpolation(37) (fminbnd in MATLAB) was used for the FOV scaling search. The search range was set to ±7% of initial guess. The nominal k-space trajectory was used as an initial guess for the optimization in UTE imaging, and the GIRF-corrected trajectory was used as an initial guess for spiral imaging and ramp sampling. To scale the 1D image and k-space data in each iteration of optimization, cubic interpolation was applied. L2-norm and negative linear correlation were used as an error function for k-space (E_K) and image (E_I) respectively. Image domain SPI data was used for GIRF estimation, while k-space and image domain data was used for direct gradient measurement in UTE imaging, spiral imaging, and ramp sampling. To scale the unitless, relative gradient shape to an absolute gradient shape, estimated amplitudes in plateau of the first readout gradient was compared with the corresponding part in prescribed gradient shape in UTE imaging. In spiral imaging, entire gradient shape was compared with the GIRF-distorted gradient shape to scale the estimated gradient shape to obtain the correct FOV in image reconstruction. In multi-echo GRE imaging and all GIRF measurements in three systems (S1, S2, and S3), the DC component of Fourier transform measured and prescribed gradient waveform was used to obtain the absolute gradient shape.

In multi-echo bipolar GRE imaging, conventional Cartesian data (non-ramp sampled data) was directly reconstructed with no additional phase correction. Data acquired with ramp sampling was reconstructed using the GIRF-corrected trajectory or the measured trajectory. After reconstructing multi echo images, Iterative Decomposition of Water and Fat With Echo Asymmetry and Least-Squares Estimation (IDEAL) was applied to obtain fat and water separated images(38), and the fat fraction was calculated.

RESULTS

GIRF estimation

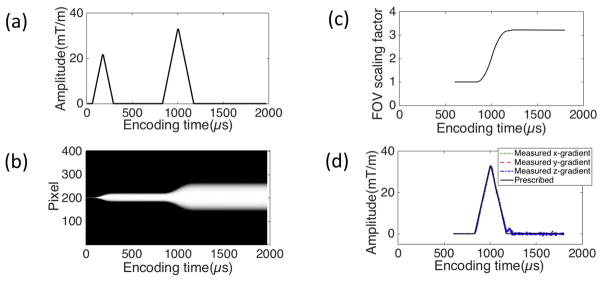
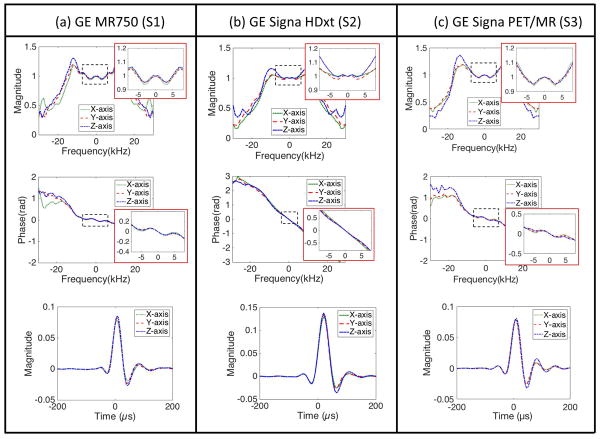
Figure 4-a shows one input gradient with amplitude of 33 mTm⁻¹ following a pre-dephasing gradient, which was used for GIRF estimation in S1. Figure 4-b shows the normalized magnitude of the 1D SPI images over encoding time obtained in y-axis, and Figure 4-c shows the estimated FOV scaling factors. Figure 4-d shows the measured gradient shape. Figure 5-a,b,c shows the estimated transfer function in the Fourier transform domain and the corresponding GIRF in the time domain for three different systems, S1, S2, and S3, respectively. The magnitude and phase of the estimated transfer functions (discrete Fourier transform of GIRF) in the frequency domain and the corresponding GIRFs in the time domain are shown here, which shows suppressed noise up to 20 kHz. The GIRFs were obtained by low-pass filtering and performing the inverse discrete Fourier transform to the transfer function. The parameters for the low-pass filter was empirically determined to suppress the amplified noise, where full width half max was 44.4 kHz, and the transition band was 16 kHz. The off-centered peak in the GIRF implies a group delay of approximately 8 μs for S1 and S3 and 20 μs for S2, which matches with an empirically observed delay in the three systems in our group.

Figure 4.

SPI based GIRF estimation. (a) A prescribed gradient, (b) normalized magnitude of 1D SPI images over phase encoding time delays in the y-gradient, (c) estimated FOV scaling factors, (d) measured gradient shape. The size of the 1D projected object in (b) directly reflects the FOV scaling factor (or relative k-space trajectory) in (c).

Figure 5.

Estimated GIRF. Magnitude and phase of GIRF in the Fourier transform domain and the corresponding time domain representation in (a) S1, (b) S2, and (c) S3. Note that the off-centered peak in GIRF implies group delay in gradient system.

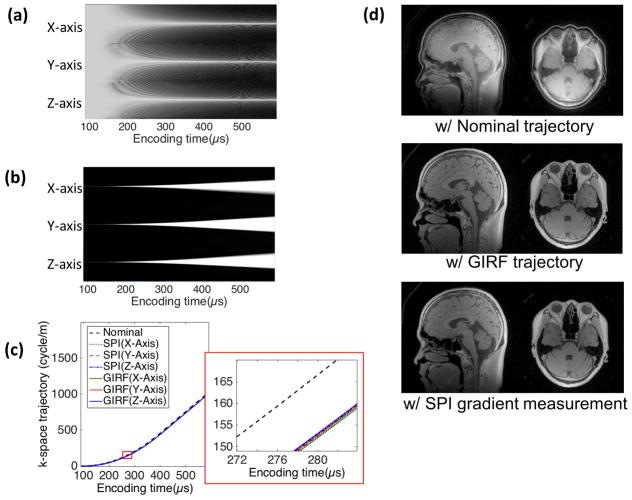
Ultra-short echo imaging

Figure 6-a shows the log magnitude of 1D k-space obtained using SPI encoding for gradient measurement in the x, y, and z-axis, and Figure 6-b shows the magnitude of the corresponding 1D SPI images that are normalized by the maximum amplitude in each encoding time. Under the mono-polar trapezoidal gradient, the encoded 1D k-space shows time-narrowing line shape over encoding, while the 1D image shows a time-broadening shape, where the both k-spaces and images exhibit time-decreasing FOV. Figure 6-c shows the GIRF measured trajectory, the SPI measured trajectory, and the nominal trajectory in physical x, y, z-axis, and a zoomed-in view, where group delay is shown between the nominal and the measured k-space trajectories. Figure 6-d show the UTE images reconstructed with the nominal, GIRF, and SPI measured trajectory for a sagittal and axial slice. The image reconstructed with the GIRF and SPI measured trajectory shows good quality with no visible imaging artifact such as ringing, while the image with the nominal trajectory exhibits ringing and mis-aligned image components.

Figure 6.

3D UTE imaging. (a) Log magnitude of k-spaces and (b) normalized images over encoding time in SPI data used for gradient measurement, (c) nominal, GIRF, and SPI measured k-space trajectory, (d) sagittal and axial slice of the image reconstructed with nominal trajectory, GIRF, and SPI measured trajectory. In the images with measured trajectory, no ringing artifact is visible, which is present in the images with nominal trajectory. Note that the coil component is also visible in the images with GIRF and SPI measured trajectory.

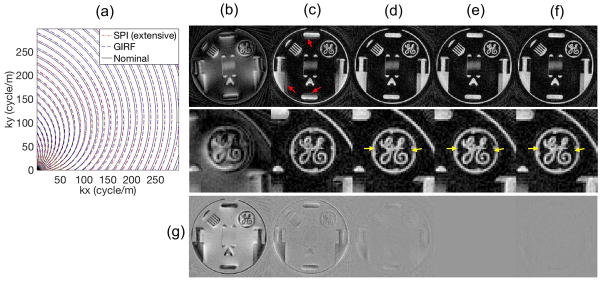
Spiral imaging

Figure 7-a shows the nominal, GIRF measured, and SPI measured trajectory. Figure 7-b shows the image reconstructed using the nominal trajectory, and Figure 7-c shows images reconstructed with the delay-corrected trajectory where a group delay of 20 μs was used. Figure 7-d shows images reconstructed with trajectory estimated using GIRF. Figure 7-e and f show images reconstructed using the trajectory obtained by extensive and quick measurement, where all 48 spiral arms were measured independently or only 4 arms of measurement, respectively. Figure 7-g shows a difference image relative to the image using the extensively measured trajectory in Figure 7-e. The image reconstructed with the delay-uncorrected trajectory shows a severe blurring artifact, while the image with delay-corrected trajectory shows reduced blurring artifact, however there is remaining blurriness artifact as indicated by the red arrows. Images reconstructed using the GIRF-trajectory, extensively measured trajectory, or quickly measured trajectory show a much better result, while images with the measured trajectory show sharper edges as indicated by yellow arrows. The quick gradient measurement shows a comparable result to the full measurement as shown in the difference image in Figure 7-g, with 8.3% of the scan time compared to the extensive measurement time.

Figure 7.

2D Spiral imaging. Reconstructed images with (a) Nominal and measured trajectory, image reconstructed with (b) nominal trajectory, (c) delay-corrected trajectory, (d) GIRF trajectory, (e) extensively measured trajectory, (f) quickly measured trajectory, and (g) difference image with respect to (e). Note that all 48 arms were individually processed in the extensive measurement in (e), while only 4 basis arms were processed in quick measurement in (f).

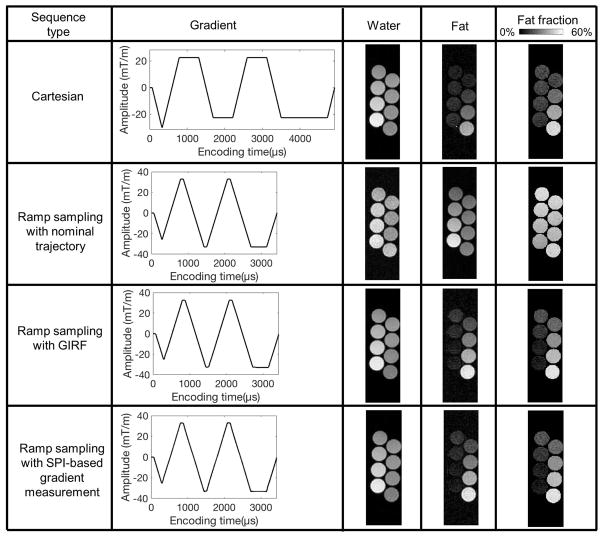
Multi-echo bipolar GRE imaging

Figure 8 shows fat and water separated images and the resultant fat fraction map obtained by three different imaging and reconstruction schemes: conventional Cartesian imaging, ramp sampling with nominal trajectory, ramp sampling with GIRF, and ramp sampling with SPI-based gradient measurement. The measured gradients show the raw data (unfiltered) of the estimated gradient waveform. The SNR measured from the separated water in all tubes, the mean and standard deviation of estimated fat fraction in each tube are shown in Table 2. In conventional Cartesian sampling, erroneous estimation of fat faction is shown due to the phase error between the echoes acquired with positive and negative readout gradient. In ramp sampling with GIRF-estimated or SPI-measured trajectory, the estimation of fat fraction is significantly improved, which is likely due to a combination of the improved accuracy in the k-space sampling position that center-aligns k-spaces across echoes as well as the reduced echo spacing, while use of the nominal trajectory yields an incorrect estimation of fat fraction with lower SNR than in ramp sampling with the corrected trajectory. The SNR measured in ramp sampling was comparable with the SNR in Cartesian sampling. The estimated fat fraction shows both GIRF and SPI-based gradient measurement method allow robust measurement of the readout gradient.

Figure 8.

Multi-echo bipolar GRE imaging. Ramp sampling images were reconstructed with nominal, GIRF-estimated, or SPI-measured trajectory. A cross sectional view of tubes with 0, 5, 10, 15, 20, 30, 40, and 50% fat fraction is shown here.

Table 2.

Fat fraction. Conventional Cartesian imaging shows apparent error in fat fraction estimation due to the artefactual phase caused by mis-aligned k-spaces between gradient echoes. SNR was measured with separated water in all tubes.

	SNR	0% fat (%)	5% fat (%)	10% fat (%)	15% fat (%)	20% fat (%)	30% fat (%)	40% fat (%)	50% fat (%)
Cartesian	55.3	10.4 ±13.2	12.2 ±21.5	13.0 ±2.3	13.8 ±3.1	13.2 ±2.8	21.5 ±2.1	34.6 ±1.6	47.3 ±1.8
Ramp sampling with nominal trajectory	45.9	37.9 ±1.9	42.3 ±1.7	46.7 ±1.9	50.4 ±1.8	48.1 ±2.0	43.5 ±2.1	42.6 ±1.7	48.2 ±1.7
Ramp sampling with GIRF	56.1	5.9 ±2.1	6.2 ±2.0	9.9 ±2.4	14.8 ±2.6	19.7 ±2.6	29.0 ±1.6	39.6 ±1.5	50.6 ±1.7
Ramp sampling with SPI-based measurement	56.4	5.4 ±2.1	6.2 ±2.2	10.3 ±2.3	15.3 ±3.0	19.8 ±2.5	29.1 ±1.7	39.8 ±1.5	50.3 ±1.8

DISCUSSION

The proposed SPI-based gradient measurement technique does not require any special hardware unlike other reported methods for PGM and MFM that need specialized equipment such as NMR field probes(11,12,20,39). While these methods have been shown to be viable techniques to measure gradient waveforms, the use of external hardware adds complication and may be cost prohibitive. In the proposed method, a 15 cm spherical phantom was used to perform gradient waveform measurement; however in theory, any object (including a human patient) can be used to perform gradient measurement. However, the imaged object does require definite boundaries (determined either by object size, coil sensitivity, or slice selectivity) to allow computation of the relative scale factors. The proposed method is robust to rigid motion of the object in two ways: the k-space scheme that only use magnitude that does not influenced by motion, and short measurement times that mitigate possible motion during the scan. The proposed SPI-based gradient measurement technique requires very minor modifications to the targeted pulse sequence, requiring only an additional loop during which the to be measured gradient amplitude is scaled for each gradient channel measured. Thus, this gradient waveform measurement can be added into existing sequences with little effort.

Compared with previously reported PGM(18–20) methods, where the number of RF pulses determines the resolution of estimated trajectory or gradient, the proposed technique allows higher resolution sampling of the gradient waveform (determined by the sampling bandwidth of the readout event). Therefore, the k-space position can be directly estimated from the measurement without any interpolation using the identical sampling rate for image acquisition. Furthermore, acquisition of the gradient measurement can be extremely rapid when the scan TR is short (e.g., ~1.5 sec per gradient axis). Furthermore, the use of the proposed methodology to perform in vivo measurement is feasible, where, for example, a database gradient measurement (e.g., obtained using a phantom) could be used to provide robust estimates for rapid gradient measurements. In vivo gradient measurement time for longer readouts (e.g., spiral and echo-planar imaging) could be further reduced by sub-sampling the number of phase encoding steps, particularly when a database calibration measurement is used. Note that in vivo calibration could be challenged when static field gradients due to magnetic field distortion is significant.

One additional feature of the SPI-based gradient measurement is that k-space trajectory can be independently recovered without knowing the history of previous k-space position. Theoretically, the FOV itself in a 1D SPI image is a direct and independent measure of k-space position as implied in equation 1. This allows flexibility to measure k-space trajectory in any type of pulse sequences even when the central region of k-space is not acquired as in hybrid encoding(40,41) and zero TE imaging(42–45). Furthermore, in the SPI-based method, noise or mis-estimation at earlier encoding times is not propagated to the later estimation since no integration or cumulative summation is required to obtain k-space position.

As demonstrated herein, the proposed gradient waveform method can be used to improve the quality of reconstructed images. This is particularly important for non-Cartesian imaging where small k-space trajectory errors lead to significant artifacts as seen in Figure 6. Another application is the use of the technique to measure trajectories in more conventional Cartesian-type acquisitions. In Figure 8, improvement is seen in chemical-shift encoded imaging (IDEAL) with a multi-echo bipolar readout by reconstructing to a measured trajectory which reduces artefactual phase due to an inaccurate k-space trajectory(46–48). Furthermore, ramp sampling reduced the total scan time by approximately 30%. The ability to perform a robust and rapid gradient measurement technique to enable ramp sampling, particularly for oblique slice orientations would be beneficial to many MRI sequences (e.g., fast gradient echo, echo-planar imaging, balanced SSFP, fast-spin echo) to provide moderate scan time reductions (20–30%) with minimal effect upon SNR.

The key idea of the proposed SPI-based gradient measurement technique is based on the assumption of linearity of the gradient distortion. This is typically a reasonable assumption when distortions are mostly caused by eddy currents that linearly scale with gradient amplitude. However, these conditions may be violated in certain instances such as gradient operation close to the limit of slew rate and amplitude, resulting in nonlinear distortion in the realized gradient shape, which is a limitation of the proposed method based upon this LTI assumption. Furthermore, the demonstration of the proposed method relies upon accurate gradient amplitude calibration (which is already a requirement to enable geometrically precise MR imaging). If mis-calibrated, global geometric distortions will be apparent relative to the physical x, y, and z gradient errors. However, this scaling can readily be compensated for by imaging a phantom with known geometry (for which the proposed method would be particularly well-suited).

Concomitant field effects are another nonlinear factor that cause deviations in the k-space trajectory. These time-variant, non-linear magnetic fields depend on gradient amplitudes and are inversely proportional to field strength. The concomitant field effects become more problematic in imaging with long readout duration and preparation gradients (e.g. velocity encoding). Despite the efficacy of the proposed gradient measurement method as shown in the experiments herein, it is difficult to directly measure the concomitant magnetic field or higher order fields since in the proposed method (and other FGM and PGM methods) the gradient measurement is performed independently in each axis, based on the linearity assumption of the gradient system. In practice, concomitant magnetic fields are modeled as second order approximations and several successful correction methods have been proposed and implemented (10,49–51). Thus, these additional correction terms could be readily applied to gradient measurement data obtained using the proposed method.

The proposed technique can be used as a calibration technique to estimate the GIRF without external hardware. As shown hereinbefore, the data collection for GIRF requires only 25~35 sec per gradient axis, making it very feasible for measurement during routine (e.g., daily or weekly) quality assurance imaging. In the present experiment using triangular gradient blips, the spectral resolution is inherently limited, and hence it may not be sensitive to long lasting eddy currents which is not visible in the estimated GIRF. This could potentially be overcome by applying frequency sweep methods (26,52), which we will explore in future work.

CONCLUSIONS

In this study, we implemented a robust and rapid gradient measurement method based on dynamic SPI, which allowed accurate measurement of k-space trajectory with high fidelity and no need of additional equipment to improve reconstructed image quality.