Recent developments and comprehensive evaluations of a GPU-based Monte Carlo package for proton therapy

Abstract

Monte Carlo (MC) simulation is commonly considered as the most accurate dose calculation method for proton therapy. Aiming at achieving fast MC dose calculations for clinical applications, we have previously developed a GPU-based MC tool, gPMC. In this paper, we report our recent updates on gPMC in terms of its accuracy, portability, and functionality, as well as comprehensive tests on this tool. The new version, gPMC v2.0, was developed under the OpenCL environment to enable portability across different computational platforms. Physics models of nuclear interactions were refined to improve calculation accuracy. Scoring functions of gPMC were expanded to enable tallying particle fluence, dose deposited by different particle types, and dose-averaged linear energy transfer (LETd). A multiple counter approach was employed to improve efficiency by reducing frequency of memory writing conflict at scoring. For dose calculation, accuracy improvements over gPMC v1.0 were observed in both water phantom cases and a patient case. For a prostate cancer case planned using high-energy proton beams, dose discrepancies in beam entrance and target region seen in gPMC v1.0 with respect to the gold standard tool for proton Monte Carlo simulations (TOPAS) results were substantially reduced and gamma test passing rate (1%/1mm) was improved from 82.7% to 93.1%. Average relative difference in LETd between gPMC and TOPAS was 1.7%. Average relative differences in dose deposited by primary, secondary, and other heavier particles were within 2.3%, 0.4%, and 0.2%. Depending on source proton energy and phantom complexity, it took 8 to 17 seconds on an AMD Radeon R9 290x GPU to simulate 10⁷ source protons, achieving less than 1% average statistical uncertainty. As beam size was reduced from 10×10 cm² to 1×1 cm², time on scoring was only increased by 4.8% with eight counters, in contrast to a 40% increase using only one counter. With the OpenCL environment, the portability of gPMC v2.0 was enhanced. It was successfully executed on different CPUs and GPUs and its performance on different devices varied depending on processing power and hardware structure.

1. Introduction

Monte Carlo (MC) method is widely regarded as the gold standard for proton therapy dose calculations (Paganetti et al., 2008; Schuemann et al., 2014; Schuemann et al., 2015). Computational efficiency has been a major issue preventing its wide application in the clinic and hindering its utilization in research. Over the years, there have been tremendous efforts devoted to accelerating proton MC dose calculation (Kohno et al., 2003; Fippel and Soukup, 2004; Li et al., 2005). In particular, graphics-processing unit (GPU) platforms have been recently employed to speed up the computations and significant acceleration factors have been achieved (Yepes et al., 2009; Jia et al., 2012; Jia et al., 2014; Ma et al., 2014; Wan Chan Tseung et al., 2015). We have developed a proton MC dose calculation package, gPMC v1.0 on GPU (Jia et al., 2012). The transport physics of gPMC was mainly based on that developed by Fippel and Soukup (2004). GPU-friendly implementations were designed to achieve a high computational efficiency. With an NVIDIA Tesla C2050 GPU, the simulation time for 10⁷ source protons ranged from 6 to 22 seconds depending on the source proton energy and the phantom or patient complexity (Jia et al., 2012).

Despite the success, the gPMC code left room for improvement regarding its accuracy, functionality, and suitability for clinical uses. It is desirable to refine the model for nuclear interaction to improve accuracy. There existed a few approximations in the original gPMC physics model (Fippel and Soukup, 2004). In a study evaluating dose calculation in 30 patients, gPMC was compared to the gold standard MC package TOPAS (Perl et al., 2012; Testa et al., 2013). Sufficient accuracy of gPMC in most cases was reported with gamma passing rate (1%/1mm) over 94% for voxels within 10% isodose line. However, ∼2% systematic overestimation of dose in the entrance region and 1∼2% underestimation in the target was observed for prostate cancer cases (Giantsoudi et al., 2015). This discrepancy was ascribed to the relatively simple model of nuclear interactions, which appeared less accurate in dose calculations for a high-energy proton beam because of the ∼1% primary protons undergoing a nuclear interaction per cm water equivalent depth. Recently, another GPU-based proton MC simulation package was developed (Wan Chan Tseung et al., 2015), which utilized a more accurate nuclear interaction model. Yet the inclusion of a complex model inevitably impacted the computational efficiency. Hence, it was our motivation to refine the physics model in gPMC to maintain its simplicity, while achieving a sufficient level of dose calculation accuracy for clinical applications.

Furthermore, the suitability of gPMC for clinical and research applications was previously limited by several factors. First, the use of NVidia's Compute Unified Device Architecture (CUDA) (NVIDIA, 2011) tied gPMC to NVidia GPU cards, hindering its portability to other GPUs and conventional CPUs. Recently, Open Computing Language (OpenCL) was introduced into the high-performance computing field. It provides a framework for developers to write programs that are executable across different platforms, including conventional CPUs, CPU clusters, and GPUs from different manufacturers. There has been an initial study regarding the use of OpenCL as the development platform for GPU-based MC dose calculation (Tian et al., 2015). In this paper, we will present our implementations of gPMC on the OpenCL environment.

In addition, there is a great desire to use MC to compute quantities other than just physical dose. For instance, there has been growing interest in research to consider variation of the proton relative biological effectiveness (RBE) in treatment planning instead of using a constant value of 1.1 (Paganetti, 2014). Due to the complexity of computing tissue specific RBE values, it was proposed to use linear energy transfer (LET) as a surrogate (Giantsoudi et al., 2013). Enabling accurate and fast computation of LET in gPMC would greatly facilitate its application in proton biology. Hence, we have included functions in gPMC to score LET.

Our new study also includes a comprehensive evaluation of gPMC's accuracy. This evaluation yields an in-depth understanding about the capability and limitation of gPMC depending on different applications. Total physical dose has typically been the quantity of interest when establishing the accuracy of a fast MC code. To obtain a more detailed evaluation of the performance of our updated gPMC code, this paper will also compare dose deposited differentiated by particle types, LET, and particle fluence to gold standard results computed by TOPAS.

2. Methods

2.1. Updates in physics model

Protons undergo different types of interactions when propagating in a medium. For electromagnetic (EM) interaction channel, gPMC employed a class II condensed history simulation scheme. The accuracy of transport in this channel has been previously demonstrated (Jia et al., 2012) by performing simulations with only this channel and comparisons with TOPAS.

Protons also undergo interactions with nuclei. gPMC v1.0 followed the empirical strategy developed previously by Fippel and Soukup (2004) to model interactions in three channels: proton-proton elastic interaction, proton-oxygen elastic interaction and proton-oxygen inelastic interaction. The total cross section data in this model were obtained through an empirical fit. In gPMC v2.0, the data were extracted and tabulated from the Geant4 system (release 10.2). In addition, we employed a new model to sample the proton angular distribution after nuclear interactions. For proton-proton elastic scattering, the kinetic energy of the scattered proton was sampled from a uniform distribution in gPMC v1.0 and the scattering angle was determined via kinematics. In the new version of the code, we sample the proton scattering angle θ according to the differential cross section in the center-of-mass frame given by (Ranft, 1972)

$$\frac{d{\sigma }_{\mathit{\text{el}}}}{d\mathrm{\Omega }}\approx A^{1.63}exp(14.5A^{0.66}t)+1.4A^{0.33}exp(10t),$$ (1)

where A is the mass number of the target and t = −2p²(l − cos θ) is the invariant momentum transfer (p being the momentum of the scattered proton). Sampling of the variable t is achieved via a rejection method. Specifically, we first sample t uniformly in the interval [0, −4p²]. Then another random variable ξ is uniformly sampled between 0 and A^1.63 + 1.4A^0.33 to reject the sampled t, if ξ is greater than $\frac{d{\sigma }_{\mathit{\text{el}}}}{d\mathrm{\Omega }}$. Other kinematic quantities including the θ and recoil proton momentum are determined and transformed to the laboratory coordinate system.

For proton-oxygen inelastic scattering, the deflection angle of secondary protons in gPMC v1.0 was sampled such that cos θ is uniformly distributed in the interval [2T_s/T_p − 1, l], where T_s and T_p are the kinetic energies of the secondary proton and incidental primary proton, respectively. However, the proton scattering angles generated as such were not sufficiently forward peaked and the unphysical cutoff at cos⁻¹(2T_s/T_p − l) excluded some large scattering angles. To overcome these problems, we empirically modified the sampling methods to yield a distribution of cos θ that is forward peaked within [0, π]. The new probability density function is

$$\mathrm{P}\{x\le cos\theta <x+\mathit{\text{dx}}\}=\frac{\xi e^{\xi x}}{e^{\xi }-e^{-\xi }}\mathit{\text{dx}}.$$ (2)

This is achieved by sampling cos θ as

$$cos\theta =ln[(\eta (e^{\xi }-e^{-\xi })+e^{-\xi })]\frac{1}{\xi },$$ (3)

where η is a random number uniformly distributed in [0,1] and ξ = λT_s/T_p. λ is a parameter fitted to be 6.5 according to nuclear data published by the ICRU (Malmer, 2001).

The main difference between gPMC and TOPAS lies in simulation of nuclear interactions. By default, TOPAS uses Quark Gluon String model for high-energy hadronic interactions of protons and binary cascade model for low energy interaction of protons and ions (Agostinelli et al., 2003). These models describe physics processes in detail and provide good agreement with experiments (Wenzel et al., 2015). Due to the sophisticated calculations involved, simulating according to these models is time consuming. On the contrary, gPMC employs simpler models as described above to achieve high efficiency and sufficient accuracy for dose calculations in radiation therapy. The empirical cross section for elastic collision in Eq. (1) matches with experimental data (Bellettini et al., 1966) and is convenient for sampling. The total cross section data for inelastic collisions are from the fitted model developed in (Fippel and Soukup, 2004). The angular distribution of secondary protons is empirically chosen to match published data.

2.2. OpenCL implementation

We have rewritten gPMC in Open Computing Language (OpenCL) to improve code portability across various platforms and devices. An OpenCL program is composed of a host program and one or more kernel functions. A host program is the outer control logic that performs the configuration and usually runs on a general purpose CPU. Kernel functions are C-based routines executed on a computing device, e.g. a GPU. In OpenCL, parallel computing is achieved by simultaneously executing kernel functions with independent elements, namely work-items (which NVIDIA refers to as “CUDA threads”). At hardware level, each work-item corresponds to a multiple processing core. A collection of related work-items that execute on a single computing unit (composed of one or more multiple processing cores) is called a work-group. Devices such as GPUs and CPU clusters that have a large number of processing cores can thus be programed to accomplish high performance computation. This structure is essentially the same as in CUDA. Hence, we transformed gPMC from the previous CUDA platform to the OpenCL platform with the code structure remaining unchanged.

Memory management is another critical issue in parallel computing. The memory model in OpenCL defines four virtual memory regions on the computing device with different size, accessibility, read/write speed and other features. The global memory is accessible to all work-items and has the largest size but low speed. In gPMC v2.0 physics data and patient data are stored as image objects in the global memory. Image object also supports fast hardware interpolations using built-in sampler functions. The position, momentum and weight of the protons are initialized as buffer objects, which are dynamically allocated on the host side and transferred to the global memory. Because the protons frequently change position, direction and energy, it is inefficient to repeatedly visit the buffer objects in the global memory during simulation. Therefore, at the beginning of the particle transport kernel execution, the information of one particle is read by the corresponding work-item from the global memory into its individual private memory, which is small but allows fast access. The dose, LET and fluence counters as well as the stack for secondary protons are allocated as buffer objects in the global memory, since they require relatively large memory space and need to be accessible to all work-items.

Since there is no OpenCL-based library for random number generators, we implemented a random number generator (RNG) using the MT19937 algorithm (Matsumoto and Nishimura, 1998) to generate a random sequence with a period of 2¹⁹⁹³⁷ − 1. The random seeds in each work-item are initialized with the system clock and its unique thread ID at the code initialization stage. Therefore the random number sequences generated by different work-items are assumed to be independent.

To achieve high efficiency, single precision floating-point variables are used, because GPUs have much higher processing power on single precision than double precision (e.g. ∼3.5 times higher in peak performance in GFLOPS (giga-floating-point operations per second) for NVidia TITAN GPU and ∼8 times higher for AMD Radeon R9 290x GPU). In addition, the image objects and their associated fast hardware interpolation on GPU cards are only available for single precision. However, a pitfall of using single precision floating-point variables is potential loss of precision, particularly when two numbers with a largely different order of magnitude are added (Magnoux et al., 2015). This could occur during a simulation, when a large number of protons are simulated and hence the dose deposition from an additional proton is much smaller than the total dose. To avoid such a problem, gPMC runs in a batched fashion. After each batch of simulation, the code copies data from dose counters to an additional memory buffer. This method effectively eliminates the large difference between each dose deposition and the total dose, hence avoiding the potential loss of precision (Magnoux et al., 2015).

2.3. Memory writing conflict

The memory conflict during dose scoring limited the overall computational efficiency in gPMC v1.0 (Jia et al., 2012). Specifically, when more than one work-items tried to write to the same block of memory, the writing actions were serialized to avoid unpredictable results. This serialization counteracts the parallel processing efficiency achieved by GPUs. To mitigate this problem, a multi-counter technique is employed in gPMC v2.0. As such, a number of M dose counters are allocated at the code initialization stage. During particle transport simulation, when a work-item tries to update a dose counter, it randomly chooses one counter and deposits dose to it. This approach reduces the scoring time, because the probability of two work-items updating the same counter is inversely proportional to the number of counters. However, the number of counters M, is limited by the memory size of computing devices, especially in the cases with a high-resolution phantom. gPMC v2.0 checks the memory size at its initialization stage and notifies users, if the memory becomes a limitation. The use of multiple counters also leads to additional overhead such as memory allocation, memory addressing when depositing energy to a certain counter, and combining data from different counters. The impact of these factors will be analyzed in detail later in Sec 3.5.

2.4. Scoring quantities

In gPMC v1.0, only physical dose was scored. However, recent research on proton RBE suggests using LET for biological dose calculations (McNamara et al., 2015; Polster et al., 2015). We thus implemented the scoring of dose averaged LET (LETd) in gPMC v2.0. LETd in each voxel was calculated as

$$\mathit{\text{LETd}}=\frac{{\sum }_i\delta E_i\times \frac{\delta E_i}{\delta l_i}}{\rho {\sum }_i\delta E_i},$$ (4)

Where ρ is the voxel density, δE_i is the energy deposition corresponding to a step δl_i plus the energy of the δ-electron that were created along the step, and the summation is over all energy deposition events in a given scoring volume. During simulation, it is possible to have a proton moving a very small step but kicking out a δ-electron with relatively large energy. In such cases δE_i/δl_i can give values of several thousand MeV/cm, known as LET spikes. Given that the maximum proton LET in water is around 830 MeV/cm (ICRU 49), we applied a cutoff at 1000 MeV/cm on δE_i/δl_i to avoid these spikes. In case an event is neglected by the cutoff, its energy is not taken into account when averaging the LET by dose.

gPMC v2.0 also supports scoring particle fluence defined as

$${\varphi }_j=\frac{{\sum }_i\delta l_{ij}}{V},$$ (5)

for voxel j where Σ_i δl_ij is the summation of all step lengths in that voxel and V is the voxel volume. During proton transport, secondary protons and other heavier ions are produced in nuclear interactions. To distinguish contribution of different components, dose of primary protons, secondary protons and other heavier ions are scored separately in gPMC v2.0.

2.5. Validation cases

A set of studies was performed to demonstrate the functionality of the new gPMC code, as well as to comprehensively validate its accuracy. Specifically, total dose, dose of primary protons, secondary protons and other heavier ions, fluence of primary protons and secondary protons, as well as LETd were compared to the results computed by TOPAS (Perl et al 2012). For dose comparison, pencil beam with zero width was simulated and the result was integrated laterally to obtain the dose distribution of a broad beam with a size of 5×5 cm². The choice of a pencil beam was because dose and fluence distributions on the central beam axis from this infinitesimal beam are very sensitive to discrepancies in angular deflection and angular distribution of protons. In contrast, the broad beam is more realistic and was hence used to evaluate the accuracy in a more clinically relevant setup. For LETd comparison, 2×2 cm² broad beams were studied. The phantom we used was a pure water phantom of 10.1×10.1×30 cm³ in dimension with a voxel size of 0.1×0.1×0.1 cm³. 100 MeV and 200 MeV mono-energetic beams normally impinged on the phantom surface.

The second scenario studied was a prostate cancer patient. gPMC v1.0 was reported to have a systematic overestimation in dose at the entrance region and underestimation at the target for prostate cases due to approximations in nuclear interaction models (Giantsoudi et al., 2015). To demonstrate the improvements made in this new version, a prostate cancer patient with two laterally opposite beams was used. Dose in this patient was computed with gPMC v1.0, gPMC v2.0 and TOPAS.

The efficiency and cross-platform portability of gPMC v2.0 were tested with several different devices including an NVidia GeForce GTX TITAN GPU card, an AMD Radeon R9 290x GPU card, an Intel i7-3770 CPU processor and an Intel Xeon E5-2640 CPU processor. We also conducted tests with different numbers of dose counters to investigate its impact on the memory conflict issue.

3. Results

3.1. Angular distribution corrections

The physics model of proton-proton elastic scattering and proton-oxygen inelastic scattering was modified in gPMC v2.0. The total cross section data was updated as well. The improvement of proton-proton elastic scattering is illustrated in Figure 1a. In gPMC v1.0, distributions of the scattering angle are almost identical among different incoming proton energies. On the contrary, the distributions are energy dependent and are more forward-peaked in gPMC v2.0, according to Eq. (1). The improvement of scattering angle distributions in the proton-oxygen inelastic interaction channel are in Figure 1b showing a better agreement of scattering angles with the ICRU data (Malmer, 2001) in gPMC v2.0 as compared to gPMC v1.0. The inaccurately modeled scatter angle in gPMC v1.0 does not cause large dose discrepancy in broad beam cases. However, the problem will appear in pencil beam cases that are more sensitive to proton scattering angles, as will be shown later.

Figure 1.

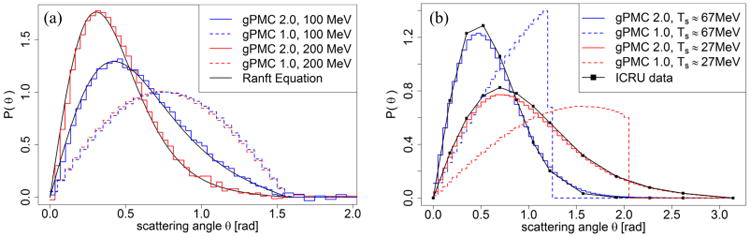
(a) Angular distribution of scattered protons after proton-proton elastic scattering with incoming proton energies of 100 MeV and 200 MeV. (b) Angular distributions of secondary protons with kinetic energy around 67 MeV and 27 MeV after proton-oxygen inelastic scattering with incoming proton energy of 100 MeV.

3.2. Dose and fluence distributions in water phantom

Figures 2 and 3 present the dose calculations in comparison with TOPAS results. Dose distributions of pencil beams were computed and the results were integrated laterally to obtain the corresponding result of broad beams. The uncertainty σ in each voxel is estimated by the dose results in all multi-counters in our simulation. In all the figures below the error bars for the gPMC v2.0 results correspond to 2σ values after simulating 1×10⁷ primary protons. Those for the TOPAS results are not drawn for clarity. We have also calculated average uncertainty $\overline{\sigma /D}$, over a high dose region where the local dose exceeds 10% of D_max inside the entire phantom. For all the cases $\overline{\sigma /D}$ is less than 1%.

Figure 2.

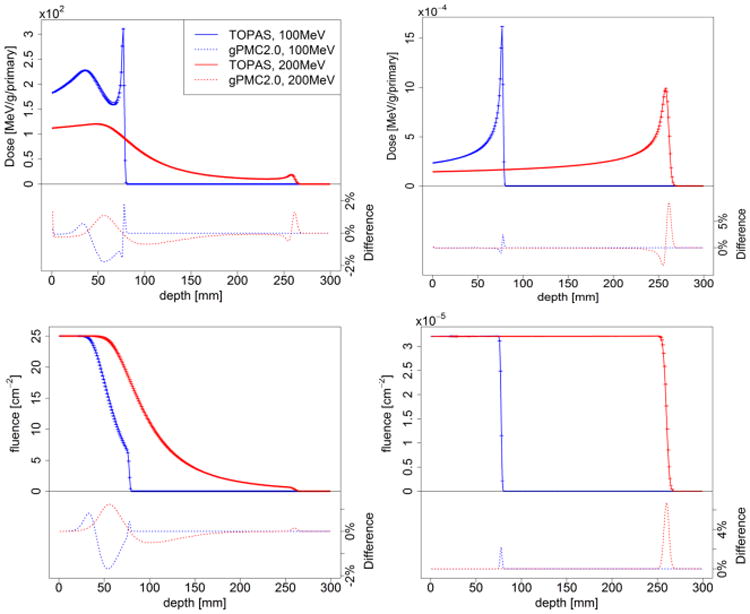
Depth dose (top row) and fluence (bottom row) curves of 100 MeV (blue) and 200 MeV (red) proton pencil beams (left column) and broad beams (right column) in a homogeneous water phantom considering only electromagnetic interactions.

Figure 3.

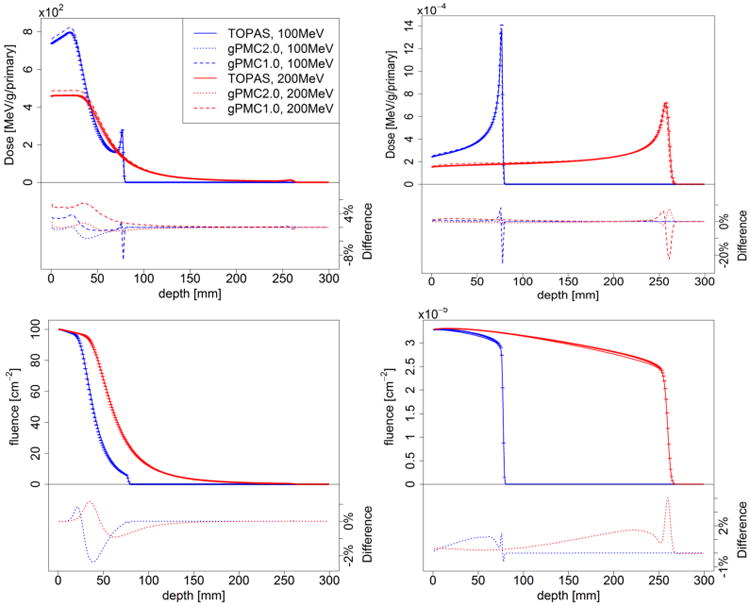
Depth dose (top row) and fluence (bottom row) curves of 100 MeV (blue) and 200 MeV (red) proton pencil beams (left column) and broad beams (right column) in a homogeneous water phantom with all interactions considered.

3.2.1. Electromagnetic interactions

We first present the simulation results in the water phantom with only electromagnetic interactions, because protons deposit energy mainly through this channel. Figure 2 shows the depth dose and fluence curves of 100 MeV and 200 MeV protons. The broad beam doses and fluences match very well with the TOPAS simulation results except at the gradient Bragg peak region. The accuracy of broad beam dose calculations has been demonstrated previously (Jia et al., 2012). For the pencil beam cases considered in this paper small dose differences (within 2%) are observed and can be ascribed to the difference in modeling of multiple scattering. Because pencil beams are the most sensitive cases, these simulations are where discrepancies in multiple scattering become apparent. In contrast, differences smeared out rapidly with increasing beam width leading to a negligible difference for broad beams. The relatively large discrepancy at the beam's end of range was due to sub-mm difference in the beam ranges.

3.2.2. Nuclear interactions

Figure 3 illustrates the depth dose and fluence curves of 100 MeV and 200 MeV protons transport in water when switching on the feature of simulating nuclear interactions. For comparison, dose distributions calculated with gPMC v1.0 are also presented. The most significant improvement is in the entrance region, where the dose overestimation from gPMC v1.0 was removed in gPMC v2.0 as a result of the improved nuclear interaction models. Dose discrepancies around the Bragg peak region are also significantly reduced. For gPMC v2.0, the dose distributions of broad beams match well with TOPAS, but for pencil beams relative difference up to 3% were observed. The relatively large dose discrepancy at the end of the beam due to small range difference was also observed.

In Figure 4 we present the dose contributions from different particle components for both 100 MeV and 200 MeV broad beams. The dose from primary protons is the major component and matches well with TOPAS. However, discrepancies in secondary proton dose and other heavier particle dose can be identified for two reasons. First, gPMC and TOPAS use different physics models for nuclear interactions. Second, in gPMC, secondary ions (heavier than protons) are assumed to have ranges smaller than a voxel and hence their energies are locally deposited instead of tracking.

Figure 4.

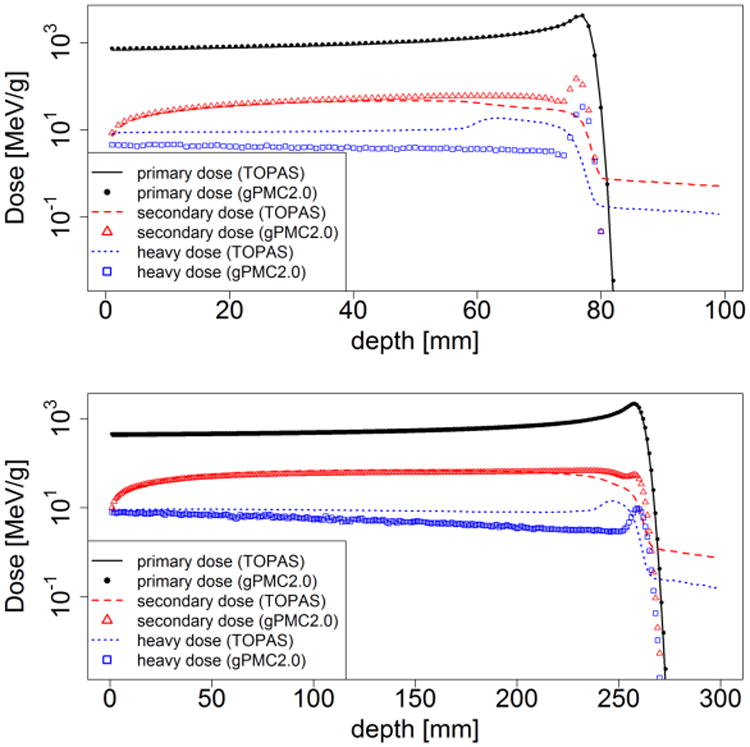
Dose from different components including primary protons, secondary protons and heavy ions after 100 MeV (top) and 200 MeV (bottom) broad proton beams impinging on a homogeneous water phantom.

To quantitatively evaluate the agreement, the relative dose difference was computed for each component, defined as $|d_{\mathit{\text{gPMC}}}^i-d_{\mathit{\text{TOPAS}}}^i|/d_{\mathit{\text{max}}}^t$. Here |.| is the standard L2 vector norm, dⁱ is a vector consisting of dose for the ith component (i = 1,2,3 for primary protons, secondary protons, and heavy particles) in voxels with doses greater than 10% of the maximum dose (within 10% isodose line), and $d_{\mathit{\text{max}}}^t$ is the maximal value of the total dose computed by TOPAS. The results are 1.1%, 0.1%, and 0.2% for the 100 MeV beam and 2.3%, 0.4%, and 0.2% for the 200 MeV beam, respectively.

3.3. LETd distributions

Figure 5 illustrates LETd distributions in water for 100 MeV and 200 MeV mono-energetic broad beams. Physical dose calculated by gPMC is also presented for reference. The LETd spikes are observed laterally outside the beam width and beyond the Bragg peak region due to secondary protons in low dose regions (Granville and Sawakuchi, 2015). This artifact needs to be corrected for biological dose computations (this is done within TOPAS by evoking different user-defined scoring techniques). The low proton numbers in these regions resulted in LETd values with a large uncertainty. Quantitatively, we computed the relative difference between the two LETd results as |LETd_gPMC−LETd_TOPAS|/LETd_max, where LETd is a vector consisting of calculated results in voxels within the 10% isodose line. This difference was found to be 0.7% and 1.1% for 100 MeV and 200 MeV beams respectively, indicating a good agreement.

Figure 5.

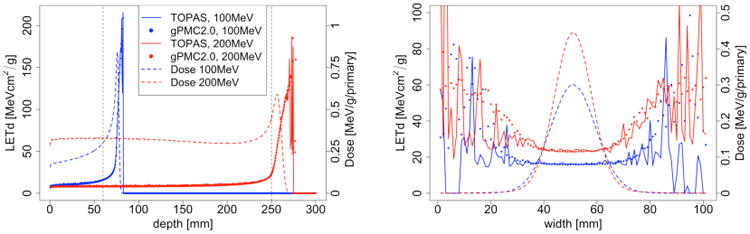
Left: LETd depth curves of 100 MeV (blue) and 200 MeV (red) proton beams; right: lateral profile of 100 MeV beam at 60 mm depth and 200 MeV beam at 250 mm depth as indicated by dashed vertical lines in left.

3.4. Patient case

One of the motivations to improve physics modeling was to resolve the dose discrepancies observed between gPMC v1.0 and TOPAS calculations for prostate cancer cases (Giantsoudi et al., 2015). The main reason was the inaccuracy of the nuclear interaction model and data. After the model refinement in this study, significant improvements are observed as illustrated in Figure 6. Both the overestimation in the entrance region and the underestimation in the target region seen in gPMC v1.0 are largely reduced. To further investigate the accuracy, we calculated the gamma index with a GPU-based gamma index computational tool (Gu et al., 2011). The passing rate for the 1%/1mm criterion improved from 82.7% to 93.1% in the region with doses greater than 10% of the maximum dose.

Figure 6.

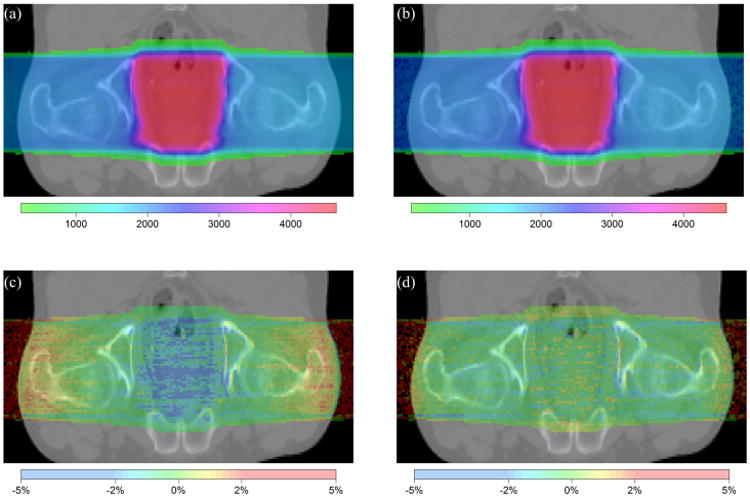
2D comparison between gPMC v2.0 and TOPAS for doses in a prostate cancer patient. (a) TOPAS-calculated dose distribution. (b) gPMC v2.0-calculated dose distribution. (c) Relative dose difference of gPMC v1.0 as ((gPMC v1.0 - TOPAS)/prescribed dose). (d) Relative dose difference of gPMC v2.0 as ((gPMC v2.0 - TOPAS)/prescribed dose).

3.5. Efficiency and portability evaluations

We first compared the computational efficiency of gPMC v2.0 with a different number of dose counters to study the impact of the memory writing conflict. Table 1 illustrates the simulation time of different beams on two GPUs with 1, 4, 8 and 16 dose counters. As expected, memory conflicts are more severe for pencil beams, because most protons are not scattered beyond the central axis voxels and hence almost all the threads simultaneously update the same memory address when scoring dose. With multiple dose counters, the speed of simulating pencil beams is significantly improved, especially for low energy protons since most of them still remain in the central axis voxels at the end of their range where energy deposition events and consequent memory writing happens more frequently. On the other hand, the memory writing conflict was not a significant problem for broad beams and hence a single dose counter worked well. To further understand this effect, we recorded dose deposition time as a function of field size and number of dose counters. The results are plotted in Figure 7. As beam size was reduced from 10×10 cm² to 1×1 cm², time on scoring was only increased by 4.8% with 8 counters, in contrast to a ∼40.0% increase of the scoring time when using only one counter.

Table 1.

Simulation time in seconds for cases with different number of dose counters on NVidia and AMD GPUs. For each case 1×10⁷ primary protons in water were simulated.

Beam	Device	Number of dose counters
		1	4	8	16
100 MeV pencil beam	NVidia GeForce GTX TITAN	50.35	8.36	7.73	7.77
	AMD Radeon R9 290x	23.07	8.27	7.99	10.44
100 MeV 10×10 cm2 beam	NVidia GeForce GTX TITAN	5.63	6.32	6.89	7.71
	AMD Radeon R9 290x	4.85	6.44	7.77	10.72
200 MeV pencil beam	NVidia GeForce GTX TITAN	35.51	20.59	20.03	20.39
	AMD Radeon R9 290x	27.92	16.26	16.57	18.95
200 MeV 10×10 cm2 beam	NVidia GeForce GTX TITAN	16.77	19.05	20.21	21.19
	AMD Radeon R9 290x	13.46	15.93	17.41	20.67

Figure 7.

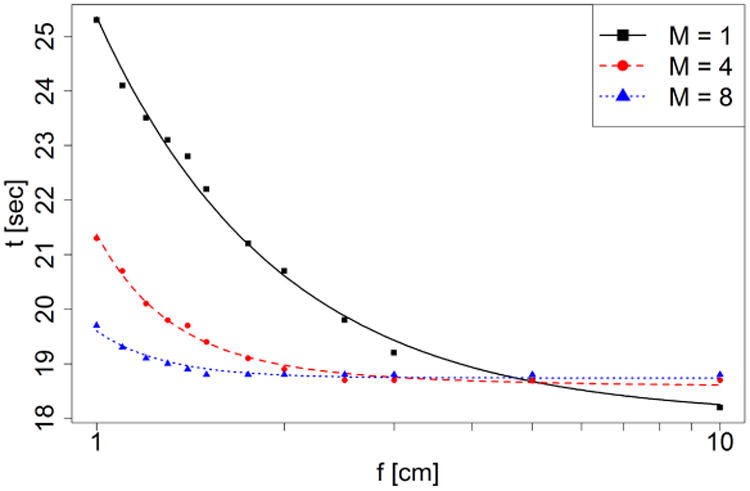
Dose deposition time as a function of field size f and number of dose counters M.

To further understand the factors of scoring time, let us denote the number of dose deposition events in a simulation as N and the probability of memory conflict as p. The total dose deposition time can be expressed as the sum of three terms t = t_{Non–conflict} + t_Conflict + t_Counter. The first term is the time for deposition events executed in parallel by all GPU threads without encountering the memory conflict issue. Hence t_{Non–conflict} = N(1−p)Δt/N_t, where Δt is the dose deposition time per event and N_t is the total number of threads. The second term t_Conflict is the time for dose deposition events with memory conflict. Suppose these events occurred in N_v voxels. Since events at different voxels do not encounter any memory conflict, t_Conflict = NpΔt/N_v. Furthermore, let us denote the field size as f². N_v is then proportional to f², namely N_v = βf². The probability of memory conflict p is inversely proportional to f² and the number of dose counters M, namely p = α/(Mf²). The third term corresponds to the overhead due to the use of multiple dose counters, which is proportional to M, namely t_Counter = λM. Putting everything together, we can write the total dose deposition time as

$$t=\frac{N\mathrm{\Delta }t}{N_t}(1-\frac{\alpha }{M{f}^2})+\frac{\alpha N\mathrm{\Delta }t}{\beta M{f}^4}+\lambda M.$$ (4)

With this model, we fitted our experimental data as a function of M and f and the results are shown in Figure 7. The successful data fitting confirms our model. Note that multiple dose counters also require a larger memory space, so one should be careful when running the code on computing devices which have limited memory. gPMC v2.0 allows users to specify the number of dose counters.

To test the portability of gPMC v2.0, we ran it on two Intel CPUs and two GPUs manufactured by NVidia and AMD, respectively. Simulation times are presented in Table 2. The performances on the two GPUs were of the same order, as the two cards have similar computation power. For high energy beams, performance of the AMD card was slightly better than the NVidia card. This was also observed in a previous article of an OpenCL MC dose engine for photon radiation therapy (Tian et al., 2015), in which it was attributed to the superiority of the AMD card over the NVidia card at the hardware level. Speed on CPUs was lower than on GPUs since CPUs have much fewer cores. Between the two CPUs, the 32-core Intel Xeon E5-2640 CPU performed much better compared to the Intel i7-3770 CPU that has only 8 cores.

Table 2.

Simulation time in seconds of gPMC v2.0 on different devices. For each case we used 8 dose counters to simulate 1×10⁷ primary protons in water.

Beam	NVidia GeForce GTX TITAN GPU	AMD Radeon R9 290x GPU	Intel i7-3770 CPU	Intel Xeon E5-2640 CPU
100 MeV pencil beam	7.73	7.99	187.06	24.29
200 MeV pencil beam	20.03	16.57	554.13	67.68

4. Conclusion and Discussion

Our recent updates on the GPU-based MC dose calculation package, gPMC, are reported in this paper. The new version, gPMC v2.0, was developed under the OpenCL environment to enable portability across different platforms. Physics models of nuclear interactions were refined to improve calculation accuracy. Scoring functions of gPMC were expanded to enable tallying particle fluence and LET in addition to absorbed dose. A multiple counter approach was employed to mitigate memory writing conflict problems. Comprehensive evaluations on accuracy, efficiency and portability of gPMC v2.0 were also performed. Accuracy improvements over gPMC v1.0 were observed for both homogeneous water phantoms as well as a prostate patient case. In particular, for a prostate cancer treatment requiring high-energy beams, dose discrepancy in beam entrance and target regions seen in gPMC v1.0 with respect to the gold standard TOPAS calculations has been substantially reduced, as a consequence of refined nuclear interaction models. Besides total dose, particle fluence, LETd, and dose contributed by different particle components were also compared with TOPAS results, showing reasonable agreements.

The computation time of gPMC v2.0 was found comparable to the previous 1.0 version. The multi-counter approach was also found to be effective. As the beam size is reduced from 10×10 cm² to 1×1 cm², the time for scoring only increased by 4.8% with 8 counters in contrast to a 40.0% increase of the scoring time when using only one counter. With the OpenCL environment, the portability of gPMC was enhanced. It was successfully executed on different CPUs and GPUs and its performance on different devices was found to vary depending on hardware processing power and structure. Meanwhile, the OpenCL code is not always the best option for a specific GPU type in terms of performance. For instance, CUDA has higher efficiency than OpenCL on NVidia's GPU. Hence, we have also maintained the CUDA version of gPMC. The physics refinement, LETd scoring and multi-counter approach reported in this manuscript were also included in the CUDA version.

Scoring of LET is a new and useful feature in gPMC v2.0 that could facilitate a number of studies regarding proton radiobiological effects. It has been proposed in recent studies to use LET as a surrogate for RBE in order to evaluate plan quality from a biological perspective. It can be incorporated into treatment planning to develop treatment plans not only optimal in terms of physical dose, but also in terms of LET (Giantsoudi et al., 2013; Paganetti, 2014; Wan Chan Tseung et al., 2016). For plan optimization studies, the new gPMC version is expected to be beneficial compared to Monte Carlo codes such as TOPAS because of its capability of rapid LET calculation. Especially for LET-based inverse treatment planning, the fast computation will be critical to ensure clinical applicability of this method.

The validity of using gPMC does depend on specific problems of interest. For clinical studies on dose calculation, the overall agreement between gPMC and TOPAS is acceptable. There is a discrepancy between the two MC engines in terms of secondary proton and heavier particle doses, as illustrated in Figure 4. This is mainly due to the fact that different nuclear interaction models are employed in gPMC and TOPAS. Because these components account for only a small fraction of primary proton dose (2∼3 orders of magnitude less), this discrepancy does not significantly impact the total dose distribution. Yet, one should be cautious when using gPMC to study effects sensitive to secondary protons or other heavier particles in proton therapy.

The RNG used in gPMC was implemented in a straightforward fashion. Each GPU thread kept its own random number state, which was updated each time a random number was produced. It is noted that efficient RNG SFMT19937 under single instruction multiple data (SIMD) scheme has been previously developed (Saito and Matsumoto, 2008). This method stores a global state array of 128-bit integers of length 156. The block generation approach can efficiently produce a group of random numbers employing the SIMD scheme. However, it may be difficult to incorporate this method in our MC simulation. If only one global state array is allocated, since different GPU threads perform particle transport simulation in a random fashion, they will need to access and modify the state array randomly, which will cause memory-writing conflict. On the other hand, if each GPU thread holds its own global state array, due to the large number of GPU threads, GPU memory size would become a limiting factor. The solution to incorporate the SFMT19937 in our MC simulation problem is to develop novel schemes to coordinate transport simulations among GPU threads. Investigations along this direction will be in our future study.