Greedy Outcome Weighted Tree Learning of Optimal Personalized Treatment Rules

Summary

We propose a subgroup identification approach for inferring optimal and interpretable personalized treatment rules with high-dimensional covariates. Our approach is based on a two-step greedy tree algorithm to pursue signals in a high-dimensional space. In the first step, we transform the treatment selection problem into a weighted classification problem that can utilize tree-based methods. In the second step, we adopt a newly proposed tree-based method, known as reinforcement learning trees, to detect features involved in the optimal treatment rules and to construct binary splitting rules. The method is further extended to right censored survival data by using the accelerated failure time model and introducing double weighting to the classification trees. The performance of the proposed method is demonstrated via simulation studies, as well as analyses of the Cancer Cell Line Encyclopedia (CCLE) data and the Tamoxifen breast cancer data.

1. Introduction

Personalized medicine has drawn tremendous attention in the past decade (Hamburg and Collins, 2010), especially in the area of cancer treatments. Heterogeneous responses to a variety of anti-cancer compounds (Buzdar, 2009) and treatment strategies (McLellan et al., 2000) motivated the development of individualized treatment rules to maximize drug responses and extend patients’ survival. Of different types of information that may assist this decision making, genetic and genomic information might be the richest and the most promising due to the development of affordable and accurate high-throughput technologies. While these data are potentially useful for researchers to better understand the functionalities of chemical compounds and their interactions in patients, the high-dimensional nature of such data also poses great challenges to the development of statistically sound, computationally efficient, and biologically interpretable methods that infer individualized treatment rules, which is the focus of this article.

The aim of individualized treatment rule is to construct a decision rule that maximizes a patient’s outcome at the population level. There are two types of methods to infer the optimal treatment decision rule: indirect methods and direct methods.

Indirect methods usually involve two steps: first, a model is built for predicting the outcome, using the treatment label, the covariates (consisting of clinical, genomic and other variables), and their interactions. Second, based on the prediction model, the optimal treatment that maximizes the treatment outcome is inferred. For a single stage problem, such as the setting used by (Qian and Murphy, 2011), where the decision is made at a single time point, a widely used indirect method is basic regression, which is a special case of Q-learning for multistage decision problems. In general, the regression model for the treatment outcome needs to be correctly specified to infer the optimal treatment. Lu et al. (2013) proposed a penalized least squares loss based approach and proved that the correct specification of interaction terms between treatment and covariates is sufficient for consistently estimating the treatment rule when the data are from randomized trials and the outcome is continuous. Geng et al. (2015) extended the work of Lu et al. (2013) to censored outcomes. Recently, Tian et al. (2014) proposed an l₁ penalty regression model to directly estimate treatment-covariate interactions on the outcome (continuous, binary, or right censored) without modeling the marginal covariate effects of a single stage problem. However, these methods are based on parametric models, which may not be flexible enough to handle the complex interactions between treatment and covariates, and the methods tend to select very large models. Other indirect methods include g-estimation for structural nested models and its variations (Murphy, 2003; Robins, 2004), regret-regression (Henderson et al., 2010), Virtual Twins (Foster et al., 2011), and the boosting approach (Kang et al., 2014).

Direct methods focus on the direct estimation of treatment decision rules. Recent statistical work in this area includes marginal structural mean models (Orellana et al., 2010), augmented value maximization (Zhang et al., 2012, 2013), outcome weighted learning (Zhao et al., 2012), and doubly robust weighted least square procedures (Wallace and Moodie, 2015). These methods circumvent the need to model the conditional mean function of the outcome given the treatment and covariates. However, they do not necessarily provide interpretable and parsimonious decision rules, which are desirable when informing clinical practices.

Tree-based methods (Breiman et al., 1984; Breiman, 2001) have emerged as one of the most commonly used machine learning tools that produce simple and interpretable decision rules. The last decade has seen promising extensions of tree-based methods in statistical modeling (Meinshausen, 2006; Ishwaran et al., 2008; Zhu and Kosorok, 2012) and theoretical understanding (Scornet et al., 2014; Wager, 2014; Zhu et al., 2015). Many tree-based methods have been proposed for personalized medicine either to identify subgroups of patients who may have an enhanced treatment effect (Su et al., 2008, 2009; Foster et al., 2011; Lipkovich et al., 2011), or to construct interpretable treatment decision rules (Zhang et al., 2012; Laber and Zhao, 2015; Zhang et al., 2015). Most of these methods are indirect methods, with the exception of Laber and Zhao (2015). However, as we shall see from our simulation analysis that, the performances of these methods can be greatly affected by the dimensionality due to the marginal search of splitting rules.

In this article, we propose a greedy outcome weighted tree learning procedure that combines the strength of the outcome weighted learning framework (Zhao et al., 2012) and the interpretability of single tree method, where a single tree model is used to determine the treatment decision. In the following sections, we first review the outcome weighted learning framework and the optimal treatment rules (Section 2). The proposed weighted greedy splitting rule is introduced in Section 3.1 to improve performance in high-dimensional data settings. A modification of the subject weight is used to facilitate the tree building process (Section 3.3). An adaptation of right censored survival data using an accelerated failure time model is provided in Section 3.4. Simulation studies (Section 4) and real data analyses (Section 5) are followed by a discussion (Section 6).

2. Outcome Weighted Learning and the Optimal Treatment Rule

Let a p-dimensional vector X ∈ 𝒳 denote a patient’s features, which may include demographic variables and genetic/genomic profiles. Let A be the treatment assignment taking values in the set of all possible treatments 𝒜. Let Y be the clinical outcome dependent upon the patient’s features X and the treatment assignment A, with larger values being more desirable. We assume that n independent and identically distributed (i.i.d) copies of the triplets {X, A, Y} are observed, denoted as ${\{{\mathbf{X}}_i,A_i,Y_i\}}_{i=1}^n$. We search for a treatment rule D^*(X) in a class of functions 𝒟: 𝒳 ↦ 𝒜, such that the following value function V(D) (Qian and Murphy, 2011) is maximized,

$$D^{\ast }(\mathbf{X})=\underset{D\in \mathcal{D}}{argmax}V(D)=\underset{D\in \mathcal{D}}{argmax}E\left[\frac{Y{\mathbf{1}}_{\{A=D(\mathbf{X})\}}}{P(A\mid \mathbf{X})}\right].$$ (1)

D^*(X) is the optimal treatment rule in the sense that it maximizes the value function V(D), which represents the population benefit for implementing a particular treatment rule D(X). In this article, we mainly focus on a two-armed randomized trial, i.e., 𝒜 = {0, 1}, and we assume that P(A|X) is known. For simplicity, we consider the case in which A is independent of the features X, with P(A = 1|X) = 1 − P(A = 0|X) = 1/2. We shall discuss a simple extension of the proposed method in Section 5.2 to account for observational studies and for a situation when treatment assignment probabilities P(A|X) are unknown.

3. Proposed Method

Zhao et al. (2012) solved (1) as a weighted classification problem. In particular, the optimal treatment rule is solved by minimizing the empirical weighted classification error

$${\widehat{D}}^{\ast }(\mathbf{X})=\underset{D\in \mathcal{D}}{argmin}\frac{1}{n}\sum _{i=1}^n{w}_i{\mathbf{1}}_{\{A_i\ne D({\mathbf{X}}_i)\}},$$ (2)

where $w_i=\frac{Y_i}{P(A_i\mid {\mathbf{X}}_i)}$ is a subject specific weight. If any Y_i has a negative value, Zhao et al. (2012) add a positive constant to all weights, i.e., $w_i=\frac{Y_i+m}{P(A_i\mid {\mathbf{X}}_i)}$, where m = −min_i(Y_i, 0). In the following, we always assume that w_i is positive, and the training dataset ${\{{\mathbf{X}}_i,A_i,Y_i\}}_{i=1}^n$ is used to determine the optimal treatment. In section 3.3, we discuss the particular choice of m, rather than using a constant, to facilitate the splitting rules in tree-based methods.

3.1. Greedy Splitting Rules

D̂^*(X) solved by a single tree method enjoys interpretability and nonparametric model structure, which are both desirable in precision medicine. A tree-based method works by recursively partitioning the feature space 𝒳. Starting with the entire feature space as the root node, a binary splitting rule is created that separates the node into two daughter nodes. This process is then recursively applied to each daughter node. Hence, creating splitting rules is the most crucial step in the tree building process. We first provide a pseudo algorithm of a general subject-weighted ensemble tree model in Table 1, which facilitates our presentation in later sections. This algorithm can be used in both regression and classification settings. A single tree model is a special case of this algorithm. The splitting rules score_cla(T, T_L, T_R) and score_reg(T, T_L, T_R) that are implemented in traditional tree-based methods are essentially a measure of the immediate variation reduction after a candidate split 1_{X(^j)<c}. It is easy to see that this marginal search of signals may fail to detect interactions, such as the checker-board model. This potential drawback has been previously discussed in the literature (Biau et al., 2008). Zhu et al. (2015) suggest that when the splitting variable is searched through a nonparametric embedded model, universal consistency can be archived. Following this approach, we propose a weighted classification score that evaluates the potential contribution of each variable j at an internal node T:

$${\mathit{score}}_{\mathit{cla}}^{\ast }(T,j)=\frac{1}{M}\sum _{m=1}^M\frac{{\sum }_{i\in {\mathcal{L}}_{T,m,o}}{w}_i{\mathbf{1}}_{\{A_i\ne {\widehat{f}}_{T,m}({\mathbf{X}}_i^{(-j)},{\stackrel{\sim }{X}}_i^{(j)})\}}}{{\sum }_{i\in {\mathcal{L}}_{T,m,o}}{w}_i{\mathbf{1}}_{\{A_i\ne {\widehat{f}}_{T,m}({\mathbf{X}}_i^{(-j)},X_i^{(j)})\}}}-1.$$ (3)

Table 1.

Pseudo algorithm: subject-weighted ensemble trees

Input: training data ${\mathcal{L}}_n={\{{\mathbf{X}}_i,w_i,Y_i\}}_{i=1}^n$ for regression and ${\{{\mathbf{X}}_i,w_i,A_i\}}_{i=1}^n$ for classification output: an ensemble tree model Draw bootstrap sample ℒb from the training data, with replacement and equal probability on each subject. Denote the out-of-bag data as ℒo. At an internal node T, stop if the sample size is sufficiently small. Otherwise, randomly generate candidate splitting variables and cutting point. For each candidate split, denote TL and TR as the two daughter notes resulting from the candidate split. Calculate the score: $$\begin{array}{c}{\mathit{score}}_{\mathit{reg}}(T,T_L,T_R)=V_T^w-\frac{w_{T_L}}{w_T}{V}_{T_L}^w-\frac{w_{T_R}}{w_T}{V}_{T_R}^w\text{for}\text{regression},\\ {\mathit{score}}_{\mathit{cla}}(T,T_L,T_R)=G_T^w-\frac{w_{T_L}}{w_T}{G}_{T_L}^w-\frac{w_{T_R}}{w_T}{G}_{T_R}^w\text{for}\text{classification}.\end{array}$$ In the above definitions, wT, wTL and wTR are the sum of subject weights within the corresponding node. $V_T^w=\frac{1}{w_T}{\sum }_{X_i\in T}{w}_i{(Y_i-{\overline{Y}}_T^w)}^2$ is the weighted variance, with ${\overline{Y}}_T^w=\frac{1}{w_T}{\sum }_{X_i\in T}{w}_i{Y}_i$. $G_T^w={\sum }_k{\varphi }_{T_k}^w(1-{\varphi }_{T_k}^w)$ is the weighted gini impurity, with ${\varphi }_{T_k}^w=\frac{1}{w_T}{\sum }_{X_i\in T}{w}_i{\mathbf{1}}_{\{A_i=k\}}$ for class k = 1, …, K. The other quantities are defined accordingly. Select the candidate split with the highest score, and apply b) and c) to each of the resulting daughter nodes. Repeat a)–c) until the desired number of trees are fited.

In the above definition, an ensemble of M trees are fitted to the within-node data ℒ_T,m. For each tree, a bootstrap sample ℒ_T,m,b is drawn from ℒ_T,m, and a single tree model f̂_T,m is fitted using ℒ_T,m,b. The out-of-bag data ℒ_T,m,o, defined as ℒ_T,m\ℒ_T,m,b, are used to calculate the misclassification error. $X_i^{(-j)}$ is the sub-vector of X_i after removing the jth entry. ${\stackrel{\sim }{X}}_i^{(j)}$ is an independent copy of variable X^(j) in the out-of-bag data, following the definition in Zhu et al. (2015). Hence, ${\stackrel{\sim }{X}}_i^{(j)}$ is independent of the vector X_i, and follows the same distribution as X^(j)|X ∈ T. It is easy to see that, when the embedded classification model f̂_T,m(X_i) is consistent, the proposed splitting score converges to a true weighted variable importance measure defined as

$$\begin{array}{l}V{I}_T^w(j)=\frac{E\left\{w{\mathbf{1}}_{\{A\ne D^{\ast }({\mathbf{X}}^{(-j)},{\stackrel{\sim }{X}}^{(j)})\}}|({\mathbf{X}}^{(-j)},{\stackrel{\sim }{X}}^{(j)})\in T\right\}}{E\left\{w{\mathbf{1}}_{\{A\ne D^{\ast }({\mathbf{X}}^{(-j)},X^{(j)})\}}\right|({\mathbf{X}}^{(-j)},X^{(j)})\in T\}}-1\\ =\frac{V_T(D^{\ast }({\mathbf{X}}^{(-j)},X^{(j)}))-V_T(D^{\ast }({\mathbf{X}}^{(-j)},{\stackrel{\sim }{X}}^{(j)}))}{E(w\mid \mathbf{X}\in T)-V_T(D^{\ast }({\mathbf{X}}^{(-j)},X^{(j)}))},\end{array}$$ (4)

where V_T (D(X)) = E[w1_{A=D(X)}|X ∈ T] is the within node value function. Interestingly, this is the proportion of the value function sacrificed by removing signals carried in $X_i^{(j)}$. Hence, the splitting variable is chosen as the one that has the most influence on the value function within node T. With our greedy splitting rule defined, we present the algorithm for the proposed method in Table 2.

Table 2.

Pseudo algorithm: single RLT for optimal treatment rule

Input: training data ${\{{\mathbf{X}}_i,w_i,A_i\}}_{i=1}^n$ output: a tree classification model At any node T, if |T| < nmina or Ai’s are identical, terminate this node with class $arg{max}_k{\varphi }_{T_k}^w$. Fit embedded model and calculate ${\mathit{score}}_{\mathit{cla}}^{\ast }(T,j)$ (equation 3) for each variable. Use variable $arg{max}_j{\mathit{score}}_{\mathit{cla}}^{\ast }(T,j)$ as the splitting variable, and search for the best cutting point that maximizes the classification score(T, TL, TR) defined in Table 1. Split T into TL and TR based on this best splitting rule, and apply a)–d) to both TL and TR.

^an_min is a tuning parameter for the terminal node size.

3.2. Tree Pruning

To obtain an accurate yet interpretable tree model, tree pruning is necessary. Tree pruning can be viewed as a penalization in the tree model size, where each split represents an extra parameter in the fitted model. Here, we adopt the cost complexity pruning proposed by Breiman et al. (1984), with details presented in the Web Appendix A.

3.3. Weight Transformation

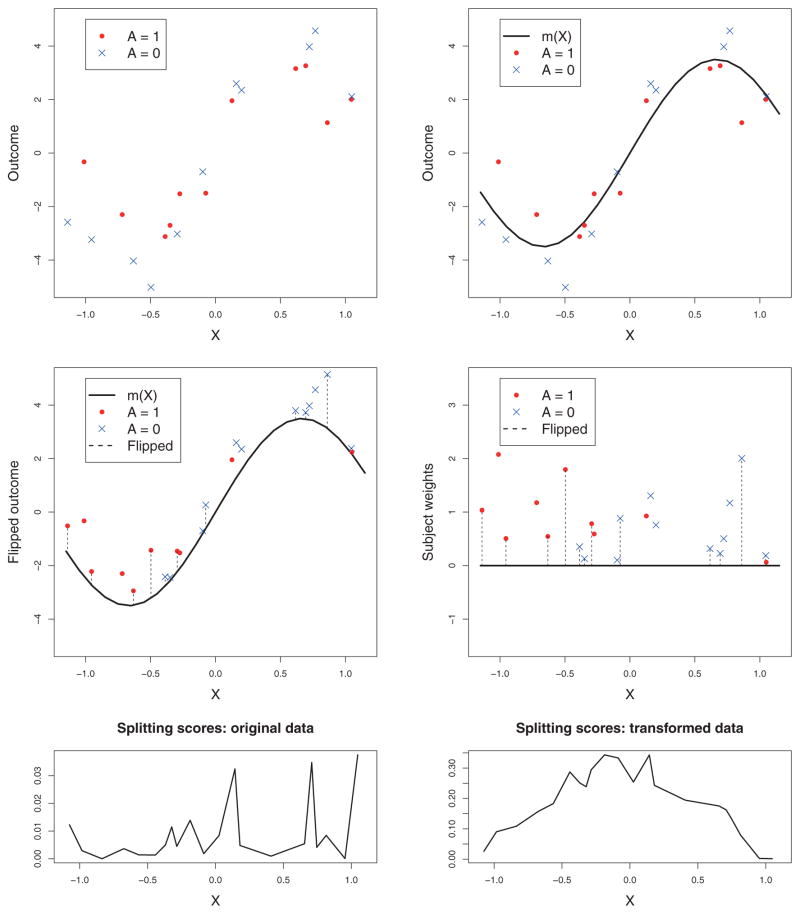
In this section, we discuss the particular choice of m for constructing the weight $w_i=\frac{Y_i}{P(A_i\mid {\mathbf{X}}_i)}$. Many different methods have been proposed, the simplest one using m = − min_i(Y_i, 0) (Zhao et al., 2012). However, such implementation may not be ideal for tree-based methods due to the nature of the splitting rules, which are sequentially constructed based on marginal signals rather than optimized globally. Figure 1 demonstrates this phenomenon under forced positive weights and our proposed model adjusted weights. The observations are created under the optimal decision rule D^*(X) = 1_{X<0}. Under forced positive weights, the marginal signal presented in the data is extremely weak, which leads to splitting near the boundary (bottom-left panel of Figure 1). This “end-cut preference” property for weak signals has been discussed in a recent analysis of random forests (Ishwaran, 2015). Our solution is to first adjust the weights using m = m(X) = E(Y|X), which is the expected outcome if a random treatment is received, and then flip the treatment label of subjects with negative weights. The new weights and treatment labels are given in the mid-right panel. Clearly, the improved marginal signal encourages a new cutting point near X = 0, as shown in the bottom-right panel. Note that the proposed m(X) will lead to minimum variance of the residuals as in Zhou et al. (2015), which enjoys improved stability as compared to (Zhao et al., 2012). Other types of weight can also be used. For example, Zhang et al. (2012) proposed the use of the contrast function as the weight, yet the conditional mean function for both treatments still needs to be estimated.

Figure 1.

Estimating optimal treatment rules using flipped treatment label. The top-left panel shows a plot of original observations. In Zhao et al. (2012) the vertical axis is equivalent to subject weights up to a constant difference. The top-right panel shows the mean response curve regardless of the treatment effects. The mid-left panel shows observations with flipped treatment labels and flipped outcomes. The mid-right panel shows the transformed classification problem with subject weights. The bottom two plots show the splitting scores for the original data and transformed data, respectively. This figure appears in color in the electronic version of this article.

Motivated by the above example, we can then transform (2) into a classification problem for minimizing the weighted misclassification error:

$${\widehat{D}}^{\ast }(\mathbf{X})=\underset{D\in \mathcal{D}}{argmin}\frac{1}{n}\sum _{i=1}^{n}w(X_i){\mathbf{1}}_{\{{\stackrel{\sim }{A}}_i\ne D({\mathbf{X}}_i)\}},$$ (5)

where w(X_i) is a plug-in subject weight defined as $\frac{\mid Y_i-\widehat{m}({\mathbf{X}}_i)\mid }{P(A_i\mid {\mathbf{X}}_i)}$, where m(X) = E(Y|X), and Ã_i is the flipped treatment label defined as Ã_i = A_i, if Y_i ≥ m(X), and 1 − A_i otherwise.

Hence, the proposed method involves two steps. Step 1), estimate a mean response function m(X) = E(Y|X) using ${\{X_i,Y_i\}}_{i=1}^n$ and perform weight and treatment label transformations; and Step 2), solve for the optimal treatment in equation (5) using the reconstructed data ${\{{\mathbf{X}}_i,w({\mathbf{X}}_i),{\stackrel{\sim }{A}}_i\}}_{i=1}^n$. In the first step, a standard random forests model is used. In the second step, the single tree model is fitted using the proposed greedy splitting score. However, it should be noted that since the tree-based method is not an exact optimization approach, the restrictions posted on the model space 𝒟 can be complicated. The resulting optimal decision rule 𝒟^*(X) should be viewed as a projection on the tree model space.

Finally, we make one more note on the equivalence between the classifiers defined in (2) and (5). In particular, our proposed modification of the weights and treatment labels will not change the decision rule at any terminal node. To see this, we focus on a single terminal node, say T, of a tree-model. Then, for any function m(X), the optimal treatment rule defined in (2) is simply the indicator function of ${\sum }_{{\mathbf{X}}_i\in T}\frac{Y_i-m({\mathbf{X}}_i)}{P(A_i\mid {\mathbf{X}}_i)}{\mathbf{1}}_{\{A_i=1\}}>{\sum }_{{\mathbf{X}}_i\in T}\frac{Y_i-m({\mathbf{X}}_i)}{P(A_i\mid {\mathbf{X}}_i)}{\mathbf{1}}_{\{A_i=0\}}$. Noting that

$$\begin{array}{l}\sum _{{\mathbf{X}}_i\in T}\frac{Y_i-m({\mathbf{X}}_i)}{P(A_i\mid {\mathbf{X}}_i)}{\mathbf{1}}_{\{A_i=1\}}-\sum _{{\mathbf{X}}_i\in T}\frac{Y_i-m({\mathbf{X}}_i)}{P(A_i\mid {\mathbf{X}}_i)}{\mathbf{1}}_{\{A_i=0\}}\\ =\sum _{{\mathbf{X}}_i\in T}\frac{\mid Y_i-m({\mathbf{X}}_i)\mid }{P(A_i\mid {\mathbf{X}}_i)}\left[{\mathbf{1}}_{\{A_i=1\}}{\mathbf{1}}_{\{Y_i>m({\mathbf{X}}_i)\}}-{\mathbf{1}}_{\{A_i=1\}}{\mathbf{1}}_{\{Y_i<m({\mathbf{X}}_i)\}}-{\mathbf{1}}_{\{A_i=0\}}{\mathbf{1}}_{\{Y_i>m({\mathbf{X}}_i)\}}+{\mathbf{1}}_{\{A_i=0\}}{\mathbf{1}}_{\{Y_i<m({\mathbf{X}}_i)\}}\right]\\ =\sum _{{\mathbf{X}}_i\in T}w({\mathbf{X}}_i){\mathbf{1}}_{\{{\stackrel{\sim }{A}}_i=1\}}-\sum _{{\mathbf{X}}_i\in T}w({\mathbf{X}}_i){\mathbf{1}}_{\{{\stackrel{\sim }{A}}_i=0\}},\end{array}$$ (6)

the decision rule is equivalent to (5) at any terminal node T in a tree model.

In observational studies, where the treatment labels are not randomized, a common strategy is to estimate the propensity score P(A|X) (Lee et al., 2010; Austin, 2011; Imai and Ratkovic, 2014) and incorporate it into the weight w_i. The other approach is to conduct matching and use only matched pairs of samples for the follow-up analysis (Rosenbaum, 2010). Both approaches can be naturally incorporated into our framework, and the propensity score is used in one of our real analyses. However, choosing the optimal strategy is beyond the scope of this article.

3.4. Double Weighted Trees for Right Censored Survival Outcome

Clinical outcomes are often subjected to censoring from the right. In this section, we propose a simple extension of the proposed method to a right censored survival outcome. In such a scenario, the observed outcome is Y = min(Y⁰, C), where Y⁰ is the true outcome of survival time, and C is the censoring time. One also observes the censoring indicator δ = 1_{Y⁰≤C}. To account for right censoring, we adopt the popular accelerated failure time model (AFT, Stute, 1993; Huang et al., 2006). Suppose that a set of random samples ${\{Y_i,{\delta }_i,{\mathbf{X}}_i\}}_{i=1}^n$ is observed, let u_i be the Kaplan–Meier weights, which can be expressed as,

$$\begin{array}{ll}\hfill u_1& =\frac{{\delta }_{(1)}}{n},\text{and}{u}_i=\frac{{\delta }_{(i)}}{n-i+1}\prod _{j=1}^{i-1}{\left(\frac{n-j}{n-j+1}\right)}^{{\delta }_{(i)}},\\ \hfill i& =2,\dots ,n,\end{array}$$ (7)

where δ₍₁₎, …, δ_(n) are the censoring indicators associated with the ordered statistics Y₍₁₎ ≤ … ≤ Y_(n) of Y_i’s. Further, let $u_i^{\ast }$ be the corresponding Kaplan–Meier weight of subject i in the unordered list, i.e., $u_i^{\ast }=u_k$, if k = Σ_j1_{Y(j)≤Yi;}. Then in our proposed estimating procedure, we first estimate the mean response function m̂ by minimizing the weighted regression least squares loss

$$\frac{1}{2}\sum _{i=1}^n{u}_i^{\ast }{(log(Y_i)-m({\mathbf{X}}_i))}^2,$$ (8)

which is solved using subject-weighted ensemble trees (Table 1). Furthermore, the optimal treatment rule is obtained through a double weighted classification problem:

$${\widehat{D}}^{\ast }(\mathbf{X})=\underset{D\in \mathcal{D}}{argmin}\frac{1}{n}\sum _{i=1}^n{u}_i^{\ast }w({\mathbf{X}}_i){\mathbf{1}}_{\{{\stackrel{\sim }{A}}_i\ne D({\mathbf{X}}_i)\}}.$$ (9)

4. Simulation Studies

We compare the proposed method with some existing tree-based methods for treatment recommendations, including the virtual twins (VT, Foster et al., 2011) and minimum impurity decision assignments (MIDAs, Laber and Zhao, 2015). The VT fit two random forests for each treatment label and summarize the preference using a single tree model. It is implemented using the R packages of “randomForest” and “rpart.” MIDAs uses a marginal impurity guided splitting rule, which is implemented in the R package “MIDAs.” An alternative choice of the weight w_i using the contrast function proposed by Zhang et al. (2012) is implemented. The contrast function E(Y_i|X_i,A_i = 1) − E(Y_i|X_i,A_i = 0) is estimated using random forests, similar to the VT method, while the decision rule is determined using the proposed weighted greedy trees. We refer to this method as Proposed-cw. We also include three penalized linear methods for high-dimensional data, Lasso and Lasso-cox (Tian et al., 2014) (through R package “glment”), optsel (Lu et al., 2013), and optsel-ipcw (Geng et al., 2015) (both through author provided R codes), as non-tree alternatives for comparison. Four simulation scenarios are created: two scenarios with complete continuous outcome; the other two scenarios with right censored survival outcome. We also consider both low-dimensional (p = 50) and high-dimensional (p = 500) settings for each scenario. Existing tree-based methods can not handle survival outcomes, hence, to make the comparisons more interesting, we propose a simple extension of the virtual twins model to right censored survival data. The idea is to replace the regression random forests in VT’s first stage with a random survival forest (Ishwaran et al., 2008). The integrated survival function is computed up to the maximum observed failure time and then compared between different treatments. The second stage of VT follows exactly the original method. We denote this extension as VT-rsf.

Each simulation setting is repeated 200 times. For each simulation run, 1000 testing samples are generated. The correct optimal treatment selection rates against the testing data are reported. Furthermore, we report the model size, the true positive identification rate of the features that are involved in the optimal treatment rule, and the total reward (empirical version of V(D) evaluated on the testing set) for the two complete outcome scenarios. For tree-based methods, the model size is the number of unique features involved in the entire tree, while the model size for penalized methods is the number of parameters involved in differentiating the treatment effects. All tree-based methods include a tuning parameter for tree pruning, which controls the tree complexity and prevents overfitting. For the three penalized methods, a penalty level is used to control sparsity. To eliminate the impact of tuning parameters, we produce a series of models for each method along the changes of its corresponding tuning parameter, and report the result of the best model against the testing data. Such an implementation is popular in penalized model literature, and the results reflect the true potential of each method. The simulation scenarios are provided below. Treatment assignment A is generated from {0, 1} with equal probability. In scenarios 1, 2, and 3, X is generated from 𝒩(0,Σ), where Σ_i,j = ρ ^|i−j|. ε’s follow i.i.d 𝒩(0, 1).

• Scenario 1 (regression): Y = 1_{A=0}1_{{X⁽¹⁵⁾<−0.5∪X⁽²⁰⁾<−0.5}} + 1.5 1_{A=1}1_{{X(15) ≥−0.5∩X⁽²⁰⁾ ≥−0.5}} + 0.5X⁽²⁾ + 0.5X⁽⁴⁾ − X⁽⁶⁾ + X⁽⁸⁾X⁽¹⁰⁾ + ε, ρ = 0.5 and n = 300.

• Scenario 2 (regression): $Y={\sum }_{j=1}^p{\beta }_j{X}^{(j)}+(2A-1)(X^{(40)}+X^{(50)})+\epsilon$, where for each simulation run, β_j’s are generated independently from uniform [−0.25, 0.25], if i = 5, 10, 15, 20, 25, 30, and 0 otherwise. ρ = 0.8 and n = 300.

• Scenario 3 (survival): μ = e^{X(1)+0.5X(5)+(3A−1.5)(|X(10)|−0.67)}, ρ = 0.25, Y⁰ ~ Exp(μ) and C ~ Exp(e^{0.1(X(25)+X(30)+X(35)+X(40))}). n = 400 and the censoring rate is 22.2%.

• Scenario 4 (survival): X ~ uniform [0, 1]^p. Y⁰’s are generated from Weibull distribution with shape parameter 2, and scale parameter e^μ where $\mu =\frac{1}{5}{\sum }_{j=6}^{10}{X}^{(j)}+A({\mathbf{1}}_{\{X^{(1)}<0.6\cap X^{(2)}>0.2\}}-0.5)$. C ~ Exp(0.3e^−μ), n = 400, and the censoring rate is 22.6%.

4.1. Simulation Results

All simulation results are summarized in Table 3 and Table 4. Scenarios 1 and 3 are tree-structured, and Scenario 4 has symmetric effects. Hence under these scenarios, tree-based models are preferred over linear models. Our proposed method dominates the performance under these models, especially in Scenarios 1 and 4, and it also demonstrates a better resilience of the increased dimension p as compared to other tree-based methods. Moreover, in all scenarios, the proposed method tends to select smaller models with larger true positive rates. This suggests that our splitting variable selection is more stable than other tree-based methods. Scenarios 2 is linear, with oblique cutting lines of the optimal treatment rule, hence it prefers Lasso and optsel, with optsel having a smaller model size. Under this scenario, the proposed method performs similarly to VT and Proposed-cw and is better than MIDAs. Moreover, tree-based methods usually result in a more parsimonious model as compared to penalized linear models. The Proposed-cw method enjoys the benefit of the greedy splitting rule, which leads to higher true positive rates; however, the performance generally lies between VT and Proposed.

Table 3.

Simulation results: continuous outcome

Scenario 1
p	Method	Correct rate (sd)	Rewarda (sd)	Model size (sd)	TP (sd)
50	Proposed	92.3% (8.0%)	1.81 (0.11)	2.38 (1.37)	1.73 (0.51)
	Proposed-cw	87.2% (9.0%)	1.74 (0.11)	3.04 (2.30)	1.71 (0.52)
	VT	86.4% (8.4%)	1.75 (0.11)	2.92 (1.86)	1.53 (0.62)
	Midas	78.4% (9.5%)	1.66 (0.12)	1.05 (0.36)	0.84 (0.55)
	Lasso	80.3% (4.4%)	1.65 (0.07)	5.30 (3.19)	1.44 (0.60)
	optsel	80.0% (4.8%)	1.63 (0.08)	5.05 (3.26)	1.40 (0.63)
500	Proposed	86.5% (11.2%)	1.74 (0.14)	2.03 (1.59)	1.39 (0.70)
	Proposed-cw	81.1% (12.6%)	1.69 (0.14)	2.75 (2.54)	1.19 (0.72)
	VT	78.0% (11.1%)	1.66 (0.13)	2.87 (2.41)	1.05 (0.76)
	Midas	75.8% (11.1%)	1.64 (0.13)	0.96 (0.38)	0.72 (0.52)
	Lasso	76.7% (6.8%)	1.60 (0.09)	6.92 (10.76)	1.24 (0.67)
	optsel	77.2% (5.6%)	1.61 (0.08)	4.94 (10.13)	1.20 (0.66)
Scenario 2
p	Method	Correct rate (sd)	Rewardb (sd)	Model size (sd)	TP (sd)
50	Proposed	81.8% (4.0%)	0.49 (0.04)	2.79 (1.45)	1.82 (0.41)
	Proposed-cw	82.5% (3.9%)	0.50 (0.04)	3.58 (1.92)	1.84 (0.40)
	VT	81.9% (3.4%)	0.49 (0.04)	3.94 (1.69)	1.76 (0.46)
	Midas	74.5% (3.1%)	0.41 (0.04)	1.00 (0.00)	0.84 (0.37)
	Lasso	96.7% (2.5%)	0.59 (0.02)	3.66 (1.82)	2.00 (0.00)
	optsel	96.2% (3.2%)	0.59 (0.02)	3.02 (1.78)	2.00 (0.07)
500	Proposed	80.5% (4.3%)	0.48 (0.05)	2.42 (1.18)	1.70 (0.50)
	Proposed-cw	80.7% (4.2%)	0.48 (0.05)	3.14 (2.06)	1.75 (0.49)
	VT	79.7% (4.3%)	0.47 (0.05)	3.30 (1.72)	1.52 (0.59)
	Midas	74.6% (2.8%)	0.41 (0.04)	1.00 (0.00)	0.84 (0.37)
	Lasso	96.3% (2.7%)	0.59 (0.02)	3.89 (2.17)	2.00 (0.00)
	optsel	97.4% (2.2%)	0.59 (0.02)	2.13 (0.42)	2.00 (0.05)

^aMaximum reward is 1.90; reward for a random rule is 1.26.

^bMaximum reward is 0.59; reward for a random rule is 0.

Table 4.

Simulation results: survival outcome

Scenario 3
p	Method	Correct rate (sd)	Model size (sd)	TP (sd)
50	Proposed	92.3% (7.6%)	2.36 (1.43)	1.72 (0.47)
	Proposed-cw	93.5% (5.0%)	2.62 (1.68)	1.84 (0.36)
	VT-rsf	94.4% (4.8%)	2.33 (1.17)	1.89 (0.32)
	Lasso-cox	78.8% (4.4%)	9.95 (4.88)	1.84 (0.37)
	optsel-ipcw	77.9% (6.3%)	5.59 (4.54)	1.62 (0.49)
500	Proposed	87.6% (11.1%)	1.87 (1.44)	1.39 (0.57)
	Proposed-cw	89.6% (6.4%)	2.00 (1.28)	1.45 (0.50)
	VT-rsf	87.0% (8.1%)	2.13 (1.91)	1.41 (0.49)
	Lasso-cox	73.3% (7.2%)	14.10 (14.18)	1.16 (0.51)
	optsel-ipcw	69.3% (9.2%)	10.50 (6.02)	1.11 (0.47)
Scenario 4
p	Method	Correct rate (sd)	Model size (sd)	TP (sd)
50	Proposed	86.6% (6.5%)	1.22 (0.56)	1.00 (0.00)
	Proposed-cw	79.6% (13.6%)	2.07 (2.46)	0.96 (0.19)
	VT-rsf	69.1% (11.1%)	5.41 (4.13)	0.95 (0.22)
	Lasso-cox	51.9% (1.1%)	16.75 (16.93)	0.38 (0.49)
	optsel-ipcw	51.8% (1.2%)	14.11 (15.89)	0.32 (0.47)
500	Proposed	84.9% (9.3%)	1.30 (1.40)	0.97 (0.17)
	Proposed-cw	72.4% (17.5%)	2.72 (3.46)	0.73 (0.44)
	VT-rsf	60.9% (11.3%)	6.18 (5.22)	0.61 (0.49)
	Lasso-cox	52.2% (1.1%)	58.04 (62.13)	0.18 (0.38)
	optsel-ipcw	52.5% (1.1%)	53.74 (43.52)	0.17(0.35)

In Scenario 1, the proposed method assigns the correct treatment with a rate of 92.3% when p = 50. Compared to other methods, the improvement ranges from 6.8 to 17.7%. True Positives (TP) for the proposed method is 1.73 on average, while the average sample size is 2.28. When p is increased to 500, the correct decision rate for all competing methods drops to a similar level at approximately 77%. Since the two linear models can always detect marginal monotone signals, this suggests that splitting rules implemented in VT and Midas can be heavily affected by the dimensionality. This phenomenon is also observed in Scenario 4, where the signal is completely symmetric. The proposed method maintains high accuracy at 84.9% when p = 500, which is only 1.7% less than the p = 50 setting. In Scenario 2, due to the linear structure, Lasso and optsel perform better that all tree-based methods, which is expected. Among all tree-based methods, the proposed method has the highest correct decision rate and largest TP. In Scenario 3, the proposed method and VT-rsf perform similarly.

5. Real Data Analyses

5.1. CCLE Dataset

Cancer Cell Line Encyclopedia (CCLE, Barretina et al., 2012) is one of the largest publicly available datasets that provide detailed genetic/genomic characterizations and drug treatment responses of human cancer cell lines. Gene expression, DNA copy number, mutation, and other genetic information are measured on over 1000 cell lines. A total set of 24 anticancer drugs/compounds are applied across 504 cell lines, with most of the drugs targeting a specific pathway. Furthermore, pharmacologic profiles and clinical outcomes are provided, making this dataset a unique testbed for our proposed method. In this analysis, the gene expression profiles, pharmacologic profiles, and cell line clinical data are obtained from the CCLE project website. For the outcome variable Y, we use the drug activity area calculated from the drug responses, which is an area under curve measurement that simultaneously captures the efficacy and potency of a drug. For each of the cell lines, the outcomes for all 24 anticancer drugs are measured, which provides information for the true optimal decision. For comparing any pair of drugs, say Drug 1 versus Drug 2, on an observed cell line i, the optimal decision rule can be defended as $D^{\ast }({\mathbf{X}}_i)={\mathbf{1}}_{\{Y_i^{\text{Drug}1}>Y_i^{\text{Drug}2}\}}$, where $Y_i^{\text{Drug}}$ is the outcome of cell line i when the drug is applied. In this analysis, we focus on a pair of drugs PD-0325901 versus RAF265. We choose this pair because the population proportion of preferring either treatment is close to 0.5, i.e., $\frac{1}{n}{\sum }_i{D}^{\ast }({\mathbf{X}}_i)=\frac{1}{n}{\sum }_i{\mathbf{1}}_{\{Y_i^{\text{PD-}0325901}>Y_i^{\text{RAF}265}\}}=54.1\%$, and the population benefit for selecting the better treatment $\frac{1}{n}\sum \mid Y_i^{\text{PD-}0325901}-Y_i^{\text{RAF}265}\mid =1.10$, which is the largest among all pairs with $\frac{1}{n}\sum D^{\ast }({\mathbf{X}}_i)$ between 0.4 and 0.6. Our final dataset contains 18,989 gene expressions measured on 447 cell lines. We further include three clinical variables: gender (male, female, and unknown); primary site type (24 categories including lung, haematopoietic and lymphoid, breast, nervous system, large intestine, and others); and histology type (22 categories such as carcinoma, lymphoid neoplasm, glioma, malignant melanoma, etc.). With the ultrahigh dimension, pre-screening is usually required. We first compute the marginal variance for each gene expression and select the top 500 genes. Furthermore, to incorporate pharmacologic profiles of the two drugs, we include their target genes.

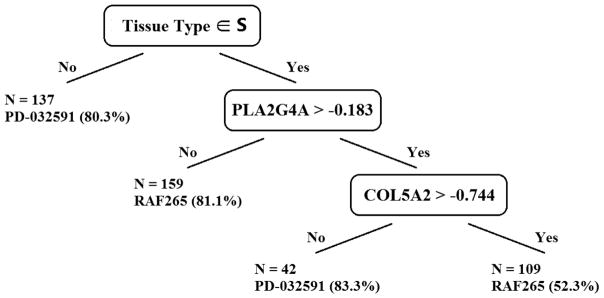
In real data analysis, parameter turning is required to select the final model. For all methods, we use 10-fold cross-validation to select the best tuning parameter. The final model for the proposed method is reported in Figure 2. The selected splitting variables have important biological implications. Tissue type is used as the first split, where tissues that belong to the categories of lung, haematopoietic and lymphoid, central nervous system, breast, ovary, kidney, upper aerodigestive tract, bone, endometrium, liver, soft tissue, pleura, prostate, salivary gland, mall intestine prefer PD-032591. When the tissue type is not in these categories, two other splits are created using gene expressions of PLA2G4A and COL5A2. When PLA2G4A is less than −0.183, RAF265 is preferred. This gene is closely related to the targeted MEK genes (MEK1 and MEK2) of PD-0325901. The enzyme encoded by this gene is phosphorylated on key serine residues by MAPKs, which are activated by MEK (according to www.atlasgeneticsoncology.org). In comparison, the final model of VT also selects tissue type as the first splitting variable with an almost identical splitting value except in three categories: urinary tract, upper aerodigestive tract, and salivary gland. However, VT uses gene S100P instead of PLA2G4A as the splitting variable in the second split. We did not detect its close relation with the targeted genes of PD-0325901 or RAF265. The final model selected by MIDAs uses the genes DUSP6, EREG, MYLK, and MANSC1 as splitting variables, yet it does not use tissue type.

Figure 2.

Fitted model for PD-0325901 versus RAF265. S is a set of tissue types that includes lung, haematopoietic and lymphoid, central nervous system, breast, ovary, kidney, upper aerodigestive tract, bone, endometrium, liver, soft tissue, pleura, prostate, salivary gland, mall intestine.

We also conducted analysis to compare different methods by randomly selecting half of the cell lines as training data and the rest as testing data. It should be noted that this approach is possible only when the outcomes of both treatments are available, which is a unique study design of the CCLE data. However, in other situations, measurement errors used in Kang et al. (2014) or Geng et al. (2015) could be more appropriate. In our analysis, the proposed method achieves the best performance when the model size is 3 (63.4% accuracy), while the accuracies of competing methods under the same model size are 62.4, 62.3, 59.1, and 59.0% for VT, MIDAs, Lasso, and optsel, respectively. Comparing with the simulation study, these accuracies are low, due to the complexity nature of biological data. However, when only the clinical variables are used, all tree-based methods give prediction accuracy at approximately 59.8%, suggesting the genetic profile does carry valuable information regarding the treatment selection. VT achieves its best performance when the model size is 7 (63.2% accuracy); however, all tree-based methods have generally reduced accuracy once the model size becomes large. This is due to the small terminal node size and overfitting. In contrast, both linear models Lasso and optsel perform worse than tree-based methods when the model size is less than 7. However, their accuracy increases gradually with the model size, e.g., Lasso’s accuracy increases up to 67.1% when the model size is 27.

5.2. Tamoxifen Treatment for Breast Cancer Patients

We apply our method to the cohort GSE6532 of data collected by Loi et al. (2007). Analysis results are presented in Web Appendix B.

6. Discussion

Tree-based methods, especially single tree methods, have unique advantages in personalized medicine due to their flexible model structure and interpretability. We have proposed a tree-based method in this manuscript for finding optimal treatment decision rules in high-dimensional data settings based on the outcome weighted learning framework. To pursue the strongest signal in the high-dimensional setting, an embedded model is utilized in the tree building process to construct greedy splitting rules. We further extend the method to right censored survival data by introducing double weighting. Simulation results suggest that the proposed method outperforms existing tree-based methods under a variety of settings and has an advantage over sparse linear models when the true underlying decision rule is tree structured. Analyses of the Cancer Cell Line Encyclopedia data and the Tamoxifen data show that the proposed method can identify predictors with important implications while having a relatively smaller model.

The method can be extended to multiple treatment settings with straightforward modification. In Section 3.3, we described a treatment label flipping procedure to handle negative outcomes and facilitate tree splitting rules. When there are multiple treatments involved, the flipped weight for a negative outcome can be distributed evenly to all alternative treatments. To be more specific, define m(X) as the mean curve of conditional response if a randomized treatment is received, i.e., $m(\mathbf{X})=\frac{1}{K}{\sum }_{k=1}^{K}E(Y\mid \mathbf{X},A=k)$. Then if Y_i < m̂(X), we create K − 1 flipped outcomes for the alternative treatments with each of them sharing equal weight |Y_i − m̂(X)|/(K − 1). The intuition is that if a treatment does not yield a favorable outcome, then all the alternative treatments are equally favored. Remaining steps of the proposed method can carry through since tree-based methods can naturally handle multi-category classification problems.

The proposed method also has limitations. From our CCLE data analysis, we observed that when the model size is small, the proposed method tends to achieve better performance than the alternatives. This suggests that the first several splitting variables tend to capture the true signals. However, as the model size increases, the sample size within the node decreases rapidly. Extremely greedy splitting rules will likely result in overfitting. This is possibly due to the complexity and weak signals of biological data, and, such a phenomenon is commonly encountered in tree-based methods. In the Tamoxifen data analysis, the final model we identified has only two subgroups. But considering the small effective sample size (139 failure observations), a smaller model is preferred to avoid potential overfitting.

7. Supplementary Materials

The Web Appendix referenced in Sections 3.2 and 5.2, along with the R code, is available with this article at the Biometrics website on Wiley Online Library.