Mechanocellular models of epithelial morphogenesis

Abstract

Embryonic epithelia achieve complex morphogenetic movements, including in-plane reshaping, bending and folding, through the coordinated action and rearrangement of individual cells. Technical advances in molecular and live-imaging studies of epithelial dynamics provide a very real opportunity to understand how cell-level processes facilitate these large-scale tissue rearrangements. However, the large datasets that we are now able to generate require careful interpretation. In combination with experimental approaches, computational modelling allows us to challenge and refine our current understanding of epithelial morphogenesis and to explore experimentally intractable questions. To this end, a variety of cell-based modelling approaches have been developed to describe cell–cell mechanical interactions, ranging from vertex and ‘finite-element’ models that approximate each cell geometrically by a polygon representing the cell's membrane, to immersed boundary and subcellular element models that allow for more arbitrary cell shapes. Here, we review how these models have been used to provide insights into epithelial morphogenesis and describe how such models could help future efforts to decipher the forces and mechanical and biochemical feedbacks that guide cell and tissue-level behaviour. In addition, we discuss current challenges associated with using computational models of morphogenetic processes in a quantitative and predictive way.

This article is part of the themed issue ‘Systems morphodynamics: understanding the development of tissue hardware’.

1. Introduction

The past decade has witnessed remarkable progress in quantitative studies of morphogenesis fuelled by advances in microscopy, image analysis and fluorescent reporter methods [1]. The resulting toolkit has enabled processes to be quantified and correlated across multiple scales: from the spatio-temporal dynamics of specific molecules within cells [2,3]; to individual cell shape changes and movement; to tissue-scale growth and deformation [4]. This has led to an increasing recognition that morphogenesis involves a complex interplay between cell signalling and mechanical forces [5]. Gene expression and protein activity modulate the cellular generation of, and response to, forces. In turn, mechanical cues may have a direct role in regulating these biochemical processes, and affecting cell behaviour, for example by controlling growth [6] or triggering apoptosis [7]. Improving our understanding of such feedbacks enables a more holistic view of development and may have future implications for improved tissue engineering and repair strategies.

Morphogenesis is frequently driven by the growth and deformation of epithelial tissues, which form polarized sheets of cells with distinct apical and basal surfaces, and tight lateral attachments located nearer their apical surface. The coordinated movement, shape change and intercalation of cells in an epithelial sheet facilitate complex morphogenetic processes, from tissue elongation through convergent extension [8] to bending and invagination [3] and tube formation [9]. The mechanical forces driving these processes are multiscale in nature [10] and include the action of molecular motors, membrane-bound adhesion components and extrinsic forces from underlying tissues [11,12]. Until recently, such forces were not experimentally measurable, and thus the role of mechanics in morphogenetic processes not well characterized. This has changed, however, with recent advances in measurement techniques, in particular in vivo [13,14].

The resulting force measurements, combined with cell- and tissue-level summary statistics on geometry and morphology that can be extracted from long-term live imaging, constitute an incredibly rich amount of data on morphogenetic processes. Computational modelling offers a useful framework for integrating such data and disentangling the roles of mechanics and signalling [15]. The iterative development of models and experiments allows us to refine our mechanistic understanding of biological observations and test competing hypotheses [16]. In particular, quantitative measurements enable us to constrain models, for example through parameter estimation, increasing the potential of such models to be used in a predictive way.

A variety of approaches have been developed to model how processes at the cell level determine tissue size, shape and function during morphogenesis [17].

A large class of these models neglect cytoplasm and cell junctions, treating an epithelial tissue as a continuum (e.g. viscoelastic) material [18–21] and employing finite elements or similar methods to discretize the tissue for simulation purposes. In essence, the continuum approximation averages over length scales much larger than the typical diameter of a cell. It can thus be difficult to incorporate heterogeneity between cells within a population. Accelerated, in part, by the reduction in cost of computing power, a number of discrete or ‘cell-based’ approaches have also been developed that treat cells as discrete entities. They provide natural candidates for studying the regulation of cell-level processes but are less amenable to mathematical analysis than their continuum counterparts. We restrict our focus to this burgeoning class of models in this review.

Cell-based models vary in complexity from those that consider the movement of cells on a fixed lattice [22,23] to models that account for continuous cell movements and consider cell shape to be fixed [24] or varying. The latter include models that track the centre of each cell as a point, determining cell neighbours through an ‘overlapping spheres’ or Delaunay triangulation approach [25–27], and vertex models that include an explicit description of cell shape. Such models are well suited to investigating the ‘passive’ mechanics of autonomous epithelial monolayer deformations. However, few existing models properly integrate descriptions of cell mechanics with models of biochemical signalling or genetic programming, or allow for the complex cell shapes that arise owing to localized adhesion, constriction and protrusion.

Here we summarize how several recent cell-based models have sought to overcome these limitations, and discuss how these models could help future efforts to study the interplay between chemical and mechanical signals in epithelial morphogenesis. Our aim is to provide a biologically accessible overview of the models' underlying assumptions, strengths and weaknesses, and the computational challenges associated with their further development, rather than an exhaustive comparison of the constitutive laws and material behaviour of the different models; for more detailed physical descriptions of recent approaches see, for example, [28]. We present these models, broadly speaking, in order of increasing computational complexity, starting with vertex models that contain the simplest explicit, dynamic description of cell shape. An overview of the strength, limitations and example applications of each class of model is presented in table 1.

Table 1.

Summary of applications to date of different modelling approaches for epithelial tissue morphogenesis. CA, Cellular automata; CPM, cellular Potts model; IBM, immersed boundary method; SEM, subcellular element model.

modelling approach	example applications	strengths	limitations
continuum models	brain cortical folding [18] cephalic furrow formation [19] ventral furrow formation [20]	strong mathematical foundation; typically few parameters; well placed to study buckling and folding phenomena	difficult to incorporate cell-level heterogeneity or subcellular processes
lattice-based models (CA, CPM)	epiboly [23] branching morphogenesis [22]	computationally cheap; straightforward to simulate many cells	risk of lattice anisotropies and cell fragmentation; difficult to relate parameters to experimentally accessible quantities
off-lattice cell-centre models	C. elegans germ line [29]	more physically motivated and easily parametrized than lattice-based models	more computationally costly than lattice-based models Lack explicit description of cell shape dynamics
vertex models	tissue size regulation [30,31] germband extension [32,33]	explicitly incorporate cell neighbour rearrangements; straightforward to generate experimentally testable summary statistics	typically neglect cell–matrix adhesion, medial actomyosin contractility, active cytoskeletal remodelling
viscoelastic models	ventral furrow formation [34–36] cell sorting [37] germband retraction [38]	include active cytoskeletal remodelling	like vertex models, require cells to be in confluent tissues
‘multi-node’/curved edge models	gastrulation [39] cell sorting [40]	detailed description of cell shape dynamics	more computationally costly than vertex and ‘finite-element’ models
IBM	limb bud morphogenesis [41] Turing patterns [42]	do not require confluent tissues; allow detailed modelling of regulated growth and death processes; straightforward to incorporate subcellular structures	unclear how to estimate ‘fluid’ properties from biological data; require sophisticated numerical solvers to avoid fluid ‘leakage’
SEM	primitive streak formation [43]	allow detailed and emergent cell shape changes in response to mechanical stimuli	computationally intensive; difficult to associate interactions functions directly with particular cytoskeletal components

2. Vertex models

We take as our starting point two-dimensional vertex models, a popular example of off-lattice cell-based models that approximate cell apical surfaces geometrically by polygons defined through the interfaces between adjacent cells [44]. In these models, the movement of junctional vertices is assumed to be governed by the strength of cell–cell adhesion, actomyosin cortical contractility and cell elasticity. Originating from models of inorganic structures such as soap bubbles, vertex models have been widely used to investigate the deformations of homogeneous and patterned epithelial tissues.

A highly cited example of the utility of vertex models is the work of Farhadifar et al. [45], who performed a systematic analysis of the equilibrium cell packing geometries and their dependence on cell mechanical and proliferative parameters with application to the Drosophila wing epithelium. By comparing simulations with experimental results on laser ablation of individual cell–cell interfaces, the authors arrived at a set of parameter values for which their model accounts for the observed vertex movements induced by laser ablation, epithelial packing geometries and area variations. This work demonstrates how such models may be parametrized, and their predictions tested, against experimental data.

3. Incorporating mechanical complexity

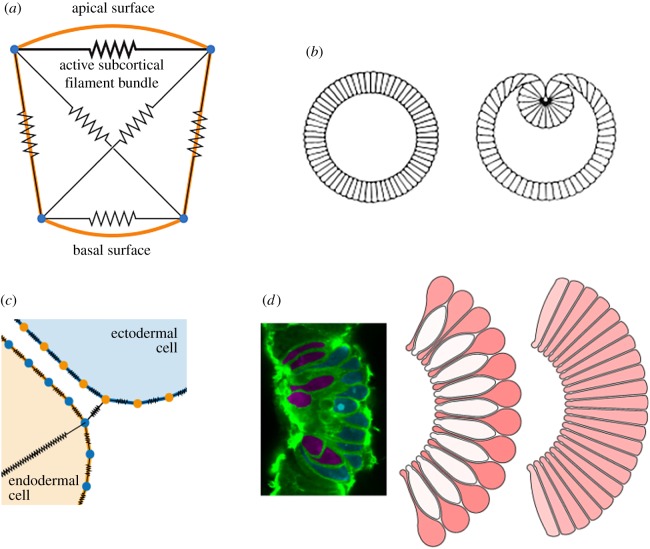
While successful in recapitulating much of the gross behaviour of planar epithelial sheets, vertex models typically ignore contributions such as cell–matrix adhesion [46] and medial actomyosin contractility [47]. These models also tend to neglect active remodelling of cytoskeletal components. One approach to including cytoskeletal remodelling is to introduce viscoelastic elements representing the cell membrane and cytoplasm (figure 1a). This approach was first adopted by Odell et al. [34,35], who modelled a cross section of an embryo as a ring of cells with interconnected vertices subject to a viscoelastic force. The authors assumed that apical edges actively contract in response to stretch. With additional system-specific assumptions, this model recapitulated patterns of deformation as observed in, for example, sea urchin gastrulation or Drosophila ventral furrow formation (figure 1b). Several more recent studies have focused on the different patterns of cell mechanical properties that can generate observed tissue deformations. For example, models of Drosophila ventral furrow formation have suggested a possible role for pushing by cells neighbouring the furrow, or buckling owing to uniform tissue-wide changes in apical tension [36].

Figure 1.

Polygon-based models of gastrulation. (a) Model of an epithelial cell cross section, incorporating viscoelastic cytoskeletal elements and active apical contractility. Adapted from [35]. (b) Simulating this model from a cylindrically symmetric configuration, while imposing a constant inner volume representing a yolk-filled lumen, leads to behaviour redolent of Drosophila ventral furrow formation. Reproduced from [35]. (c) Model of endodermal (yellow) and ectodermal (blue) cells in the Nematostella vectensis blastula, showing contractile elements (black) within and between cells. Adapted from [39]. (d) Simulation of bottle cell formation with this model. Left: In vivo image showing bottle (red) and squat (blue) cells. Middle/right: two model configurations, where endodermal cells are bound apically only (middle) or also basally (right), resulting in distinct cell shapes during apical constriction. Reproduced from [39].

An alternative extension of the vertex model has been developed by Brodland and co-workers [48], who decompose each polygonal cell into triangular ‘finite elements’, joined at the centroid of the polygon. This approach treats the cytoplasm as a continuous viscous material and assumes that cell–cell interfaces experience a constant force. As in vertex models, the motion of cell vertices is driven by interfacial tension between cells of the same and different types; however, here the volume of each cell is held constant. This model has, for example, been successfully used to test the roles of differential adhesion [49] and differential surface contraction to cell sorting and engulfment [37], to assess the mechanical efficiencies of different tissue-reshaping mechanisms [50], and study the contributions of applied stress and edge-tension anisotropies to germband retraction in the Drosophila embryo [38].

4. Incorporating additional geometric complexity

The models discussed in §§2 and 3 share the assumption that cell shape is well approximated by a polygon of specified degree. In recent work by Tamulonis et al. [39], the cross section of each cell is modelled by a polygon comprising a large number of vertices, allowing for more complex cell shapes (figure 1c). Membrane elasticity is modelled by associating a linear spring with each cell edge, whose stiffness and equilibrium length varies according to whether the edge is apical, basal or lateral. The apical (and, in some simulations, basal) corners of neighbouring cells are also connected by very stiff springs, representing adherens junctions. Apical constriction is implemented via an intracellular spring between each endodermal cell's apical corners. The authors do not impose a constant cell volume, instead assuming the cytoplasm to be linearly elastic, resulting in an additional force acting at each vertex. This model was applied to study gastrulation of the starlet sea anemone Nematostella vectensis, which culminates some cells adopting a characteristic ‘bottle’ shape. The model successfully reproduces several key features of gastrulation and suggests that bottle cell formation may emerge from the balance of spatially patterned mechanical forces: strong apico-basal contractility, reduced cell–cell adhesion and a lateral constraint (figure 1d). It will be interesting to see how widely conserved this combination of apical constriction and reduced cell–cell adhesion is as a mechanism for generating complex cell shapes in embryonic epithelia.

While the model by Tamulonis et al. [39] assumes a fixed number of nodes per cell, a recent development of the finite-element model by Brodland and co-workers [40] replaces straight edges by polylines with an arbitrary number of segments, allowing for curved cell boundaries. The authors allow the number of nodes per cell to vary dynamically according to some threshold on segment length, and also replace the triangular decomposition with an orthogonal dashpot system. By comparing simulations of annealing, engulfment and cell sorting, the authors show that cells with polyline boundaries exhibit a more fluid, biologically realistic behaviour than those with straight edges, which experience shape constraints limiting their movement and deformation.

In other work, Ishimoto & Morishita developed a ‘bubbly’ vertex model [51], motivated by observations of curved cell boundaries within a range of epithelia and ‘two-vertex’ cells within the mouse olfactory epithelium. The framework uses a generalized form of the tissue potential energy that is a function of the curvatures and vertex positions, where the Young–Laplace law represents the force balance along the cell boundary. This significantly increases the computational cost of simulation, but provides an interesting extension to the standard vertex model that may be applicable to a variety of morphogenetic processes.

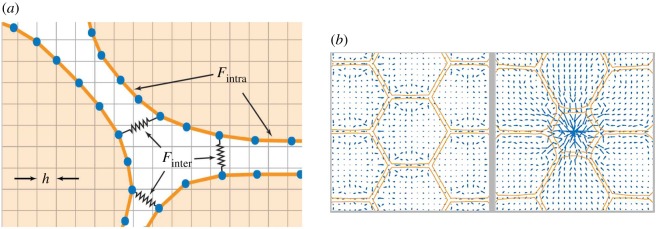
We conclude our discussion of models that allow complex cell morphologies by considering the immersed boundary method (IBM) [42,52–56]. Originally developed to study the flow of blood around heart valves [57], the IBM considers the dynamics of one or more elastic membranes, which represent cell boundaries, immersed in a viscous incompressible fluid (figure 2a), which represents the cytoplasm and extracellular matrix [53]. The IBM has been applied to three-dimensional problems, such as the deformation of leucocytes and [58] and red blood cells [59], but for simplicity, we restrict our focus to two dimensions here. We emphasize that the fluid does not interact directly with the immersed boundaries, and the boundaries do not directly partition the fluid. The fluid obeys the Navier–Stokes equations with an imposed body force acting owing to the elastic interactions of each cell. The precise functional form of this body force may be formulated rigorously as a strain relation [56], or else by decomposing it into inter- and intracellular interaction contributions (figure 2a) [53]. The immersed boundaries move owing to the fluid flow without slipping. The numerical solution of this model involves discretizing the fluid onto a regular square grid, whereas the immersed boundaries are represented by a finite number of points along their length.

Figure 2.

The immersed boundary method. (a) Model schematic shows an off-lattice discretization (blue nodes) of the immersed boundaries representing individual cells (orange) and the regular grid use to discretize the fluid flow problem. Adhesion links exist between blue nodes within each immersed boundary, as well as between neighbouring boundaries. (b) A simulation viewed at two time points shows the computed fluid velocity (blue arrows) and immersed boundary geometry (orange lines). Immersed boundaries are initially at rest in a honeycomb pattern before reacting to the central cell reducing its surface area.

The first application of the IBM to collective cell dynamics, by Rejniak and co-workers, focused on the growth of solid tumours under differing geometric configurations, initial conditions and progression models [53,54]. Although not yet used extensively to model epithelial morphogenesis, the IBM has been applied extensively in biology and elsewhere [52,55,60]. The flexibility of the IBM is exemplified by an application by Dillon and co-workers to vertebrate limb bud morphogenesis, where an immersed boundary now represents a tissue domain rather than a cell [41].

Although still primarily used in other settings, the IBM has several features that make it well suited to modelling epithelial morphogenesis, as argued by Tanaka et al. [42]. First, the IBM allows cell shapes to be an emergent property rather to be than a constraint of the model. In particular, in contrast to the vertex and finite-element models, the IBM does not require cells to be in confluent tissues, and thus appears well suited for detailed modelling of problems involving cell–cell interface dynamics such as intercalation, shear, loss of epithelial organization and delamination, with less need for explicit rules for processes such as T1 and T2 transitions. Second, unlike most vertex models, cells maintain a constant area in the absence of fluid sources or sinks, and thus the IBM enables detailed modelling of regulated growth and death processes. Third, the IBM also lends itself well to efficient numerical solution on periodic domains [60], which may be a sensible choice for considering a small snapshot of a larger tissue. Fourth, it is straightforward to explicitly incorporate subcellular structures such as the nucleus within the IBM using additional immersed boundaries, for example to investigate the role of intracellular mechanical heterogeneity in morphogenetic processes where significant cell bending or deformation occurs [61]. Finally, as already briefly mentioned, the extension to three dimensions is conceptually straightforward without the need to specify large numbers of different types of vertex rearrangements [62].

We illustrate the utility of the IBM in figure 2b, which shows a simulation of epithelial cell packing where neighbouring cell shapes evolve in response to a central cell shrinking (e.g. in preparation for extrusion from the sheet).

5. Three-dimensional models

Models of embryonic epithelia can reduce complexity by adopting a two-dimensional approximation (either in plane, as in convergent extension [47]; or cross section, as in ventral furrow formation [35]). However, some morphogenetic events require a three-dimensional model. A number of studies have extended vertex models to three dimensions. These include models of systems where apical patterns of myosin appear to control morphogenesis that allow a two-dimensional sheet of cells to buckle out of the plane, as in the case of dorsal appendage formation [63], as well as models that represent cells as three-dimensional prisms [64–66]. Examples of three-dimensional finite-element models include studies of neurulation by Brodland and co-workers [67]. Another relevant model in this context was proposed by Savin et al. [68] to describe the development of gut looping. The IBM has not yet been applied to three-dimensional cell populations, and existing software implementations are not straightforward to generalize to three dimensions [42].

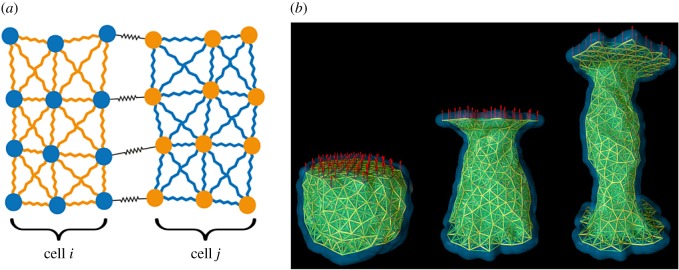
We conclude by considering the subcellular element model (SEM), where now discrete elements are used to represent both the cell membrane and cytoplasm. The SEM was initially developed by Newman [69] as a flexible framework for simulating the detailed dynamics of emergent cell shape changes in response to mechanical stimuli. In the SEM, each cell is composed of a large, and possibly varying, number of small volumes of cytoplasm (or other organelles) called subcellular elements. Each subcellular element of a cell is modelled as a single point at its centre of mass, which changes position over time subject to three processes: (i) weak random fluctuations; (ii) elastic interaction with elements of the same cell; and (iii) elastic interaction with elements of other cells (figure 3a).

Figure 3.

The subcellular element model. (a) Model schematic diagram shows two cells and a subset of the intra- and intercellular interactions between their elements. (b) SEM simulation under a creep-stress protocol. Reproduced from [70]. © IOP Publishing. Reproduced with permission. All rights reserved.

The motion of each subcellular element is subject to a strong viscous drag owing to the surrounding cytoplasm. As with most cell-based models, it is assumed that viscous terms dominate inertial terms. The biomechanical properties of cells are encoded in elastic interactions between elements that are defined using phenomenological potential functions encoding close-range repulsion and medium-range attraction [71] for elements of the same or different cells. It is difficult to associate such functions directly with particular cytoskeletal components or other structural protein systems. However, computational studies of bulk properties at the tissue scale suggest that the precise functional form of the potential has little impact on the system dynamics [25,72].

By carrying out in silico bulk rheology experiments on a single cell over a timescale of around 10 s, it is possible to scale the parameters of the SEM such that its passive biomechanical properties are independent of the number of elements that make up each cell [72]. These experiments follow a creep-stress protocol in which a constant extensile force is applied to a cell's surface, whereas the opposite surface is fixed, before the extensile force is released, and the strain is measured as the extension of the cell in the direction of the force, relative to its initial linear size (figure 3b). The SEM agrees qualitatively with in vitro rheology measurements [73], exhibiting a finite strain that plateaus after around one second, with complete recovery of the original cell shape after the force is released [72]. Over longer timescales (100 s), cells instead respond actively to external stresses, for example by undergoing cytoskeletal remodelling, making them more fluid-like. This can be incorporated into the SEM by inserting and removing subcellular elements of a cell in the regions of high and low stress, respectively [70].

To date, the SEM has not been widely used to study biological processes outside the area of epithelial morphogenesis. Christley et al. [74] developed a model of epidermal growth on a basal membrane that incorporates a simple algorithm for cell growth (through the incremental addition of subcellular elements) and division (through the redistribution of subcellular elements to two daughter cells) coupled to a subcellular gene network representing intercellular Notch signalling. The SEM has also been coupled to a fluid flow model to simulate the attachment of platelets to damaged blood vessel walls in thrombus development [75]. By using a detailed mechanical model of the platelets, the authors determine the relationship between platelet stiffness and movement in the fluid and, consequently, how platelets attach to injured sites on the vessel wall. In the context of developmental biology, the primary application of the SEM to date has been a computational study of primitive streak formation by Sandersius et al. [43]. Like the IBM, the SEM enables straightforward inclusion of subcellular structures such as nuclei for the study of processes such as (pseudo-)stratification; and cell rearrangements are emergent rather than imposed as constraints. There are already three-dimensional examples of the SEM, which allows for efficient library algorithmic implementations that can simulate tissues comprising several thousands of cells [74,76].

6. Incorporating signalling

While some morphogenetic processes can be modelled by assuming a specified patterning of cell mechanical properties [30,63], in the case of mechanotransduction the mechanism underlying such patterning may need to be treated explicitly. An appealing property of cell-based models is the ease with which they may be modified to incorporate such feedback. Vertex and cellular Potts models now frequently couple descriptions of morphogen transport and signalling to cell behaviour [31,66,77–79], whereas a recent vertex model of active cell intercalation during Drosophila germband extension incorporates an explicit description of planar cell polarity and medial myosin II dynamics [80]. A similar approach has been taken to describe the role of myosin II patterning in driving intercalation during germband extension [32]. Such biological detail is rarer in the more complex mechanocellular models described above; though recent examples include [42,74]. Further development of increasingly detailed mechanocellular models will require the careful derivation of key relationships between the fluorescence intensity of relevant proteins and mechanical properties from live-imaging datasets.

7. Outlook

We conclude by highlighting some of the technical developments required to increase the utility of the cell-based models discussed above as computational tools for the study of epithelial morphogenesis.

(a). Model choice and implementation

An increasingly important consideration is availability of software. At present, Chaste [81] is the only open-source simulation tool publically available for off-lattice models of cell populations, including vertex and finite-element models. Implementations of the IBM and SEM also exist within this framework. The more widespread availability of such tools and, in particular, the use of industrial-grade software engineering approaches to ensure robust, extensible code and reproducible results, are crucial as computational modelling evolves from a qualitative to a quantitative tool in cell biology. A technical requirement for this is the development and use of stable, accurate and efficient numerical algorithms for solving models.

Related to this problem is the choice of a particular cell-based model for a given problem. The decision as to which is the best model to interrogate a specific research question is subjective, and often based on the experience of the modeller and the software they have access to obtaining and extending. Moreover, the issue is often exacerbated by the fact that it is difficult to accurately compare different modelling approaches, because the modeller cannot generally distinguish between differences that are due to model assumptions and those that arise from the specific details of the numerical implementation of the model [82]. A systematic comparison of the relative strengths and weaknesses of each model, and the underlying biophysical assumptions, remains lacking; this would go a long way towards addressing the above problem. A rare example of such a comparison is the simulation study by Pathmanathan et al. [25]; this type of analysis could be extended to other cell-based approaches.

(b). Key challenges in future model development

The majority of existing models of epithelial morphogenesis neglect interactions with neighbouring tissues, yet there is increasing evidence for their importance. While a small number of theoretical studies have included an explicit representation of basement lamina or stromal tissue [83,84], further work is required to make progress in this area. In particular, the development of methodologies to interface models that include descriptions of cell shape, mechanics and biochemical signalling in different ways and on different scales, will be crucial. As mentioned above, the extension of cell-based models to three dimensions is both an urgent requirement and technically challenging. An overarching question in this context is what physics needs to be included in a cell-based model, and how to implement this across different frameworks, as we continue to add greater amounts of biological detail. This requires balancing mechanical realism with computational tractability.

(c). Integrating models and quantitative data

Recent years have witnessed dramatic changes in our ability to extract multiplex, quantitative data, on a range of spatio-temporal scales, from actomyosin dynamics within single cells, to tissue-level morphogenetic changes, including folding, bending and within-plane reorganization. A major remaining challenge for the modelling community is to understand how to best integrate and interpret these data with cell-based modelling frameworks. A goal for the future should be a concrete pipeline that includes: data acquisition, analysis and fusion; model development, reduction and parametrization; model validation/selection and the guidance of future experimental directions. Key challenges in this regard involve developing efficient methods for computational inference and experimental design, and designing standardized approaches to report uncertainty.

(d). Summary

Here we have sought to provide some representative examples (in order of increasing complexity and geometric realism) that give a clear picture of developments to date, rather than an exhaustive list of models. These models are most suited for situations where we are particularly interested in capturing irregular cell shapes because they are important for the system-level behaviour, such as bottle cells in gastrulating embryos [39]. The development of such models, in combination with recent advances in the live imaging of embryogenesis and image analysis, means that the field is now in a position to develop and validate biologically realistic models in a quantitative manner. Having the ability to extract geometric and mechanical summary statistics from data and parametrize models in an integrated manner will be crucial if we are to exploit the full potential of combined experiment-modelling efforts.

Authors' contributions

A.G.F., F.C. and R.E.B. contributed to the development of the ideas presented in the paper and wrote the paper.

Competing interests

We have no competing interests.

Funding

F.C. is supported by an EPSRC-supported Systems Biology Doctoral Training Centre Studentship (EP/G03706X/1).