The hidden treasure in your data: phasing with unexpected weak anomalous scatterers from routine data sets

Weak anomalous signals from serendipitously acquired surface-bound Ca atoms/native S atoms from routine data sets, that were not optimized for SAD phasing, were used to successfully phase protein structures.

Abstract

Single-wavelength anomalous dispersion (SAD) utilizing anomalous signal from native S atoms, or other atoms with Z ≤ 20, generally requires highly redundant data collected using relatively long-wavelength X-rays. Here, the results from two proteins are presented where the anomalous signal from serendipitously acquired surface-bound Ca atoms with an anomalous data multiplicity of around 10 was utilized to drive de novo structure determination. In both cases, the Ca atoms were acquired from the crystallization solution, and the data-collection strategy was not optimized to exploit the anomalous signal from these scatterers. The X-ray data were collected at 0.98 Å wavelength in one case and at 1.74 Å in the other (the wavelength was optimized for sulfur, but the anomalous signal from calcium was exploited for structure solution). Similarly, using a test case, it is shown that data collected at ∼1.0 Å wavelength, where the f′′ value for sulfur is 0.28 e, are sufficient for structure determination using intrinsic S atoms from a strongly diffracting crystal. Interestingly, it was also observed that SHELXD was capable of generating a substructure solution from high-exposure data with a completeness of 70% for low-resolution reflections extending to 3.5 Å resolution with relatively low anomalous multiplicity. Considering the fact that many crystallization conditions contain anomalous scatterers such as Cl, Ca, Mn etc., checking for the presence of fortuitous anomalous signal in data from well diffracting crystals could prove useful in either determining the structure de novo or in accurately assigning surface-bound atoms.

1. Introduction  

The direct determination of macromolecular structures from X-ray diffraction data alone is a major goal for the crystallo­graphic community. Seminal work by Hendrickson and Teeter demonstrated that anomalous scattering from native S atoms alone is sufficient to support de novo structure determination (Hendrickson & Teeter, 1981 ▸). Interestingly, this daring sulfur-SAD experiment was performed long before the advent of density modification and the maturation of detectors and software for maximizing signals from carefully formulated synchrotron data-collection strategies. It took another ∼20 years (Dauter et al., 1999 ▸) for the crystallographic community to embrace the power of sulfur anomalous scattering for the de novo structure determination of proteins. Since then, several experiments have highlighted the necessity for highly redundant data in order to attain the accuracy required to use the weak anomalous signal for phasing (see, for example, Dauter & Dauter, 1999 ▸; Dauter & Adamiak, 2001 ▸; Ramagopal et al., 2003b ▸; Debreczeni et al., 2003 ▸; Usón et al., 2003 ▸; Sarma & Karplus, 2006 ▸; Wagner et al., 2006 ▸). A recent comprehensive study covering ∼140 structures determined using sulfur anomalous signal further highlights the necessity of collecting accurate data (Rose et al., 2015 ▸).

Single-wavelength anomalous dispersion (SAD) has become the method of choice for de novo determination of protein crystal structures (Hendrickson, 2014 ▸), accounting for 73% of the structures determined by experimental phasing deposited in the Protein Data Bank (PDB; Berman et al., 2000 ▸) in 2013 (Bunkóczi et al., 2015 ▸). The use of intrinsic S atoms and selenomethionine derivatives for the experimental phasing of protein structures has been extensively discussed (see, for example, Hendrickson & Teeter, 1981 ▸; Hendrickson et al., 1990 ▸; Doutch et al., 2012 ▸; Kim et al., 2013 ▸; Ramagopal et al., 2003b ▸; Sarma & Karplus, 2006 ▸; Dauter et al., 1999 ▸). When it is not possible to use the anomalous signals from intrinsic S atoms, or selenomethionine derivatives cannot be prepared, derivatives of anomalous scatterers such as Zn, As, Mn, halide ions, halogenated fragments etc. have been exploited for the purpose of experimental phasing (see, for example, Dauter & Dauter, 2007 ▸; Kim et al., 2013 ▸; Liu et al., 2011 ▸; Ramagopal et al., 2003a ▸; Salgado et al., 2005 ▸; Bauman et al., 2016 ▸). There have also been reports of the utilization of anomalous signal at short wavelengths (∼1 Å) from serendipitously acquired scatterers for experimental phasing, either with data collection optimized for SAD (Gadd et al., 2015 ▸) or the use of unexpected anomalous signal from routine data sets (Cuesta-Seijo et al., 2006 ▸; McClelland et al., 2016 ▸), with McClelland and coworkers reporting the utilization of anomalous signal from Cd²⁺ collected near the selenium edge from a protein that crystallized in space group P1. The use of longer wavelength X-rays (∼2.0 Å or above) for native SAD has been proposed and has been in practice since the early part of this century (Weiss et al., 2001 ▸; Liu et al., 2000 ▸; Djinović Carugo et al., 2005 ▸; Micossi et al., 2002 ▸), with continued interest in this decade (Weinert et al., 2015 ▸; Cianci et al., 2016 ▸; Liebschner et al., 2016 ▸; Gorgel et al., 2015 ▸; Zhu et al., 2012 ▸; Liu et al., 2012 ▸; Goulet et al., 2010 ▸; Lakomek et al., 2009 ▸), as it avoids the need to prepare selenomethionine or other derivatives. The current state of the art in native SAD has been comprehensively discussed by Rose et al. (2015 ▸). At the wavelengths typically accessible at synchrotron beamlines and home sources, the anomalous signal from sulfur is weak. The use of longer wavelengths at a synchrotron source is expected to result in stronger anomalous signal, for example at a wavelength of 2.1 Å f′′ for sulfur is 0.98 e, which is close to double the value at the wavelength of 1.54 Å (0.55 e) corresponding to a copper-anode home source. However, most beamlines are not optimized to operate at longer wavelengths, and the use of longer wavelengths limits the data quality owing to a number of factors, including the maximum resolution that can be achieved, increased absorption, radiation damage and the possibility of harmonic contamination (Doutch et al., 2012 ▸).

Although longer wavelengths are preferred for the exploit­ation of weak anomalous signal from atoms with Z < 20, an initial diffraction experiment on a new protein usually aims at obtaining the highest resolution data, even when the sequence identity of the protein to that of known structures is below the ‘twilight zone’ for molecular replacement. Moreover, most beamlines are optimized to collect data at a wavelength of around 1.0 Å, where the expected anomalous signal from anomalous scatterers such as calcium and sulfur is low. Many crystallization conditions contain metals such as calcium and manganase as well as chloride ions, and it has been noted in a study on the phasing of 23 proteins that in 90% of cases light ions such as chloride, phosphate, sulfate, potassium or calcium were interacting with the protein molecule (Mueller-Dieckmann et al., 2007 ▸). Anomalous signals from these serendipitous anomalous scatterers can potentially be used in experimental phasing of protein structures. However, the use of weak anomalous signals from adventitiously bound weak anomalous scatterers for phasing in macromolecular crystallo­graphy is seldom discussed. Here, we present two such cases where anomalous signal from surface-bound Ca atoms acquired from the mother liquor were exploited for phasing: (i) PSPTO_5518 from Pseudomonas syringae pv. tomato (PSPTO) and (ii) the hypothetical protein PTO0218 from Picrophilus torridus (PTO). Although there have been previous reports of successful calcium/sulfur SAD phasing at ∼1 Å wavelength using the combined anomalous signal from structural Ca atoms together with intrinsic sulfurs (Wang et al., 2006 ▸; Koch et al., 2010 ▸), to the best of our knowledge PSPTO and PTO represent the first two cases where anomalous signal from surface-bound Ca atoms was used for phasing. We also examined hen egg-white lysozyme (HEWL), where data collected at ∼1.0 Å wavelength were sufficient to drive de novo structure solution using the sulfur anomalous signal alone. To the best of our knowledge, HEWL is the first case where just the sulfur anomalous signal at ∼1.0 Å wavelength has been shown to be sufficient for de novo structure determination. Also, for PSPTO the data were collected near the selenium edge and for PTO they were collected near the iron edge; moreover, the multiplicity was near or below 10 in all cases. However, the anomalous signals from these atoms, with the Bijvoet ratio being close to Wang’s limit of 0.6% (Wang, 1985 ▸) in two cases (PSPTO and HEWL) and around 1.5% in the case of PTO, could nevertheless be used to obtain the structures. These results suggest that a careful analysis of supposedly native data and with judicious manual intervention can lead to the unanticipated determination of structures.

2. Materials and methods  

PSPTO and PTO were expressed in Escherichia coli BL21 (DE3) cells using suitable vector constructs [the clones are available at the PSI Material Repository at DNASU, with clone IDs PsCD00298173 (PSPTO) and PtCD00370250 (PTO)], purified using size-exclusion chromatography and concentrated to 7.8 and 10 mg ml⁻¹, respectively. PSPTO was crystallized by hanging-drop vapour diffusion from a drop consisting of 7.8 mg ml⁻¹ protein solution mixed in a 1:1 ratio with reservoir solution consisting of 30% PEG 400, 0.1 M HEPES, 0.2 M calcium chloride pH 7.5 and maintained at 293.0 K. PTO was crystallized by sitting-drop vapour diffusion from a drop consisting of 10 mg ml⁻¹ protein solution mixed in a 1:1 ratio with reservoir solution consisting of 0.2 M calcium chloride, 0.1 M HEPES–Na pH 7.5, 28%(v/v) polyethylene glycol 400 maintained at 298 K. HEWL was purchased from Sigma–Aldrich and used without further purification. It was crystallized by hanging-drop vapour diffusion from a drop consisting of 20 mg ml⁻¹ protein solution mixed in a 1:1 ratio with reservoir solution consisting of 10% sodium chloride, 50 mM sodium acetate pH 4.6 and maintained at 293 K. All three proteins were dissolved in 20 mM HEPES pH 7.5, 150 mM NaCl, 10%(v/v) glycerol, 0.5 mM TCEP.

Diffraction data for PSPTO and PTO were collected on the X4A beamline at NSLS using an ADSC Quantum 4 CCD detector. Diffraction data for HEWL were collected on the X29A beamline at NSLS (Brookhaven National Laboratory) using an ADSC Quantum 315 CCD detector. The data for PTO were processed using HKL-2000 (Otwinowski & Minor, 1997 ▸) and those for PSPTO and HEWL were processed using HKL-3000 (Minor et al., 2006 ▸). All data were collected from crystals maintained at 100 K in a stream of cold nitrogen gas. CC_1/2(anom) for each of the data sets was calculated as follows: each data set was split into two equal sets and these were treated as MAD data, with one set input as peak data and the other set input as inflection data in HKL2MAP (Pape & Schneider, 2004 ▸) to calculate the anomalous correlation coefficients, and these were used as CC_1/2(anom).

For all three proteins, the SHELX program suite (Sheldrick, 2010 ▸), as incorporated in the HKL2MAP GUI, was used for experimental phasing. Substructure solution was performed using SHELXD, with 1000 cycles of substructure search and an E-value cutoff of 1.7 unless otherwise mentioned, to include only strong reflections, with anomalous data to 2.1, 2.8 and 2.0 Å resolution for PSPTO, PTO and HEWL, respectively, followed by density modification in SHELXE. The density-modified phases were input to ARP/wARP (Langer et al., 2008 ▸) for model building. For PTO, the quality of the electron-density map obtained after density modification alone was not sufficient for model building, and three cycles of iterative chain tracing with 20 cycles of density modification were used. To check the feasibility of an automated structure-solution workflow, the anomalous data were input into the AutoSol routine in PHENIX (Adams et al., 2010 ▸).

PSPTO and PTO did not have models in the PDB that were appropriate for molecular replacement, and the data sets described here were used for phasing, as well as for refining the structures. The coordinates have been deposited in the PDB as entries 2pag and 2i52 for PSPTO and PTO, respectively. For lysozyme (HEWL), the coordinates from PDB entry 1lz8 (Dauter et al., 1999 ▸) were used as a reference structure. Since in all three cases we had nearly complete models from phasing, the phases that yielded the model were refined against the final deposited structure (moving the final structure to the same origin as the experimental model) with 20 cycles of restrained refinement in REFMAC5 (Murshudov et al., 2011 ▸) to obtain the final phases. The initial and final phases were merged together into one file using CAD, and the average phase errors before and after density modification (d.m.) were calculated using PHISTATS using the final refined map as a reference. Similarly, map correlations before and after density modification were calculated using OVERLAPMAP (Brändén & Jones, 1990 ▸; Jones & Stuart, 1991 ▸). All of these programs are available as part of the CCP4 software suite (Winn et al., 2011 ▸).

3. Results  

Table 1 ▸ presents the diffraction data for each of the three proteins and Table 2 ▸ presents the absorption edges, with the corresponding X-ray energies, of the anomalous scatterers encountered in this study. In the following subsections, the phasing approach used for each of these proteins is described.

Table 1. Diffraction data.

Unless otherwise mentioned, values in parentheses are for the highest resolution shell.

Protein	PSPTO	PTO	HEWL†
Beamline	X4A	X4A	X29A
No. of amino acids in asymmetric unit	145	726‡	129
No. of non-H atoms in asymmetric unit	1190	5814‡	1001
Anomalous scatterers§	Ca (2), S (4)	Ca (7.3), S (30)	S (10)
Space group	P41212	C2221	P43212
Unit-cell parameters
a (Å)	47.43	90.76	78.81
b (Å)	47.43	143.49	78.81
c (Å)	122.49	129.80	37.04
Wavelength (Å)/energy (keV)	0.979/12.664	1.743/7.113	1.075/11.533
Resolution (Å)	40.0–1.60 (1.63–1.60)	50–2.08 (2.12–2.08)	50–1.46 (1.49–1.46)
Total rotation range (°)	270	360	357
Anomalous multiplicity¶	10.4 (6.2)	6.3 (2.3)	12.2 (4.7)
Multiplicity	18.9 (11.6)	12.0 (4.2)	22.7 (8.8)
Completeness (%)	99.2 (92.5)	96.7 (67.0)	99.7 (96.4)
R merge (%)	3.6 (21.6)	5.0 (22.1)	4.0 (14.8)
R anom (%)	2.15	4.03	2.0
R p.i.m. (%)	1.2 (10.3)	2.0 (17.2)	1.2 (7.3)
CC1/2 in highest resolution shell	0.959	0.900	0.977
〈I/σ(I)〉	53.64 (8.14)	34.07 (4.06)	57.64 (13.04)
B Wilson (Å2)	13.8	21.5	12.9
Solvent content	0.38	0.48	0.35
f′′†† (e)	0.56 (Ca), 0.24 (S)	1.6 (Ca), 0.70 (S)	0.28 (S)
〈ΔF anom〉/〈F〉‡‡ (%)	0.57	1.6	0.61

^†For data set HEWLAll (see Table 3 ▸).

^‡With six molecules in the asymmetric unit.

^§The value in parentheses is the number of anomalous scattering atoms in the asymmetric unit. In lysozyme there are eight cysteines and two methionines.

^¶Multiplicity with Friedel pairs kept separate.

^†† f′′ values were obtained from http://skuld.bmsc.washington.edu/scatter/AS_periodic.html.

^‡‡Calculated using the formula 〈ΔF ^anom〉/〈F〉 = 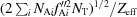, where N _Ai is the number of and f′′_Ai is the imaginary scattering contribution of an anomalous scatterer of type i, N _T is the total number of non-H atoms in the molecule and Z _eff is the effective number of electrons of the ‘average’ protein atom (6.7; Wang et al., 2006 ▸).

Table 2. Absorption edges of the anomalous scatterers observed in this study and the difference between the energy at the absorption edge and the energy at the wavelength used for data collection.

The difference between f′′ values (Δf′′) at the absorption edge and the wavelength used for data collection is also included.

Absorption edges				Difference in energy and f′′ between the absorption edge and the X-ray wavelength used for data collection
Atom	Wavelength (Å)	Energy (keV)	f′′† (e)	Protein	Energy used (keV)	Difference from absorption edge (keV)	Δf′′ (e)
Ca	3.070	4.038	4.05	PSPTO	12.664	8.626 (Ca)	3.49 (Ca)
S	5.016	2.472	4.1	PTO	7.113	4.043 (Ca)	2.45 (Ca)
				HEWL	11.533	9.061 (S)	3.82 (S)

^† f′′ values were obtained from http://skuld.bmsc.washington.edu/scatter/AS_periodic.html.

3.1. PSPTO  

PSPTO crystallized in space group P4₁2₁2 with one molecule in the asymmetric unit and X-ray diffraction data were collected to 1.6 Å resolution. This protein has three cysteine residues. A BLAST search (Altschul et al., 1990 ▸) against the PDB did not reveal any suitable models, suggesting that the sequence is highly unique and ruling out the possibility of determining the structure by molecular replacement. Native X-ray diffraction data were collected at a wavelength of 0.979 Å with a crystal rotation of 0.5° per frame, and a total of 540 frames were collected covering a 270° wedge, with an exposure time of 10 s. Although the intention was to collect an accurate and high-resolution native data set, it is our practice to check for the presence of anomalous scatterers in most high-resolution data sets (>1.8 Å). It should be noted that scaling the data in HKL-2000 with the ‘scale anomalous’ option did not indicate the presence of any anomalous signal (see §4.2 and Fig. 2). This observation is not surprising as the sulfur edge is almost 10 200 eV (or 4.037 Å) from the energy of the X-rays used in this experiment. However, to our surprise, a substructure search in space group P4₁2₁2 in SHELXD, looking for four anomalous scatterers, using anomalous data to 2.1 Å resolution, produced two strong peaks followed by four additional peaks (see Supporting Information), which were consistent in most correct solutions. The map obtained with the original coordinates showed better CC, contrast, connectivity and FOM compared with that obtained from inverted coordinates, confirming that the space group was indeed P4₁2₁2 and not P4₃2₁2. Model building resulted in a model containing residues 4–135 of the 145-amino-acid protein. The two strong peaks in the substructure solution suggested an anomalous scatterer slightly larger than sulfur. The crystallization conditions contained calcium chloride, from which Ca atoms could have been acquired. On refinement of the model, two strong difference density peaks were observed on the surface near Gln101, Asp103 and Thr105. The coordination with the amino-acid side chains and water molecules together with the anomalous difference Fourier map suggested that these were likely bound Ca atoms (Supplementary Fig. S1a), which were modelled in the refined structure.

To examine the efficacy of a completely automated crystal structure-determination workflow, the anomalous data were input to the AutoSol routine in PHENIX. Interestingly, when the anomalous scatterers were input as two Ca atoms PHENIX was able to build residues 4–111 and 124–136, but when the anomalous scatterers were input as four sulfurs it was able to build only 53 residues (7–24, 72–80, 86–106 and 126–130), about 37% of the structure. The modelled segments correspond to correct elements of the structure, but PHENIX appeared to be unable to build a more complete model. However, searching for either calcium or sulfur in SHELXD yielded the same substructure solution with exactly matching coordinates/occupancies, and in both the cases the density-modified map was sufficient for completely automated building.

3.2. PTO  

PTO is a 13 kDa hypothetical protein PTO0218 from P. torridus. Again, a BLAST search did not identify a useful molecular-replacement model. PTO crystallized in space group C222₁ with six molecules in the asymmetric unit and X-ray diffraction data were collected to 2.08 Å resolution. PTO contains 121 residues, including one cysteine and four methionines. X-ray diffraction data were collected at a wavelength of 1.743 Å (7113 eV), near the iron edge, with a crystal rotation of 1° per frame, with the goal of determining the structure by sulfur phasing. As the data were collected on the bending-magnet beamline X4A, each frame required 4 s of exposure. Given the speed of SHELXD (and thanks to HKL2MAP), there was sufficient time to check the sub­structure solution at frequent intervals. After approximately 300 frames, substructure solution looking for 30 sulfurs yielded several solutions with a high CC/PATFOM in SHELXD (Supplementary Fig. S2b). A significant drop in occupancy was observed between the first and second heavy-atom peaks and between the second and third, with a smooth transition in the occupancies of additional sites (see Supporting Information). In general, for substructures involving Se or S atoms (i.e. covalently bonded to the protein) such variation in occupancy is rare. The observed drop in occupancy between the third and the fourth atom suggested the presence of anomalous scatterers other than sulfur. Model building with the phases obtained after SHELXC/D/E resulted in a model with 678 of the 726 residues.

The asymmetric unit in the crystal of PTO consists of four molecules arranged in a rugby-ball-like shape, with the other two adopting a half rugby-ball-like shape positioned parallel to the long side of the ball (Supplementary Fig. S1b). To exploit noncrystallographic symmetry (NCS) information in density modification, NCS operators were used in DM (Cowtan & Zhang, 1999 ▸), and the resulting map was input to ARP/wARP for model building, allowing 659 residues in 12 chains to be built (the structure deposited as PDB entry 2i52 was originally determined exploiting NCS, but for this study, to check the feasibility of the SHELXC/D/E pipeline, we carried out the structure-solution workflow elucidated above without the use of NCS). To examine the efficacy of a completely automated crystal structure-determination workflow, the anomalous data were input to the AutoSol routine in PHENIX, which was able to build 640 of the 726 residues.

In the final structure there were 12 Ca atoms, which refined with varying occupancies. Two Ca atoms were refined with full occupancy and the rest with partial occupancies, with a total occupancy of Ca atoms of 7.3 (which is approximately one calcium per chain). All of the Ca atoms, which were derived from the crystallization medium, are in the solvent region, either between molecules or on the surface. One of the two Ca atoms that refined with full occupancy mediated a crystal contact.

Although this case represents a data set optimized for phasing using sulfur anomalous signal, anomalous signal from surface-bound Ca atoms contributed significantly to the phasing and de novo structure determination of this protein. PSPTO represents a data set where the anomalous signal from surface-bound Ca atoms at 0.979 Å wavelength was utilized for phasing, whereas PTO represents a data set where the anomalous signal from surface-bound Ca atoms at 1.743 Å wavelength is utilized. Hence, despite not being a routine data set, we included the PTO data set in this study along with that of PSPTO to compare the quality of the phases obtained in the two data sets (discussed further in §4.2).

3.3. HEWL  

The above two cases prompted us to test the feasibility of structure determination using sulfur anomalous signal from a ‘routine’ data set collected without optimization for sulfur phasing. Beamline X29 at NSLS employs a mini-gap undulator source, with the maximum flux observed around 11.5 keV (a wavelength of ∼1.078 Å; Shi et al., 2006 ▸). As a test case, we used hen egg-white lysozyme, a well studied 129-amino-acid protein with eight cysteines and two methionines (referred to as HEWL). At this wavelength, the f′′ value for sulfur is 0.28 e and the expected anomalous signal is as low as 0.61%. The protein crystallized in space group P4₃2₁2 with one molecule in the asymmetric unit and X-ray diffraction data were collected to 1.46 Å resolution. X-ray diffraction data were collected at a wavelength of 1.075 Å (11.533 keV) with a crystal rotation of 1° per frame and 0.5 s exposure. Owing to the strong diffraction, 200 frames were collected with the detector at ∼200 mm (corresponding to ∼1.46 Å) with a sevenfold attenuation followed by another 157 frames with an unattenuated beam, both with a crystal rotation of 1°. Although the high-exposure data were expected to have a large number of overloaded reflections, this would lead to a more accurate measurement of low-intensity reflections owing to the higher beam flux, thus providing a more accurate measurement of the anomalous differences. Hence, the two data sets were merged and used for phasing. Substructure solution was attempted by searching for 14 S atoms to include surface-bound Cl atoms (observed in most structures with crystallization conditions containing NaCl), with three disulfide bonds resolved (DSUL 3 command in SHELXD), using anomalous data to 2.0 Å resolution. Considering the facts that (i) the data were collected approximately 9000 eV (or 3.941 Å) away from the sulfur edge, (ii) the total wedge for both data sets together is only around 360° and (iii) the f′′ value at this wavelength for sulfur is very low (0.28 e), we did not anticipate successful identification of the sulfur positions. However, out of 1000 cycles, three solutions with high CC/PATFOM and clear bimodal distribution distinguishing the correct and wrong solutions (Supplementary Fig. S2c) gave a clear indication that the substructure solution was successful. The coordinates of the first few anomalous scatterers in all three putative solutions were manually checked for consistency of the sulfur positions and the coordinates from the best solution were used for phasing with SHELXE with the solvent content set to 35%. As expected for lysozyme, the map obtained from the original coordinates (space group P4₃2₁2) after 20 cycles of density modification had a better CC, contrast, connectivity and FOM compared with that obtained from the inverted substructure coordinates (space group P4₁2₁2). The resulting map was input to ARP/wARP for model building; a single chain of 126 residues was docked into the map.

To determine the minimal data needed for phasing, different data sets were prepared (where the data set obtained with an unattenuated beam is referred to as the high-intensity data and that obtained on attenuating the beam is called the low-intensity data) using the first 100 frames from the high-intensity data merged with last 100 frames from the low-intensity data (data set 1), the first 150 frames from both data sets merged together (data set 2), the first 100 frames from both data sets merged together (data set 3), all 200 frames of the low-intensity data alone (data set 4) and all 157 frames of the high-intensity data alone (data set 5). Table 3 ▸ provides a comparison of the various parameters for these data sets. Henceforth, HEWLAll refers to the data set obtained from merging all of the high- and low-intensity data. We were able to successfully phase and build a model with all of the data sets. For data sets 3 and 4, 20 cycles of density modification alone were not able to produce a map that was good enough for ARP/wARP to build a model, but three iterative cycles of tracing with 20 cycles of density modification yielded a map that ARP/wARP could use to build 126 of the 129 residues of the protein chain. Data sets 1 and 3 have similar multiplicity and resolution, but the total wedge covered in data set 1 is 200°, whereas it is 100° in data set 3.

Table 3. Comparison of HEWL data sets.

Values in parentheses are for the highest resolution shell.

	HEWLAll	Data set 1†	Data set 2‡	Data set 3	Data set 4	Data set 5
Total rotation range (°)	357	200	300	200	200	157
Resolution (Å)	50–1.46 (1.49–1.46)	50–1.46 (1.49–1.46)	50–1.46 (1.49–1.46)	50–1.46 (1.49–1.46)	50–1.46 (1.49–1.46)	50–1.46(1.49–1.46)
Anomalous multiplicity	12.2 (4.7)	6.9 (2.6)	10.3 (4.2)	7.2 (3.5)	7.1 (2.7)	5.2 (2.2)
Completeness (%)	99.7 (96.4)	99.6 (95.9)	99.0 (89.3)	96.3 (74.3)	99.7 (96.3)	96.6 (89.1)
R merge (%)	4.0 (14.8)	4.1 (13.3)	4.0 (13.7)	3.7 (12.5)	3.6 (16.3)	3.5 (7.3)
R anom (%)	2.04	2.21	2.33	2.50	2.22	2.91
CC1/2 in highest resolution shell	0.977	0.968	0.975	0.978	0.957	0.989
〈I/σ(I)〉	57.6 (13.0)	40.6 (8.8)	50.0 (14.8)	40.6 (14.2)	47.3 (5.3)	39.2 (13.8)
Wilson B (Å2)	12.9	13.6	13.0	13.0	12.5	12.0
Successful phasing†	Yes	Yes	Yes	Yes	Yes	Yes
Average phase error before d.m.‡ (°)	64.3	63.8	66.4	67.3	69.8	74.8
Average phase error after 20 cycles of d.m.‡ (°)	49.2	51.7	54.3	60.5	57.7	67.7
Average phase error after d.m.‡ and autotracing in SHELXE (°)	N/A†	N/A†	N/A†	48.7	45.3	42.9
Map correlation before d.m.‡	0.408	0.408	0.392	0.294	0.296	0.163
Map correlation after 20 cycles of d.m.‡	0.655	0.611	0.590	0.471	0.541	0.378
Map correlation after d.m.‡ and autotracing in SHELXE	N/A§	N/A§	N/A§	0.647	0.714	0.725

^†The first 100 frames from the high-intensity data merged with the last 100 frames from the low-intensity data.

^‡The first 150 frames from both data sets merged together.

^§The first 100 frames from both data sets merged together.

^¶All 200 frames of the low-intensity data.

^††All 157 frames of the high-intensity data.

^‡‡Multiplicity with Friedel pairs kept separate.

^§§An electron-density map from which a near-complete model could be built was generated.

^¶¶d.m. indicates density modification in SHELXE.

^†††Tracing was not necessary for phasing and hence was not performed.

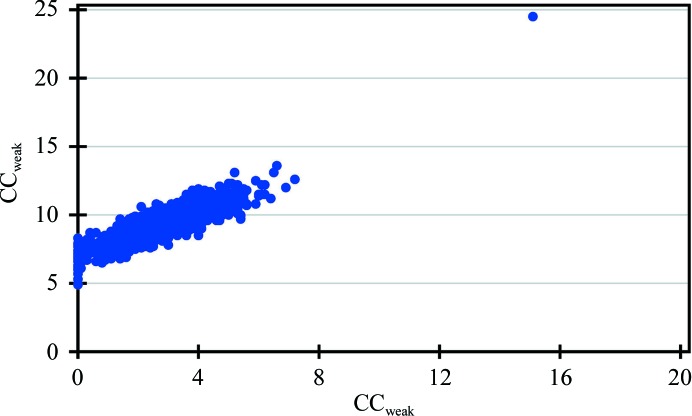
Determining the substructure solution using data set 5 required several attempts that involved tuning the E-values (normalized structure factor) and resolution. In one such attempt, using anomalous data extending to 1.7 Å resolution with an E-value cutoff of 1.7, one correct solution was obtained from 1000 cycles (Fig. 1 ▸). The difficulty in finding the substructure solution is not surprising considering the fact that these data had a completeness of only ∼70% in the range 50–3.5 Å (Supplementary Fig. S3), owing to a high number of overloads, and a multiplicity as low as 5.2 (Table 3 ▸). These missing high-intensity reflections are expected to contain a disproportionate amount of information about the structure.

Figure 1.

CC_all/CC_weak from a SHELXD run of 1000 cycles representing 999 incorrect substructure solutions and one correct solution that resulted in successful phasing of data set 5 for HEWL, which has a data completeness of only ∼70% to 3.5 Å resolution owing to overloads, with an average multiplicity as low as 5.2.

To evaluate the impact of losing high-intensity reflections owing to overloads on the success of substructure solution, we artificially removed the top 5, 10, 15, 20, 25, 30 and 35% of intense reflections from the HEWLAll data set and attempted substructure solution for each of the data sets. The CC_all/CC_weak from SHELXD for each of the data sets is shown in Supplementary Fig. S4. As more of the intense reflections were removed, determining the substructure solution required tuning of the E-values and resolution. Also, the number of correct substructure solutions obtained decreased as more of the intense reflections were removed (as observed on moving from Supplementary Fig. S4a to Fig. S4f), with the removal of the top 30% intense reflections, similar to the case of data set 5, yielding only one correct solution. When the top 35% of intense reflections were removed, tuning the E-values and resolution with 10 000 cycles in SHELXD did not yield a correct substructure. This corroborates our suggestion that the missing high-intensity reflections owing to overloads are expected to contain a disproportionate amount of information about the structure. Hence, a X-ray diffraction experiment should strive to minimize/completely avoid the collection of overloaded reflections.

Interestingly, when we used the HEWLAll data set in AutoSol in PHENIX, v.1.9 and earlier versions were not able to produce a correct substructure solution and hence we were not able to determine the structure using this program. However, when the correct substructure from SHELXD was input to AutoSol in PHENIX it was able to build a single chain of 120 residues. Interestingly, in v.1.10 of PHENIX, AutoSol was able to generate models of varying lengths with the HEWLAll data, data set 2 and data set 4 and was unable to generate a model with data sets 1, 3 and 5.

3.4. Examples from the PDB  

We evaluated the feasibility of experimental phasing using data sets for three crystal structures deposited in the PDB: mouse acirecutone dioxygenase (PDB entry 5i91; Deshpande et al., 2016 ▸), human carbonic anhydrase isozyme II (PDB entry 3m5e; Sūdžius et al., 2010 ▸) and the main protease of Coronavirus HKU4 (PDB entry 2yna; Q. Ma, Y. Xiao & R. Hilgenfeld, unpublished work). All three structures were solved by molecular replacement with data collected at wavelengths of 0.979, 0.812 and 0.91841 Å to resolutions of 1.76, 1.7 and 1.5 Å for PDB entries 5i91, 3m5e and 2yna, respectively. However, the presence of Ni²⁺ in PDB entries 5i91 and 2yna and of Zn²⁺ in PDB entry 3m5e provided sufficient anomalous signal for successful determination of the substructure and model building.

4. Discussion  

As mentioned earlier, PSPTO and PTO had no models in the PDB and de novo structure determination was necessary in both cases. The data-acquisition strategies were not optimized for anomalous scattering, as these crystals unexpectedly acquired anomalous scatterers from the crystallization solution. In addition, our experiment with the HEWL test case was performed to mimic most routine experiments that are used to acquire native data sets. In the cases of PTO and HEWL (high-intensity data alone; see Table 3 ▸) we were able to determine structures with multiplicities near 6.0; for PSPTO this value is around 10.0. Moreover, the actual energies of the X-rays used for data collection were ∼8500, 4000 and 9000 eV away from the resonance edges associated with the relevant anomalous scatterers in PSPTO, PTO and HEWL, respectively (Table 2 ▸). All three cases mimic data-collection strategies that are typically employed for the collection of native data. Despite not being optimized for experimental phasing, these data sets yielded very good quality phases that were sufficient for automatic model building.

4.1. Multiplicity, radiation damage and data accuracy  

It is an accepted fact that high multiplicity is one of the key factors for successful sulfur phasing, even when X-ray energies corresponding to higher f′′ values (e.g. 5–8 keV) are used. One must be mindful that multiplicity comes with the detrimental effects of radiation-damage-induced errors (Garman & Nave, 2002 ▸; Holton, 2009 ▸; Ravelli & Garman, 2006 ▸; Garman, 2010 ▸). A dose limit of 2 × 10⁷ Gy (1 Gy = 1 J kg⁻¹) was proposed by Henderson for cryocooled protein crystals, at which the intensities of diffracted rays are reduced by half (D ₅₀; Henderson, 1990 ▸). Based on a recent experiment, this limit has been relaxed to 3 × 10⁷ Gy or 30 MGy, where the average diffraction intensities reduce to 70% of their original value (D ₇₀; Owen et al., 2006 ▸). Another recent study (Liebschner et al., 2015 ▸) suggests that the damage rate may be different for different crystals and indicates that the damage D ₇₀ was 30% greater at 6.33 keV (7.5 MGy) compared with 12.66 keV (11 MGy), highlighting that longer wavelengths result in greater damage. The acceptable extent of damage depends on the objective of the experiment, based on which the quality of the data obtained requires a different level of accuracy. For example, when the experimenter is looking for overall structural information, acceptable damage could be higher compared with the situation where critical biological information or exploitation of weak anomalous signal for de novo structure solution is sought. In the latter two cases, the involvement of highly radiation-sensitive residues such as aspartate or glutamate either in the active site or in the coordination with metal ions might severely affect the outcome of the experiment, as the extent of damage can affect the binding of ligands and/or the occupancy of the metal ions. A series of 20 consecutive data sets collected from a single crystal of thaumatin, covering the same rotation range 0–90° at a second-generation bending-magnet beamline, showed intensity variations as great as 300% for some reflections (Banumathi et al., 2004 ▸). In this case, the overall dose received by the crystal was approximately 3.4% of the Henderson limit for each data set (covering only a 90° wedge). These data indicate that even a relatively small received dose can cause as much as a 10–15% variation in the intensity of some reflections between consecutive data sets, although not all reflections may be affected to this extent. The allowed variation owing to radiation damage is much more stringent for the case of anomalous phasing with very weak anomalous signal. Liu and coworkers proposed that for multi-crystal native SAD, a dose of 5 MGy is the upper limit for the data set from each individual crystal (Liu et al., 2014 ▸). In the case of PSPTO, PTO and HEWL the overall doses, as calculated by RADDOSE (Zeldin et al., 2013 ▸), are 0.10, 0.03 and 0.13 MGy, which are 0.5, 0.15 and 0.65% of the Henderson limit, respectively. For the low-intensity data set of HEWL, this value is only 0.02 MGy. These values indicate that the crystals experienced very minimal damage, and consequently the accumulated intensity error owing to radiation damage is also minimal. It should be noted that when collecting data for multi-crystal native SAD, the variation owing to non-isomorphism may not be insignificant; however, it has been shown that by properly choosing and merging compatible data sets, structures can be determined from weakly diffracting crystals (Liu et al., 2014 ▸). It appears that the accumulated error resulting from radiation damage is more serious than slight non-isomorphism between crystals.

Errors owing to X-ray beamline instability are also detrimental to data quality. Multiple measurements of the same and symmetry-related reflections can improve the overall accuracy of the data. The accuracy of measurement also increases with the strength of the diffraction data. As shown in Table 1 ▸, the overall I/σ(I) values were as high as 50 for the PSPTO and HEWL data sets. In these cases, although the expected anomalous signal and multiplicities were low [compared with the high multiplicity (20–100) with which data are usually collected for native/sulfur SAD], the accurate measurement of very strong reflections and their Friedel mates, as well as the overall low X-ray dose, appears to compensate for the low signal and low multiplicity.

As described above, two sweeps of data were collected for HEWL, one with sevenfold attenuation covering a 200° wedge and the other unattenuated covering a 157° wedge. As expected, substructure solutions from merged data had a higher overall CC_all/CC_weak and PATFOM compared with other low-multiplicity data sets. Although there were a few overloads in the low-intensity data, the overall data completeness was close to 100% (Supplementary Fig. S3). To determine the minimum data required to determine the HEWL structure and to examine whether the high-intensity data contributed to successful phasing, we merged various wedges from the low- and high-intensity data. The multiplicity in these data sets was around 7.0 in most of them (Table 3 ▸) and phasing was almost universally successful, albeit with some difficulty for the data set where only high-intensity data were used, where almost 30% of the low-resolution data to 3.5 Å were missing owing to overloads; the overall I/σ(I) for these data was nearly 40, whereas it was 50 for the low-exposure data. Although substructure solution was difficult when using the high-intensity data set alone (data set 5), the quality of the map was comparable to other HEWL data sets (Table 3 ▸). These observations highlight the contribution of missing reflections to the overall I/σ(I), which in turn could determine the ease/success of phasing.

4.2. Anomalous signal and phasing  

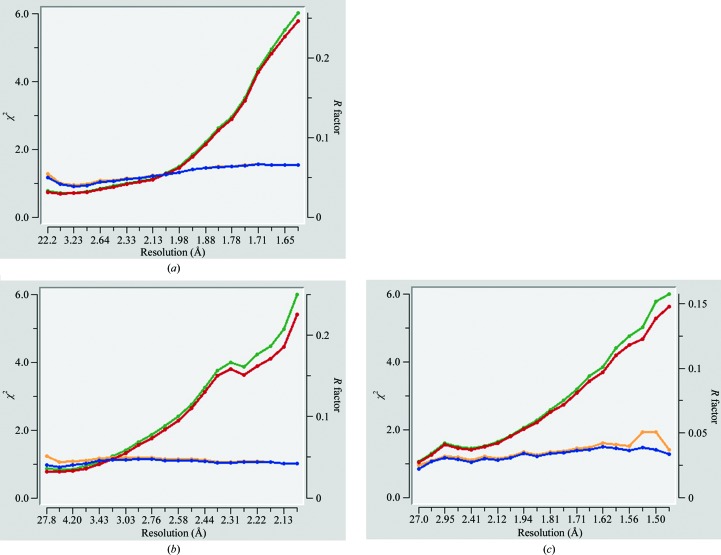
Several indicators for the estimation of anomalous signal have been proposed (Zwart, 2005 ▸; Dauter, 2006 ▸). While such indicators are very useful in most phasing experiments, they may not be fully accurate when dealing with very weak anomalous signal. One such indicator, the χ² statistic provided by the HKL-2000 data-reduction program, is very useful for detecting the presence of anomalous signal at the time of data collection itself. The presence of anomalous signal results in a noticeable difference in χ² plots with Friedel mates separated and Friedel mates merged, owing to the inequality in the intensities of Friedel mates, and this can be used as an initial indication of the presence of anomalous signal in the data. However, for very weak anomalous scatterers with Z ≤ 20, the χ² statistic may not reliably report the presence of anomalous signal (Fig. 2 ▸). In a multi-crystal native SAD experiment, it was observed that data with higher multiplicity from multiple crystals produce better substructure solutions and final maps compared with data sets with better values for some of these indicators, including CC_1/2, but with lower multiplicity (Liu et al., 2014 ▸).

Figure 2.

χ² versus resolution plots for (a) PSPTO, (b) PTO and (c) HEWL. The blue and red lines represent χ² and R factor, respectively, for the data with Friedel mates separated; orange and green lines represent χ² and R factor, respectively, for the data with Friedel mates merged.

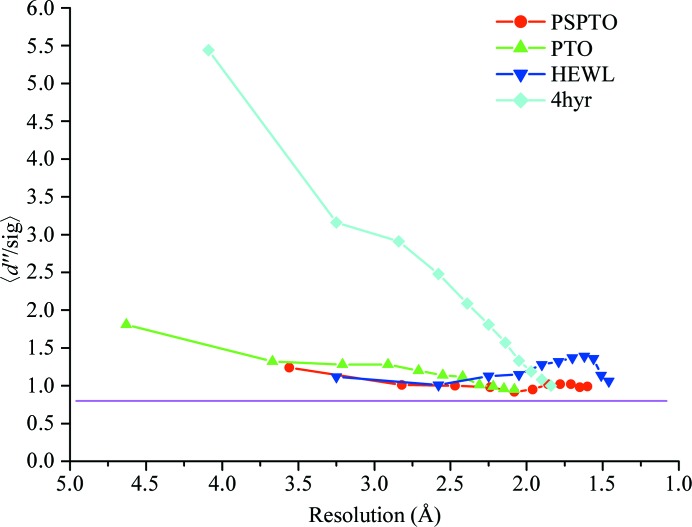
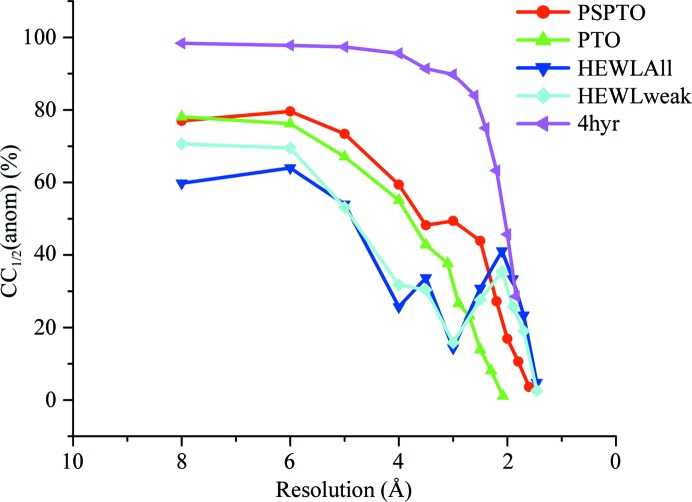
In all three of the cases discussed above, none of these tests were performed before determining the structures. Analysis of these data sets suggests that detectable anomalous signal was present in all cases. Fig. 3 ▸ shows the 〈d′′/σ〉 values as calculated by SHELXD plotted against resolution for all of the proteins along with the values corresponding to selenomethionine-derivatized putative glucarate dehydratase from Acidamino­coccus sp. D21 (PDB entry 4hyr; New York Structural Genomics Research Consortium, unpublished work) as a representative of data collected for an anomalous scatterer at an energy closer to its peak (Se in this case) to highlight the differences in the indicator as observed for a strong anomalous scatterer versus a weak one. The CC_1/2(anom) values for all three data sets clearly indicate significant anomalous signal extending to at least 3.0 Å resolution (Fig. 4 ▸). Since the data sets were collected at 1.74 and 0.979 Å, respectively, for PTO and PSPTO (f′′ values of 1.6 and 0.56, respectively, for Ca atoms), it was expected that higher CC_1/2(anom) values would be observed for PTO compared with PSPTO. Surprisingly, CC_1/2(anom) did not vary between the two data sets (Fig. 4 ▸), underscoring the suggestion that in cases with very weak anomalous signal this metric might not fully predict the likelihood of succeeding in substructure solution and phasing. However, consistent with the CC_1/2(anom) values, both of the data sets produced maps with similar quality (Table 4 ▸).

Figure 3.

A plot of 〈d′′/sig〉 versus resolution for the three proteins discussed in this paper along with representative selenomethionine data collected at the Se edge of a putative glucarate dehydratase from Acidaminococcus sp. D21 (PDB entry 4hyr). The values for HEWL correspond to the data set HEWLAll. The purple line is drawn at 〈d′′/sig〉 = 0.8, at which the signal is considered to be negligible. All three proteins show weak anomalous signal throughout the resolution range.

Figure 4.

A plot of CC_1/2(anom) versus resolution for the three proteins discussed in this paper with representative selenomethionine data collected at the Se edge of a putative glucarate dehydratase from Acidaminococcus sp. D21 (PDB entry 4hyr). For HEWL, CC_1/2(anom) versus resolution is plotted for both the data set with high-intensity and low-intensity data merged (HEWLAll) and for the weak-intensity data alone (HEWLweak, corresponding to data set 4 in Table 3 ▸).

Table 4. Map correlation coefficients and phase errors.

	Map correlation		Average phase error (°)
Protein	Before d.m.†	After d.m.‡	Before d.m.†	After d.m.‡	Solvent content
PSPTO	0.382	0.539	71.4	61.1	0.38
PTO	0.391	0.596 (0.730)§	70.6	61.5 (49.8)§	0.48
HEWL	0.396	0.6	66.8	52.7	0.35

^†Comparison between initial phases before density modification in SHELXE and the final phases (from the refined model).

^‡Comparison between phases after density modification in SHELXE and the final phases.

^§Autotracing in SHELXE was required before these could be phased successfully. The value in parentheses is the phase error/map correlation after three cycles of autotracing with 20 cycles of density modification before each cycle of autotracing in SHELXE.

^¶Corresponds to the HEWLAll data set.

Similarly, it is notable that the data for PTO were collected at a wavelength of ∼1.743 Å and the substructure contained ∼7 Ca atoms (12 atoms, ten of which were refined with partial occupancy), with calcium having an f′′ value of 1.6 e at this wavelength. The quality of the phases obtained from these data was not superior to those obtained from the HEWLAll data set (Table 4 ▸), where the wavelength for data collection was 1.075 Å and anomalous contribution was from S atoms, with sulfur having an f′′ value of 0.28 e at this wavelength. Both of these data sets have a similar multiplicity, although the calculated 〈ΔF ^anom〉/〈F〉 value (Table 1 ▸) for PTO was nearly three times that for HEWL. However, HEWL has a higher overall I/σ(I) (Table 1 ▸), indicating that while the collection of redundant data is critical for successful phasing, redundancy should not be achieved at the expense of overall data strength. It should be noted that most successful cases of multi-data-set native SAD experiments at low resolution were from strongly diffracting crystals having an overall I/σ(I) of around 50 and high symmetry (Weinert et al., 2015 ▸; Liu et al., 2014 ▸).

The observed strength of the anomalous signal from a given scatterer not only depends on the wavelength of the X-rays and the number of scatterers, but also on the B factor of the anomalous scatterers and the quality of the data (Shen et al., 2003 ▸; Zwart, 2005 ▸; Terwilliger et al., 2016 ▸). The impact of the B factor can be clearly seen in the case of the HEWL data set (Supplementary Table S1 and Fig. S5). Although the expected f′′ values for Cl and S atoms are 0.36 and 0.28 e, respectively, the first surface-bound Cl atom was observed as a seventh peak in the substructure solution of the HEWLAll data (Supplementary Table S1) and the other five Cl atoms were not consistent in all of the solutions; they either appeared after all of the S atoms in the substructure solution or did not appear at all. Anomalous difference Fourier peaks for the HEWL data set are shown in Fig. 5 ▸ at the 3, 5 and 7σ levels. It is clear that some of these surface-bound chlorine peaks cannot be seen in the map contoured at the 5σ level (cyan spheres in Fig. 5 ▸ b), while the anomalous peaks of the sulfurs, which were part of the protein chain and hence were more ordered than the chlorines, were observed.

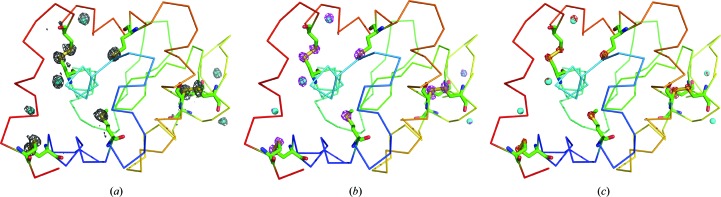
Figure 5.

Anomalous maps around the sulfurs and chlorines in HEWL shown at (a) 3σ, (b) 5σ and (c) 7σ. The maps were calculated using the HEWLAll data set. The S atoms in the side chains are in yellow and the Cl atoms are in cyan. An anomalous difference Fourier map at 7σ is not seen around most Cl atoms. This figure was produced using PyMOL (Schrödinger).

The above-mentioned indicators for estimation of anomalous signal are the most commonly used and thus have been considered in this study. A recent paper elucidates a theor­etical framework that is intended to provide a more accurate value for the expected anomalous signal taking into consideration ‘useful anomalous correlation’, the ratio of the number of unique reflections in the data set to the number of sites in the substructure and the atomic displacement factors of the atoms in the substructure (Terwilliger et al., 2016 ▸). The anomalous_signal tool within the PHENIX suite based on this framework estimates the probability P(Substr) that the substructure can be found, the signal strength and the likely figure of merit of phasing (if the substructure is found). P(Substr) as calculated by the tool for different resolution cutoffs varies between 26 and 99%, 26 and 76% and 22 and 79% for the PSPTO, PTO and HEWLAll data sets, respectively. The signal as provided by the tool varies from 3.7 to 17.0, from 4.4 to 12.0 and from 1.7 to 12.9 for PSPTO, PTO and HEWLAll, respectively. Comparing this with the selenomethionine case of PDB entry 4hyr, P(Substr) varies from 32 to 100% and the signal varies from 6.0 to 32.1. For data set 5 of HEWL, P(Substr) and the signal vary from 22 to 74% and from 1.7 to 11.0, respectively, which are comparable to those for HEWLAll, but the substructure solution required several attempts, as detailed in the previous section. Terwilliger et al. (2016 ▸) suggest that data sets with an anomalous signal greater than 10–15 could be solved, and the data sets presented in this paper all have anomalous signal greater than 10 only at certain resolution cutoffs.

5. Conclusions  

The exploitation of very weak anomalous signal is becoming an increasingly common practice, and native SAD with redundant data collected from multiple crystals or as multiple data sets from the same crystal but at different locations of the crystal has been shown to work with crystals diffracting to worse than 3.0 Å resolution (El Omari et al., 2014 ▸; Liu et al., 2014 ▸; Akey et al., 2014 ▸). In most cases it is essential to have highly redundant data (with a multiplicity of 20–100) collected using long-wavelength (1.5–2.5 Å) X-rays to maximize the accuracy and strength of the anomalous signal. Here, we show that routinely collected high-resolution data sets from strongly diffracting crystals using X-rays of shorter wavelength (around 1.0 Å) with f′′ values of 0.28 e for S atoms and 0.56 e for Ca atoms can drive de novo structure determination.

Whether the data are for anomalous phasing or molecular replacement, checking for the presence of anomalous signal in the data has at least two advantages. Firstly, calculation of anomalous difference Fourier maps with refined phases would help in the accurate assignment of bound atoms. In two of the cases presented here, although the wavelength used was around 1.0 Å, the anomalous difference Fourier peaks varied between 30 and 5σ (Supplementary Table S1; Supplementary Fig. S5 illustrates this for HEWL) depending on the anomalous scatterer and the B factor of these atoms. It appears that strongly bound atoms with Z > 15 can be assigned from the strength of the anomalous difference Fourier peaks together with the coordination geometry/environment around the bound atoms, even from data collected using a wavelength of ∼1.0 Å. Secondly, in fortuitous cases unexpected anomalous signal can be used for phasing the structure de novo where the starting model is of poor quality (for example, using anomalous signal from Cd²⁺ acquired from the crystallization solution for experimental phasing, as reported in McClelland et al., 2016 ▸).

6. Related literature  

The following reference is cited in the Supporting Information for this article: Thorn & Sheldrick (2011 ▸).