Skip to main content
NCBI home page
Scientific Reports logoLink to Scientific Reports
. 2014 Jan 28;4:3910. doi: 10.1038/srep03910

Kinetic behaviour of the cells touching substrate: the interfacial stiffness guides cell spreading

Jianjun Li 1, Dong Han 2,b, Ya-Pu Zhao 1,a
PMCID: PMC5379211  PMID: 24468681

Abstract

To describe detailed behaviour of cell spreading under the influence of substrate stiffness, A549 cells cultured on the surfaces of polydimethylsiloxane (PDMS) and polyacrylamide (PAAm) with bulk rigidities ranging from 0.1 kPa to 40 kPa were in situ observed. The spreading behaviour of cells on PAAm presented a positive correlation between spreading speed and substrate stiffness. After computing the deformations of PAAm gels and collagen, the bulk stiffness of PAAm, rather than matrix tethering, determined the cell behaviour. On the other hand, spreading behaviour of the cells was unaffected by varying the bulk stiffness of PDMS. Based on simulation analyses, the elasticity of silica-like layer induced by UV radiation on PDMS surface dominated cell-substrate interaction, rather than the bulk stiffness of the material, indicating that it is the interfacial stiffness that mainly guided the cell spreading. And then the kinetics of cell spreading was for the first time modeled based on absolute rate theory.

The interactions between cells and their surrounding substrate (extracellular matrix, ECM) trigger numerous responses that play essential roles in regulating their behaviours and fates1. As the ECM provides physical support for cell anchorage and is responsible for transmitting environment signals to cell, the cell-ECM biointerface is an indispensable part for cell's life. Thus a cell can sense and respond to a wide range of external signals, including chemistry, topography and mechanics of the interface, which leads to the change of its morphology, dynamics, behaviour and function2. In the study of chemical and topographical pattern on this surface, we have already known that cells respond differently to variations in surface chemistry and can specifically distinguish between proteins or even peptides of a few amino acids3. Directional control of cell movement along preset paths can be realized on the microarrays of asymmetric cell-adhesive islands4. In recent years, it has become increasingly evident that the cellular response to environmental signals goes far beyond the ability of the cell to surface chemistry and topography, and thus emphasis has been focused on the mechanics of biointerface, especially on matrix stiffness5,6,7. Furthermore, according to the principle of biomechenophamarcology8,9, a newly developed multidisciplinary study demonstrated that the substrate stiffness could also affect the response of the cells like cancer cells to medication10.

The process of stiffness sensing, i.e. cells sense the mechanical properties of their surrounding environment by pulling and pushing it, and transduce the force into biochemical signals in response, is called mechanotransduction. It is important to understand the mechanotransduction process, since this relationship contributes to the maintenance of tensional homeostasis and normal tissue structure and function11,12,13 as mentioned above. As the complexity of these processes is daunting, our understanding is still in its infancy.

Cell spreading is the initial kinetic process following adhesion events once the cell touches the substrate, which presents a good prototype of simplifying the cell-substrate interactions14. To investigate the influence of substrate stiffness on cell behaviours and explore underlying physical mechanism, we chose two types of artificial substrate, i.e. PAAm and PDMS modified with collagen I. Herein, the PAAm with different bulk rigidities always shows different porous network structures. In contrast, the same stiffness of silica-like layer on the PDMS surface is really induced by UV radiation no matter how soft the PDMS bulk is. The in situ observation of cell spreading behaviours was performed and explanations were explored accordingly, mostly in theoretical ways.

Results

Characterization of membrane extension and scaling law in cell spreading

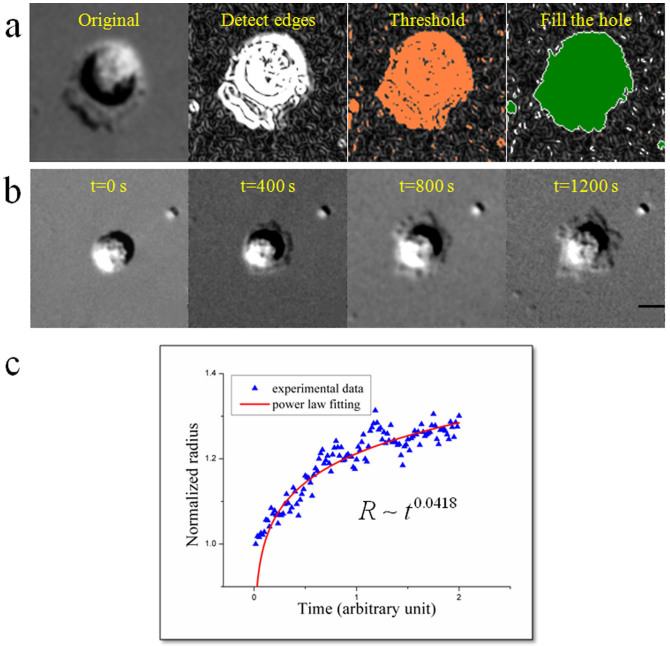
Cell spreading, which comprises actin-dependent membrane extensions and integrin-mediated adhesions, is the initial process of close contact between the cell and the substrate. An obvious feature of this dynamic process is the variations of contact areas on 2-D surface. Here we used DIC microscopy to reveal the contact region and calculated the changes of contact area with submicron and second precision. A time-lapse series of bright-field images shown in Fig. 1b demonstrate that the contact areas increase with time during the spreading assay. When the cell first gets in touch with the substrate, it changes from a rough sphere to a thick disk on the surface, and receives a signal from the liganded integrins during this process. The competition between two membrane motions, extension caused by actin polymerization at the cortex and retrograde flow by myosin contraction and membrane tension, dominates the area variations15. Similarly in anisotropic spreading14, extensions supported by filopodia are irregular with many stochastic transient extension periods (STEPs). The cell spreading area, a widely used statistics in establishing the role of a particular molecule or disease state that plays in cytoskeleton regulation16, as a function of time is well described by a sigmoid curve17. This sigmoid curve can be fitted by a power exponential function (Fig. 1c); hence the cell spreading is characterized by a scaling law R ~ tα. The scaling factor α of the power law is a universal and dimensionless parameter, and is a better one to describe the kinetics of cell spreading than other dimensional parameters, such as cell edge velocities. The behaviour of cell spreading is analogous to that of droplet spreading18, though the underlying mechanism is totally different.

Figure 1.

Figure 1

Open in a new tab

(a) Steps of computing cell areas. From left to right: original DIC image, detecting edge, optimizing threshold, filling the hole with removing noise. (b) Time-lapse recording of cell spreading in the first 20 min. (c) Relative contact radius as a function of time. This relationship can be fitted well by the power laws. Scale bar: 10 μm.

Influences of stiffness of PAAm and PDMS substrates on cell spreading

The mechanical properties of the ECM, especially the rigidity (“bulk stiffness”) defined by its elastic modulus, play an important role in regulating the behaviours of a multitude of cell types both in vitro and in vivo. Based on their responses to the rigidity of substrates, the cell lines can be divided into two categories: “rigidity dependent” (those which show distinctly different cell behaviours with varied substrate rigidities), and “rigidity independent” (those which show equally on both soft and stiff substrates)7. As the rigidity is an intrinsic quantity of the material, it is interesting to find that the spreading behaviours of A549 cells showed “rigidity dependent” on PAAm and “rigidity independent” on PDMS in the same rigidity range.

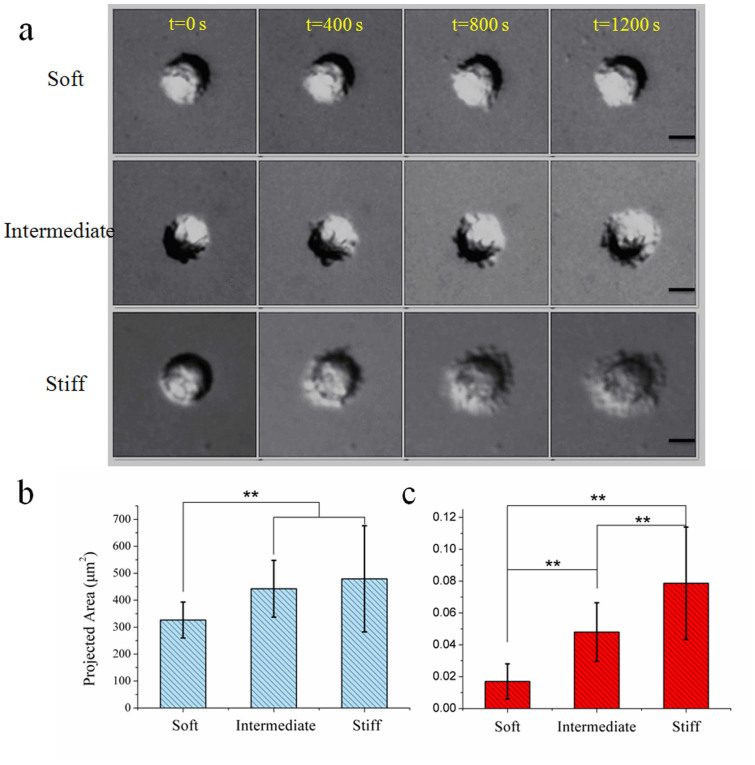
As shown in Fig. 2 and Movie S1, A549 cells exhibited distinct responses on the PAAm substrates. On PAAm, the morphology of A549 cells at 1200 s after seeding varied in response to the change of substrate rigidity. Rounded, nearly spherical cells with few irregular membrane protrusions seen on soft gels of 0.3 kPa is a sharp contrast to the flat, large spread cells with evident protrusions on the stiffest gels of 32.6 kPa. Cells seeded on gels of intermediate rigidity of 2.3 kPa showed in-between behaviours. The projected areas of cells after 20 minutes seeding increased with increasing substrate stiffness, e.g., increased from 326 ± 67 μm2 (n = 17) on soft substrate to 479 ± 196 μm2 (n = 21) on stiff substrate. The projected areas of cells on the gels of 2.3 kPa were 442 ± 106 μm2 (n = 23), which is in the middle. Besides, the cells on stiffer substrates showed more membrane protrusions in the spreading process, while those extensions on soft substrates quickly retracted and did not contribute to the net increase in cell areas. As described in the above section, a general parameter, “the scaling law factor α”, was used to characterize the velocities of membrane extension, and to quantify this spreading dynamics. Fitted to the experimental data, the scaling law factor of stiff substrate has a higher value of 0.079 ± 0.035, which means that the cells spread more quickly. The scaling law factors of soft and intermediate substrate are 0.017 ± 0.011 and 0.048 ± 0.018, respectively. The above results demonstrate that the spread speed of cells increases with increasing stiffness.

Figure 2. Different behaviours of cell spreading on different substrates of PAAm.

Figure 2

Open in a new tab

(a) Time-lapse recording of cell spreading on different substrates. The extensions of lamellipodia or filopodia rely on substrate elasticity. (b) The projected areas of cells after 20 min seeding. They increase with the elasticity. (c) The speed of cell spreading on different substrates. Cells on stiffer substrate spread much faster than those on soft substrate. ** p < 0.01, obtained by one-way ANOVA analysis. Scale bar: 10 μm.

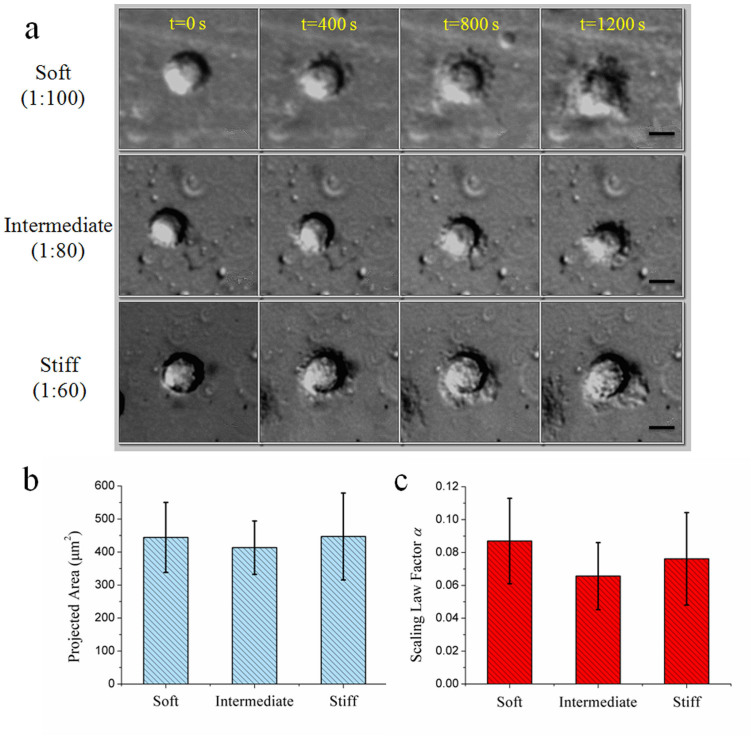
For PDMS, no obvious difference of cell morphology appeared on the substrates with different rigidities (Fig. 3a and Movie S2). The soft substrate did not suppress cell spreading. Even on the substrate of 0.1 kPa, the cells were flat, fully spread with apparent lamellipodia or filapodia, which were indistinguishable from those grew on stiff substrate. As shown in Fig. 3b, the projected areas after 20 minutes in culture were nearly the same for all three substrates, around 440 μm2 (447 ± 132, 413 ± 80, 444 ± 106, from stiff substrate to soft one). When analyzing the spreading speed, we found that the scaling law factors of all substrates were much the same, which means that the rigidity variations of PDMS substrates had no obvious effect on cell spreading speed (seen in Fig. 3c). The scaling factor of soft substrate was 0.087 ± 0.026 (n = 15), whereas that of intermediate and stiff substrate was 0.066 ± 0.020 (n = 15) and 0.076 ± 0.028 (n = 19), respectively. The values of scaling law factor on PDMS equal to that on the stiffest substrate of PAAm, which means that the cells spread very fast on PDMS.

Figure 3. Independence of cell spreading behaviours on the bulk stiffness of PDMS.

Figure 3

Open in a new tab

(a) Time-lapse recording of cell spreading on different substrates in the same range of rigidity as PAAm. (b) Nearly the same projected areas, showing no significant statistical differences. (c) Cells spreading fast on both stiff substrate and soft substrate. Scale bar: 10 μm.

Silica-like layer on the PDMS surface

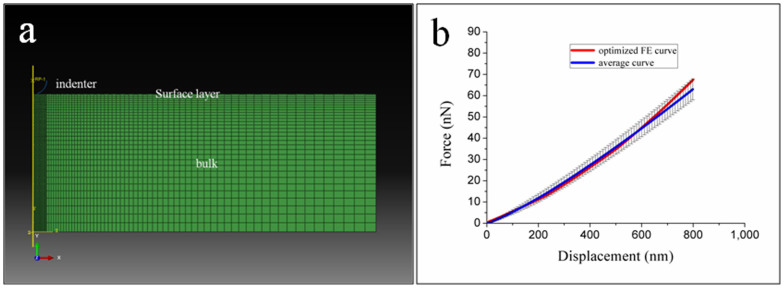
In the process of investigating how the rigidities of PAAm and PDMS influence cell behaviours, we standardize the method of linking the collagen onto the surface of the substrate by using the same heterobifunctional protein crosslinker, sulfo-SANPAH. This standardization minimizes the influence of surface chemical properties in comparing the two types of substrates. During the modification, a UV light source is needed to activate the N-hydroxysuccinimide ester in sulfo-SANPAH to react with the primary amines of collagen. However, previous studies showed that a thin and brittle silica-like layer would emerge on the surface of PDMS after UV radiation19,20,21,22. Our experiments also demonstrated the existence of surface layer on PDMS (shown in Fig. S1, S2, and S3). Here we firstly used an optimization method based on finite element method (FEM) and AFM indentations to obtain the mechanical properties of the surface layer (elastic modulus and thickness) and then to quantify the influence of silica-like layer on the bulk stiffness of PDMS in FEM.

Following the optimization procedure, the elastic modulus and thickness of surface layer on PDMS (60:1) was found to be 7.0 MPa and 200 nm. The appropriateness of these results was qualitatively (curve shape) and quantitatively (mean error < 5%) confirmed by comparison of the FE-generated force-displacement curve with the experimental data (Fig. 4b). The parameter of surface layer on PDMS (80:1) is very close to that on PDMS (60:1) (Fig. S4). As previous literature22 showed that plasma stiffening effects were similar in different mix ratio formulations of PDMS, we applied the parameters of surface layer (here 60:1) to other mix ratios of PDMS (80:1 and 100:1).

Figure 4.

Figure 4

Open in a new tab

(a) Finite element model of indentation simulation composed of indenter and PDMS substrate with surface layer. (b) AFM averaged curve and optimized FE curve.

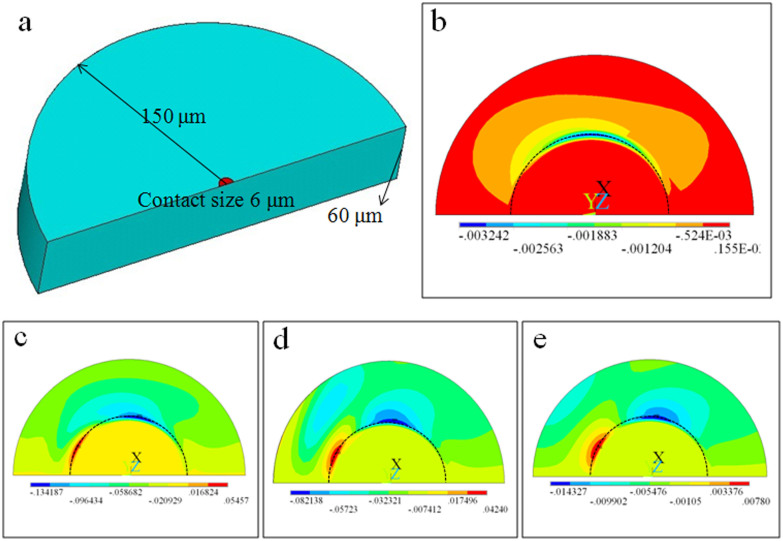
The substrate was deformed by the forces transmitted from the cell through focal adhesion; therefore we focused on the forces in the contact region between the cell (focal adhesions) and the PDMS substrate to investigate cell-substrate interactions. As the shear stress in the contact region mattered a great deal to cell spreading, the influence of surface layer could be quantitatively reflected in the shear stress. Adopting the optimized parameter, a silica-like layer (200 nm) with modulus of 7.0 MPa is deposited on the bulk materials of 40 kPa in this model. The displacement constraint condition23 is used based on the idea of strain sensing of the cells24. When bulk stiffness was varied over a wide range, the force that cells exerted increased while the extent to which the cells deformed was nearly the same. Compared with the bare material without stiff layer, the maximum shear stresses of the composite material at the surface are approximately ten times larger, of the order of 10 kPa (Fig. 5b and Fig. 5e). This means that interfacial stiffness dominates the elasticity of the whole materials. As can be seen from Fig. 5 (c–e), varying the bulk stiffness from 0.1 kPa to 40 kPa shows little impact on the shear stresses. This result further confirms that silica-like surface dominates the bulk materials, which means that the “real” elasticity that cells sense is not the bulk stiffness, and is much larger than it. This “real” elasticity is usually out of the rigidity range that cell can sense (Fig. S5). This may be the reason why cells behave “rigidity independently” on PDMS.

Figure 5. FEM analysis of the influence of silica-like layer on PDMS.

Figure 5

Open in a new tab

(a) The PDMS modeled as a half cylinder (150 μm in radius and 60 μm in thickness). Contact area was treated as a semi-circle with the radius of 6 μm, close to the size of focal adhesion. The model comprising a hard surface layer and compliant bulk materials is pulled at a given distance. (b) Shear stress at the surface of bare PDMS on the contact region with meshing buffering region. The contact region (focal adhesion size) was inside the dashed half circle. The maximum value was of the order of 1 kPa. (c–e) Shear stress at the surface of PDMS with hard layer. Owing to the hard layer, the shear stress at the contact area was ten times bigger, of the order of 10 kPa. Changing the bulk stiffness of PDMS from 0.1 kPa (c) to 40 kPa (e) does not contribute much to the shear stress on the surface. Unit in (b–e): MPa.

Which is the key determinant of cellular response on PAAm, extracellular matrix tethering or bulk stiffness of the substrate?

In the process of mechanotransduction, endogenous cytoskeleton contractility of cells is balanced by resistant forces generated from the deformation of the ECM, the magnitude of which is determined by the elastic modulus of ECM25. As the substrate, such as petri dish/glass/hydrogels, is often used to support the ECM, the forces will transmit to the substrate and cause deformation as long as the junctions between the ECM and the substrate are strong enough. In this way, the ECM and substrate work as a series system that cells sense and respond to. The equivalent elasticity of this system E* can be determined as follows

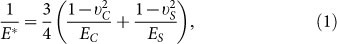graphic file with name srep03910-m1.jpg

where EC, UC and ES, US are elastic modulus and Poisson's ratio of the matrix and the substrate, respectively.

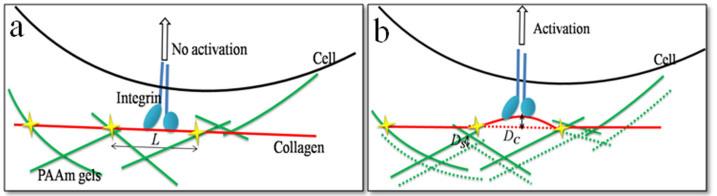
As shown in equation (1), the component of the series system, which has a lower value of elastic modulus, will make more contributions to the whole system. It means that the soft part dominates the system. Whether it is soft or not can be judged by the extent of deformation under the same load. As the network of the ECM is complex and unstable26, we often ignore the influence of ECM part, and the elasticity of the whole system is referred to the elasticity of the substrate. For PAAm, a simple method proposed by Trappmann et al. was established to estimate the elasticity of ECM based on the feature of porous materials27. The pores on the surface determine the anchoring sites of ECM (Fig. S6), which means that the distance between covalent anchoring points is longer with greater pore size and shorter with smaller pore size. When cells apply a tensile force to the collagen (the ECM used in our research), the mechanical feedback will involve a certain movement of that collagen segment which was coupled to the soft network of substrate. As the collagen is a semiflexible polymer with persistence length ≥ 15 nm28, the deformation of collagen can be obtained by modeling the collagen anchoring the surface as a simple supported beam with two fixed ends (Fig. 6). Then the deflection DC of the collagen fiber segment is determined by the load W (the tensile force exerted by the cell) and the characteristic length of collagen segment L29:

graphic file with name srep03910-m2.jpg

where E′ is the modulus of collagen (not EC), about 1 MPa30, and I is the moment of inertia; for the round collagen fiber, I = πd4/64, d is the diameter of the collagen fiber, about 100 nm31.

Figure 6. A simple model using relative deformation of collagen and PAAm gels under cell contraction.

Figure 6

Open in a new tab

It is established to evaluate the key factor of extracellular matrix tethering and bulk stiffness.

As PAAm gels were originally used in gel electrophoresis to separate proteins, varying crosslinker density not only results in different pore sizes but also different rigidities of gels. In this model, the deflection of collagen decreases rapidly with increasing segment length, which means that the collagen network becomes softer when the anchored substrate has greater pore sizes. As pore size was inversely correlated with rigidity27, greater pore size also means lower rigidity of gels. Thus it is important to evaluate the role of collagen network and substrate rigidity.

The forces generated by collagen at the anchoring site transmit to the gels and cause deformation. Since the collagen fiber is more rigid than the gels, the deformation of the substrate can be obtained using the model in which a rigid, flat rod pulls into an elastic half-space. The deflection is expressed as32

graphic file with name srep03910-m3.jpg

For PAAm of 100 kPa, L is around 2.5 nm. Then the comparative deformation of collagen and PAAm can be computed as

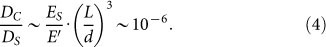graphic file with name srep03910-m4.jpg

Compared with the magnitude of substrate deformation, the collagen fiber deforms very little and behaves in a much more rigid manner, which means that the elasticity of the substrate is the main contribution to the elasticity of the whole system. As the deformation of collagen fiber is determined by the porous network of the substrate, it also indicates that the bulk stiffness of the gels is the key factor. In this case, it is precise enough to use the elasticity of the substrate to characterize the rigidity of the environment.

Theoretical model of cell spreading

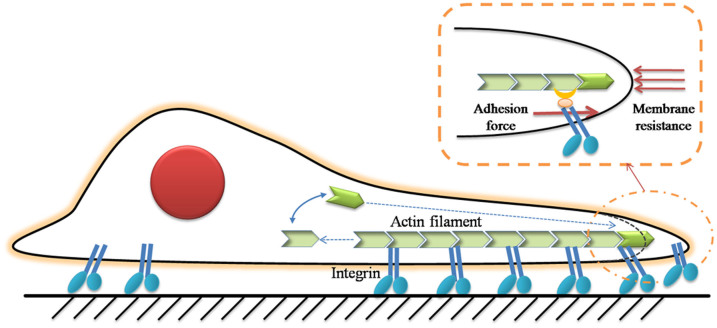
From the biological point of view, cell spreading is an active process and also a rate process33. It involves complex biochemical and biophysical events, like actin-based membrane extensions and integrin-mediated adhesions (Fig. 7). Continuous extensions are sustained by continued integrins bindings14. Then chemical and physical signals of the ECM can be transferred to cell's internal proteins which govern the constant remodeling of cell shape. Although cells are complicated biochemical automata, we believe that the physical principles of cell spreading can be captured using a set of microscopic parameters. Here we presented a theoretical model to describe this characteristic of cell spreading.

Figure 7. Schematic of cell spreading over a substrate.

Figure 7

Open in a new tab

The chemical process of actin assembly is affected by the integrin-ECM binding force and membrane resistance.

The cell areas increase caused by membrane extensions can be mostly attributed to actin polymerization at the membrane periphery. During this process, the chemical reaction of actin polymerization is affected by integrin-ECM binding and membrane resisting. Without considering the network of filapodia or lamellipodia, isotropic spreading is studied here as the simplest form of this model34. We also ignored the capping proteins, nucleation proteins and other proteins which function in reactions of filaments35. Thus the speed of cell spreading can be characterized by a competition between polymerization and depolymerization rate. Actin polymerization involves initiation and dimerization of G-actin monomers, followed by the propagation of actin filaments. If initiation and dimerization are neglected for simplicity, actin polymerization can be treated as a simple bimolecular binding reaction, where a free subunit binds to the end of a filament that contains n subunits to generate a filament of length n + 136. At chemical equilibrium, the rate of addition of new subunits to the filament ends is balanced by the rate of subunit dissociation. As long as the free energy is negative, this reaction will spontaneously proceed. The equation of this binding reaction can be written as:

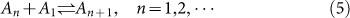graphic file with name srep03910-m5.jpg

As this chemical reaction is a rate process, absolute rate theory (or transition state theory) can be adopted to obtain the scaling law of cell spreading33, and investigate the influence of substrate rigidity. At equilibrium, the advancing frequency of actin polymerization should be the same as the receding frequency, that is

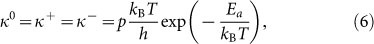graphic file with name srep03910-m6.jpg

where kB is the Boltzmann constant, T is absolute temperature, h is the Planck constant, Ea = 14kBT is the activation energy for the binding reaction37, p is the steric factor33, about 10−7, kBT/h is the fundamental frequency, it is about 1013/s at room temperature, which can be denoted by ω0.

When external forces are applied to the end of filament, the reaction equilibrium will drift so that the probability of monomer addition will be changed. Under the driving work w on the filament end, the advancing and receding frequencies can be written in the following form,

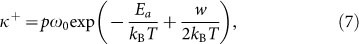graphic file with name srep03910-m7.jpg
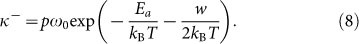graphic file with name srep03910-m8.jpg

The driving forces alter the well depth of surface potential, and change the probability of monomer assembly and disassembly. Thus the velocity of filament growth can be expressed as

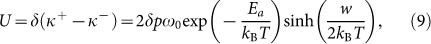graphic file with name srep03910-m9.jpg

where δ is the characteristic length of single monomer, about 2.7 nm38.

To solve equation (9), we need to obtain the driving work w. Based on previous understanding of cell spreading, the driving force is comprised of chemical energy released by integrin binding and resisting force by membrane tension and membrane deformation. Similar to a ribbon lying on an elastic layer, the shear stress in the adhesion area, which is controlled by driving force, can be obtained from

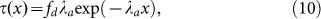graphic file with name srep03910-m10.jpg

where 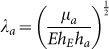Inline graphic is a characteristic reciprocal length with μa being the shear modulus of ECM. E is the Young's modulus of A549 cells, hE is the characteristic distance between the surface and the actin work, hE ≈ 20 nm, and ha is the thickness of the actin cytoskeleton, ha ≈ 0.5 μm39. By referring to previous study40, the resultant force fd is a combination of adhesion and membrane resistance, i.e.

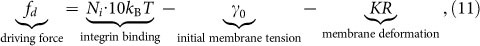graphic file with name srep03910-m11.jpg

where Ni is the density of integrins41, about 800/μm2, 10 kBT is the binding energy of a single integrin, γ0 is the initial membrane tension, 0.01 pN/nm42, K is the elastic stiffness coefficient of coupled membrane and cytoskeleton deformation, 30 pN/nm43, R is the radius of cell, varying with time. If we assume that the forces at the tip of membrane play a leading role, the shear stress related to driving work is written as τ(0) = fdλa. Considering the average area occupied by each monomer S (about 0.01 μm2)40, the driving work can be expressed as

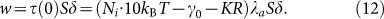graphic file with name srep03910-m12.jpg

With substitution of the expression of driving work into equation (9), the relation between spreading radius and time is rewritten as

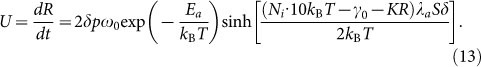graphic file with name srep03910-m13.jpg

In our case, compared with thermal fluctuation kBT, the driving work w is quite small (w/kBT < 0.1). According to the properties of hyperbolic sine function, we approximate 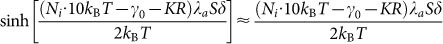Inline graphic for simplicity. Then equation (13) can be solved as

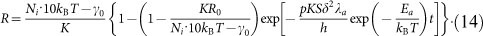graphic file with name srep03910-m14.jpg

In dealing with experimental data, the normalized radius (R′ = R(t)/R0) is used to find the universal relations with normalized time (τ = t/T0). In this way, the unit of time is arbitrary, since there is no constraint on T039. Using the first-order Taylor expansion at τ = 1, we can get a simple approximation:

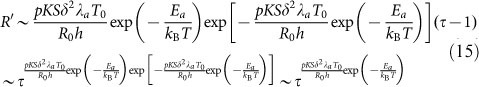graphic file with name srep03910-m15.jpg

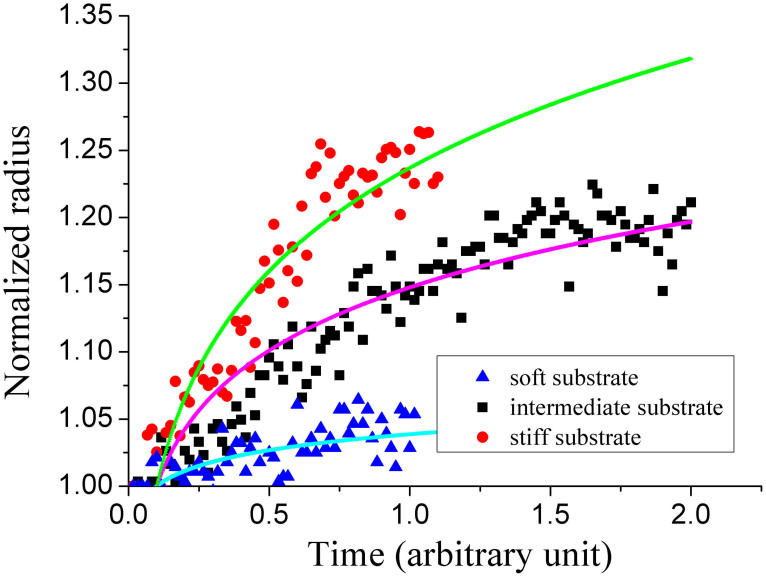
In this way, the scaling law of radius-time relation is derived from our biophysical model, and the scaling factors, which are used to characterize the spreading speed in the experiment, can be obtained. For PAAm in our study, the rigidity of substrate varies from 0.3 kPa to 33 kPa, and the scaling factor can be obtained as 0.013, 0.06 and 0.095 by substituting the values of other quantities given in this section into equation (15). The typical experimental data for different PAAm substrates are well fitted with our model (Fig. 8). So it also allows us to explore the influence of substrate stiffness on the above model. For PDMS, the shear stresses on all substrates were larger than that of stiff substrate of PAAm. It means that the “real” elasticity of PDMS is too large and goes beyond the rigidity range that cell can sense. Thus the curves of three substrates predicted by our model are identical and coincide with the stiff curve for PAAm (shown in Fig. S7).

Figure 8. Normalized contact radius as a function of time.

Figure 8

Open in a new tab

This result is consistent with the typical data on PAAm in our experiment.

Discussion

This study addresses the physical mechanism underlying the spreading behaviour of A549 cells on two different substrates, PAAm and PDMS: the scaling law that cell spreading follows and the reasons cells distinguish between two substrates with varying degrees of bulk stiffness in the same range. Based on the experimental observations and theoretical analysis, we have found out that:

  1. The spreading behaviour of cells on PAAm presents a positive correlation with substrate stiffness, while spreading behaviour of the cells is unaffected by varying the bulk stiffness of PDMS.

  2. For PDMS, the stiffness of silica-like layer on the surface dominates the cell spreading rather than its bulk stiffness.

  3. Compared with extracellular matrix tethering, the stiffness of PAAm plays a more important role in determining cell behaviour.

  4. Kinetics of cell spreading is described based on absolute rate theory, and the influences of interfacial stiffness are also focused on.

Cell spreading is the initial process once the cell touches the substrate, and interactions between the cell and the substrate occur at the interface. As the ECM and substrate provide physical support for cell anchorage, the “real” stiffness which cells can sense and respond to is contributed by the bulk stiffness of substrate, the interfacial stiffness of separable layer at the surface of substrate and the stiffness of ECM (which is determined by extracellular matrix tethering).

Bulk stiffness is generally, though by no means always, regarded as the key factor in determining cell behaviours. Previous studies showed that bulk stiffness played an important role in regulating cellular function, such as proliferation44, migration5, differentiation6, and apoptosis7. And the relationship between cell spreading and bulk stiffness has also been reported in experiments and theories39,40,45. In a separate study of cell spreading performed by Wang et al.45, it was concluded that NIH3T3 fibroblasts spread faster and showed greater projected areas on stiffer PAAm gels than on softer ones. And this phenomenon can also be modeled39,40 to describe the spreading kinetics and investigate the influence of substrate stiffness. The cell spreading behaviour on PAAm gels in our studies is consistent with their results.

The interfacial stiffness mainly guided cell spreading on PDMS. As comparative studies on PDMS and PAAm are difficult, little work has been reported and the underlying mechanism is still unclear. In previous reports, the loss modulus which denotes the viscosity influenced MSC differentiation46, and the variations in the viscoelasticity of PDMS may influence epithelial sheet movement47. This suggested that the viscosity of PDMS, which influenced the cell behaviour by diminishing cells' sensitivity to the stiffness, was a possible reconciliation for this apparently contradictory finding. It is different from our explanation. Cell behaviour influenced by stiff layer on the surface of PDMS was previously studied with FEM analysis22, however we are the first to observe it in experiments. As UV/UVO/plasma treatments are widely used to functionalize the hydrophobic PDMS surface, this surface modification which can dominate cell-substrate interface should be noticed. Additionally, coating a thin layer of gold (E ~ 70 GPa) on the surface makes the substrate rigid27, which will highly enhance the importance of interfacial stiffness and outweigh the bulk stiffness.

The stiffness of ECM also contributes to the “real” elasticity. Trappmann and colleagues27 pushed forward the current understanding at the intersection of stem-cell biology and biomaterials by showing that stem-cell spreading and differentiation are influenced by how ECM molecules are tethered to PAAm substrate, rather than bulk stiffness of substrate. However, the conclusion of our research is opposite. In our model, there is a criterion to evaluate the competition between bulk stiffness and extracellular matrix tethering. In this way, the deformation of the substrate should be considered, not just for the softest substrate, but also for the stiffer one. This can be proved by the traction force microscopy23, in which the positions of fluorescent particles are changed when the cells apply contractile forces. As the local stiffness of collagen tethers is much larger than the bulk stiffness in our computation, ignoring the local stiffness and treating bulk stiffness as the “real” rigidity seems reasonable. Our model also suggests that changing a parameter value only contributes to variation of one part (local stiffness of collagen tethers or bulk stiffness), and does not testify the comparative importance of this part. For example, coating a thin layer of gold (E ~ 70 GPa) on the surface increases the interfacial stiffness of the substrate, and the deformation of substrate will be fairly small. Then the elasticity of the whole system is dominated by the variable pore sizes. But minimizing the importance of bulk stiffness does not mean that it can be ruled out. Using gold nanoparticles spacing from 60 nm to 190 nm on stiff substrate (3 MPa) also indicates that local stiffness of collagen tethers affects cell behaviours, which neither means that the bulk stiffness can be ruled out. What we should note in our model is that the relative distance L relates to, but may not equal to the pore sizes of the hydrogels. The collagen may also be decoupled from the hydrogels, then it shows more compliant and the role of local stiffness of collagen tethers may be reconsidered. Although the stiffness of ECM contributes little in 2D cell culture compared with bulk stiffness, it will play a more important role in 3D cell culture environment, because the cells are encapsulated in pure ECM.

The relationship between cell radius and spreading time can be obtained from the experiments, and it was found to satisfy the scaling law39. Studying cell spreading within the scaling law allows us to quantify the cellular dynamics through two observable quantities, projected areas Amax and scaling factor α. Different but constant scaling factor αi in different phases of spreading are evident in a double logarithmic plot, which divides the whole process into three phases48. Due to the limitation of our experimental techniques, the membrane dynamics at the earliest spreading phase cannot be obtained since the cell body usually occludes in bright field imaging. The universal power-law behaviour of cell spreading49 in the initial phase is omitted in our study.

The application of absolute rate theory to cell spreading, which is performed for the first time in our study, is based on the fact that all biochemical reactions are rate processes33. Our model predicts the scaling law of radius-time relationship, which is similar to Brownian Ratchet model38. It is not surprising that both models have the same form and Boltzmann factors, as long as we realize that actin polymerization can be treated as Markov process. The addition of monomer onto the end of actin filament is an independent process, and has nothing to do with previous polymerization. Brownian motion is another typical Markov process. In this way, our model based on absolute rate theory is established and linked to other models. To incorporate the influence of interfacial stiffness in our model, we introduce the shear stress of the interface between cell and substrate to disturb the biochemical reactions, as the shear stress at the margin of the contact area guides cell spreading39. For PAAm, which has no separable surface layer, the shear stress is determined by the bulk stiffness of the substrate. For PDMS, the shear stress obtained by FEM simulation is much larger, which indicates that the stiffness of stiffen layer at the surface outweighs the bulk stiffness of PDMS. In this way, cell spreading behaviours on PAAm and PDMS can be described and characterized as one model in the context of interfacial environments.

In summary, not only experimental results from distinguishing between PAAm and PDMS with varied bulk stiffness but also theoretical analysis on the two systems indicate that the interfacial stiffness of substrate mainly guides cell spreading behaviours. Our finding suggests that the interfacial stiffness should be taken into account in regulating cell behaviours, including cell adhesion, spreading and subsequent migration, and may have a major impact on the design of materials for tissue engineering applications.

Methods

Preparation of PAAm and PDMS substrates for cell spreading

The preparations of PAAm hydrogels were adapted from a previously described protocol50. PAAm gels were mixed with acrylamide at final concentrations of 3, 5, 10 wt/vol% and bis-acrylamide at the corresponding concentration of 0.06, 0.15, 0.3 wt/vol%. 3/1000 total volume of ammonium persulfate (APS) and 1/1000 total volume of Tetramethylethylenediamine (TEMED) were added to gel solutions to accelerate the polymerizing process. A thin film of PAAm hydrogels (about 100 μm) was formed like a “sandwich” by carefully placing an amino-silanated glass coverslip (15 mm in diameter) on top of 20 μl of gel precursor solution which sit in the middle of the chloro-silanated confocal dish (Shengyou). Three hours later, we added PBS buffer into the confocal dish, and peeled off the top coverslip. The remaining monomer and crosslinker were removed by washing with PBS three times. For cell seeding, collagen I protein was conjugated to the surface of hydrogel using the heterobifunctional linker Sulfo-SANPAH (ProteoChem). 500 μl of a 0.2 mg ml−1 solution in 50 mM HEPES were pipetted onto the gel surface in a confocal dish (with a 20 mm diameter glass bottom), which was then placed under a homemade 365 nm ultraviolet light and irradiated for 10 minutes. Afterwards, the gels were washed with 50 mM HEPES in PBS and this procedure was repeated once. The substrates were coated with 500 μl of a 0.1 mg ml−1 solution of rat type I collagen (Invitrogen) in acetic acid for three hours at 37°C. Samples were washed three times with PBS before the seeding of cells.

The two parts of the PDMS kit (Sylgard 184, Dow Corning) were mixed in different ratios at the 100:1, 80:1, 60:1 base: crosslinker. The mixture was stirred sufficiently and degassed for one hour. Then the PDMS gels were spun on the plasma-treated confocal dish, and cured at 80°C for 24 hours. For cell seeding, the PDMS substrates were treated in a similar way with PAAm gels as described above.

Mechanical characterization of substrate stiffness

The mechanical properties of PAAm and PDMS were tested at the micro-scale by atomic force microscopy (AFM, Agilent 5500). To apply the Hertz model appropriately, a glass sphere (around 8.0 μm and 5 μm in diameter) was glued on the cantilever of AFM tip. The spring constant of tip was calibrated using the method of “Thermal K” before experiment. The resonant frequency is around 35 kHz and the measured spring constant is 0.368 N/m and 0.043 N/m, respectively. The stiffer cantilever was used in the measurement of stiffer substrates, and the soft cantilever was used for soft ones. The indentation speed was set as 5.0 μm/s. The z-position ranged from 2 μm to −1.5 μm during the indentation, and can be adjusted in Pico View. The elastic modulus of the substrate was calculated from the force-curve using our homemade software and obtained as an average of multiple measurements. The elastic modulus of all substrates used in our research is shown in Table 1. The value of softest PDMS was obtained from other paper27, because this substrate is too viscous to hold the load for a longer time. The experiment on UV treated PDMS was performed in the same way. 3 samples were tested and force curve was obtained for at least 30 locations per sample. All AFM curves were averaged, resulting in a single curve.

Table 1. Elastic modulus of PAAm and PDMS substrates.

  %Aryacrylamide %Bis-acrylamide E ± St. Dev (kPa)
PAAm 3 0.06 0.32 ± 0.24
5 0.15 2.29 ± 1.09  
10 0.3 32.6 ± 8.0  
Open in a new tab

Optimized method based on finite element simulation and AFM indentation

An optimization method based on finite element analysis was performed to evaluate the effects of plasma treatment (the thickness and elastic modulus of surface layer). The final goal was to match simulated indentation process with the corresponding AFM experiments. The indentation process can be treated as an axisymmetric problem in which a glass microsphere was glued on the AFM tip (Fig. 4a). The model was composed of the AFM spherical indenters and the bi-layer PDMS substrate consisting of a surface layer (Esurf, t) and the bulk. The indenter was modeled as a rigid body. The material description of PDMS followed a hyperelastic and nearly incompressible neo-Hookean law. To fit with the experimental data, neo-Hookean material properties were used as the initial “E modulus” defined by the following relationship E = 3μ, where μ is the shear modulus. The contact between the indenter and the substrate was modeled as frictionless. The force-indention curve was derived from the displacement and reaction force of rigid sphere. Initial elastic modulus (range from 1000 to 20000 kPa) and thickness (100 to 300 nm) of the surface layer was defined and then adjusted to fit the experimental data, until an “optimized” model of the material was found.

Finite element analysis of cell-substrate interactions on the PDMS surface

Based on the determined PDMS structure and mechanical properties, an x-axisymmetric model of substrate was built, as shown in Fig. 5a. To mimic the substrate deformed by the cellular force transmitted through focal adhesion, we established such a model that the substrate was pulled by a rod at a given displacement (200 nm in z-axis, 300 nm in y-axis) as a Neo-Hookean solid (Fig. 5a). The contact region was a half circle with 12 μm in diameter which is near to the size of focal adhesions. Then the contact region was fine-meshed to facilitate contact detection and processing. As the shear stress in contact region mattered a great deal to cell spreading, the influence of surface layer could be reflected in the shear stress quantitatively.

Cell culture and seeding onto substrates

A549 cells (adenocarcinomic human alveolar basal epithelial cells) were maintained in Dulbecco's modified Eagle's medium-high glucose (DMEM) supplemented with 10% fetal bovine serum (FBS) and 1% penicillin-streptomycin at 37°C in 5% CO2. When the assay was conducted, A549 cells were harvested with trypsin and EDTA and seeded onto PAAm and PDMS substrates (functionalized with collagen I) at a density of 10,000 per cm2. All reagents in this section were purchased from HyClone.

Measurement of cell spreading and motility

To address the dynamics of cell spreading, we used differential interference contrast microscopy (DIC), with a 20× air objective (Ti-E, Nikon) to quantitatively record the spreading process of individual A549 cell. The temperature of assays was controlled by a heated stage (Model 321 Autotuning Temperature Controller, LakeShore). Time-lapse imaging of a field containing 10 to 20 cells was performed with a charge-coupled device (CCD) camera (Cool SNAP HQ2, Photometrics) at a 10 s interval for 40–60 minutes after plating on different substrates. To settle the problem of focus drift in the whole assay, a solution termed the Perfect Focus System (PFS) was used. Each assay under this specific condition was repeated at least three times. The parameters were controlled by the MetaMorph software. Cell areas were measured using MetaMorph as well. At least 15 cells in three assays per substrate type were analyzed. The measurements of the cell area were conducted at ten second interval and normalized to the initial area of the digested cells.

Data process

To obtain the radical parameters of cells on the plane of the substrate, we used MetaMorph to transform the 16-bit digital gray scale images into binary images which can separate the cell area from the background. This separation involves the following major steps: detect edges, confirm threshold, fill holes and remove noise, as illustrated in Fig. 1a. In the process of edge detecting, we used Kirsch convolution to isolate and enhance the edges in the image by comparing brightness changes in the neighboring pixels. After that, we applied segmentation to the image to differentiate between objects of interest (cell) and other parts of the image (background) based on the image's grayscale levels. Too low or too high threshold will lead to incorrect fragment of cell and background. To solve this problem, a tool called “Auto Threshold for Light Objects” was used to optimize the threshold. Once finished, the image was transformed into a binary image (orange cell and black background). The last step is filling the holes inside the edges and removing the background to obtain the data of cell areas. Because we are primarily interested in the dynamics of cells during spreading, we did not include any activity such as polarization, migration, quiescence that followed the cells reaching their fully spreading states.

Supplementary Material

Supplementary Information

Movie S1

Download video file (305.1KB, mov)
Supplementary Information

Movie S2

Download video file (603.9KB, mov)
Supplementary Information

Supplementary infomation

srep03910-s3.doc (2.2MB, doc)

Acknowledgments

This work was jointly supported by the National Natural Science Foundation of China (NSFC, Grant No. 11072244), the Key Research Program of the Chinese Academy of Sciences (Grant No. KJZD-EW-M01), the Instrument Developing Project of the Chinese Academy of Sciences (Grant No. Y2010031) and the project of 973 in Ministry of Science and Technology of China (Grant No. 2012CB933800).

The authors declare no competing financial interests.

Author Contributions J.J.L., D.H. and Y.P.Z. contributed the ideas. J.J.L. and D.H. designed and performed all the experiments. J.J.L. and Y.P.Z. performed the FEM simulation and carried out the theoretical analysis. All authors wrote the paper, discussed the results and commented on the manuscript.

07/07/2014

A correction has been published and is appended to both the HTML and PDF versions of this paper. The error has not been fixed in the paper.

References

  1. Geiger B., Bershadsky A., Pankov R. & Yamada K. M. Transmembrane crosstalk between the extracellular matrix and the cytoskeleton. Nat. Rev. Mol. Cell Biol. 2, 793–805 (2001). [DOI] [PubMed] [Google Scholar]
  2. Geiger B., Spatz J. P. & Bershadsky A. D. Environmental sensing through focal adhesions. Nat. Rev. Mol. Cell Biol. 10, 21–33 (2009). [DOI] [PubMed] [Google Scholar]
  3. Hersel U., Dahmen C. & Kessler H. RGD modified polymers: biomaterials for stimulated cell adhesion and beyond. Biomaterials 24, 4385–4415 (2003). [DOI] [PubMed] [Google Scholar]
  4. Kumar G., Ho C.-C. & Co C. C. Guiding cell migration using one-way micropattern arrays. Adv. Mater. 19, 1084–1090 (2007). [Google Scholar]
  5. Lo C. M., Wang H. B., Dembo M. & Wang Y. Cell movement is guided by the rigidity of the substrate. Biophy. J. 79, 144–152 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Engler A. J., Sen S., Sweeney H. L. & Discher D. E. Matrix elasticity directs stem cell lineage specification. Cell 126, 677–689 (2006). [DOI] [PubMed] [Google Scholar]
  7. Tilghman R. W. et al. Matrix rigidity regulates cancer cell growth and cellular phenotype. PLoS One 5, e12905 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Liao F. L. & Han D. Biomechanopharmacology: a new discipline interfacing hemorheology and pharmacology. Biorheology 39, 652–653 (2002). [Google Scholar]
  9. Liao F. L., Li M., Han D., Cao J. & Chen K. Biomechanopharmacology: A new borderline discipline. Trends Pharmacol. Sci. 27, 287–289 (2006). [DOI] [PubMed] [Google Scholar]
  10. Feng J. T. et al. Substrate stiffness influences the outcome of antitumor drug screening in vitro. Clin. Hemorheol. Micro. 10.3233/CH-131696 (2013). [DOI] [PubMed] [Google Scholar]
  11. DuFort C. C., Paszek M. J. & Weaver V. M. Balancing forces: architectural control of mechanotransduction. Nat. Rev. Mol. Cell Biol. 12, 308–319 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Vogel V. & Sheetz M. Local force and geometry sensing regulate cell functions. Nat. Rev. Mol. Cell Biol. 7, 265–275 (2006). [DOI] [PubMed] [Google Scholar]
  13. Jaalouk D. E. & Lammerding J. Mechanotransduction gone awry. Nat. Rev. Mol. Cell Biol. 10, 63–73 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Dubin-Thaler B. J., Giannone G., Döbereiner H. G. & Sheetz M. P. Nanometer analysis of cell spreading on matrix-coated surfaces reveals two distinct cell states and STEPs. Biophy. J. 86, 1794–1806 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Giannone G. et al. Periodic lamellipodial contractions correlate with rearward actin waves. Cell 116, 431–443 (2004). [DOI] [PubMed] [Google Scholar]
  16. de Hoog C. L., Foster L. J. & Mann M. RNA and RNA binding proteins participate in early stages of cell spreading through spreading initiation centers. Cell 117, 649–662 (2004). [DOI] [PubMed] [Google Scholar]
  17. Bardsley W. G. & Aplin J. D. Kinetic analysis of cell spreading. I. Theory and modelling of curves. J. Cell Sci. 61, 365–373 (1983). [DOI] [PubMed] [Google Scholar]
  18. Yuan Q. Z. & Zhao Y. P. Precursor film in dynamic wetting, electrowetting, and electro-elasto-capillarity. Phys. Rev. Lett. 104, 246101 (2010). [DOI] [PubMed] [Google Scholar]
  19. Efimenko K., Wallace W. E. & Genzer J. Surface modification of Sylgard-184 poly (dimethyl siloxane) networks by ultraviolet and ultraviolet/ozone treatment. J. Colloid Interf. Sci. 254, 306–315 (2002). [DOI] [PubMed] [Google Scholar]
  20. Béfahy S. et al. Thickness and elastic modulus of plasma treated PDMS silica-like surface layer. Langmuir 26, 3372–3375 (2009). [DOI] [PubMed] [Google Scholar]
  21. Mills K., Zhu X., Takayama S. & Thouless M. The mechanical properties of a surface-modified layer on poly(dimethylsiloxane). J. Mater. Res. 23, 37–48 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Bartalena G., Loosli Y., Zambelli T. & Snedeker J. Biomaterial surface modifications can dominate cell–substrate mechanics: the impact of PDMS plasma treatment on a quantitative assay of cell stiffness. Soft Matter 8, 673–681 (2012). [Google Scholar]
  23. Legant W. R. et al. Multidimensional traction force microscopy reveals out-of-plane rotational moments about focal adhesions. Proc. Natl. Acad. Sci. USA 110, 881–886 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Saez A., Buguin A., Silberzan P. & Ladoux B. Is the mechanical activity of epithelial cells controlled by deformations or forces? Biophy. J. 89, L52–L54 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Hoffman B. D. & Crocker J. C. Cell mechanics: dissecting the physical responses of cells to force. Annu. Rev. Biomed. Eng. 11, 259–288 (2009). [DOI] [PubMed] [Google Scholar]
  26. Hynes R. O. The extracellular matrix: not just pretty fibrils. Science 326, 1216–1219 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Trappmann B. et al. Extracellular-matrix tethering regulates stem-cell fate. Nat. Mater. 11, 642–649 (2012). [DOI] [PubMed] [Google Scholar]
  28. Storm C., Pastore J. J., MacKintosh F. C., Lubensky T. C. & Janmey P. A. Nonlinear elasticity in biological gels. Nature 435, 191–194 (2005). [DOI] [PubMed] [Google Scholar]
  29. Landau L. D. & Lifshitz E. M. Theory of Elasticity. 3rd Edition. (Elsevier, 1986).
  30. Collet J.-P., Shuman H., Ledger R. E., Lee S. & Weisel J. W. The elasticity of an individual fibrin fiber in a clot. Proc. Natl. Acad. Sci. USA 102, 9133–9137 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Wenger M. P., Bozec L., Horton M. A. & Mesquida P. Mechanical properties of collagen fibrils. Biophy. J. 93, 1255–1263 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Johnson K. L. Contact Mechanics. (Cambridge university press, Cambridge, 1987). [Google Scholar]
  33. Glasstone S., Laidler K. J. & Eyring H. The Theory of Rate Processes. (McGraw-Hill, 1941). [Google Scholar]
  34. Carey S. P., Charest J. M. & Reinhart-King C. A. Forces during cell adhesion and spreading: implications for cellular homeostasis. Cellular and Biomolecular Mechanics and Mechanobiology. Gefen, A. (ed.), 29–69 (Springer, Berlin, 2011). [Google Scholar]
  35. Pollard T. D. & Cooper J. A. Actin, a central player in cell shape and movement. Science 326, 1208–1212 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Theriot J. A. The polymerization motor. Traffic 1, 19–28 (2002). [DOI] [PubMed] [Google Scholar]
  37. Drenckhahn D. & Pollard T. D. Elongation of actin filaments is a diffusion-limited reaction at the barbed end and is accelerated by inert macromolecules. J. Biol. Chem. 261, 12754–12758 (1986). [PubMed] [Google Scholar]
  38. Peskin C. S., Odell G. M. & Oster G. F. Cellular motions and thermal fluctuations: the Brownian ratchet. Biophy. J. 65, 316 (1993). [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Chamaraux F., Fache S., Bruckert F. & Fourcade B. Kinetics of cell spreading. Phys. Rev. Lett. 94, 158102 (2005). [DOI] [PubMed] [Google Scholar]
  40. Li Y., Xu G. K., Li B. & Feng X. Q. A molecular mechanisms-based biophysical model for two-phase cell spreading. Appl. Phys. Lett. 96, 043703 (2010). [Google Scholar]
  41. Reinhart-King C. A., Dembo M. & Hammer D. A. The dynamics and mechanics of endothelial cell spreading. Biophy. J. 89, 676–689 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Morris C. & Homann U. Cell surface area regulation and membrane tension. J. Membrane Biol. 179, 79–102 (2001). [DOI] [PubMed] [Google Scholar]
  43. Brevier J., Vallade M. & Riveline D. Force-extension relationship of cell-cell contacts. Phys. Rev. Lett. 98, 268101 (2007). [DOI] [PubMed] [Google Scholar]
  44. Hadjipanayi E., Mudera V. & Brown R. Close dependence of fibroblast proliferation on collagen scaffold matrix stiffness. J. Tissue Eng. Regen. M. 3, 77–84 (2009). [DOI] [PubMed] [Google Scholar]
  45. Yeung T. et al. Effects of substrate stiffness on cell morphology, cytoskeletal structure, and adhesion. Cell Motil. Cytoskeleton 60, 24–34 (2005). [DOI] [PubMed] [Google Scholar]
  46. Cameron A. R., Frith J. E. & Cooper-White J. J. The influence of substrate creep on mesenchymal stem cell behaviour and phenotype. Biomaterials 32, 5979–5993 (2011). [DOI] [PubMed] [Google Scholar]
  47. Murrell M., Kamm R. & Matsudaira P. Substrate viscosity enhances correlation in epithelial sheet movement. Biophy. J. 101, 297–306 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Döbereiner H. G., Dubin-Thaler B., Giannone G., Xenias H. S. & Sheetz M. P. Dynamic phase transitions in cell spreading. Phys. Rev. Lett. 93, 108105 (2004). [DOI] [PubMed] [Google Scholar]
  49. Cuvelier D. et al. The universal dynamics of cell spreading. Curr. Biol. 17, 694–699 (2007). [DOI] [PubMed] [Google Scholar]
  50. Tse J. R. & Engler A. J. Preparation of hydrogel substrates with tunable mechanical properties. Curr. Protoc. Cell Biol. 47, 10.16.1–10.16.16 (2010). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Movie S1

Download video file (305.1KB, mov)
Supplementary Information

Movie S2

Download video file (603.9KB, mov)
Supplementary Information

Supplementary infomation

srep03910-s3.doc (2.2MB, doc)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES