Abstract
Despite the enormous increase in computer power, it is still extremely challenging to obtain computationally converging sampling of ab initio QM/MM (QM(ai)/MM) free energy surfaces in condensed phases. The sampling problem can be significantly reduced by the use of the reference potential paradynamics (PD) approach, but even this approach still requires major computer time in studies of enzymatic reactions. To further reduce the sampling problem we developed here a new PD version where we use an empirical valence bond reference potential that has a minimum rather than a maximum at the transition state region of the target potential (this is accomplished conveniently by shifting the EVB of the product state). Hence, we can map the TS region in a more efficient way. Here, we introduce and validate the inverted EVB PD approach. The validation involves the study of the SN2 step of the reaction catalyzed by haloakene dehalogenase (DhlA) and the GTP hydrolysis in the RasGAP system. In addition, we have also studied the corresponding reaction in water for each of the systems described here and the reaction involving trimethylsulfonium and dimethylamine in solution. The results are encouraging and the new strategy appears to provide a powerful way of evaluating QM(ai)/MM activation free energies.
Graphical abstract

I. Introduction
Simulation of chemical processes in the condensed phases using the QM/MM1 technique has become a mainstream approach in computer simulation studies.2 Recent methodological advances in electronic structure calculations, increased computer power, as well as parallel computing have opened new opportunities for predictive ab initio QM/MM simulations and for understanding chemical processes in polar environment on a molecular level.3–6 One of the recent advances is a powerful computational scheme for the QM(ai)/MM free energy calculations using a reference potential (RP) approach,7–9 which was implemented in the Paradynamics (PD) model.10–13 The PD model is based on a number of earlier studies, including those which have established ways of efficient sampling of the RP using the empirical valence bond14 (EVB) method, as well as the ideas of refining the EVB RP9 to minimize the energy difference between the EVB RP and the target QM(ai)/MM potential (TP), and the idea of using the linear response approximation15,16 (LRA) or the free energy perturbation (FEP) approach, while moving from the RP to the TP at the TS and at the reactant states (RS) (Figure 1a). The refinement of the EVB RP is important for fast convergence of the LRA and FEP approaches. That is, evaluation of the activation free energy barrier by the PD approach using the EVB RP was estimated10 to require ∼200 times fewer calls to the TP compared to metadynamics (MTD) studies involving a direct sampling of the TP.17 The PD approach provides a rigorous way of dealing with the high computational cost of the sampling on the QM(ai)/MM potential, necessary to get the accurate free energy barrier.
Figure 1.
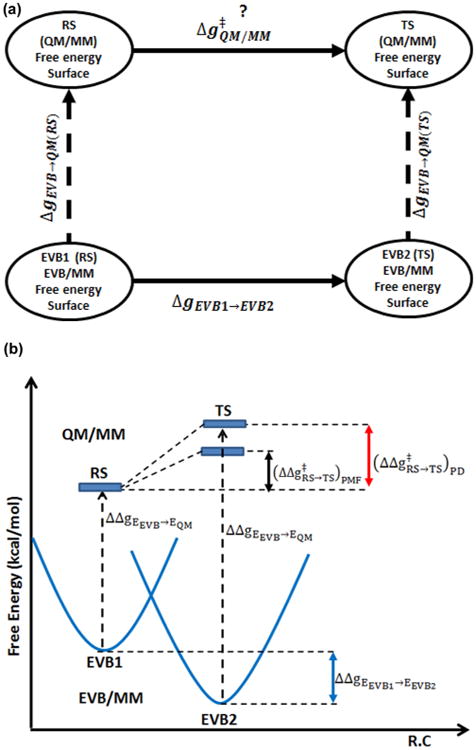
(a) Thermodynamic cycle used in the Paradynamics approach to calculate free energy barriers. To achieve that, we estimate free energy of moving from the reference potential to the target potential at the RS and at the TS. (b) A thermodynamic cycle that provides a pictorial way of calculating the QM/MM activation free energy, where the QM/MM barrier obtained by moving from the EVB/MM to the QM/MM potential is shown by a red arrow. EVB2 represents a reference potential whose minimum is placed at the position of the TS of the TP.
Unfortunately, despite the effectiveness of the PD, its computational cost in evaluating free energy surfaces in proteins does not allow us to determine reliable surfaces for enzymatic reactions with both high enough ab initio level and sufficient sampling. Thus, for example we found it necessary recently18 to perform QM(ai)/MM free energy calculations only in solution and then calibrated an EVB surface on the calculated solution surface and used we introduced here a new twist of the PD idea. That is, instead of addressing the great challenge of obtaining an EVB surface that has maximal similarity to the QM(ai)/MM at the transition state region, we generate two EVB states where the second state has a minimum at the TS region of the target potential (see Figure 1b and the discussion below). Placing the minimum of the second EVB state at the location of the QM(ai)/MM TS allows for an efficient sampling in the TS region using the EVB as a reference potential. In this case, we do not put a major effort into finding the best reference potential and therefore use a free energy perturbation (FEP) from the reference to the target potential.
We would like to clarify at this point that having a minimum at the TS position has similarity to the approach of Houk and co-workers,19 who used MM force fields with a minimum at the TS position. However, the similarity ends at this point, since in our approach the TS of the QM/MM surface has a true TS (maximum along the reaction coordinate) and the minimum on the EVB reference potential only serves to improve the convergence in evaluating the QM/MM TS free energy by an FEP mapping from the reference potential to the target potential (which has not been done in the approach of ref 19). On the other hand, an approach that has a closer relationship to our strategy has been used in a recent work by Heimdal and Ryde,20 who explored our reference potential idea with different classical MM potentials, that also included the quantum-to-molecular mechanics (Q2MM) method, and the MM potential of the type proposed by ref.19 However, this study mainly used a fixed solute (which avoids the main challenge in the field). Reference 20 also tried an approach called “QCTP – free” that allows the solute to move, but the FEP was still performed only on the reference surface (eq 4 of ref 20). Thus, they did not obtain a true FEP from the MM to the QM/MM and encounters convergence problems. Furthermore, no attempt was made to verify the results by obtaining the PMF on the QM/MM surface by direct umbrella sampling.
Here, we examine the effectiveness of the new PD version in addressing the challenge of evaluating QM(ai)/MM activation free energies of reactions catalyzed by haloakene dehalogenase (DhlA) and RasGAP system. We have also studied the corresponding reaction in water for these systems and the reaction of trimethylsulfonium and dimethylamine in solution.
II. Methods
The central idea of the PD (RP) approach is that the extensive configurational sampling required to calculate the QM(ai)/MM free energy barrier is done on a computationally inexpensive reference potential,7–9,16 rather than directly on the expensive target QM(ai)/MM potential. Our standard PD approach, described in Figure 1, involves a construction of the free energy surface (FES) for the RP using the EVB14 method and the FEP/US technique.21,22 This is followed by evaluating the free energy difference between the RP and TP, at the RS and TS region, using the LRA or FEP approach. In the ideal case when the TS position is very similar for the RP and TP surfaces we can write10
| (1) |
where is the reaction coordinate (RC) at the TS region of the TP target potential, ETP is the target potential, and ERP is the reference potential. We have the same approximation for the RS position
| (2) |
In this expression, ξETP is the RC for the RS at the target potential. It is also worth mentioning that the potentials used here were contained within the RS and TS regions at the TP by
| (3) |
| (4) |
where the Econs is a harmonic potential given by
| (5) |
Note that ξ is the reaction coordinate and can assume different values for the RS and TS regions.
The derivation of eqs 1 and 2 has been based on the linear response approximation (LRA),12,13 which becomes less reliable when the target potential and the reference potential are different. In such cases, we can use a treatment, which is a variant of the EVB FEP/US mapping formulation.21,22 That is, we are interested here in
| (6) |
where the free energy function is given by
| (7) |
and
| (8) |
where
| (9) |
This potential moves from ERP (m = 0) to the target potential ETP (m = N + 1), where N is the number of frames. The ΔΔGm in eqs 7 and 8 is the result of moving from ERP + Econs to ETP + Econs by the FEP procedure, where the second term removes the effect of the constraining potential and selects the particular values of RC. It is important to point out that in the cases where the contribution of Econs term is very small one can write
| (10) |
With eqs 6, 7, and 8 we can use the thermodynamic cycle depicted in Figure 1 to determine the QM(ai)/MM free energy barrier . In this cycle, the free energy for moving from EVB1 to EVB2 (ΔgEVB1→EVB1) is obtained by an EVB surface that was constructed using two diabatic surfaces; the first one (EVB1) corresponds to the RS region of the target QM/MM surface and the second (EVB2) has a minimum that resembles the TS region of the target QM/MM surface. The cycle can be evaluated by either the LRA or FEP approaches, using the cycle depicted in the Figure 1 we can determine using
| (11) |
where ΔgEVB1→QM(RS) is the free energy for moving from EVB1 to the RS and ΔgEVB2→QM(TS) is the free energy for moving from EVB2 to the TS.
It is important to point out that in the regular EVB/MM the free energy surface at the TS region may not be similar to the corresponding region on the QM(ai)/MM surface. This problem can be reduced by the PD procedure (that involves iterative refinement of the EVB parameters) but this requires a significant effort.13 On the other hand, if we are not interested in refining the EVB surface but just in using it as a stable reference potential, we may construct a second EVB state with a minimum whose structure resembles the geometry of the TS in QM/MM surface (Figure 1B). In addition, the EVB offers a very convenient and effective way of having the minimum of EVB2 shifted to the position of the TS of the TP (see section III.1).
In this work, we explored the performance of our approach in evaluation of the activation free energy of the SN2 step of the reaction catalyzed by DhlA, the reaction of trimethylsulfonium and dimethylamine in solution, and GTP hydrolysis in water and in RasGAP. The initial structures for the calculations were taken from the Protein Data Bank (PDB) with the 1WQ123 PDB code for the RasGAP system, the PDB with the 2DHC code for the DhlA24 system, and the 3F9X PDB code for trimethylsulfonium and dimethylamine in solution.25
The EVB and the QM/MM calculations were carried out by the MOLARIS simulation program,11,26 using the ENZYMIX force field. The EVB free energy profiles were calculated at configurations selected by the same free energy perturbation umbrella sampling (FEP/US) approach used in our previous studies (e.g., ref 27, 28). The simulation systems were solvated by the surface constrained all atom solvent (SCAAS) model26 using a water sphere of 18 Å radius centered on the substrates and surrounded by a 2 Å grid of Langevin dipoles and finally by a bulk solvent. Long-range electrostatic effects were treated by the local reaction field (LRF) method.26
The next step of the PD involved FEP mapping from the EVB surface to the QM/MM surface. This was done by running 100 ps of QM/MM relaxation for each and then 11 frames (where the simulation of each frame started with 10 ps relaxation and then 20 ps of production) for moving from the EVB potential to QM/MM potential. In other words, a total of 660 ps mapping simulations were performed when moving from the EVB potential to the QM potential at the TS and at the RS regions.
It is also worth mentioning that all the protein systems were equilibrated running 100 ps of EVB/MM MD simulation, followed by a FEP mapping procedure that involved the use of 11 frames with 20 ps each for moving from EVB1 to EVB2. The EVB parameters are described in the Supporting Information (Tables S1, S2, and S3). In order to evaluate the convergence of our results, we also ran longer MD simulation for DhlA system, which involved 11 frames with 100 ps each. It is important to clarify that this was done both for moving from EVB1 to EVB2 and for moving from EVB to PM6 potential at RS and TS region (see Table S6).
It is also important to point out that for the DhlA system the ionizable protein residues were represented by their neutral states. In general, we add the effect of the ionized residues by using Coulomb's law with large effective dielectric, but here we neglect the effect of the ionized residues following our finding that adding the effect of the ionized residues (ASP260, ARG229, LYS176, ASP178, GLU293, ASP266, LYS221, LYS224, LYS261) decreases the EVB barrier by only 1.6 kcal/mol. In the case of RasGAP we selected ionized residues within the first solvation shells of the substrate (see Table S4 in SI). In addition, the tautomers of histidine residues (in its neutral form) were determined automatically by our standard procedure (included in MOLARIS), which automatically selects the configuration with lower electrostatic energy. The histidine residues where taken to be neutral with the proton on ND1 leaving to further work the evaluation of the pKa in the protein.
All the simulations were performed at 300 K using a 1 fs time step for the RasGAP system and a 0.5 fs step for DhlA and trimethylsulfonium and dimethylamine in solution. A harmonic constraint of 100 kcal mol−1 Å−2 was applied to select the particular values of RC on the TP. The effect of the constraint could be removed using eq 9, but in the cases analyzed here, the effect of constraining the RC was quite small. Finally, for QM/MM calculations with the B3LYP functional29,30 and the 6-31g* basis set, we used the Qchem 4.031 package, while for the QM/MM calculations with the PM6 and PM3 potentials, we used MOPAC2009.32 In order to obtain reliable results, the FEP frame simulations were repeated for the PM6 cases with different initial conditions (obtained from arbitrary points on the relaxation trajectory).
III. Results and Discussion
III.1. Using the Inverted (Shifted) EVB as a Reference Potential
This work tried to both validate and use the new PD version. The corresponding study started by considering the DhlA system that catalyzes the SN2 reaction step described by the EVB states of Figure 2. The simulation of the corresponding catalytic effect has already been the subject of several PD studies.1,2,1,3 The general features of the PD are discussed elsewhere33 where in general the performance depends on the similarity between the RP and the TP. Here, however, we are proposing an EVB RP with a minimum close to the TS of the QM/MM TP. This new PD version reduces the sampling problem and minimizes the structural difference between the RP and TP at the QM/MM TS region. In other words, refining the bonds, angles, and torsion parameters allows us to describe the inverted EVB potential in terms of two key resonance structures: the first corresponds to the RS and the second corresponds to the TS of the QM/MM surface. In this way, we force the inverted EVB to have a minimum at a structure that will be as close as possible to the TS of the TP.34 The actual construction of the inverted EVB is extremely simple, within the EVB formulation. That is, we pull the product resonance structure EVB2 (see Figure 1b) down by changing the EVB parameters (bond, angles, and torsions) and/or gas phase shift (the constant that is added to the energy of EVB2), and this allows us to move the TS of the inverted minima backward along the reaction coordinate and then we change the bonding parameters for the bonds that are changed during the given reaction step, until the minimum of EVB2 moves to the approximate position of the QM/MM TS. Since the original EVB has very reliable features in the directions appendicular to the RC (e.g., angle bending) it is easy to retain the reliability in these directions and only generate a minimum along the reaction coordinate. We provide below a benchmark example of application of inverted EVB as RP.
Figure 2.
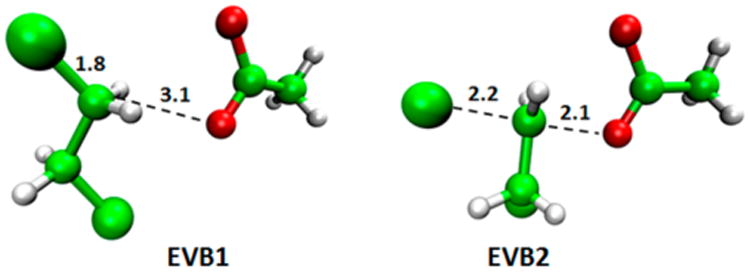
EVB resonance structure for the reaction catalyzed by haloalkane dehalogenase. The figure illustrates the structures that correspond to the minima of EVB1 and EVB2 in the reference potential of the SN2 step of the reaction catalyzed by DhlA. The initial structure was taken from the PDB with the 2DHC PDB code.
In our first example, we used the EVB/MM as the reference potential and the semiempirical PM6/MM35 as a target potential, where we evaluated the activation barrier of the target potential using a reference potential composed of EVB1 and EVB2, whose minima correspond the geometries shown in Figure 2. The reaction coordinate we considered here was the standard solute RC defined by ξ = d(Cl−C) − d(C−O), where we selected ξ = −1.3 for RS and ξ = 0.2 for the TS using information from ref 13 and Figure S1 in the SI. The free-energy change of moving from the EVB to the MO-based PM6/MM potential at the RS and TS was calculated using the FEP method (eq 6).
The validation of the proposed inverted EVB PD approach requires us to demonstrate that the barrier calculated for the TP using the PD cycle is close to the corresponding barrier obtained by PMF calculations. Here we must emphasize that the issue is not the ability to obtain the correct activation free energy with a high level of quantum theory, but rather the comparison of the results obtained using the new PD version with the PMF results. Thus, we have compared our results with full PM6/MM PMF scheme described in ref 13 for the reaction in DhlA and the reference reaction in water. As seen from Figure 3 the PM6/MM barriers estimated by the inverted EVB PD approach were found to be 26.0 and 14.0 kcal/mol (Table 1) in water and in the protein, respectively. The result found here gave higher barriers than those obtained in ref 13, which have reported from the calculated PMF a PM6/MM activation barriers of 19.0 and 10 kcal/mol for the same reaction in water and protein, respectively. The origin of the difference will be explored in subsequent studies. In addition, the protocol employed here reproduced closely the experimental catalytic effect of 11.7 kcal/mol36 and activation barrier for the reaction in the protein (15.3 kcal/mol) and in water (27 kcal/mol).36
Figure 3.
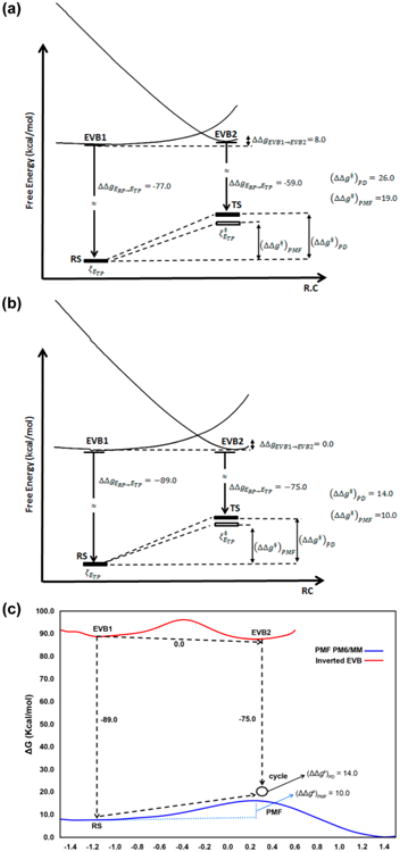
PD cycles obtained with a PM6/MM as target potential and an inverted EVB reference potential for the SN2 step in the reaction catalyzed by DhlA. (a) Reaction in water and (b) reaction in the protein. (c) Activation free energy computed from PMF PM6/MM and activation free energy obtained from the thermodynamic cycle in the protein.
Table 1. Evaluating the Free Energies for Transferring from the EVB to the PM6 Free-Energy Surface, where the PD Thermodynamic Cycle Was Computed by FEP for the SN2 Step in the Catalytic Reaction of Haloakene Dehalogenase and Watera.
| system | ΔΔgEVB→PM6 (EVB1) | ΔΔgEVB→PM6 (EVB2) | ΔΔgEVB1→EVB2 |
|
|
||
|---|---|---|---|---|---|---|---|
| water | −77.0 (−78.0) | −59.0 (−59.0) | 8.0 | 26.0 (27.0) | 19.0b\ | ||
| DhlA | −89.0 (−89.0) | −75.0 (−74.0) | 0.0 | 14.0 (15.0) | 10.0b\ 9.4d |
Energies in kcal/mol. EVB1 corresponds to the RS region and EVB2 corresponds to the TS region for the SN2 step of the reaction of haloakene dehalogenase. The results for the two-step LRA are shown in parentheses.
Results from ref 13.
Error range is discussed in the text.
From the present work.
In order to establish the reliability of our approach we moved the minimum of EVB2 forward across the reaction coordinate and obtained a change of about 1 kcal/mol in the PD activation free energy (see Table S5). We also ran longer MD simulations to evaluate the convergence of our results. This was done for the DhlA system with PM6 as the target potential. The simulation involved 11 frames with 100 ps each. The results suggest that the PD prediction using longer MD deviate only 1.0 kcal/mol from the PD prediction using shorter MD simulation (see Table 1 and Table S6), which is a very encouraging result for those interested in using DFT as a target potential. Finally, we also changed the position of the RS and obtained about 2 kcal/mol deviation upon changing the minimum along the RC (Table S5). In addition, we built a histogram for the MD trajectories to see the distribution of the energy gap between the two potentials (see Figure S3). The distribution of the energy gap for the MD trajectories propagated on the EVB MD and the PM6 MD is centered at −100 kcal/mol and −80, respectively. Similarly, for the TS region, the distribution of the energy gap for the MD trajectories propagated on EVB MD and PM6 MD is centered at −84 kcal/mol and −66, respectively. The overlap between the distributions of the EVB and PM6 distributions indicates that we should have a good convergence.
In trying to estimate the error range of the calculations one can follow ref 37 or simpler estimate like looking at a single step LRA (ETP(ξETP) − ERP(ξETP)ERP) and evaluating the standard deviation for results that are obtained from sections that are taken at 10 ps spacing. In this case, we obtained a standard deviation of 1.8 and 1.6 kcal/mol for the FEP at the TS region and the PMF, respectively. However, in our view a more useful estimate is obtained by evaluating the FEP (or PMF) barrier using trajectories that start from different initial points (obtained from collecting structures in a fixed time interval of a long trajectory) and then finding the statistical error between the different FEP (PMF) results. This approach has some similarity to the philosophy of the replica exchange method, and if we had the resources for running many trajectories we would have obtained a reliable estimate of the error range. In the present case, we found that the FEP and the PMF have errors of 2.1 kcal/mol (from 7 trajectories) and 1.3 kcal/mol (from 5 trajectories), respectively. Note, however, that our main estimate of the error of the current method is the difference between the barrier obtained by the PMF on the QM/MM potential and the same activation barrier evaluated by the PD cycle (see Figure 3b). This error extends from 1.0 kcal/mol in the proton transfer (PT) in the RasGAP example (see section III.4) to about 6 kcal/mol in a SN2 reaction in water. More work is needed to reduce the error, but it is not likely to be resolved just by running longer runs.
In order to validate the new PD version described above, we also explored the reaction involving a methyl group migration from trimethylsulfonium and dimethylamine in solution.38 Of course, this example was done by changing the system and the TP in order to evaluate the effectiveness of the inverted EVB/MM in the determination for the activation barrier using different system and target potential. Again, the reaction is described by two diabatic states that correspond to classical valence bond (VB) structures that represent the reactant and transition state of the TP (Figure 4). This test system was studied using the PM339 level of theory as target potential. The PM3/MM free energy barrier calculated for the reaction in water with full PMF (see Figure S2 in the SI for the PMF) gives 33 kcal/mol, while the result with the PD cycle is 27.0 kcal/mol for the reaction involving trimethylsulfonium and dimethyl-amine in solution (see Figure 5 and Table 2). In this case, the PD prediction is in agreement with the experimental estimate of 28.0 kcal/mol.30 However, it underestimates by ∼6 kcal/mol the results obtained from PM3/MM PMF. It is important to point out that it is hard to identify the source of the deviation between the PM3/MM PMF and PD cycles; performing such analysis is a nontrivial task that is left for future studies.
Figure 4.
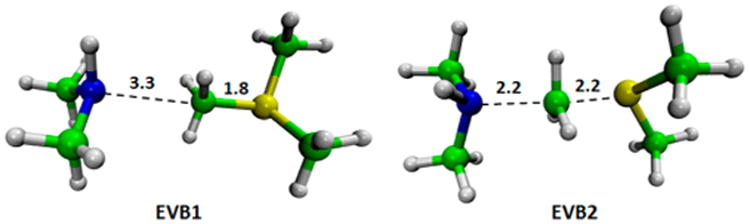
EVB resonance structures for the reaction involving trimethylsulfonium and dimethylamine in solution.
Figure 5.
A PD cycle obtained with a PM3/MM as target potential and an inverted EVB reference potential for the SN2 reaction involving trimethylsulfonium and dimethylamine in solution.
Table 2. A PD cycle for the SN2 Reaction Involving Trimethylsulfonium and Dimethylamine in Solutiona.
Energies in kcal/mol. EVB1 corresponds to the RS at TP and EVB2 corresponds to the TS at TP. In this example, we show the evaluation of the free energies for transfer from the EVB to the PM3 free-energy surface.
The error range is discussed in the text.
The above SN2 study provides an ideal tool for exploring the related reaction catalyzed by catechol O-methyltransferase (COMT), expanding on our latest study40 where we reproduced the catalytic effect of COMT and its mutants and show that this effect is not a near-attack conformation (NAC) effect. A PD study will have particular value in allowing us to clarify the problems with the recent work of Klinman and co-workers,41 presuming that our EVB study has not established the origin of the catalytic effect of COMT (despite our published results) and arguing that this effect is due to a NAC type “active site compression” in COMT. Furthermore, ref 41 has implied that graphics processing unit (GPU) based QM/MM is the only way to explore the active site compression, although the GPU calculations reported in ref 41 only give information on the ground state and incorrectly imply that one must use a very large QM region, while our EVB studies have established that QM/MM calculations with a limited-sized QM region work very well when they involve comparison of native and mutants or comparison of water and protein reactions. At any rate, while we and others believe that the NAC idea has been shown to be invalid, we would like to point out that the current PD approach offers a way to explore the NAC idea with proper sampling while using QM regions of different sizes and to examine the reliability of the calculated catalytic effect and the mutational effects, as well as a consistent analysis of the NAC effect. Such PD studies can also use the wt as the reference potential for calculating the mutant activation barrier and even to use our QCP centroid calculations42 to evaluate the kinetic isotope effect (KIE), while using non-EVB QM/MM models.
III.2. LRA Calculations
The use of the LRA approach to calculate the free energy differences between the RP and TP drastically reduced the computational cost of implementation of the PD approach.43 However, the convergence of the LRA may be problematic when the difference between the RP and the TP is significant. On the other hand, it is important to point out that the LRA is just the end point approximation of the full FEP treatment which can be implemented by using eq 1. Thus, while the full FEP can take into account cases when the two surfaces are very different, the LRA is not expected to give reliable results in such cases. In this study, we start our examination of the validity of the LRA treatment by evaluating the FEP and LRA perturbations between the EVB/MM and PM6/MM potentials of the MOPAC200932 package; this is done for the same reaction described in Figure 2. Here we would like to emphasize that the thermodynamic cycle used to estimate activation free energy can be evaluated by either the LRA or FEP approaches; using the cycle depicted in Figure 1 we can determine using eq 11.
Using the inverted EVB PD combined with the LRA approach, we obtained barriers of about 27.0 and 15.0 kcal/mol for the reaction in water and protein, respectively (see Table 1 and Figure S4 for comparison between the FEP and LRA results). The calculated difference of the activation barrier in FEP and LRA is ∼1 kcal/mol for the reaction in water and in protein, which suggest a good performance of the end-point LRA treatment with nearly identical results to those of the full FEP treatment for this case. However, in other cases the performance of the LRA is much less impressive (see section III.4).
III.3. Moving from EVB to DFT Potentials
In the previous section, we demonstrate the PD cycle with FEP treatment for moving from the EVB/MM (RP) to the PM6/MM (TP). We also used EVB/MM (RP) and a hybrid DFT B3LYP//6-31G*/MM (TP). In the PM6/MM example, we used full n-step FEP in computing the free energy of switching from the EVB to the PM6 potential, where it was computed with 11 mapping steps the for the RS region and 11 mapping steps for the TS region, which correspond to 22 trajectories. In the case with the DFT RP it is important to try to save computer time, and thus we might try to use the LRA approach. That is, using the two-step LRA also allows us to compute the activation free energies at a significantly reduced computational cost, which includes two trajectories at reactants and two trajectories at the transition state. Therefore, the LRA may be a feasible approach in terms of computational cost in calculating the B3LYP//6-31G*/MM free-energy barriers for an enzymatic reaction. However, this strategy will only work when the TP and RP are similar.
Using the inverted EVB PD and LRA approaches, we evaluated the activation free energy of the reaction of DhlA using the inverted EVB PD(RP) and the B3LYP//6-31g*/MM (TP), where the EVB parameters are given in Table S1. The results of the calculations are also summarized in Table 3. The computed barrier is about 11 kcal/mol which is overestimating the 8.8 kcal/mol B3LYP//6-31g*/MM calculated by ref 13. Apparently, the inverted EVB PD approach is overestimating the results obtained by ref 13. The origin for this discrepancy would require further examination and it may reflect a difference in sampling of the protein configurations. Note that the catalytic effect is well described in both cases. Using the inverted EVB PD approach we obtained barriers of 22.04 and 10.71 kcal/mol for the reaction in water and protein, respectively, with the B3LYP//6-31g* potential. It is important to point out that the EVB PD and LRA approaches closely reproduced the experimental catalytic effect of 11.7 kcal/mol using inverted EVB PD and B3LYP//6-31g*/MM as target potential (Table 3).
Table 3. PD Thermodynamic Cycle Computed by the LRA for the SN2 Step in the Catalytic Reaction of Haloakene Dehalogenase (B3LYP//6-31g*/MM)a.
| system | ΔΔgEVB→DFT (EVB1) | ΔΔgEVB→DFT (EVB2) | ΔΔgEVB1→EVB2 |
|
|
||
|---|---|---|---|---|---|---|---|
| water | −42.0 | −28.0 | 8.0 | 22.0 | - | ||
| DhlA | −44.0 | −33.0 | 0.0 | 11.0 | 8.8b |
Energies in kcal/mol. EVB1 corresponds to the RS and EVB2 corresponds to the TS for the SN2 step of the reaction of haloakene dehalogenase.
Results from ref 13.
III.4. PD for More Complex Systems
Although the present study provides encouraging results, one can wonder whether we found the correct ab initio TS. In the previous example, we have used RS and TS structures obtained from the PMF reported in ref 13. However, in most cases one deals with problems where the TS structure is unknown. One possible way to obtain more conclusive results is to first find the reasonable target region and then to calculate the PMF on the target surface at the neighborhood of this RTS. Of course, it is important to have some idea about the geometry of the TP and some options are possible. In this respect, it is useful to comment on the work of ref 13 which suggested the computation of the full free-energy surface using a low level of accuracy (PM3, AM1, PM6, etc.) to identify the reaction path and then select regions, which correspond to RS, TS, or PS to perform a local PMF moving to TP.13 Another option is to start with a free energy surface for the reaction in solution and then using the corresponding TS geometries in the protein. Recently, we reported QM(ai)/MM free energy calculations for the reaction of phosphate monoester hydrolysis in aqueous solution,44 exploring the relevant free-energy surfaces by several approaches, including QM(DFT)/MM MD. In this example we report the study reaction in RasGAP using TS structural information from the solution calculation of ref 44.
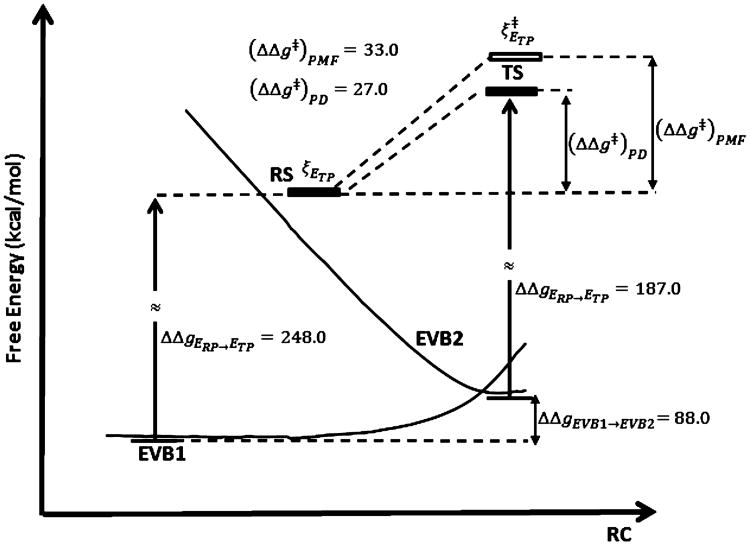
As commented above, in this example we chose a particularly challenging system, namely, the GTP hydrolysis in the reaction of RasGAP. The mechanistic options for the reference reaction in water is described in ref 44 where a very careful and systematic study was performed, and the corresponding free energy surfaces established that the mechanism that involves an additional water molecule (the 2W mechanism,see Figure6) has at least 6 kcal/mol lower barrier and is the likely mechanism in the protein. More specifically, the reaction involves an attack by the nucleophilic water that reaches a plateau on the free energy surface and then performs a proton transfer (PT) to another water (with a very low barrier), and then continues in a subsequent PT to the phosphate oxygen. Calibrating an EVB surface on the solution ab initio results and using this surface in studies of G-proteins confirmed our previous view (see ref 45) that the activation of G-proteins involved electrostatic stabilization of the TS, which is exerted, in the 2W mechanism, almost entirely at the plateau. Nevertheless, obtaining the same conclusions from the ab initio surface in the protein would provide further confirmation.
Figure 6.
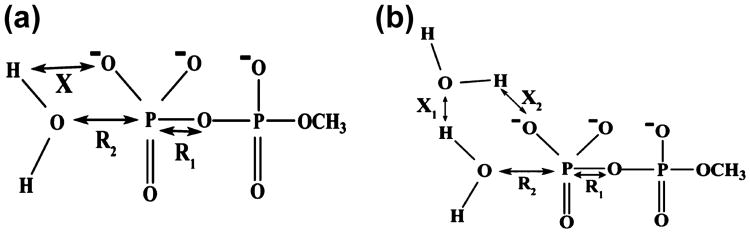
Mechanistic options for the hydrolysis of phosphate monoester. (A) Structural model where the proton is directly transferred from the attacking nucleophilic water to the substrate. (B) Structural model where the proton transfer occurs through the assistance of an additional water (2 water mechanism).
With the above considerations in mind, we tried to move one step further and explore the protein ab initio activation barrier. In order to progress in this direction we start with the examination of our approach for the reference solution reaction. It is important emphasize that our main strategy is simply to create to EVB type force fields where one (EVB1) has a minimum at the RS state and the second (EVB2) at the location of the TP TS. As commented in the previous section, using these two states, we can complete the thermodynamic cycle of Figure 1. The calculations for the 1W mechanism used EVB diabatic states with minima at the structures of EVB1 and EVB2 and the corresponding PD results are summarized in Table 4. As seen from this table we obtained a barrier of around 11 kcal/mol in a good agreement with the values found previously in the extensive QM(ai)/MM PMF calculations of ref 44 (see Table 3 of ref 44), while the results for the proton transfer in the 2W mechanism in water are summarized in Table 5.
Table 4. PD Thermodynamics for the PT from the Nucleophilic Water to the Phosphate Oxygen in the Hydrolysis of Phosphate Monoester in the 1W Mechanisma.
| method | ΔgEVB→DFT EVB1 | ΔgEVB→DFT EVB2 | ΔΔg(EVB1→EVB2) |
|
|
||
|---|---|---|---|---|---|---|---|
| FEP | 168.0 | 200.0 | −21.0 | 11.0 | 14.0b | ||
| LRA | 167.0 | 221.0 | −21.0 | 33.0 | 14.0b |
The table considered the perturbation from the EVB/MM reference potential to B3LYP//6-31g*/MM target potential (ΔGEVB→DFT), where EVB1 corresponds to the RS and EVB2 corresponds to the TS for proton transfer from the nucleophilic water to the phosphate oxygen in a system containing H2PO4− in solution (1W mechanism). Energies in kcal/mol.
Results from ref 44.
Table 5. PD Thermodynamic Cycle for the PT from the Nucleophilic Water to a Second Water in the Hydrolysis of Phosphate Monoester in the 2W Mechanisma.
| method | ΔgEVB→DFT (EVB1) | ΔgEVB→DFT (EVB2) | ΔΔg(EVB1→EVB2) |
|
|
||
|---|---|---|---|---|---|---|---|
| FEP | 246.0 | 268.0 | −22.0 | 0.0 | 1.4b | ||
| LRA | 228.0 | 264.0 | −22.0 | 14 | 1.4b |
The Table considers the perturbation from EVB/MM reference potential to B3LYP//6-31g*/MM target potential (ΔGEVB→DFT), where EVB1 corresponds to the RS and EVB2 corresponds to the TS for proton transfer from the nucleophilic water to a second water in a system containing H2PO4− plus H2O in solution (2W mechanism). Energies in kcal/mol. The estimate activation free energy is close to zero using results from FEP and 13.76 using the LRA approach results.
Results from ref 44.
In the 2W case the FEP estimate of the activation free energy of moving from the plateau is very reasonable and similar to the B3LYP//6-31g* activation free energy of 1.4 kcal/mol obtained in ref 44 (note that the result obtained by the PD cycle can also be negative if the result of the cycle deviates by more than 1.4 from the PMF). In this case, the LRA result is not in agreement with FEP results (see Tables 4 and 5). The reason for this discrepancy between FEP and LRA results may reflect the convergence of the LRA that may be problematic when there is a significant difference between the RP and the TP potential. Next, we constructed the reference EVB for the reaction in the protein and explored the crucial first step (the formation of the plateau). This was done using the EVB structures shown in Figure 7 and the corresponding results are summarized in Table 6 and Figure 8. The resulting plateau free energy of about 20 kcal/mol overestimated the actual barrier of about 15 kcal/mol18 (which should be similar to the value at the plateau) but it still presents a significant catalysis relative to the about 27 kcal/mol obtained at the same level for the plateau in water.44 The lower value of about 15 kcal/mol18 obtained by EVB calculations calibrated on the QM(ai)/MM solution surface probably reflects a more extensive sampling. Interestingly, the best agreement between the PMFs and the PD was obtained when both calculations started from the same configurations. The same trend appears in regular EVB studies when we usually average over different starting points. This type of averaging is also necessary for the PD calculations. Finally, it is useful to point out that obtaining proper converging surfaces for the reaction of RasGAP and related systems is of major importance, when one tries to explore the validity of energy minimization studies, that obtained very small energy at the plateau region (ref 46) as well as the issue of the two water path that was not explored in ref 46.
Figure 7.
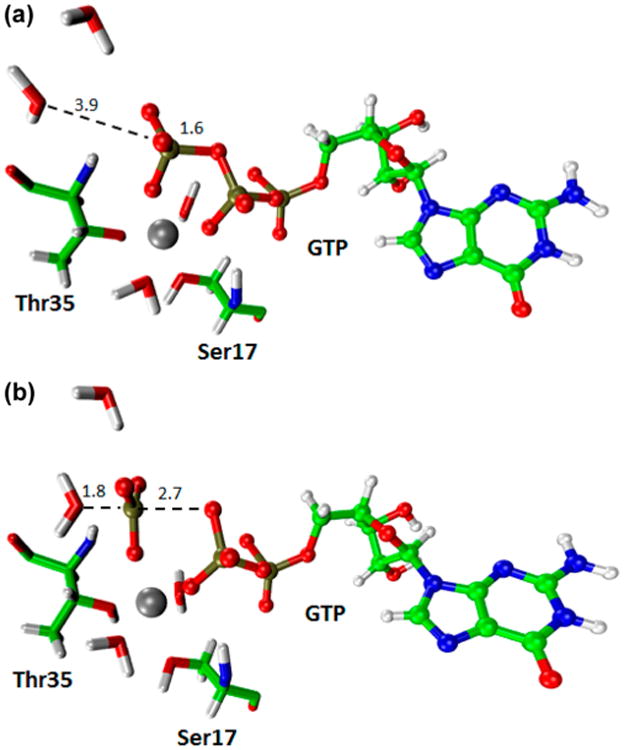
(a) EVB1 and (b) EVB2 structures for the approach to the plateau in the hydrolysis of GTP in the active site of the RasGAP system, where the initial structure was taken from Protein Data Bank (PDB) with the 1WQ1 PDB code.
Table 6. Free Energies for Transferring from the EVB to the DFT Free-Energy Surfacea.
| method | ΔΔgEVB→DFT (EVB1) | ΔΔgEVB→DFT (EVB2) | ΔΔgEVB1→EVB2 |
|
||
|---|---|---|---|---|---|---|
| FEP | 1176.0 | 1376.0 | −179.0 | 21.0 | ||
| LRA | 1176.0 | 1375.0 | −179.0 | 21.0 |
PD thermodynamic cycle for the arrival to the plateau in the hydrolysis of GTP in the RasGAP system.
Figure 8.
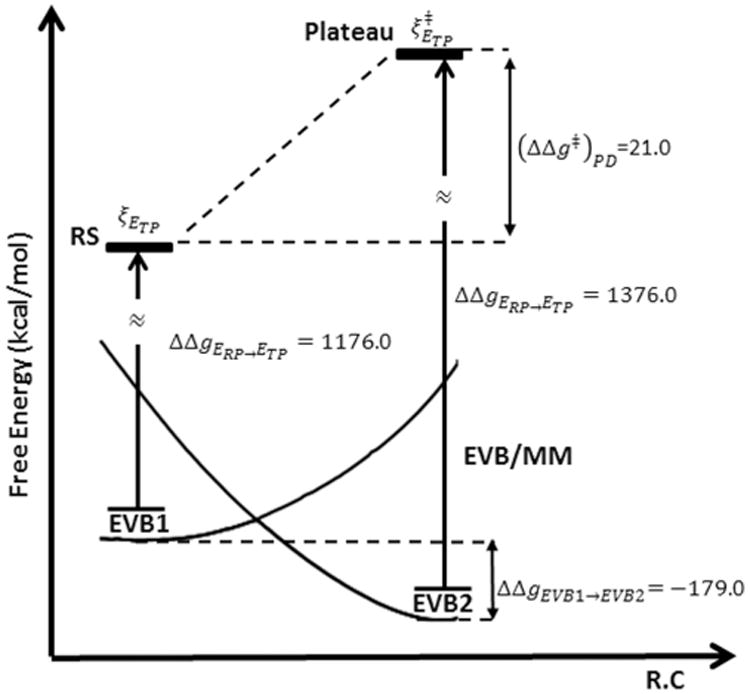
Thermodynamic cycle for the arrival to the plateau in the hydrolysis of phosphate monoester in the active site of RasGAP, where B3LYP//6-31g*/MM was used as the target potential.
IV. Concluding Discussion
This work introduced a new version of the PD approach where the reference potential at the TS region is represented by the minimum of the product diabatic state. The approach is found to be convenient and quite powerful. Of course, in this case we are not trying to obtain the best realistic adiabatic EVB but simply to use a reference potential with a very convenient way of evaluating the free energy for moving from EVB1 to EVB2. The new PD approach seems to be powerful enough to allow one to obtain QM(ai)/MM activation free energies in enzymatic reactions. However, we still recommend examination of the calculated results by using EVB surfaces that are calibrated on the solution reaction and then transferred to the enzyme environment. In this way, one can repeat the EVB calculations with different initial conditions and find the true convergence error in the calculations. We would like to clarify again that the main difficulty in our PD approach is capturing the effect of the variation in the solute (substrate) coordinate and not in capturing the effect of the environment. In general, it is quiet trivial to obtain the free energy contribution of the environment for a fixed solute, but capturing the correct reaction coordinate along the solute surface has been a major challenge. This work only discussed briefly what type of problems can be explored by our general approach, in addition to exploring complex issues like enzyme design where we have one or two metals. It can also be used in challenging problems like the action of G-proteins and in exploring the action and the mutational effects on COMT and related systems (see above). At any rate, the inverted PD approach is expected to be very useful in exploring ab initio QM/MM free energy surfaces in enzyme.
Supplementary Material
Acknowledgments
This work was supported by NIH grants GM 24492 and NSF grant MCB-08364000. We gratefully acknowledge the University of Southern California's High Performance Computing and Communications Center for and Extreme Science and Engineering Discovery Environment (XSEDE) for computer time. J.L. thanks the Conselho Nacional de Desenvolvimento Cientifico e Tecnológico and Programa Ciência sem Fronteiras. We also would like to thank Dr. Nikolay V. Plotnikov of Department of Chemistry, Stanford University, for many important discussions about paradynamics and for providing the mapping program.
Footnotes
Supporting Information: The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcb.5b11966.
Parameters used to describe the EVB potential, the PMF for reaction catalyzed by DhlA and for reaction involving trimethylsulfonium and dimethylamine in solution, distribution for the energy gap for EPM6 − EEVB; FEP results for moving from reference to the target potential in the DhlA case, ionized residues for the RasGAP system, free energies for transferring from the EVB to the PM6 moving along the RC, longer time simulations for computing thermodynamic cycle for reaction catalyzed by DhlA (PDF)
Notes: The authors declare no competing financial interest.
References
- 1.Warshel A, Levitt M. Theoretical Studies of Enzymic Reactions: Dielectric, Electrostatic and Steric Stabilization of the Carbonium Ion in the Reaction of Lysozyme. J Mol Biol. 1976;103:227–249. doi: 10.1016/0022-2836(76)90311-9. [DOI] [PubMed] [Google Scholar]
- 2.Warshel A. Multiscale Modeling of Biological Functions: From Enzymes to Molecular Machines (Nobel Lecture) Angew Chem, Int Ed. 2014;53:10020–10031. doi: 10.1002/anie.201403689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kamerlin SCL, Warshel A. Multiscale Modeling of Biological Functions. Phys Chem Chem Phys. 2011;13:10401–10411. doi: 10.1039/c0cp02823a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kamerlin SCL, Haranczyk M, Warshel A. Progress in Ab Initio QM/MM Free-Energy Simulations of Electrostatic Energies in Proteins: Accelerated QM/MM Studies of Pka, Redox Reactions and Solvation Free Energies†. J Phys Chem B. 2009;113:1253–1272. doi: 10.1021/jp8071712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hu H, Yang W. Free Energies of Chemical Reactions in Solution and in Enzymes with Ab Initio Quantum Mechanics/Molecular Mechanics Methods. Annu Rev Phys Chem. 2008;59:573–601. doi: 10.1146/annurev.physchem.59.032607.093618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Senn HM, Thiel W. QM/MM Methods for Biomolecular Systems. Angew Chem, Int Ed. 2009;48:1198–1229. doi: 10.1002/anie.200802019. [DOI] [PubMed] [Google Scholar]
- 7.Muller RP, Warshel A. Ab Initio Calculations of Free Energy Barriers for Chemical Reactions in Solution. J Phys Chem. 1995;99:17516. [PubMed] [Google Scholar]
- 8.Luzhkov V, Warshel A. Microscopic Models for Quantum Mechanical Calculations of Chemical Processes in Solutions: LD/AMPAC and SCAAS/AMPAC Calculations of Solvation Energies. J Comput Chem. 1992;13:199–213. [Google Scholar]
- 9.Bentzien J, Muller RP, Florian J, Warshel A. Hybrid Ab Initio Quantum Mechanics/Molecular Mechanics Calculations of Free Energy Surfaces for Enzymatic Reactions: The Nucleophilic Attack in Subtilisin. J Phys Chem B. 1998;102:2293–2301. [Google Scholar]
- 10.Plotnikov NV, Kamerlin SCL, Warshel A. Paradynamics: An Effective and Reliable Model for Ab Initio Qm/Mm Free-Energy Calculations and Related Tasks. J Phys Chem B. 2011;115:7950–7962. doi: 10.1021/jp201217b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Warshel A, Chu ZT, Villa J, Strajbl M, Schutz CN, Shurki A, Vicatos S, Chakrabarty S, Plotnikov NV, Schopf P. Molaris-Xg, v 9 11. University of Southern California; Los Angeles, CA: 2012. [Google Scholar]
- 12.Rosta E, Klahn M, Warshel A. Towards Accurate Ab Initio QM/MM Calculations of Free-Energy Profiles of Enzymatic Reactions. J Phys Chem B. 2006;110:2934–2941. doi: 10.1021/jp057109j. [DOI] [PubMed] [Google Scholar]
- 13.Plotnikov NV. Computing the Free Energy Barriers for Less by Sampling with a Coarse Reference Potential While Retaining Accuracy of the Target Fine Model. J Chem Theory Comput. 2014;10:2987–3001. doi: 10.1021/ct500109m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Warshel A, Weiss RM. An Empirical Valence Bond Approach for Comparing Reactions in Solutions and in Enzymes. J Am Chem Soc. 1980;102:6218–6226. [Google Scholar]
- 15.Lee FS, Chu ZT, Bolger MB, Warshel A. Calculations of Antibody-Antigen Interactions: Microscopic and Semi-Microscopic Evaluation of the Free Energies of Binding of Phosphorylcholine Analogs to McPC603. Protein Eng, Des Sel. 1992;5:215–228. doi: 10.1093/protein/5.3.215. [DOI] [PubMed] [Google Scholar]
- 16.Rosta E, Klahn M, Warshel A. Towards Accurate Ab Initio QM/MM Calculations of Free-Energy Profiles of Enzymatic Reactions. J Phys Chem B. 2006;110:2934. doi: 10.1021/jp057109j. [DOI] [PubMed] [Google Scholar]
- 17.Mones L, KulhaInek P, Simon I, Laio A, Fuxreiter M. The Energy Gap as a Universal Reaction Coordinate for the Simulation of Chemical Reactions. J Phys Chem B. 2009;113:7867–7873. doi: 10.1021/jp9000576. [DOI] [PubMed] [Google Scholar]
- 18.Prasad BR, Plotnikov NV, Lameira J, Warshel A. Quantitative Exploration of the Molecular Origin of the Activation of Gtpase. Proc Natl Acad Sci U S A. 2013;110:20509–20514. doi: 10.1073/pnas.1319854110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Norrby PO, Rasmussen T, Haller J, Strassner T, Houk KN. Rationalizing the Stereoselectivity of Osmium Tetroxide Asymmetric Dihydroxylations with Transition State Modeling Using Quantum Mechanics-Guided Molecular Mechanics. J Am Chem Soc. 1999;121:10186–10192. [Google Scholar]
- 20.Heimdal J, Ryde U. Convergence of QM/MM Free-Energy Perturbations Based on Molecular-Mechanics or Semiempirical Simulations. Phys Chem Chem Phys. 2012;14:12592–12604. doi: 10.1039/c2cp41005b. [DOI] [PubMed] [Google Scholar]
- 21.King G, Warshel A. Investigation of the Free Energy Functions for Electron Transfer Reactions. J Chem Phys. 1990;93:8682. [Google Scholar]
- 22.Torrie GM, Valleau JP. Nonphysical Sampling Distributions in Monte Carlo Free-Energy Estimation: Umbrella Sampling. J Comput Phys. 1977;23:187–199. [Google Scholar]
- 23.Scheffzek K, Ahmadian MR, Kabsch W, Wiesmuller L, Lautwein A, Schmitz F, Wittinghofer A. The Ras-Rasgap Complex: Structural Basis for Gtpase Activation and Its Loss in Oncogenic Ras Mutants. Science. 1997;277:333–338. doi: 10.1126/science.277.5324.333. [DOI] [PubMed] [Google Scholar]
- 24.Verschueren KHG, Seljee F, Rozeboom HJ, Kalk KH, Dijkstra BW. Crystallographic Analysis of the Catalytic Mechanism of Haloalkane Dehalogenase. Nature. 1993;363:693–698. doi: 10.1038/363693a0. [DOI] [PubMed] [Google Scholar]
- 25.Couture JF, Dirk LMA, Brunzelle JS, Houtz RL, Trievel RC. Structural Origins for the Product Specificity of Set Domain Protein Methyltransferases. Proc Natl Acad Sci U S A. 2008;105:20659–20664. doi: 10.1073/pnas.0806712105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Lee FS, Warshel A, Chu ZT. Microscopic and Semimicroscopic Calculations of Electrostatic Energies in Proteins by the Polaris and Enzymix Programs. J Comput Chem. 1993;14:161. [Google Scholar]
- 27.Warshel A. Computer Modeling of Chemical Reactions in Enzymes and Solutions. John Wiley & Sons; New York: 1991. [Google Scholar]
- 28.Warshel A, Sharma PK, Kato M, Xiang Y, Liu HB, Olsson MHM. Electrostatic Basis for Enzyme Catalysis. Chem Rev. 2006;106:3210–3235. doi: 10.1021/cr0503106. [DOI] [PubMed] [Google Scholar]
- 29.Lee CT, Yang WT, Parr RG. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron-Density. Phys Rev B: Condens Matter Mater Phys. 1988;37:785–789. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- 30.Becke AD. Density-Functional Thermochemistry 0.3. The Role of Exact Exchange. J Chem Phys. 1993;98:5648–5652. [Google Scholar]
- 31.Shao Y, Molnar LF, Jung Y, Kussmann J, Ochsenfeld C, Brown ST, Gilbert ATB, Slipchenko LV, Levchenko SV, O'Neill DP, et al. Advances in Methods and Algorithms in a Modern Quantum Chemistry Program Package. Phys Chem Chem Phys. 2006;8:3172–3191. doi: 10.1039/b517914a. [DOI] [PubMed] [Google Scholar]
- 32.Stewart JJP. Mopac2009. Colorado Springs, CO, USA; 2008. [Google Scholar]
- 33.Kamerlin SCL, Warshel A. The Empirical Valence Bond Model: Theory and Applications. Wiley Interdiscip Rev-Comput Mol Sci. 2011;1:30–45. [Google Scholar]
- 34.Nakayama H, Shimamura T, Imagawa T, Shirai N, Itoh T, Sako Y, Miyano M, Sakuraba H, Ohshima T, Nomura N, et al. Structure of a Hyperthermophilic Archaeal Homing Endonuclease, I-Tsp061i: Contribution of Cross-Domain Polar Networks to Thermo-stability. J Mol Biol. 2007;365:362–378. doi: 10.1016/j.jmb.2006.09.066. [DOI] [PubMed] [Google Scholar]
- 35.Stewart JJP. Optimization of Parameters for Semiempirical Methods V: Modification of Nddo Approximations and Application to 70 Elements. J Mol Model. 2007;13:1173–1213. doi: 10.1007/s00894-007-0233-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Olsson MHM, Warshel A. Solute Solvent Dynamics and Energetics in Enzyme Catalysis: The S(N)2 Reaction of Dehalogenase as a General Benchmark. J Am Chem Soc. 2004;126:15167–15179. doi: 10.1021/ja047151c. [DOI] [PubMed] [Google Scholar]
- 37.Straatsma TP, Berendsen HJC, Stam AJ. Estimation of Statistical Errors in Molecular Simulation Calculations. Mol Phys. 1986;57:89–95. [Google Scholar]
- 38.Callahan BP, Wolfenden R. Migration of Methyl Groups between Aliphatic Amines in Water (Pg 125, Pg 310, 2003) J Am Chem Soc. 2003;125:10481–10481. doi: 10.1021/ja021212u. [DOI] [PubMed] [Google Scholar]
- 39.Stewart JJP. Optimization of Parameters for Semiempirical Methods 0.1. Method. J Comput Chem. 1989;10:209–220. [Google Scholar]
- 40.Lameira J, Bora RP, Chu ZT, Warshel A. Methyltransferases Do Not Work by Compression, Cratic, or Desolvation Effects, but by Electrostatic Preorganization. Proteins: Struct, Funct Genet. 2015;83:318–330. doi: 10.1002/prot.24717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Zhang JY, Kulik HJ, Martinez TJ, Klinman JP. Mediation of Donor-Acceptor Distance in an Enzymatic Methyl Transfer Reaction. Proc Natl Acad Sci U S A. 2015;112:7954–7959. doi: 10.1073/pnas.1506792112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Liu HB, Warshel A. Origin of the Temperature Dependence of Isotope Effects in Enzymatic Reactions: The Case of Dihydrofolate Reductase. J Physn Chem B. 2007;111:7852–7861. doi: 10.1021/jp070938f. [DOI] [PubMed] [Google Scholar]
- 43.Plotnikov NV, Warshel A. Exploring, Refining, and Validating the Paradynamics QM/MM Sampling. J Phys Chem B. 2012;116:10342–10356. doi: 10.1021/jp304678d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Plotnikoy NV, Prasad BR, Chakrabarty S, Chu ZT, Warshel A. Quantifying the Mechanism of Phosphate Monoester Hydrolysis in Aqueous Solution by Evaluating the Relevant Ab Initio QM/MM Free-Energy Surfaces. J Phys Chem B. 2013;117:12807–12819. doi: 10.1021/jp4020146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Kamerlin SCL, Sharma PK, Prasad RB, Warshel A. Why Nature Really Chose Phosphate. Q Rev Biophys. 2013;46:1–132. doi: 10.1017/S0033583512000157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Khrenova MG, Grigorenko BL, Kolomeisky AB, Nemukhin AV. Hydrolysis of Guanosine Triphosphate (GTP) by the Ras Center Dot Gap Protein Complex: Reaction Mechanism and Kinetic Scheme. J Phys Chem. 2015;119:12838–12845. doi: 10.1021/acs.jpcb.5b07238. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.