Coarse graining from variationally enhanced sampling applied to the Ginzburg–Landau model

Significance

A multiscale description is believed to be the only feasible route toward the simulation of complex systems. Yet moving from one scale to another is not a trivial task, and many different approaches can be taken. We propose here a systematic approach to go from a fine scale to a coarser one, based on the recently introduced variationally enhanced sampling method. Contrary to other coarse-graining methods, it combines in the same algorithm the sampling enhancement and the optimization of the coarse-graining parameters. We illustrate the method in the case of the vapor–liquid critical transition of a Lennard–Jones fluid. This is done in the context of the Ginzburg–Landau field theoretical description of second-order phase transitions.

Abstract

A powerful way to deal with a complex system is to build a coarse-grained model capable of catching its main physical features, while being computationally affordable. Inevitably, such coarse-grained models introduce a set of phenomenological parameters, which are often not easily deducible from the underlying atomistic system. We present a unique approach to the calculation of these parameters, based on the recently introduced variationally enhanced sampling method. It allows us to obtain the parameters from atomistic simulations, providing thus a direct connection between the microscopic and the mesoscopic scale. The coarse-grained model we consider is that of Ginzburg–Landau, valid around a second-order critical point. In particular, we use it to describe a Lennard–Jones fluid in the region close to the liquid–vapor critical point. The procedure is general and can be adapted to other coarse-grained models.

Computer simulations of condensed systems based on an atomistic description of matter are playing an ever-increasing role in many fields of science. However, as the complexity of the systems studied increases, so does the awareness that a less detailed, but nevertheless accurate, description of the system is necessary.

This has been long since recognized, and branches of physics like elasticity or hydrodynamics can be classified in modern terms as coarse-grained (CG) models of matter. In more recent times, a field theoretical model suitable to describe second-order phase transitions has been introduced by Landau (1) and later perfected by Ginzburg (2). In recent decades a number of coarse-grained models that aim at describing polymers or biomolecules have also been proposed (3, 4). In all these approaches some degrees of freedom, deemed not essential to study the phenomenon at hand, are integrated out and the resulting reduced description contains a number of parameters that are not easily determined.

Here we use the recently developed variationally enhanced sampling (VES) method (5) to suggest a procedure that allows the determination of such parameters, starting from the microscopic Hamiltonian. This illuminates a somewhat unexpected application of VES, which has been introduced as an enhanced sampling method. We show that it also provides a powerful framework for the optimization of CG models, due to the combination of its enhanced sampling capabilities and its variational flexibility. Moreover, VES takes advantage of its deep connection with relative entropy, a quantity that has been shown to play a key role in multiscale problems (6, 7).

As a first test case for our procedure we consider the Ginzburg–Landau (GL) model for continuous phase transitions. An advantage of using this model is that its strengths and limits are well known and that other researchers have already attempted to perform such a calculation (8–14). A system that undergoes a second-order phase transition is described in the GL model by the following free energy, valid in a rotationally invariant one-component real-order parameter scenario,

$$F[\psi ]=g\int {|\nabla \psi (\overrightarrow{r})|}^2{d}^{3}r+a\int {\psi }^2(\overrightarrow{r})d^{3}r+b\int {\psi }^4(\overrightarrow{r})d^{3}r,$$ [1]

where the field $\psi (\overrightarrow{r})$ describes the order parameter fluctuations, and $g$, $a$, and $b$ are phenomenological quantities that we call Landau’s parameters. To be defined, we apply our method close to the liquid–vapor critical point of a Lennard–Jones fluid.

Variationally Enhanced Sampling

Before discussing our method, we briefly recall some of the ideas at the basis of VES. The VES method shares with metadynamics (15, 16) the idea of enhancing the sampling by adding an external bias potential, which is a function of a few coarse-grained order parameters, so-called collective variables (CVs). Contrary to metadynamics and other similar methods, VES does not generate the bias potential by periodically adding on the fly small contributions, but as the result of the minimization of a convex functional. Various extensions have been proposed, where VES has been used in different ways (17–22).

Let us suppose that the physical behavior of interest is well described by a set of CVs $𝐬=𝐬(𝐑)$, which are function of the coordinates $𝐑$ of the $N$ particles that compose the system. Then we can write the associated free-energy function as $F(𝐬)=-(1/\beta )\log \int d𝐑\delta [𝐬-𝐬(𝐑)]e^{-\beta U(𝐑)}$, where $\beta =1/(k_{\mathrm{B}}T)$ is the inverse temperature and $U(𝐑)$ is the interparticle potential energy.

In VES a functional that depends on an externally applied bias $V(𝐬)$ is introduced,

$$\mathrm{\Omega }[V]=\frac{1}{\beta }\log \frac{\int d𝐬e^{-\beta [F(𝐬)+V(𝐬)]}}{\int d𝐬e^{-\beta F(𝐬)}}+\int d𝐬p(𝐬)V(𝐬),$$ [2]

where $p(𝐬)$ is a chosen probability distribution that we call target distribution. The functional is convex and for the value of $V(𝐬)$ that minimizes $\mathrm{\Omega }[V]$, we have

$$P_V(𝐬)=p(𝐬),$$ [3]

where

$$P_V(𝐬)=\frac{e^{-\beta [F(𝐬)+V(𝐬)]}}{\int d𝐬e^{-\beta [F(𝐬)+V(𝐬)]}}$$ [4]

is the distribution of $𝐬$ in the ensemble biased by $V(𝐬)$. Neglecting immaterial constants, Eq. 3 can also be written as

$$F(𝐬)=-V(𝐬)-\frac{1}{\beta }\log p(𝐬).$$ [5]

Thus, finding the minimizing bias potential $V(𝐬)$ is equivalent to finding the free energy $F(𝐬)$.

We note here that the functional $\mathrm{\Omega }[V]$ has close connections to the relative entropy or Kullback–Leiber divergence $D_{KL}$ (23–25), in particular $\beta \mathrm{\Omega }[V]=D_{KL}(p\parallel P_V)-D_{KL}(p\parallel P_0)$. Furthermore, at the minimum we have $\mathrm{\Omega }[V]\le 0$, which is a rewrite of the Gibbs–Bogoliubov inequality (26).

To minimize $\mathrm{\Omega }[V]$ we express $V(𝐬)$ as a linear function of a finite set of variational parameters $𝜶=\{{\alpha }_i\}$ and thus $V(𝐬;𝜶)$. By doing so, our functional becomes a function of $𝜶$ that can be minimized using the gradient and the Hessian

$$\frac{\partial \mathrm{\Omega }(𝜶)}{\partial {\alpha }_i}=-{⟨\frac{\partial V(𝐬;𝜶)}{\partial {\alpha }_i}⟩}_{V(𝜶)}+{⟨\frac{\partial V(𝐬;𝜶)}{\partial {\alpha }_i}⟩}_p$$ [6]

$$\frac{{\partial }^2\mathrm{\Omega }(𝜶)}{\partial {\alpha }_i\partial {\alpha }_j}=\beta \left[{⟨\frac{\partial V(𝐬;𝜶)}{\partial {\alpha }_i}\frac{\partial V(𝐬;𝜶)}{\partial {\alpha }_j}⟩}_{V(𝜶)}-{⟨\frac{\partial V(𝐬;𝜶)}{\partial {\alpha }_i}⟩}_{V(𝜶)}{⟨\frac{\partial V(𝐬;𝜶)}{\partial {\alpha }_j}⟩}_{V(𝜶)}\right],$$ [7]

where the averages in the right-hand side of the equations are calculated either in the biased ensemble ${⟨\cdot ⟩}_{V(𝜶)}$ or in the $p(𝐬)$ ensemble ${⟨\cdot ⟩}_p$, and second derivatives in $𝜶$ have been omitted due to the linearity assumption.

Because the forces in Eqs. 6 and 7 are calculated as statistical averages, a stochastic optimization method (27) is needed. We describe in detail the minimization procedure in Minimization Procedure.

Minimization Procedure

The minimization of the VES functional $\mathrm{\Omega }[V]$, Eq. 2, was carried out following the iterative procedure of Bach and Moulines (27), as described also in refs. 5 and 17. In this scheme we consider two distinct sequences of parameters: the instantaneous ${𝜶}^{(n)}$ and the averaged ${\overline{𝜶}}^{(n)}$. The instantaneous sequence is updated using the gradient and the full Hessian (Eqs. 6 and 7), evaluated at the last available average parameter values ${\overline{𝜶}}^{(n)}$,

$${\alpha }_i^{(n+1)}={\alpha }_i^{(n)}-\mu \left[\frac{\partial \mathrm{\Omega }\left({\overline{𝜶}}^{(n)}\right)}{\partial {\alpha }_i}+\sum _j\frac{{\partial }^2\mathrm{\Omega }\left({\overline{𝜶}}^{(n)}\right)}{\partial {\alpha }_i\partial {\alpha }_j}\times \left({\alpha }_j^{(n)}-{\overline{\alpha }}_j^{(n)}\right)\right],$$ [S1]

where $\mu$ is a fixed step size that we keep on the order of $0.1$ in all our simulations. An important feature of this algorithm is that it does not require a long sampling time for each iteration; in fact, we typically estimate the gradient and the Hessian with a stride $S=2,000$ simulation time steps. We also implemented a multiple-walkers framework (37) to further improve the sampling, using two independent walkers that share the same bias.

To accelerate convergence, we found it useful to calculate $\overline{𝜶}$ as an exponentially decaying average; namely,

$${\overline{\alpha }}_i^{(n+1)}={\overline{\alpha }}_i^{(n)}+\frac{{\alpha }_i^{(n+1)}-{\overline{\alpha }}_i^{(n)}}{W},$$ [S2]

which is the discretized equivalent of

$${\overline{\alpha }}_i(t)={\int }_0^{t}dt\prime {\alpha }_i(t\prime )e^{-(t-t\prime )/\tau }.$$ [S3]

The weight $W$ is linked to the decaying time $\tau$ by the relation $1/W=1-e^{-S\mathrm{\Delta }t/\tau }\approx S\mathrm{\Delta }t/\tau$, where $\mathrm{\Delta }t$ is the simulation time step and $S$ is the stride between the parameter updates. In the runs reported here we aimed at a $\tau$ of about $1/10$th of the total simulation length, which amounts to taking $W=500$.

Within reasonable bounds, the precise choice of the parameters $\mu$, $S$, and $\tau$ does not affect much the rate of convergence of the optimization algorithm. In fact, we found that the choice of the target distribution parameters $g_t$ and $a_t$ plays a more important role in this.

Free-Energy Model

We consider a Lennard–Jones fluid of $N$ particles confined in a periodically repeated cubic box of volume $V=L^3$. The order parameter of such a system is linked to the density $\rho (\overrightarrow{r})$,

$$\psi (\overrightarrow{r})=\frac{\rho (\overrightarrow{r})-{\rho }_c}{{\rho }_0},$$ [8]

where ${\rho }_0=N/V$ and ${\rho }_c$ is the critical density. The order parameter can be expanded in a discrete Fourier series as

$$\psi (\overrightarrow{r})=\sum _{\overrightarrow{k}}{e}^{i\overrightarrow{k}\cdot \overrightarrow{r}}{\psi }_{\overrightarrow{k}},$$ [9]

where $\overrightarrow{k}=\frac{2\pi }{L}\overrightarrow{n}$, with $\overrightarrow{n}\in {\mathbb{Z}}^3$. The Ginzburg–Landau model implicitly relies on a characteristic CG length $\mathrm{\Lambda }$. This is defined by including in the series expansion, Eq. 9, only those wave vectors $\overrightarrow{k}$ whose modulus is less than $k_M=2\pi /\mathrm{\Lambda }$. We refer to this as “wave vector cutoff of order $n_M$,” where $n_M$ is an integer such that ${|\overrightarrow{k}|}^2\le k_M^2=n_M{(2\pi /L)}^2$ for all of the included $\overrightarrow{k}$. Close to $T_c$ the system is dominated by long-wavelength fluctuations and the presence of a cutoff should become physically irrelevant.

We consider as collective variables these Fourier components of the order parameter, $𝐬={\{{\psi }_{\overrightarrow{k}}\}}_{|\overrightarrow{k}|\le k_M}$. In terms of $𝐬$ the GL free energy can be rewritten as

$$F(𝐬)=g{I}_G(𝐬)+a{I}_2(𝐬)+b{I}_4(𝐬),$$ [10]

where the integrals in Eq. 1 are rewritten in Fourier space as

$$I_G(𝐬)=V\sum _{|\overrightarrow{k}|\le k_M}{k}^2{|{\psi }_{\overrightarrow{k}}|}^2$$ [11]

$$I_2(𝐬)=V\sum _{|\overrightarrow{k}|\le k_M}{|{\psi }_{\overrightarrow{k}}|}^2$$ [12]

$$I_4(𝐬)=V\sum _{|\overrightarrow{q}|\le 2k_M}|\sum _{|\overrightarrow{k}|\le k_M}{\psi }_{\overrightarrow{k}}{\psi }_{\overrightarrow{q}-\overrightarrow{k}}{|}^2$$ [13]

and in the last convolution it is implied that if $|\overrightarrow{q}-\overrightarrow{k}|>k_M$, then ${\psi }_{\overrightarrow{q}-\overrightarrow{k}}=0$. We note that because the order parameter is a real quantity, its Fourier transform has the property ${\psi }_{\overrightarrow{k}}={\psi }_{-\overrightarrow{k}}^{\ast }$. This symmetry property is used to reduce the number of independent collective variables. With a cutoff of order $n_M=3$ we have $26$ CVs, but in our simulations we have dealt with up to $364$ CVs, in the $n_M=19$ case (see Table S1).

Table S1.

Number of independent CVs for a given wave vector cutoff order $n_M$

$n_M$	CVs
3	26
7	80
12	178
16	256
19	364

Bias Potential and Target Distribution

To proceed, we have to choose a variational form for $V(𝐬)$ and introduce a suitable $p(𝐬)$. As a general principle we use for $V(𝐬)$ and $p(𝐬)$ expressions that, when combined as in Eq. 5, lead to an $F(𝐬)$ with exactly the functional form suggested by the considered CG model. In the present case we have as reference the GL free energy, Eq. 10, and thus we take

$$V(𝐬)=g_V{I}_G(𝐬)+a_V{I}_2(𝐬)+b_V{I}_4(𝐬)$$ [14]

and

$$p(𝐬)=\frac{e^{-\beta [g_t{I}_G(𝐬)+a_t{I}_2(𝐬)]}}{\int d𝐬e^{-\beta [g_t{I}_G(𝐬)+a_t{I}_2(𝐬)]}}.$$ [15]

These two expressions can be used in $\mathrm{\Omega }[V]$, which then can be minimized relative to the variational parameters $g_V$, $a_V$, and $b_V$. At the minimum the estimated $F(𝐬)$ has the desired GL structure, with parameters $g=g_t-g_V$, $a=a_t-a_V$, and $b=-b_V$.

Because $V(𝐬)$ in Eq. 14 has only a limited variational flexibility, our estimate of the free energy $F(𝐬)$ is only approximated. However, given that our $V(𝐬)$ is based on sound physical considerations, we still expect the $F(𝐬)$ obtained to be a good approximation.

Using the $p(𝐬)$ in Eq. 15 has some advantages. It is a product of univariate Gaussian distributions, so the averages over $p(𝐬)$ that are needed to minimize $\mathrm{\Omega }[V]$ (Eqs. 6 and 7) can easily be evaluated. And, more importantly, it can be used to guide sampling and accelerate the optimization convergence.

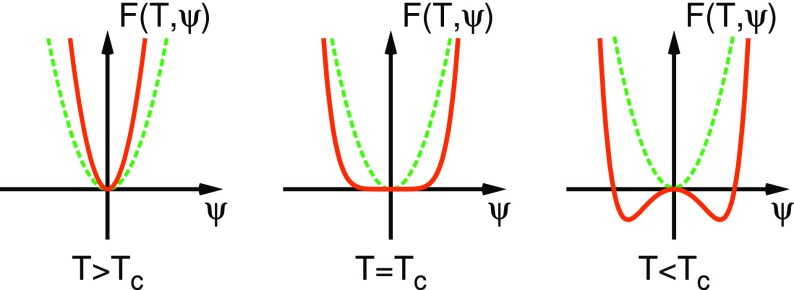
To understand this point we refer to Fig. 1, which gives an artist’s impression of a Landau free energy as a function of a one-dimensional order parameter as the system crosses the critical temperature $T_c$. For $T>T_c$ the order parameter fluctuations are predominantly Gaussian and the effect of the non-Gaussian quartic term is hidden in the tail of the distribution, as pointed out also by other authors (10, 13). By using a $p(𝐬)$ that is broader than the natural Gaussian fluctuations, we can enhance the probability with which the tails are sampled, thus improving the computation of the parameter $b$ proportional to the quartic term $I_4(𝐬)$.

Fig. 1.

A simplified one-dimensional representation of the chosen quadratic target free energy $F_t=-(1/\beta )\log p(𝐬)$ (green dashed line) and the expected Landau free energy (orange solid line).

For $T<T_c$ we enter into the coexistence region, where different problems arise. The symmetry is broken, and the system spontaneously separates into two slab-shaped regions of finite but different value of the order parameter. These two phases, vapor and liquid, correspond to the two minima in Fig. 1, Right. By using a $p(𝐬)$ that focuses on the transition region we can keep the system homogeneous and avoid to a certain extent some finite-size drawbacks (28). However, as the temperature is lowered, the interface between the two phases sharpens up with respect to the CG length $\mathrm{\Lambda }$. This situation cannot be described quantitatively by a GL model that takes into account only long-wavelength fluctuations of the order parameter. In our simulations there is some clear evidence that the underlying model is no longer suited for describing the system. In fact, the convergence in the optimization of $\mathrm{\Omega }[V]$ slows dramatically, and the obtained parameters no longer follow the expected linear behavior.

The use of a higher wave vector cutoff, and thus a smaller CG length $\mathrm{\Lambda }$, can mitigate this issue, but only marginally. In fact, there is another important feature that is not taken into account by this simple model, that is, the so-called field mixing due to the lack of particle–hole symmetry (29), which induces an asymmetry between the two phases at low $T$. Nevertheless the GL model we adopted can still give us some relevant information, as shown at the end of Results.

Computational Setup

We simulate an Argon fluid, described by the classical two-body Lennard–Jones potential ${\varphi }_{LJ}(r)=4ϵ[{(\sigma /r)}^{12}-{(\sigma /r)}^6]$ truncated and shifted at $R_c=2.5\sigma$:

$${\mathrm{\Phi }}_{LJ}(r)=\{\begin{array}{cc}{\varphi }_{LJ}(r)-{\varphi }_{LJ}(R_c)\hspace{1em}\hfill & r<R_c\hfill \\ 0\hspace{1em}\hfill & r\ge R_c.\hfill \end{array}$$ [16]

This simple system has been intensively studied (28–31) and exhibits in its phase diagram the needed second-order phase transition, at the liquid–vapor critical point. All of the physical quantities in this paper are expressed in terms of Lennard–Jones reduced units.

We perform canonical molecular dynamics simulations at a fixed average density equal to the critical one, ${\rho }_c=0.317$ (30). We are aware that in a finite-size system the critical density is not exactly ${\rho }_c$, but for our purposes we just need to be close to that value. The temperature $T$ is kept constant by the velocity-rescaling stochastic thermostat (32). The time step used is $0.002$, and typically we used ${10}^7$ steps for each run.

All of the simulations are performed with the molecular dynamics package Gromacs 5.0.4 (33), patched with a development version of the Plumed 2 (34) enhance sampling plugin, in which we implemented the VES method for our specific GL free-energy model.

The choice of $g_t$ and $a_t$, which define $p(𝐬)$in Eq. 15, was based on the amplitude of the fluctuations observed in the unbiased runs and on some trial-and-error simulations performed on small systems ($N=128,256$). The values thus obtained were then used as reference for the larger systems. The adopted values were between $0.05$ and $0.2$, and generally $g_t>a_t$.

Results

The Ginzburg–Landau model expects the parameter $a$ to have a linear temperature dependence close to the critical point, and thus

$$a(T)=a_c(T-T_c),$$ [17]

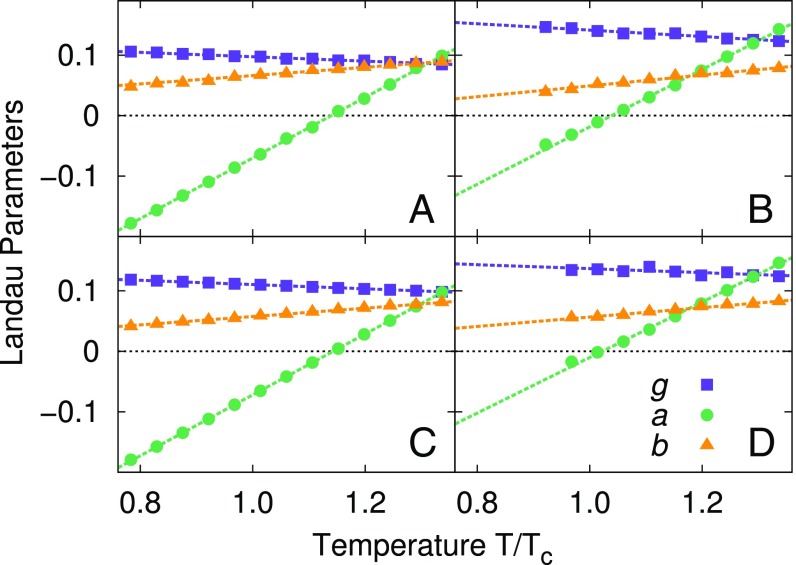
whereas the other two parameters should be constant, $g(T)=g_c$ and $b(T)=b_c$. We run multiple simulations varying both the size of the system and the cutoff order and consequently also the CG length $\mathrm{\Lambda }$. As noted at the end of Bias Potential and Target Distribution, depending on the system size and $\mathrm{\Lambda }$, convergence can become problematic at low temperatures. Nevertheless we can, somewhat conservatively, refer only to the region $T>0.95T_c$, where convergence is safely reached for all of the systems studied here. In this region our estimates are always in qualitative agreement with Landau’s ansatz, as can be seen in Fig. 2. The temperature dependence of the three parameters can be well fitted linearly, and all of the results obtained are provided in Table S2. Here we note only that the slope of $g(T)$ and $b(T)$ is roughly $10$ times smaller than the one of $a(T)$. This nonconstant behavior has been reported also in previous literature, for other Landau free-energy models (10).

Fig. 2.

(A–D) Landau’s parameters optimized for systems with (A) $N=128$, $n_M=3$ and thus $\mathrm{\Lambda }=4.267$; (B) $N=2,048$, $n_M=3$ and thus $\mathrm{\Lambda }=10.75$; (C) $N=2,048$, $n_M=19$ and thus $\mathrm{\Lambda }=4.272$; and (D) $N=8,192$, $n_M=3$ and thus $\mathrm{\Lambda }=17.07$. Data at temperatures where convergence was not clearly reachable are omitted. The linear fits are obtained using only data at $T>0.95T_c$, and error bars are smaller than the data points.

Table S2.

Landau parameters for different systems sizes $N$ and wave vector cutoff orders $n_M$

$N$	$n_M$	$\mathrm{\Lambda }$	$g_1$	$g_0$	$a_c$	$T_c^{\ast }$	$b_1$	$b_0$
128	3	4.27	−0.03(3)	0.13(3)	0.46(2)	1.23(6)	0.06(3)	−0.00(2)
256	3	5.38	−0.03(3)	0.15(1)	0.46(1)	1.19(4)	0.07(0)	−0.02(0)
256	7	3.52	−0.03(2)	0.13(0)	0.46(4)	1.29(7)	0.05(8)	0.00(3)
512	3	6.77	−0.04(4)	0.17(5)	0.45(8)	1.16(8)	0.07(3)	−0.02(4)
512	7	4.43	−0.03(4)	0.14(9)	0.46(9)	1.22(8)	0.06(2)	−0.00(9)
512	12	3.39	−0.03(3)	0.13(0)	0.46(0)	1.31(4)	0.05(9)	−0.00(0)
1,024	3	8.53	−0.03(5)	0.17(4)	0.44(4)	1.14(3)	0.05(9)	−0.00(9)
1,024	7	5.59	−0.04(1)	0.16(9)	0.46(6)	1.18(4)	0.06(8)	−0.02(2)
1,024	12	4.27	−0.03(4)	0.14(7)	0.46(8)	1.23(8)	0.06(1)	−0.00(8)
1,024	16	3.70	−0.03(5)	0.14(2)	0.46(8)	1.27(6)	0.06(1)	−0.00(3)
2,048	3	10.75	−0.04(8)	0.19(4)	0.43(7)	1.12(7)	0.08(2)	−0.04(0)
2,048	7	7.04	−0.03(3)	0.16(8)	0.45(2)	1.15(4)	0.07(1)	−0.03(1)
2,048	12	5.38	−0.04(0)	0.16(7)	0.46(7)	1.19(1)	0.06(3)	−0.01(6)
2,048	16	4.66	−0.03(3)	0.15(3)	0.46(3)	1.21(4)	0.06(7)	−0.01(8)
2,048	19	4.27	−0.03(2)	0.14(5)	0.46(4)	1.24(0)	0.06(3)	−0.01(1)
4,096	3	13.55	−0.01(8)	0.15(5)	0.42(9)	1.11(5)	0.06(8)	−0.01(8)
4,096	7	8.87	−0.03(4)	0.17(6)	0.44(3)	1.13(3)	0.06(9)	−0.03(1)
4,096	12	6.77	−0.03(3)	0.16(8)	0.45(4)	1.15(6)	0.07(2)	−0.03(4)
8,192	3	17.07	−0.03(0)	0.16(9)	0.42(3)	1.10(9)	0.07(1)	−0.02(1)
8,192	7	11.17	−0.02(4)	0.17(0)	0.43(1)	1.12(0)	0.07(1)	−0.03(3)

We recall that the coarse-grained length is $\Lambda =N^{1/3}/\left({\rho }_0^{1/3}\sqrt{n_M}\right)$ and that in the thermodynamic limit the critical temperature is T_c =1:08(5).

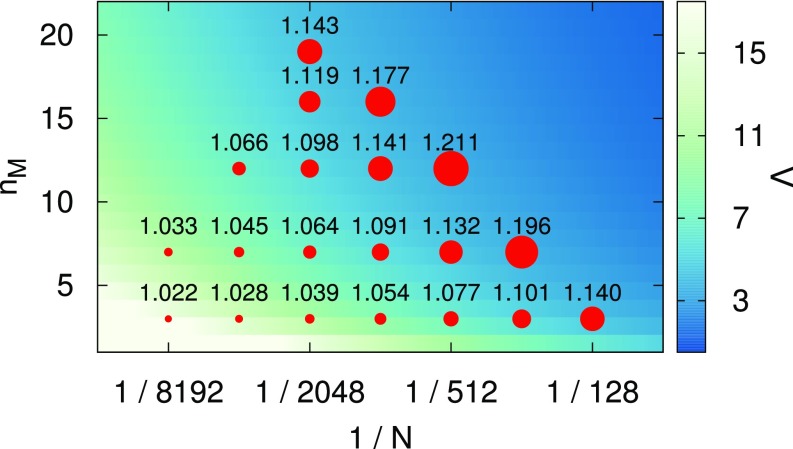
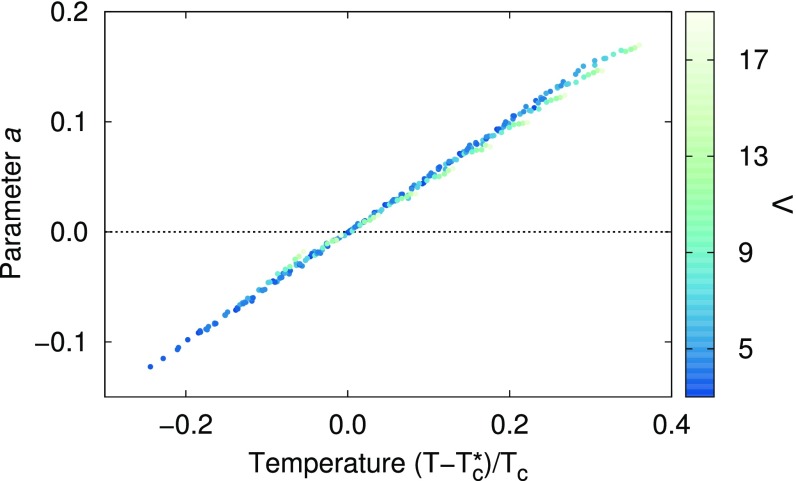
It is possible to define an effective critical temperature $T_c^{\ast }$ as the temperature at which the parameter $a(T)$ becomes zero. This is different from the critical temperature in the thermodynamic limit, $T_c=1.085\pm 0.005$ (30), due to finite-size effects. Contrary to the effective critical temperature that could be defined by looking at the specific heat, $T_c^{\ast }$ is always greater than $T_c$, as noted already in ref. 8. In Fig. 3 we show our estimate of $T_c^{\ast }/T_c$ as a function of both the system size $N$ and the wave vector cutoff order $n_M$. As expected, increasing the size at fixed cutoff, we have that $T_c^{\ast }$ approaches $T_c$. Maybe less intuitively, when we increase the number of wave vectors, $T_c^{\ast }$ moves away from $T_c$. What we observe is that $T_c^{\ast }$ is mainly linked to the coarse-graining length $\mathrm{\Lambda }$; in fact, we find that roughly $(T_c^{\ast }-T_c)\propto 1/\mathrm{\Lambda }$. Despite the great variations in the value of $T_c^{\ast }$, all our data on $a(T)$ can be collapsed into a single line when plotted as a function of $(T-T_c^{\ast })/T_c$ (Fig. 4). These are all empirical observations and do not necessarily imply rigorous scaling laws.

Fig. 3.

The effective critical temperature $T_c^{\ast }/T_c$ for different system sizes $N$ and wave vector cutoff orders $n_M$. The dimension of the points is proportional to $(T_c^{\ast }/T_c-1)$. The background colors are related to the coarse-graining length $\mathrm{\Lambda }\propto N^{1/3}/\sqrt{n_M}$, according to the scale on the right.

Fig. 4.

Parameter $a$, the one proportional to the quadratic term in Eq. 10, as a function of the rescaled temperature $(T-T_c^{\ast })/T_c$. The effective critical temperature $T_c^{\ast }$ is different for each system, as shown in Fig. 3. Only points with $T>0.95T_c$ are plotted.

Simulations from the Coarse-Grained Model

Having obtained a coarse-grained description, we can ask to what an extent the GL model can represent the microscopic properties of the system. To try to answer this question, we run Monte Carlo simulations, using as variables the Fourier components ${\psi }_{\overrightarrow{k}}$ and as Hamiltonian the GL free energy. We define the model at all temperatures by assuming that the parameters depend linearly on $T$. Despite the limitations of the GL model (end of Bias Potential and Target Distribution), we find that some of the properties of our system are well described for a wide range of temperatures.

The most remarkable one is maybe the description of the Binder cumulant (35, 36), a quantity often used to obtain a good estimate of the critical temperature $T_c$, from finite-size simulations. Using our notation, we can handily express the Binder cumulant as

$$U(T)=1-\frac{⟨I_4⟩}{3{⟨I_2⟩}^2},$$ [18]

where $⟨\cdot ⟩$ is the ensemble average at temperature $T$, and $I_2$ and $I_4$ are defined in Eqs. 12 and 13, respectively. The important property of the Binder cumulant is that $U(T_c)$ does not depend on the system size, and thus it is possible to evaluate $T_c$ by looking at the crossing point of the curves obtained with different $N$.

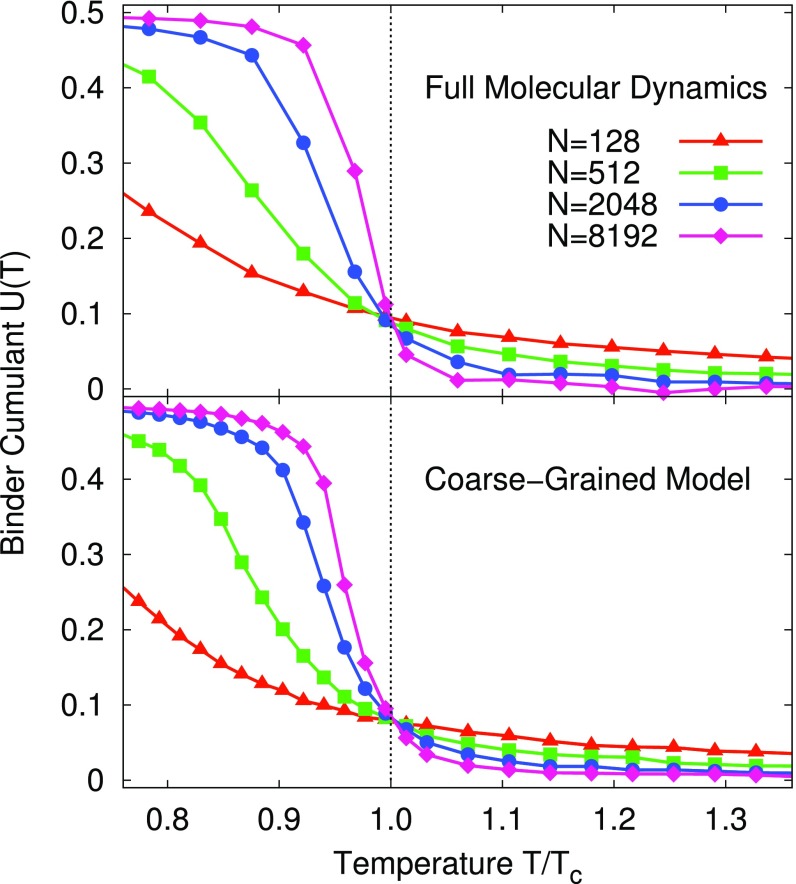
The behavior of $U(T)$ for different system sizes is reported in Fig. 5, obtained with unbiased molecular dynamics and Monte Carlo coarse-grained simulations. Remarkably the CG simulations well reproduce the $U(T)$ curve, even at $T<T_c$, and give an estimate of $T_C$ in good agreement with the literature (30). To calculate $I_2$ and $I_4$ for Fig. 5 we used a wave vector cutoff of order $n_M=3$, but it is important to note that the inclusion of higher-order wave vectors does not change the crossing point, even though the shape of the curves $U(T)$ may change. This reflects the fact that the critical behavior is dominated by long-wavelength fluctuations.

Fig. 5.

The Binder cumulant $U(T)$ defined in Eq. 18 obtained with full molecular dynamics simulations and with Monte Carlo simulations using the optimized GL free energy as a Hamiltonian. In both cases a wave vector cutoff of order $n_M=3$ was used, and thus for the CG simulations only $26$ independent variables were used for each system size. The interception of the curves gives an estimate of the critical temperature. We take as reference $T_c=1.085$ (30). Error bars are smaller than the data points, and lines are drawn only to guide the eyes.

Conclusions

In this paper we have shown that VES not only is a method for enhanced sampling, but also provides a formidable tool to approach coarse graining in a systematic and rigorous way. It combines the strength of relative entropy optimization methods with the intriguing ability to orient the sampling toward a desired statistical distribution.

In the present application we treated the case of a second-order phase transition, for which the well-established GL theory provided a good CG model, with a clear functional form for the free energy. In other fields of application careful consideration will have to be paid, and the structure of the CG model and the corresponding free energy might not be easily determinable. However, we can envisage several cases in which this might be possible. For instance, we could use as a CG model the classical density functional theory or models such as those introduced in refs. 3 and 4. Then VES provides a way to link rigorously and effectively the parameters of the coarse-graining model to the microscopic Hamiltonian.

Collective Variables

We report here explicitly the CVs used for our Lennard–Jones system. We can write the density of the system as a sum of delta functions centered in the atom’s positions ${\overrightarrow{R}}_j$:

$$\rho (\overrightarrow{r})=\sum _j^N\delta \left(\overrightarrow{r}-{\overrightarrow{R}}_j\right).$$ [S4]

This is a safe approximation, because the wave vector cutoff will then actually limit our study to distances greater than $\mathrm{\Lambda }$. Being the order parameter $\psi (\overrightarrow{r})=(\rho (\overrightarrow{r})-{\rho }_c)/{\rho }_0$, its Fourier components ${\psi }_{\overrightarrow{k}}$ are

$$\mathrm{Re}({\psi }_{\overrightarrow{k}})=\frac{1}{N}\sum _j^N\cos \left(\overrightarrow{k}\cdot {\overrightarrow{R}}_j\right),$$ [S5]

$$\mathrm{Im}({\psi }_{\overrightarrow{k}})=-\frac{1}{N}\sum _j^N\sin \left(\overrightarrow{k}\cdot {\overrightarrow{R}}_j\right),$$ [S6]

and it is now easy to note that ${\psi }_{\overrightarrow{k}}={\psi }_{-\overrightarrow{k}}^{\ast }$, which halves the number of independent Fourier components.

The number of independent CVs is directly related to the cutoff order $n_M$. For each independent Fourier component ${\psi }_{\overrightarrow{k}}$, we have two independent CVs, its real and imaginary parts. The number of CVs as a function of $n_M$ is reported in Table S1.

Landau Parameters

We report here the Landau parameters obtained with the variational enhanced sampling method, as described in the main text. The parameters in Table S2 are obtained with a linear fit of the optimized parameters at temperatures

$$T=\{1.05,1.10,1.15,1.20,1.25,1.30,1.35,1.40,1.45,1.50\}.$$ [S7]

The lowest temperature for the fit is chosen in such a way that a good convergence is ensured at any $T$ even for the bigger systems. Given Ginzburg–Landau free energy, Eq. S10, the fitting parameters are defined as follows:

$$g(T)=g_{1}T+g_0$$ [S8]

$$a(T)=a_c(T-T_c^{\ast })$$ [S9]

$$b(T)=b_{1}T+b_0.$$ [S10]

The errors in our estimate of the GL parameters arise from two sources: the statistical error coming from the stochastic optimization and the error provided by the linear fit. The statistical error is significantly smaller than the fit error.