Monostable superrepellent materials

Significance

Existence of monostable Cassie states is exhibited using simple pillars exposed to mercury and dual-length-scale structures exposed to water, respectively. Then, transitions from the Cassie state to the Wenzel state are repaired without energy input, which prevents the often-reported irreversible breakdowns of superhydrophobicity. Constructing a phase diagram where both the texture density and the surface chemistry are varied allows us to establish the conditions of monostability. Furthermore, the region in the phase diagram where monostable Cassie states are observed is found to be large enough to guide further design and engineering of robust superrepellent materials.

Abstract

Superrepellency is an extreme situation where liquids stay at the tops of rough surfaces, in the so-called Cassie state. Owing to the dramatic reduction of solid/liquid contact, such states lead to many applications, such as antifouling, droplet manipulation, hydrodynamic slip, and self-cleaning. However, superrepellency is often destroyed by impalement transitions triggered by environmental disturbances whereas inverse transitions are not observed without energy input. Here we show through controlled experiments the existence of a “monostable” region in the phase space of surface chemistry and roughness, where transitions from Cassie to (impaled) Wenzel states become spontaneously reversible. We establish the condition for observing monostability, which might guide further design and engineering of robust superrepellent materials.

Water repellency describes the ability of materials to repel water and make it flow with negligible friction and adhesion, compared with usual situations. It is achieved by combining chemical hydrophobicity with micro- and/or nanotextures (1, 2). Water meeting such materials remains at the textures’ tops, which generates a composite interface made of hydrophobic solid and air trapped inside the textures (Cassie state) (3). As a consequence, water hardly contacts these solids on which its dynamical behaviors are spectacular (4–7). Repellency also holds if the liquid has a higher surface tension than water (salty water, mercury); using special texture designs, it can even be extended to liquids with smaller surface tension (8), and/or to water at small scale (such as dew) (9, 10), so it was proposed (11) to call such materials “superhygrophobic,” from the Greek “hygros” meaning humid.

Repellent materials are classically found in nature, in particular at the surface of many plants and insects, two situations where the control of water is crucial for surviving (1, 12). It was reported that these natural surfaces often (yet not always) exhibit dual structures, with microbumps on the scale of 10–100 µm coated by nanostructures of typically 100 nm (1). This results in an amplification of static (13–17) and dynamical (18) repellency, because we can then expect the generation of composite solid/air interfaces at different scales––where we mean by amplification an improved nonwettability (13–15, 17) and a smaller adhesion (16, 18, 19), two factors that contribute to the liquid mobility.

This field of research has been very active for about 20 years, with theoretical, experimental, and computational viewpoints. Researchers discussed the surface energy of materials having different kinds of structures (20–23), various adhesion properties (24–26), diverse geometries of solid–liquid–vapor contact lines (27, 28), or flow interactions between the liquid and its substrate (29–32). In many studies, model hydrophobic textures (such as lines or pillars) were considered, and wetting was found to be usually “bistable”: Depending on the history of the system, two states can be observed (33–35). A drop gently deposited on the texture often is in the Cassie levitating state (33, 36), whereas after an impact it can get impaled in the so-called Wenzel state (37). Most generally, one of the states is metastable (33, 34, 38), with an energy barrier large enough to prevent spontaneous transition to the other state (39, 40). Metastability is beneficial for achieving relatively robust slippery Cassie states (1, 2, 32, 41–44), but detrimental in strongly pinned sticky Wenzel situations (33, 45). Hence, a key to optimize water-repellent materials and guarantee their promising technological applicability would be to suppress the energy barrier between Wenzel and Cassie states. In this context, it is worth exhibiting monostable Cassie states where even an accidental transition to the undesired Wenzel state, due to force fluctuations such as encountered in an impact (37) or to pressure applied on the liquid (16, 17, 33, 46–50), can be repaired owing to the absence of barrier between both states. Because reported Wenzel-to-Cassie (W2C) transitions generally involve either an external energy input (17, 49, 51–53) or a potential energy release (35, 54–56), monostable Cassie states might be seen as unreal (57), but we describe here such situations and criteria for achieving them. Our hope is that these findings will shed new light on our fundamental understanding of water repellency.

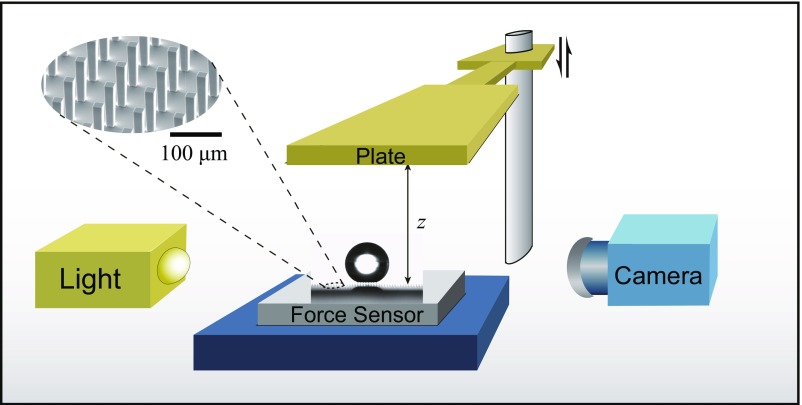
We probe Cassie and Wenzel configurations by pressing and releasing drops against hydrophobic textured substrates (Fig. 1), which we do with a superhydrophobic plate of very low adhesion (58, 59), allowing us to leave the bottom interface as free as possible: In the lifting stage, an adhesive plate would induce a depression in the liquid and trigger transitions between Wenzel and Cassie state (16). However, we show in SI Appendix that using a stickier, simply hydrophobic plate does not modify our conclusions. Rates of change of plate height are chosen to be in a quasi-static limit, that is, in situations where viscous forces are negligible compared with surface tension, so that contact angles are virtually not affected by motion.

Fig. 1.

Schematic of the experiment. A millimeter-size water drop is placed on hydrophobic pillars (side a = 19 μm, height h = 100 μm, spacing b = 80 μm, as shown in the inset), and pressed with a superhydrophobic plate, until inducing a transition from Cassie to Wenzel state. Then the plate motion is reversed and side views allow us to extract the drop profile and surface energy as a function of distance z. The force exerted by the liquid on its substrate is simultaneously measured with a sensitive force sensor.

The substrate is made of silicon and decorated by a square array of posts with side a = 19 µm, height h = 100 µm, and spacing b = 80 µm (Fig. 1). The corresponding surface fraction f = a²/(a+b)² occupied by the pillars and the roughness factor r = 1 + 4ah/(a+b)² are 0.04 and 1.8, respectively. At such scales and surface fraction, Cassie and Wenzel states can be distinguished from backlighted side views (36): A thin ray of light below the liquid is the signature of the Cassie state (Fig. 1). In addition, we place under the textured material a force sensor (Mettler Toledo, XA205), and we monitor the force (typically 1–10 mN, with a precision <0.1 mN) exerted by the drop as it is squeezed. We use two kinds of hygrophobic surface chemistry. (i) Silicon can be coated with OTS (octadecyl-trichlorosilane) molecules. The samples are first cleaned and oxygen-plasma-treated before being placed in a 0.4% vol/vol solution of OTS in hexadecane; samples are then washed with chloroform and ethanol, and dried with nitrogen (see more details in SI Appendix). Contact angles on OTS-treated flat materials were measured by moving drops of water or mercury at 50 µm/s. The respective advancing and receding contact angles deduced from side views are found to be θ_a = 113 ± 3° and θ_r = 91 ± 2° for water, and θ_a = 165 ± 2° and θ_r = 137 ± 4° for mercury (see SI Appendix for details). (ii) To make the substrates more water repellent, they can be coated with silanized silica nanobeads with diameter 30 nm dispersed in isopropanol (Glaco, Soft99). The treatment consists of drawing a clean sample out of the dispersion, letting the solvent evaporate, and consolidating the coating at 150 °C for 15 min (60). To minimize its adhesion to liquids, the glass plate used to squeeze the drops is similarly Glaco-treated, which provides water contact angles θ_a = 167 ± 2° and θ_r = 159 ± 2°.

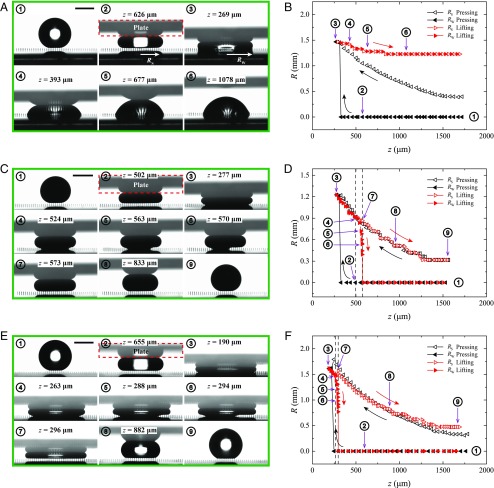
We compare in Fig. 2 the common case of an irreversible Cassie-to-Wenzel (C2W) transition (Fig. 2 A and B) to the more exceptional situation of monostable Cassie states (Fig. 2 C–F). In the first series of experiments (Fig. 2 A and B), pillars are OTS-coated and the advancing angle of water (visible in the first picture of Fig. 2A) is 161 ± 3°, much larger than the 113° observed on flat treated silicon, an increase arising from the Cassie state. Then, the drop (with radius R₀ = 0.9 mm, smaller than the capillary length) is pressed by the upper plate. As the gap distance z quasi-statically decreases (dz/dt = −50 µm/s), the drop undergoes a C2W transition (33) (third picture in Fig. 2A), as also seen in Fig. 2B where the impaled Wenzel radius R_W abruptly increases from 0 to 1.45 mm at z = 313 µm. Liquid impales where it sits, so that the apparent radius of contact R_S with the substrate is continuous at the transition. After further pressing (down to z = 269 µm), motion of the upper plate is reversed (red data in Fig. 2B) at a lower speed, dz/dt = 20 µm/s. However, the drop remains pinned (R_S = R_W), so that the radius R_S hardly changes as the two solid surfaces are separated. The final (receding) angle is acute, a consequence of the strong pinning in the Wenzel state (33).

Fig. 2.

States and contact radii of nonwetting drops squeezed against a microtextured surface. (A) Snapshots for water pressed against silicon pillars treated with OTS (see also Movie S1). A Cassie drop with radius R₀ = 0.9 mm (circle 1) is squeezed (circle 2) until it reaches the Wenzel state (circle 3). Upon lifting (circles 4 and 5), the drop remains strongly pinned in this state (circle 6). (Scale bar, 1 mm.) (B) Liquid footprint as a function of the plate/substrate gap z. The apparent radius of liquid/substrate contact is denoted as R_S (empty triangles), and the Wenzel contact as R_W (full triangles). Symbols are black and left-pointed in the pressing stage, and they are red and right-pointed in the lifting stage. Numbers correspond to A. (C) Same experiment with mercury (R₀ = 0.78 mm) instead of water (see also Movie S2). The initial Cassie drop (circle 1) is pressed (circle 2) so as to reach the Wenzel state in the pillars (circle 3). Upon lifting, the drop first shrinks (circle 4) before liquid dewets the microposts from the edge (circles 5 and 6); this mixed state eventually leads to a compressed Cassie state (circle 7) conserved over lifting (circles 8 and 9) (D) Drop radii R_W and R_S as functions of z. Vertical dashed lines show the boundaries of the W2C transition and numbers refer to C. (E) Same experiment after treating micropillars with a Glaco nanotexture and pressing water (see also Movie S3). The succession of events is similar to that in C. (F) Drop radii R_W and R_S as functions of z. Vertical dashed lines indicate the boundaries of the W2C transition and numbers refer to E.

The sequence of events is markedly different when the receding angle on the material is significantly higher, that is, on a more hygrophobic material. This situation is generated (i) either by considering mercury instead of water (Fig. 2 C and D), with corresponding angles on OTS-coated flat surfaces of θ_a = 165 ± 2° and θ_r = 137 ± 4°, or (ii) by adding on the pillars a nanotexture (Glaco treatment, described above and in SI Appendix) and using water (Fig. 2 E and F). Contact angles on Glaco-coated flat materials are θ_a = 164 ± 2° and θ_r = 150 ± 3°, comparable to the previous case, and water then is in a nano-Cassie state, even when pressed.

Results obtained in the latter two situations are similar. The C2W transition in the pillars is observed for a gap z comparable to that in the first experiment, but the lifting stage is very different. On the one hand, the curve for the contact radius R_S (empty triangular symbols in Fig. 2 D and F) is nearly reversible, so that the final state is very close to the initial one; the only difference at large z in Fig. 2C arises from the fact that the initial angle corresponds to an advancing drop, whereas the final one is obtained after the drop receded. This difference is hardly visible in Fig. 2C, where we pass from 168 ± 4° to 164 ± 1°, but it is clearer in Fig. 2E, where the angle varies from 163 ± 4° to 146 ± 1°. On the other hand, whereas the C2W transition is critical in both cases, the W2C transition is continuous. Its existence and location depend on the receding angle: the larger θ_r (water on Glaco), the smaller the gap z at which a compressed Cassie state appears; in addition, spontaneous W2C transitions with water are only observed if a substructure is added to the pillars (leading to smaller adhesion), which justifies the common existence of such dual-length-scale structures in natural systems.

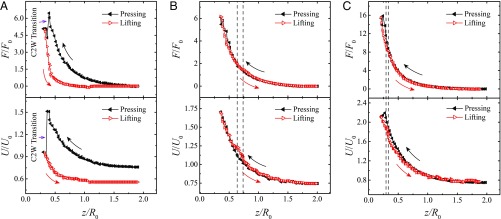
A squeezed liquid exerts on its substrate a force denoted as F. As sketched in Fig. 1, F can be measured with a force sensor at a frequency of 2 Hz. The corresponding results are displayed in Fig. 3 for the three situations of Fig. 2. Data are completed by evaluating in each case the surface energy of the drop U = (γ _SL – γ _SV)Σ_SL + γ Σ_LV, obtained after extracting from side views the surface areas Σ_SL and Σ_LV of the solid/liquid and liquid/vapor interfaces (on both plates), respectively, and using Young’s formula: γ _SL – γ _SV = – γ cosθ_E, where we take for the equilibrium angle θ_E the mean angle (θ_a + θ_r)/2 measured on each surface.

Fig. 3.

Force and energy for the three experiments reported in Fig. 2. The force F exerted by the liquid on its substrate is measured with a force sensor and it is plotted as a function of the gap z normalized by the drop radius R₀. The interfacial energy U of the deformed drop is deduced from image analysis and it is also plotted as a function of z/R₀. Force and energy are normalized by 2πR₀γ and 4πR₀²γ, respectively. Data are full and black in the pressing stage, and empty and red in the lifting stage. (A) Force and energy for water on OTS-coated pillars, corresponding to the experiments in Fig. 2 A and B. (B) Force and energy for mercury on OTS-coated pillars (experiments in Fig. 2 C and D). Vertical dashed lines mark the boundaries of the mixed WC state observed during the W2C transition. (C) Force and energy for water on Glaco-coated pillars (experiments in Fig. 2 E and F).

Data in Fig. 3 quantitatively confirm our first observations. Instead of (classical) irreversible C2W transitions with a marked hysteresis loop (Fig. 3A), we observe quasi-reversible trajectories on repellent (i.e., higher contact angle), weakly adhesive substrates (Fig. 3B and C). For all curves, the pressing stages are similar. Interfacial energy then increases by ΔU ∼ 0.5 µJ, an amplitude comparable to the typical scale of surface energy U₀ = 4πR₀²γ ∼ 0.7 µJ for a water drop with radius R₀ = 0.9 mm. The amplitude is larger (ΔU ∼ 3 µJ) for mercury, of higher surface tension. However, plots become different at the C2W transition: in case A, force and energy both decrease in a discontinuous fashion, which highlights the existence of a large energy barrier (∼U₀) between the two states, as generally expected (33, 35). This behavior is in sharp contrast with what can be observed on substrates with larger contact angles (Fig. 3 B and C): both F(z) and U(z), respectively scaled by F₀ = 2πR₀γ and U₀ = 4πR₀²γ, become continuous at the W2C and C2W transitions; in addition, pressing and lifting stages are nearly superimposed. Later, the total energy monotonously decreases during the lifting process as the liquid undergoes a transition from the pressed Wenzel state to the Cassie state. The energy landscape shows that the Cassie state here is monostable, rather than metastable as it is on usual superhydrophobic surfaces (33, 39, 40, 52). We show in SI Appendix that changing the pillar spacing b of the substrate to 100 μm or using a stickier pressing plate do not modify our conclusions (see also Movies S4–S8).

To get a criterion of monostability, we first consider the case of an “ideal” material, which when flat does not provide any pinning and thus can be characterized by a unique (Young) contact angle θ_E. Because (– cosθ_E) can be viewed as a dimensionless surface energy, a necessary condition for observing a spontaneous W2C transition is that the (negative) cosine of the Wenzel angle, rcosθ_E, is smaller than the (negative) cosine of the Cassie angle, that is, − 1 + f + f cosθ_E. This yields (1 – f)/(r – f) < – cosθ_E (33), where f and r are the surface fraction and roughness factor, respectively. However, on a “real” material, even flat, the movement of the contact line is accompanied by dissipation due to pinning and relaxation of the line. Because we discuss here the dewetting process in a W2C transition, we propose to consider the receding contact angle (that includes this dissipation) to build a criterion for monostable Cassie states. This condition for a spontaneous W2C transition can be written:

$$(1-f)/(r-f)<-\cos {\theta }_{\text{r}}.$$ [1]

Because a receding angle θ_r is smaller than the equilibrium angle θ_E, Eq. 1 is more demanding than that on an ideal surface, which is a first reason why spontaneous W2C transitions are so rarely observed. This criterion is increasingly challenging when hydrophobicity gets weaker (smaller θ_r), which makes it more difficult to dislodge a drop from the Wenzel state (40). For water, a typical receding angle on (flat) hydrophobic materials is 100°; because droplet mobility is obtained for a surface fraction f of order 0.1, Eq. 1 implies that spontaneous W2C transitions should only occur if the pillar aspect ratio h/a is larger than 11. This is not only difficult to produce, it is generally irrelevant in natural systems where such slender structures are flexible, which leads to different physics (61). Hence is the necessity of having a subtexture, which induces a nano-Cassie state and much higher receding angles (17), making criterion 1 much easier to satisfy: for θ_r = 150°, it becomes h/a < 0.4––a condition always satisfied in our experiments.

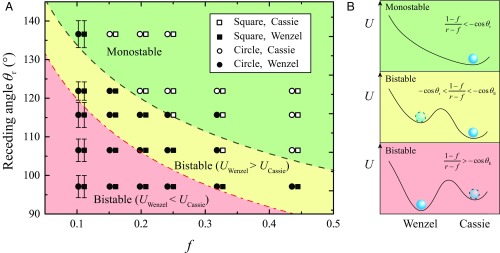
Criterion 1 was tested by varying both θ_r and f. We used two families of silicon pillars (square and circular) with side a =100 μm, height h = 100 μm, and variable mutual distance b, allowing us to vary f from 0.1 to 0.44. Then Eq. 1 can be explicitly expressed as a function of the sole variable f, because r(f) is a known function of f only. To tune θ_r in a wide range, we used mercury as a liquid and five different surface treatments (oxygen plasma, air plasma, air plasma with aging, no treatment, and OTS), allowing us to vary the receding angle in quite a continuous fashion, from 97° to 137° (see SI Appendix for details). A copper plate nanostructured with CuO (62) with negligible angle hysteresis (63) was used for pressing and releasing the drops. We conducted experiments similar to those shown in Fig. 2, which allows us to determine whether the drop is monostable or bistable––the latter term being the usual case of a drop remaining in the Wenzel state whereas thermodynamics favors a Cassie state (that is, metastable Wenzel state), or vice versa (metastable Cassie state).

Results are displayed in Fig. 4A, where empty and full dots, respectively, stand for the observation of monostable and bistable states during cycles of loading and discharge. At least five experiments were done for each data point, whose symbol shape refers to the pillar section (square or circular). For a given surface, at fixed f, a monostable Cassie state requires large receding angles. Hence, the energy barrier usually encountered in the W2C transition can be circumvented using highly repellent materials. Conversely, at fixed surface chemistry, a monostable Cassie state can be obtained by increasing the surface fraction, so that the Wenzel state becomes of high surface energy. Even at large surface fraction, the drop can leave the Wenzel state, despite its strong (potential) anchoring in the dense network of pillars. We compare the observations with criterion 1 drawn with a black dashed line, and indicate in green the expected region of monostability. Most data nicely agree with this criterion. Considering the Young angle θ_E rather than θ_r (red dot-dashed line in Fig. 4A) provides a much less convincing frontier between the two behaviors. However, we plotted this second line because it separates metastable Wenzel states (in yellow) from metastable Cassie states (in red), as sketched in Fig. 4B, which shows the three possible energy diagrams with the same color code.

Fig. 4.

(A) Experimental observation of monostable (open dots) or bistable (solid dots) Cassie states. The phase space decouples surface chemistry (expressed by θ_r) from texture (expressed by the surface fraction f). Silicon posts are either square (squares) or circular (circles), with height h =100 μm and side (or diameter) a = 100 μm. The surface fraction f is varied by changing the post separation b. The receding angle is tuned by changing the treatment applied to the material, and averaged over five measurements; error bars indicate the SD of data. The dashed black line is Eq. 1, found to separate quite nicely the green region of monostability from the regions of bistability. The red dashed line is drawn by replacing in Eq. 1 the receding angle by the equilibrium contact angle. Background colors correspond to the respective energy diagrams drawn in B.

Criterion 1 is a necessary condition for monostability but it might in some cases not be sufficient. It considers pinning on the hydrophobic material but not on the pillar edges, which can also block a W2C transition. In our scenario, liquid in the Wenzel state dewets the substrate from the side, which allows it to gradually lift to the Cassie state, as clearly observed in Fig. 2 C and E where pillar edges do not prevent dewetting––a consequence of the high values of contact angles in these two experiments. When contact angles approach 90°, pinning on textures may impede the W2C transition even if Eq. 1 is obeyed. This extra condition of dewetting depends on the exact shape of the pillars. It can be seen as a local condition whereas Eq. 1 is a more global one. In SI Appendix, we simulate pinning on pillars similar to the ones used in this study, and we find that this additional barrier is overcome when the contact angle is large enough (typically above 105°), as it is in our experiments in Fig. 4.

We proposed here a method to probe C2W and W2C transitions that consists of squeezing and releasing a drop between a textured surface and a nonadhesive plate. Direct observations coupled to measurements of the corresponding force and energy of the drop allow us to show the existence of monostable Cassie states and to exhibit a region of significant size in the phase diagram of the textured material (Fig. 4A). Then, C2W transitions induced by pressure, as can happen by pressing on drops (16, 33), by impact (37), or underwater (47–49), are reversible. Monostability was found to be mainly triggered by a combination of chemical hydrophobicity and minimized pinning, and obtained either by considering water on a doubly textured surface [so that the Wenzel state in the larger texture is accompanied by a nano-Cassie state in the smaller one (17)], or mercury (of higher cohesion) on a simply textured surface. Our findings might contribute to understand why dual-length-scale structures are often observed in natural systems (1, 12): the absence of an irreversible trapping of water inside smaller textures provides a surface that remains hydrophobic and slippery enough to recover from the penetration of water in larger textures, as can occur under rains. Such nano-Cassie states are a consequence of the small feature size, and can further be favored by water density fluctuations, as recently shown by molecular simulations (64). However, they are not necessary if the degree of nonwetting is high enough, as shown here with mercury on single textures, emphasizing the importance of surface chemistry in such processes.