Experimental comparison of two quantum computing architectures

Significance

Quantum computers are an emerging technology promising to be vastly more powerful at solving certain problems than any conventional computer. These devices are now moving out of the laboratory and becoming generally programmable. This allows identical quantum tasks or algorithms to be implemented on radically different technologies to inform further development and scaling. We run a series of algorithms on the two leading platforms: trapped atomic ions and superconducting circuits. Whereas the superconducting system offers faster gate clock speeds and a solid-state platform, the ion-trap system features superior qubits and reconfigurable connections. The performance of these systems is seen to reflect the topology of connections in the base hardware, supporting the idea that quantum computer applications and hardware should be codesigned.

Abstract

We run a selection of algorithms on two state-of-the-art 5-qubit quantum computers that are based on different technology platforms. One is a publicly accessible superconducting transmon device (www.research.ibm.com/ibm-q) with limited connectivity, and the other is a fully connected trapped-ion system. Even though the two systems have different native quantum interactions, both can be programed in a way that is blind to the underlying hardware, thus allowing a comparison of identical quantum algorithms between different physical systems. We show that quantum algorithms and circuits that use more connectivity clearly benefit from a better-connected system of qubits. Although the quantum systems here are not yet large enough to eclipse classical computers, this experiment exposes critical factors of scaling quantum computers, such as qubit connectivity and gate expressivity. In addition, the results suggest that codesigning particular quantum applications with the hardware itself will be paramount in successfully using quantum computers in the future.

Inspired by the vast computing power a universal quantum computer could offer, several candidate systems are being explored. They have allowed experimental demonstrations of quantum gates, operations, and algorithms of ever-increasing sophistication. Recently, two architectures, superconducting transmon qubits (1–5) and trapped ions (6, 7), have reached a new level of maturity. They have become fully programmable multiqubit machines that provide the user with the flexibility to implement arbitrary quantum circuits from a high-level interface. This makes it possible for the first time to test quantum computers irrespective of their particular physical implementation.

Whereas the quantum computers considered here are still small scale and their capabilities do not currently reach beyond small demonstration algorithms, this line of inquiry can still provide useful insights into the performance of existing systems and the role of architecture in quantum computer design. These will be crucial for the realization of more advanced future incarnations of the present technologies.

The standard abstract model of quantum computation assumes that interactions between arbitrary pairs of qubits are available. However, physical architectures will in general have certain constraints on qubit connectivity, such as nearest-neighbor couplings only. These restrictions do not in principle limit the ability to perform arbitrary computations, because swap operations may be used to effect gates between arbitrary qubits using the connections available. For a general circuit, reducing a fully connected system to the more sparse star-shaped or linear nearest-neighbor connectivity requires an increase in the number of gates of $O(n)$, where $n$ is the number of qubits (8). How much overhead is incurred in practice depends on the connections used in a particular circuit and how efficiently they can be matched to the physical qubit-to-qubit interaction graph.

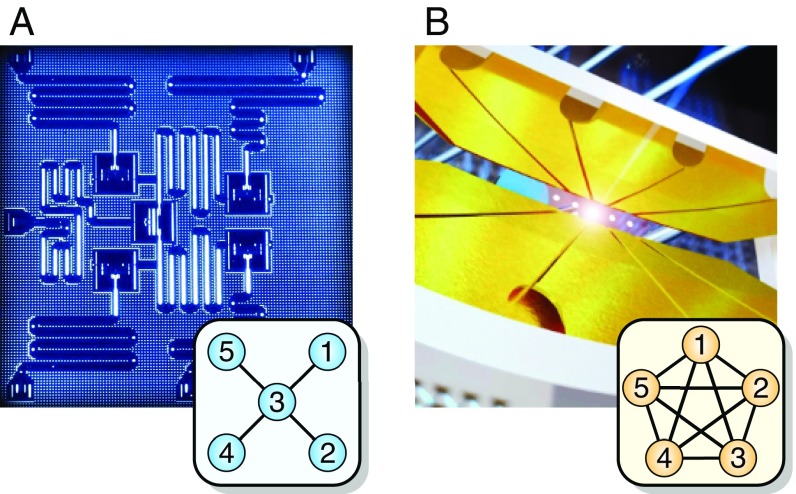
In this article, we make use of the public access recently granted by IBM to a $5$-qubit superconducting device (illustrated in Fig. 1A) via their “Quantum Experience” cloud service (www.research.ibm.com/ibm-q). This allows us to repeat algorithms that we perform in our own ion-trap experiment on an independent quantum computer of identical size and comparable capability but with a different physical implementation at its core.

Fig. 1.

Graphic representations of the two systems. (A) the superconducting qubits connected by microwave resonators (credit: IBM Research). (B) The linear chain of trapped ions connected by laser-mediated interactions. (A and B, Insets) Qubit connectivity graphs: (A) star shaped and (B) fully connected.

Physical Systems

The ion-trap system consists of five ¹⁷¹Yb⁺ ions that are confined in a linear Paul trap and laser cooled close to their motional ground state (Fig. 1B) (6). The qubits are magnetic-field–insensitive pairs of states in the hyperfine-split ${}^{2}S_{1/2}$ ground level of each atom, which gives a qubit frequency of $12.642821\text{GHz}$. All control and measurement are performed optically. State preparation and readout are accomplished by optical pumping and state-dependent fluorescence detection (9). Qubit operations are realized via pairs of Raman beams, derived from a single 355-nm mode-locked laser. These optical controllers consist of an array of individual addressing beams and a counterpropagating global beam that illuminates the entire chain (6). Single-qubit rotations are driven by a Raman beat note of defined amplitude, phase, and duration resonant with the qubit frequency. Two-qubit operations are produced by applying Raman beams to a pair of ions, with beat-note frequencies near the motional sidebands. This creates an effective XX–Ising interaction between the spins mediated by all modes of motion (10–12). We use a pulse-shaping scheme to ensure spin and motion are disentangled at the end of the operation (13, 14). Because all ions partake in the collective motion of the chain, gates between any pair can be invoked in this way (Fig. 1B, Inset). The addressing during operations and the distinction between qubits during readout are both achieved by spatially resolving the ions. The fidelities for single- and 2-qubit gates are typically $99.1(5)$% and $97(1)\%$, respectively. The single-qubit readout fidelity is $99.7(1)\%$ for state $|0⟩$ and $99.1(1)\%$ for state $|1⟩$. The latter is lower because off-resonant excitation during readout predominantly causes $|1⟩\to |0⟩$ pumping. The average readout fidelity for an entire $5$-qubit state is $95.7(1)\%$. This is lower than one would expect from the average single-qubit readout fidelity, because there is crosstalk that leads to $|0⟩\to |1⟩$ errors on adjacent channels. Typical gate times are $20\mu$s for single-cubit and $250\mu$s for 2-qubit gates. Spin depolarization is negligible for hyperfine ground-level qubits ($T_1\sim \mathrm{\infty }$). The spin-dephasing time ($T_2^{\ast }$) is $\sim 0.5$ s in the current setup and can be easily extended by suppressing magnetic-field noise.

In analogy to atoms given by nature, the man-made superconducting circuits in the IBM quantum computer can be thought of as “artificial atoms” (16). They are transmon qubits (17) or superconducting islands connected by Josephson junctions and shunt capacitors that provide superpositions of charge states that are insensitive to charge fluctuations. The device used here has a range of qubit frequencies between $5$ GHz and $5.4$ GHz (www.research.ibm.com/ibm-q). The qubits are connected to each other and the classical control system by microwave resonators. State preparation (18) and readout, as well as single- (19) and 2-qubit gates (20), are achieved by applying tailored microwave signals to this network and measuring the response. Qubits are resolved in the frequency domain during addressing and readout. In the Quantum Experience hardware, the qubits are connected in a star-shaped pattern that provides four 2-qubit interactions (Fig. 1A, Inset), which are controlled-NOT (CNOT) gates targeting the central qubit. Single-qubit readout fidelities are typically $\sim 96\%$ (www.research.ibm.com/ibm-q), and the average readout fidelity for an arbitrary $5$-qubit state is $\sim 80\%$ (www.research.ibm.com/ibm-q). Typical gate fidelities are $99.7\%$ and $96.5\%$ for single- and 2-qubit gates, respectively. Typical gate times are $130$ ns for single-qubit and 250–450 ns for 2-qubit gates, whereas coherence times are $\sim 60\mu$s for both depolarization ($T_1$) and spin dephasing ($T_2$). The publicly accessible system runs autonomously, not requiring any human intervention over many weeks (www.research.ibm.com/ibm-q). This level of reliability may come at a cost due to drifts between periodic calibrations. Higher connectivity can in general be achieved by coupling three to four transmons to one resonator, limited by spectral resolution. The present layout could be modified to provide connections from qubit $1$ to $5$ and from qubit $2$ to $4$ (www.research.ibm.com/ibm-q). Furthermore, other superconducting architectures involving multimode resonators (3) can offer higher connectivity.

On these two machines, we compare a selection of composite gates and algorithms that represent a variety of circuit connectivities. In each case, we map the algorithms to the device by breaking them down into circuits made up of gates native to the specific hardware. We rely on an optimization protocol (21) to accomplish this task for the trapped ions and CNOT $+$ T/Z^a algebra (22) with further manual optimization to compose the experiments for the IBM machine (23). The available gate set for the ion-trap system consists of the 2-qubit XX gate, as well as arbitrary single-qubit ${\text{R}}_{\alpha }^{\theta }$ gate rotations by an angle $\theta$ about any axis (given by $\alpha$) on the equator of the Bloch sphere. We call this the R/XX library. The IBM system makes available the family of gates [X, Y, Z, H, S, CNOT, and T (15)], known as the Clifford $+$ T library. Because each gate is subject to errors, the circuits are optimized to minimize the number of operations used. The resulting gate numbers are optimal for 2-qubit gates and either optimal or close to optimal for single-qubit gates. The total number of single- and 2-qubit gates for each algorithm is shown in Table 1. The R/XX library offers a better overall expressive power. However, we note that the Clifford $+$T library was likely chosen for didactic reasons and is not native to superconducting systems, which do in principle offer continuous parameters for single- and 2-qubit gates.

Table 1.

Single- and 2-qubit gate counts for the circuits on the superconducting (star-shaped) and the ion-trap (fully connected) system after mapping to the respective hardware using the respective gate libraries

Connectivity	Star		LNN		Full
Hardware	Superconductor		Superconductor		Ion Trap
Gate type	1-qubit	2-qubit	1-qubit	2-qubit	1-qubit	2-qubit
Margolus	20	3	20	3	11	3
Toffoli	17	10	9	10	9	5
Bernstein–Vazirani	10	0–4	10	0–10	14–26	0–4
Hidden shift	28–34	10	20–26	4	42–50	4
QFT-3	42	19	11	7	8	3
QFT-5	*	*	35	28	22	10

For comparison, the gate counts for a linear nearest-neighbor (LNN) architecture as implemented in ref. 1 are included. We also note the gate count for the quantum Fourier transform (QFT) for 3 and 5 qubits. The latter was implemented in ref. 6, using a sequence of modular gates that was not optimized for gate count. The QFT-5 cannot be implemented exactly using the current IBM gate library.

^*If we assume Z^a operations are possible, the counts shown are 47 for singlecubitand 29 for 2-qubit gates.

In addition to the two systems considered here, Table 1 also gives the numbers for an LNN connectivity architecture as used, e.g., in superconducting qubits (1) as well as semiconductor gated quantum dots (24). The numbers in Table 1 show that the 2-qubit gate count strongly depends on the matching between the circuit and the qubit connectivity graph. The LNN architecture is as efficient as the fully connected system for the hidden shift algorithm, whereas the star-shaped system incurs overheads; the reverse is true for the Bernstein–Vazirani algorithm (Fig. 2).

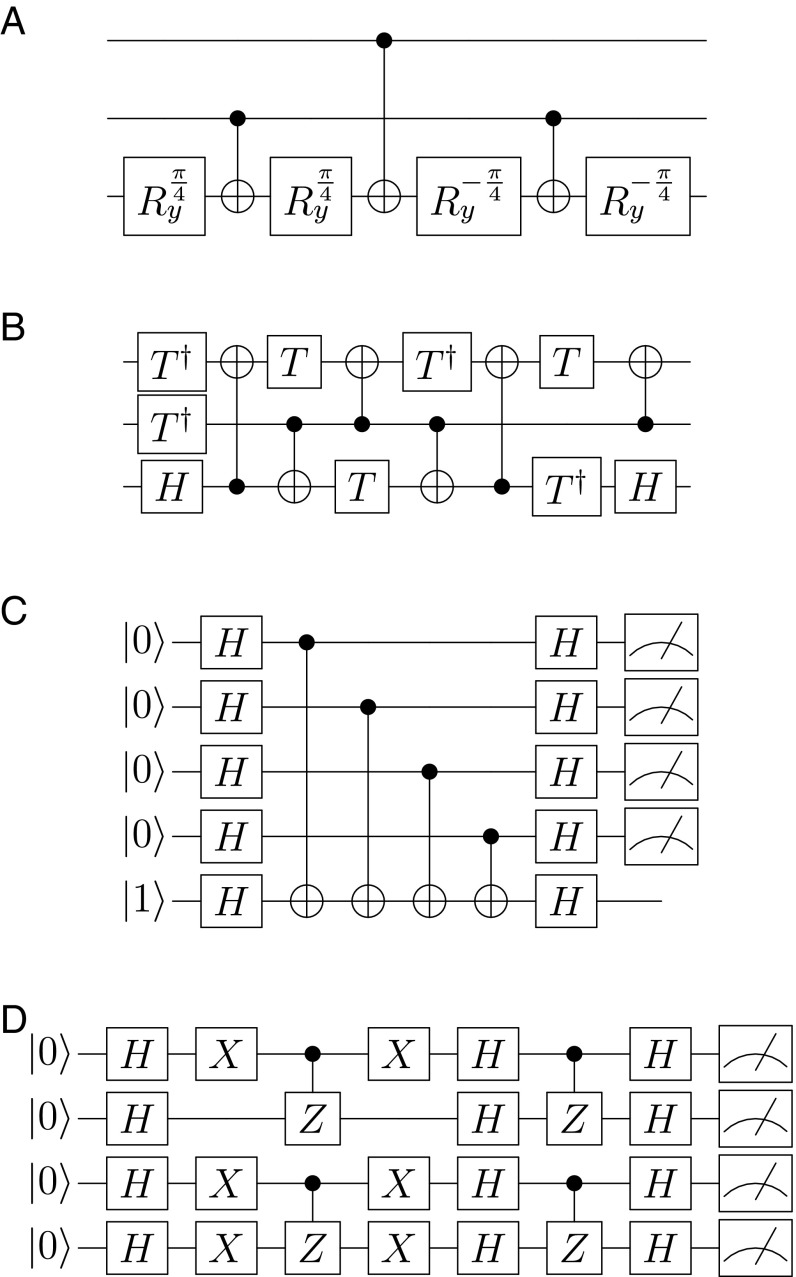
Fig. 2.

High-level circuits of the implemented example computations (gates defined in ref. 15). (A–D) Margolus gate (A), Toffoli gate (B), Bernstein–Vazirani (C), and hidden shift (D). The Bernstein–Vazirani algorithm is shown for the oracle $c=(1111)$, where all CNOTs are present. The hidden shift circuit is shown for the shift pattern $s=(1011)$, where X operations are present on qubits $1$, $3$, and $4$.

Algorithms

Margolus and Toffoli Gates.

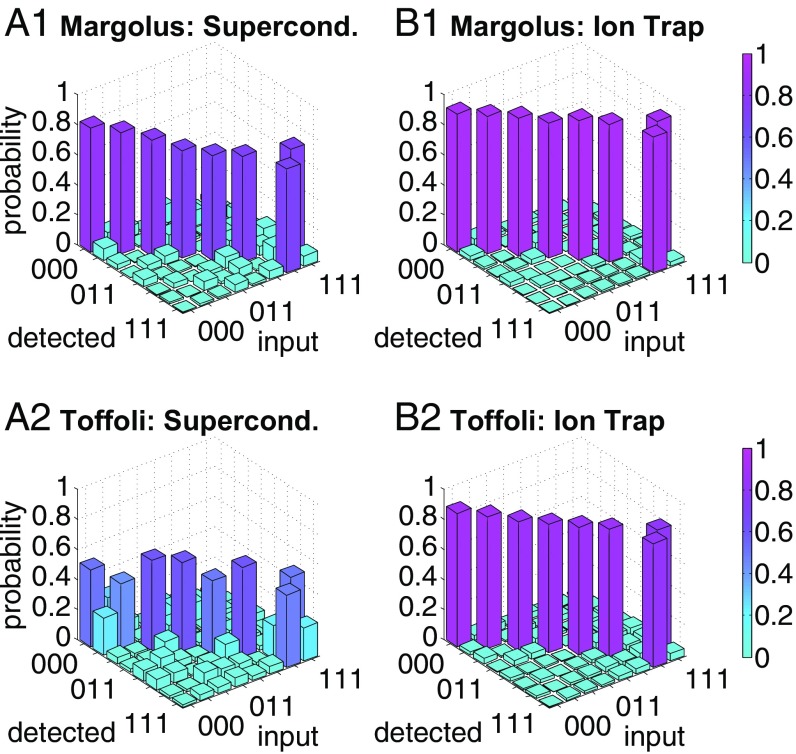
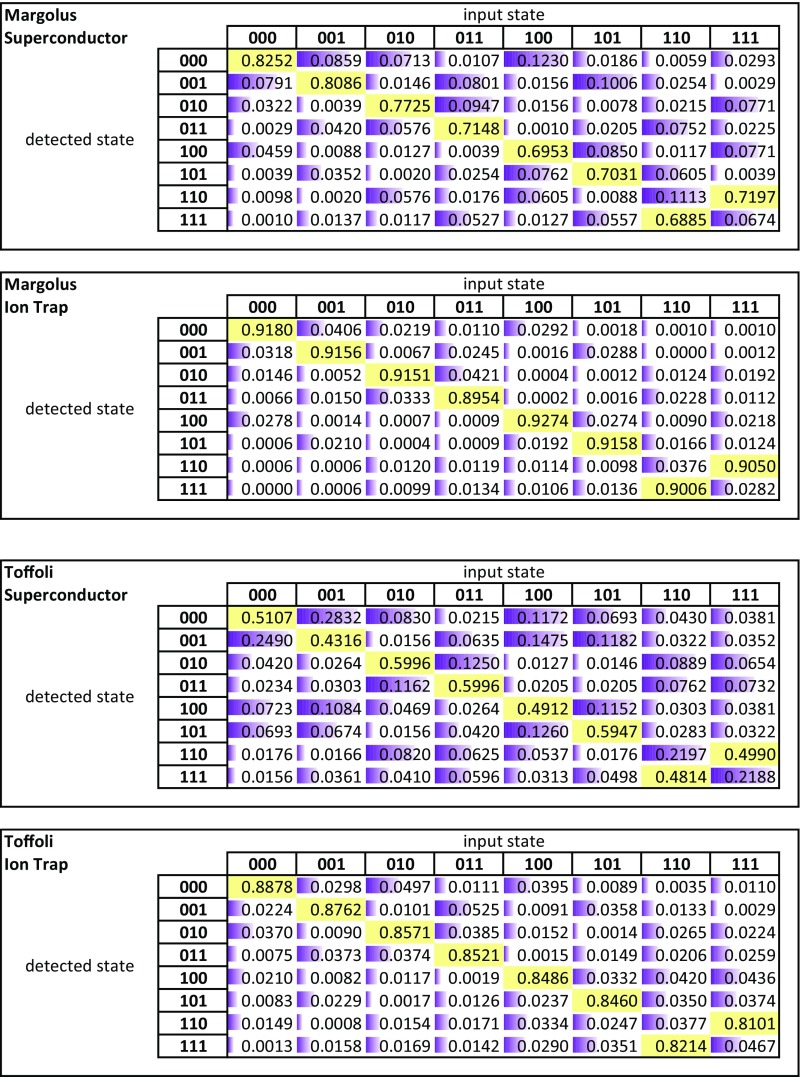
The Toffoli gate is a $3$-qubit controlled-controlled–NOT gate that requires six CNOT gates (25, 26). It is possible to implement the Toffoli gate with five entangling gates if the square root of the CNOT operation is available (15), which is the case with the trapped-ion XX gate. The Margolus gate is a simplified version of the Toffoli operation, which introduces an additional phase on the state corresponding to $|100⟩$. It can be realized with just $3$ CNOT gates (27, 28). The circuits are shown in Fig. 2 A and B. Note that for the Margolus gate, all entangling operations connect to the same qubit, which means that this circuit can be realized efficiently with star-shaped qubit connectivity. The systems perform this circuit at success probability $74.1(7)\%$ for superconductors and $90.1(2)\%$ for ions (Fig. 3 A1 and B1).

Fig. 3.

Margolus gate results from the star-shaped superconductor (A1) and the fully connected ion trap system (B1). The fidelities are $74.1(7)$% and $90.1(2)\%$, respectively. The full Toffoli gate results give success probabilities of $52.6(8)\%$ for the superconducting (A2) and $85.0(2)\%$ for the ion-trap (B2) system. The axes represent states as $3$-bit binary numbers. For each input state, the probabilities of detecting each state are shown.

The full Toffoli circuit uses the same 3 qubits as the Margolus implementation so that preparation and measurement errors remain the same. The optimized circuit for the fully connected ion-trap system contains five 2-qubit gates and the additional operations lower the fidelity to $85.0(2)\%$ (Fig. 3B2). For the star-shaped system, an additional seven 2-qubit gates are needed to effect the swap operations necessary to go from the Margolus to the full Toffoli gate. This leads to a reduced success rate of $52.6(8)\%$ for the superconducting system (Fig. 3A2). Note that the transformation $|a,b,c⟩\to |c\oplus ab,b,a⟩$ may be obtained with the Clifford $+$ T library on a star-shaped graph with the provably minimal number of seven CNOT gates. We do not consider such input-to-output mappings of the composite gates in this work. However, we always choose the most favorable input-to-output mapping for the IBM star and LNN architectures when executing entire quantum algorithms, which is merely a classical swap between physically measured signals.

Bernstein–Vazirani and Hidden Shift Algorithms.

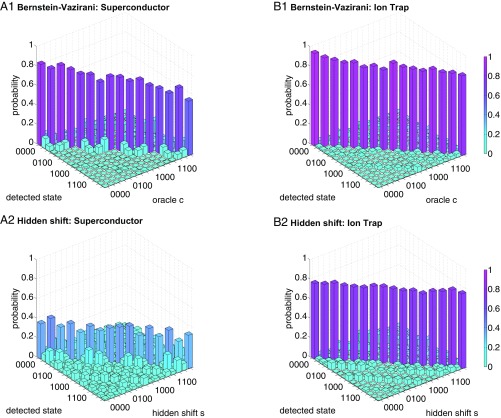
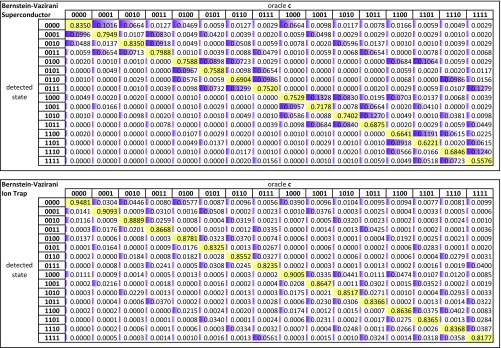
In the Bernstein–Vazirani algorithm, an oracle implements the function $f_c(x)=x\cdot c$. The algorithm finds the unknown bit string c in a single shot. In the oracle, c is encoded in a pattern of CNOT gates, all of which target the ancilla qubit (29). As can be seen from the circuit in Fig. 2C, the entire algorithm maps well onto a star-shaped architecture. This algorithm is very similar to a parity check circuit used in error correction applications, and indeed the IBM system was laid out with this application in mind (5). The single-shot success probabilities are $72.8(5)\%$ for the star-shaped superconducting system and $85.1(1)\%$ for the fully connected ion-trap system (Fig. 4 A1 and B1).

Fig. 4.

Results from the Bernstein–Vazirani algorithm implementing the oracle function $f_c(x)=x_0{c}_0\oplus c_1{x}_1\oplus c_2{x}_2\oplus c_3{x}_3$ for all possible $4$-bit oracles c performed on the star-shaped (A1) and the fully connected (B1) systems. The average success probabilities are $72.8(5)\%$ for the superconductor and $85.1(1)\%$ for the ion-trap system. The hidden shift algorithm for $f(x)=x_0{x}_1\oplus x_2{x}_3$. All possible $4$-bit shifted oracle functions are implemented on the superconducting system (A2) as well as the ion trap (B2). The average success probabilities are $35.1(6)$% and $77.1(2)\%$, respectively. The axes represent states and oracle parameters as $4$-bit binary numbers.

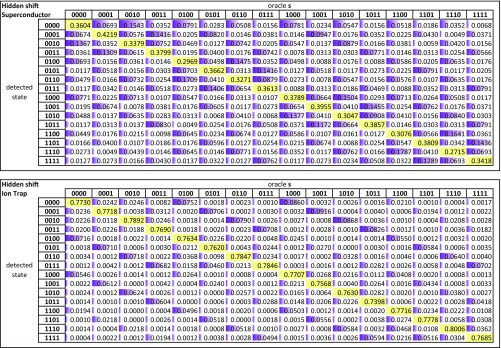
To compare this to a similar algorithm with different connectivity requirements, we implement the hidden shift algorithm (30) for a black box bent function (31, 32). An oracle implements the shifted version $f(\text{𝐱}+\text{𝐬})$ of the known Boolean function $f$. We want to determine the $n$-bit string s that constitutes the “hidden shift.” For a subset of Boolean functions, there exists a quantum algorithm that can solve this problem in a single oracle query, whereas classical algorithms require $\mathrm{\Omega }(\sqrt{2^n})$ queries. This subset contains functions that have a flat Fourier spectrum and whose dual $f^{\sim }$ can be calculated efficiently, i.e., so-called bent functions of the Maiorana–McFarland class (32). Here we choose the $4$-bit function $f(\text{𝐱})=x_1{x}_2\oplus x_3{x}_4$ for which $f=f^{\sim }$. We implement all possible $4$-bit shift patterns s using the circuit shown in Fig. 2D. The algorithm output state directly corresponds to the hidden shift s. The circuit involves gates between two disconnected pairs of qubits, which creates an overhead of six two-qubit gates for a star-shaped architecture. The results are shown in Fig. 4 A2 and B2. The fidelity of the fully connected ion-trap implementation is $77.1(2)\%$, compared with $35.1(6)\%$ for the superconducting device. The numerical values of the data plotted in Figs. 3 and 4 are displayed in Figs. S1–S3.

Fig. S1.

Numerical quantum computer 3-qubit input/output matrix for the Margolus gate (Top two panels) and the Toffoli gate (Bottom two panels), corresponding to Fig. 3 of the main text. For each gate, the results from both superconductor and ion-trap quantum computers are displayed.

Fig. S3.

Numerical quantum computer 4-qubit input/output matrix for the hidden shift algorithm for the superconductor system (Top) and the ion-trap system (Bottom), corresponding to Fig. 4 A2 and B2 of the main text.

The errors in both devices appear concentrated in certain sets of states, leading to patterns in the off-diagonal elements of the result plots (Fig. 4). These highly structured signatures suggest that systematic errors dominate, especially readout errors. The grouped patterns such as in Fig. 4A1 indicate flips of the least-significant bits, whereas parallel lines correspond to the most significant bits changing their state. In the trapped-ion results, these lines can be modulated in height due to readout crosstalk and are more pronounced on the lower-numbered state side due to $1\to \mathrm{\hspace{0.17em}0}$ being the dominant detection error channel. Finally, we stress that comparing quantum computations across systems depends on the specifics of error propagation, which will vary between different hardware implementations, through their particular connectivity and physical errors. We summarize the success probabilities for the implemented circuits on both machines in Table 2. We also show the expected values for two simple error propagation models based on the errors of the individual gates ${ϵ}_g$ and of $M$-qubit single-shot readout ${ϵ}_M$ for both systems. The first model assumes random error propagation per operation with overall error ${(1-{ϵ}_M)}^M{(1-{ϵ}_g)}^{\sqrt{N}}$, where $N$ is the number of gates. Because the errors for each step are independent and comparable to a random walk, the overall error involves $\sqrt{N}$ factors. The second model is based on systematic (coherent) over- or underrotations with overall error ${(1-{ϵ}_M)}^M{(1-{ϵ}_g)}^N$, which accumulates with $N$ factors. We see that the numbers are broadly consistent, with systematic errors better predicting the superconducting system, whereas the ion-trap performance falls in between the two. The superconducting hidden shift algorithm is the only example with a significantly lower experimental result, perhaps from inhomogeneous errors in the device.

Table 2.

Summary of the achieved success probabilities for the implemented circuits, in percentages

Connectivity	Star shaped			Fully connected
Hardware	Superconducting			Ion trap
Success probability/%	Obs	Rand	Sys	Obs	Rand	Sys
Margolus	74.1(7)	82	75	90.1(2)	91	81
Toffoli	52.6(8)	78	59	85.0(2)	89	78
Bernstein–Vazirani	72.8(5)	80	74	85.1(1)	90	77
Hidden shift	35.1(6)	75	52	77.1(2)	86	57

The observed probabilities (“Obs”) are tabulated alongside two simple error propagation models given the gate number N and the individual gate and readout errors of the two systems encapsulated in the parameters ϵ_g and ϵ_M, respectively (main text). The first stimate assumes random (“Rand”) error propagation with overall error ${\left(1-{ϵ}_g\right)}^{\sqrt{N}}$ whereas the second one is based on systematic (“Sys”) coherent over- or underrotations with overall error (1 − ϵ_g)^N, where N is the number of gates. The readout error for M qubits is (1 − ϵ_M)^M in both cases.

Outlook

Comparing quantum computing architectures involves many interrelated factors. Quantum gate operation fidelities, qubit numbers, primitive gate speeds, and coherence times are obviously important low-level metrics in a large-scale quantum computer. The results presented here show higher absolute fidelities and coherence times in the trapped-ion system, with higher clock speeds for the superconducting system. However, these metrics are moving targets: Whereas these systems are the most advanced and versatile quantum computing platforms built to date, both technologies are currently advancing rapidly.

In any case, such metrics should not be considered in isolation. Our comparison points to important higher-level considerations in scaling a quantum computer. The overall performance of a quantum circuit and the “time to solution” will depend critically on architectural restrictions, qubit connectivity, gate reconfigurability, and gate expressivity, and these attributes will become ever more important as the system is scaled up. Even with 5-qubit systems, we find that the qubit connectivity graph is best codesigned to mirror the structure of the particular quantum circuit and that the choice of a more expressive gate library affects the efficiency of the computations.

The physical scaling of each of these leading technologies has many challenges, and how they will be connected and reconfigured at large scales is an open question. One of the biggest challenges is the management of the control complexity in larger systems and potential crosstalk from overlapping qubit interactions or control buses. In most superconducting designs, there are many current-carrying wires necessary for control and biasing the individual qubits, and this may be difficult to route through a large superconducting chip (1–5). It will likely become a great challenge to manage the dilution refrigerator heat budget with such circuitry. Alternative modular superconducting architectures improve connectivity by integrating qubits with microwave cavity modes, at the expense of significant added volume per qubit (33). Ion-trap designs will hinge upon the stable and accurate delivery of laser beams (or near-field microwave sources) to address each qubit individually in a vacuum chamber. The fully connected nature of the ion-trap architecture may not scale to arbitrarily large numbers of qubits, owing to the spectral overlap of collective normal modes of motion. However, full connectivity between 20 and 100 trapped-ion qubits appears possible (6) and a modular approach for scaling to much larger systems with high connectivity and distance-independent operations seems promising (34, 35). In any hardware, an automated calibration procedure and powerful user interface will likely provide a higher level of integration. Such system-level attributes will become even more important as quantum circuits grow in complexity, regardless of physical platform.

Numeric probability values of the results presented in Figs. 3 and 4 in the main text are shown in Figs. S1–S3. The target populations, with nominal unit probabilities, are highlighted in yellow. The others, representing errors, show a bar graph scaled from 0 to 0.1 to emphasize the systematic error patterns.

Fig. S1 is a compilation of the Margolus/Toffoli gate data shown in Fig. 3 of the main text. Fig. S2 is a compilation of the Bernstein–Vazirani data shown in Fig. 4 A1 and B1 of the main text, and Fig. S3 is a compilation of the hidden shift data shown in Fig. 4 A2 and B2 of the main text.

Fig. S2.

Numerical quantum computer 4-qubit input/output matrix for the Berstein–Vazirani algorithm for the superconductor system (Top) and the ion-trap system (Bottom), corresponding to Fig. 4 A1 and B1 of the main text.