Effect of material flexibility on the thermodynamics and kinetics of hydrophobically induced evaporation of water

Significance

The evaporation of water in hydrophobic confinement is important for the formation and function of both natural and synthetic hydrophobic self-assemblies. Using advanced computational techniques, we find that the thermodynamic and kinetic stability of water in hydrophobic confinement is extremely sensitive to the flexibility of the confining material. In the context of engineered systems, this work suggests that the mechanical properties of the building blocks in a self-assembled system are a crucial design consideration. With respect to biophysical phenomena, it suggests that small changes in flexibility can induce switch-like responses such as the opening and closing of membrane channels and the conversion between active and inactive states in receptors, both of which are common drug targets.

Abstract

The evaporation of water induced by confinement between hydrophobic surfaces has received much attention due to its suggested functional role in numerous biophysical phenomena and its importance as a general mechanism of hydrophobic self-assembly. Although much progress has been made in understanding the basic physics of hydrophobically induced evaporation, a comprehensive understanding of the substrate material features (e.g., geometry, chemistry, and mechanical properties) that promote or inhibit such transitions remains lacking. In particular, comparatively little research has explored the relationship between water’s phase behavior in hydrophobic confinement and the mechanical properties of the confining material. Here, we report the results of extensive molecular simulations characterizing the rates, free energy barriers, and mechanism of water evaporation when confined between model hydrophobic materials with tunable flexibility. A single-order-of-magnitude reduction in the material’s modulus results in up to a nine-orders-of-magnitude increase in the evaporation rate, with the corresponding characteristic time decreasing from tens of seconds to tens of nanoseconds. Such a modulus reduction results in a 24-orders-of-magnitude decrease in the reverse rate of condensation, with time scales increasing from nanoseconds to tens of millions of years. Free energy calculations provide the barriers to evaporation and confirm our previous theoretical predictions that making the material more flexible stabilizes the confined vapor with respect to liquid. The mechanism of evaporation involves surface bubbles growing/coalescing to form a subcritical gap-spanning tube, which then must grow to cross the barrier.

A canonical manifestation of hydrophobicity (1) is the fact that liquid water confined between hydrophobic objects of sufficiently large size becomes metastable with respect to its vapor at small-enough separations (2–4). The resulting strong attractive force between the objects upon water evaporation is thought to provide a mechanism of self-assembly (5–7) and has been suggested to underlie the experimentally observed long-range hydrophobic attraction (8, 9). In addition, hydrophobically induced evaporation has recently been proposed as an important feature of protein–ligand binding (10, 11) and is also thought to provide a functional role in the operation of membrane-bound protein assemblies, such as ion channels (12, 13) and receptors (14).

Motived by these examples, a number of computational studies have investigated hydrophobically induced evaporation in idealized systems with regular geometries (e.g., pore slits and cylinders) that are often chemically uniform, perfectly rigid, and topologically smooth (15, 16). Such studies have provided fundamental insights into water evaporation in hydrophobic confinement. However, to develop a quantitative basis for the rational design of hydrophobic assemblies it is necessary to consider how less-idealized features inherent to real materials affect both the thermodynamics and kinetics of hydrophobic evaporation. It is also expected that a more comprehensive picture would provide deeper insights into the mechanisms and rates of important biophysical phenomena (10, 12–14). Features that have received some attention to date include chemical heterogeneity (17–20) and surface geometry/topography (21–23).

The present work considers how hydrophobically induced evaporation is influenced by the flexibility of the confining material, that is to say, the ability of the material to deform under load. Such a fundamental material property has largely eluded consideration in the present context, but as will be demonstrated here flexibility has a profound impact on the thermodynamics and kinetics of evaporation. Only a few computational studies have explicitly considered flexibility in the context of hydrophobic evaporation (24–26), with two studies suggesting that flexibility promotes evaporation (24, 25), whereas another study suggests that flexibility has no effect (26). The present work is motived by our recent thermodynamic analysis (27) that suggests that making the confining material more flexible stabilizes a confined vapor with respect to the liquid phase. The arguments in ref. 27 take into the account the geometric and energetic aspects of the deformation that accompanies evaporation in a confined open region bounded by flexible walls and surrounded by liquid. We show that $D_c$, the critical separation below which the liquid becomes metastable with respect to its vapor, can be rigorously decomposed into rigid and flexible contributions, $D_c=D_{rigid}+D_{flex}$. For a linear elastic material $D_{flex}>0$, meaning that flexible surfaces will have a $D_c$ larger than otherwise identical rigid surfaces.

A distinguishing aspect of this work is that, in addition to assessing thermodynamic stability, we calculate the rates and determine the mechanism of evaporation. For hydrophobic evaporation to provide a functional role in either natural or engineered systems transitions must be kinetically accessible on appropriate time scales. Because evaporation is a rare, activated process, transition rates and mechanisms are only accessible with the aid of computationally demanding path sampling techniques (28–31) for systems of even moderate chemical or geometric complexity. Such technical challenges underlie the relatively few studies of the kinetics of evaporation in nanoscopic confinement and even fewer using molecular water models.

Pioneering studies of the kinetics of hydrophobically induced evaporation performed by Luzar and coworkers used lattice-gas representations with Glauber dynamics Monte Carlo (3, 17, 32, 33) as well as a molecular model of water with the reactive flux formalism (34). Notably, ref. 17 examined the role of chemical heterogeneity on the kinetics of evaporation. Bolhius and Chandler (35) performed transition path sampling calculations of drying of a Lennard-Jones liquid confined between solvophobic disks. Xu and Molinero (26) studied vapor–liquid oscillations of the coarse-grained mW water model (36) confined between hydrophobic disks. Sharma and Debenedetti (37, 38) used forward flux sampling (FFS) (39) to calculate the rates and barriers to evaporation of SPC/E water (40) between rigid hydrophobic plates, for a range of separations. In addition, the kinetics of binding of a spherical ligand to a hydrophobic pocket (41, 42), an event which requires dehydration of the cavity, has been characterized using direct molecular dynamics (MD) simulations interpreted using a diffusive surface hopping model (41) as well as a recent extension of metadynamics (43) to calculate transition rates (42).

Here we present calculations of the rate, mechanism, and free energy profiles of evaporation of water confined between the nanoscale hydrophobic plate-like solutes displayed in Fig. 1, using FFS (31, 39, 44) in conjunction with MD. Within each atomically detailed solute, each nearest-neighbor pair interacts via a harmonic spring, the strength of which dictates the flexibility of the plate. We keep the strength of the interactions between water molecules and plate atoms fixed and tune flexibility to assess how it influences the thermodynamics and kinetics of hydrophobically induced evaporation.

Fig. 1.

Simulation environment displayed in both the confined liquid (Left) and vapor (Right) states. The two (∼3 × 3 nm²) atomistic hydrophobic surfaces are composed of three ABA stacked hexagonal lattices. Each nearest neighbor within a wall is harmonically bonded, and the spring constant strength $K$ is tuned to control the flexibility of the material. The row of atoms on the top and bottom of the walls (i.e., those with largest and smallest y coordinates) remain fixed in space, and the remaining ones are time-integrated. The separation between the walls is defined as the distance between the atomic centers of the innermost immobile atoms.

Rates of Evaporation

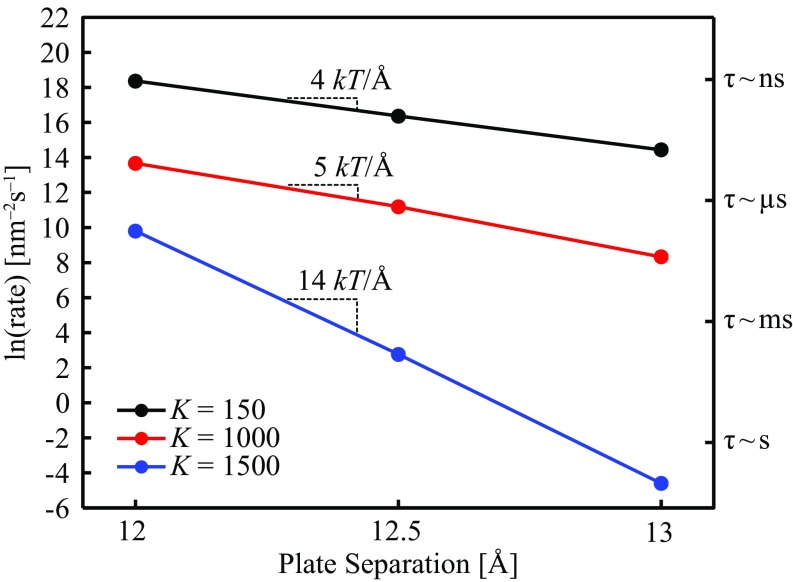
Fig. 2 shows the dependence of the calculated evaporation rates upon plate separation $D$ for three flexibilities, spanning an order of magnitude. Here, the harmonic bond spring constant ($K\hspace{0.17em}[=]\frac{\text{kcal}}{\text{mole}{\text{Å}}^2}$) connecting each nearest-neighbor pair within a plate is used as a measure of the material’s flexibility. Increasing $K$ results in a stiffer material, and lowering $K$ softens it. In the present study, $K$ was varied between 150 and 1,500. The axis on the right-hand side of the figure displays the characteristic time scale of evaporation, $\tau ={\left({\text{rate}}^{\ast }A\right)}^{-1}$, where $A$ is the area of a plate (∼3 × 3 nm²).

Fig. 2.

Evaporation rates calculated via FFS as a function of plate separation for three different flexibilities ($K\hspace{0.17em}[=]\frac{\text{kcal}}{{\text{mole}\mathrm{\AA }}^2}$), spanning an order of magnitude. The right-hand axis displays the characteristic time scales of evaporation.

For the range of separations and flexibilities we have studied, water confined between rigid hydrophobic objects takes longer to evaporate than an otherwise identical softer material at the same separation [i.e., ${\left(\frac{\partial \tau }{\partial K}\right)}_D>0$]. The three lines of constant $K$ have different slopes, meaning that the change in rate for a given change in $K$ depends on the separation [i.e., ${\left(\frac{\partial \tau }{\partial K}\right)}_D=f\left(D\right)$]. The difference in slopes implies that the distance dependence of the free energy barrier to evaporation ${\text{ΔΩ}}^{\ast }$ depends on flexibility [i.e., ${\left(\frac{\partial {\text{ΔΩ}}^{\ast }}{\partial D}\right)}_K=f\left(K\right)$], and as long as the linearity in $\text{ln}\left(\text{rate}\right)$ versus $D$ holds, for separations between 12 and 13 $\AA ,$ the barrier varies by 14, 5, and 4 $kT/\AA$ for $K$ = 1,500, 1,000, and 150, respectively. $\text{Ω}$ here refers to the grand potential, the appropriate thermodynamic potential for an open system that can exchange mass and energy with the surrounding bulk liquid.

For this range of $D$–$K$ parameter space, the evaporation time scales vary across some 10 orders of magnitude, spanning from nanoseconds to tens of seconds. The largest change at fixed flexibility occurs for the most rigid material ($K$ = 1,500), ranging from tens of seconds at $D=13\hspace{0.17em}\AA$ to microseconds at $D=12\hspace{0.17em}\AA$, a remarkably pronounced response to a mere 1 Å change in separation. The most pronounced change at fixed separation occurs at $13\hspace{0.17em}\AA$, where a single order of magnitude change in the degree of flexibility results in a nine-orders-of-magnitude change in the rate of evaporation.

Previous calculations of evaporation between perfectly rigid nanoscale plates found that the rate and the corresponding barrier to evaporation depend sensitively upon the plate separation (37, 38). Such a sensitivity can result in switch-like behavior, where a confined, possibly metastable, liquid is “flipped” to the vapor due to a small reduction in separation, dramatically reducing the time scale for evaporation. Indeed, studies suggest that Å-level reductions in protein channel diameter are enough to induce the transition from an open, hydrated state to a closed, dewetted state in an ion channel (13). The present results suggest that rigidity can enhance switch-like responses to separation perturbations. However, rigidity also substantially increases the time scale of evaporation for all separations. Thus, the design of a hydrophobic switch must consider the trade-off between the time scale of evaporation and its sensitivity to separation perturbations. In addition, our work suggests that small perturbations in the flexibility of the confining material can also promote a switch-like response. Indeed, differences in flexibility and corresponding internal hydration have been observed as distinguishing features of the active and inactive states of G protein-coupled receptors (GPCRs), an important family of membrane-bound protein assemblies (14, 45, 46), a point we will discuss further in the context of the free energy profiles and barriers.

We have performed energy-strain calculations on the plates to determine Young’s modulus $E$ for each $K$. The results show that by this measure our plates are extremely rigid. For $K$ = 1,500, $E\sim {10}^4$ Gpa, and for K = 150, $E\sim {10}^3$ Gpa. For reference, $E$ of diamond is roughly 10³ Gpa (47). However, the resistance of a plate to bending is a combination of its elastic properties and thickness, quantified by its flexural rigidity, $f=E{h}^3/12\left(1-\hspace{0.17em}{\nu }^2\right)$, where $h$ is the thickness and $\nu$ is Poisson’s ratio (48). In general, $\nu$ varies between 0 and 0.5, so the denominator is of $\mathcal{O}\left(10\right)$. Thus, the relative ease of bending a given plate-like material (i.e., fixed $E$) scales with $h^3$. The thickness of the plates considered in this work is 0.23 nm, a dimension of the order of a few carbon–carbon bond lengths. If we take the denominator of $f$ to be of order 10, $f\sim 300-\mathrm{3,000}\hspace{0.17em}{k}_{B}T$, where $k_B$ is Boltzmann’s constant and $T$ is temperature, 298 K in this case. Proteinaceous materials such as β-sheet crystals, which have thicknesses of roughly 1 nm and $E$ of roughly 20 Gpa (49), have $f\sim 500\hspace{0.17em}{k}_{B}T$, which falls within the range of our plates. Thus, the plates considered here are mechanically similar to an important class of biological materials, which suggests that the parameter space we have explored here, $f\sim 300-\mathrm{3,000}\hspace{0.17em}{k}_{B}T$ and nanometer dimensions, may be relevant to those biological systems, namely protein channels and receptors, that have been proposed to integrate hydrophobic evaporation into their function.

Effect of Flexibility on the Mechanism of Evaporation

In an FFS calculation (31) one partitions the evolution between the two states of interest into a series of milestones along a suitable order parameter $\lambda$, which in our case is the number of confined water molecules (herein referred to as $N$). The initial configurations are captured during a sufficiently long MD simulation. Specifically, if the system originates in the liquid basin and undergoes a fluctuation that reaches the predetermined first milestone ${\lambda }_1$, the configuration at ${\lambda }_1$ is stored. One advances to the next milestone by randomizing the initial linear and angular velocities of these configurations, running an MD simulation, and capturing configurations that reach the next milestone before returning to the starting liquid basin. This process is repeated over and over until the transition is completed. This procedure alone will yield the transition rate (Methods). However, additional inspection of the configurations captured at each milestone can yield insights into the type of fluctuations required for the transition to occur.

For the purpose of calculating the rate via FFS, using the number of confined water molecules as the order parameter is convenient and appropriate, yet not all configurations with the same local density are equally likely candidates to transition to the vapor. Particular arrangements of water molecules will constitute better or worse configurations. At a given milestone a select set of configurations contributes to the pathway between the liquid and vapor basins and contains the relevant information about what types of fluctuations eventually promote a phase transition. It is these configurations that tell us which arrangement the water molecules adopt as the system transitions to a vapor. During evaporation one expects that a vapor-like region of sufficient size promotes the nucleation of the impending phase, and the associated classical nucleation picture links the free energy barrier to the formation of a gap-spanning vapor tube of sufficiently large radius (34, 37, 50).

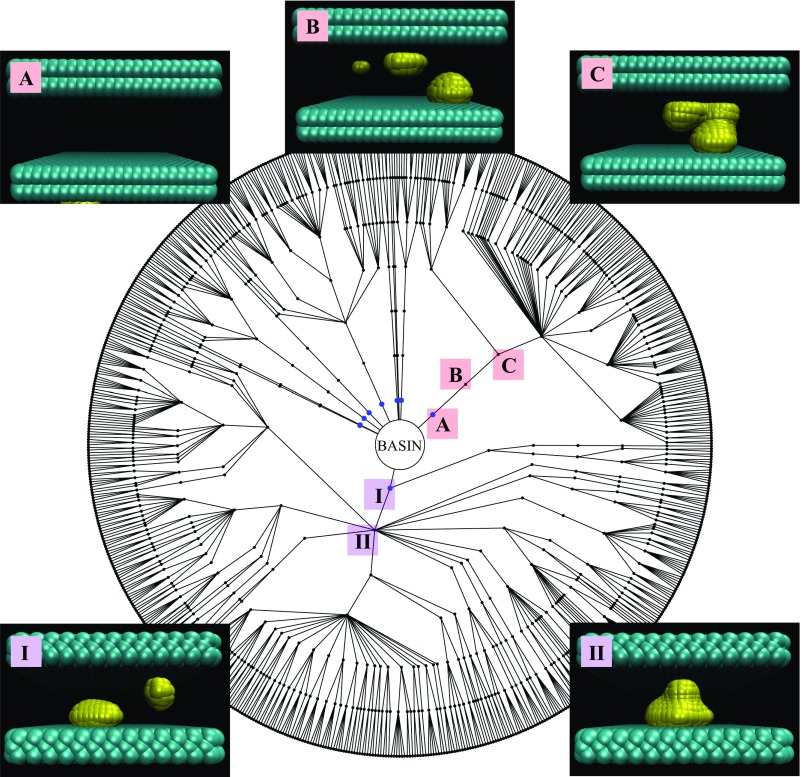
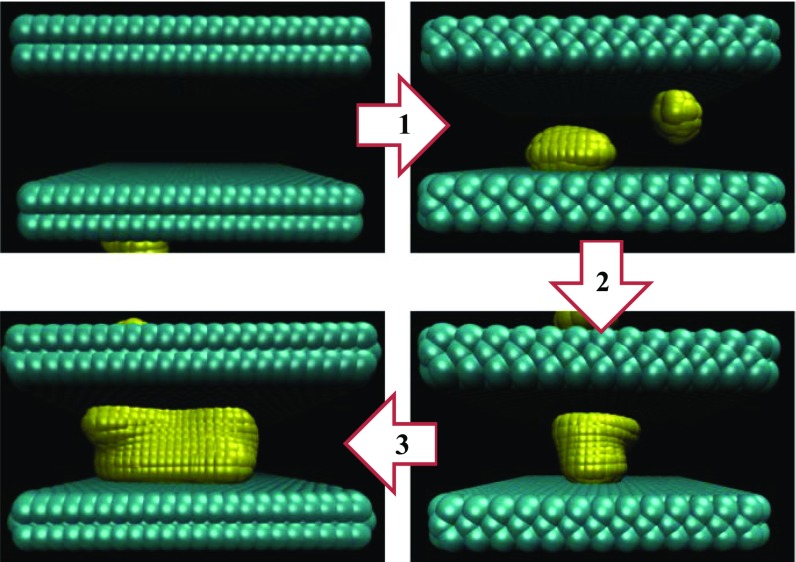
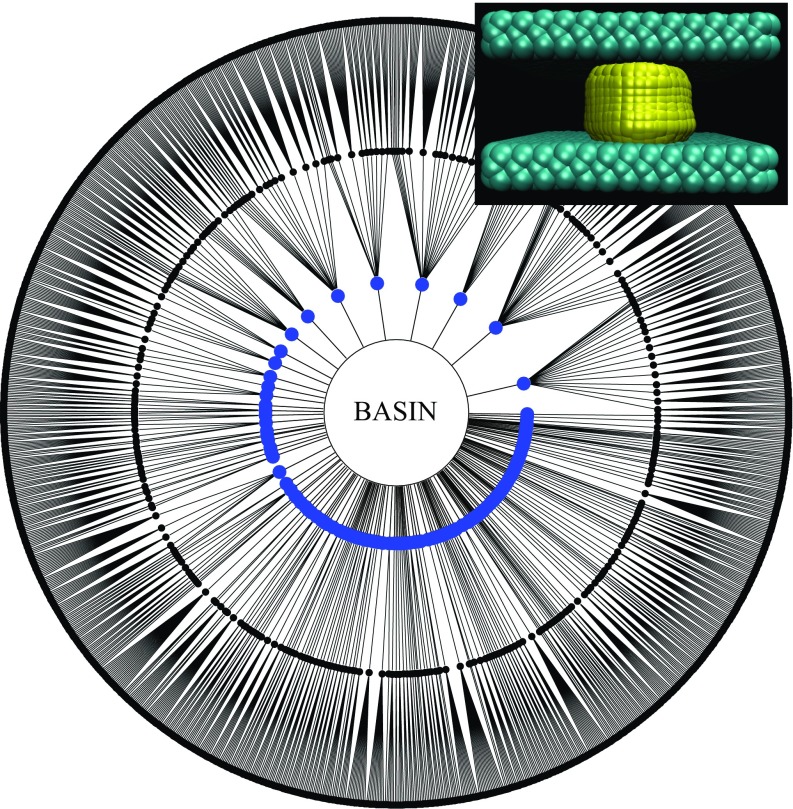
We have produced connectivity maps (see discussion below as well as Figs. 4 and 6) of all configurations that form a pathway between the liquid and vapor. Rendering instantaneous interface representations (51) of these configurations allowed us to determine how the shape of the vapor-like regions develops as the system evaporates. Such representations provide a set of points that delineate the boundary between the liquid and vapor-like regions. In Fig. 3 we show a schematic of the mechanism of evaporation, based on the configurations at D = 13 Å for each flexibility. However, we have confirmed that the mechanism illustrated in Fig. 3 is general for all separations studies in this work. We observe three steps. First, the transition proceeds through the formation of surface bubbles on opposite plates, a consequence of the enhanced density fluctuations of water proximal to extended hydrophobic surfaces (52, 53). These surface bubbles then grow/coalesce to form a gap-spanning vapor tube. In all pathways, the first configuration that includes a gap-spanning tube has a transition probability to the next milestone smaller than 0.5. Because the probability of advancing to the next milestone is greater than or equal to the probability of reaching the vapor basin, we can conclude that these first instances of tubes represent subcritical configurations. Thus, after bubbles transition to vapor tubes, an additional “uphill” fluctuation is required for the tube to grow to sufficient size and cross the nucleation barrier.

Fig. 4.

Diagram display of all of the reactive pathways to evaporation for $D=13\mathrm{\AA }$ and $\mathit{K}=\mathrm{1,500.}$ Each node corresponds to a particular configuration and connecting lines are successful FFS steps. Each concentric circle of nodes corresponds to a milestone. The center is the liquid basin; a radial step outward represents advancing an FFS milestone; each outermost node is a configuration reaching the vapor. Instantaneous interface rendering of the initial steps of two distinct reactive trajectories (which start with configurations I and A and account for roughly 85% of configurations reaching the vapor) are displayed. In both cases, surface bubbles (configurations I and B) on opposite faces grow/coalesce to form a gap-spanning vapor bridge (configurations II and C). The remaining FFS steps (configurations not illustrated) are associated with the growth of these gap-spanning tubes.

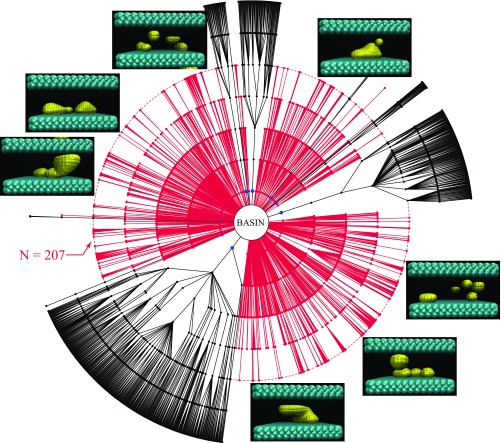
Fig. 6.

Diagram displaying the connections of all configurations that advance past the first milestone for $D=13\mathrm{\AA }$ and $\mathit{K}=\mathrm{1,500}$. Reactive trajectories are shown in black and trajectories that fail to reach the vapor are shown in red. Nearly every unsuccessful trajectory fails to progress beyond the milestone at $\mathit{N}=207$, which corresponds to the kink in the corresponding free energy diagram (Fig. 5). A representative selection of configurations that fail to advance beyond $\mathit{N}=207$ is shown and exhibits a mixture of bubbles and gap-spanning vapor tubes. The configurations at this milestone that advance (configurations not shown) are exclusively gap-spanning vapor tubes. Note that all bubbles shown abut one of the walls.

Fig. 3.

Schematic of the mechanism of evaporation showing how the vapor-like portions develop as the system transitions from a confined liquid to vapor. The yellow portions delineate the instantaneous liquid/vapor interface (51) and the water molecules are removed for visual clarity. The mechanism proceeds in three steps: 1, surface bubbles form; 2, surface bubbles grow/coalesce to form a gap-spanning subcritical vapor tube; and 3, the vapor tube expands and crosses the nucleation barrier. Note that all bubbles shown abut one of the walls.

We have already noted the dramatic nine-orders-of-magnitude change in the evaporation rate for a single-order-of-magnitude change in the flexibility of the plates. We have found that a large portion of this difference can be attributed to the respective frequency at which $K=150$ and $K=\mathrm{1,500}$ systems traverse steps labeled as 1 and 2 in Fig. 3. We note that whereas the difference in rates and thermodynamic stabilities (Free Energy Profiles and Barriers) is substantial the differences in deformations are subtle.

Fig. 4 displays the connectivity map of all configurations that link the liquid and vapor for the D = 13 Å , $K$ = 1,500 system. The center of the figure represents the liquid basin and each radial step outward represents a milestone on the path toward the vapor. The points along the outer perimeter are configurations that reach the vapor. Surprisingly, very few among the roughly 1,000 configurations at the first milestone ultimately connect to the vapor, and there are several bottlenecks before the configurations branch out to produce many reactive pathways. The steps associated with the two major bottlenecks are displayed in Fig. 4. In both of these cases surface bubbles grow/coalesce to form a gap-spanning vapor-bridge. Although not shown, well-formed tubes, like that displayed in Fig. 3, do not appear until the third or fourth milestone. In other words, for the most rigid plates considered here, tubes are not observed without the use of advanced sampling.

From the above we conclude that in order for the water confined between the $D=13\hspace{0.17em}\AA$, $K=\mathrm{1,500}$ plates to evaporate, two rare events must occur in series. First, surface bubbles must grow/coalesce to form vapor tubes, which occurs roughly on the timescale of a microsecond, a value estimated by calculating the “rate” to the fourth milestone. Second, once such a tube has formed, roughly 1 out of every 10 million instances will then undergo a fluctuation that propels it over the barrier, estimated by dividing the time scale of evaporation by the time scale of tube formation.

However, for $K$ = 150 (the most flexible case) at the same separation, many configurations captured at the first milestone already contain well-formed gap-spanning vapor tubes, and there are no bottlenecks in the connectivity map (Fig. S1). Recall that configurations at the first milestone are captured through a straightforward MD simulation. Thus, formation of tubes in this instance is not a rare event, and the rate of evaporation is largely governed by the probability that a tube grows to become supercritical.

Fig. S1.

Diagram display of all of the reactive pathways to evaporation for $D=13\hspace{0.17em}\AA$ and $K=150$ (i.e., the most flexible walls). The configuration on the top right containing a well-formed gap-spanning tube is a representative of a typical configuration found at the first milestone. In other words, for the most flexible case, gap-spanning tubes are sampled during a regular MD simulation, without the use of advanced sampling.

In all of the cases we have considered the barrier to evaporation is the formation of a gap-spanning vapor tube of sufficient size. The first instances of tubes encountered along a pathway are always subcritical, and additional milestones are required to capture fluctuations that drive these configurations over the barrier. In this sense, once tubes are formed the progression is consistent with the classical picture. However, far from the barrier the picture is nonclassical and associated with the growth of surface bubbles. The growth/coalescence that results in subcritical tubes changes the pathway to evaporation from nonclassical to classical.

Free Energy Profiles and Barriers

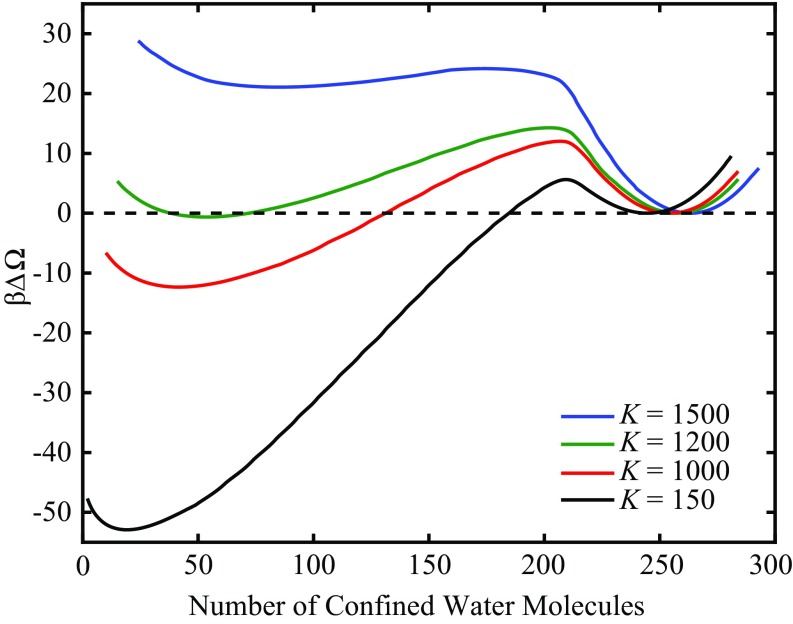
The free energy profiles $\beta \mathrm{\Delta }\mathrm{\Omega }\left(N\right)$ for four flexibilities at $D=13\hspace{0.17em}\AA$ are presented in Fig. 5. The profiles shown here are calculated by performing FFS in the forward (evaporation) and reverse (condensation) directions to produce the stationary distribution of the order parameter (44). All curves are shifted such that the minimum of liquid basin, in the neighborhood of 250 confined water molecules, is at $\text{ΔΩ}=0$. Precise values of the barriers to evaporation ${\text{ΔΩ}}^{\ast }$, location of the barrier $N^{\ast }$, free energy difference between the confined vapor and liquid ${\text{ΔΩ}}_{vl}$, and locations the liquid $N_l$ and vapor basins $N_v$ are displayed in Table 1.

Fig. 5.

Free energy profiles as a function of the number of confined water molecules for walls separated by 13 Å, for four different flexibilities ($\mathit{\beta }=1/\mathit{kT}$, where $\mathit{k}$ is Boltzmann’s constant). Making the material more flexible (i.e., reducing $\mathit{K}$) lowers the barriers to evaporation and stabilizes the vapor. $\mathit{K}=\mathrm{1,200}$ is roughly the coexistence flexibility at this fixed separation.

Table 1.

Effect of flexibility $K$ on the barrier to evaporation $\mathrm{\Delta }{\Omega }^{*}/kT$, location of the barrier $N*$, free energy difference between vapor and liquid $\mathrm{\Delta }{\mathrm{\Omega }}_{\mathit{vl}}/kT$, and location of the liquid $N_l$ and vapor $N_v$ basins

$K$	${\text{ΔΩ}}^{\ast }/kT$	$N^{\ast }$	${\text{ΔΩ}}_{vl}/kT$	$N_l$	$N_v$
1,500	24.2	174	21.1	263	85
1,200	14.2	203	−0.642	258	53
1,000	12.0	207	−12.4	254	41
150	5.62	209	−52.9	245	19

In agreement with our theoretical arguments (27), making the plates more flexible stabilizes the vapor with respect to the liquid. The macroscopic thermodynamic arguments suggested that flexibility stabilizes the vapor by reducing its absolute free energy, without affecting the liquid state. The fact that the curvature of the vapor free energy minimum increases with increasing flexibility (i.e., reducing $K$), whereas the curvature of the liquid minimum remains roughly unchanged, supports this formulation (27).

Typically, studies focus on the critical drying distance (4, 16, 26), the separation below which the confined liquid becomes metastable with respect to its vapor. Here, we show that there is a critical flexibility (∼$K$ = 1,200 in this example) that supports coexistence between the two confined fluid phases. The consequence for real materials is that rather than a single critical separation for materials that have similar interactions with water (e.g., similar contact angle), there is a locus of points in the flexibility-separation plane where this transition becomes thermodynamically favored.

We suggested above that tuning flexibility can result in switch-like behavior due to a large separation of time scales of evaporation. However, as Fig. 5 suggests, this behavior is not symmetric. Whereas the separation of evaporation time scales is nine orders of magnitude, the 55.4 $kT$ difference in the barriers to condensation in going from $K$ = 150–1,500 results in a 24-orders-of-magnitude change in the time scales of condensation, spanning from nanoseconds to tens of millions of years. In this example, the most sensitive switch is a system with $K$ = 150, which condenses on geological time scales, that upon rigidification can condense on practically any desired time scale (e.g., nanoseconds for $K$ = 1,500 or milliseconds for $K$ = 1,200). The default state of a switch-like system may more effectively be the vapor state, which can then rapidly condense if the confining material is made more rigid. Of course, physical restrictions come into play, such as the requirement that the open state of an ion channel remain hydrated (12, 13).

Another set of membrane-bound proteins, GPCRs, may offer an example where nature has adopted the above-described physics into biomolecular function. Recently, simulations of several members of this superfamily (adenosine A_2A, β₂-andrenergic, and rhodopsin) have suggested that the default inactive state has an interior dehydrated region, which upon activation undergoes a transition to a continuous interior water channel (14). Independently, Müller and coworkers have performed single-molecule force spectroscopy experiments to determine the mechanical properties of GPCRs in various states. Upon activation through chromophore removal, rhodopsin becomes more rigid in all domains (46). In the case of β₂-andrenergic receptor, the domain containing the conserved NPxxY motif, the region where the simulations observed substantial changes in hydration (14), becomes more rigid when bound to agonists (i.e., drugs inducing activation) and more flexible when bound to an inverse agonist or neutral antagonist (45). It seems that rigidification-induced hydrophobic condensation may be an integral feature of GPCR activation.

Shape of the Free Energy Profiles

Recently, Remsing et al. (53) used an umbrella sampling technique to compute the free energy profiles of evaporation between perfectly rigid plate-like solutes for a range of separations. A highlighted feature of their profiles was an apparent discontinuity in slope, which they referred to as a “kink,” occurring either at or in the neighborhood of the barrier. The authors concluded that this kink corresponds to the intersection of distinct free energy profiles between surface bubbles and gap-spanning vapor tubes. The mechanistic implication is that along the pathway to evaporation the kink represents an abrupt transition from surface bubbles to gap-spanning tubes. Recall that we observe that such a transition is indeed part of the mechanism of evaporation (Figs. 3 and 4).

Revisiting the free energy profiles in Fig. 5, the most rigid case considered ($K$ = 1,500) exhibits an apparent kink at $N$ = 207, which also happens to be one of the milestones in the evaporation FFS calculation. For the three other flexibilities the region around the maximum is asymmetric, but a discernible kink is not present. In the free energy profile corresponding to the most rigid plate the kink does not coincide with the barrier. If our findings were consistent with those of Remsing et al. (53), one should expect that during evaporation, at $N$ = 207, bubbles transition to subcritical vapor tubes. Such tubes would need to undergo an additional fluctuation to become supercritical.

In Fig. 6 we present a connectivity map of the $D=13\hspace{0.17em}\AA$, $K=\mathrm{1,500}$ calculation including the pathways of configurations that advance beyond the first milestone yet fail to connect to the vapor, shown in red. One salient feature of this diagram is that nearly all (there are exactly two exceptions) of the unsuccessful pathways fail to advance beyond the fifth milestone at $N$ = 207, which coincides with the kink in the free energy diagram.

We have examined instantaneous interface renderings of all of the 759 configurations at this milestone. Of the 198 configurations that advance to the next milestone, every single one already contains a gap-spanning vapor bridge, which for convenience we call a tube. The 198 tubes found at N = 207 have become tubes well before the kink. As shown in Fig. 4, the vast majority of reactive pathways feature tubes by the third milestone at $N$ = 221. The remaining 561 configurations that fail to advance are a collection of isolated surface bubbles and tubes. Rather than a transition occurring at the kink in our examples, this feature in the free energy profile seems to represent a sifting event. Capturing configurations that fluctuate to low $N$ (i.e., the FFS order parameter) results in a mixture of bubbles and tubes successfully advancing early in the process. However, beyond a certain point, coinciding with the kink in our free energy profile, only gap-spanning tubes will continue to advance.

Conclusions

The calculations presented here suggest that the mechanical properties of the confining material constitute an extremely important parameter in the context of hydrophobic evaporation. By tuning the modulus of a model hydrophobic material by an order of magnitude, the evaporation rate can vary by nine orders of magnitude (seconds to nanoseconds) and the condensation rate by 24 orders of magnitude (nanoseconds to tens of millions of years). In agreement with the thermodynamic arguments of ref. 27, making the material more flexible stabilizes the confined vapor. We have also found that the mechanism of evaporation involves a transition from surface bubbles to a gap-spanning tube. Whereas the barrier to evaporation corresponds to forming a tube of sufficient size, a large portion of the ability of increasing flexibility to lower the barriers to evaporation is due to facilitating the transition from surface bubbles to tubes that are subcritical.

In the context of the engineering design of hydrophobic assemblies, our findings suggest that subtle differences in the mechanical properties may result in assemblies with vastly differently thermodynamic and kinetic stabilities. Although we have provided arguments as to why flexibility stabilizes the vapor thermodynamically (27), the precise mechanism underlying the large increase in rate with flexibility requires further investigation, certainly across the range of moduli considered here, none of which allows large-scale plate deformations. It also seems that the switch-like behavior induced by small changes in flexibility may have implications in the function of membrane-bound protein assemblies, such as GPCRs (14, 45, 46). Given that this class of receptors is a target for roughly one-third of all drugs (10), exploring this connection in more detail would likely be a fruitful topic of further research.

Methods

MD Setup and Simulations.

The hydrophobic walls are composed of three hexagonal lattices, with a lattice constant of 1.4 Å, that are hexagonally close-packed (i.e., ABA stacking). Each nearest-neighbor pair within a given wall is harmonically bonded with a spring constant, meaning $U\left(r_{ij}\right)=K{\left(r_{ij}-1.4\hspace{0.17em}\AA \right)}^2$, where the usual 1/2 factor is included in $K$. Otherwise, the wall atoms do not interact with each other. The first layer of atoms on the top and bottom of each wall remain fixed in space, which fixes the separation between the walls, and the remaining ones are time-integrated. The 8,505 water molecules are modeled by the SPC/E potential (40) and they interact with the walls through their oxygen sites. The water molecules are constrained via the SHAKE algorithm (54). For both walls, the atoms on the interior lattice interact with water molecules via a Lennard-Jones potential with a very weak minimum ($\sigma =3.283\hspace{0.17em}\AA$ and $\mathit{ϵ}=0.01445\hspace{0.17em}\text{kJ/mol}$) and the remaining two layers interact via the corresponding Weeks–-Chandler–Andersen (55) purely repulsive interaction. MD simulations in the NpT ensemble were performed at 298 K and 1 atmosphere using a Nosé–Hoover thermostat and barostat (56, 57) with a time step of 2 fs, thermostat damping of 200 fs, and barostat damping of 2,000 fs. Time integration was performed with the LAMMPS software package (58) used as a library within an in-house FFS code (59). Electrostatic interactions were handled via the PPPM Ewald method (60) on a 36 × 36 × 36 grid with a target relative error of 10⁻⁴.

FFS.

The methodology here follows the “direct” FFS variant for calculating transition rates from state $A$ to $B$ as described in detail in a recent review (31). We note that previous work using rigid walls found excellent agreement between the results of FFS and direct MD (37). A short MD simulation is performed in the initial basin $A$, and the order parameter $\lambda$ is monitored to obtain an estimate of its distribution in the neighborhood of the basin. In our work, $\lambda$ is the number of confined water molecules. The boundary of the basin is defined as ${\lambda }_0=<\lambda {>}_A\hspace{0.17em}\pm \hspace{0.17em}{\sigma }_{\lambda }$ (e.g., ${\lambda }_0=<\lambda {>}_A-\hspace{0.17em}{\sigma }_{\lambda }$ for ${\lambda }_1<{\lambda }_0)$, where $<{>}_A$ denotes the average in basin $A$ and and ${\sigma }_{\lambda }$ is the corresponding SD. The first milestone ${\lambda }_1$ is chosen as roughly the 0.5% point of the cumulative distribution function. A set of MD simulations are then performed and configurations at ${\lambda }_1$ produced from trajectories originating at ${\lambda }_0$ are captured until there are at least 750 configurations captured exactly at ${\lambda }_1$. The flux from the basin to the first milestone $\text{Φ}\left({\lambda }_1/{\lambda }_0\right)$ is given by the total number of crossings divided by the total simulation time and normalized by the wall’s area. Because the evaporation here is surface-induced and nucleation-limited, it is reasonable to normalize by the area. Using equation S12 from ref. 53, we estimate that the roughly cylindrical critical nuclei have radii ranging from 0.65 to 1.0 nm. These dimensions are smaller than, but comparable to, the linear dimension of our plates (∼3 nm). Accordingly, we expect some edge effects, with true linear scaling of rate with area arising at somewhat larger plate sizes.

The conditional probability of the system at milestone ${\lambda }_i$ reaching the next milestone ${\lambda }_{i+1}$ was calculated by randomly selecting a configuration at ${\lambda }_i$, randomizing the linear velocities of the center of mass of and angular momenta of the water molecules and the velocities of the mobile wall atoms according to the Maxwell–Boltzmann distribution, and launching an MD simulation. $\lambda$ is then monitored to see whether the trajectory reaches ${\lambda }_{i+1}$ before returning to the basin at ${\lambda }_0$. After many trials, the total number of successes reaching ${\lambda }_{i+1}$ divided by the total number of attempts yields the conditional probability $P\left({\lambda }_{i+1}\text{|}{\lambda }_i\right)$. At least 750 configurations were captured at each milestone, and the next milestone was typically chosen so that the transition probability was roughly 0.01. This procedure is propagated starting with the set of configurations captured at ${\lambda }_1$ until reaching the basin of the final state $B$, at which point the transition probabilities converge to unity. The rate from $A$ to $B$ is given by

$$rat{e}_{AB}=\mathrm{\Phi }({\lambda }_1/{\lambda }_0){\displaystyle \prod }_{i=1}^{i=n-1}P\left({\lambda }_{i+1}\text{|}{\lambda }_i\right),$$

where $n$ is the total number of milestones.

Free Energy Profiles.

Free energy profiles were calculated by performing FFS in both forward and reverse directions (44). The stationary distribution of $\lambda$ is formulated as $P\left(\lambda \right)={\psi }_A\left(\lambda \right)+{\psi }_B\left(\lambda \right)$, where ${\psi }_A\left(\lambda \right)$ is the contribution to the probability density from the trajectories that originated in basin $A$, and ${\psi }_B\left(\lambda \right)$ is the contribution from those originating in $B$. ${\psi }_A\left(\lambda \right)$ is calculated through ${\psi }_A\left(\lambda \right)=p_A\mathrm{\Phi }({\lambda }_1/{\lambda }_0){\tau }_A\left(\lambda ;{\lambda }_0\right)$, where $p_A$ is the probability that the system is observed in basin $A$ (i.e., ${\lambda }_0=\hspace{0.17em}<\lambda {>}_A\hspace{0.17em}\pm \hspace{0.17em}{\sigma }_{\lambda }$) and ${\tau }_A\left(\lambda ;{\lambda }_0\right)$ is the characteristic time that a trajectory originating at ${\lambda }_0$ spends at $\lambda$, given by ${\tau }_A\left(\lambda ;{\lambda }_0\right)={\pi }_A\left({\lambda }_1;{\lambda }_0\right)+{\displaystyle \sum }_{i=1}^{n-1}{\pi }_A(\lambda ;{\lambda }_i){\displaystyle \prod }_{j=0}^{i-1}P\left({\lambda }_{j+1}\right|{\lambda }_j)$. ${\pi }_A\left(\lambda ;{\lambda }_i\right)$ is the average time a trajectory originating at ${\lambda }_i$ spends at $\lambda$ and, if the MD time step remains constant throughout the calculation, is given by ${\pi }_A\left(\lambda ,{\lambda }_i\right)=\frac{H_{\lambda }}{\text{Δ}\lambda M_i}$, where $H_{\lambda }$ is the number of the times $\lambda$ is sampled for a set of trials originating at ${\lambda }_i$, $\text{Δ}\lambda$ is the discretization of $\lambda$ (1 in this work because $N$ is discrete), and $M_i$ is the total number of trajectories launched from ${\lambda }_i$. ${\psi }_B\left(\lambda \right)$ is calculated in an identical manner via an FFS calculation in the reverse direction. $p_A$ and $p_B$ are estimated via $p_{A}rat{e}_{AB}=\hspace{0.17em}{p}_{B}rat{e}_{BA}$ and $p_A\hspace{0.17em}+\hspace{0.17em}{p}_B=1$. The above relations come from the fact that, aside from a miniscule fraction of time, the system resides in either state $A$ or $B$.

Instantaneous Interface Calculation

Here, we use the instantaneous interface technique of Willard and Chandler (51) to delineate the vapor/liquid interface and follow the specific procedure advanced by Remsing et al. (53) to account for the density of the confining surface. For a specific configuration $\overline{\mathbf{R}}$ the coarse grained density profile ${\rho }_{\alpha }(x,y,z;\overline{\mathbf{R}})$ of an individual atom $\alpha$ (taken as either oxygen or plate atoms in this work) is found through convolution of its local density with a coarse-graining function $\varphi$:

$${\rho }_{\alpha }\left(x,y,z;\overline{\mathbf{R}}\right)={\displaystyle \sum }_{i=1}^{N_{\alpha }}\varphi \left(x_i-x\right)\varphi \left(y_i-y\right)\varphi \left(z_i-z\right),$$

where $N_{\alpha }$ is the number of $\alpha$ atoms and $(x_i,y_i,z_i)$ is the Cartesian coordinate of atom $i$. The total normalized coarse-grained density is given by

$$\overline{\rho }\left(x,y,z;\overline{\mathbf{R}}\right)=\frac{{\rho }_{water}\left(x,y,z;\overline{\mathbf{R}}\right)}{{\rho }_{bulk\hspace{0.17em}water}}+\frac{{\rho }_{plate}\left(x,y,z;\overline{\mathbf{R}}\right)}{\text{max}\left[{\rho }_{plate}\left(x,y,z;\overline{\mathbf{R}}\right)\right]},$$

where ${\rho }_{bulk\hspace{0.17em}water}$ is the coarse-grained density of bulk water. Such a definition provides that $\overline{\rho }$ is nearly 1 both in bulk water and within a plate. The interface is then defined to be the set of points such that $\overline{\rho }=0.5$. A configuration is divided into a 3D grid with a 1 Å spacing in each dimension. $\varphi$ is chosen as a Gaussian, with a width of 2.4 Å, which is truncated and shifted at 7 Å and then normalized. Linear interpolation between nearest-neighbor grid points that bracketed $\overline{\rho }=0.5$ was used to estimate the precise location of the interface.

Strain-Energy Calculation

A linear elastic material subject to an engineering strain $\mathit{ϵ}$, will exhibit a stress $\sigma =E\mathit{ϵ}$, where the constant of proportionality $E$ is Young’s modulus (48). The strain energy per unit volume in the material accompanying deformation $\text{Δ}u$ is found through integrating $\sigma$:

$$\mathrm{\Delta }u=\frac{1}{2}E{\mathit{ϵ}}^2+\hspace{0.17em}{u}_0,$$

where $u_0$ is the intensive strain energy at zero deformation.

To calculate $E$ in the plates, the location of the top rows of atoms in both plates was strained upward (Fig. 1) by increments of 0.01 Å up to 0.55 Å (corresponding to engineering strains from 0 to 0.0175). At each strain, an NVT simulation was used to calculate the average total strain energy $<U>$ in the plates. The slope of a linear fit of $\frac{<U>-<U_0>}{V}$ vs. $\frac{1}{2}{\mathit{ϵ}}^2$, where $V$ is the volume of an unstrained plate, yielded $E$.