Biological regulation of atmospheric chemistry en route to planetary oxygenation

Significance

It has been proposed that enhanced methane fluxes to Earth’s early atmosphere could have altered atmospheric chemistry, initiating a hydrocarbon-rich haze reminiscent of Saturn’s moon Titan. The occurrence, cause, and significance of haze development, however, remain unknown. Here, we test and refine the “haze hypothesis” by combining an ultra-high-resolution sulfur- and carbon-isotope dataset with photochemical simulations to reveal the structure and timing of haze development. These data suggest that haze persisted for ∼1 million years, requiring a sustained biological driver. We propose that enhanced atmospheric CH₄, implied by the presence of haze, could have had a significant impact on the escape of hydrogen from the atmosphere, effectively contributing to the terminal oxidation of Earth’s surficial environments ∼2.4 billion years ago.

Abstract

Emerging evidence suggests that atmospheric oxygen may have varied before rising irreversibly ∼2.4 billion years ago, during the Great Oxidation Event (GOE). Significantly, however, pre-GOE atmospheric aberrations toward more reducing conditions—featuring a methane-derived organic-haze—have recently been suggested, yet their occurrence, causes, and significance remain underexplored. To examine the role of haze formation in Earth’s history, we targeted an episode of inferred haze development. Our redox-controlled (Fe-speciation) carbon- and sulfur-isotope record reveals sustained systematic stratigraphic covariance, precluding nonatmospheric explanations. Photochemical models corroborate this inference, showing Δ³⁶S/Δ³³S ratios are sensitive to the presence of haze. Exploiting existing age constraints, we estimate that organic haze developed rapidly, stabilizing within ∼0.3 ± 0.1 million years (Myr), and persisted for upward of ∼1.4 ± 0.4 Myr. Given these temporal constraints, and the elevated atmospheric CO₂ concentrations in the Archean, the sustained methane fluxes necessary for haze formation can only be reconciled with a biological source. Correlative δ¹³C_Org and total organic carbon measurements support the interpretation that atmospheric haze was a transient response of the biosphere to increased nutrient availability, with methane fluxes controlled by the relative availability of organic carbon and sulfate. Elevated atmospheric methane concentrations during haze episodes would have expedited planetary hydrogen loss, with a single episode of haze development providing up to 2.6–18 × 10¹⁸ moles of O₂ equivalents to the Earth system. Our findings suggest the Neoarchean likely represented a unique state of the Earth system where haze development played a pivotal role in planetary oxidation, hastening the contingent biological innovations that followed.

Quadruple sulfur isotope fractionation is one of the most robust geochemical tools available to constrain the atmosphere’s redox state, owing to intrinsic links between atmospheric photochemistry and oxygen (1–11). Prior to ∼2.4 billion years ago (5, 6), sedimentary S-phases display mass-independent S-isotope fractionation (S-MIF; Δ³³S and Δ³⁶S≠ 0),* which is conspicuously absent in the younger geological record (5–7, 11). The disappearance of S-MIF is widely cited as reflecting a critical change in the Earth’s atmospheric state, where oxygen exceeded 0.001% of present atmospheric levels (3) during the so-called Great Oxidation Event (GOE; 4–6, 12). More recently, however, the perception of the GOE sensu stricto has been questioned by emerging data derived from 3.0–2.5-billion-year-old sedimentary rocks, interpreted to represent both earlier accumulation(s) of atmospheric oxygen/ozone (13–16) as well as transient descents toward a reduced methane-rich atmospheric state (8, 9, 17, 18).

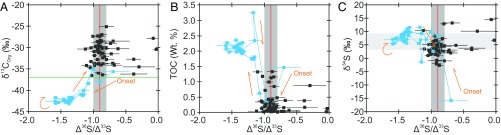
Interrogation of the temporal S-MIF record reveals additional details—variable magnitude and changes in Δ³⁶S/Δ³³S slope—that are suggested to reflect subtle atmospheric compositional changes beyond the simple presence or absence of oxygen (6–10, 12, 17, 19–21). Specifically, geochemical records from multiple continents reveal a broad correlation between changes in the S-MIF record and highly ¹³C-depleted organic carbon—termed C-S anomalies (8)—that have been interpreted to reflect the periodic formation of a hydrocarbon haze reminiscent of that observed on Saturn’s moon Titan (8–10). Although these records have been used to paint an intriguing picture of Neoarchean atmospheric dynamics in the prelude to the GOE (8, 9), a critical appraisal of the Neoarchean haze hypothesis awaits (22). We present high-resolution, coupled quadruple sulfur- and carbon-isotope, Fe-speciation, and total organic carbon (TOC) records (Fig. 1) from the youngest of the three C-S anomalies identified in core GKF01, obtained from Griqualand West Basin, South Africa (Fig. 1A, Fig. S1, Geological Setting and Age Model, Dataset S1, and refs. 9, 15, 23, and 24), resulting in the highest temporal-resolution stratigraphic study yet conducted in the Archean. Critical to testing the haze hypothesis, our geochemical records reveal the timing and structure of a C-S anomaly, which when combined with an updated photochemical model demonstrate a connection between changes in Δ³⁶S/Δ³³S ratios and atmospheric haze. Following this, we speculate on the wider role of episodic haze formation in planetary oxidation.

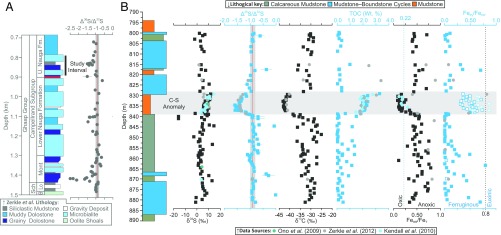
Fig. 1.

Preexisting lithological and geochemical data from core GKF01 (9) combined with new high-resolution geochemical data. (A) The published low-resolution GKF01 Δ³⁶S/Δ³³S record (9), the Neoarchean reference array (red line), and its ±0.1 uncertainty envelope (gray vertical band; ref. 8). (B) The new δ³⁴S, Δ³⁶S/Δ³³S, δ¹³C, TOC, and Fe-speciation (Fe_HR/Fe_T, Fe_Py/Fe_HR) data (squares) along with published data (filled circles; refs. 9, 15, and 24). The horizontal gray band signifies the C-S anomaly (discussed in the text). The vertical red line and gray envelope in the Δ³⁶S/Δ³³S plot represent the Neoarchean reference array and its associated uncertainty (± 0.1; ref. 8). Vertical lines in the Fe-speciation plots distinguish oxic from anoxic (Fe_HR/Fe_T ≥ 0.38) and ferruginous from definitively euxinic (Fe_Py/Fe_HR > 0.7) water column conditions. The open symbols in the Fe_HR/Fe_Py plot have Fe_HR/Fe_T <0.22, signifying oxic sedimentation (9, 15, 67). Assimilating these observations, sedimentation during the examined interval was likely dynamic, with a generally ferruginous background state (Fe_HR/Fe_T >0.38; Fe_Py/Fe_HR <0.7), becoming oxygenated during the C-S anomaly (Fe_HR/Fe_T <0.22; ref. 15). The definition of Fe_HR, Fe_Py, and Fe_T are given as a footnote to the text in Constraining the Timing and Drivers of Atmospheric Haze Formation, whereas the derivation of the diagnostic Fe-speciation threshold values are given in Methodology, Sedimentary Fe Speciation. Analytical uncertainties (1 SD, 1σ) are typically encompassed within each individual data point with the exception of a few Δ³⁶S/Δ³³S ratios whose uncertainty was computed from larger of the internal or external 1σ uncertainties associated with the raw Δ³³S and Δ³⁶S data (9). The large-scale lithological log (A) follows that presented in Zerkle et al. (9), whereas the new data (B) are plotted against the detailed sedimentary logs, which along with core photos are available online (general.uj.ac.za/agouron/index.aspx).

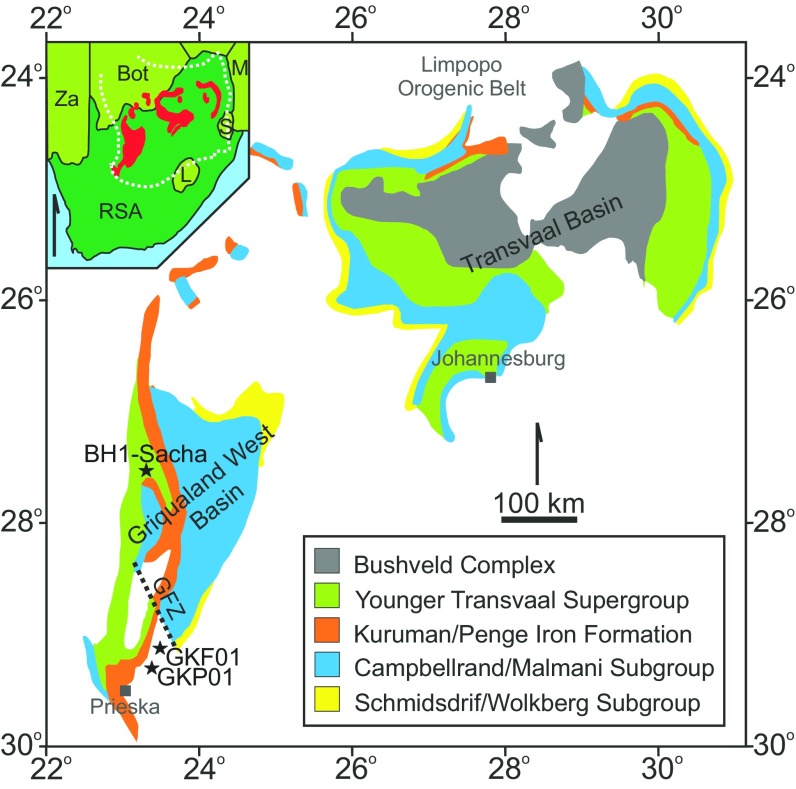
Fig. S1.

Geological map of the Transvaal Supergroup preserved on the Kaapvaal Craton with a geographical insert, modified from refs. 53 and 68. The position of cores where Δ³⁶S/Δ³³S–δ¹³C covariation has been previously reported (core GKF01, ref. 9; core BH1-Sacha, ref. 8) is indicated by labeled stars. Additionally the extra Agouron core (GKP01) that we discuss below in terms of chronological constraints is also given. The shallow-water Ghaap plateau facies are separated from their deep-water equivalents by the fault at Griquatown (GFZ; refs. 37 and 53), hence the different stratigraphic nomenclature between Zerkle et al. (9) and Izon et al. (8).

Results

In core GKF01, the upper Nauga Formation reveals large multiple S-isotope variability, with nonzero Δ³³S and Δ³⁶S (Figs. 1 and 2, Fig. S2, and Dataset S1), reflecting photochemical production in an atmosphere devoid of significant free oxygen (1–3, 6, 7). The majority of these data form a linear Δ³⁶S/Δ³³S array (Fig. 2), typifying core GKF01 (9, 18) and the wider Neoarchean as a whole (Δ³⁶S ≈ −0.9 × Δ³³S). Of importance for this study, the Δ³⁶S/Δ³³S record reveals a coherent stratigraphic structure with a remarkably stable background (Δ³⁶S/Δ³³S = −0.9) punctuated by a spectacular negative excursion between 840.0 and 827.87 m core depth. During the excursion Δ³⁶S/Δ³³S ratios become increasingly negative (Fig. 1B), attaining a steeper slope of ∼−1.5, before relaxing back toward the background Δ³⁶S/Δ³³S (−0.9; Figs. 1 and 2). Whereas the Δ³⁶S/Δ³³S data display little variability outside of the identified excursion (Fig. 2), the magnitude of the Δ³³S and Δ³⁶S is highly variable, carrying positive and negative arithmetic signs, respectively (Fig. S2 and Dataset S1). Consequently, it seems that the dominant sulfur source for pyrite formation over the examined interval was elemental sulfur, inferred to carry a positive Δ³³S (7, 18, 25). Atypically, the δ³⁴S record displays little variability, with the exception of two relatively more ³⁴S-depleted samples seen at ∼840 m (Fig. 1).

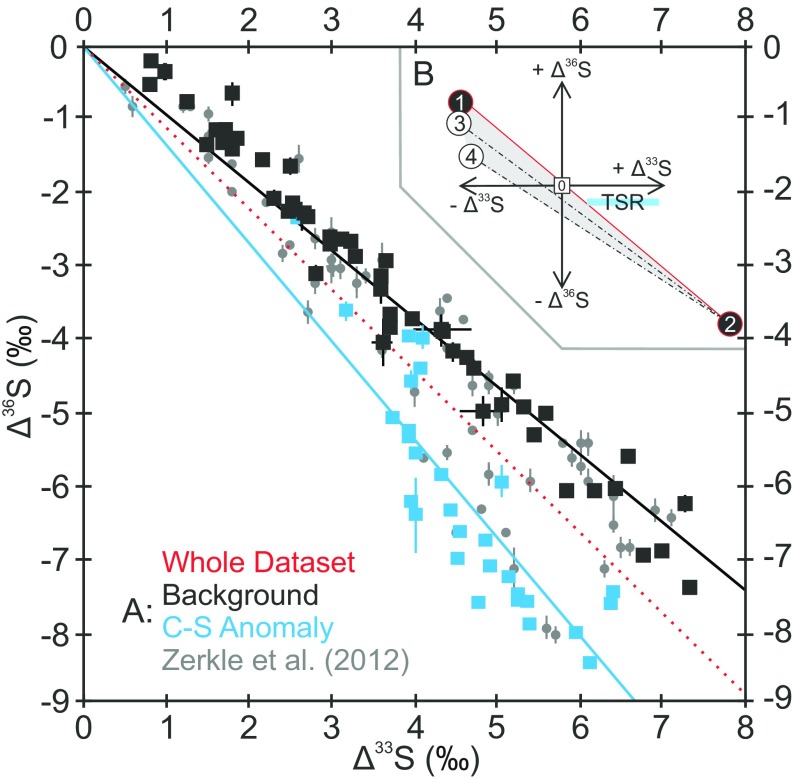
Fig. 2.

Quadruple S-isotope data from core GKF01 (A) with a schematic mixing scenario (B). Δ³⁶S vs. Δ³³S trends for the new data (black and blue) superimposed on previously published data (gray circles; ref. 9). Regressions are given through the whole dataset (red) as well as through the C-S anomaly (blue) and background (black). Uncertainties are plotted conservatively, using the larger of the internal or external uncertainty (1σ), and are consistently smaller than a single data point. The insert (B) schematically illustrates the range of Δ³³S and Δ³⁶S values that can be expressed in pyrite (shaded gray area) formed via mixing of sulfide derived from MSR (open circles 3–4) with atmospherically derived S-MIF carried by sulfate (filled circle 1) and elemental sulfur (filled circle 2). The horizontal blue bar illustrates the Δ³⁶S-Δ³³S systematics of TSR derived sulfide. Note, biological activity has the potential to exert greater influence on Δ³⁶S/Δ³³S when pyrite carries a negative Δ³³S (i.e., derived from sulfate) rather than a positive Δ³³S (29) as observed in the C-S anomaly (Fig. 1). Additionally, mixing with TSR-derived sulfide moves the Δ³⁶S/Δ³³S to less negative values.

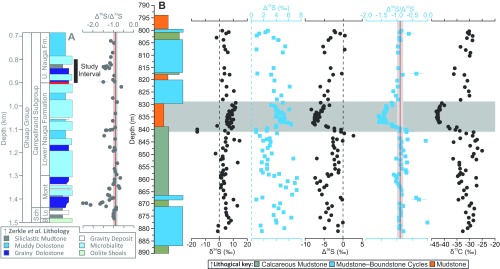
Fig. S2.

A depicts the stratigraphic distribution of the preexisting data (9) and B illustrates the new S- and C-isotope data (δ³⁴S, Δ³³S, Δ³⁶S, Δ³⁶S/Δ³³S, and δ¹³C_Org). The horizontal gray band illustrates the C-S anomaly, whereas the vertical red lines and their gray envelopes depict the Neoarchean reference array and its associated uncertainty (8). Analytical uncertainties are generally encompassed within individual datapoints, whereas uncertainty on the Δ³⁶S/Δ³³S ratio is computed from the larger of the internal or external uncertainties for Δ³⁶S and Δ³³S. Note the C-S anomaly predates the lithological change (see also Fig. S3).

Moving in phase, or perhaps even leading the S-isotope record, δ¹³C_Org is also observed to descend to extremely low values (less than −37‰; Fig. 1B), a relationship that is particularly apparent in Fig. 3A where Δ³⁶S/Δ³³S ratios less than −1 correspond to δ¹³C_Org^† less than −37‰, and the most ¹³C-depleted samples relate to the lowest Δ³⁶S/Δ³³S. We observe additional low δ¹³C_Org values (∼−35‰) below the C-S anomaly that are not associated with changes in Δ³⁶S/Δ³³S but correspond to small-scale increases in TOC typical of the intercalated mudstones that are below the scale to be illustrated in Fig. 1.

Fig. 3.

Carbon isotope (δ¹³C) (A), TOC (B), and δ³⁴S (C) vs. Δ³⁶S/Δ³³S data from 800- to 900-m core depth in core GKF01. In each plot the data have been color-coded, differentiating the background (black) from the C-S anomaly (blue), with orange arrows illustrating its temporal evolution. Vertical red lines in each plot give the average Neoarchean Δ³⁶S/Δ³³S with a ±0.1 uncertainty envelope (vertical gray bar; ref. 8). The horizontal green line in A marks δ¹³C = −37‰, a threshold commonly used to identify methanotrophy (8, 9, 26). The horizontal gray bar in C represents the range of seawater δ³⁴S estimates derived from carbonate associated sulfate (55). Typically analytical uncertainty is encompassed within the data points, with the exception of a few Δ³⁶S/Δ³³S ratios as in Fig. 2.

The C-S anomaly is not confined wholly to the mudstone interval, as cursory consideration of Fig. 1 would suggest. The decreases in both geochemical parameters are observed to have occurred by 840-m core depth; however, closer inspection of detailed core logs/photos (Fig. S3, Geological Setting and Age Model, and Dataset S1) shows that the lithological change from carbonate to mudstone occurs 0.6–1.0 m above this chemostraigraphic horizon. Similarly, whereas the most depleted Δ³⁶S/Δ³³S ratios are confined to the basal half of the mudstone, the return to background Δ³⁶S/Δ³³S is not established until 827.8 m, some 1.5 m above the reestablishment of calcareous sedimentation (Fig. 1, Fig. S3, Geological Setting and Age Model, and Dataset S1). These observations require chemostratigraphic controls beyond simple facies or lithological changes.

Fig. S3.

Initial core photographs corresponding to the onset of the C-S anomaly. The cores become progressively younger up the page, as signaled by the bold yellow arrow and initial core markings. The older (deeper) core tray (A) is joined to the younger (shallower) tray B by the bold black arrows. The onset of the C-S anomaly (in both Δ³⁶S/Δ³³S and δ¹³C) is seen by 840-m core depth (annotated), whereas the change in lithology (from calcareous mudstone to mudstone) occurs at least 1 m up-core, in younger rocks. Thin red arrows highlight this nontrivial stratigraphic difference. Core photographs and detailed lithological logs of cores GKF01 and GKP01 are available via the Agouron-Griqualand Paleoproterozoic drilling project online database (general.uj.ac.za/agouron/index.aspx). These photos feature overlap (core markings and vertical blue boxes), and hence repetition of strata, to ensure the entire core was imaged.

Discussion

The Causes and Significance of the Sulfur and Carbon Isotope Covariation.

The broad correspondence between low Δ³⁶S/Δ³³S and δ¹³C_Org has formed the cornerstone of the “haze hypothesis,” whereby enhanced methane flux (manifested as low δ¹³C_Org) is hypothesized to have promoted organic-haze formation and altered atmospheric chemistry (registered as Δ³⁶S/Δ³³S; refs. 8 and 9). The low-resolution records generated in these prior studies, however, have precluded rigorous examination of this hypothesized link, which in turn has obfuscated the wider role of haze formation within the evolution of the ancient Earth system. As a result this early work failed to reveal the stratigraphic structure of a C-S anomaly beyond a few scattered data points. Our geochemical records (Fig. 1, Fig. S2, and Dataset S1) provide a framework from which to examine the origin of the observed C- and S-isotope covariation.

The δ¹³C of sedimentary organic matter (δ¹³C_Org) is an integrated product, combining varying contributions from different biological sources. Contemporary and Phanerozoic δ¹³C_Org records display restricted variability owing to the limited C-isotope fractionation associated with heterotopic respiration. The Neoarchean, by contrast, features a more pronounced range of δ¹³C_Org, indicating more pervasive incorporation of ¹³C-depleted substrates, particularly methane (26). Accordingly, the low δ¹³C_Org (<−37‰) seen in the C-S anomaly, and probably the intermediate δ¹³C_Org (<−35‰) in the basal part of the examined succession (<840 m; Fig. 1), speak to substantial methane incorporation into sedimentary organic matter. In greater detail, this incorporation involves the interplay between localized methane production (methanogenesis), oxidation, and assimilation (methanotrophy; ref. 26). Therefore, the low δ¹³C_Org data observed in GKF01 (and other Neoarchean sedimentary successions) can be explained in two ways: (i) increased methanotrophy assimilating more methane into the sedimentary record independent of the methane flux (26, 27) or (ii) enhanced methanogenesis increasing environmental methane availability, with a parallel increase in methanotrophy (8, 9). Sedimentary δ¹³C_Org values are controlled locally and reflect the carbon utilization strategies of the microbial communities from which the organic matter is sourced. Therefore, the haze hypothesis does not require every inflection in the δ¹³C_Org record to correspond to altered atmospheric chemistry. In fact, one prediction of the haze hypothesis is that there should be instances where Δ³⁶S/Δ³³S and δ¹³C_Org are decoupled (8), such as below 840 m in core GKF01 (Fig. 1).

An Alternate, Nonatmospheric, Control on Δ³⁶S/Δ³³S?

The haze hypothesis is reliant on the Δ³⁶S/Δ³³S parameter faithfully recording what is inferred to be regional to global-scale atmospheric chemistry. The high-resolution dataset we present here (Fig. 1) provides the perfect opportunity to test alternative hypotheses, whereby nonatmospheric, sediment-hosted processes could have produced the observed changes in the Δ³⁶S/Δ³³S record.

Biological metabolic processes are known to impart small mass-dependent effects during inter- and intracellular (un)mixing processes (19, 28). Biologically mediated mass conservation effects are known to preferentially affect Δ³⁶S, resulting in distinctive Δ³⁶S/Δ³³S slopes (∼−7; ref. 28), potentially overprinting the atmospheric Δ³⁶S/Δ³³S signal. The extent of such a biological overprint is quasi-predictably governed by initial source of pyrite sulfur, producing a scalene mixing field in Δ³⁶S-Δ³³S quadruple-isotope space (Fig. 2B and ref. 29). Because microbial sulfate reduction (MSR) imparts the largest biological S-isotope fractionations, this biological effect is most pronounced when the pyrite sulfur is dominated by a sulfate precursor (negative Δ³³S) and becomes progressively more muted when elemental sulfur (positive Δ³³S) dominates the pyrite-sulfur pool (29). Examination of Fig. 2, Fig. S2, and Dataset S1 reveals the pyrite throughout the studied interval carries a pronounced and exclusively positive Δ³³S, in turn implying an elemental sulfur source, which is expected to be less susceptible to modification by MSR (Fig. 2). In addition to altering Δ³³S and Δ³⁶S, microbial processes are also generally associated with pronounced changes in δ³⁴S (60–70‰; ref. 30). However, as described above, the δ³⁴S record in the succession we examined is remarkably stable (Figs. 1 and 3C), offering little support for a biologically mediated model (19).

Thermochemical sulfate reduction (TSR) can also impart a distinctive S-MIF signature (Fig. 2B); however, this process also cannot explain our S-isotope observations. First, we see no evidence for selective hydrothermal activity associated with TSR in strata between 840.0 and 827.87 m. Decisively, TSR has been shown experimentally to impart large Δ³³S enrichments without significant changes in Δ³⁶S (31). Addition of TSR-derived sulfur, therefore, would serve to increase Δ³⁶S/Δ³³S ratios above the Neoarchean reference array, which is contrary to what we observe (Fig. 2).

A final possibility invokes an additional, and isotopically distinct, S-MIF production pathway capable of producing an additional sulfur pool with a distinct and different Δ³⁶S/Δ³³S (<−1.5), which could selectively contribute to pyrite genesis under variable conditions (32). The observed change in Δ³⁶S/Δ³³S could, therefore, reflect electron donor availability, highlighting a potential localized control on the degree of pyritization, whereby high TOC permitted selective access to a recalcitrant sulfur pool. Following this scenario, the increased TOC observed in the C-S anomaly (Fig. 1), could potentially provide a sediment-hosted explanation for the observed coupled C- and S-isotope covariation. This explanation would require a ubiquitous association between low Δ³⁶S/Δ³³S, δ¹³C_Org, and high TOC, which is not observed in our data or in previous datasets (Figs. 1–3 and refs. 8, 9, and 22). For example, closer examination of Fig. 3B shows there are samples that are enriched in TOC (∼1 wt %) yet display typical Δ³⁶S/Δ³³S ratios (−0.9). Similar trends are also obvious in published records, with typical Δ³⁶S/Δ³³S ratios being frequently observed in tandem with high TOC abundances (5% wt %; ref. 9). Also, if sedimentary Δ³⁶S/Δ³³S ratios were truly independent of time-dependent changes in atmospheric chemistry, the necessary refractory sulfur pool should be ever-present (independent of lithology) and should be observed in other portions of the geological record. For instance, a secondary sedimentary sulfur pool might be expected to be intermittently incorporated into pyrite under a particular range of depositional conditions, producing highly variable Δ³⁶S/Δ³³S values. This is not the case here (Fig. 1) and is also at odds with the wider Archean Δ³⁶S/Δ³³S record (19). Moreover, secondary ion mass spectrometry (SIMS) analyses reveal that Δ³⁶S/Δ³³S trends are conserved at the grain scale between different populations of pyrite within the GKF01 core as a whole (18). Therefore, any model driven by electron donor availability, reliant on a “ghost sulfur pool,” cannot be responsible for the observed change in Δ³⁶S/Δ³³S revealed in the C-S anomaly (Fig. 1). Taken together, sediment-hosted processes, such as biological modification, thermochemical alteration, and differential pyrite genesis, fail to satisfactorily explain the systematic changes in Δ³⁶S/Δ³³S starting at 840 m, leaving an atmospheric origin as the most parsimonious explanation of these data.

Photochemical Modeling of Δ³⁶S/Δ³³S.

Assimilating the arguments presented above, the two isotopic systems (C and S) that form the crux of the haze hypothesis are sensitive to perturbations on different spatial, and potentially temporal, scales. In principle, low δ¹³C_Org, and hence methane production/consumption, should be ubiquitous in the Archean, responding to local-scale changes in organic matter quality and quantity (8, 9, 26). In an atmospheric sense, however, it is unlikely that a short-lived change akin to what we observed in the intercalated subordinate mudstones in the basal part of the succession (>840-m core depth; Fig. 1) would result in a change in atmospheric methane concentrations capable of instigating haze formation. Instead, it would require a sustained regional increase in methane fluxes, caused by changes in nutrient delivery or redistribution in the oceans (discussed below), to plausibly increase atmospheric methane concentrations sufficiently to instigate haze formation. If haze development was substantial enough to enshroud the planet, it is also possible that Δ³⁶S/Δ³³S could be decoupled from δ¹³C_Org, if the site of methane production/consumption was occurring elsewhere.

To examine the direct link between Δ³⁶S/Δ³³S values and atmospheric chemistry, we updated and validated an Archean 1D photochemical model (7) to predict Δ³³S, Δ³⁶S, and trace Δ³⁶S/Δ³³S ratios through an atmospheric reaction network (Fig. S4 and Methodology, Photochemical Modeling). The most significant changes from the initial predictions of Claire et al. (7) arise from the inclusion of new data allowing Δ³⁶S predictions, and the use of newly measured SO₂ photodissociation cross-sections (33). As noted previously (7, 34), the earlier SO₂ cross-sections (35) produced results at odds to the commonly accepted interpretation of the geologic record: predicting positive Δ³³S in sulfate and negative Δ³³S in elemental sulfur. Incorporating the revised cross-sections (33) resolves this data–model mismatch and now predicts exit channels with the arithmetic sign commonly seen in the rock record (Figs. 4 and 5). However, it is important to note our model still fails to reproduce both the magnitude of the S-MIF and the Δ³⁶S/Δ³³S ratio archived in the geological record (Figs. 1, 4, and 5, Fig. S2, Methodology, Photochemical Modeling, and Dataset S1). A detailed exploration of this discrepancy exceeds the scope of this study, but likely reflects uncertainties concerning the primary S-MIF generating mechanism(s) included within the model and/or the composition of the Archean background state (Methodology, Photochemical Modeling and ref. 7). Both of these potential sources of uncertainty are the focus of ongoing research and remain fundamental to successful inverse reconstruction of the chemical composition of the Archean atmosphere.

Fig. S4.

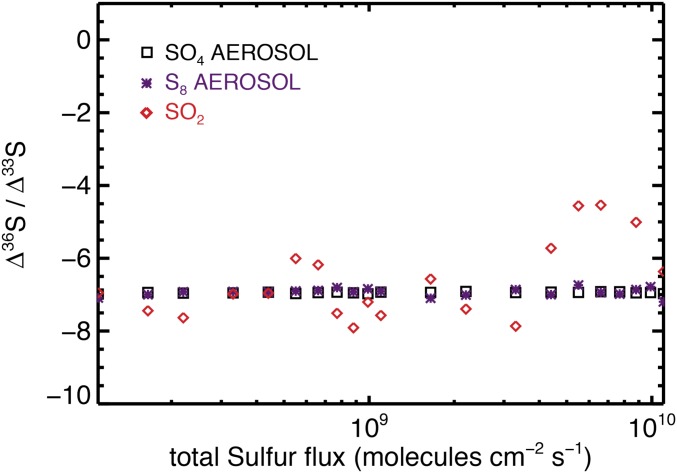
Model validation of the updated photochemical model presented herein. Here, multiple simulations have been run with variable atmospheric sulfur loading, with only mass-dependent fractionation factors included. Integrated over the whole atmospheric reaction pathway, the average Δ³⁶S/Δ³³S carried by sulfur (SO₄) aerosols, octasulfur (S₈) aerosols, and sulfur dioxide (SO₂) are given by black squares, purple crosses, and red diamonds, respectively.

Fig. 4.

Photochemical Δ³⁶S and Δ³³S predictions for the “standard atmosphere” (7) under normal conditions (A) and with differential sulfur loading (B). Under standard atmospheric conditions, in A sulfur leaves the model atmosphere unequally divided between three exit channels (SO₂, 56%; S₈, 24%; and SO₄, 18%). Values of Δ³⁶S/Δ³³S are displayed for the entire troposphere (filled circles), with the large squares showing the ground-level signal carried by a specific exit channel combining both wet and dry deposition. B recreates the experiment illustrated in figures 6 C and D in Claire et al. (7), where the total volcanic sulfur flux to the model atmosphere is varied over two orders of magnitude (10⁸–10¹⁰ molecules⁻² s⁻¹). The spatial distribution of atmospherically important species within the standard atmospheric framework is displayed in figure 2 of Claire et al. (7), where the following boundary conditions were adopted: volcanic sulfur flux of 3.85 × 10⁹ molecules⁻² s⁻¹ (∼1 Tmole y⁻¹) at an H₂S:SO₂ ratio of 1:10 and a volcanic H₂ flux of 1 × 10¹⁰ molecules⁻² s⁻¹ (∼3 Tmole y⁻¹). Fixed ground-level mixing ratios of 100 ppm and 10 ppb for CH₄ and O₂, respectively. Carbon dioxide concentrations were fixed at 1% at all heights, and N₂ provided a total atmospheric pressure of 1 bar. Full details of the model, validation, and its limitations are appended (Methodology, Photochemical Modeling).

Fig. 5.

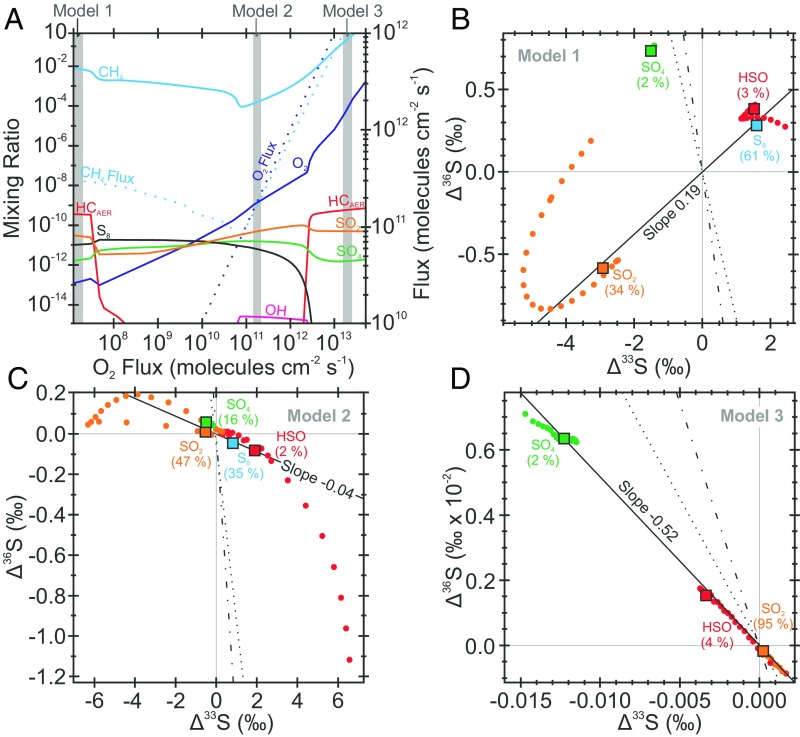
Simulated Δ³⁶S/Δ³³S response to varying O₂ and CH₄ fluxes. (A) The three distinct atmospheric states (models 1–3, B–D) that were chosen to examine the effect of a hydrocarbon haze on atmospheric chemistry (numbered vertical gray bands in A). The first model simulates a thick hydrocarbon haze before the advent of oxygenic photosynthesis (B), whereas the second and third models represent haze-free (C) and hazy (D) states after the advent of oxygenic photosynthesis (7, 10). Under each atmospheric regime (B–D) the Δ³⁶S/Δ³³S carried by each atmospheric exit channel, at specific atmospheric height, is plotted as color-coded circles, whereas the atmospherically integrated signal (the ground-level value) of each vector is represented by a color-coded square. The relative importance of each exit channel is given in parentheses. In A the mixing ratios of atmospheric species are shown as solid lines (left axis), and fluxes are shown as dashed lines (right axis). In B–D the Archean reference array (Δ³⁶S/Δ³³S = −0.9; ref. 8), the steepened slope reflecting the C-S anomaly (Fig. 1) and the best fit to the simulated data are given by the dotted, dot-dashed, and solid lines, respectively. Full details of the model, validation, and its limitations are given in Methodology, Photochemical Modeling. Zero Δ³⁶S and Δ³³S data are given as gray lines to illustrate the change in scale between B–D.

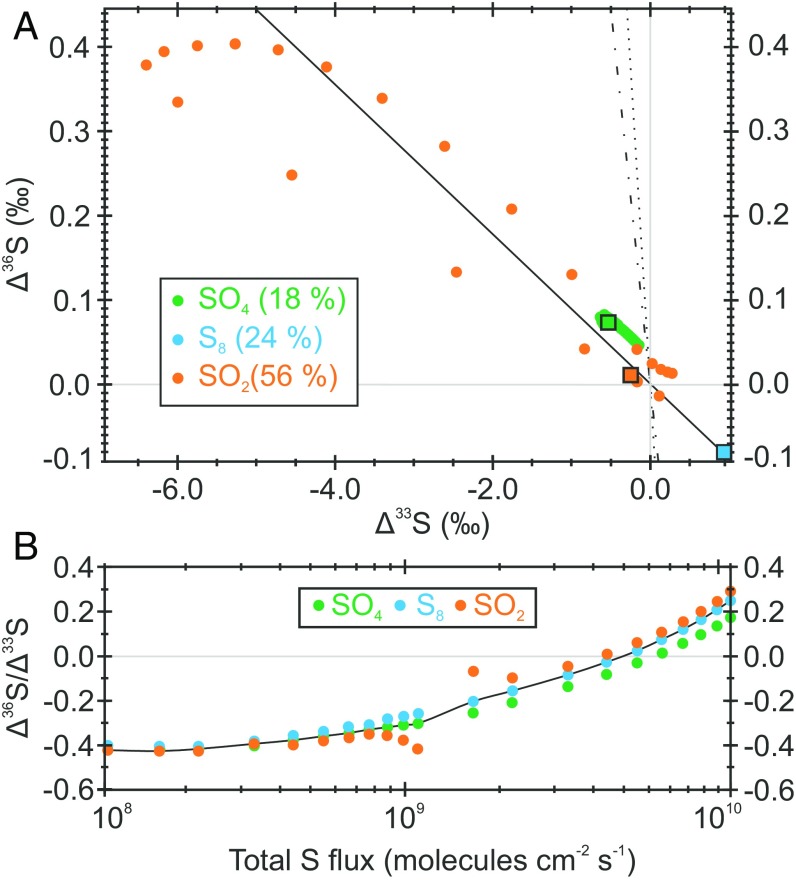
Fig. 4A provides insight into the transmittance of Δ³⁶S/Δ³³S ratios through an atmospheric reaction network. Exploiting the putative Neoarchean atmospheric composition (the “standard model”) envisaged by Claire et al. (7), sulfur species leave the atmosphere unequally divided between three exit channels. The model predicts that aerosol exit channels (SO₄ and S₈) feature fairly homogeneous Δ³⁶S/Δ³³S signatures irrespective of the height of their tropospheric genesis. By contrast, the predicted Δ³⁶S/Δ³³S ratios communicated to SO₂ vary substantially through the troposphere. Sulfur dioxide (SO₂) exits the atmosphere primarily dissolved in rainwater, so homogenization likely precludes the expression of the modeled Δ³⁶S/Δ³³S variability (Figs. 4 and 5). Aerosol species, by contrast, should serve as more instantaneous vectors carrying the entire range of Δ³⁶S/Δ³³S to the Earth’s surface, resulting in spatial variability independent of atmospheric chemistry. Consequently, the modeled Δ³⁶S/Δ³³S stability in aerosols is reassuring, advocating Δ³⁶S/Δ³³S ratios as a conservative parameter reflective of a given atmospheric state; that, unlike the absolute S-MIF magnitude (32), would be unlikely to display significant widespread spatial variability under a truly global atmospheric state. This fits well with the stable background Δ³⁶S/Δ³³S (−0.9) that is observed throughout the majority of the 100 m [11.7 ± 3.3 million years (Myr); Geological Setting and Age Model] of examined core (Fig. 1) and the wider Archean record (19).

The utility of Δ³⁶S/Δ³³S ratios is extended via examination of Fig. 4B. Here, we present results from 22 distinct model atmospheres where the total volcanic sulfur flux was varied over two orders of magnitude. This experiment alters the atmospheric redox state, enhancing the relative importance of the S₈ exit channel in the more sulfur-laden atmospheres. Fig. 4B shows that within each model atmosphere the Δ³⁶S/Δ³³S ratios of all exit channels remain homogenous (±0.1), in turn supporting our claim that Δ³⁶S/Δ³³S reflects the instantaneous state of atmospheric chemistry. The range and systematic decrease in Δ³⁶S/Δ³³S observed between simulations (+0.2 to −0.4) highlights the sensitivity of Δ³⁶S/Δ³³S ratios to atmospheric composition, advocating Δ³⁶S/Δ³³S as a promising atmospheric probe—a conclusion that extends beyond both the chosen experiment (sulfur loading) and our predicted magnitudes.

To examine the ability of an organic haze to modulate Δ³⁶S/Δ³³S, we varied the O₂ and CH₄ fluxes (7, 10) to create two different hazy states (models 1 and 3 in Fig. 5 B and D) along with an additional clear-skies atmospheric state (model 2 in Fig. 5C). Similar to the cases presented previously (Fig. 4A), the incorporation of the new cross-sections (33) causes the Δ³³S predictions to deviate from those presented previously (7), qualitatively approximating the geological record. Our simulated hazy atmospheric states produce Δ³⁶S/Δ³³S slopes (+0.19, Fig. 5B and −0.52, Fig. 5D) that differ from the clear-skies simulation (−0.04, Fig. 5C). The clear-skies simulation in Fig. 5C has distinct boundary conditions that are broadly similar to the “standard atmosphere” (Fig. 4A and ref. 7) so their similar Δ³⁶S/Δ³³S provides additional confidence that Δ³⁶S/Δ³³S slopes are the product of specific atmospheric states and do not vary widely with minor fluctuations in atmospheric state. We stress again that the absolute values of these predictions are preliminary and will likely change with additional model complexity (Methodology, Photochemical Modeling). Our approach here is not sufficient to make the claim that haze is uniquely responsible for variations in the Δ³⁶S/Δ³³S slope from −0.9 to −1.5. Rather, our more simple aim is to test the assertion that atmospheric reaction rates, exit channels, and UV transparency vary sufficiently underneath a hazy atmosphere to modulate the Δ³⁶S/Δ³³S ratios (7–10). The predicted uniformity of Δ³⁶S/Δ³³S ratios, expressed in all atmospheric exit channels, ultimately facilitates transmission from the atmosphere where they may be preserved in the geological record (8, 9, 18)—a key prediction of the haze hypothesis. Furthermore, the different Δ³⁶S/Δ³³S ratios produced under different atmospheric hazy regimes provide support to the idea that hazes in different parts of Earth history (e.g., before and after substantial biospheric O₂ fluxes) might yield unique S-MIF signatures (compare Fig. 5B and Fig. 5D) (8).

A caveat to these inferences hinges on pyrite genesis, the global vs. regional extent of the haze, and the photochemical origin of the pyrite-sulfur precursor. Under a global hazy atmospheric configuration, after mixing into the seawater sulfate reservoir putative hazy-type Δ³⁶S/Δ³³S ratios (−1.5) would be preserved within pyrite independent of its initial sulfur source (e.g., sulfate or elemental sulfur; Figs. 4 and 5). If regional haze development were possible, then conceivably pyrite could have inherited either a typical Archean Δ³⁶S/Δ³³S (−0.9) or a steeper hazy-type Δ³⁶S/Δ³³S (−1.5). Here, elemental sulfur would have carried the atmospheric Δ³⁶S/Δ³³S, and thus the localized instantaneous chemical state directly to pyrite. Contrastingly, pyrite produced from seawater sulfate would be expected to preserve a globally integrated signal, facilitated via oceanic mixing. Therefore, sulfate-sourced pyrite could carry a slope more characteristic of haze beneath a localized clear-skies atmospheric regime. Unfortunately, the current dataset displays exclusively positive Δ³³S (Fig. 2, Fig. S2, and Dataset S1), thus precluding a definitive appraisal of the precursor sulfur (18) in this particular C-S anomaly. Given that our pyrite record is derived from predominantly sulfur aerosols, reflecting instantaneous atmospheric chemistry, the shift in Δ³⁶S/Δ³³S indicates core GKF01 was deposited beneath a hazy sky, consistent with the observed C- and S-isotope covariation (Figs. 1 and 3A).

Constraining the Timing and Drivers of Atmospheric Haze Formation.

These geochemical and computational arguments lend credence to the haze hypothesis. Accordingly, we interpret the C-S anomaly as a chemostratigraphic marker of atmospheric haze development. The well-defined structure of the high-resolution C-S anomaly (Fig. 1) allows us to extract time constraints to reveal the tempo and duration of an inferred episode of haze development. Using existing radiometric age constraints (refs. 36–40 and Geological Setting and Age Model), and assuming linearity, application of average sedimentation rates suggests that haze persisted for 1.4 ± 0.4 Myr, attaining maximum haze thickness (lowest Δ³⁶S/Δ³³S) over 0.3 ± 0.1 Myr (3 m). Adopting these temporal constraints, even acknowledging the potential uncertainties of our approach (Geological Setting and Age Model) the development of Neoarchean atmospheric haze is inconsistent with rapid release of methane from a standing methane reservoir (such as methane hydrates) and requires a more sustained methane flux to the atmosphere.

Although contemporary sedimentary methane production is substantial, little escapes to the ocean–atmosphere system owing to efficient consumption by either aerobic methanotrophs or by a consortium of anaerobic methanotrophs and sulfate reducers (AOM) at the sulfate–methane transition zone (41–43). Nevertheless, within the oxygen- and sulfate-starved Neoarchean oceans (44–46) methanogens would have proliferated, whereas methanotrophs and AOM would have been spatially restricted. Correspondingly, enhanced Neoarchean methanogenesis would have likely translated into elevated atmospheric methane fluxes (41–43), supporting large background Archean methane concentrations (7, 10, 20, 21, 41, 47). When the CH₄:CO₂ mixing ratio exceeded a critical threshold of ∼0.1 this CH₄ flux would have formed an organic-rich hydrocarbon haze (9, 10, 20, 47), although the regional/global extent of these haze(s) requires further study.

Methanogens feature a complex biochemistry dependent on nickel-based metalloenzymes (48), which they use to produce methane at the expense of simple carbon compounds and molecular hydrogen (49, 50). Although reconstructed marine nickel concentrations suggest that post-2.7-Ga oceans were nickel-limited (49, 50), it is improbable that nickel alone was a stimulus for episodically heightened methane production necessary for haze production. The envisaged Neoarchean oceanic nickel depletion has been attributed to long-term unidirectional mantle cooling, changing the chemical composition of igneous rocks and concomitant marine nickel delivery (49, 50). In contrast, haze formation was geologically rapid and occurred repeatedly in the prelude to the GOE (8, 9), thus requiring a recurrent, yet geologically short-lived, driver. Although it is feasible that episodic volcanism could supply reactive igneous rocks, secular mantle cooling should have ensured their nickel content was progressively lower (49, 50). Perhaps more importantly, it is difficult to envisage a solely volcanic/hydrothermal driver that effectively decouples nickel delivery from other bioessential elements [e.g., P, N, Fe, Mo, etc. (13)].

Alternatively, episodic top-down stimulation of the entire biosphere, via enhanced primary productivity in the surface waters, could provide a more satisfactory trigger for haze development. This inference is supported by relatively high total organic-carbon (TOC) abundances (≥2%) within the C-S anomaly (Fig. 3B) compared with the Neoarchean average (1.5 ± 1.3 wt %; ref. 51). Although high TOC abundances could reflect diminished dilution by carbonate, enhanced productivity or preservation, the consistently low primary Fe_HR/Fe_T (<0.38) ratios observed during the C-S anomaly (Fig. 1B) suggest that oxic sedimentation persisted^‡ (9, 15), arguing against a preservational control. Contrasting redox inferences gleaned from the S-MIF and the Fe-speciation records further implicate marine productivity with atmospheric haze development. Here, the low Fe_HR/Fe_T (<0.38) ratios, in concert with limited enrichments in redox sensitive trace metals [e.g., Mo, Re and U (15)], signal mildly oxic sedimentation against an anoxic atmospheric backdrop (Fig. 1B). Given that atmospheric models insinuate O₂ residence times on the order of a few hours (7) and extremely reducing tropospheric conditions, these data can only be reconciled by oxygenic photosynthesis (15) creating locally oxygenated water column conditions and the development of an oxygen oasis (52). The production of oxygen and organic matter in surface environments and their destruction in deeper waters, the sediment–water interface and below, had the potential to spatially decouple oxygen and methane production, thereby offering a mechanism where methane could have escaped water column reoxidation and contributed to the atmospheric methane burden.

Excluding a facies control on the observed TOC increase is more difficult. The deepening experienced during the mudstone deposition probably inhibited carbonate deposition via isolation from the photic zone (23), hence reducing the dilutive effects of the biogenic carbonates during the C-S anomaly. That said, the small-intercalated mudstones in the basal part of the examined section (<840 m) represent the same facies change yet do not display the isotopic covariation that defines the C-S anomaly. This difference we explain as a function of scale: The mudstone containing the C-S anomaly has known lateral facies equivalents in core GKP01 (15, 23, 53), so independent of dilution-type effects, TOC-rich sediments were deposited across a larger area of the Griqualand West basin during the C-S anomaly. Thus, increased TOC deposition could have supplied ample organic carbon to fuel regionally pervasive methanogenesis, potentially enhancing methane fluxes to the atmosphere. Importantly, consistent with the predictions of atmospheric simulations (7), the persistence of large-magnitude S-MIF with changing Δ³⁶S/Δ³³S (Figs. 1 and 2, Fig. S2, and Dataset S1) demonstrates that the atmosphere remained essentially oxygen-free (1–3, 6, 7, 10) despite evidence for enhanced oxygen production (9, 15). Apparently the global sinks of water column reductants [(e.g., Fe²⁺ (4)], combined with reduced atmospheric gases (e.g., H₂ and CH₄), were still sufficient to prevent atmospheric oxygenation at this time (7, 10).

Deciphering the ultimate stimulus for the inferred biospheric invigoration, and associated ecological shifts, remains difficult, yet given the persistence of large-magnitude S-MIF (Figs. 1 and 2, Fig. S2, and Dataset S1) there is no need to invoke planetary-scale oxidative weathering by free atmospheric O₂ (13, 14). Alternate mechanisms such as episodic chemical weathering driven by changes in climate and/or tectonics could directly, or indirectly (via changes in ocean circulation and upwelling efficiency), have delivered the necessary nutrients to the photic zone over widespread areas. Additionally, the emergence and proliferation of terrestrial life (51) should have also revolutionized weathering efficiency via ground-level oxidative weathering (54), providing another mechanism to flux nutrients (e.g., P and bioessential trace elements), along with sulfate to the ocean, without any significant leak of O₂ to the atmosphere.

Pyrite δ³⁴S values are lowest at the base of the C-S anomaly (∼−15‰) before stabilizing to values close to those reconstructed from contemporaneous carbonate-associated sulfate from the Campbellrand carbonate platform (Figs. 1 and 3C, Fig. S2, and ref. 55). Whereas these few ³⁴S-depleted samples could easily reflect changes in sediment-housed microbial sulfur cycling and associated pyrite formation (19, 56), these data can also be reconciled with an initial weathering pulse delivering sulfate, and presumably other nutrients, to the biosphere. Beyond the fortuitous placement of the low δ³⁴S at the base of the C-S anomaly within an otherwise stable δ³⁴S record (Figs. 1 and 3C), unequivocal discrimination between these two potential explanations of the δ³⁴S data are challenging on the basis of bulk SF₆ measurements alone. Enigmatically, however, radiogenic ¹⁸⁷Os/¹⁸⁸Os_i ratios have recently been reported from the Mt. McRae shale, which can only be reconciled with crustal ¹⁸⁷Os ingrowth via β⁻ decay of ¹⁸⁷Re, followed by remobilization and delivery to the marine reservoir (14). The Mt. McRae succession is perhaps one of the most celebrated Archean sedimentary successions, containing the ∼2.5-billion-year-old trace-element enrichments that have been interpreted to represent pre-GOE whiffs of oxygen (13). Interestingly, as noted by Zerkle et al. (9), the upper Mt. McRae shale also features a change in Δ³⁶S/Δ³³S to lower values (57), which is broadly associated with a change in δ¹³C_Org—exhibiting some interesting parallels with the data presented herein. Unfortunately, the Mt. McRae shale data are of insufficient resolution to make meaningful comparisons with our own, and no Re-Os data exist for the C-S anomaly examined in Fig. 1. Clearly further targeted SF₆ and SIMS analysis, coupled with the application of sensitive radiogenic isotope tracers [e.g., Re-Os (58)], to this and other C-S anomalies (8, 9) has the potential to elucidate the source of the nutrients (weathering vs. oceanic nutrient redistribution) and should be a fruitful avenue of future research.

From an Earth system perspective, low seawater sulfate concentrations were likely an important prerequisite for haze formation, allowing methane to escape AOM in the sediment pile and enter the atmosphere. The Neoarchean oceans as a whole are inferred to have had historically low sulfate concentrations (16, 45), poising the biosphere at a tipping point, allowing the balance between methane production and consumption to shift rapidly following pulses of marine fertilization and attendant sedimentary carbon delivery (8). Consequently, enhanced productivity would be expected to strengthen methane production, creating inflections in the δ¹³C isotope record that are only coupled with changes in Δ³⁶S/Δ³³S when methane fluxes are sufficient to affect atmospheric chemistry. Eventually, however, enhanced terrestrial colonization (51, 54), combined with increasing biological oxygen production (9, 15) and waning availability of residual reductants (e.g., Fe²⁺), would have changed the marine budgets of electron acceptors [e.g., sulfate (51)], curbing biogenic methane fluxes via enhanced AOM (43) and ultimately changing the atmospheric response to biospheric stimulation (13, 15).

Haze Formation as a Harbinger of Planetary Oxidation?

Biogenic methane production has been proposed as an efficient hydrogen shuttle to the exosphere (41). Empirical studies throughout the solar system reveal that multiple processes combine to enable hydrogen escape from the upper atmosphere at its maximum theoretical rate (59), meaning that planetary hydrogen loss can be approximated by the diffusive supply of H-bearing compounds from the stratosphere (e.g., H₂, H₂O, and CH₄). Whereas freeze distillation confines water vapor to the troposphere, methane escapes Earth’s cold trap and supplies hydrogen to the stratosphere through photolysis, which can be lost instantaneously to space—irreversibly shedding reducing power and potentially explaining how the Earth’s surficial environment became irreversibly oxidized over long timescales (41, 59).

The abrupt change in Δ³⁶S/Δ³³S correlated to a decrease in sedimentary δ¹³C_Org seen in the C-S anomaly (Fig. 1B and ref. 3) demonstrates a rapid change in atmospheric chemistry, which we have interpreted to represent the development of a hydrocarbon haze formed at elevated methane concentrations. As such, our data and models provide support for the presence of substantial methane in the Archean atmosphere, confirming predictions made in multiple theoretical studies (3, 20, 41–43, 47, 59). Our previous work (8, 9, 17, 18), and the work of others (57), has shown that similar tandem decreases in Δ³⁶S/Δ³³S and δ¹³C_Org occur in other Neoarchean strata, suggesting the Neoarchean atmospheric composition was dynamic, and atmospheric haze development was potentially frequent in the overture to the GOE. Experimental data (60, 61) and photochemical models (7, 9, 10, 20, 47) both predict that hydrocarbon hazes form when CO₂:CH₄ mixing ratios exceed ∼0.1. Given the strong dependency of hydrogen escape on atmospheric methane availability (41, 59), conceptually, therefore, intervals of haze development could have served as intervals of heightened hydrogen loss, implicating more reduced atmospheric chemistry as a harbinger of planetary oxidation.

Catling et al. (41) performed three time-resolved calculations where they fixed the partial pressure of CO₂ (pCO₂) (0.0003, 0.003, and 0.01 bar) and calculated the pCH₄ necessary to maintain a surface temperature of 290 K against the evolving luminosity of the Archean sun. Using their figure 1A, pCH₄ was calculated to approximate 950, 170, and 130 ppm when pCO₂ was fixed at 0.0003, 0.003, and 0.01 bar. Simplifying atmospheric pressure to approximate 1 bar equates to background CH₄:CO₂ mixing ratios of 3.16 (950 ppm/300 ppm), 0.06 (170 ppm/3,000 ppm), and 0.01 (130 ppm/10,000 ppm) for each scenario, respectively. Excluding the first scenario because the climatically necessitated CH₄:CO₂ mixing ratio requires the development of a potentially improbably thick organic haze (7, 9, 20, 47) leaves two clear-skies solutions to explore. Assuming organic haze forms when the CH₄:CO₂ mixing ratio exceeds 0.1, haze development in each scenario requires either a 1.67- (0.1/0.06) or 10- (0.1/0.01) fold increase in atmospheric methane concentrations, or a factor of 1.5–10 increase in planetary oxidation rate representing 2.6–18 × 10¹² moles O₂ equivalents y⁻¹, assuming the background state was 1–1.5 × 10¹² moles O₂ y⁻¹. Consequently, given our estimate of haze duration (1.4 ± 0.4 Myr; Methodology, Geological Setting and Age Model), a single episode of haze development could equate to a net gain of up to ∼2.6–18 × 10¹⁸ moles of O₂ equivalents to the Earth system (41).

It is important to stress that the absolute gain of oxygen equivalents, or the rate of hydrogen loss, depends on both the composition of the atmosphere and on predictions of their resulting climate. Catling et al. (41) used the climate model of Pavlov et al. (62), which has a substantial error in the methane absorption coefficients as rectified by Haqq-Misra et al. (47). When combined with more recent predictions of greenhouse and anti-greenhouse cooling effects (63), Archean pCO₂ in excess of 0.01 is required to warm the planet in lieu of the lower solar luminosity (47). A higher pCO₂ would reduce the background CH₄:CO₂ mixing ratio, requiring a more substantial methane flux to instigate haze formation. Logically, therefore, larger fluxes of methane would promote greater hydrogen escape rates, with concomitant greater oxidative effect, rendering our estimates conservative. A more accurate and precise treatment is dependent on emerging modeling approaches, incorporating more appropriate particle physics and coupled climate modules to calculate accurate radiative transfer through hazy atmospheres (63). However, for now, the most appropriate models reconcile haze development with available geological evidence and suggest that runaway haze development was inhibited by self-shielding (i.e., haze prevents methane photolysis), implicating intricate feedback systems between biological methane production, atmospheric chemistry, and surface-incident UV radiation (63).

Assimilated, core GKF01 reveals a pronounced and stratigraphically systematic excursion toward low Δ³⁶S/Δ³³S and δ¹³C that requires a change in the chemical composition of the atmosphere. This contests the notion of homogenous atmospheric chemistry across vast swaths of Archean time (64) while providing the strongest evidence to date that the Neoarchean was dynamic on million-year time scales. These atmospheric oscillations are best explained via a strong teleconnection between the biosphere and atmospheric chemistry, whereby increased nutrient availability instigated a biogeochemical cascade, prompting organic-haze formation. Episodic haze formation should have hastened hydrogen escape and likely acted as a counterintuitive mechanism of generating significant oxidizing equivalents to the whole Earth system against an oxygen-free atmospheric backdrop.

Methods

The geochemical data presented herein have been generated following established methodologies. Similarly, the photochemical model has been updated, via the inclusion of updated SO₂-photodisasociation cross-sections (33), from that developed in Claire et al. (7). Here, we précis our approach, reserving a complete description for Methodology. Briefly, sulfur isotope analysis was performed on purified SF₆, following CRS pyrite distillation, at the University of Maryland (8, 9). Analytical uncertainties are estimated from the long-term reproducibility of Ag₂S fluorinations and estimated to be 0.02, 0.008, and 0.20‰ (1 SD, 1σ) for δ³⁴S, Δ³³S, and Δ³⁶S ratios, respectively. Organic carbon isotope and TOC data were generated at the Jet Propulsion Laboratory (JPL) astrobiogeochemistry laboratory (abcLab) using 10% (vol/vol) HCl decarbonated sample residues. The average reproducibility of δ¹³C_Org and TOC sample duplicates was found to be ± 0.22‰ and 0.02%, respectively. Iron speciation analyses were conducted at the University of St. Andrews, exploiting an empirically calibrated sequential extraction (65), as detailed in ref. 66, with an extract precision of ∼5%. All raw data are tabulated in Dataset S1.

Geological Setting and Age Model

The study that initially noted covariation between Δ³⁶S/Δ³³S and δ¹³C exploited samples from core GKF01 (Fig. S1 and ref. 9) and focused on the basal Ghaap group, spanning the Boomplaas–Upper Nauga Formations (Fig. 1). Core GKF01, and its companion core GKP01, were recovered southwest of Griquatown (Fig. S1), capturing proximal to midplatform slope sedimentation. Core GKF01 bottomed-out in the Boomplaas Formation of the Schmidtsdrif Subgroup and recovered a complete record Schmidtsdrif–Campellrand sediments, encompassing the Boomplaas and Lokammona Formations of the Schmidtsdrif Subgroup, overlain by the Monteville, Nauga, and Klein Naute Formations of the Campbellrand Subgroup (Fig. 1 and refs. 23, 36, and 53).

In contrast to the Schmidtsdrif Subgroup, the Campbellrand Subgroup displays spatial heterogeneity within Griqualand West Basin, being subdivided into two facies domains (68, 69). Each domain features different sedimentary facies resulting from the basinal configuration and the paleowater depth, with shallow water facies (Ghaap Plateau facies) restricted to the north of Griquatown Fault Zone and the deeper-water (Prieska facies) equivalents to the south (Fig. S1 and refs. 68 and 69). Core GKF01 documents Prieska-type Transvaal sedimentation, whereas BH1-Sacha is further north and represents thicker, shallow-water sedimentation. Despite the difference in stratigraphic nomenclature, Δ³⁶S/Δ³³S–δ¹³C covariation has been recorded in each core, suggesting the chemostratigraphic trends are insensitive to water depth (an inference borne out by our new data). To better our understanding of haze formation we revisited core GKF01 and constructed a high-resolution geochemical record from ∼900–800 m (Figs. 1–3). We target this stratigraphic interval based on the initial work of Zerkle et al. (9). This is the youngest known C-S anomaly for which good core recovery exists but, importantly, it overlies the Kamden Iron formation (∼905 m)—a prominent and pervasive stratigraphic marker—meaning our efforts should be directly traceable into other cores.

The chronostratigraphic framework for the Prieska–Koegas area, along the southwestern margin of the Kaapvaal craton, is developed predominately from SHRIMP U-Pb ages derived from zircons concentrated from the various intercalated tuff beds. Within this framework the zircon population ages young systematically and show good agreement between studies (36–40). Knoll and Beukes (36) exploited the unusually large number of marker beds present in core GKP01 (companion core to GKF01) to correlate the core to outcrop-derived “type-profiles” and to exploit the existing precise U-Pb radiometric age constraints (see figure 8 in ref. 36).

Although the tuff horizons in GKF01 are not as well documented as in GKP01, the proximity of the two cores (∼24 km), combined with the presence of well-defined lithological, sequence stratigraphic, and impactite horizons (23), allows us to develop a crude linear age-depth model. We use these age controls to place the first constraints on the duration of the C-S anomaly and hence an episode of Neoarchean haze formation. The implications of these temporal constraints are discussed in the main text. Specifically, using the age constraints on Tuff 4 at ∼905-m core depth beneath the Kamden member (2,581 ± 9 Ma, ref. 39; 2,588 ± 6 Ma, ref. 37) and Tuff 0 beneath Bruno’s band (2,521 ± 3 Ma, ref. 40; 2,516 ± 4 Ma, ref. 37) at 325-m core depth results in a calculated compacted sedimentation rate (CSR) of 9.5 ± 2.5 m Myr⁻¹. Applying these estimates to our new chemostratigraphic record suggests that the haze persisted for 1.4 ± 0.4 Myr (12.13 m), attaining maximum haze thickness in 0.3 ± 0.1 Myr (3 m).

We stress that these time estimates on haze formation are subject to numerous sources of uncertainty and are reliant on poorly known sedimentation rates. The errors we have quoted above are simply propagated from those offered in the initial papers (36–40) and do not account for deviation from linear sedimentation. Deviation from linear sedimentation—our implicit assumption—could result from (i) facies-dependent sedimentation rates, (ii) differential compaction histories, (iii) instantaneous sedimentation (e.g., turbidites), and (iv) unrecognized sedimentary hiatuses. Although there are no reports of hiatuses, sedimentary facies are observed to vary on a number of scales throughout core GKF01. The Nauga formation, for example, features pronounced cyclicity, with microbialite–slope carbonate couplets occasionally passing into siliciclastic mudstones. On a broader scale, in the basal part of core GKF01, microbialite facies are more volumetrically important than in the younger part of the succession. Consequently, there is good reason to suspect slight deviation from linear behavior (23), with variable and scale-dependent sedimentation rates. To examine this potential scale dependency, we constructed CSRs over a longer stratigraphic interval (Lokammona–Klein Naute Formations). Here, we adopt the age from the dated Lokammona tuff to constrain the age of the uppermost surface of Lokammona Formation at 1,440-m core depth (2,650 ± 8 Ma, ref. 39) and repeat the same exercise as above. Taking these data we calculate the CSR to be 8.5 ± 0.9 m Myr⁻¹, which is statistically inseparable from our previous estimate. This agreement, providing that there are no substantial unrecognized sedimentary hiatuses, suggests that that uncertainty implicit in radiometric age determinations dominates our rate calculations. Given that the presented chronostratigraphic framework is unusually detailed, a reduction in these uncertainties will require precise dating of the core directly, thus circumnavigating complications involved with correlations to the regionally developed geochronology.

Methodology

Quadruple S-Isotope Determination.

Sedimentary sulfide phases were extracted via sequential reflux with 6 M HCl and acidified with 1 M CrCl₂ at the University of St. Andrews (8). The first reduction step yielded operationally defined acid volatile sulfur (AVS) and the second stage reduced pyritic sulfur, which was precipitated as silver sulfide (8, 9, 70). The purified Ag₂S (1–3 mg) was reacted with a 10-fold excess of fluorine gas (F₂) at 250 °C for ∼8–12 h in Ni bombs. The reaction product, sulfur hexafluoride (SF₆), was cryogenically separated from residual F₂ (at −196 °C) and from HF and other trace contaminants (at −115 °C) using liquid nitrogen (LN₂) and an ethanol-LN₂ slurry, respectively. Finally, the SF₆ was purified via gas chromatography using a composite column composed of a type 5A molecular sieve (3.18-mm diameter, 1.8 m long), followed by a Hayesp-Q column (3.18-mm diameter, 3.6 m long). Under these conditions SF₆ was eluted after ∼13 min using an He carrier gas (20 mL⋅min⁻¹ at 50 °C) and the yield was quantified to >95%.

The S-isotope composition of the pure SF₆ was measured via dual-inlet isotope ratio mass spectrometry (Thermo-Finnigan MAT 253) using four collectors arranged to measure the intensity of SF₅⁺ ion beams at mass charge ratios (m/z) of 127, 128, 129, and 131 (³²SF₅⁺, ³³SF₅⁺, ³⁴SF₅⁺, and ³⁶SF₅⁺). Analytical uncertainties are estimated from the long-term reproducibility of Ag₂S fluorinations and are deemed to be 0.02, 0.008, and 0.20‰ (1 SD, 1σ) for δ³⁴S, Δ³³S, and Δ³⁶S ratios, respectively. The accuracy of the presented data was assessed via analysis of IAEA S1 and S3 standards, producing data in line with published accepted values (8, 9).

Carbonate Abundance and Organic Carbon Isotope Analyses.

The carbonate-carbon fraction was quantitatively removed from homogenized sample powders via multiple overnight 10% (vol/vol) HCl acid attacks, allowing the carbonate abundance to be calculated gravimetrically. The resulting carbonate-free residues were then rinsed to neutrality using Milli-Q ultrapure water (18.2 MΩ·cm) before being dried at 40 °C at the University of St. Andrews (8).

The dry sample residues were homogenized and weighed into tin cups ready for organic carbon isotope (δ¹³C_Org) and TOC determination at the JPL abcLab over four analytical sessions. During each session, an acetanilide standard (Costech Analytical) was analyzed in multiple (n = 8) to monitor external precision, linearity, and instrument response for TOC calculation. Carbon-isotope data are expressed as permil deviations from the V-PDB standard, via normalization after duplicate analysis of NBS19 (1.95‰) and LSVEC (−46.6‰) within each analytical session. External reproducibility is deemed to be 0.07‰ (1σ), based on the replicate analysis of between 1.5 and 4.5 μmol of acetanilide-C.

Initially 1-mg sample aliquots were analyzed with the intention to introduce ∼2 μmol C into the mass spectrometer. Many of these initial analyses yielded 1.5–4.5 μmol C; however, most (51 of 91) were analyzed a second time with variable sample weights to yield ∼2 μmol C. Average reproducibility of δ¹³C_Org and TOC sample duplicates was found to be ± 0.22‰ and 0.02%, respectively. Consequently, where available, the data are calculated and plotted as averages with their associated reproducibility (Dataset S1).

Sedimentary Fe Speciation.

Iron speciation analyses were conducted at the School of Earth & Environmental Sciences, University of St. Andrews to determine the paleoredox of the investigated samples (9). Highly reactive Fe (Fe_HR), comprising pyrite Fe and other Fe phases that are reactive to sulfide to form pyrite in the water column or during early digenesis, were quantified via only minor modification from established techniques (65–67, 71). Briefly, 0.1 g of sample powder was exposed to acetic acid-buffered (pH 4.5), 1 M sodium acetate solution at 50 °C for 48 h to liberate carbonate Fe (Fe_Carb), including siderite and ankerite. The leached residues were attacked for 2 h at ambient temperature by 0.29 M sodium dithionite solution, buffered to pH 4.8 using a mixed 0.3/0.2 M acetic acid/sodium citrate solution, to target diagenetically reducible Fe oxides (Fe_Ox) such as goethite and hematite. Finally, the remaining magnetite (Fe_Mag) was extracted with a mixed 0.2/0.17 M ammonium oxalate/oxalic acid solution. Iron concentrations were determined using a Thermo Scientific iCAP 6300 inductively coupled plasma optical emission spectrometer after 20-fold dilution. Standardization was achieved using synthetic, matrix matched, 0–10 μg mL⁻¹ Fe standards. Reproducibility, based on 10 replicate extractions of PACS-2, is demonstrated to be better than 5%; however, this is likely to be an underestimate of some low-Fe samples where analytical reproducibility is more likely to approximate 10%.

The Ag₂S precipitated for S-isotope analysis allowed the final Fe-pool(s) to be quantified gravimetrically, with AVS representing monosulfides (FeS) and CRS representing pyrite (FeS₂), whose sum represents the inorganic sulfurized pool (Fe_Py = Fe_AVS + Fe_CRS). Repeat extraction of (n = 6) demonstrates that reproducibility is better than 5% for sedimentary CRS distillation (70).

Comprehensive surveys of both contemporary (72) and Phanerozoic sediments (73) demonstrate that products of anoxic sedimentation generally have Fe_HR/Fe_T ratios above 0.38, and hence this is the diagnostic threshold used to discriminate between oxic and anoxic sedimentation (9, 15, 67). In detail, 0.38 is a conservative discriminator of anoxic deposition because ancient rocks deposited beneath an oxic water column feature lower Fe_HR/Fe_T ratios (0.14 ± 0.08; ref. 74). Accordingly Fe_HR/Fe_T ratios below 0.22 are considered to unequivocally indicate an oxygenated water column, whereas intermediate Fe_HR/Fe_T (0.22–0.38) ratios remain ambiguous and could be a product of either oxic or anoxic deposition and require careful examination to reach robust conclusions (65–67, 75). Differentiating whether anoxic sediments (Fe_HR/Fe_T >0.38) were deposited under ferruginous or euxinic water column can be achieved by considering the extent of pyritization of the Fe_HR pool (65–67, 75–77). Modern euxinic environments have been used to set the upper limit for ferruginous deposition (Fe_Py/Fe_HR; ref. 74); however, early calibration attempts exploited an Fe extraction technique that failed to adequately define the Fe_Carb and Fe_Mag pools (67). In light of these shortcomings, recent work suggests that 70% pyritization of the Fe_HR pool (Fe_Py/Fe_HR = 0.7) may be a more appropriate threshold (65–67, 75–77) to distinguish between ferruginous and euxinic sedimentation.

The Fe-speciation proxy was originally developed to be applied to siliclastic sediments and has only recently been calibrated in carbonate-rich facies (71). Clarkson et al. (71), via analysis of modern and ancient samples, demonstrated that reliable redox inferences, using the aforementioned discriminators, can be made providing the analyte contains more than 0.5 wt % Fe. These authors (71) also found via analysis of burial dolomites that the Fe-speciation proxy seems to be susceptible to deep burial dolomitization, where there has been a source of mobile Fe during recrystallization. Our carbonate-rich samples contain more than 0.5 wt % Fe and therefore should encode reliable redox information. That said, we acknowledge that some of these samples have experienced dolomitization, which may have increased their Fe contents. Accordingly we have opted to conservatively only place emphasis on the Fe-speciation data derived from the center of the C-S anomaly, which are derived from siliclastic lithologies and hence not influenced by dolomitization.

Photochemical Modeling.

The model used to predict and examine the utility of the Δ³⁶S/Δ³³S parameter is updated from that presented previously by Claire et al. (7). The 1D photochemical model comprises 74 gas-phase species undergoing 392 photochemical reactions and includes vertical transport by eddy and molecular diffusion, rainout, lightning, particle condensation, and diffusion-limited hydrogen escape. Altitude-dependent computation is based on incremental 0.5-km grid steps over 100 km. Within this structure a fixed tropopause is adopted at 11 km. Radiative transfer was computed using a two-stream approximation using Rayleigh and Mie scattering for gaseous and particulate species, respectively. Photolysis rates were diurnal averages based on a 50° solar zenith angle. Model integration was performed using a variable time-step reverse-Euler method, which relaxes to Newton’s method when large time steps are large. Only fully converged steady-state solutions were analyzed.

The present model incorporates updated SO₂-isotopologue absorption cross-sections (33). The previous cross-sections (35) used by Claire et al. (7) have been questioned by numerous authors (7, 34) and predict Δ³³S with the opposite sign from that expected from empirical observations (7). Incorporation of the new cross-sections (33) reverses the Δ³³S predictions (Figs. 4 and 5), producing Δ³³S with signs that align with that recorded in the geological record. Importantly for this contribution, Endo et al. (33) measured the ³⁶SO₂ isotopologue, allowing Δ³⁶S/Δ³³S to be traced through an atmospheric reaction network for the first time (Figs. 4 and 5). To validate the numerical self-consistency of our isotopic model we ran the same simulations presented in Fig. 4B but included only mass-dependent fractionation factors. This test scenario (Fig. S4) consistently produced Δ³⁶S/Δ³³S slopes near −7.0 as predicted by the theory of mass conservation (28) (Fig. S4).

Although there is evidence for the persistence of a Mesoarchean organic haze (10, 20, 78), and the subject of our study is to examine the hypothesized development of periodic Neoarchean haze(s) (8, 9), the apparent longevity of Δ³⁶S/Δ³³S = −0.9 (64) argues that a clear-skies atmospheric configuration was a more appropriate background state. Accordingly we adopted a haze-free standpoint for our standard atmosphere (Figs. 4A and 5C) for our modeling efforts, approximating the background atmospheric state following the advent of photosynthesis, yet before the GOE. Here, the atmosphere was computed using 2.5-Ga solar flux (79) with a volcanic sulfur flux of 3.85 × 10⁹ molecules cm⁻² s⁻¹ (∼1 Tmol y⁻¹) at an H₂S:SO₂ ratio of 1:10 and a volcanic H₂ flux of 1 × 10¹⁰ molecules cm⁻² s⁻¹ (∼3 Tmol y⁻¹). The volcanic inputs were log-normally distributed vertically throughout the troposphere. Carbon dioxide concentrations were fixed at 1% irrespective of height, and N₂ provided a balance atmospheric pressure of 1 bar. Further boundary conditions include fixed ground-level mixing ratios of CH₄ (100 ppm) and O₂ (10 ppb). To maintain these mixing ratios in steady state with all other processes, the model computed fluxes of CH₄ (3.6 × 10¹¹ molecules cm⁻² s⁻¹) and O₂ (6.2 × 10¹¹ molecules cm⁻² s⁻¹), which are broadly consistent with predictions of Archean biospheric fluxes after the evolution of oxygenic photosynthesis (3, 21, 42). A reducing atmosphere is maintained by elevating volcanic H₂ and H₂S fluxes slightly above their contemporary levels (case V2 in ref. 21) and by a CH₄:O₂ flux ratio >1:2 (10).

As highlighted in the main text, our hazy simulations do not produce Δ³⁶S/Δ³³S slopes of −1.5 (Fig. 5), and the standard model atmosphere fails to reproduce Δ³⁶S/Δ³³S of −0.9 (Fig. 4A). The absolute source of this data–model mismatch is unknown; however, it reflects some combination of (i) the uncertainties associated with the prescribed isotopic fractionation factors and/or (ii) the background chemical composition of the Archean atmosphere. Another complication with hazy simulations involves aspects of the numerical computation schemes. Although the internal mechanics of clear-skies simulations are well-constructed and well-behaved, the same cannot be said regarding the preliminary simulations presented herein. These model convergence issues decrease our ability to make confident predictions across the entire suite of runs shown in Fig. 5. These convergence concerns arise from poor coupling between the chemical, radiative, particle-formation, and particle-distribution modules and are compounded by the assumed invariant atmospheric temperature profile. Very recently, major strides have been made in coupling this 1D photochemical model with a radiative-convective climate model specifically for hazy atmospheres, which rectifies many of the aforementioned problems (63). Incorporation of these changes into the isotopic scheme is substantial and beyond the scope of the present contribution, whose aim was more simply to test the utility of the Δ³⁶S/Δ³³S parameter as a proxy for atmospheric chemical composition. Incorporation of these changes will be necessary for future accurate predictive computations of the magnitudes of minor S-isotope effects in a hazy atmosphere. Although our detailed numerical predictions will certainly be updated, we have satisfied our aim and demonstrated that the altered UV transparency and exit channel importance underneath an organic haze can result in distinct changes in Δ³⁶S/Δ³³S, thereby demonstrating the feasibility of the overall hypothesis.