Significance
Walking through any forest, one is struck by the variety of plant forms coexisting. Given that all plants compete for the same basic resources, why is there not a single winner? Our study shows that when key ingredients common to all forests are accounted for—including disturbance events, competition for light, and two widely observed trait-based tradeoffs—models of niche differentiation predict forests of considerably greater diversity than was previously thought possible. In particular, our model accurately predicts the proliferation of species occupying niche space in low light, a feature of tropical forests that motivated the so-called neutral theory of biodiversity and biogeography. The presented results thereby provide a platform for understanding diversity in forests worldwide.
Keywords: niche, coexistence, trait, plant, adaptive dynamics
Abstract
To explain diversity in forests, niche theory must show how multiple plant species coexist while competing for the same resources. Although successional processes are widespread in forests, theoretical work has suggested that differentiation in successional strategy allows only a few species stably to coexist, including only a single shade tolerant. However, this conclusion is based on current niche models, which encode a very simplified view of plant communities, suggesting that the potential for niche differentiation has remained unexplored. Here, we show how extending successional niche models to include features common to all vegetation—height-structured competition for light under a prevailing disturbance regime and two trait-mediated tradeoffs in plant function—enhances the diversity of species that can be maintained, including a diversity of shade tolerants. We identify two distinct axes of potential niche differentiation, corresponding to the traits leaf mass per unit leaf area and height at maturation. The first axis allows for coexistence of different shade tolerances and the second axis for coexistence among species with the same shade tolerance. Addition of this second axis leads to communities with a high diversity of shade tolerants. Niche differentiation along the second axis also generates regions of trait space wherein fitness is almost equalized, an outcome we term “evolutionarily emergent near-neutrality.” For different environmental conditions, our model predicts diverse vegetation types and trait mixtures, akin to observations. These results indicate that the outcomes of successional niche differentiation are richer than previously thought and potentially account for mixtures of traits and species observed in forests worldwide.
The central challenge of community ecology is to discern the rules governing the assembly of species and growth types. The problem is acute for vegetation, because trait differences do not differentiate species in terms of resource requirement (1–3). However, most forests accommodate tens to hundreds of plant species (1, 2, 4). Hence, niche-based theories of biodiversity have sought to identify mechanisms through which multiple species can coexist while competing for a single resource such as light (2, 5–10). Tradeoffs in plant function are key, because they prevent one species from monopolizing available resources. In particular, a tradeoff between growth in high light and survival in low light (shade tolerance) has been shown theoretically to allow different successional types (species with different shade tolerances) to coexist in vegetation subject to recurrent disturbance (8). In tropical forests, diverse assemblages are distributed along this growth–mortality axis (11, 12), suggesting that this tradeoff is potentially important for community assembly. However, species in the field are distributed unevenly along this axis, with a proliferation of species clustered at the slow-growing, shade-tolerant end (4, 11, 13). By contrast, in existing niche models, only a few species are maintained at equilibrium through successional processes, including only a single slow-growing, shade-tolerant type (6, 14–18). This mismatch between theory and observation has led many to question the importance of successional niche differentiation for community assembly and to seek alternative explanations for forest diversity (1, 4, 11, 16, 18, 19).
So far, however, conclusions about the potential for niche differentiation in forests have been drawn from models encoding a very simplified view of plant communities. Most theoretical investigations have relied on models lacking size-structured dynamics in their populations (8–11, 15, 17, 20). Where size-structured models have been used (6, 16, 21), only a single axis of potential differentiation has been considered. In reality, size-structured growth and competition are key processes in plant communities, so adding them to models impacts strongly on the population dynamics (6, 8, 22–24). The richer population dynamics could extend opportunities for coexistence. Also, coexisting species are known to vary in multiple aspects of plant function (25, 26). However, it remains unknown whether different traits offer separate and potentially synergistic mechanisms of ecological differentiation.
Here, we show how a more realistic modeling of successional niche differentiation can naturally lead to communities with a higher diversity of types than was previously thought possible, including a key feature some researchers have claimed could not be explained by niche theory (19): a proliferation of slow-growing, shade-tolerant strategies (Fig. 1). Further, we show how the same model can produce a variety of other vegetation types and trait mixtures under different conditions of the physical environment. To reach these conclusions, we extend classic models of successional niche differentiation (6, 8, 14–16) by including four features that are ubiquitous in real-world vegetation. Although each feature is known to be important, they have not yet been simultaneously integrated into a model of niche differentiation. It is this combination of features, more than any single feature alone, that leads to additional insight.
Fig. 1.
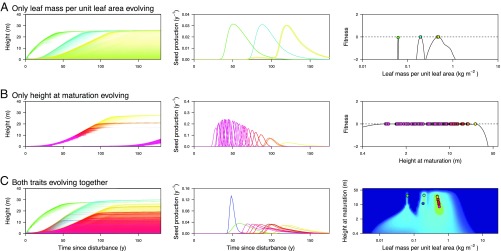
Multitrait successional dynamics enable diverse species coexistence. We consider a model in which plant species inhabiting a metacommunity of patches can differ in two functional traits, leaf mass per unit leaf area and height at maturation. (A) After a disturbance, vegetation development in a patch follows successional dynamics under height-structured competition for light. A, Upper shows the height of individual plants in a patch as it ages, and A, Lower shows the prevalence of species (left vertical axis and colored areas) as the probability that a patch remains undisturbed decreases (right vertical axis and black line). The black line therefore shows the distribution of patch ages in the metacommunity, with an average interval between disturbances of 60 y. After a disturbance, patches start at age 0 with a total shading of zero (A, Lower shows the successional dynamics starting from age 1 y). Note the log scaling of the horizontal axis. (B) Across the metacommunity, patches are in different successional stages, linked through seed rain. In this schematic illustration, patches are shown with finite size and internal horizontal structure, whereas in the model they are treated as being infinitely large and horizontally homogeneous. (C) Evolutionary dynamics in the two functional traits give rise to a metacommunity with a characteristic pattern of coexisting species (white circles), comprising a few early-successional fast-growing species (green and blue regions) and a high diversity of late-successional shade-tolerant species (yellow and red regions). Colors in A and B indicate trait combinations as shown in C.
First, we explicitly model the size-structured nature of growth, mortality, and reproduction, in the context of a prevailing disturbance regime and based on a well-established mechanistic understanding of growth and competitive shading (Fig. 1 and SI Appendix, Fig. S1; Materials and Methods). The ecological structure of our model is standard across many successional frameworks (6, 14–16, 22). We consider a vegetation landscape as represented by a metacommunity of patches in different stages of development, linked via seed dispersal. Disturbance events clear established plants within a patch. As patches age after a disturbance, the population within the patch develops through the processes of growth, mortality, and reproduction, under height-structured competitive shading (Fig. 1A). In contrast to much previous work, where dynamics are simulated in patches of fixed size and number, we model continuous density distributions of both patch ages (reset at the time of disturbance) and plant heights within each patch (22, 27, 28). This enables us deterministically to model entire metapopulations and evaluate the fitness of competing types over their life cycle (29).
Second, we incorporate specific, well-known, physiological tradeoffs in plant function. Species are represented by trait values indicating their position along these physiological tradeoffs. Here we consider two prominent functional traits—leaf mass per unit leaf area (LMA) and height at maturation (HMAT). Demographic tradeoffs are not assumed a priori, but emerge naturally from these trait differences via a carbon-based growth model (Materials and Methods). Based on empirical data, LMA is involved in a tradeoff between the cost of building leaves and leaf turnover rate (25, 26, 30) (SI Appendix, Fig. S2A). Via the growth model, variation in LMA generates a demographic tradeoff between the height growth rate and shade tolerance of seedlings, reflecting empirical patterns (26) (SI Appendix, Fig. S2B). The trait HMAT specifies the height at which the allocation of surplus energy shifts from vegetative growth toward reproduction (SI Appendix, Fig. S3A). In the growth model, changes in HMAT thereby affect several demographic outcomes, including age at maturation, survival to maturation, and maximum fecundity (SI Appendix, Fig. S3B). Whereas other traits are undoubtedly important for plant communities, we focus on these two because they capture different aspects of plant growth strategy, are involved in central and well-established tradeoffs, and are known to vary widely among coexisting species in real plant communities (25, 26).
Third, in assessing the possibilities for niche differentiation, we allow for species simultaneously to differentiate along two axes, quantified by LMA and HMAT, whereas most existing niche models consider only a single axis. Theoretically, it is known that adding new traits will enhance diversity, provided the different traits offer separate or potentially synergistic mechanisms of ecological differentiation (31). Because LMA and HMAT have quite different demographic consequences, we investigate the capacity of each trait to maintain diversity, as well as that of the two traits combined.
Fourth, metacommunities are assembled evolutionarily as well as ecologically, using methods of adaptive dynamics theory (32, 33). We not only ask whether specific trait mixtures can coexist ecologically, but also determine the mixtures likely to emerge through repeated rounds of immigration, mutation, and selection on an evolving fitness landscape. The reproductive success of plants in our system is frequency and density dependent (32). A new strategy can invade if, and only if, its net rate of population increase across the metacommunity (i.e., its invasion fitness) is positive. The current resident species mixture gives rise to a fitness landscape in trait space, which comprehensively determines the potential for future demographic and evolutionary change. Adaptive dynamics methods thus focus on determining the long-term outcomes of the intricate dynamical feedback between a community’s composition and its fitness landscape. Although previous models of trait evolution in size-structured vegetation exist (34, 35), none have generated stable coexistence of multiple types. This is most likely because, to maintain analytical solutions, some of the key features outlined above, such as disturbance regimes, were omitted. By contrast, our model covers a more realistic combination of salient ecological details.
A model simultaneously incorporating these four enhancements allows us to investigate how two trait-mediated tradeoffs interact to shape forest diversity and structure. We begin by investigating possibilities for coexistence with first one, and then two, traits evolving under environmental conditions broadly akin to those in tropical rainforests: high site productivity and disturbance regimes with intermediate return intervals of 60 y (36). We then extend the analysis to show how the same tradeoffs can produce different trait mixtures for different site productivities and disturbance intervals.
Results
Our analyses focus on determining the coexistence patterns of trait combinations resulting from the underlying ecological model. The two trait-mediated tradeoffs included in our model each promote diversity, meaning that, unless mutation and immigration cease entirely, a metacommunity with a single type cannot prevent other types from invading. This applies when only LMA is evolving (SI Appendix, Figs. S4 and S5), when only HMAT is evolving (except where noted; SI Appendix, Figs. S6 and S7), and when both traits are evolving (SI Appendix, Figs. S12 and S13). To see how this tendency to promote diversity plays out, we assemble metacommunities under a scenario akin to that experienced in real vegetation, with new types generated via two mechanisms: through small variation arising from mutations in the trait values of the resident (or existing) types and through introduction of new residents with trait values drawn from a uniform probability distribution across the entire viable trait space (these can be thought of as dispersers from a regional species pool). The assembly algorithm uses a discrete time step, with each step corresponding approximately to the length of the mean interval between disturbances. At each step, we update the abundance of resident types via Eq. 1, introduce new types at a minimum density, and remove resident types that have dropped below that minimum. Thus, only types that experience positive fitness during invasion are able to establish as residents. The number of mutants and immigrants introduced is drawn from a Poisson distribution, with an average rate of 0.1 and 1 per step, respectively. The assembly process is continued for up to 5,000 steps, after which the assembled metacommunities are functionally fully differentiated and evolutionarily stable, as indicated by a stable mean and covariance of trait values and a fitness landscape with no regions of positive fitness (Figs. 2 and 3 and SI Appendix, Figs. S4–S7, S12, and S13). Generally, we find that the ecological model enables the stable coexistence of different types across the metacommunity. Moreover, we find that similar trait mixtures are predicted when the rates of immigration and mutation are lowered 10-fold (SI Appendix, Figs. S8 and S9), indicating that mixtures primarily reflect the underlying tradeoffs.
Fig. 2.
Multitrait evolution under physiological tradeoffs offers alternative pathways of niche differentiation, leading to a high diversity of late-successional shade-tolerant types. A–C show metacommunities resulting when (A) only leaf mass per unit leaf area evolves, (B) only height at maturation evolves, and (C) both functional traits evolve together. A–C, Left and Center, respectively, show the size distributions and seed rains of each species within a patch in the wake of a disturbance. Seed rains are expressed as fractions of total lifetime seed production. In A–C, Right, each circle represents a single species. Colors indicate trait combinations as in Fig. 1. The intensity of shading in A–C, Left indicates the density of plants at a given height and patch age. A–C, Right shows evolved trait mixtures and corresponding fitness landscapes, with C, Right colored as in Fig. 3.
Fig. 3.
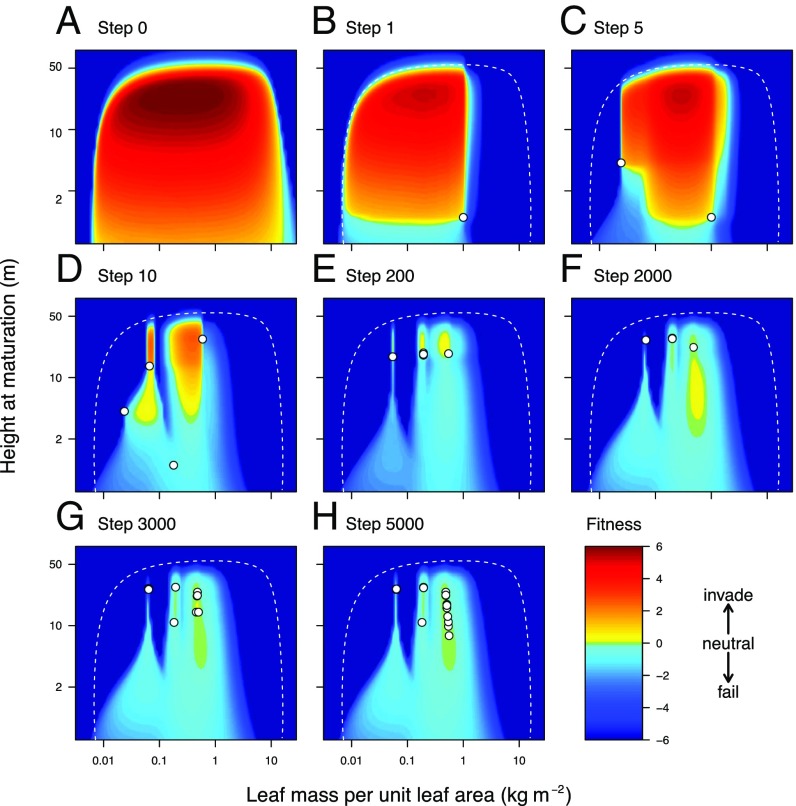
Community assembly leads to characteristically structured fitness landscapes, including peaks, valleys, and plateaus. A–H show fitness landscapes at different stages of assembly of the metacommunity shown in Figs. 1, 2C, and 4C. Coloring across trait space indicates the invasion fitness of rare species competing with the resident species (circles). In each panel, the dashed curve delimits trait combinations that are not viable even in the absence of any competition. Community assembly starts with a species randomly selected across the trait space (step 1). At each subsequent step, the abundances of resident species are updated according to their fitness, and new invaders are added around existing residents and across trait space. Invasion is successful only in regions with positive invasion fitness (colored yellow to red), whereas species that successfully invade but then find themselves in regions of negative invasion fitness (colored blue to cyan; e.g., lowest circle in D) are ultimately driven extinct. A ridge-shaped fitness plateau (green region in H) naturally forms in the course of the community assembly, after a high diversity of late-successional shade-tolerant species establish in regions of positive fitness.
Single-Trait Evolution.
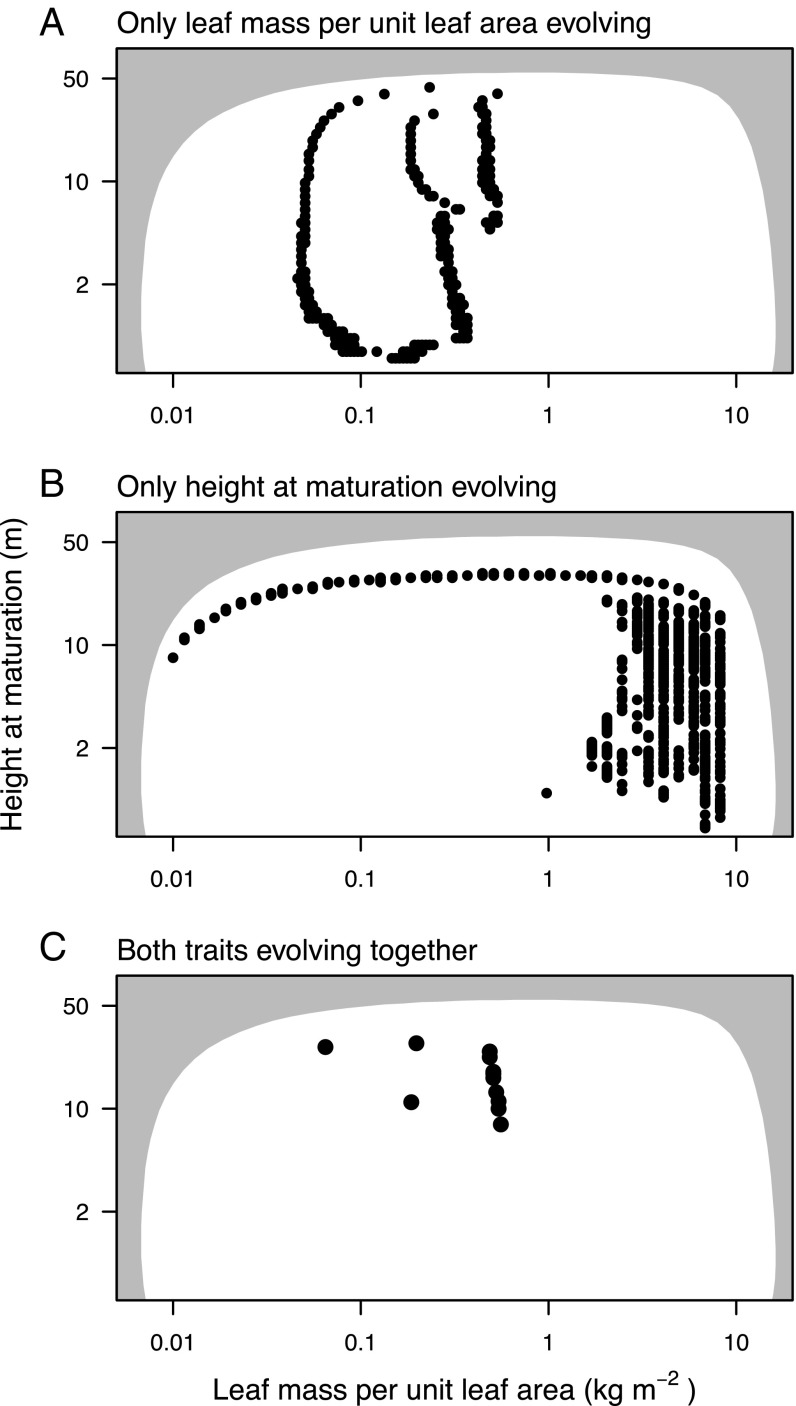
Evolution of LMA in the model leads to stable coexistence of up to three different types (Figs. 2A and 4). Embedding the tradeoff between LMA and leaf turnover rate in our physiological growth model gives rise to a demographic tradeoff between the height growth rate and shade tolerance of seedlings (SI Appendix, Fig. S2B). In the evolved metacommunities, low-LMA strategies correspond to fast-growing, early-successional types that flourish in high-light conditions immediately following a disturbance. Due to their fast leaf turnover, low-LMA strategies pay high costs of leaf replacement and are intrinsically shade intolerant. They are unable to regenerate in older patches, where higher-LMA strategies prevail, corresponding to mid- and late-successional types. The exact number of LMA strategies also varies with the value of HMAT, from two strategies when plants are constrained to be short to three strategies when they are allowed to grow taller (Fig. 4A).
Fig. 4.
Rich interactions between the two functional traits determine the evolution of bivariate trait mixtures. A and B show the evolved univariate mixtures in each trait when the other trait is fixed at a specific value, and C shows the bivariate trait mixture that results when both traits are evolving together. Each circle represents a single species. The shaded region is the same in each panel and indicates trait combinations that are not viable even in the absence of any competition (Fig. 3A).
Differentiation in HMAT also promotes niche diversification in the model, but through a different mechanism, allowing strategies with similar successional types (similar LMA) to coexist with one another via the partitioning of reproductive opportunity (Fig. 2B). By reproductive opportunity, we refer to the potential of a plant with positive carbon budget to produce seeds. As they have similar LMA strategies, different HMAT strategies show the same patterns before maturation of seedling recruitment, growth rate, shade tolerance, and reproductive opportunity. However, as they begin to reproduce, species differentiate based on how much they capitalize on current reproductive opportunity vs. deferring reproduction into the future. These differences in reproductive allocation generate differences in growth rate and seed output among older plants (Fig. 2B). Within a set of similar LMA strategies, there is first a period of joint establishment and growth, and then early-maturing strategies are progressively overtopped by strategies with higher HMAT (Fig. 2B).
Importantly, we find that coexistence of different HMAT strategies is possible only once LMA exceeds a threshold (Fig. 4B). Below that threshold, only a single strategy can be supported, whereas above it, a diversity of types can be maintained. The reason mixtures are easier to maintain at higher than at lower LMA values is that competitive thinning during stand development is less intense. The equilibrium population size in single-strategy systems tends to decrease toward higher LMA values (SI Appendix, Fig. S10). The lower density of seeds implies a lower density of germinating seedlings and thus a lower density of plants during development of the stand. When the density of competitors is lower, plants shifting to reproduction take longer to be overtopped and thus have more opportunity to reproduce before they eventually die.
The two traits considered here not only offer alternative pathways of niche differentiation, but also have different effects on the resultant fitness landscapes. A fitness landscape describes whether variants with new trait combinations can invade a resident community. During the process of community assembly, new residents establish in positive regions of the landscape, until these disappear. Residents can also be competitively excluded. Whether the eventual metacommunities predicted by our model contain one, few, or many types results from differences in the way fitness landscapes are progressively reshaped during community assembly, which in turn reflects the way traits influence community dynamics. We find that differentiation in LMA creates a fitness landscape with distinct adaptive peaks, allowing only a finite number of types to coexist competitively (Fig. 2A; for the pattern arising through the assembly, see SI Appendix, Figs. S4 and S5). Differentiation in HMAT, on the other hand, creates an almost flat fitness landscape (Fig. 2B; for the pattern arising through the assembly, see SI Appendix, Figs. S6 and S7). This can support many more types compared with LMA. We use the term “evolutionarily emergent near-neutrality” for these flattened fitness landscapes. Importantly, they do not start out flat, but rather become leveled by density-dependent and frequency-dependent selection, with nonresident strategies invading at trait combinations having positive fitness and resident strategies climbing up nearby peaks through gradual evolution under directional selection (SI Appendix, Figs. S6 and S7).
The emergence of a peaked fitness landscape for LMA and a flat fitness landscape for HMAT reflects the underlying nature of the tradeoffs mediated by these traits. Because LMA generates a demographic tradeoff between growth rate and shade tolerance, niche differentiation occurs when these types can regenerate successfully at different patch ages (Fig. 1A). The spacing of LMA types and the deep valley in the fitness landscape between the lower two LMA strategies in the evolved metacommunity (Fig. 2A) arise because there is a substantial cost in having an LMA value only slightly higher than the resident. This occurs because the intrinsic dynamics of size-structured growth produce undulations in the total amount of shading at ground level, with total shading during the first wave of recruitment jumping up (Fig. 1A) (24). As a result, species with only a marginally higher LMA are unable to recruit below the canopy of an early-successional strategy, whereas species with a substantially higher LMA are able to recruit. The dynamics of recruitment thereby impose a form of limiting similarity in LMA values. Because the amplitude of these undulations in total shading decreases with patch age (Fig. 1A), the relief of the fitness landscape is more subdued around mid- and late-successional types. In contrast to LMA, HMAT does not generate deep valleys or limiting similarity in the fitness landscape. Having the same LMA (and thereby the same potential growth rate and shade tolerance), plants differing only in their HMAT strategies establish at the same time. Any undulations in total shading thus impact similarly on species during establishment, irrespective of HMAT. Coexistence of different HMAT types then becomes possible when the shorter species are able to produce sufficient seed to survive into the next generation, despite being overtopped by species with greater HMAT. Nothing in the shading profile or dynamics prevents two species from maturing at similar heights.
Two-Trait Evolution.
When LMA and HMAT coevolve, differentiation in both produces a metacommunity with a limited number of early- and midsuccessional strategies and a larger number of late-successional, shade-tolerant trees and shrubs (Figs. 1, 2C, and 3). Except for the lowest-LMA strategy—the first to reach its evolutionary attractor—the trait values favored when the traits coevolve cannot be inferred either from the evolution of each trait in isolation (Fig. 4) or from the fundamental niche space given by the fitness landscape before competition begins (Fig. 3A). The tendency remains for differentiation in HMAT to occur only at higher LMA values. However, coexistence in the HMAT dimension becomes possible at lower values of LMA than when the traits are evolving in isolation (Fig. 4). This occurs because the presence of lower-LMA strategies in the metacommunity reduces the abundance of the high-LMA types and thus the intensity of competition within the high-LMA populations. As noted above, it is this reduced competitive intensity within the recruiting cohort that potentially allows for the partitioning of reproductive opportunity. Also, the possibility for strategies with lower HMAT to invade arises only once the tallest late-successional strategy has neared its attractor (Fig. 3 E and F).
Joint evolution of the two traits crucially modifies the number of types that can be maintained. As when each trait evolves in isolation, the range of supported LMA types is still low, with three broad types emerging (Fig. 2C). Within the type with highest LMA, there is a subtle negative covariation between LMA and HMAT. Still, the high-LMA strategies are overall tightly clustered along the LMA axis. Compared with when HMAT evolves in isolation, the range of supported HMAT types is lower. Nevertheless, the evolved metacommunity has a concentration of types within the late-successional group. A nearly level plateau is generated in the fitness landscape at high LMA and across a range of HMAT (Figs. 2C and 3). Once the plateau has been generated, the nearly flat fitness landscape makes competitive advantage very weak, so further competitive exclusion proceeds extremely slowly.
Environmental Factors.
So far, we have focused on the functional composition and diversity of a metacommunity experiencing environmental conditions similar to those of tropical forests (high site productivity and intermediate disturbance interval), because this is where previous niche models seemed least satisfying. We now expand our results from this focus: Fig. 5 shows how, by varying the disturbance interval and site productivity, our model readily generates a much wider variety of trait mixtures and metacommunities, via the same fundamental set of processes.
Fig. 5.
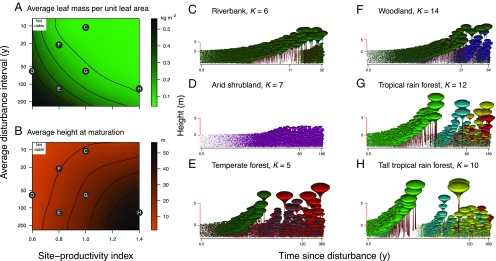
Extended niche models allow for natural variation of forest structure and diversity with environmental conditions, recovering widely observed empirical patterns. (A and B) Mean trait values vary across metacommunities evolved for different average disturbance intervals and site productivities. The resultant fitness landscapes are shown in SI Appendix, Fig. S13. Letters refer to the metacommunities illustrated in C–H. (C–H) Resultant successional dynamics in a patch in the wake of a disturbance. The center tick labels along the logarithmically scaled horizontal axes indicate the average disturbance intervals. Colors indicate trait combinations as in Fig. 1. Panel labels suggest real vegetation types bearing likeness to our model-evolved metacommunities. Also shown is the number of distinct functional types in each metacommunity (determined as the number of trait combinations with positive seed rain differing from one another by at least 1% in each functional trait after 5,000 steps of community assembly).
Across the range of metacommunities that result, several features are notable. First, mean trait values shift across the environmental space (Fig. 5 A and B). Lower LMA values are favored in locations with higher productivity and shorter disturbance intervals, whereas higher HMAT values are favored in locations with higher productivity and longer disturbance intervals. Second, the number of successional types (LMA values) drops from three down to two and then to one as disturbances become more frequent, such that shade-tolerant types are absent at locations with shortest intervals between disturbances (SI Appendix, Fig. S13). Third, metacommunities occurring on productive sites that are infrequently disturbed lack the diversity of late-successional species that arise at intermediate disturbance intervals, thus resembling tall temperate forests (Fig. 5E). Fourth, diversity is highest within the last successional type, irrespective of whether the metacommunity comprises one, two, or three successional types. As before, these diversity hotspots in trait space correspond to plateaus of evolutionarily emergent near-neutrality (SI Appendix, Fig. S13). Also, in more frequently disturbed metacommunities, coexistence of different HMAT strategies becomes possible at lower values of LMA. This occurs because the relative value of the seed output that plants can produce before being overtopped increases as disturbances become more frequent, even if competitive intensity within the first successional type is still high.
Sensitivity Analysis.
Overall, we find that our results are robust to changes in model parameters. In SI Appendix, Figs. S11, S14, and S15 show how parameter changes affect mainly the quantitative details of the evolved trait mixtures, while leaving the qualitative features of the reported coexistence patterns mostly unaffected. In particular, we find that reducing the maximum allocation to reproduction does not change the tendency for coexistence of different HMAT types on a flat fitness landscape when HMAT evolves alone (SI Appendix, Fig. S11). When both traits evolve together, we find that reducing the maximum allocation to reproduction causes a narrower range of HMAT strategies to be maintained, but these still exist within a cluster of strategies on a relatively flat plateau of the fitness landscape (SI Appendix, Fig. S15).
Discussion
Although niche differentiation is widely regarded as a key process maintaining diversity in forests, models based on successional niche differentiation have so far been unable to demonstrate how more than a few functional types can stably coexist; in particular, they have predicted only a single late-successional type (6, 15–18). The fact that such niche models could not explain “why niches are more finely partitioned under low-light conditions than under high-light conditions” (ref. 19, p. 169) has provided continued motivation for an alternative neutral theory of biodiversity and biogeography based on the controversial assumption of fitness equivalence (11, 19, 37). However, our results suggest that this perception of successional niche differentiation being able to support only a few strategies may have arisen only because previous models lacked critical features of real forests—most importantly, the ability of species to differentiate in traits influencing both seedling growth rate and reproductive allocation. Here we have demonstrated that when these features are added, successional niche models can indeed account for the relatively denser occupation of niche space in low light, as well as for other empirically observed patterns of forest structure, such as the shifts in trait mixtures along environmental gradients. These results highlight the importance of successional dynamics and trait-mediated tradeoffs in shaping forest diversity. Additionally, our eco-evolutionary framework for modeling forest composition bridges to, and potentially enhances, models of ecosystem function, the neutral theory of biodiversity, and trait-based approaches in ecology.
Multiple Axes of Successional Differentiation.
Coexistence of different strategies in our model, which occurs at the metacommunity level, becomes possible as species specialize in growing or reproducing in patches of particular ages within the successional process. A distribution of patch ages in the metacommunity is thus essential for stable coexistence. Under different environmental conditions, a variety of vegetation types emerge from the same successional processes (Fig. 5). But if disturbance is removed, the metacommunity collapses to a single patch and the opportunity for coexistence disappears.
The two traits we have studied offer distinct mechanisms of successional differentiation. Differences in LMA produce different successional types (i.e., strategies differing in growth rate and shade tolerance), whereas differences in HMAT allow for differentiation within a successional type. Previously, it has been recognized that the widely cited competition–colonization tradeoff actually entails two distinct tradeoffs, one involving differences in the ability of species to colonize vacant patches and another involving differences in their ability to grow in high vs. low light (8). Here, we have identified a third dimension of differentiation in the maturation schedule of larger plants having the same seedling demography. Also, we have shown how the latter two dimensions potentially interact to shape diversity (Figs. 2 and 4). Our results demonstrate how joint differentiation in LMA and HMAT can lead to metacommunities exhibiting the archetypal structure of most tropical forests (4, 19): a limited number of early-successional, shade-intolerant strategies and a larger number of late-successional, shade-tolerant trees and shrubs (Fig. 2C). This is exactly the feature of tropical forests that was thought unattainable by niche models (19).
At the same time, the finding that only a limited number of LMA types can be maintained suggests that differences in reproductive allocation (here via HMAT) may play a stronger role than differences in growth rate (here via LMA) in maintaining total species richness in forests. Our analysis for LMA is undoubtedly more realistic than those of earlier niche models, as we explicitly link to a prominent physiological trait as a driver of successional niche differentiation. However, our results for LMA are also aligned with core conclusions from earlier successional models: that successional processes can maintain only a limited number of types differing in growth rate and shade tolerance, including only a single shade-tolerant species (6, 15–17). Increased diversity in our model becomes possible through introducing HMAT as the second trait. Indeed, HMAT has been proposed before as a potentially independent axis of differentiation among late-successional species (13, 14, 38). Our results support this view, but with the caveat that the mechanism allowing coexistence of different HMAT types still relies on the successional process. Furthermore, our results support the idea (13) that the higher diversity of tropical forests in part can be attributed to an absence of short, shade-tolerant types in temperate forests (compare Fig. 5 E–G).
Predicting Trait Mixtures and Vegetation Structure.
It is well known that coexisting plant species often exhibit a wide range of physiological traits, affecting various aspects of plant function (25, 30). However, it has been less clear how such trait mixtures are maintained (3, 25, 34). The model we have introduced and analyzed here has uncovered unique insights into what sort of mechanisms can maintain a trait mixture. Building on well-established empirical results (12, 26, 30), we show how mixtures for two prominent traits can be maintained through differentiation along a successional niche axis. Moreover, we find that the conditions enabling diversification along the two considered trait axes are at least widespread, if not universal, in forests. These are size-structured competition for light, a disturbance regime, and tradeoffs in plant function related to leaf turnover and reproductive allocation.
How much of plant trait diversity can be accounted for by successional processes remains unclear, but a wide range of traits have been implicated in such processes, including properties of leaves, seeds, wood, and xylem. Fundamentally, one can expect any trait influencing growth, mortality, or fecundity to have implications for successional dynamics. Successional processes therefore hold promise for explaining mixtures in many traits, not only with regard to LMA and HMAT.
The eco-evolutionary framework applied here also holds promise for predicting trait mixtures over environmental gradients, complementing previous efforts, which succeeded in using evolutionary algorithms to predict carbon allocation among roots and stems (35). Under different environmental conditions, our model predicts a variety of vegetation types and trait mixtures (Fig. 5). These evolved forests capture two well-known empirical patterns whereby LMA values tend to be lower in more productive sites with shorter disturbance intervals (30, 39, 40) and plants tend to be taller on more productive sites with longer disturbance intervals (39, 41).
In addition, our model provides testable hypotheses about other features of vegetation for which good data are as yet lacking. For example, we find that the number of LMA types varies with the disturbance regime and that HMAT diversity is always highest within the last successional type, irrespective of whether the metacommunity comprises one, two, or three successional types. More generally, frameworks like the one used here have potential to bridge between models focusing alternatively on the function and composition of forests (42), which have until recently remained separate and largely incompatible.
Evolutionarily Emergent Near-Neutrality.
The unified neutral theory of biodiversity (UNT) (11) was proposed as a conceptual alternative to the theory of niche differentiation, for explaining species diversity in forests and, in particular, the high diversity of late-successional types in tropical forests (19). Unlike niche theory, the UNT assumes that all plants are functionally identical, having equal growth rates, shade tolerance, and fitness. Trait differences do not affect community assembly; rather, stochastic speciation and population dynamics maintain diversity via the continual introduction of new species combined with slow competitive exclusion. The parameters of the UNT can be tuned so that it captures the high species diversity observed in tropical forests. However, to most forest ecologists, including Hubbell himself (11, 19), the core assumption of fitness equivalence on which the UNT rests seems implausible, partly for theoretical reasons (43), but mainly because coexisting species are known to vary greatly in the demographic rates contributing to fitness (4, 11, 19, 44).
Since its publication, multiple studies have therefore attempted either to reconcile the UNT with traditional niche-based theories of diversity (10, 45–47) or to justify the assumption of fitness equivalence (19, 37, 45). In attempts thus far, slow competitive exclusion has been imposed on the system, rather than emerging intrinsically. For example in the model by Hubbell (37), strong dispersal and recruitment limitations are introduced to bring the process of competitive exclusion to a near standstill. Under such conditions a variety of types can be maintained, but if competitive exclusion resumes, then diversity collapses to a single type. How conditions of near-neutrality or slow competitive exclusion might arise in nature therefore remains hotly debated (10, 37, 45).
Our study goes one step farther toward reconciling niche theory and neutral theory by showing how a central assumption of the UNT—fitness equivalence—can arise intrinsically as an outcome of trait-based niche differentiation. Importantly, the fitness equivalence arises not as a global property, but in specific regions of trait space. Niche differentiation is often thought of as creating a fitness landscape with distinct adaptive peaks, supporting a finite number of types that are able to persist without competitive exclusion (9, 15). Such a landscape does indeed result when LMA is evolving alone (Fig. 2B). However, our model shows that fitness landscapes of quite different shapes are also possible. When HMAT is evolving alone, this produces a flattened fitness landscape (Fig. 2B; for the emergence of this fitness landscape in the course of community assembly, see SI Appendix, Fig. S7). When LMA and HMAT evolve jointly, a nearly level (near-neutral) plateau arises, but only in a specific region of trait space, corresponding to shade-tolerant, late-successional types (Figs. 2C and 3). These plateaus in fitness landscapes are what we call evolutionarily emergent near-neutrality. The definition of “neutrality” used here is the same as that in the UNT: equivalence in per capita fitness among all individuals of every species (11, 45). However, evolutionarily emergent near-neutrality differs from the complete neutrality assumed in the UNT in two important ways. First, the flattened fitness landscape appears only toward the end of community assembly—it is a product of a competition process, not a property assumed or imposed as in the UNT (11). Second, evolutionarily emergent near-neutrality does not apply globally across the whole assemblage, but rather emerges in particular regions of trait space. The fitness landscape as a whole can thus include both peaks and plateaus.
The question then naturally arises whether the near-neutral fitness landscapes created via trait-based niche differentiation are sufficiently flat to enable ecological drift to contribute to the range of types and species maintained in the community. In general, flattened fitness landscapes slow down the process of competitive exclusion. When combined with demographic stochasticity, they sustain a considerably larger number of species than landscapes with steep relief and spaced peaks.
Generality and Limitations.
Many theoretical studies have identified mechanisms that potentially promote diversity, using models with simplified population dynamics. In this study, we set out to investigate whether niche differentiation can generate and maintain richer trait mixtures than had previously been recognized, by making the details of the population dynamics one step more realistic. By linking to explicit traits, whose tradeoffs can be quantified empirically, we have also sought to increase the connection between field observations and theoretical research. Nevertheless, the question remains how well the dynamics of our model reflect those of real ecosystems.
Overall, the assumptions underlying our model seem well supported. The key demographic processes captured by our model—disturbance, size-asymmetric shading, successional dynamics, and trait-mediated tradeoffs in plant function—are found in nearly all vegetation and have been applied broadly in successional models (22, 48). Predictions about the effects of traits on growth made using the growth model applied in this study (24) were found to be well supported in a meta-analysis of more than 100 studies (49). Whereas some previous theoretical models have been shown to suffer from pathologies arising from discontinuous competition kernels (17, 50), the competitive interactions in our model are not generated from a fixed kernel, but instead dynamically arise from plants shading each other, with the effects of this shading varying continuously with respect to size (via integration through photosynthesis) across the entire life cycle of a plant (SI Appendix, Fig. S16).
However, some limitations of our approach and results should be made clear. Compared with previous niche models lacking size structure and traits of known importance, our approach is an improvement. However, we focus on competition for a single resource (light) and model abstract disturbance events that remove all vegetation. We also assume that competition can be described in terms of vertical spatial structure within patches without accounting for intricacies of horizontal spatial structure and that the patches in the metacommunity are equally coupled by dispersal. Although these are essential simplifications, they are commonly used across a number of vegetation models to render tractable the computational analysis of size-structured populations (6, 14, 22). Additionally, we have considered only traits involved in two tradeoffs. Although this is more than previously considered in niche models, species in real forests are known to vary widely in other traits involved in other tradeoffs (12, 25). In extending our work, it will be interesting to investigate whether the addition of extra traits further enhances the opportunities for niche differentiation reported here.
The parameters of the physiological growth model applied in our analysis would benefit from further empirical support and testing. Here, we have used a previously published parameter set (24): Although drawing on available data as much as possible, data for some parameters were limited. As an example, we assume that mature plants eventually allocate all surplus energy to reproduction. Data to test this assumption are almost entirely absent (51). Because we have defined surplus energy as that being left over after tissues lost via turnover are replaced, trees allocating 100% of surplus energy to reproduction still produce new cohorts of leaves and continue to expand in stem diameter. Moreover, we have established that our results are not sensitive to varying the parameter values used in our analysis (SI Appendix, Figs. S11, S14, and S15). In particular, we have shown that relaxing the assumption that plants shift to allocating 100% of surplus energy to reproduction does not change our core results: HMAT mixtures can be maintained when HMAT evolves alone even when we reduce the maximum fraction allocated to reproduction to as low as 20% (SI Appendix, Fig. S11). When HMAT and LMA evolve jointly, we find that reducing the maximum fraction allocated to reproduction narrows the range of HMAT coexisting strategies, without affecting our key result of finding a cluster of strategies on a relatively flat plateau of the emergent fitness landscape (SI Appendix, Fig. S15).
Closing Remarks.
Overall, our work demonstrates that when a few key ingredients common to all forests are added, successional niche models can readily produce forests of considerably higher diversity than was previously thought possible, including the particular feature of tropical forests that helped motivate the UNT: the proliferation of species occupying niche space in low light. We have shown how the core tradeoffs underpinning two prominent traits are sufficient to maintain stable coexistence of species differing in those traits, via distinct pathways of successional behavior. Finally, we have shown how niche differentiation can create regions in trait space where fitness landscapes are nearly flat and, through this evolutionarily emergent near-neutrality, promote rich patterns of coexistence enhanced by ecological drift across the resultant fitness plateaus.
Materials and Methods
SI Appendix, Fig. S1 summarizes the processes represented in the model, and in SI Appendix, Tables S1 and S2 summarize all variables and parameters defined below.
Population Dynamics.
We consider a metacommunity of patches, with the age of each patch corresponding to the time since its last disturbance (Fig. 1). Disturbance events remove all plants within a patch. Following a disturbance, patches are colonized by seeds arriving from a global pool of dispersers; any seeds produced within the patch contribute to this global pool of dispersers. Different patches within the metacommunity are assumed to have similar abiotic properties and thus differ only in their age. The state of a metacommunity can therefore be characterized by the density distribution of patch ages and, for each patch age, the height distribution of plants of all species within patches of that age. With continuous distributions, the model captures the ensemble behavior of an infinitely large number of patches and thus plants.
The distribution is affected by the disturbance regime. We assume that disturbances are caused externally and can be described fully by the average time interval between disturbances, (by default 60 y). Further, we let the age-dependent probability of patch disturbance increase linearly with patch age . Incorporating these assumptions into von Foerster’s equation for age-structured population dynamics (52) leads to a Weibull distribution of patch ages (53), , as shown in Fig. 1A.
Competitive hierarchies among plants within developing patches are modeled by tracking the height distribution of plants as patches age after a disturbance. We denote by the traits of plant species , where is the LMA and is the HMAT of plant species ; by the traits of resident species; and by their average seed rain across the metacommunity (details below). Here traits refer to heritable characteristics of plants that are constant throughout ontogeny, in contrast to a plant’s height, which changes through ontogeny. We denote by the density of plants with height given their traits and a competitive environment and by , , and the height growth rate, death rate, and fecundity rate of those plants in that environment. These variables depend on the vertical profile of shading within the patch, , which in turn depends on the resident traits , the seed rains of these resident types, and the patch age . For each , the seed rain is given by the cumulative seed output across the metacommunity,
| [1] |
where is the probability of offspring surviving dispersal.
The dynamics of the metacommunity, as described by the density distribution , are then given by a partial differential equation
| [2] |
(22, 27, 28). Eq. 2 has two boundary conditions. The first,
| [3] |
equates the inflow of plants at the lower bound of the height distribution to the rate at which offspring are produced in the metacommunity. Here, is the probability of offspring successfully establishing themselves in a new patch, set to decrease as the growth rate of seedling declines (SI Appendix, Eq. S16). The second boundary condition states that patches are completely cleared after a disturbance,
| [4] |
Plants and species interact via their influences on the vertical shading profile . Specifically, canopy openness at height in a patch of age is calculated from the total leaf area above that height (54),
| [5] |
where is the total leaf area above height for plants of height and is the light-extinction coefficient.
Invasion Fitness.
We denote by the (invasion) fitness of plants with traits growing in a metacommunity with one or more resident strategies with traits and seed rains (32, 33). Invasion fitness is ideally calculated as the long-term per capita growth rate of the population with traits when rare; however, in structured metacommunities, the most convenient indicator of per capita growth rate is the logarithm of the basic reproduction ratio, (29), where is the average number of dispersing seeds with traits produced by each dispersing seed. The trait combination can invade when or equivalently .
Recalling that patches of age have frequency density in the landscape, it follows that a dispersing seed with traits has probability of landing in a patch of age to .The basic reproduction ratio for plants with traits is thus
| [6] |
where is the expected number of dispersing seeds with traits produced by a single dispersing seed with traits arriving in a patch of age (29). Here, is calculated by integrating a plant’s fecundity, , over the expected lifetime of the patch, taking into account competitive shading from residents with traits , the plant’s probability of surviving, and its traits:
| [7] |
and , respectively, are the height and the cumulative survival probability at the patch age of seeds with traits arriving in a patch of age , and is the probability that the patch remains undisturbed from age to .
Physiological Dynamics.
Rates of growth, mortality, and fecundity are given by a physiological submodel specifically formulated for height-structured metacommunity models (24). This submodel is fully described in SI Appendix, section 1, Eqs. S1–S16. The principal ingredients are (i) growth driven by carbon assimilation and light interception, (ii) an allometric model linking a plant’s leaf area to its height and mass of supporting tissues, (iii) a continuous vertical distribution of leaf area within the crown of each plant, (iv) net dry-matter production given by gross photosynthesis (calculated by integrating instantaneous assimilation rates in a given light profile over the annual solar environment) minus costs of tissue respiration and turnover, (v) fecundity calculated from reproductive investment and mass per seed, and (vi) an exponential increase in mortality with declining carbon income per leaf area (24).
The two evolving traits, LMA () and HMAT (), generate demographic differences by influencing rates of net biomass production and allocation. The details of the trait-mediated tradeoffs are as follows. LMA determines the cost of deploying leaf area and is related to leaf turnover via an allometric relationship observed in a global dataset (30), , with fitted parameters and (SI Appendix, Fig. S2). We also vary the mass-based leaf respiration rate so that it stays constant per unit leaf area as LMA is varied, as is empirically observed (30), HMAT affects the fraction of mass increment allocated to reproduction, varying with height ,
| [8] |
where is the maximum allocation (ranging between 0 and 1) and determines the sharpness of the transition. By default, we set and , implying a rapid transition to reproduction at (SI Appendix, Fig. S3). The remaining fraction of mass increment is allocated to growth.
Parameters.
We use parameter values as provided for the previously published growth model (24) (SI Appendix, Table S2). To vary environmental conditions, we change the mean disturbance interval, , and a dimensionless index of site productivity, which acts as a multiplier on the maximum photosynthesis per leaf area, . Default values for these parameters are y and . We assess the sensitivity of our results to changes in other parameters by evolving trait mixtures for parameter values at 90% and 110% of the default values (SI Appendix, Figs. S11, S14, and S15).
Numerical Methods.
To solve Eq. 2, we use a refined version of the Escalator Boxcar Train (EBT) method (27, 55) powered by an embedded fourth-order Runge–Kutta ordinary differential equation solver. This solver is also used to calculate invasion fitness by numerically integrating Eqs. 6 and 7. The original EBT method proceeds by introducing cohorts at fixed time intervals and then approximating the first and second moments of the density distribution N within each cohort (27). We extend this method by adaptively refining the time points at which new cohorts are introduced into the metacommunity. This is necessary to handle the strongly size-asymmetric interactions occurring in our model. To generate Figs. 1 and 5, we sample from the continuous distribution N for a series of patch ages (SI Appendix, section 2).
Supplementary Material
Acknowledgments
We thank five anonymous reviewers and many colleagues for helpful discussions and comments on earlier versions of this paper. This work was supported by Australian Research Council (ARC) Grants DP110102086 and DP0877064 (to D.S.F.). Å.B. was supported by the Swedish Research Council Formas (2012-2008). M.W. was supported by a fellowship from the ARC. U.D. was supported by the European Commission, the European Science Foundation, the Austrian Science Fund, the Austrian Ministry of Science and Research, and the Vienna Science and Technology Fund.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
Data deposition: Code and data reproducing the results in this paper have been deposited on Figshare, https://doi.org/10.6084/m9.figshare.4649800.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1610206114/-/DCSupplemental.
References
- 1.Wright JS. Plant diversity in tropical forests: A review of mechanisms of species coexistence. Oecologia. 2002;130(1):1–14. doi: 10.1007/s004420100809. [DOI] [PubMed] [Google Scholar]
- 2.Tilman D, Pacala S. The maintenance of species richness in plant communities. In: Ricklefs RE, Schluter D, editors. Species Diversity in Ecological Communities: Historical and Geographical Perspectives. Univ of Chicago Press; Chicago: 1993. pp. 13–25. [Google Scholar]
- 3.Adler PB, Fajardo A, Kleinhesselink AR, Kraft NJB. Trait-based tests of coexistence mechanisms. Ecol Lett. 2013;16(10):1294–1306. doi: 10.1111/ele.12157. [DOI] [PubMed] [Google Scholar]
- 4.Condit R, et al. The importance of demographic niches to tree diversity. Science. 2006;313(5783):98–101. doi: 10.1126/science.1124712. [DOI] [PubMed] [Google Scholar]
- 5.Grubb PJ. The maintenance of species-richness in plant communities: The importance of the regeneration niche. Biol Rev. 1977;52(1):107–145. [Google Scholar]
- 6.Huston M, Smith T. Plant succession: Life history and competition. Am Nat. 1987;130(2):168–198. [Google Scholar]
- 7.Rees M, Westoby M. Game-theoretical evolution of seed mass in multi-species ecological models. Oikos. 1997;78(1):116–126. [Google Scholar]
- 8.Pacala SW, Rees M. Models suggesting field experiments to test two hypotheses explaining successional diversity. Am Nat. 1998;152(5):729–737. doi: 10.1086/286203. [DOI] [PubMed] [Google Scholar]
- 9.Chesson P. Mechanisms of maintenance of species diversity. Annu Rev Ecol Syst. 2000;31:343–366. [Google Scholar]
- 10.Adler PB, HilleRisLambers J, Levine JM. A niche for neutrality. Ecol Lett. 2007;10(2):95–104. doi: 10.1111/j.1461-0248.2006.00996.x. [DOI] [PubMed] [Google Scholar]
- 11.Hubbell SP. 2001. The Unified Neutral Theory of Biodiversity and Biogeography, Monographs in Population Biology (Princeton Univ Press, Princeton)
- 12.Wright SJ, et al. Functional traits and the growth–mortality trade-off in tropical trees. Ecology. 2010;91(12):3664–3674. doi: 10.1890/09-2335.1. [DOI] [PubMed] [Google Scholar]
- 13.King DA, Wright SJ, Connell JH. The contribution of interspecific variation in maximum tree height to tropical and temperate diversity. J Trop Ecol. 2006;22(1):11–24. [Google Scholar]
- 14.Kohyama T. Size-structured tree populations in gap-dynamic forest: The forest architecture hypothesis for the stable coexistence of species. J Ecol. 1993;81(1):131–143. [Google Scholar]
- 15.Parvinen K, Meszéna G. Disturbance-generated niche-segregation in a structured metapopulation model. Evol Ecol Res. 2009;11(4):651–666. [Google Scholar]
- 16.Gravel D, Canham CD, Beaudet M, Messier C. Shade tolerance, canopy gaps and mechanisms of coexistence of forest trees. Oikos. 2010;119(3):475–484. [Google Scholar]
- 17.D’Andrea R, Barabás G, Ostling A. Revising the tolerance-fecundity trade-off; or, on the consequences of discontinuous resource use for limiting similarity, species diversity, and trait dispersion. Am Nat. 2013;181(4):E91–E101. doi: 10.1086/669902. [DOI] [PubMed] [Google Scholar]
- 18.Purves DW, Vanderwel MC. Traits, states and rates: Understanding coexistence in forests. In: Coomes DA, Burslem DFRP, Simonson WD, editors. Forests and Global Change, Ecological Reviews. Cambridge Univ Press; Cambridge, UK: 2014. pp. 161–194. [Google Scholar]
- 19.Hubbell SP. Neutral theory in community ecology and the hypothesis of functional equivalence. Funct Ecol. 2005;19(1):166–172. [Google Scholar]
- 20.Tilman D. Competition and biodiversity in spatially structured habitats. Ecology. 1994;75(1):2–16. [Google Scholar]
- 21.Sakschewski B, et al. Leaf and stem economics spectra drive diversity of functional plant traits in a dynamic global vegetation model. Glob Chang Biol. 2015;21(7):2711–2725. doi: 10.1111/gcb.12870. [DOI] [PubMed] [Google Scholar]
- 22.Moorcroft PR, Hurtt GC, Pacala SW. A method for scaling vegetation dynamics: The ecosystem demography model (ED) Ecol Monogr. 2001;71(4):557–586. [Google Scholar]
- 23.Strigul N, Pristinski D, Purves D, Dushoff J, Pacala S. Scaling from trees to forests: Tractable macroscopic equations for forest dynamics. Ecol Monogr. 2008;78(4):523–545. [Google Scholar]
- 24.Falster DS, Brännström Å, Dieckmann U, Westoby M. Influence of four major plant traits on average height, leaf-area cover, net primary productivity, and biomass density in single-species forests: A theoretical investigation. J Ecol. 2011;99(1):148–164. [Google Scholar]
- 25.Westoby M, Falster DS, Moles AT, Vesk PA, Wright IJ. Plant ecological strategies: Some leading dimensions of variation between species. Annu Rev Ecol Syst. 2002;33:125–159. [Google Scholar]
- 26.Poorter L, Bongers F. Leaf traits are good predictors of plant performance across 53 rain forest species. Ecology. 2006;87(7):1733–1743. doi: 10.1890/0012-9658(2006)87[1733:ltagpo]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- 27.de Roos AM. A gentle introduction to physiologically structured population models. In: Taljapurkar S, Caswell H, editors. Structured Population Models in Marine, Terrestrial and Freshwater Systems. Springer; New York: 1997. pp. 119–204. [Google Scholar]
- 28.Hara T. A stochastic model and the moment dynamics of the growth and size distribution of plant populations. J Theor Biol. 1984;109(2):173–190. [Google Scholar]
- 29.Metz JAJ, Gyllenberg M. How should we define fitness in structured metapopulation models? Including an application to the calculation of evolutionarily stable dispersal strategies. Proc R Soc Lond B Biol Sci. 2001;268(1466):499–508. doi: 10.1098/rspb.2000.1373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Wright IJ, et al. The world-wide leaf economics spectrum. Nature. 2004;428(2403):821–827. doi: 10.1038/nature02403. [DOI] [PubMed] [Google Scholar]
- 31.Barabás G, D’Andrea R, Rael R, Meszéna G, Ostling A. Emergent neutrality or hidden niches? Oikos. 2013;122(11):1565–1572. [Google Scholar]
- 32.Metz JAJ, Nisbet RM, Geritz SAH. How should we define ‘fitness’ for general ecological scenarios? Trends Ecol Evol. 1992;7(6):198–202. doi: 10.1016/0169-5347(92)90073-K. [DOI] [PubMed] [Google Scholar]
- 33.Brännström Å, Johansson J, von Festenberg N. The hitchhiker’s guide to adaptive dynamics. Games. 2013;4(3):304–328. [Google Scholar]
- 34.Falster DS, Westoby M. Plant height and evolutionary games. Trends Ecol Evol. 2003;18(7):337–343. [Google Scholar]
- 35.Dybzinski R, Farrior C, Wolf A, Reich PB, Pacala SW. Evolutionarily stable strategy carbon allocation to foliage, wood, and fine roots in trees competing for light and nitrogen: An analytically tractable, individual-based model and quantitative comparisons to data. Am Nat. 2011;177(2):153–166. doi: 10.1086/657992. [DOI] [PubMed] [Google Scholar]
- 36.Chambers JQ, et al. The steady-state mosaic of disturbance and succession across an old-growth Central Amazon forest landscape. Proc Natl Acad Sci USA. 2013;110(10):3949–3954. doi: 10.1073/pnas.1202894110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hubbell SP. Neutral theory and the evolution of ecological equivalence. Ecology. 2006;87(6):1387–1398. doi: 10.1890/0012-9658(2006)87[1387:ntateo]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- 38.Thomas SC, Bazzaz FA. Asymptotic height as a predictor of photosynthetic characteristics in Malaysian rain forest trees. Ecology. 1999;80(5):1607–1622. [Google Scholar]
- 39.Douma JC, Shipley B, Witte J-PM, Aerts R, van Bodegom PM. Disturbance and resource availability act differently on the same suite of plant traits: Revisiting assembly hypotheses. Ecology. 2012;93(4):825–835. doi: 10.1890/10-1961.1. [DOI] [PubMed] [Google Scholar]
- 40.Fortunel C, Paine CET, Fine PVA, Kraft NJB, Baraloto C. Environmental factors predict community functional composition in Amazonian forests. J Ecol. 2014;102(1):145–155. [Google Scholar]
- 41.Toledo M, et al. Climate and soil drive forest structure in Bolivian lowland forests. J Trop Ecol. 2011;27(4):333–345. [Google Scholar]
- 42.Mokany K, et al. Integrating modelling of biodiversity composition and ecosystem function. Oikos. 2016;125(1):10–19. [Google Scholar]
- 43.Purves DW, Turnbull LA. Different but equal: The implausible assumption at the heart of neutral theory. J Anim Ecol. 2010;79(6):1215–1225. doi: 10.1111/j.1365-2656.2010.01738.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Westoby M, Wright IJ. Land-plant ecology on the basis of functional traits. Trends Ecol Evol. 2006;21(5):261–268. doi: 10.1016/j.tree.2006.02.004. [DOI] [PubMed] [Google Scholar]
- 45.Chave J. Neutral theory and community ecology. Ecol Lett. 2004;7(3):241–253. [Google Scholar]
- 46.Scheffer M, van Nes EH. Self-organized similarity, the evolutionary emergence of groups of similar species. Proc Natl Acad Sci USA. 2006;103(16):6230–6235. doi: 10.1073/pnas.0508024103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Chisholm RA, Pacala SW. Niche and neutral models predict asymptotically equivalent species abundance distributions in high-diversity ecological communities. Proc Natl Acad Sci USA. 2010;107(36):15821–15825. doi: 10.1073/pnas.1009387107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Kunstler G, et al. Plant functional traits have globally consistent effects on competition. Nature. 2016;529(7585):204–207. doi: 10.1038/nature16476. [DOI] [PubMed] [Google Scholar]
- 49.Gibert A, Gray EF, Westoby M, Wright IJ, Falster DS. On the link between functional traits and growth rate: Meta-analysis shows effects change with plant size, as predicted. J Ecol. 2016;104(5):1488–1503. [Google Scholar]
- 50.Barabás G, D’Andrea R, Ostling AM. Species packing in nonsmooth competition models. Theor Ecol. 2013;6(1):1–19. [Google Scholar]
- 51.Thomas SC. Age-related changes in tree growth and functional biology: The role of reproduction. In: Meinzer FC, Lachenbruch B, Dawson TE, editors. Size- and Age-Related Changes in Tree Structure and Function. Vol 4. Springer; Dordrecht, The Netherlands: 2011. pp. 33–64. [Google Scholar]
- 52.Von Foerster H. Some remarks on changing populations. In: Stohlman F, editor. The kinetics of Cellular Proliferation. Grune et Stratton; New York: 1959. pp. 382–407. [Google Scholar]
- 53.Clark JS. Ecological disturbance as a renewal process: Theory and application to fire history. Oikos. 1989;56(1):17–30. [Google Scholar]
- 54.Yoda K. Three dimensional distribution of light intensity in a tropical rain forest of west Malaysia. Jpn J Ecol. 1974;24(4):247–254. [Google Scholar]
- 55.Brännström Å, Carlsson L, Simpson D. On the convergence of the escalator boxcar train. SIAM J Numer Anal. 2013;51(6):3213–3231. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.