Significance
Deep neural networks are currently the most successful machine-learning technique for solving a variety of tasks, including language translation, image classification, and image generation. One weakness of such models is that, unlike humans, they are unable to learn multiple tasks sequentially. In this work we propose a practical solution to train such models sequentially by protecting the weights important for previous tasks. This approach, inspired by synaptic consolidation in neuroscience, enables state of the art results on multiple reinforcement learning problems experienced sequentially.
Keywords: synaptic consolidation, artificial intelligence, stability plasticity, continual learning, deep learning
Abstract
The ability to learn tasks in a sequential fashion is crucial to the development of artificial intelligence. Until now neural networks have not been capable of this and it has been widely thought that catastrophic forgetting is an inevitable feature of connectionist models. We show that it is possible to overcome this limitation and train networks that can maintain expertise on tasks that they have not experienced for a long time. Our approach remembers old tasks by selectively slowing down learning on the weights important for those tasks. We demonstrate our approach is scalable and effective by solving a set of classification tasks based on a hand-written digit dataset and by learning several Atari 2600 games sequentially.
Achieving artificial general intelligence requires that agents are able to learn and remember many different tasks (1). This is particularly difficult in real-world settings: The sequence of tasks may not be explicitly labeled, tasks may switch unpredictably, and any individual task may not recur for long time intervals. Critically, therefore, intelligent agents must demonstrate a capacity for continual learning: that is, the ability to learn consecutive tasks without forgetting how to perform previously trained tasks.
Continual learning poses particular challenges for artificial neural networks due to the tendency for knowledge of the previously learned task(s) (e.g., task A) to be abruptly lost as information relevant to the current task (e.g., task B) is incorporated. This phenomenon, termed catastrophic forgetting (2–6), occurs specifically when the network is trained sequentially on multiple tasks because the weights in the network that are important for task A are changed to meet the objectives of task B. Whereas recent advances in machine learning and in particular deep neural networks have resulted in impressive gains in performance across a variety of domains (e.g., refs. 7 and 8), little progress has been made in achieving continual learning. Current approaches have typically ensured that data from all tasks are simultaneously available during training. By interleaving data from multiple tasks during learning, forgetting does not occur because the weights of the network can be jointly optimized for performance on all tasks. In this regime—often referred to as the multitask learning paradigm—deep-learning techniques have been used to train single agents that can successfully play multiple Atari games (9, 10). If tasks are presented sequentially, multitask learning can be used only if the data are recorded by an episodic memory system and replayed to the network during training. This approach [often called system-level consolidation (4, 5)] is impractical for learning large numbers of tasks, as in our setting it would require the amount of memories being stored and replayed to be proportional to the number of tasks. The lack of algorithms to support continual learning thus remains a key barrier to the development of artificial general intelligence.
In marked contrast to artificial neural networks, humans and other animals appear to be able to learn in a continual fashion (11). Recent evidence suggests that the mammalian brain may avoid catastrophic forgetting by protecting previously acquired knowledge in neocortical circuits (11–14). When a mouse acquires a new skill, a proportion of excitatory synapses are strengthened; this manifests as an increase in the volume of individual dendritic spines of neurons (13). Critically, these enlarged dendritic spines persist despite the subsequent learning of other tasks, accounting for retention of performance several months later (13). When these spines are selectively “erased,” the corresponding skill is forgotten (11, 12). This provides causal evidence that neural mechanisms supporting the protection of these strengthened synapses are critical to retention of task performance. These experimental findings—together with neurobiological models such as the cascade model (15, 16)—suggest that continual learning in the neocortex relies on task-specific synaptic consolidation, whereby knowledge is durably encoded by rendering a proportion of synapses less plastic and therefore stable over long timescales.
In this work, we demonstrate that task-specific synaptic consolidation offers a unique solution to the continual-learning problem for artificial intelligence. We develop an algorithm analogous to synaptic consolidation for artificial neural networks, which we refer to as elastic weight consolidation (EWC). This algorithm slows down learning on certain weights based on how important they are to previously seen tasks. We show how EWC can be used in supervised learning and reinforcement learning problems to train several tasks sequentially without forgetting older ones, in marked contrast to previous deep-learning techniques.
Results
EWC.
In brains, synaptic consolidation might enable continual learning by reducing the plasticity of synapses that are vital to previously learned tasks. We implement an algorithm that performs a similar operation in artificial neural networks by constraining important parameters to stay close to their old values. In this section, we explain why we expect to find a solution to a new task in the neighborhood of an older one, how we implement the constraint, and finally how we determine which parameters are important.
A deep neural network consists of multiple layers of linear projection followed by element-wise nonlinearities. Learning a task consists of adjusting the set of weights and biases of the linear projections, to optimize performance. Many configurations of will result in the same performance (17, 18); this overparameterization makes it likely that there is a solution for task B, , that is close to the previously found solution for task A, . While learning task B, EWC therefore protects the performance in task A by constraining the parameters to stay in a region of low error for task A centered around , as shown schematically in Fig. 1. This constraint is implemented as a quadratic penalty and can therefore be imagined as a spring anchoring the parameters to the previous solution, hence having the name elastic. Importantly, the stiffness of this spring should not be the same for all parameters; rather, it should be greater for parameters that most affect performance in task A.
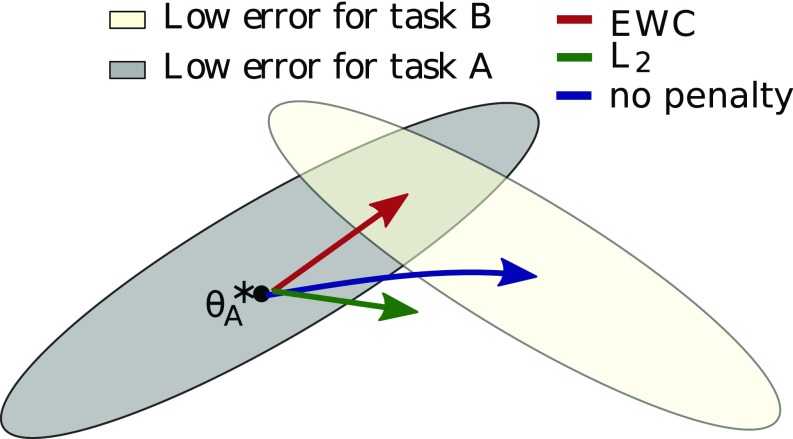
Fig. 1.
EWC ensures task A is remembered while training on task B. Training trajectories are illustrated in a schematic parameter space, with parameter regions leading to good performance on task A (gray) and on task B (cream color). After learning the first task, the parameters are at . If we take gradient steps according to task B alone (blue arrow), we will minimize the loss of task B but destroy what we have learned for task A. On the other hand, if we constrain each weight with the same coefficient (green arrow), the restriction imposed is too severe and we can remember task A only at the expense of not learning task B. EWC, conversely, finds a solution for task B without incurring a significant loss on task A (red arrow) by explicitly computing how important weights are for task A.
To justify this choice of constraint and to define which weights are most important for a task, it is useful to consider neural network training from a probabilistic perspective. From this point of view, optimizing the parameters is tantamount to finding their most probable values given some data . We can compute this conditional probability from the prior probability of the parameters and the probability of the data by using Bayes’ rule:
| [1] |
Note that the log probability of the data given the parameters is simply the negative of the loss function for the problem at hand . Assume that the data are split into two independent parts, one defining task A () and the other defining task B (). Then, we can rearrange Eq. 1:
| [2] |
Note that the left-hand side is still describing the posterior probability of the parameters given the entire dataset, whereas the right-hand side depends only on the loss function for task B, . All of the information about task A must therefore have been absorbed into the posterior distribution . This posterior probability must contain information about which parameters were important to task and is therefore the key to implementing EWC. The true posterior probability is intractable, so, following the work on the Laplace approximation by Mackay (19), we approximate the posterior as a Gaussian distribution with mean given by the parameters and a diagonal precision given by the diagonal of the Fisher information matrix . has three key properties (20): (i) It is equivalent to the second derivative of the loss near a minimum, (ii) it can be computed from first-order derivatives alone and is thus easy to calculate even for large models, and (iii) it is guaranteed to be positive semidefinite. Note that this approach is similar to expectation propagation where each subtask is seen as a factor of the posterior (21). Given this approximation, the function that we minimize in EWC is
| [3] |
where is the loss for task B only, sets how important the old task is compared with the new one, and labels each parameter.
When moving to a third task, task C, EWC will try to keep the network parameters close to the learned parameters of both tasks A and B. This can be enforced either with two separate penalties or as one by noting that the sum of two quadratic penalties is itself a quadratic penalty.
EWC Extends Memory Lifetime for Random Patterns.
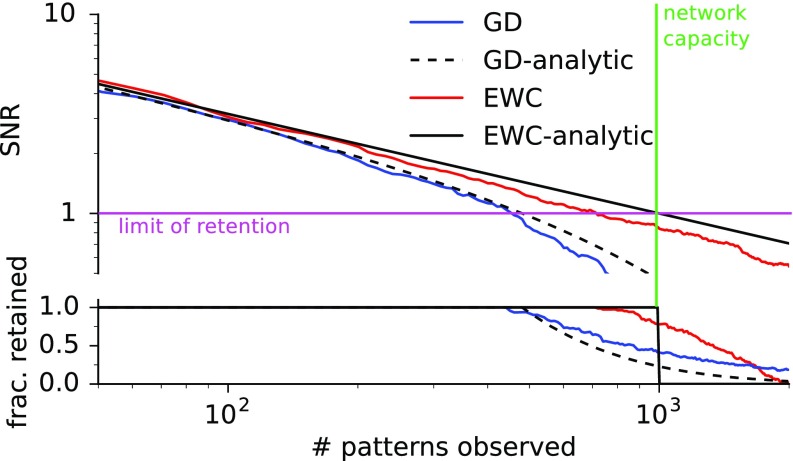
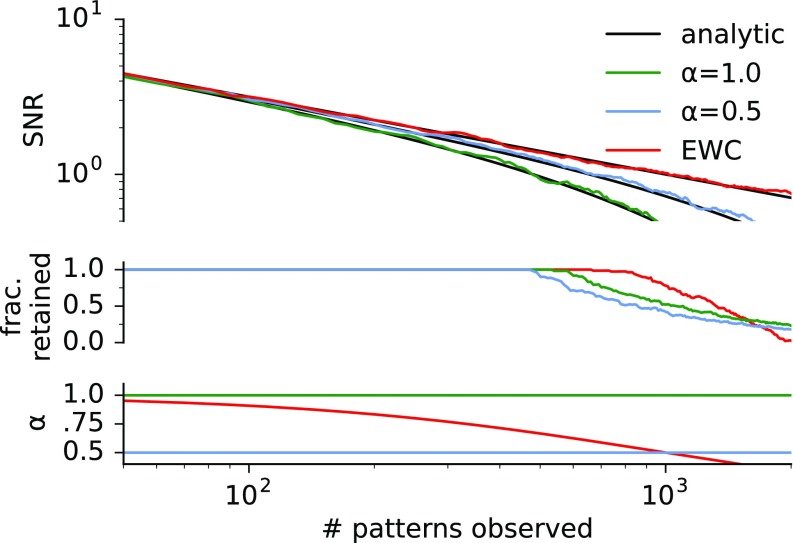
As an initial demonstration, we trained a linear network to associate random (i.e., uncorrelated) binary patterns to binary outcomes. Whereas this problem differs in important ways from more realistic settings that we examine later, this scenario admits analytical solutions and thus provides insights into key differences between EWC and plain gradient descent. In this case, the diagonal of the total Fisher information matrix is proportional to the number of patterns observed; thus in the case of EWC the learning rate lowers as more patterns are observed. Following ref. 15, we define a memory as retained if its signal-to-noise ratio (SNR) exceeds a certain threshold. Fig. 2, Top shows the SNR obtained using gradient descent (blue lines) and EWC (red lines) for the first pattern observed. At first, the SNR in the two cases is very similar, following a power-law decay with a slope of . As the number of patterns observed approaches the capacity of the network, the SNR for gradient descent starts decaying exponentially, whereas EWC maintains a power-law decay. The exponential decay observed with gradient descent is due to new patterns interfering with old ones; EWC protects from such interference and increases the fraction of memories retained (Fig. 2, Bottom). In the next sections we show that in more realistic cases, where input patterns have more complex statistics, interference occurs more easily with consequently more striking benefits for EWC over gradient descent.
Fig. 2.
Log-log plot of the SNR for recalling the first pattern after observing random patterns. If no penalty is applied (blue), the SNR decays as only when is smaller than the number of synapses and then decays exponentially. When EWC is applied (red), the decay takes a power-law form for all times. The dashed and solid lines show the analytic solutions derived in Eqs. S28 and S30. The fraction of memories retained (Bottom) is defined as the fraction of patterns whose SNR exceeds . EWC results in a higher fraction of memories being retained when the network is at capacity (). After network capacity is exceeded (Right), EWC performs worse than gradient descent (Discussion). More detailed plots can be found in the Supporting Information, Figs. S1 and S2.
EWC Allows Continual Learning in a Supervised Learning Context.
We next addressed the problem of whether EWC could allow deep neural networks to learn a set of more complex tasks without catastrophic forgetting. In particular, we trained a fully connected multilayer neural network on several supervised learning tasks in sequence. Within each task, we trained the neural network in the traditional way, namely by shuffling the data and processing them in small batches. After a fixed amount of training on each task, however, we allowed no further training on that task’s dataset.
We constructed the set of tasks from the problem of classifying hand-written digits from the Mixed National Institute of Science and Technology (MNIST) (22) dataset, according to a scheme previously used in the continual-learning literature (23, 24). For each task, we generated a fixed, random permutation by which the input pixels of all images would be shuffled. Each task was thus of equal difficulty to each other, but would require a different solution.
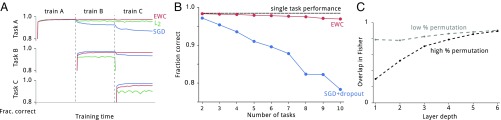
Training on this sequence of tasks with plain stochastic gradient descent (SGD) incurs catastrophic forgetting, as demonstrated in Fig. 3A. The blue curves show performance on the testing sets of two different tasks. At the point at which the training regime switches from training on the first task (A) to training on the second one (B), the performance for task B falls rapidly, whereas for task A it climbs steeply. The forgetting of task A compounds further with more training time and the addition of subsequent tasks. This problem cannot be countered by regularizing the network with a fixed quadratic constraint for each weight (green curves, L2 regularization): here, the performance in task A degrades much less severely, but task B cannot be learned properly as the constraint protects all weights equally, leaving little spare capacity for learning on B. However, when we use EWC, and thus take into account how important each weight is to task A, the network can learn task B well without forgetting task A (red curves). This is exactly the behavior described diagrammatically in Fig. 1.
Fig. 3.
Results on the permuted MNIST task. (A) Training curves for three random permutations A, B, and C, using EWC (red), regularization (green), and plain SGD (blue). Note that only EWC is capable of maintaining a high performance on old tasks, while retaining the ability to learn new tasks. (B) Average performance across all tasks, using EWC (red) or SGD with dropout regularization (blue). The dashed line shows the performance on a single task only. (C) Similarity between the Fisher information matrices as a function of network depth for two different amounts of permutation. Either a small square of 8 × 8 pixels in the middle of the image is permuted (gray) or a large square of 26 × 26 pixels is permuted (black). Note how the more different the tasks are, the smaller the overlap in Fisher information matrices in early layers.
Previous attempts to solve the continual-learning problem for deep neural networks have relied upon careful choice of network hyperparameters, together with other standard regularization methods, to mitigate catastrophic forgetting. However, on this task, they have achieved reasonable results only on up to two random permutations (23, 24). Using a similar cross-validated hyperparameter search to that in ref. 24, we compared traditional dropout regularization to EWC. We find that stochastic gradient descent with dropout regularization alone is limited and that it does not scale to more tasks (Fig. 3B). In contrast, EWC allows a large number of tasks to be learned in sequence, with only modest growth in the error rates.
Given that EWC allows the network to effectively squeeze in more functionality into a network with fixed capacity, we might ask whether it allocates completely separate parts of the network for each task or whether capacity is used in a more efficient fashion by sharing representation. To assess this, we determined whether each task depends on the same sets of weights, by measuring the overlap between pairs of tasks’ respective Fisher information matrices (Fisher Overlap). A small overlap means that the two tasks depend on different sets of weights (i.e., EWC subdivides the network’s weights for different tasks); a large overlap indicates that weights are being used for both of the two tasks (i.e., EWC enables sharing of representations). Fig. 3C shows the overlap as a function of depth. As a simple control, when a network is trained on two tasks that are very similar to each other (two versions of MNIST where only a few pixels are permutated), the tasks depend on similar sets of weights throughout the whole network (gray dashed curve). When then the two tasks are more dissimilar from each other, the network begins to allocate separate weights for the two tasks (black dashed line). Nevertheless, even for the large permutations, the layers of the network closer to the output are indeed being reused for both tasks. This reflects the fact that the permutations make the input domain very different, but the output domain (i.e., the class labels) is shared.
EWC Allows Continual Learning in a Reinforcement Learning Context.
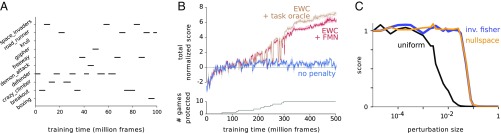
We next tested whether EWC could support continual learning in the far more demanding reinforcement learning (RL) domain. In RL, agents dynamically interact with the environment to develop a policy that maximizes cumulative future reward. We asked whether Deep Q Networks (DQNs)—an architecture that has achieved impressive successes in such challenging RL settings (25)—could be harnessed with EWC to successfully support continual learning in the classic Atari 2600 task set (26). Specifically, each experiment consisted of 10 games chosen randomly from those that are played at human level or above by DQN. At training time, the agent was exposed to experiences from each game for extended periods of time. The order of presentation of the games was randomized and allowed for returning to the same games several times. At regular intervals we would also test the agent’s score on each of the 10 games, without allowing the agent to train on them (Fig. 4A).
Fig. 4.
Results on Atari task. (A) Schedule of games. Black bars indicate the sequential training periods (segments) for each game. After each training segment, performance on all games is measured. The EWC constraint is activated only to protect an agent’s performance on each game once the agent has experienced 20 million frames in that game. (B) Total human-averaged scores for each method across all games. The score is averaged across random seeds and over the choice of which 10 games are played (Fig. S3). The human-normalized score for each game is clipped to 1. Red curve denotes the network that infers the task labels using the FMN algorithm; brown curve is the network provided with the task labels. The EWC and SGD curves start diverging when games start being played again that have been protected by EWC. (C) Sensitivity of a single-game DQN, trained on Breakout, to noise added to its weights. The performance on Breakout is shown as a function of the magnitude (standard deviation) of the weight perturbation. The weight perturbation is drawn from a zero mean Gaussian with covariance that is either uniform (black; i.e., targets all weights equally), the inverse Fisher (; blue; i.e., mimicking weight changes allowed by EWC), or uniform within the nullspace of the Fisher (orange; i.e., targets weights that the Fisher estimates that the network output is entirely invariant to). To evaluate the score, we ran the agent for 10 full game episodes, drawing a new random weight perturbation for every time step.
Notably, previous reinforcement learning approaches to continual learning have relied either on adding capacity to the network (27, 28) or on learning each task in separate networks, which are then used to train a single network that can play all games (9, 10). In contrast, the EWC approach presented here makes use of a single network with fixed resources (i.e., network capacity) and has minimal computational overhead.
In addition to using EWC to protect previously acquired knowledge, we used the RL domain to address a broader set of requirements that are needed for successful continual-learning systems: In particular, higher-level mechanisms are needed to infer which task is currently being performed, detect and incorporate novel tasks as they are encountered, and allow for rapid and flexible switching between tasks (29). In the primate brain, the prefrontal cortex is widely viewed as supporting these capabilities by sustaining neural representations of task context that exert top–down gating influences on sensory processing, working memory, and action selection (30–33).
Inspired by this evidence, we augmented the DQN agents with extra functionality to handle switching task contexts. Knowledge of which task is being performed is required for the EWC algorithm as it informs which quadratic constraints are currently active and also which quadratic constraint to update when the task context changes. To infer the task context, we implemented an online clustering algorithm that is trained without supervision and is based on the forget-me-not (FMN) process (34) (see Materials and Methods for more details). We also allowed the DQN agents to maintain separate short-term memory buffers for each inferred task. These allow action values for each task to be learned off-policy, using an experience replay mechanism (25). As such, the overall system has memory on two timescales: Over short timescales, the experience replay mechanism allows learning in the DQN to be based on the interleaved and uncorrelated experiences (25). At longer timescales, know-how across tasks is consolidated by using EWC. Finally, we allowed a small number of network parameters to be game specific. In particular, we allowed each layer of the network to have biases and per-element multiplicative gains that were specific to each game.
We compare the performance of agents that use EWC (red) with ones that do not (blue) over sets of 10 games in Fig. 4. We measure the performance as the total human-normalized score across all 10 games; the score on each game is clipped to 1 such that the total maximum score is 10 (at least at human level on all games) and 0 means the agent is as good as a random agent. If we rely on plain gradient descent methods as in ref. 25, the agent never learns to play more than one game and the harm inflicted by forgetting the old games means that the total human-normalized score remains below one. By using EWC, however, the agents do indeed learn to play multiple games. As a control, we also considered the benefit to the agent if we explicitly provided the agent with the true task label (Fig. 4B, brown), rather than relying on the learned task recognition through the FMN algorithm (Fig. 4B, red). The improvement here was only modest.
Whereas augmenting the DQN agent with EWC allows it to learn many games in sequence without suffering from catastrophic forgetting, it does not reach the score that would have been obtained by training 10 separate DQNs (Fig. S3). One possible reason for this is that we consolidated weights for each game based on a tractable approximation of parameter uncertainty, the Fisher information. We therefore sought to test the quality of our estimates empirically. To do so, we trained an agent on a single game and measured how perturbing the network parameters affected the agent’s score. Regardless of which game the agent was trained on, we observed the same patterns, shown in Fig. 4C. First, the agent was always more robust to parameter perturbations shaped by the inverse of the diagonal of the Fisher information (blue), as opposed to uniform perturbations (black). This validates that the diagonal of the Fisher information is a good estimate of how important a parameter is. Within our approximation, perturbing in the null space should have no effect on performance. Empirically, however, we observe that perturbing in this space (orange) has the same effect as perturbing in the inverse Fisher space. This suggests that we are overconfident about certain parameters being unimportant: It is therefore likely that the chief limitation of the current implementation is that it underestimates parameter uncertainty.
Fig. S3.
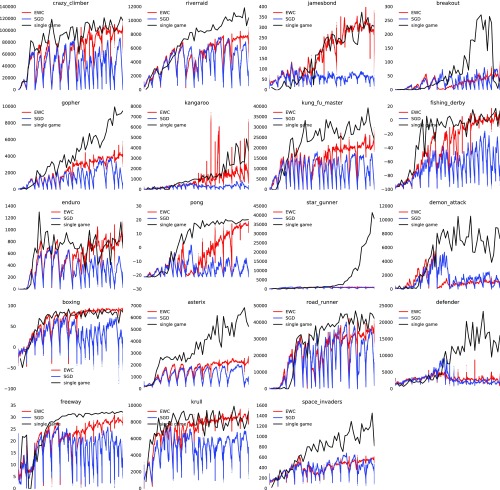
Score in the individual games as a function of steps played in that game. The black baseline curves show learning on individual games alone.
Fisher Overlap
To assess whether different tasks solved in the same network use similar sets of weights (Fig. 3C in the main text), we measured the degree of overlap between the two tasks’ Fisher matrices. Precisely, we computed the two tasks’ Fishers, and ; normalized these to each have unit trace, and ; and then computed their Fréchet distance, a metric on the space of positive-semidefinite matrices (44),
which is bounded between zero and one. We then define the overlap as , with a value of zero indicating that the two tasks depend on nonoverlapping sets of weights and a value of one indicating that for some .
Discussion
We present an algorithm, EWC, that allows knowledge of previous tasks to be protected during new learning, thereby avoiding catastrophic forgetting. It does so by selectively decreasing the plasticity of weights and thus has certain parallels with neurobiological models of synaptic consolidation (15, 16). We implement EWC as a soft, quadratic constraint whereby each weight is pulled back toward its old values by an amount proportional to its importance for performance on previously learned tasks. In analytically tractable settings, we demonstrate that EWC can protect network weights from interference and thus increase the fraction of memories retained over plain gradient descent. To the extent that tasks share structure, networks trained with EWC reuse shared components of the network. We further show that EWC can be effectively combined with deep neural networks to support continual learning in challenging reinforcement learning scenarios, such as Atari 2600 games.
The EWC algorithm can be grounded in Bayesian approaches to learning. Formally, when there is a new task to be learned, the network parameters are tempered by a prior which is the posterior distribution on the parameters given data from the previous task(s). This enables fast learning rates on parameters that are poorly constrained by the previous tasks and slow learning rates for those that are crucial.
There has been previous work (35, 36) using a quadratic penalty to approximate old parts of the dataset, but these applications have been limited to small models. Specifically, ref. 35 used random inputs to compute a quadratic approximation to the energy surface. Their approach is slow, as it requires recomputing the curvature at each sample. The ELLA algorithm described in ref. 36 requires computing and inverting matrices with a dimensionality equal to the number of parameters being optimized; therefore it has been mainly applied to linear and logistic regressions. In contrast, EWC has a run time that is linear in both the number of parameters and the number of training examples. We could achieve this low computational complexity only by using a crude Laplace approximation to the true the posterior distribution of the parameters. Despite its low computational cost and empirical successes—even in the setting of challenging RL domains—our use of a point estimate of the posterior’s variance (as in a Laplace approximation) does constitute a significant weakness (Fig. 4C). Our initial explorations suggest that one might improve on this local estimate by using Bayesian neural networks (37).
Whereas this paper has primarily focused on building an algorithm inspired by neurobiological observations and theories (15, 16), it is also instructive to consider whether the algorithm’s successes can feed back into our understanding of the brain. In particular, we see considerable parallels between EWC and two computational theories of synaptic plasticity.
Cascade models of synaptic plasticity (15, 16) construct dynamical models of synaptic states to understand the trade-off between plasticity and memory retention. Cascade models have important differences from our approach. In particular, they aim to extend memory lifetimes for systems at steady state (i.e., the limit of observing an infinite number of stimuli). As such, they allow for synapses to become more or less plastic and model the process of both retaining and forgetting memories. In contrast, we tackle the simpler problem of protecting the network from interference when starting from an empty network. In fact in EWC weights can only become more constrained (i.e., less plastic) with time and thus we can model only memory retention rather than forgetting. Therefore when the number of random patterns observed exceeds the capacity of the network and steady state is reached, EWC starts to perform even worse than plain gradient descent (Fig. 2, Bottom). Further, the EWC model—like standard Hopfield networks (38)—is prone to the phenomenon of blackout catastrophe when network capacity is saturated, resulting in the inability to retrieve any previous memories or store new experiences. Notably, we did not observe these limitations under the more realistic conditions for which EWC was designed—likely because the network was operating well under capacity in these regimes.
Despite these key differences, EWC and cascade share the basic algorithmic feature that memory lifetimes are extended by modulating the plasticity of synapses. Whereas prior work on cascade models (15, 16) has tied the metaplastic state to patterns of potentiation and depression events—i.e., synaptic-level measures—our approach focuses on the computational principles that determine the degree to which each synapses might be consolidated. It may be possible to distinguish these models experimentally, because the plasticity of a synapse depends on the rate of potentiation events in the cascade model, but on task relevance in EWC.
In this respect, the perspective we offer here aligns with a recent proposal that each synapse stores not only its current weight, but also an implicit representation of its uncertainty about that weight (39). This idea is grounded in observations that postsynaptic potentials are highly variable in amplitude (suggestive of sampling from the weight posterior during computation) and those synapses that are more variable are more amenable to potentiation or depression (suggestive of updating the weight posterior). Although we do not explore the computational benefits of sampling from a posterior here, our work aligns with the notion that weight uncertainty should inform learning rates. We take this one step farther, to emphasize that consolidating the high precision weights enables continual learning over long timescales. With EWC, three values have to be stored for each synapse: the weight itself, its variance, and its mean. Interestingly, synapses in the brain also carry more than one piece of information. For example, the state of the short-term plasticity could carry information on the variance (39, 40). The weight for the early phase of plasticity (41) could encode the current synaptic strength, whereas the weight associated with the late phase of plasticity or the consolidated phase could encode the mean weight.
The ability to learn tasks in succession without forgetting is a core component of biological and artificial intelligence. In this work we show that an algorithm that supports continual learning—which takes inspiration from neurobiological models of synaptic consolidation—can be combined with deep neural networks to achieve successful performance in a range of challenging domains. In doing so, we demonstrate that current neurobiological theories concerning synaptic consolidation do indeed scale to large-scale learning systems. This provides prima facie evidence that these principles may be fundamental aspects of learning and memory in the brain.
Materials and Methods
Full methods for all simulations can be found in Random Patterns, MNIST Experiments, and Atari Experiments. Hyperparameters for the MNIST experiment are described in Table S1. For the Atari 2600 experiments, we used an agent very similar to that described in ref. 42. The only differences are that we used (i) a network with more parameters, (ii) a smaller transition table, (iii) task-specific bias and gains at each layer, (iv) the full action set in Atari, (v) a task-recognition model, and (vi) the EWC penalty. Full details of hyperparameters are described in Table S2. Here we briefly describe the two most important modifications to the agent: the task-recognition module and the implementation of the EWC penalty.
Table S1.
Hyperparameters for each of the MNIST figures
| Hyperparameter | Fig. 3A | Fig. 3B | Fig. 3C |
| Learning rate | – | ||
| Dropout | No | Yes | No |
| Early stopping | No | Yes | No |
| No. hidden layers | 2 | 2 | 6 |
| Width hidden layers | 400 | 400–2,000 | 100 |
| Epochs/dataset | 20 | 100 | 100 |
Table S2.
Hyperparameters for the Atari experiment
| Hyperparameter | Value | Brief description |
| Action repeat | 4 | Repeat the same action for four frames. Each agent step will occur every fourth frame. |
| Discount factor | 0.99 | Discount factor used in the Q-learning algorithm. |
| No-op max | 30 | Maximum number of do nothing operations carried out at the beginning of each training episode to |
| provide a varied training set. | ||
| Max. reward | 1 | Rewards are clipped to 1. |
| Scaled input | 84 × 84 | Input images are scaled to 84 × 84 with bilinear interpolation. |
| Optimization algorithm | RMSprop | Optimization algorithm used. |
| Learning rate | 0.00025 | The learning rate in RMSprop. |
| Max. learning rate | 0.0025 | The maximum learning rate that RMSprop will apply. |
| Momentum | 0.0 | The momentum used in RMSprop. |
| Decay | 0.95 | The decay used in RMSProp. |
| Clip | 1.0 | Each gradient from Q-learning is clipped to 1. |
| Max. norm | 50. | After clipping, if the norm of the gradient is greater than 50., the gradient is renormalized to 50. |
| History length | 4 | The four most recently experienced frames are taken to form a state for Q-learning. |
| Minibatch size | 32 | The number of elements taken from the replay buffer to form a minibatch training example. |
| Replay period | 4 | A minibatch is loaded from the replay buffer every four steps (16 frames including action repeat). |
| Memory size | 50,000 | The replay memory stores the last 50,000 transitions experienced. |
| Target update period | 7,500 | The target network in Q-learning is updated to the policy network every 7,500 steps. |
| Min. history | 50,000 | The agent will start learning only after 50,000 transitions have been stored into memory. |
| Initial exploration | 1.0 | The value of the initial exploration rate. |
| Exploration decay start | 50,000 | The exploration rate will start decaying after 50,000 frames. |
| Exploration decay end | 1,050,000 | The exploration rate will decay over 1 million frames. |
| Final exploration | 0.01 | The value of the final exploration rate. |
| Model update period | 4 | The Dirichlet model is updated every fourth step. |
| Model downscaling | 2 | The Dirichlet model is downscaled by a factor of 2; that is, an image of size 42 × 42 is being modeled. |
| Size window | 4 | The size of the window for the task recognition model learning. |
| Num. samples Fisher | 100 | Whenever the diagonal of the Fisher is recomputed for a task, 100 minibatches are drawn from the |
| replay buffer. | ||
| Fisher multiplier | 400 | The Fisher is scaled by this number to form the EWC penalty. |
| Start EWC | 20E6 | The EWC penalty is applied only after 5 million steps (20 million frames). |
We treat the task context as the latent variable of a hidden Markov model. Each task is therefore associated to an underlying generative model of the observations. The main distinguishing feature of our approach is that we allow for the addition of new generative models if they explain recent data better than the existing pool of models by using a training procedure inspired by the FMN process in ref. 33 (see Atari Experiments for full description). To apply EWC, we compute the Fisher information matrix at each task switch. For each task, a penalty is added with the anchor point given by the current value of the parameters and with weights given by the Fisher information matrix times a scaling factor that was optimized by hyperparameter search. We added an EWC penalty only to games that had experienced at least million frames.
Random Patterns
In this section we show that using EWC it is possible to recover a power-law decay for the SNR of random patterns. The task consists of associating random -dimensional binary vectors to a random binary output by learning a weight vector . The continual-learning aspect of the problem arises from the fact that at time step , only the pattern is accessible to the learning algorithm. Before providing a detailed derivation of the learning behavior, we provide a sketch of the main ideas. Learning consists of minimizing an objective function at each time step. This objective function contains the square loss for the current pattern plus a penalty that minimizes the distance of the weight vector to its old value. This corresponds to EWC if the distance metric used is the diagonal of the total Fisher information matrix. Conversely, if a fixed metric is used, we recover gradient descent. In this particular case, the diagonal of the Fisher information matrix is proportional the number of patterns observed, so EWC simply consists of lowering the learning rate at each time step. We then obtain an exact solution for the average response (signal) of a pattern observed at time at a later time in both the gradient descent (constant learning rate) and the EWC cases. We find that EWC leads to a power-law decay in the signal whereas gradient descent leads to an exponential one. Our analysis of the variance in the response (noise) shows that in both the EWC and gradient descent cases, for small time, the noise increases as . Conversely, for large the noise tends to 1 in the gradient descent case, and it decays as in the EWC case.
We assume that , such that each element is . We regress to the targets with the dot product and optimize the parameters , using least-squares minimization. Therefore, the loss at step can be written as
| [S1] |
The first term on the right-hand side is simply a squared error, and the second term makes the problem well defined by constraining the parameters to be close to the old ones under a metric . We consider two possible choices for the metric: In the steepest descent case, we use a fixed, uniform metric, and in the EWC case we use the diagonal of the Fisher information matrix. Note that in this problem, the diagonal of the Fisher information matrix at time step is simply an identity matrix multiplied by . To cover both cases, we refer to the norm of the metric at time step as . This quantity is fixed in the case of steepest descent and is increasing with time as for the EWC case. Let us take the derivative of Eq. S1 with respect to and set it to 0. We then find that
| [S2] |
Let us solve Eq. S2 for to find
| [S3] |
We simplify the previous equation by using the Sherman–Morrison formula for matrix inverses and by defining :
| [S4] |
Note that this is exactly the same equation that one would obtain if performing gradient descent with a learning rate .
If we assume that the initial conditions are a null vector and define the matrix and the vector , then unfolding the recurrence relation from [S4] leads to
| [S5] |
To measure the average memory strength of a memory from time at a later time , we need to compute the signal that is the mean response to a stimulus from time step ,
| [S6] |
where the angle brackets denote averaging over all of the patterns seen, except .
To be retrieved, it is important for this average signal to exceed the noise by a certain margin. The noise is simply defined as the standard deviation of the quantity above; that is,
| [S7] |
In what follows, we first derive the expression for the signal and then that for the noise term in both the steepest-descent and EWC cases.
Because each term in each term of the sum of Eq. S5 pertains to one time step only, averaging Eq. S6 factors out, and it is sufficient to be able to compute the following average,
| [S8] |
where is the identity matrix. Of each term in the sum of Eq. S5, all of the terms starting with an with will average to 0, and the only term remaining will therefore be
| [S9] |
which, using Eq. S8, will result in
| [S10] |
We consider two cases: In the steepest-descent case and in the EWC case . Note that we chose the magnitude for the regularization for the steepest-descent case in such a way that they both agree for the first time step. In the steepest-descent case, after some manipulation we reach
| [S11] |
If we are interested in cases when , the previous expression can be rearranged into
| [S12] |
In the EWC case we have
| [S13] |
To compute the noise term, we assume that the weight vector is uncorrelated from the observed vector , and we can simplify Eq. S7:
| [S14] |
Note that this assumption is tantamount to averaging the quantity over all , including .
Therefore, the key to computing the noise term is to be able to predict the average norm of the weight vector. To deduce what form this must take, let us rearrange Eq. S3 slightly to yield
| [S15] |
Define the vector as
| [S16] |
Then the expected change in the norm of the weight vector can we written as
| [S17] |
These two terms are readily computed as
| [S18] |
| [S19] |
Therefore, the expected change in the norm can be written as
| [S20] |
To proceed, we take a continuous approximation of this difference equation to yield a linear, first-order, inhomogeneous ordinary differential equation for the norm of the weight vector,
| [S21] |
with boundary condition
| [S22] |
In the case of steepest descent, the function is simply a constant and the above equation simplifies to
| [S23] |
Let us assume that to simplify that expression to
| [S24] |
with solution
| [S25] |
If, instead, we are in the EWC case, the function is and Eq. S21 becomes
| [S26] |
It is possible to obtain an analytic solution to this ordinary differential equation,
| [S27] |
where Ei is the exponential integral function.
For the gradient descent case the analytical form of the SNR is simple. Using Eqs. S12 and S25 we find
| [S28] |
This expression is a power law when and an exponential when is the same order of magnitude as or greater.
The expression for the noise in Eq. S27, however, is harder to interpret. If , it is equivalent to the solution for the steepest descent, that is, Eq. S25. If conversely , noting that for large x, we can get a simplified form for the norm of the weight as a function of time:
| [S29] |
Thus, we can obtain the expression for the behavior of the SNR in the EWC case in the small time and large time regimes. When , the signal expressed in [S13] is ∼ and the noise term from [27] can be approximated as . So the SNR can be written as
| [S30] |
If, however, the time is of the same magnitude as different outcomes are observed for steepest descent and for EWC, as the time step approaches in the EWC case, the signal from Eq. S13 will fall as and the noise from Eq. S29 will also as ; therefore the overall SNR will take the form
| [S31] |
The main distinction that we expect between using steepest descent and EWC is therefore that EWC should show a power law in the SNR with an exponent of −0.5 for both the small time and large time regimes. Gradient descent, conversely, will show a power law only for times shorter than the capacity of the network, and subsequently the memories are forgotten exponentially.
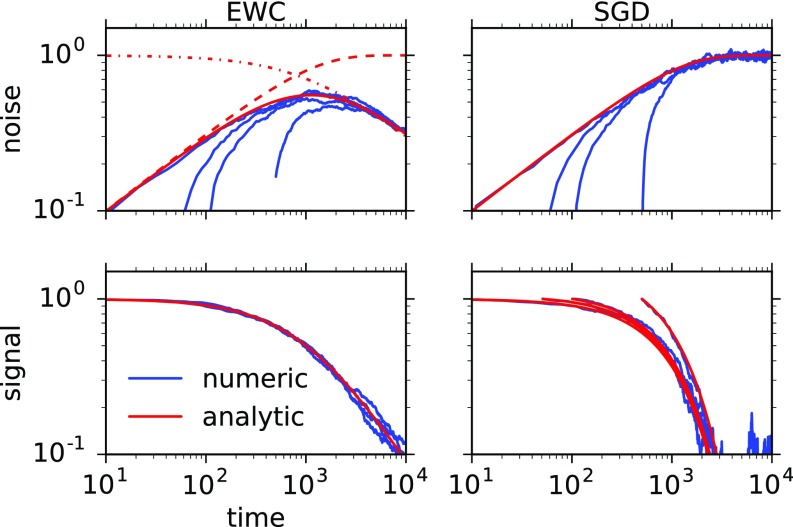
Our analytic computation of the noise term is approximate, because of the approximation that weights and input can be considered to be uncorrelated and also because we make a continuous approximation. To validate these assumptions, and to check our computations, we compare the analytic expression with numerical simulations. The numerical simulations were obtained by making several (400) simulations of the weights and patterns observed with a value of . We then simply computed the signal as the mean response at time from a pattern observed at time and the noise as the SD. In Fig. S1 we show the value of the signal and noise obtained numerically and for the analytic expressions in Eqs. S11, S13, S25, S27, and S29. Note that agreement between the observed signal and the numerical one is always very good. For the noise term agreement is good except when is small and our assumptions that weights and the patterns are uncorrelated does not hold. When our assumption on the noise breaks down, we observe that the magnitude of the noise is smaller than we predict and the SNR is higher than expected by our analysis.
Fig. S1.
Signal (Bottom row) and noise (Top row) terms for the EWC (Left column) and gradient descent (Right column) cases as a function of time . The blue curves are the results of numeric simulations, whereas the red curves show the analytic results. Each panel contains stimuli observed at different times . (Top Left) (noise in the EWC case) The solid red curve is the full form of Eq. S27, the dashed line is Eq. S25 (which is valid for small times), and the dashed-dotted line is the long time approximation of the noise in Eq. S29. The different solid blue curves correspond to the noise from patterns observed at times 1, 50, 100, and 500. (Top Right) (noise in the gradient descent case) The red curve shows Eq. S25. (Bottom Left) (signal in the EWC case) The red curve is Eq. S13. (Bottom Right) (signal for the gradient descent case) The red curves are Eq. S11.
It should be noted that in this analysis we have chosen a particular value for the regularization term . This is equivalent to the value used for the first pattern observed in EWC. Because this regularization term effectively sets the learning rate, this means we have picked a learning rate for gradient descent equivalent to that used at the start of learning in EWC. To make a fair comparison we should also test gradient descent using the smaller learning rates used at later stages by EWC. First, we generalize the expressions for the signal and noise terms in the gradient descent case with arbitrary learning rate . Remembering that , the generalization of Eqs. S12 and S25 becomes
| [S32] |
| [S33] |
In Fig. S2 we show a comparison of the SNR in the EWC case (red curves) and in the plain gradient descent case with different learning rates (green lines, ; blue lines, ). These learning rates are chosen to match the learning rate in EWC at the beginning of training () and at capacity, that is, when , at which point . The SNR plot (Fig. S2, Top) shows that irrespective of the learning rate used, the SNR in the gradient descent case eventually follows an exponential decay, albeit with a different rate. EWC, conversely, maintains a power-law decay. Fig. S2, Middle shows that the fraction of memories retained is higher using EWC than with either the learning rates, although a higher percentage is retained with the lower learning rate.
Fig. S2.
Comparison of EWC (red lines) with gradient descent with different learning rates (green, ; blue, ). Bottom shows these two learning rates correspond to the learning rate used in EWC at the first pattern and at network capacity () Top shows log-log plot of the SNR for the first pattern observed. The black lines show the analytic expressions from Eqs. S13, S27, and S32. Note that EWC has a power-law decay for the SNR, whereas gradient descent eventually decays exponentially, albeit at a later time for the lower learning rate. Middle shows the fraction of memories retained (i.e., with ) in the three cases. Note that the lower rate has a moderately higher fraction of memories retained than the larger one, but that EWC still has a higher memory retention.
MNIST Experiments
We carried out all MNIST experiments with fully connected networks with rectified linear units, using the Torch neural network framework. To replicate the results of ref. 24, we compared with results obtained using dropout regularization. As suggested in ref. 24, we applied dropout with a probability of 0.2 to the input and of 0.5 to the other hidden layers. To give SGD with dropout the best possible chance, we also used early stopping. Early stopping was implemented by computing the test error on the validation set for all pixel permutations seen to date. Here, if the validation error was observed to increase for more than five subsequent steps, we terminated this training segment and proceeded to the next dataset; at this point, we reset the network weights to the values that had the lowest average validation error on all previous datasets. Table S1 shows a list of all hyperparameters used to produce the three graphs in Fig. 3 of the main text. Where a range is present, the parameter was randomly varied and the reported results were obtained using the best hyperparameter setting. When random hyperparameter search was used, 50 combinations of parameters were attempted for each number experiment.
Atari Experiments
Atari experiments were carried out in the Torch framework. The agent architecture used is almost identical to that used in ref. 42. In this section we provide details on all of the parameters used.
Images are preprocessed in the same way as in ref. 25, namely the 210 × 160 images from the Atari emulator are down-sampled to 84 × 84, using bilinear interpolation. We then convert the red green blue (RGB) images to YUV and use the grayscale channel alone. The state used by the agent consists of the four latest down-sampled, grayscale observations concatenated together.
The network structure used is similar to the one from ref. 25, namely three convolutional layers followed by a fully connected layer. The first convolution had kernel size 8, stride 4, and 32 filters. The second convolution had kernel size 4, stride 2, and 64 filters. The final convolution had kernels size 3, stride 1, and 128 filters. The fully connected layer had 1,024 units. Note that this network has approximately four times as many parameters as the standard network, due to having twice as many fully connected units and twice as many filters in the final convolution. The other departure from the standard network is that each layer was allowed to have task-specific gains and biases. For each layer, the transformation computed by the network is therefore
| [S34] |
where the biases are and the gains are . The network weights and biases were initialized by setting them randomly with a uniform number between and , with set to the square root of the incoming hidden units (for a linear layer) or set to the area of the kernel times the number of incoming filters (for convolutional layers). Biases and gains were initialized to 0 and 1, respectively.
We used an -greedy exploration policy, where the probability of selecting random action, , decayed with training time. We kept a different timer for each of the tasks. We set for time steps and then decayed this linearly to a value of 0.01 for the next time steps.
We trained the networks with the Double Q-learning algorithm (42). A training step is carried out on a minibatch of 32 experiences every four steps. The target network is updated every time steps. We trained with RMSProp, with a momentum of , a decay of , a learning rate of , and a maximum learning rate of .
Other hyperparameters that we changed from the reference implementation were (i) using a smaller replay buffer ( past experiences) and (ii) a scaling factor for the EWC penalty of . Another subtle difference is that we used the full action set in the Atari emulator. In fact, although many games support only a small subset of the 18 possible actions, to have a unified network structure for all games we used 18 actions in each game.
We randomly chose the 10 games for each experiment from a pool of 19 Atari games for which the standalone DQN could reach human-level performance in frames. The scores for each of these games for the baseline algorithm, for EWC, and for plain SGD training, as a function of the number of steps played in that game, are shown in Fig. S3. To get an averaged performance, we chose 10 sets of 10 games and ran four different random seeds for each set.
The most significant departure from the published models is the automatic determination of the task. We model each task by a generative model of the environment. In this work, for simplicity, we model only the current observation. The current task is modeled as a categorical context that is treated as the hidden variable in a hidden Markov model that explain observations. In such a model the probability of being in a particular context at time evolves according to
where is the Kronecker delta function and is the probability of switching context. The task context then conditions a generative model predicting the observation probability . Given such generative models, the probability of being in a task set at time can be inferred by the observations seen so far as
The maximal probability context is then taken to be the current task label.
In our implementation, the generative models consist of factored multinomial distributions explaining the probability of the state of each pixel in the observation space. The model is a parameterized Dirichlet distribution, which summarizes the data seen so far using Bayesian updates. To encourage each model to specialize, we train the models as follows. We partition time into windows of a particular width . During each window, all of the Dirichlet priors are updated with the evidence seen so far. At the end of the window, the model best corresponding to the current task set is selected. Because this model was the most useful to explain the current data, it keeps its prior, and all other priors are reverted to their state at the beginning of the time window. We ensure that one hold-out uniform (i.e., uninitialized) Dirichlet multinomial is always available. Whenever the hold-out model is selected, a new generative model is created and a new task context is therefore created. This model is Bayesian, in the sense that data are used to maintain beliefs over priors on the generative models, and is nonparametric, in the sense that the model can grow as a function of the observed data. It can be seen as an implementation of the flat FMN algorithm described in ref. 34. The parameter is not learned. Instead we use the result from ref. 43 where it is shown that a time-decaying switch rate guarantees good worst-case asymptotic performance provided the number of tasks grows as .
Table S2 summarizes all hyperparameters used for the Atari experiments. Except for the parameters pertaining to the EWC algorithm (Fisher multiplier, num. samples Fisher, EWC start) or pertaining to the task recognition models (model update period, model downscaling, and size window), all of the parameter values are the same as in ref. 42 and have not been tuned for these experiments.
Acknowledgments
We thank P. Dayan, D. Wierstra, S. Mohamed, Yee Whye Teh, and K. Kavukcuoglu for constructive comments and useful discussion. C.C. was funded by the Wellcome Trust, the Engineering and Physical Sciences Research Council, and the Google Faculty Award.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1611835114/-/DCSupplemental.
References
- 1.Legg S, Hutter M. Universal intelligence: A definition of machine intelligence. Minds Mach. 2007;17(4):391–444. [Google Scholar]
- 2.French RM. Catastrophic forgetting in connectionist networks. Trends Cognit Sci. 1999;3(4):128–135. doi: 10.1016/s1364-6613(99)01294-2. [DOI] [PubMed] [Google Scholar]
- 3.McCloskey M, Cohen NJ. Catastrophic interference in connectionist networks: The sequential learning problem. In: Bower GH, editor. The Psychology of Learning and Motivation. Vol 24. Academic; New York: 1989. pp. 109–165. [Google Scholar]
- 4.McClelland JL, McNaughton BL, O’Reilly RC. Why there are complementary learning systems in the hippocampus and neocortex: Insights from the successes and failures of connectionist models of learning and memory. Psychol Rev. 1995;102(3):419–457. doi: 10.1037/0033-295X.102.3.419. [DOI] [PubMed] [Google Scholar]
- 5.Kumaran D, Hassabis D, McClelland JL. What learning systems do intelligent agents need? Complementary learning systems theory updated. Trends Cogn Sci. 2016;20(7):512–534. doi: 10.1016/j.tics.2016.05.004. [DOI] [PubMed] [Google Scholar]
- 6.Ratcliff R. Connectionist models of recognition memory: Constraints imposed by learning and forgetting functions. Psychol Rev. 1990;97(2):285–308. doi: 10.1037/0033-295x.97.2.285. [DOI] [PubMed] [Google Scholar]
- 7.Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks. In: Pereira F, Burges CJC, Bottou L, Weinberger KQ, editors. Advances in Neural Information Processing Systems 25. Curran Assoc, Red Hook; NY: 2012. pp. 1097–1105. [Google Scholar]
- 8.LeCun Y, Bengio Y, Hinton G. Deep learning. Nature. 2015;521(7553):436–444. doi: 10.1038/nature14539. [DOI] [PubMed] [Google Scholar]
- 9.Rusu AA, et al. 2015. Policy distillation. arXiv:1511.06295.
- 10.Parisotto E, Ba JL, Salakhutdinov R. 2015. Actor-mimic: Deep multitask and transfer reinforcement learning. arXiv:1511.06342.
- 11.Cichon J, Gan WB. Branch-specific dendritic ca2+ spikes cause persistent synaptic plasticity. Nature. 2015;520(7546):180–185. doi: 10.1038/nature14251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hayashi-Takagi A, et al. Labelling and optical erasure of synaptic memory traces in the motor cortex. Nature. 2015;525(7569):333–338. doi: 10.1038/nature15257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Yang G, Pan F, Gan WB. Stably maintained dendritic spines are associated with lifelong memories. Nature. 2009;462(7275):920–924. doi: 10.1038/nature08577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Yang G, et al. Sleep promotes branch-specific formation of dendritic spines after learning. Science. 2014;344(6188):1173–1178. doi: 10.1126/science.1249098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fusi S, Drew PJ, Abbott L. Cascade models of synaptically stored memories. Neuron. 2005;45(4):599–611. doi: 10.1016/j.neuron.2005.02.001. [DOI] [PubMed] [Google Scholar]
- 16.Benna MK, Fusi S. 2015. Computational principles of biological memory. arXiv:1507.07580.
- 17.Hecht-Nielsen R. Neural Netw. Suppl 1; 1988. Theory of the backpropagating network; pp. 445–448. [Google Scholar]
- 18.Sussmann HJ. Uniqueness of the weights for minimal feedforward nets with a given input-output map. Neural Networks. 1992;5:589–593. [Google Scholar]
- 19.MacKay DJ. A practical Bayesian framework for backpropagation networks. Neural Comput. 1992;4(3):448–472. [Google Scholar]
- 20.Pascanu R, Bengio Y. 2013. Revisiting natural gradient for deep networks. arXiv:1301.3584.
- 21.Eskin E, Smola AJ, Vishwanathan S. Laplace propagation. In: Thrun S, Saul LK, Schoelkopf PB, editors. Advances in Neural Information Processing Systems 16. MIT Press; Cambridge, MA: 2004. pp. 441–448. [Google Scholar]
- 22.LeCun Y, Cortes C, Burges CJ. 1998. The MNIST database of handwritten digits. Available at yann.lecun.com/exdb/mnist/. Accessed March 3, 2017.
- 23.Srivastava RK, Masci J, Kazerounian S, Gomez F, Schmidhuber J. Compete to compute. In: Burges CJC, Bottou L, Welling M, Ghahramani Z, Weinberg KQ, editors. Advances in Neural Information Processing Systems 26. Vol 26. Curran Assoc; Red Hook, NY: 2013. pp. 2310–2318. [Google Scholar]
- 24.Goodfellow IJ, Mirza M, Xiao D, Courville A, Bengio Y. 2015. An empirical investigation of catastrophic forgeting in gradient-based neural networks. arXiv:1312.6211.
- 25.Mnih V, et al. Human-level control through deep reinforcement learning. Nature. 2015;518(7540):529–533. doi: 10.1038/nature14236. [DOI] [PubMed] [Google Scholar]
- 26.Bellemare MG, Naddaf Y, Veness J, Bowling M. The arcade learning environment: An evaluation platform for general agents. J Artif Intell Res. 2013;47:253–279. [Google Scholar]
- 27.Ring MB. Child: A first step towards continual learning. In: Thrun S, Pratt L, editors. Learning to Learn. Kluwer Acadamic; Norwell, MA: 1998. pp. 261–292. [Google Scholar]
- 28.Rusu AA, et al. 2016. Progressive neural networks. arXiv:1606.04671.
- 29.Collins AG, Frank MJ. Cognitive control over learning: Creating, clustering, and generalizing task-set structure. Psychol Rev. 2013;120(1):190–229. doi: 10.1037/a0030852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.O’Reilly RC, Frank MJ. Making working memory work: A computational model of learning in the prefrontal cortex and basal ganglia. Neural Comput. 2006;18(2):283–328. doi: 10.1162/089976606775093909. [DOI] [PubMed] [Google Scholar]
- 31.Mante V, Sussillo D, Shenoy KV, Newsome WT. Context-dependent computation by recurrent dynamics in prefrontal cortex. Nature. 2013;503(7474):78–84. doi: 10.1038/nature12742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Miller EK, Cohen JD. An integrative theory of prefrontal cortex function. Annu Rev Neurosci. 2001;24(1):167–202. doi: 10.1146/annurev.neuro.24.1.167. [DOI] [PubMed] [Google Scholar]
- 33.Doya K, Samejima K, Katagiri K-i, Kawato M. Multiple model-based reinforcement learning. Neural Comput. 2002;14(6):1347–1369. doi: 10.1162/089976602753712972. [DOI] [PubMed] [Google Scholar]
- 34.Milan K, et al. The forget-me-not process. In: Lee DD, Sugiyama M, Luxburg UV, Guyon I, Garnett R, editors. Advances in Neural Information Processing Systems 29. Curran Assoc; Red Hook, NY: 2016. [Google Scholar]
- 35.French RM, Chater N. Using noise to compute error surfaces in connectionist networks: A novel means of reducing catastrophic forgetting. Neural Comput. 2002;14(7):1755–1769. doi: 10.1162/08997660260028700. [DOI] [PubMed] [Google Scholar]
- 36.Ruvolo PL, Eaton E. ELLA: An efficient lifelong learning algorithm. JMLR Workshop Conf Proc. 2013;28(1):507–515. [Google Scholar]
- 37.Blundell C, Cornebise J, Kavukcuoglu K, Wierstra D. Weight uncertainty in neural networks. JMLR Workshop Conf Proc. 2015;37:1613–1622. [Google Scholar]
- 38.Amit D. Modeling Brain Function. Cambridge Univ Press; Cambridge, UK: 1989. [Google Scholar]
- 39.Aitchison L, Latham PE. 2015. Synaptic sampling: A connection between PSP variability and uncertainty explains neurophysiological observations. arXiv:1505.04544.
- 40.Pfister JP, Dayan P, Lengyel M. Synapses with short-term plasticity are optimal estimators of presynaptic membrane potentials. Nat Neurosci. 2010;13(10):1271–1275. doi: 10.1038/nn.2640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Clopath C, Ziegler L, Vasilaki E, Büsing L, Gerstner W. Tag-trigger-consolidation: A model of early and late long-term-potentiation and depression. PLoS Comput Biol. 2008;4(12):e1000248. doi: 10.1371/journal.pcbi.1000248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.van Hasselt H, Guez A, Silver D. Deep reinforcement learning with double q-learning. In: Schuurmans D, Wellman M, editors. Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence. AAAI Press; Palo Alto, CA: 2016. pp. 2094–2100. [Google Scholar]
- 43.Veness J, Ng KS, Hutter M, Bowling M. Context tree switching. In: Malvar H, editor. 2012 Data Compression Conference. IEEE; New York: 2012. pp. 327–336. [Google Scholar]
- 44.Dowson D, Landau B. The fréchet distance between multivariate normal distributions. J Multivar Anal. 1982;12(3):450–455. [Google Scholar]