Steady-state EB cap size fluctuations are determined by stochastic microtubule growth and maturation

Significance

Essential to microtubules’ function is their property of switching between phases of growth and shrinkage, called dynamic instability. Growing microtubules are protected by the presence of a GTP cap that is thought to fluctuate in size, causing stability fluctuations that eventually result in a switch to depolymerization. Despite their importance these fluctuations had not been quantitatively characterized until now, and hence their properties were previously unknown. Here we measure these cap size fluctuations and develop a theory that explains their properties based on the kinetic network of cap formation. This study provides a quantitative description of the fundamental process of microtubule cap size fluctuations. Their properties indicate that microtubules are far from instability for most of the time during growth.

Abstract

Growing microtubules are protected from depolymerization by the presence of a GTP or GDP/Pi cap. End-binding proteins of the EB1 family bind to the stabilizing cap, allowing monitoring of its size in real time. The cap size has been shown to correlate with instantaneous microtubule stability. Here we have quantitatively characterized the properties of cap size fluctuations during steady-state growth and have developed a theory predicting their timescale and amplitude from the kinetics of microtubule growth and cap maturation. In contrast to growth speed fluctuations, cap size fluctuations show a characteristic timescale, which is defined by the lifetime of the cap sites. Growth fluctuations affect the amplitude of cap size fluctuations; however, cap size does not affect growth speed, indicating that microtubules are far from instability during most of their time of growth. Our theory provides the basis for a quantitative understanding of microtubule stability fluctuations during steady-state growth.

The dynamic nature of the microtubule cytoskeleton is essential for its function: It allows for fast adjustments and reorganizations of the internal cell architecture depending on the state of the cell and its environment (1–3). At the heart of this dynamicity is the propensity of microtubules to switch stochastically between phases of growth and shrinkage, called dynamic instability (4–6). GTP hydrolysis by lattice-incorporated tubulin is ultimately responsible for this behavior (7, 8). After addition of tubulin to the growing microtubule end, GTP hydrolysis and phosphate release occur only after a delay. Hence, GTP-tubulins are enriched in the microtubule end region, forming a protective cap that stabilizes the growing microtubule (1, 9, 10).

Although details are still debated, the fast transition from growth to shrinkage, called catastrophe, is thought to be triggered by the loss of the GTP cap, likely as a consequence of stochastic fluctuations in its size (4, 9, 11, 12). The exact properties of these cap size fluctuations are unknown because the GTP in the growing microtubule end region cannot be directly visualized. However, end-binding proteins of the EB family have been shown recently to bind to the protective cap (13–16). Fluorescent EBs can therefore be used to indirectly visualize the cap at the individual microtubule level (14).

These studies revealed that the cap consists of hundreds of tubulins in the stabilizing conformation and that they have a roughly monoexponential distribution starting from the growing microtubule end, giving rise to the comet-shaped appearance of the EB binding region (13, 15, 17, 18). The majority of this EB cap is lost during a period of several seconds before catastrophe occurs (16, 19), indicating that the EB binding region is critical for stability. In agreement with this notion, faster-growing microtubules that have larger caps were found to be more stable after sudden tubulin removal (14). During regular steady-state growth, cap size and microtubule stability seemed to fluctuate on a timescale of several seconds (14), the origin of which is unclear.

In the simplest kinetic model cap sites are generated by tubulin incorporation into the microtubule lattice, followed by a growth-speed-independent maturation process that forms the mature lattice (13, 19, 20). Maturation corresponds to a conformational change, most likely associated with GTP hydrolysis or phosphate release (15, 16, 19, 21). The maturation rate can be experimentally determined from the characteristic length of the EB binding region and the average microtubule growth speed, a procedure called “comet analysis” (13, 19, 22).

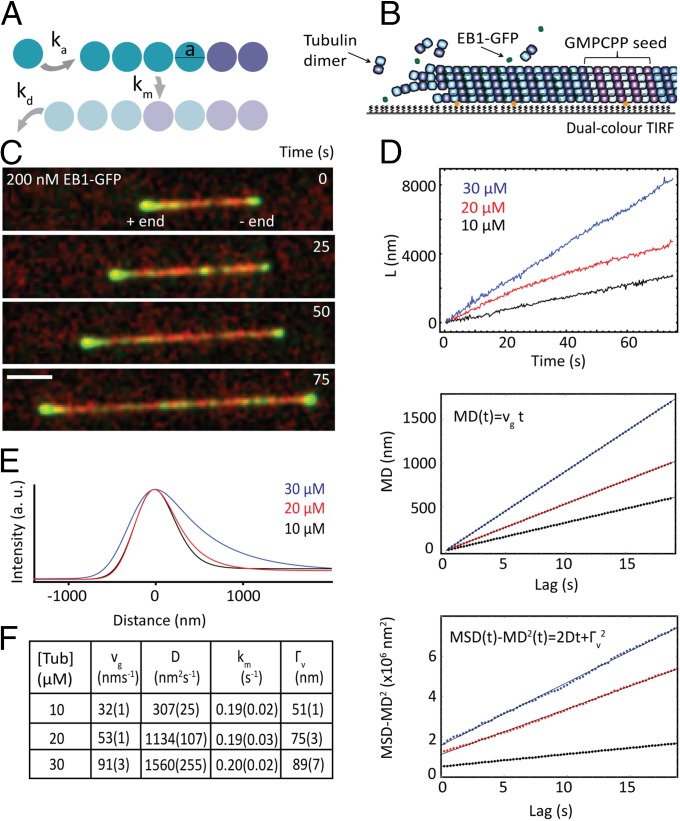
Because freshly added tubulins can also dissociate from microtubule ends, the net tubulin incorporation rate is the difference between the tubulin association and dissociation rates (23–27). Therefore, in the simplest scenario only three rates—the tubulin association, dissociation, and maturation rates—might be sufficient to describe the kinetic network of the formation of the protective cap (Fig. 1A).

Fig. 1.

Microtubule growth and cap properties from time-averaged data. (A) Illustration of the single protofilament model with three kinetic rate constants for tubulin association (k_a), dissociation (k_d) and maturation (k_m). The length of a tubulin dimer, a, is 8/13 nm. (B) Schematic of the TIRF microscopy assay. (C) Image sequence from a representative dual-color TIRF microscopy movie, acquired at a frame rate of 4 s⁻¹ (scale bar: 3 μm). (D) (Top) Representative growth trajectories (position time traces) of microtubule plus ends for three tubulin concentrations as obtained by automated end tracking. (Middle) MD plotted over time calculated from 38, 25, and 17 growth trajectories with an average duration of 193 s, 196 s, and 148 s for 10 μM, 20 μM, and 30 μM tubulin, respectively. The mean growth speed v_g was extracted from fits to the data (black lines). (Bottom) Variance of the displacement (MSD minus MD squared) plotted over time. The diffusion constant, D, and the measurement noise, Γ_v, were extracted from fits to the data (black lines). (E) Time-averaged comet-shaped spatial EB1-GFP fluorescence intensity profiles were automatically generated from TIRF movies (with a total duration of 750 s, 1,950 s, and 1,050 s of growth for increasing tubulin concentrations). The maturation rate constant, k_m, of the cap reaction network is obtained with comet analysis. (F) Table of mean growth speeds, diffusion constants, maturation rate constants, and positional measurement noise estimates obtained from MD, MSD, and comet analysis (errors given in brackets are SEM). a. u., arbitrary units.

The quantitative investigation of microtubule growth fluctuations, using mean-squared displacement (MSD) analysis, revealed large growth fluctuations, suggesting fast association and dissociation kinetics (23, 28). However, despite their presumed importance for microtubule stability, the fluctuations of the protective cap size have not yet been measured. Their properties, such as their typical amplitude and characteristic timescale, are unknown, and it is unclear whether cap size fluctuations can contribute to growth fluctuations.

Intrinsic network noise has been extensively studied for gene expression and other biochemical networks (29–34). The specific properties of the noise were often found to be of functional importance. Moreover, chemical network theory has demonstrated that the fluctuation properties of a network are determined by its topology and reaction rates.

Here, we develop a theory that predicts the fluctuation characteristics of the protective cap during microtubule growth from a simple kinetic network of cap formation. Using correlation analysis we measured the properties of the cap size fluctuations using EBs as a cap size marker and compared them to the measured properties of the growth fluctuations. We find that, in agreement with theory, growth fluctuations can be considered as Gaussian white noise and cap size fluctuations are well described by the mean-reverting Ornstein–Uhlenbeck (OU) process (35–37) with a typical timescale that is determined entirely by the maturation rate. This explains the timescale of previously observed stability fluctuations during microtubule growth (14). Furthermore, the expected and measured amplitude of the cap size fluctuations indicates that microtubules are far from instability during most of their growth time. Overall, the agreement between theory and experiment suggests that the basic properties of the fluctuations in the size of the protective cap can be explained using a simple kinetic model.

Theory

The Cap Reaction Network.

We assume a single protofilament kinetic model for microtubule growth and cap formation summarized by the following scheme and illustrated in Fig. 1A:

$$\varnothing \underset{k_d}{\overset{k_a}{\rightleftarrows }}C\underset{k_m}{\to }L.$$

The cap, C, grows by the addition of GTP-bound subunits to the microtubule end with an association rate $k_a$, which is proportional to the tubulin concentration. The cap shrinks by two processes: (i) the dissociation of subunits from the microtubule end, which occurs at a constant rate independent of the cap size, and (ii) depletion via maturation of cap sites into lattice sites, L, at rate k_mn, where k_m is the maturation rate constant and n is the number of cap sites. For simplicity this model neglects a recently reported prematuration step. This step is considerably faster than the maturation step, especially in the presence of EB1 proteins, making the pre-EB1 binding region much smaller than the EB binding region (19).

Time-Averaged Properties of the Network.

Previous studies (13, 19, 22, 23) have demonstrated how the three kinetic rate constants of the cap reaction network can be derived from the time-averaged properties of two observables: the growth trajectory of the microtubule and the spatial distribution of its cap sites. The growth trajectory represents a 1D Brownian “diffusion-with-drift” process with mean growth speed and diffusion constant given by ref. 23: $v_g=(k_a-k_d)\hspace{0.17em}a$ and $D=1/2\hspace{0.17em}(k_a+k_d)\hspace{0.17em}{a}^2$, respectively. Here a is the length of a subunit in the single protofilament model, considered to be the length of a tubulin dimer (8 nm) divided by 13 (the typical number of protofilaments in a microtubule).

From comet analysis (SI Materials and Methods) the spatial probability distribution is given by ref. 19, $\langle P\left(x,t\right)\rangle =e^{-\frac{x}{l}}$, where $P\left(x,t\right)$ is equal to 1 (0) if the subunit at position x, measured from the terminal subunit, is a cap site (lattice site). The maturation rate k_m can be obtained from the growth speed v_g and the average comet length l, because $l=v_g/k_m$. The average number of subunits in the cap, μ, is then given by l/a:

$$\mu =\left(k_a-k_d\right)/k_m.$$ [1]

Fluctuation Properties of the Network.

Growth velocity fluctuations.

In the linear noise approximation (33) (LNA) we can write an instantaneous velocity as $v\left(t\right)=v_g+{\xi }_v\left(t\right)$, where ${\xi }_v\left(t\right)$ is a Gaussian white-noise term accounting for the stochasticity of the microtubule growth (30, 32). The power in the noise term is proportional to the sum of the rates of the two Poisson processes of association and dissociation (11): $\langle {\xi }_v\left(t\right)\hspace{0.17em}{\xi }_v(t\prime )\rangle =(k_a+k_d)a^2\delta (t-t\prime )$, where $\delta \left(t\right)$ is the Dirac delta function. We calculate our measured velocity as $\widehat{v}\left(t\right)=(L\left(t+\mathrm{\Delta }t\right)-L\left(t\right))/\mathrm{\Delta }t$ and its autocovariance function (ACF) is given by $C_{\widehat{v}}\left(\tau \right)=\lambda \hspace{0.17em}{a}^2\left(k_a+k_d\right){\delta }_{\tau 0}$, where $\lambda =1/\mathrm{\Delta }t$ and ${\delta }_{ij}$ is the Kronecker delta (SI Materials and Methods for details). The form of this ACF reflects the “memorylessness” of the growth fluctuations (i.e., there is no characteristic timescale). The zero lag magnitude reveals the fluctuation amplitude,

$${\sigma }_v=\sqrt{\lambda (k_a+k_d)}a$$ [2]

Cap size fluctuations.

In the cap reaction network the size of the cap fluctuates about its mean value driven away from equilibrium by growth fluctuations. Following a perturbation the cap reverts back to its mean size via the maturation process on a characteristic “relaxation” timescale $\tau$ ; this is the “mean-reverting” property of the OU process.

To find the ACF of the cap size fluctuations we can write a deterministic equation for the evolution of the cap: $\dot{n}\left(t\right)=\hspace{0.17em}{k}_a-k_d-k_{m}n$. In the LNA we perturb this expression about its mean and again add a noise term, $\delta \dot{n}\left(t\right)=-k_m\hspace{0.17em}\delta n\left(t\right)+{\xi }_c\left(t\right)$, to get an expression for the stochastic fluctuations. The Gaussian noise term, ${\xi }_c\left(t\right)$, is the sum of a component due to the growth fluctuations, ${\xi }_v\left(t\right)$, and an independent component due to the maturation step, ${\xi }_m\left(t\right)$, characterized by the following (32): $\langle {\xi }_m\left(t\right)\hspace{0.17em}{\xi }_m(t\prime )\rangle =k_m\langle n\rangle \hspace{0.17em}\delta \left(t-t\prime \right)$. With these expressions the ACF of the cap size fluctuations is given by $C_c\left(\tau \right)=\left(k_a/k_m\right)e^{-k_m\tau }$ (SI Materials and Methods for details). The maturation rate enters here as the inverse of the relaxation time, characterizing the memory of the fluctuations. The zero lag magnitude reveals the fluctuation amplitude,

$${\sigma }_c=\sqrt{k_a/k_m}\hspace{0.17em}.$$ [3]

Cross-covariance of growth velocity and cap size fluctuations.

The cross-covariance function (CCF) can also be found from the above expressions (SI Materials and Methods for details). It is given by

$$C_{vc}\left(\tau \right)=a\hspace{0.17em}(k_a+k_d)e^{-k_m\tau }\hspace{0.17em}U\left(\tau \right),$$ [4]

where $U\left(\tau \right)$ is the unit step function. The asymmetry of the CCF results from causality in the network; the growth fluctuations drive the cap size fluctuations but there is no feedback from cap to growth (38).

Measurement Noise.

In the presence of experimental measurement noise, modeled as white Gaussian noise, the ACFs require additional terms (SI Materials and Methods and Fig. S1 for details). The ACFs of the velocity and the cap fluctuations become

$$C_{\widehat{v}}^{\prime }\left(\tau \right)=\lambda \hspace{0.17em}{a}^2\left(k_a+k_d\right){\delta }_{\tau 0}+{\lambda }^2{\mathrm{\Gamma }}_v^2(2{\delta }_{\tau 0}-{\delta }_{\tau \mathrm{\Delta }t}),$$ [5]

$$C_c^{\prime }\left(\tau \right)=\frac{k_a}{k_m}\hspace{0.17em}{e}^{-k_m\tau }+{\mathrm{\Gamma }}_c^2{\delta }_{\tau 0},$$ [6]

respectively, where Γ_v and Γ_c denote the amplitude of the position and cap size measurement noise.

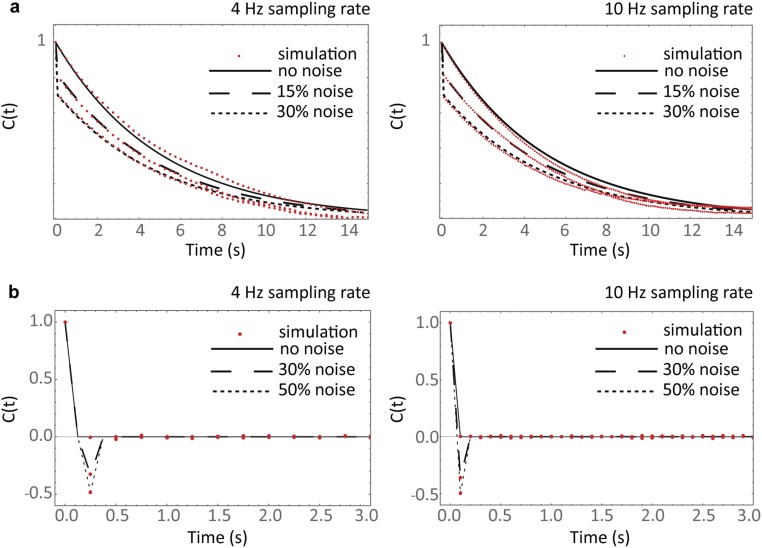
Fig. S1.

Testing the robustness of the analysis to experimental noise and sampling rate. A full stochastic simulation of the cap reaction network was implemented to generate simulated cap and growth fluctuation data. Twenty tracks with an average duration of 200 s were analyzed replicating the experimental data. (A) Autocorrelation functions of simulated cap fluctuations (red) are compared with theory (black lines, Eq. 6) for different noise conditions (modeled as additive white Gaussian noise) at a sampling rate of 4 Hz (Left) and 10 Hz (Right). (B) Autocorrelation functions of simulated growth fluctuations (red) are compared with theory (black lines, Eq. 5) under different experimental noise conditions at a sampling rate of 4 Hz (Left) and 10 Hz (Right). Agreement between theory and experiment supports the validity of the model and robustness of the analysis under relevant experimental conditions.

SI Materials and Methods

Microtubule Dynamics Assay.

Microtubule plus end growth and the GFP intensity of fission yeast EB1 (Mal3-GFP) in the plus end region were measured in flow cells assembled as described previously (39) using TIRF microscopy (19, 55). Alexa568-labeled microtubules were assembled from biotinylated, Alexa568-labeled and GMPCPP-stabilized seeds, which were attached to a functionalized glass coverslips via Neutravidin (Life Technologies). The free tubulin concentration was 10, 20, or 30 µM [of which 12.5% was labeled with Alexa568 (Life Technologies)]. For all experiments, Mal3-GFP was present at 200 nM. The final imaging buffer was 80 mM K-Pipes (pH 6.85; Sigma), 1 mM EGTA (Sigma), 1 mM DTT (Fischer), 5 mM 2-mercapothethanol (Sigma), 10 mM Na-ascorbate (Sigma), 90 mM KCl (Fischer), 1.5 mM GTP (Fermentas), 0.1% (vol/vol) methylcellulose (Sigma), 50 µg/mL β-casein (Sigma), 20 mM glucose (Fischer), 0.5 mg/mL glucose oxidase (Serva), 0.25 mg/mL catalase (Sigma), and 0.5 mM MgCl₂. A comparatively low concentration of MgCl₂ was used to obtain long uninterrupted growth episodes and good signal-to-noise ratios for Mal3-GFP, because high MgCl₂ concentrations decrease the affinity of Mal3 (24). For the lower tubulin concentrations, the final reaction mixture was supplemented with tubulin storage buffer (BRB 80) to maintain the same buffer environment for all conditions. Simultaneous imaging of the Alexa568 channel and the GFP channel was performed at 4 Hz with an exposure time of 100 ms per frame and identical laser settings for all conditions. All experiments were performed at 30 °C.

Automated Microtubule Tracking.

After image acquisition, the two fluorescent channels were aligned using a calibration grid (Compugraphics) as previously described (19) and drift-corrected using a custom macro written in ImageJ (https://imagej.nih.gov/ij/). For MSD analysis and fluctuation analysis of the microtubule growth, time traces of microtubule plus-end positions were extracted from the Alexa568 channel using a previously described MATLAB (The MathWorks) program, which has been shown to achieve subpixel resolution (19, 40). Cropped images of the microtubule’s end in the Alexa568 and GFP channel were also generated at each tracked end position. These images, 1 $\mu \text{m}$ (axial) by 0.4 $\mu \text{m}$ (lateral) in size, were aligned along the axis of the microtubule and centered 0.17 $\mu \text{m}$ away from the tracked end position to capture the full intensity from the end. From the cropped images, time-averaged EB1-GFP fluorescence intensity profiles (comets) were generated for use in comet analysis. For the cap size fluctuation analysis, mean signal intensity values were extracted from the cropped images in the GFP and Alexa568 channels, resulting in time traces of intensity fluctuations at the microtubule end. These intensity values were background-subtracted assuming a flat background obtained from the mean of the pixel values falling in the range $[I_{min},\hspace{0.17em}{I}_{max}\times 0.2]$.

Fluorescence Background Subtraction from EB1-GFP Intensity Fluctuation Data.

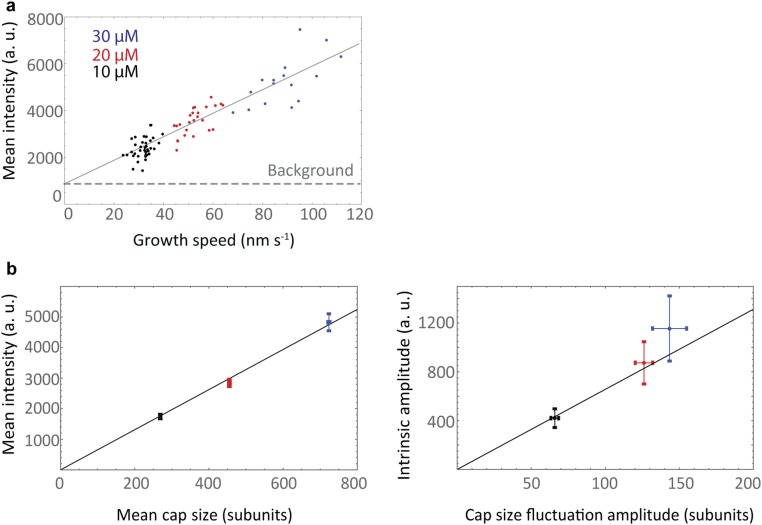
The measured mean intensity at the end of the microtubule is a combination of the signal from the cap and a background signal from EB1-GFP in solution. The EB1-GFP intensity fluctuation data therefore required a second background subtraction. Theoretically the mean size of the cap is directly proportional to the mean growth speed of the microtubule. We therefore obtained an estimate for the background fluorescence signal by plotting the mean growth speed against the mean EB1-GFP intensity for each track and making a linear fit to the data, extrapolating back to the origin (Fig. S5A). The y-intercept of the fit represented the background fluorescence signal, which was subtracted from the measured intensities before analysis.

Fig. S5.

Conversion of the background-corrected EB1-GFP fluorescence intensity into numbers of cap subunits. (A) Background signal calculation; the mean EB1-GFP fluorescence intensity from each intensity trace given in arbitrary units (a. u.) plotted against the average growth speed of the corresponding trajectory. The background signal is given by the y-intercept and was subtracted from the EB1-GFP intensity measurements. (B) Proportionality factor calculation; from the analysis of time-averaged data one obtains estimates for the mean cap size and the cap fluctuation amplitude. From the fluctuation analysis the same expressions are obtained in units of signal intensity rather than numbers of subunits. Signal intensity and numbers of subunits are expected to be proportional. A global fit of mean cap size (Left) and cap size fluctuation amplitude (Right) derived from the time-averaged analysis against the corresponding values from fluctuation analysis yields a conversion factor given by the slope of the best fit line shown in black (mean values were computed for each tubulin concentration, and error bars show SEM).

Processing Tracks and Selecting Growth Episodes.

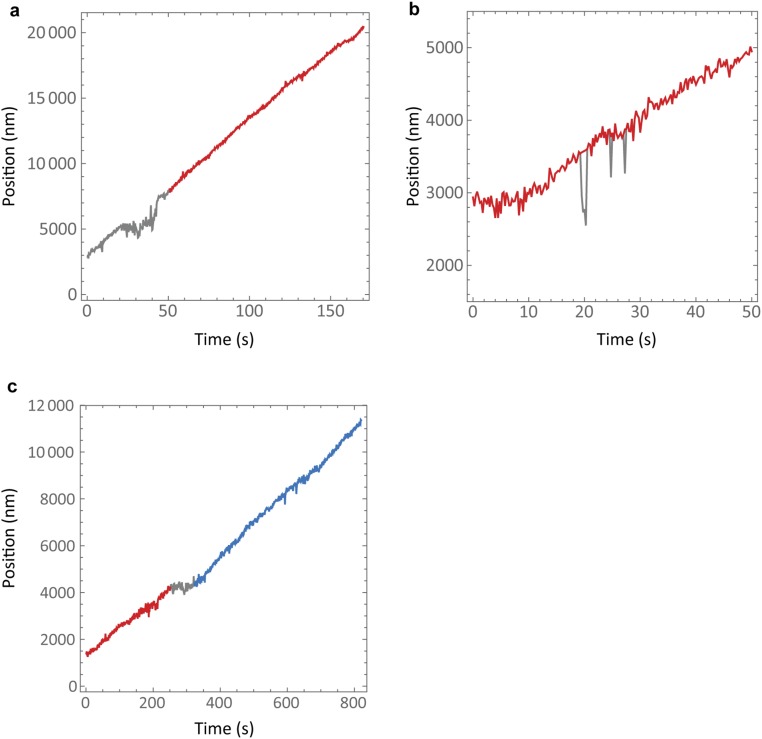
The extracted end positions occasionally showed some artifacts due to tracking errors. To mitigate the effects of these errors the tracks were further processed; at each tracked microtubule end position $x_i$ at time $t_i$ a linear fit to the track in the 50-s window $\left[t_i-25\hspace{0.17em}s,t_i+25\hspace{0.17em}s\right]$ was made to find an expected position ${\overline{x}}_i$, assuming constant growth within this window. The deviation $x_i-{\overline{x}}_i$ was then computed and the distribution of all of the deviations was found for each experimental condition. The end position $x_i$ was identified as a tracking error if its deviation from constant growth fell outside a threshold value corresponding to a deviation of 488 (4 σ), 894 (4 σ), and 1,136 (3 σ) tubulin dimers for the 10 μM, 20 μM, and 30 μM tubulin conditions, respectively. The threshold value was chosen to best identify the tracking errors observable by eye and each track was visually inspected to ensure that the procedure worked as expected. It was observed that tracking errors often occurred in close succession; hence, complete tracks or sections of tracks were deleted (Fig. S2A) until the number of tracking errors per track was less than three for each experimental condition. It was also observed that the vast majority of errors (90%) were in the negative direction, indicating that they were indeed experimental artifacts (Fig. S2B). The tracking errors left in the remaining data, which comprised 99%, 90%, and 86% of the original data for the three tubulin conditions, were then corrected by replacing $x_i$ with ${\overline{x}}_i.$

Fig. S2.

Procedure to select continuous steady-state microtubule growth. (A) An example of an experimental microtubule position trajectory with many consecutive tracking errors in the negative direction. Tracking errors were identified as very large deviations from constant growth (SI Materials and Methods) and it was observed that many errors often occurred in quick succession. Whole sections of tracks were therefore removed (gray line) before analysis. (B) Three tracking errors (gray) are shown in a partial track. In the analyzed tracks there were on average two errors per track and these were corrected by replacement with the expected microtubule position given constant growth (red line) (SI Materials and Methods). (C) An example of a track containing an episode of very slow growth (gray line) identified as a deviation from steady-state behavior. These episodes were also removed from the data and the two partial trajectories were treated separately (red and blue lines) (SI Materials and Methods). Statistics of these procedures are given in Table S1.

Short episodes of very slow growth were observed occasionally in the growth trajectories of the microtubules, reminiscent of “pauses” of growth (Fig. S2C). We considered these growth episodes to be deviations from steady-state behavior and not applicable to our analysis of steady-state growth. To identify these episodes a linear fit was made at each point $x_i$ in the window $\left[t_i-12.5\hspace{0.17em}s,t_i+12.5\hspace{0.17em}s\right]$ and a velocity $v_i$ was extracted from the gradient of the fit. The 25-s window was chosen to be smaller than the average pause length (80 s) so that the beginning and end of a pause could be accurately identified. To capture the pauses seen by eye a threshold velocity was chosen, 65% of the mean velocity for the track, and if $v_i$ fell below this threshold $x_i$ was flagged as anomalous. Manual inspection of the tracks indicated that episodes exceeding 17.5 s, 15 s, and 12.5 s for the 10 μM, 20 μM, and 30 μM conditions, respectively, were apparently deviations from steady-state growth. These episodes were removed from the data and the remaining partial tracks were subsequently considered separately (Fig. S2C). Shorter episodes were identified as anomalous at higher tubulin concentration because these microtubules grow faster. Two, four, and five anomalous episodes were identified in the 10 μM, 20 μM, and 30 μM datasets, respectively, one of which was discounted as a false positive. The data now left for analysis were 98%, 88%, and 81% of the original data comprising 38, 25, and 17 tracks for the 10 μM, 20 μM, and 30 μM tubulin conditions with an average duration of 193 s, 196 s, and 148 s. The statistics of these procedures are summarized in Table S1.

Table S1.

Table of statistics detailing processing of tracks

Tracking statistics	10 μM	20 μM	30 μM
Total time, s	7,458	5,534	3,130
Threshold for identifying tracking errors, nm	300	550	700
Total time after removal of poorly tracked episodes, s	7,358	4,979	2,684
Average no. of tracking errors remaining per track	2	2	3
No. of slow growth episodes	2	3	5
Total time after removal of slow growth episodes, s	7,339	4,889	2,521
% Total time remaining	98	88	81

Tracking statistics for three experimental conditions: 10 μM, 20 μM, and 30 μM tubulin. Tracking errors were identified as deviations from constant growth above a threshold value. Errors often appeared consecutively and so poorly tracked episodes were removed from the data entirely. The tracking errors remaining per track were then corrected. In the second step slow growth episodes were identified and also removed from the data (SI Materials and Methods and Fig. S2).

The remaining trajectories and their corresponding EB1 intensity fluctuation data were considered as representing pure steady-state growth behavior recorded with the highest possible positional tracking precision our automated tracking routine can deliver.

MSD Analysis.

The growth trajectory of the microtubule represents a Brownian diffusion-with-drift process, where the “drift” is characterized by the mean growth speed of the microtubule and the “diffusion” characterizes growth fluctuations about the mean position. The mean growth speed, $v_g$, is captured by the MD (23):

$$\langle L\left(t+\mathrm{\tau }\right)-L\left(t\right)\rangle =v_g\tau .$$ [S1]

The MSD provides additionally the diffusion constant, D, and the squared amplitude of the measurement noise, ${\mathrm{\Gamma }}_v^2$:

$$\langle {\left(\mathit{L}\left(\mathit{t+}\tau \right)-L\left(t\right)\right)}^2\rangle \mathit{-}{\mathit{v}}_{\mathit{g}}^{\mathit{2}}{\tau }^{\mathit{2}}+\mathit{2}D\tau +\mathit{2}{\mathit{\Gamma }}_v^2.$$ [S2]

The mean growth speed was obtained from a linear fit to the MD as a function of the time interval τ (Fig. 1D, Middle). The diffusion constant, D (reflecting the extent of the growth fluctuations), and the measurement noise, ${\mathrm{\Gamma }}_v$ (tracking precision), were determined from a linear fit to the variance of the displacement [i.e., the MSD minus the MD squared, as a function of the time interval τ (Fig. 1D, Bottom)]. From Eqs. S1 and S2 this gives

$$\mathrm{MSD}\left(\tau \right)-\mathrm{MD}{\left(\tau \right)}^2=2D\tau +2{\mathit{\Gamma }}_v^2.$$ [S3]

EB1 Comet Analysis.

Average EB1-GFP fluorescence intensity profiles (comets) of the growing microtubule end were generated to determine the average size of the EB cap and the maturation rate $k_m$. For each microtubule growth episode a time trace of the microtubule end position and a cropped image of the end were generated as described in Automated Microtubule Tracking. The instantaneous microtubule growth speed at each time point was calculated using a 10-s smoothing window, and the corresponding cropped images were then speed-sorted into quartiles. The lowest quartiles were discarded because they contained the greatest deviations from steady-state growth. For each remaining quartile the EB1-GFP comet profiles were extracted from the cropped images and averaged (19). The average comet profiles were then fitted with a convolved mathematical function assuming a monoexponential decay of the density of EB binding sites (figure 2 C and F in ref. 19) to obtain an estimate of $k_m$.

EB1 Binding/Unbinding Rates.

We have calculated the effect of the fast binding/unbinding turnover of EB1 molecules on the measured fluctuations of the total EB intensity. Under these growth conditions and this EB1 concentration we expect a total of ∼270 EB1 binding sites: B₀ (figure 5E in ref. 19). The EB1 binding/unbinding rates from single molecule measurements (figure 3B in ref. 19) are $k_{\text{off}}=3.4\hspace{0.17em}\hspace{0.5em}{\text{s}}^{-1}$ and $k_{\text{on}}=0.12\hspace{0.5em}\hspace{0.17em}{\text{nM}}^{-1}\hspace{0.17em}\cdot {\mathrm{s}}^{-1}=24\hspace{0.17em}{\text{s}}^{-1}$ (at an EB1 concentration $E_0=200\hspace{0.17em}\text{nM}$). These rates are much greater than the maturation rate of binding sites $(\sim 0.2\hspace{0.5em}\hspace{0.17em}{\text{s}}^{-1}$), so changes in the number of binding sites can be neglected at steady state. Hence, the mean number of occupied binding sites is $\langle \text{EB}\rangle =B_0\gamma /1+\gamma ,$ where $\gamma =E_0{k}_{\text{on}}/k_{\text{off}}$, with a corresponding variance $\text{Var}\langle \text{EB}\rangle =\langle \text{EB}\rangle /1+\gamma .$ For these experimental conditions, $\gamma =7,\langle \text{EB}\rangle =270\hspace{0.17em}\text{*}\hspace{0.17em}0.875\hspace{0.17em}=\hspace{0.17em}236$ and $\mathrm{Var}\langle \text{EB}\rangle =236/8=30$ (i.e., this would lead to an SD of $\sim 2\%$ mean signal and cannot explain the measured fluctuations). Furthermore, the characteristic correlation time of this system would be $1/E_0{k}_{\text{on}}+k_{\text{off}}=\hspace{0.17em}36\hspace{0.17em}\text{ms}$ (i.e., less than the camera exposure time of 100 ms and hence very unlikely to be observed).

Bleaching Control Experiments.

Bleaching of EB1-GFP molecules in this assay type is expected to be insignificant due to the fast binding/unbinding at microtubule ends; furthermore, the total volume of the flow cell is large in comparison with the TIRF field. To ensure that this is also true in our experimental setting, we performed control experiments at the same experimental conditions as used elsewhere (10 μM free tubulin and 200 nM EB1-GFP). We prepared a sample and imaged it for 1,100 frames (typical movie length for all other data) and then imaged the same microscope sample for another 1,100 frames. For each movie, microtubule ends were tracked and the total EB intensities were calculated over the whole movie. The mean values of EB1 intensities are shown in Table S2: They have a similar range, regardless of whether the samples have been imaged before, indicating that bleaching of EB1-GFP does not significantly contribute to the obtained values. Data were obtained from six independent experiments (six samples). For two microscope slides a third movie was recorded to further demonstrate that bleaching is insignificant.

Table S2.

Control measurements for bleaching of EB1-GFP

Sample	Mean	SD	No. of MTs	No. of samples
First (no preexposure)	2,182	517	27	6
Second	2,385	510	26	6
Third	2,144	542	9	2

The same sample was imaged for 1,100 frames up to three times in succession. From each movie, microtubule (MT) ends were tracked and total EB intensities were extracted. The mean values of EB1-GFP intensities are in a similar range regardless of if the samples have been imaged before, indicating that bleaching of EB1-GFP does not significantly contribute to the obtained values.

Generation of Velocity Time Series.

We generated velocity time series by calculating finite differences of the position time series at 2 Hz (half the image acquisition rate). Thus, two time series were generated for each track, one from even-numbered frames and one from odd-numbered frames. Velocities were not calculated at the smallest possible time difference to reduce the relative magnitude of the measurement noise. The two resulting time series were considered separately, consistent with the theoretical analysis that treats microtubule length increments (equivalently velocity fluctuations) as independent.

Correlation Analysis.

The ACF of a process x is defined as $C_x\left(\tau \right)=\langle (x\left(t\right)-\overline{x})(x\left(t+\tau \right)-\overline{x})\rangle$, where $\overline{x}=\langle x\rangle$. The CCF characterizing the correlation between two processes x and y is defined as $C_{xy}\left(\tau \right)=\langle (x\left(t\right)-\overline{x})(y\left(t+\tau \right)-\overline{y})\rangle .$

To calculate the ACF and CCF for a discrete time series $x\left(t\right)$ we can write $x\left(nT\right)=x\left[n\right]$, where T is the sampling interval and the time series runs from $n=1$ to $N.$ The asymptotically unbiased sample autocovariance is given by

$${\widehat{C}}_x\left[m\right]=\hspace{0.17em}\frac{1}{N-m}{\displaystyle \sum _{i=1}^{N-m}}\left(x\left[i+m\right]-\widehat{x}\right)\left(x\left[i\right]-\widehat{x}\right),$$ [S4]

where

$$\widehat{x}=\frac{1}{N}{\displaystyle \sum _{i=1}^N}x\left[i\right].$$ [S5]

For the relatively short time series studied here this estimator is biased toward zero. The bias of lowest order, $\mathcal{O}\left(\frac{1}{N}\right)$, can be eliminated by splitting the time series into two halves and recombining their respective ACFs ${\widehat{c}}_{\left(1\right)}$ and ${\widehat{c}}_{\left(2\right)}$ in the following way (56):

$$\widehat{C}=2\widehat{c}-\frac{1}{2}\hspace{0.17em}\left({\widehat{c}}_{\left(1\right)}+{\widehat{c}}_{\left(2\right)}\right).$$ [S6]

This bias correction was implemented using the sample autocovariance given in Eq. S4.

To calculate the cross-covariance of two fluctuating time series $x\left[n\right]$ and $y\left[n\right]$ we used the estimator

$${\widehat{C}}_{xy}\left[m\right]=\hspace{0.17em}\frac{1}{N-m}{\displaystyle \sum _{i=1}^{N-m}}\left(x\left[i+m\right]-\widehat{x}\right)\left(y\left[i\right]-\widehat{y}\right).$$ [S7]

Analysis of Velocity ACFs and Comparison with MSD Analysis.

Mean velocity ACFs are plotted for each tubulin concentration in Fig. 2C. To fit these functions we used Eq. 5: $C_{\widehat{v}}^{\prime }\left(\tau \right)=\lambda \hspace{0.17em}{a}^2\left(k_a+k_d\right){\delta }_{\tau 0}+{\lambda }^2{\mathrm{\Gamma }}_v^2(2{\delta }_{\tau 0}-{\delta }_{\tau \mathrm{\Delta }t})$. An estimate for measurement noise was obtained from the magnitude of the correlation at the shortest time lag ($\mathrm{\Delta }t$) and this was compared directly to the estimate obtained from MSD analysis. The amplitude of the velocity fluctuations was obtained from the magnitude of the correlation at zero lag and the previously obtained estimate of the measurement noise, and this was compared with the estimate of the fluctuation amplitude derived from MSD analysis because (setting $\mathrm{\Delta }t=1$) σ_v² = 2D.

Fig. 2.

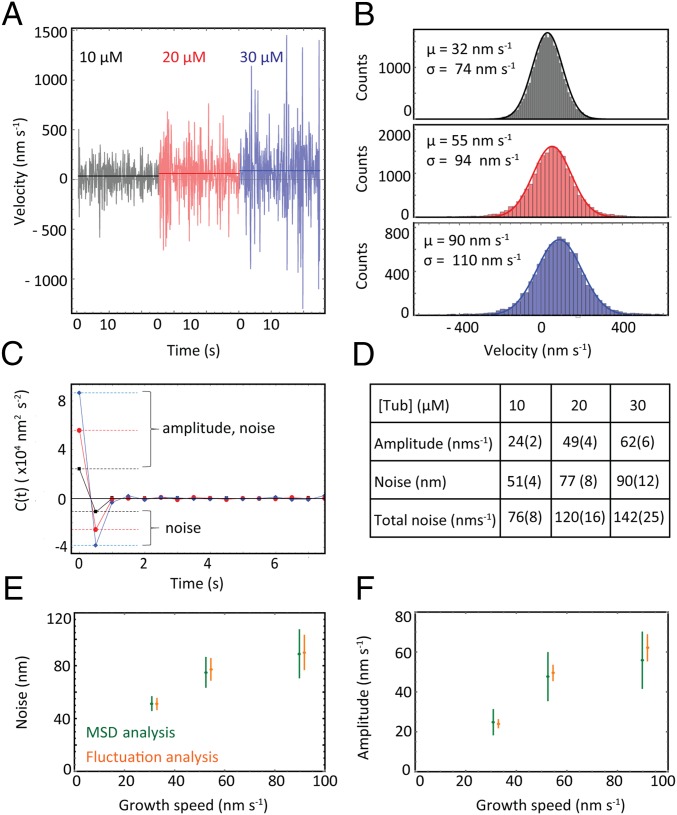
Fluctuation analysis of microtubule growth. (A) Representative velocity fluctuation traces generated from finite differencing the position data at 2 Hz. (B) Histograms of the velocity distributions (calculated with Δt = 1 s) show the average velocity and the SD increase with tubulin concentration (n = 1 × 10⁴, n = 2 × 10⁴, and n = 3 × 10⁴ with increasing tubulin concentration). (C) Plots of the average velocity ACF, indicative of Brownian diffusion in the presence of white Gaussian measurement noise. The magnitude at the origin increases with tubulin concentration due to larger growth fluctuations and higher measurement noise. Dashed lines indicate values extracted from the ACF. (D) Table of parameter estimates extracted from the ACFs in C. “Total noise” estimates are given by C_v′(0) using Eq. 5 and can be compared with the SD of the Gaussian fits to the velocity histograms in B. Errors in brackets are SEM. (E and F) Estimates of the amplitude of the growth fluctuations and the measurement noise obtained from the time-averaged analysis (MD and MSD) and the fluctuation analysis (ACFs) are compared (error bars are SEM), demonstrating good agreement between the two methods.

Analysis of EB1-GFP Autocorrelation Functions.

As a control we calculated the autocorrelation functions of the Alexa568-tubulin channel and found there was a slowly decaying correlation, revealing a source of correlated noise present in the fluorescence intensity measurements (Fig. 3D), which is likely due to thermal fluctuations of the microtubule (43). Cross-covariance analysis confirmed that the same external noise source was affecting the EB1-GFP intensity measurements (Fig. S4 A and B). The EB1-GFP autocorrelation functions therefore comprise a component from the EB1-GFP fluctuations and also a component from the correlated noise. To account for this we performed a global fit to the six curves in Fig. 3 C and D. A biexponential was fitted to the EB1-GFP autocorrelation functions (Fig. 3C) of the form

$$C_i\left(\tau \right)=A_i{e}^{-k_{m,\hspace{0.17em}i}\tau }+\alpha A_i{e}^{-k_{c,\hspace{0.17em}i}\tau },$$ [S8]

where the subscript $i=\mathrm{1,2,3}$ denotes the three experimental conditions. The first term corresponds to the cap size fluctuations (intrinsic noise) and the second term corresponds to the thermal fluctuations (correlated noise) with correlation time $1/k_c$ (Fig. S4C). For each condition the decay rate $k_{c,i}$ was shared with the decay rate from a monoexponential fit to the corresponding Alexa568-tubulin autocorrelation function (Fig. 3D),

$$C_i\left(\tau \right)=B_i{e}^{-k_{c,\hspace{0.17em}i}\tau }.$$ [S9]

Because the relative strength of the EB1-GFP fluctuations and thermal fluctuations are expected to be the same independent of tubulin concentration the parameter $\alpha$ was shared globally between the three conditions. For both fits the first data point was excluded (because this point also contains a Gaussian component due to measurement noise) and the subsequent 24 data points were fitted, which was a fitting range determined from simulated data to give accurate results (Fig. S1). The extracted parameters were also found to be robust under a range of fitting lengths (22–28 data points), with an SD in results of between 3% and 6% for all parameters and experimental conditions.

Fig. 3.

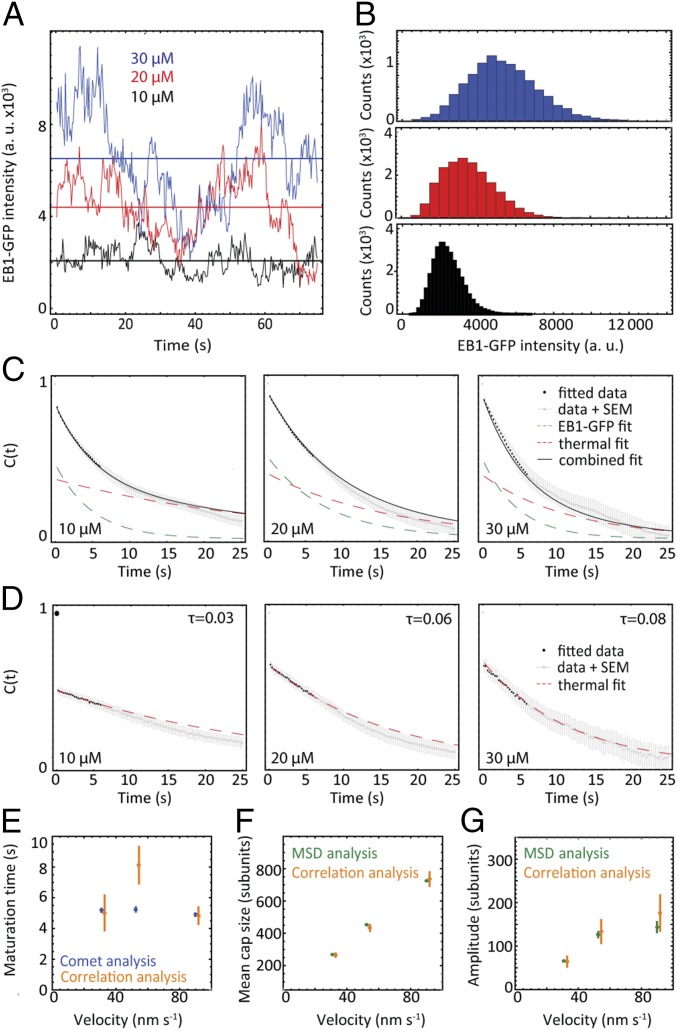
Fluctuation analysis of microtubule cap dynamics. (A) Representative time traces of the EB1-GFP fluorescence intensity fluctuations at growing microtubule ends for three tubulin concentrations. (B) Histograms of EB1-GFP intensity distributions show that the average signal and its SD increase with tubulin concentration (n values as in Fig. 2B). (C) Autocorrelation functions of the EB1-GFP intensity fluctuations. (D) Autocorrelation functions of the Alexa568-tubulin intensity fluctuations (error bars are SEM) revealing a source of correlated experimental noise. EB1-GFP intensity measurements are subject to the same correlated noise. Global fits (black lines) to pairs of autocorrelation functions (black dots) of Alexa568-tubulin (D) and EB1-GFP intensity (C) fluctuations (SI Materials and Methods and Fig. S4C) produced estimates for decay rates due to EB1-GFP fluctuations (maturation rates) and correlated noise, respectively. (E) Comparison of maturation times (k_m⁻¹) from correlation analysis (C and D) and comet analysis (Fig. 1E). (F and G) The mean cap size and the amplitude of the cap size fluctuations were obtained from EB1-GFP intensity time traces and their autocorrelation functions after finding a proportionality factor to convert fluorescence intensity into numbers of subunits (SI Materials and Methods). These values were compared with the same quantities derived from the time-averaged analysis (Fig. S5 B and C) (error bars are SEM). a. u., arbitrary units.

Fig. S4.

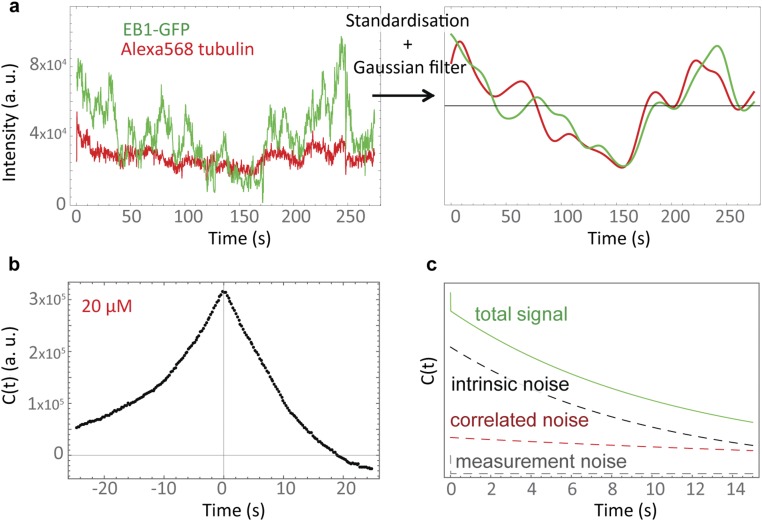
Cross-covariance of the Alexa568-tubulin and EB1-GFP fluctuations from the cap indicate correlated experimental noise is present in the data. (A) (Left) Representative time traces of the Alexa568-tubulin (red) and the EB1-GFP (green) fluorescence intensity fluctuations at the microtubule end given in arbitrary units (a. u.). (Right) Standardizing both signals and smoothing with a Gaussian kernel qualitatively reveals the existence of correlated noise. (B) The cross-covariance between the two signals shows correlation at positive and negative time lags confirming that an external noise source is correlating the two signals. (C) Illustration of the hypothetical noise components contributing to the measured ACF. The total correlation is composed of a white Gaussian measurement noise component, a correlated noise component, and the intrinsic noise of the cap size fluctuations.

Calculating Mean Cap Size and Cap Fluctuation Amplitude from Intensity Measurements.

From the time-averaged analysis (MSD and comet analysis) estimates of $D,v_g$ and $k_m$ were obtained. We used these results to predict average values for the mean cap size, $\mu$, and the squared cap size fluctuation amplitude$,\hspace{0.17em}{\sigma }^2,$ for each tubulin concentration because we have

$$\mu =\frac{1}{k_m}\frac{v_g}{a}\hspace{1em}\text{and}\hspace{1em}{\sigma }^2=\frac{1}{2k_m}\left(\frac{2D}{a^2}+\frac{v_g}{a}\right)$$ [S10]

from expressions given in the main text. The same properties, in fluorescence units rather than numbers of cap sites, can be calculated from the fluctuation analysis of EB1-GFP intensities. The mean EB1-GFP intensity is the mean cap size in fluorescence units and the intrinsic noise of the intensity fluctuations is the cap size fluctuation amplitude in fluorescence units. The intrinsic noise of the intensity fluctuations was found by multiplying the variance of the intensity measurements by the coefficient $A_i$ in Eq. S8.

To compare the results of the time-averaged analysis and the fluctuation analysis we found a proportionality factor that related the fluorescence units to numbers of cap sites by performing a global fit (weighted least-squares minimization) to the values of $\mu$ and ${\sigma }^2$ derived from the time-averaged analysis and the values of $\mu \prime$ and ${\sigma }^2\prime$ derived from the intensity measurements (Fig. S5B), where the dash denotes units of fluorescence intensity. We then converted the fluorescence intensity measurements into numbers of cap sites and made a direct comparison (Fig. 3 F and G).

ACF of the Cap Size Fluctuations.

To derive correlation functions it is useful to define the Fourier transform pairs of the ACF and the CCF, which are the power spectrum and cross-power spectrum, respectively, given by (57): $S_x\left(\omega \right)=\langle x\left(\omega \right)x^{\ast }\left(\omega \right)\rangle ,\hspace{0.17em}\omega >0$ and $S_{xy}\left(\omega \right)=\langle x\left(\omega \right)\hspace{0.17em}{y}^{\ast }\left(\omega \right)\rangle ,\hspace{0.17em}\omega >0$. The zero frequency components are removed by definition because the ACF and CCF are defined with respect to the mean. One can then obtain correlation functions by first finding power spectra and performing an inverse Fourier transform. We start with a deterministic equation for the evolution of the cap,

$$\dot{n}\left(t\right)=\hspace{0.17em}{k}_a-k_d-k_{m}n\left(t\right).$$ [S11]

In the LNA to find an equation for the stochastic fluctuations, $\delta n\left(t\right),$ we make the substitution $n\left(t\right)=\overline{n}+\delta n\left(t\right)$ where $\overline{n}=\langle n\left(t\right)\rangle$ and add a Gaussian white-noise term, ${\xi }_c\left(t\right),$ to account for the stochasticity in the reactions:

$$\begin{array}{c}\frac{d}{dt}\left(\overline{n}+\delta n\left(t\right)\right)=\hspace{0.17em}{k}_a-k_d-k_m\left(\overline{n}+\delta n\left(t\right)\right)+{\xi }_c\left(t\right)\\ \dot{\delta n}\left(t\right)=\hspace{0.17em}-k_m\hspace{0.17em}\delta n\left(t\right)+{\xi }_c\left(t\right).\hspace{0.17em}\end{array}$$ [S12]

The second line is obtained by noting that $\overline{n}=\mu =\left(k_a-k_d\right)/k_m$ (Eq. 1). With a Fourier transform Eq. S12 becomes

$$-i\omega \delta n\left(\omega \right)=-k_m\hspace{0.17em}\delta n\left(\omega \right)+{\xi }_c\left(\omega \right).$$ [S13]

The power spectrum, $\langle {\left|\delta n\left(\omega \right)\right|}^2\rangle$, is therefore given by

$$\langle {\left|\delta n\left(\omega \right)\right|}^2\rangle =\frac{\langle {\left|{\xi }_c\left(\omega \right)\right|}^2\rangle }{k_m^2+{\omega }^2}.$$ [S14]

Because ${\xi }_c\left(\omega \right)$ is the sum of the noise due to the growth fluctuations, ${\xi }_v\left(\omega \right),$ and the noise due to the maturation process, ${\xi }_m\left(\omega \right),$ we can write ${\xi }_c\left(\omega \right)=\frac{1}{a}{\xi }_v\left(\omega \right)+{\xi }_m\left(\omega \right)$ and obtain

$$\langle {\left|{\xi }_c\left(\omega \right)\right|}^2\rangle =\langle \left(\frac{1}{a}{\xi }_v\left(\omega \right)+{\xi }_m\left(\omega \right)\right)\left(\frac{1}{a}{{\xi }_v}^{\ast }\left(\omega \right)+{{\xi }_m}^{\ast }\left(\omega \right)\right)\rangle =\frac{1}{a^2}\langle {\left|{\xi }_v\left(\omega \right)\right|}^2\rangle +\langle {\left|{\xi }_m\left(\omega \right)\right|}^2\rangle$$ [S15]

because the cross-terms, that is, $\langle {\xi }_v\left(\omega \right){{\xi }_m}^{\ast }\left(\omega \right)\rangle$, are zero as the noise sources are independent. From the main text we have

$$\langle {\xi }_v\left(t\right){\xi }_v(t\prime )\rangle =\left(k_a+k_d\right)\hspace{0.17em}{a}^2\hspace{0.17em}\delta \left(t-t\prime \right)$$ [S16]

and

$$\langle {\xi }_m\left(t\right)\hspace{0.17em}{\xi }_m(t\prime )\rangle =k_m\langle n\rangle \hspace{0.17em}\delta \left(t-t\prime \right).$$ [S17]

With a Fourier transform of these expression one can obtain

$$\langle {\left|{\xi }_v\left(\omega \right)\right|}^2\rangle =a^2\left(k_a+k_d\right)$$ [S18]

$$\langle {\left|{\xi }_m\left(\omega \right)\right|}^2\rangle =k_m\langle n\rangle$$ [S19]

and

From Eqs. S15, S18, and S19 we obtain an expression for the power spectrum in Eq. S14,

$$S_c\left(\omega \right)=\frac{2\hspace{0.17em}{k}_a}{k_m^2+{\omega }^2}.$$ [S20]

An inverse Fourier transform recovers the ACF of the cap size fluctuations given in the main text,

$$C_c\left(\tau \right)=\frac{k_a}{k_m}{e}^{-k_m\tau }.$$ [S21]

Cross-Power Spectrum of Velocity and Cap Fluctuations.

A deterministic equation for the growth fluctuations is given by

$$v\left(t\right)=\left(k_a-k_d\right)a.$$ [S22]

Substituting $v\left(t\right)=\overline{v}+\delta v\left(t\right)$ into Eq. S22 and adding the Gaussian white noise term ${\xi }_v\left(t\right)$ we obtain an equation for the stochastic velocity fluctuations,

$$\delta v\left(t\right)={\xi }_v\left(t\right),$$ [S23]

where we have used $\overline{v}=v_g$ and $v_g=\left(k_a-k_d\right)a$ (see the main text). With a Fourier transform this becomes

$$\delta v\left(\omega \right)={\xi }_v\left(\omega \right).$$ [S24]

The cross-power spectrum is given by $\langle \delta v\left(\omega \right)\delta n^{\ast }\left(\omega \right)\rangle$. Using Eqs. S13 and S24 we find

$$\begin{array}{c}\langle \delta v\left(\omega \right)\delta n\ast \left(\omega \right)\rangle =\frac{\langle {\xi }_v\left(\omega \right){\xi }_c^{\ast }\left(\omega \right)\rangle }{k_m+i\omega }\\ =\frac{\langle {\xi }_v\left(\omega \right)\left(\frac{1}{a}{\xi }_v^{\ast }\left(\omega \right)+{\xi }_m^{\ast }\left(\omega \right)\right)\rangle }{k_m+i\omega }\\ =\frac{1}{a}\frac{\langle {\left|{\xi }_v\left(\omega \right)\right|}^2\rangle }{k_m+i\omega }.\end{array}$$ [S25]

Using Eq. S18 we obtain the cross-power spectrum

$$S_{vc}\left(\omega \right)=\frac{\left(k_a+k_d\right)}{k_m+i\omega }a.$$ [S26]

A Fourier transform of the above recovers the CCF (Eq. 4),

$$C_{vc}\left(\tau \right)=a\left(k_a+k_d\right)e^{-k_m\tau }U\left(\tau \right)$$ [S27]

ACF of Velocity Fluctuations in the Presence of Measurement Noise.

For a diffusion-with-drift process we can write an instantaneous velocity $v\left(t\right)=v_g+\hspace{0.17em}{\xi }_v\left(t\right)$ (see the main text). We calculate the velocity fluctuations as $\widehat{v}\left(t\right)=(L\left(t+\mathrm{\Delta }t\right)-L\left(t\right))/\mathrm{\Delta }t$. In this finite case the equivalent noise term ${\widehat{\xi }}_v\left(t\right)$ has different properties; its covariance is given by $\langle {\widehat{\xi }}_v\left(t\right){\widehat{\xi }}_v(t\prime )\rangle =\lambda a^2\left(k_a+k_d\right){\delta }_{tt\prime }$, where $\lambda =1/\mathrm{\Delta }t$ and ${\delta }_{ij}$ is the Kronecker delta. In the presence of positional measurement noise the expression for $\widehat{v}\left(t\right)$ requires two additional terms accounting for the measurement of L(t) and L(t + Δt),

$$\widehat{v}\left(t\right)=v_g+\hspace{0.17em}\hspace{0.17em}{\widehat{\xi }}_v\left(t\right)+\hspace{0.17em}{\widehat{\gamma }}_v\left(t+\mathrm{\Delta }t\right)-{\widehat{\gamma }}_v\left(t\right)$$ [S28]

Each measurement error term, ${\widehat{\gamma }}_v\left(t\right)$, is characterized by

$$\langle {\widehat{\gamma }}_v\left(t\right){\widehat{\gamma }}_v(t\prime )\rangle ={\lambda }^2{\mathrm{\Gamma }}_v^2{\mathit{\delta }}_{\mathit{tt}\prime }$$ [S29]

where ${\mathrm{\Gamma }}_v^2$ is the squared amplitude of the positional measurement noise. From the definition of the ACF and defining $\overline{v}=\langle v\left(t\right)\rangle$,

$$\begin{array}{c}{C}_{\widehat{v}}^{\prime }\left(\tau \right)=\langle \widehat{v}\left(t\right)\widehat{v}\left(t+\tau \right)\rangle -{\overline{v}}^2\\ =\langle \left(v_g+{\widehat{\xi }}_v\left(t\right)+{\widehat{\gamma }}_v\left(t+\mathrm{\Delta }t\right)-{\widehat{\gamma }}_v\left(t\right)\right)\left(v_g+{\widehat{\xi }}_v\left(t+\tau \right)+{\widehat{\gamma }}_v\left(t+\mathrm{\Delta }t+\tau \right)-{\widehat{\gamma }}_v\left(t+\tau \right)\right)\rangle -{\overline{v}}^2.\end{array}$$ [S30]

Expanding out the brackets gives

$$\begin{array}{c}{C}_{\widehat{v}}^{\prime }\left(\tau \right)=\langle {\widehat{\xi }}_v\left(t\right)\hspace{0.17em}{\widehat{\xi }}_v\left(t+\tau \right)\rangle +{\langle \widehat{\gamma }}_v\left(t+\mathrm{\Delta }t\right){\widehat{\gamma }}_v\left(t+\mathrm{\Delta }t+\tau \right)\rangle \\ -{\langle \widehat{\gamma }}_v\left(t+\mathrm{\Delta }t\right){\widehat{\gamma }}_v\left(t+\tau \right)\rangle +{\langle \widehat{\gamma }}_v\left(t\right){\widehat{\gamma }}_v\left(t+\tau \right)\rangle ,\end{array}$$ [S31]

where we have used the fact that $\langle {\xi }_v\left(t\right){\gamma }_v(t\prime )\rangle =0$ for all t, and $\overline{v}=v_g$. This can be written as

$$C_v^{\prime }\left(\tau \right)=\{\begin{array}{ll}\langle {\widehat{\xi }}_v{\left(t\right)}^2\rangle +\langle {\widehat{\gamma }}_v{\left(t+\mathrm{\Delta }t\right)}^2\rangle +\langle {\widehat{\gamma }}_v{\left(t\right)}^2\rangle \hfill & \text{for}\hspace{0.17em}\tau =0\hfill \\ -\langle {\widehat{\gamma }}_v{\left(t+\mathrm{\Delta }t\right)}^2\rangle \hfill & \text{for}\hspace{0.17em}\tau =\mathrm{\Delta }t\hfill \\ 0\hfill & \text{for}\hspace{0.17em}\tau >\mathrm{\Delta }t,\hfill \end{array}$$ [S32]

which can be written as

$$C_v^{\prime }\left(\tau \right)=\lambda (k_a+k_d)a^2{\delta }_{\tau 0}+{\lambda }^2{\mathit{\Gamma }}_v^2\left(2{\delta }_{\tau 0}-{\delta }_{\tau \mathrm{\Delta }t}\right).$$ [S33]

ACF of Cap Size Fluctuations in the Presence of Measurement Noise.

The ACF of the cap size fluctuation in the presence of measurement noise is simpler. The measurement noise ${\gamma }_c\left(t\right)$ is characterized by

$$\langle {\gamma }_c\left(t\right){\gamma }_c(t\prime )\rangle ={\mathrm{\Gamma }}_c^2{\delta }_{tt\prime }$$ [S34]

Following a similar procedure as above the ACF is given by

$$C_c^{\prime }\left(\tau \right)=\frac{k_a}{k_m}{e}^{-k_m\tau }+{\mathrm{\Gamma }}_c^2{\delta }_{\tau 0}$$ [S35]

Simulation of the Cap Reaction Network.

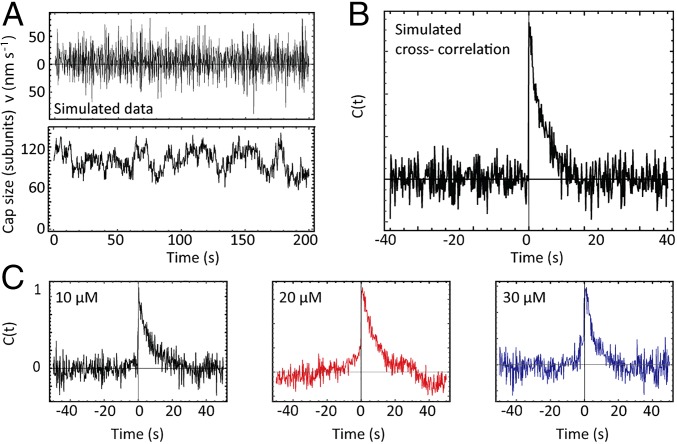
A full stochastic simulation of the cap reaction network developed in Mathematica (Wolfram) from a previous study (24) was used to test the validity of our model and the robustness of our analysis to experimentally limiting factors. Twenty simulated tracks 200 s long were analyzed to replicate our experimental datasets. We tested our analysis under a range of simulated noise conditions (modeled as additive white Gaussian noise) covering what was measured experimentally. We also analyzed simulated data at 4 Hz and a faster rate of 10 Hz (Fig. S1). We found the simulation results fitted the theory well in all cases. Example simulation data and cross-correlation analysis results are shown in Fig. 4 A and B.

Fig. 4.

Cross-correlation analysis between growth speed and cap size fluctuations. (A) An example microtubule length trajectory (Top) and its cap size fluctuations (Bottom) from a full stochastic simulation of the cap reaction network with added Gaussian noise replicating the experimentally measured noise levels. (B) Cross-correlation of simulated data (20 tracks, 200 s long) shows the expected one-sided exponential decay, demonstrating that growth fluctuations drive cap size fluctuations. (C) Experimental cross-correlation functions show a strongly asymmetric shape and the apparent monoexponential decays at positive lag times are in qualitative agreement with theory.

Results

To measure the properties of EB cap size fluctuations, microtubules were grown from surface-immobilized GMPCPP-stabilized seeds in the presence of purified Alexa568-tubulin and GFP-tagged fission yeast EB1 (Mal3) (Fig. 1B), essentially as described (13, 39) (SI Materials and Methods). Experiments were performed at three different tubulin concentrations. Microtubule growth and EB cap size fluctuations were monitored using dual-color time-lapse total internal reflection fluorescence (TIRF) microscopy, with an image acquisition rate of four frames per s (Fig. 1C). The growing plus ends of microtubules were tracked (16, 40, 41), and the corresponding intensity of the EB1-GFP signal in the microtubule end region was recorded using an automated procedure (19) (SI Materials and Methods). For analysis, we considered only continuous growth episodes of at least 200-s duration (SI Materials and Methods, Table S1, and Fig. S2), excluding catastrophe episodes.

Cap Formation Kinetics from Time-Averaged Data.

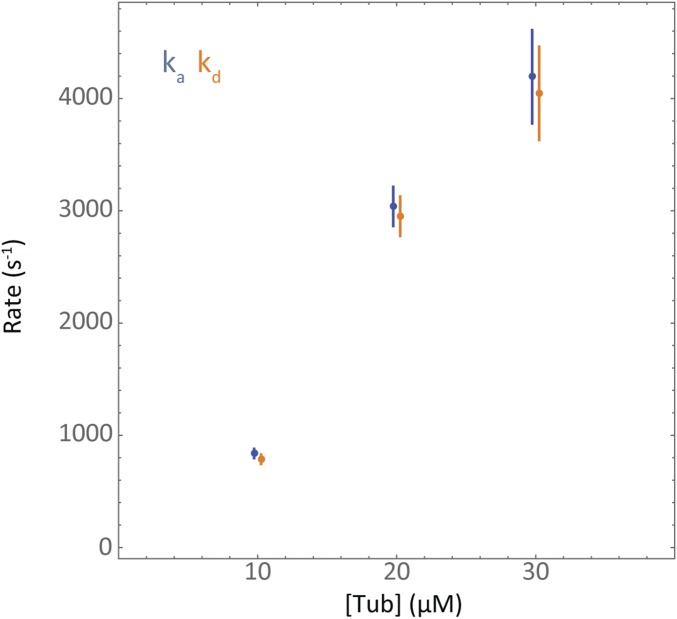
First, we extracted the time-averaged characteristics of the observed steady-state growth trajectories. Representative trajectories show visible fluctuations with faster growth at higher tubulin concentration, as expected (Fig. 1D, Top). Mean growth speeds were determined by mean displacement (MD) analysis (Fig. 1D, Middle and SI Materials and Methods) and the diffusion constant was quantified with MSD analysis (Fig. 1D, Bottom and SI Materials and Methods), characterizing the diffusion-with-drift process. From the MSD analysis an estimate for the positional measurement noise was also obtained. From the estimates of the diffusion constant and the mean growth speed the tubulin association and dissociation rates can be derived, which were found to be large compared with their difference (Fig. S3), in agreement with the notion of fast assembly kinetics (23, 42). The average EB cap length at plus ends was extracted from time-averaged EB1-GFP intensity profiles (Fig. 1E) by comet analysis (13, 14, 19). From the mean growth speeds and the comet lengths the maturation rates were derived (SI Materials and Methods). The time-averaged properties of the cap reaction network are summarized in Fig. 1F.

Fig. S3.

Association and dissociation rate constants determined by MD and MSD analysis. Values of the association rate constant $k_a$ (blue dots) and the dissociation rate constant $k_d$ (orange dots) calculated for the three tubulin concentrations (error bars are SEM). Values for the rate constants were found to increase with tubulin concentration and are large compared with their difference.

Properties of Velocity Fluctuations.

Next we used fluctuation analysis to study the growth fluctuations directly. We obtained velocity time series by calculating finite differences of the microtubule positions at 2 Hz (SI Materials and Methods). Representative velocity traces show that the velocities fluctuate randomly over time (Fig. 2A), resulting in Gaussian-shaped velocity distributions (Fig. 2B), as expected. We then calculated the ACF of the velocity traces (Fig. 2C and SI Materials and Methods). The increasing magnitude of the ACFs at the origin with increasing tubulin concentration reflects the expected larger fluctuation amplitudes (intrinsic noise) with growth speed due to faster association and dissociation kinetics (Eq. 2), as also seen in the broadening of the velocity distributions (Fig. 2B). Measurement noise also contributes to the magnitude at the origin and causes the negative correlation at the shortest time lag (Eq. 5). Estimates of the intrinsic noise and measurement noise were extracted from the ACFs (SI Materials and Methods and Fig. 2D). Their combined values agreed well with sigma values of Gaussian fits to the velocity distributions (Fig. 2 B and D), demonstrating consistency. The measurement noise was in the expected range of the microtubule end tracking precision (40). In further agreement with theory, the absence of a characteristic correlation time reflects the Poissonian nature of the association and dissociation of tubulin at growing microtubule ends.

The velocity fluctuation amplitude can also be predicted from the results of MSD analysis (SI Materials and Methods) and compared with the fluctuation analysis results. Measurement noise estimates can be compared directly. Good agreement confirms the close mathematical relationship between these two methods (Fig. 2 E and F). However, the fluctuation analysis goes further by explicitly showing that the velocity fluctuations are “memoryless,” supporting the model of microtubule growth as a Brownian diffusion-with-drift.

Properties of EB Cap Size Fluctuations.

To measure directly the properties of the EB cap size fluctuations we analyzed time series of EB1-GFP intensities in the microtubule end region at 4 Hz. As expected from theory (Eq. 1) representative time traces (Fig. 3A) and histograms of EB1-GFP intensities (Fig. 3B) show that the mean intensity, corresponding to the total cap size, increases with tubulin concentration (i.e., growth speed) (13). Also in agreement with theory (Eq. 3) the amplitudes of the fluctuations increase with tubulin concentration (Fig. 3 A and B). Interestingly, the intensity fluctuations give the impression of a strong low-frequency structure, which was not seen in the velocity fluctuations (Fig. 2A).

We computed autocorrelation functions (normalized ACFs) of the EB cap intensity fluctuations and found that in contrast to the velocity fluctuations they showed an apparently monoexponential decay on a timescale of several seconds (Fig. 3C). The loss of some correlation within the first time lag is the expected consequence of white Gaussian measurement noise (Eq. 6). As a control we also analyzed the Alexa568-tubulin intensity in the microtubule end region; autocorrelation functions revealed that in addition to the measurement noise signature a slowly decaying correlation was detectable beyond the first time lag (Fig. 3D). This correlated noise was present in both fluorescence channels as demonstrated by cross-covariance analysis (Fig. S4 A and B) and was therefore contributing to the measured autocorrelation functions (Fig. S4C). It is likely the consequence of thermal motion of the microtubules in the z-direction of the sample (“microtubule wiggling”), expected to occur at this timescale (43), leading to slow intensity fluctuations due to the exponentially decaying profile of the TIRF evanescent field in the z-direction (44).

Therefore, we performed a monoexponential fit to the autocorrelation functions of the Alexa568-tubulin intensity fluctuations and a biexponential fit to the autocorrelation functions of the EB cap size fluctuations sharing the decay time corresponding to microtubule wiggling (SI Materials and Methods). The shorter decay time of the biexponential fit gives an estimate of the maturation rate, k_m (1/τ). Extracted τ values were in the same range for all tubulin concentrations: 5.0 ± 1.1 s, 8.1 ± 1.2 s, and 4.8 ± 0.5 s for 10 μM, 20 μM, and 30 μM tubulin, respectively. These values agree well with those obtained from comet analysis (Figs. 1F and 3E), providing independent support for our simple model and confirming that the maturation rate is essentially independent of the microtubule growth velocity (13, 20), as expected theoretically.

Next we determined the mean size of the EB cap and the amplitude of the cap size fluctuations from the autocorrelation functions of the EB fluorescence intensity time traces (Fig. S5 A and B and SI Materials and Methods). We found again that both the mean cap size and the fluctuation amplitude increased with tubulin concentration (i.e., with growth velocity), consistent with theory (Eqs. 1 and 3). The mean cap size increases from 266 subunits at 10 μM to 736 subunits at 30 μM (Fig. 3F), implying a cap of 20–60 tubulin layers long (because 13 tubulin subunits comprise a layer) for our range of experimental conditions. This is in agreement with earlier estimates for microtubules growing in vitro (13, 14, 19) and in living cells (18). Over the same range of tubulin concentrations the amplitude of the fluctuations increased from 64 to 178 subunits (Fig. 3G).

The mean cap size and its fluctuation amplitude can also be predicted from the analysis of time-averaged data, that is, of spatial EB intensity profiles (comets), MD, and MSD plots (SI Materials and Methods); good agreement between the time-averaged analysis and the fluctuation analysis further supports the theory (Fig. 3 F and G). These results provide quantitative characterization of the properties of EB cap size fluctuations and their dependence on microtubule growth velocity.

Cross-Correlation of Growth Speed and Cap Size Fluctuations.

The topology of the cap reaction network defines a direction of causality: Microtubule growth fluctuations affect cap size fluctuations, but cap size fluctuations do not influence growth fluctuations. For such a model, one expects a distinct cross-correlation (normalized CCF) as shown by simulated data (Fig. 4 A and B). We computed the average cross-correlation functions between the measured growth fluctuations and cap size fluctuations for the three tubulin concentrations (Fig. 4C). The mixing of two noisy signals resulted in relatively noisy cross-correlation curves. Nevertheless, all curves clearly show an asymmetry with exponential decays on the side of positive time lags and roughly zero covariance at negative time lags, in qualitative agreement with theory (Eq. 4). These observations further support the topology of the reaction network and the derived theory for steady-state microtubule growth velocity and cap size fluctuations.

Discussion

Here we have measured the fluctuations in the size of the protective cap of growing microtubules using fluorescent EB proteins as cap markers. Using correlation analysis we have characterized the properties of these fluctuations and have found that the amplitude and characteristic timescale of the cap size fluctuations can be understood quantitatively based on a simple kinetic reaction network describing cap formation. Theoretical expressions for the properties of the fluctuations have been derived using concepts from chemical network analysis, previously applied in studies of gene expression and other biochemical networks (29–31). The measured timescale and amplitude of the cap size fluctuations agreed quantitatively with values predicted with kinetic rates obtained from time-averaged data (comet and MSD analysis), demonstrating consistency.

Interestingly, the cap size fluctuations show very different characteristics compared with the growth velocity fluctuations. This is due to the nature of the underlying chemical kinetic processes. Growth speed fluctuations are determined by two Poisson processes, tubulin association and dissociation (23, 26), whereas cap size fluctuations are additionally determined by cap site maturation, most likely the transformation of GTP (or GDP/Pi) tubulin to GDP tubulin (15, 16, 21). The instantaneous rate of cap site maturation depends linearly on the fluctuating cap size, resulting in a process formally similar to diffusion in a potential well (OU process). The cap represents a mean-reverting system characterized by the timescale at which it relaxes back to its average size following a stochastic perturbation, which is the inverse of the characteristic frequency (i.e., the maturation rate constant). The relatively slow kinetics of cap site maturation limits the response of the cap size to the fast growth fluctuations and effectively attenuates the high-frequency perturbations caused by the stochastic growth.

We can now explain the timescale of microtubule stability fluctuations, as previously observed in tubulin washout experiments (14). In these experiments, faster-growing microtubules with larger protective caps were more stable (14). However, the correlation between instantaneous microtubule stability and cap size was lost when they were measured several seconds apart (14), which is indeed in the range of the characteristic timescale of the cap size fluctuations, as shown here. Hence, the maturation time in the range of seconds as shown here (Figs. 1E and 3E) and elsewhere (13–15, 19, 20) sets the timescale of instantaneous microtubule stability fluctuations. This timescale also eliminates EB1 binding dynamics as a significant source of EB1 fluctuations: For the experimental conditions here, these dynamics occur on a ∼100-ms scale and would only contribute a few percent variation (SI Materials and Methods).

The observed asymmetry of the CCF of growth velocity and cap size fluctuations indicate that in a steady growth state velocity fluctuations drive cap size fluctuations, but not vice versa. Whereas this supports the topology of the simple kinetic reaction network of cap generation, it may also seem surprising, because the mean cap size decreases strongly over several seconds before catastrophe (16, 19), suggesting that cap size could affect growth speed. However, here we excluded catastrophe episodes and growth pauses from our analysis, because we wanted to focus on steady-state growth alone. In fact, the observed CCF shows that microtubules are remarkably stable, for most of their time in steady-state growth. Together with recent observations of a stability threshold being in the range of 10–30% of the average cap size (14, 16, 19) the amplitudes of cap size fluctuations as measured here and predicted by our theory indicate that this stability threshold is indeed far from the mean cap size (∼3 sigma).

Typical microtubule lifetimes at steady state are several hundreds of seconds, much longer than the maturation time (24, 25, 45–49); how these two timescales are linked is not clear. Currently, there is no exact agreement on the criterion for inducing catastrophe. Simple cap models have been criticized for not correctly describing the measured dependence of steady-state microtubule lifetimes on their growth speed (50). For a more comprehensive model, finer detail on the structure of the cap, potentially influenced by the nanoscale structure of the microtubule end itself, such as the tapered or sheet-like extensions observed by electron microscopy (48) may have to be considered (51). Furthermore, defects (45) or lattice cracks (52–54) have been hypothesized to exist and to provide alternative or additional constraints on microtubule stability (45, 50, 53, 54). Unfortunately, unlike cap size fluctuations, the real-time observation of these other features is currently not possible, limiting direct tests of these models.

Our quantitative understanding of the properties of the protective cap size fluctuations during steady-state growth, as developed here, will likely be useful in the future for the refinement of existing models and possibly the development of new quantitative models explaining the lifetime of microtubules based on the kinetic processes of growth and cap maturation, as well as for their regulation by accessory proteins.

Materials and Methods

In vitro microtubule dynamics assays were imaged by TIRF microscopy. Microtubule end tracking, data analysis, simulations, and theoretical work were performed using programs written in MATLAB, Mathematica, and Image J. Detailed procedures can be found in SI Materials and Methods.