Abstract
Background
After adjusting for age and body mass index (BMI), mammographic measures - dense area (DA), percent dense area (PDA) and non-dense area (NDA) - are associated with breast cancer risk. Our aim was to use longitudinal data to estimate the extent to which these risk-predicting measures track over time.
Methods
We collected 4,320 mammograms (age range, 24-83 years) from 970 women in the Melbourne Collaborative Cohort Study and the Australian Breast Cancer Family Registry. Women had on average 4.5 mammograms (range, 1-14). DA, PDA and NDA were measured using the Cumulus software and normalised using the Box-Cox method. Correlations in the normalised risk-predicting measures over time intervals of different lengths were estimated using nonlinear mixed-effects modelling of Gompertz curves.
Results
Mean normalised DA and PDA were constant with age to the early 40s, decreased over the next two decades, and were almost constant from the mid 60s onwards. Mean normalised NDA increased non-linearly with age. After adjusting for age and BMI, the within-woman correlation estimates for normalised DA were 0.94, 0.93, 0.91, 0.91 and 0.91 for mammograms taken 2, 4, 6, 8 and 10 years apart, respectively. Similar correlations were estimated for the age and BMI adjusted normalized PDA and NDA.
Conclusion
The mammographic measures that predict breast cancer risk are highly correlated over time.
Impact
This has implications for etiologic research and clinical management whereby women at increased risk could be identified at a young age (e.g. early 40s or even younger) and recommended appropriate screening and prevention strategies.
Keywords: mammographic density, breast cancer, longitudinal, tracking, correlation
Introduction
How well a measure of interest is maintained over time within an individual is called ‘tracking’ (1) and can be assessed by the correlations between measures taken at different time points. Risk-prediction biomarkers with strong tracking are particularly important because they allow characterising an individual's risk well before the onset of disease.
For women of the same age and body mass index (BMI), mammographic density (MD), the amount of white radiographic appearance of dense tissue as seen on a mammogram, is an established risk factor for breast cancer both as an absolute (dense area; DA) and a relative (percent dense area; PDA) measure (2-4). The association between the absolute amount of non-white appearance of breast tissue (non-dense area; NDA) and risk of breast cancer remains controversial (3). MD measures are also associated with the sensitivity of mammography by ‘masking’ tumours (5-7). Therefore, the extent to which a woman's risk-associated MD measures (i.e. MD measures adjusted for age and BMI) change over time (i.e. ‘track’) is important. If tracking is high from early adulthood, it might be possible to identify at young ages women at increased risk of breast cancer and/or of having tumours ‘masked’, and offer appropriate screening and prevention strategies.
When considering MD as a risk factor for breast cancer we need to adjust for age and BMI. This is because both age and BMI are negative confounders of the association between MD and risk; increasing age is associated with lower MD (both in terms of DA and PDA) and increasing BMI is associated with lower PDA while increasing age and BMI (at least post-menopausal BMI) are associated with higher risk. Therefore, when investigating the changes over time in the risk-predicting MD measures we need to first adjust the MD measures for age and BMI.
In terms of change in mean values over time, studies have found that DA and PDA decreased with age (8-10) while NDA increased with age (9, 11) after adjusting for BMI. NDA was also found to increase with age without adjusting for BMI (12). Another study, which had investigated the effects of menopause, found that DA and PDA decreased with menopause and NDA increased with menopause after adjusting for height and weight (13). Two studies found that, after adjusting for age, PDA decreased as BMI increased but found that DA did not vary with change in BMI (11, 14).
In terms of tracking, for MD measures adjusted for age and BMI the Australian Mammographic Density Twin Study (15) found the correlations between measures taken on average 8 years apart were about 0.8. Similarly, a UK longitudinal study (9) found correlations of about 0.8 for MD measures taken about 9 years apart but this estimate was obtained without adjusting for age and BMI. Both studies were of women older than 40 years, and to our knowledge no previous study has considered tracking for women younger than 40 years.
In this study, we have quantified the degree of tracking of the MD measures that predict breast cancer risk (i.e. the age- and BMI-adjusted MD measures) using a longitudinal set of mammograms from a sample of Australian women.
Methods
Melbourne Collaborative Cohort Study (MCCS)
The MCCS, established in 1990-1994, includes 24,469 women living in Melbourne aged between 27 and 76 years at recruitment when information about lifestyle and demographic characteristics were obtained through administered structured questionnaires and weights and heights were measured (16). Participants were followed up from 1995-2002 by a postal questionnaire in which weights were self-reported, and from 2003-2007 with face-to-face interviews when weights were measured. The Cancer Council Victoria's Human Research Ethics Committee approved the study protocol.
In 2009, we conducted a linkage between female MCCS participants and BreastScreen Victoria (BSV), the government-funded mammographic screening program. We identified 20,444 (84%) participants who had attended BSV at least once. These women were eligible for a nested case-control MD study (4). We randomly sampled 884 women from the nested case-control study (182 cases, 702 controls). After excluding mammograms taken after the end of follow-up at 31st December 2007 (288 mammograms, 7 women) and those taken within two years before diagnosis of breast cancer (173 mammograms, 31 women), there were 3,954 mammograms from 846 women.
Australian Breast Cancer Family Registry (ABCFR)
The ABCFR, initiated in 1992, includes a population-based case-control-family study conducted in Melbourne and Sydney (17-19). Cases with first primary invasive breast cancer were recruited from the respective population-based state cancer registries. Controls were sampled through electoral rolls and frequency matched for age. Cases and controls acted as probands for recruitment of relatives. Demographic and lifestyle characteristics and heights and weights were self-reported through questionnaires. At 10 year follow-up, weight was again self-reported. The Institutional Ethics Committees of The University of Melbourne, Cancer Council Victoria and the New South Wales Cancer Council approved the study protocol.
Mammograms were retrieved from BSV, breast clinics and the ABCFR participants themselves. A total of 855 mammograms from 301 women (89 cases, 212 controls) were identified. After excluding mammograms taken at/after diagnosis of cases (75 mammograms, 73 women) and mammograms taken within two years before diagnosis of breast cancer (11 mammograms, 10 women), 769 mammograms from 218 women remained.
Combined MCCS and ABCFR longitudinal MD studies
The combined sample included 4,714 mammograms from 1,064 women (9 mammograms were dropped because they were taken within the same year for a woman). Details of this sample are presented in Table 1. After dropping women for whom there was no information on their BMI, there were 4,320 mammograms from 970 women. Both of these datasets, before and after excluding missing BMI, were used to fit models to MD measures unadjusted for, and adjusted for BMI, respectively. For the 970 women, all mammograms were taken between the ages of 24 to 83 years (83.2% of the mammograms were taken between 50 to 74 years, the target age group for screening in Australia). Women had between 1 to 14 mammograms (average 4.5) and for those who had more than one mammogram, the time between the first and last mammogram ranged from 1.2 to 19.6 years (average 8.7 years).
Measurement of mammographic density
Mammograms were taken between years 1988 and 2009, 99% were craniocaudal views and 84% were of the right breast. For all but four women, their mammograms were of the same breast. Mammograms were digitised and measured by the Australian Mammographic Density Research Facility (AMDRF) at The University of Melbourne. Lumysis 85 and Array scanners were used to digitise mammograms from the ABCFR and MCCS, respectively. MD was measured for the MCCS and ABCFR by three readers (JS, KK, CFE) and one reader (JS), respectively, using the Cumulus software (Imaging Research Program, Sunnybrook Health Sciences Centre, University of Toronto, Toronto, Canada) with readers blinded to participants' information. For each study, mammograms were randomized into read sets of about 100 mammograms each with about 10% repeated within each read set, and mammograms repeated in read set 1 were repeated across every 5th read set to estimate reliability within and between read sets. For MCCS mammograms, the between reader reliabilities were 0.86 for DA and 0.99 for total breast area. For ABCFR mammograms, the within reader reliabilities were 0.97 for DA and 0.98 for total breast area. Since the reliabilities of MCCS were high we used the average measures of all three readers for the analyses.
Statistical analysis
The Box-Cox method (20) was used to identify the appropriate transformations to achieve approximate normal distributions; DA and PDA were transformed to (DA0.2-1)/0.2 and (PDA0.2-1)/0.2, respectively while NDA was transformed to (NDA0.4-1)/0.4. We have transformed the mammographic measures to ensure that the assumption of the mixed-effects model that the residuals have an approximately normal distribution is met.
Normalised variables, DA, PDA and NDA, were modelled as a function of age at mammogram. We considered five functions of age: 1) linear, 2) quadratic, 3) cubic, 4) logistic (with four parameters) and 5) Gompertz. The Gompertz function is described by four parameters: l, u, d and scale, example: Normalised DA = l + ((u - l)/exp(dexp(-scale(age-60)))), where age is the age at mammogram (centralised about the mean age at mammogram of 60 years), l is the lower asymptote approached as age decreases, u is the upper asymptote approached as age increases, d is the displacement along the age axis, scale is the rate of change in the measure, and d and scale are constrained to be positive.
The best fitting model, according to the Bayesian information criteria (BIC), was the Gompertz function (results not shown). Consequently, we fitted the Gompertz function to each measure using a mixed-effects model, allowing: (i) the asymptotes to vary across women (i.e. allowing random effects for the lower and upper asymptotes); and (ii) the between-women variances of the lower and upper asymptotes to be correlated (i.e. the random effects for the asymptotes were allowed to depend on each other). Random effects for d and scale were not estimated given the limited number of women with mammograms taken within the age range during which the change occurred.
BMI at time of mammogram was estimated by linear interpolation and extrapolation of BMI measures available at study entry and follow-ups. BMI and other covariates (menarche, parity, family history and study) were fitted as fixed effects to explain the woman-to-woman variation in both the asymptotes.
A sensitivity analysis was done by restricting analyses to controls only.
The within-individual correlation for measures taken 2, 4, 6, 8 and 10 years apart were defined as Correlation(u)=1-(Variogram(u))/σ2, where Variogram(u) is the average of the half-squared differences across all pairs of residuals corresponding to u, the time between mammograms, and σ2 is the variance (1).
Nonparametric bootstrapping was applied to obtain the 95% confidence interval (CI) for each within-individual correlation estimate. For each measure, we ran 1,115 bootstrap replicates for each model. The number of bootstrap replicates that converged for each model and the 95% CIs derived using the bootstrap percentile method are reported in Tables 2-4.
Lowess (i.e. smoothed) curves were fitted and visually compared to the fitted Gompertz curves derived from the mixed-effects models. Lowess curves (bandwidth, 0.5) were plotted based on smoothed y variables obtained by applying separate weighted regression for each point (xi, yi) in the data. In the weighted regression at each point, regression is based on the point of interest and several points around the main point by giving the highest weight to the point of interest and decreasing weights for the points that are further away based on their distance on the x axis to the point of interest (21).
Statistical analyses were performed using R 3.0.2 (R Foundation for Statistical Computing, Vienna, Austria) and Stata 12.1 (Stata Corporation, College Station, TX).
Results
Table 1 shows the characteristics of the study sample. The average ages at first and last mammogram were 55 years and 63 years, respectively. The average time interval between mammograms was 2.2 years (standard deviation (SD) = 1.0). The median time between the first and last mammogram was 8 years (SD = 5.0).
Table 1. Characteristics of participants in the study.
| Overall | MCCS | ABCFR | ||
|---|---|---|---|---|
| Number of women (number of mammograms) | 1064 (4714) | 846 (3951) | 218 (763) | |
| Number of mammograms per woman, median (range) | 4 (1-14) | 5 (1-10) | 3 (1-14) | |
| Number of women with one mammogram, N (%) | 141 (13) | 80 (9) | 61 (28) | |
| Mean (SD) | ||||
|
|
||||
| Time interval between mammograms, years | 2.2 (1.0) | 2.2 (0.8) | 2.2 (1.7) | |
| Age at first mammogram, years | 55.8 (9.8) | 58.9 (7.6) | 44.0 (8.3) | |
| Age at last mammogram, years | 63.4 (10.7) | 67.0 (7.8) | 49.4 (8.7) | |
| BMI at study entry, kg/m2 | 26.8 (5.1) | 27.5 (5.1) | 24.1 (4.3) | |
| BMI at first mammogram, kg/m2 | 27.0 (5.6) | 27.5 (5.1) | 24.8 (6.9) | |
| BMI at last mammogram, kg/m2 | 26.8 (5.1) | 27.5 (5.1) | 24.1 (4.3) | |
| Median (25th-75th percentile) | ||||
|
|
||||
| Time between first and last mammograms, years | 8.0 (5.0) | 8.4 (4.9) | 4.5 (4.8) | |
| At first mammogram: | ||||
| Dense area, cm2 | 14.7 (4.5-30.3) | 12.0 (3.3-26.7) | 25.0 (14.4-38.0) | |
| Nondense area, cm2 | 116.0 (77.6-161.1) | 122.6 (85.6-170.7) | 83.2 (57.6-132.7) | |
| Total area, cm2 | 135.3 (100.6-179.7) | 139.3 (107.8-187.7) | 118.0 (82.1-162.5) | |
| Percent density, % | 11.7 (3.0-26.1) | 8.7 (2.3-21.8) | 24.1 (12.3-34.7) | |
| At last mammogram: | ||||
| Dense area, cm2 | 12.1 (3.5-25.7) | 9.7 (2.8-21.7) | 23.6 (11.4-36.6) | |
| Nondense area, cm2 | 131.0 (91.0-178.2) | 138.7 (99.6-186.7) | 93.7 (60.0-139.0) | |
| Total area, cm2 | 148.3 (110.4-195.6) | 154.3 (118.1-200.9) | 123.6 (83.8-165.9) | |
| Percent density, % | 8.5 (2.4-20.4) | 6.7 (1.6-16.7) | 21.2 (8.7-31.4) | |
| Difference between first and last mammogram | ||||
| Dense area, cm2 | -0.7 (-6.0-0.6) | -0.9 (-5.5-0.4) | -0.4 (-8.1-2.9) | |
| Nondense area, cm2 | 11.2 (0-27.9) | 13.1 (0-30.4) | 0.7 (-4.4-18.7) | |
| Total area, cm2 | 8.5 (-1.2-24.4) | 10.3 (-0.4-26.8) | 0.0 (-4.5-13.4) | |
| Percent density, % | -0.9 (-6.1-0.1) | -1.0 (-5.3-0.1) | -0.5 (-9.6-2.3) | |
| N (%) | ||||
|
|
||||
| Case-Control statusa | Cases | 155 (15) | 149 (18) | 6 (3) |
| Controls | 909 (85) | 697 (82) | 212 (97) | |
| Menarche | ≤12 | 382 (36) | 311 (37) | 71 (33) |
| 13+ | 680 (64) | 533 (63) | 147 (67) | |
| Parity | Nulliparous | 120 (11) | 107 (13) | 13 (6) |
| Multiparous | 908 (85) | 739 (87) | 169 (78) | |
| Family history (number of women) | Yes | 318 (37) | 149 (22) | 169 (100) |
| No | 541 (63) | 541 (78) | 0 (0) | |
Case-control status of participants refer to the status at selection of the nested case-control MD study
Figure 1 shows that, for all three mammographic measures, the fitted Gompertz curve was close to the smoothed Lowess curve. Both DA and PDA had a similar change in pattern over time; estimated mean DA and PDA were constant up to about the early 40s, decreased thereafter and became constant again from about the mid 60s onwards. NDA had a reversed pattern compared with DA and PDA; estimated mean NDA was constant up to the mid 30s, increased thereafter and became constant again from the early 70s onwards.
Figure 1.
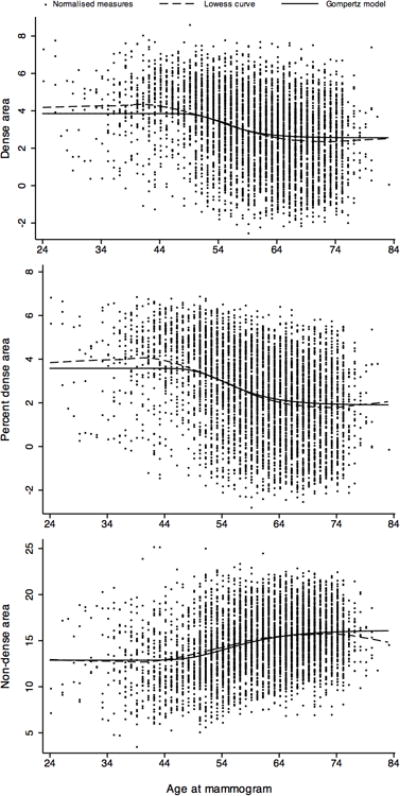
Normalised measures of dense area (DA), percent dense area (PDA) and non-dense area (NDA) as a function of age at mammogram showing the fitted Gompertz model and smoothed Lowess curve
Table 2 shows estimates of normalised DA from fitting the Gompertz model. After back transformation, the estimated mean DA was constant at 17 cm2 until the early 40s, decreased over the next two decades and slowly plateaued to almost a constant of about 8 cm2 from the mid 60s onwards. From the age of 44 to 64 years, mean DA decreased at 0.44 cm2/year and from the age of 65 to 83 years it decreased at 0.03 cm2/year. Mean DA at the younger (i.e. early 40s and younger) and older ages (i.e. older than 83) varied across women (SD for normalised DA lower and upper asymptotes = 2.0).
Table 2. Estimates of the Gompertz mixed-effects model corresponding to normalised dense area.
| Unadjusted model | Model adjusted for BMI | Fully adjusted Modela | |
|---|---|---|---|
|
|
|||
| 1064 women and 4714 mammograms | 970 women and 4320 mammograms | 859 women and 3847 mammograms | |
| Fixed effect, estimate (95% CI) | |||
| Lower asymptote (l) | 3.85 (3.69, 4.00) | 5.13 (4.66, 5.61) | 5.30 (4.58, 6.03) |
| Upper asymptote (u) | 2.56 (2.43, 2.69) | 3.11 (1.72, 3.49) | 3.52 (2.91, 4.13) |
| Displacement along the age axis | 0.27 (0.20, 0.33) | 0.26 (0.19, 0.33) | 0.29 (0.22, 0.37) |
| Scale | 0.24 (0.28, 0.20) | 0.25 (0.29, 0.21) | 0.25 (0.29, 0.21) |
| BMI, kg/m2 | |||
| lower asymptote | -0.05 (-0.07, -0.03) | -0.04 (-0.06, -0.02) | |
| upper asymptote | -0.02 (-0.03, -0.01) | -0.02 (-0.03, -0.003) | |
| Menarche (13+ vs ≤ 12) | |||
| lower asymptote | -0.11 (-0.44, 0.22) | ||
| upper asymptote | 0.23 (-0.07, 0.53) | ||
| Parity(1+ vs nulliparous) | |||
| lower asymptote | -0.78 (-1.26, -0.29) | ||
| upper asymptote | -0.82 (-1.28, -0.36) | ||
| Family history(Yes vs No) | |||
| lower asymptote | 0.68 (0.36, 1.01) | ||
| upper asymptote | 0.05 (-0.27, 0.37) | ||
| Random effect, estimate (95% CI) | |||
| SD(lower asymptote) | 1.98 (1.86, 2.11) | 1.90 (1.78, 2.03) | 1.91 (1.78, 2.05) |
| SD(upper asymptote) | 1.89 (1.79, 1.98) | 1.89 (1.79, 1.99) | 1.90 (1.79, 2.00) |
| Correlation(l, u) | 0.76 (0.69, 0.82) | 0.77 (0.69, 0.83) | 0.77 (0.69, 0.83) |
| Residuals, estimate (95% CI) | |||
| SD(Residual) | 0.55 (0.53, 0.56) | 0.55 (0.53, 0.56) | 0.55 (0.53, 0.56) |
| Correlation between mammograms taken within an individual woman (95% CI)b | |||
| 2 years apart | 0.94 (0.91, 0.94) | 0.94 (0.91, 0.94) | 0.94 (0.91, 0.94) |
| 4 years apart | 0.93 (0.90, 0.93) | 0.93 (0.89, 0.93) | 0.93 (0.89, 0.93) |
| 6 years apart | 0.92 (0.88, 0.93) | 0.91 (0.88, 0.92) | 0.92 (0.88, 0.93) |
| 8 years apart | 0.92 (0.88, 0.94) | 0.91 (0.88, 0.94) | 0.91 (0.87, 0.94) |
| 10 years apart | 0.91 (0.83, 0.95) | 0.91 (0.83, 0.95) | 0.91 (0.82, 0.95) |
Model is adjusted for BMI at each mammogram, age at menarche, parity and family history.
95% CIs are obtained using nonparametric bootstrapping. Number of bootstrap replicates that converged; 1030 for unadjusted model, 893 for model adjusted for BMI and 776 for fully adjusted model.
The correlation over time intervals between mammograms for normalised DA measures, adjusted for age, BMI and other confounders (menarche, parity and family history), was 0.94 (95% CI = 0.91 to 0.94) over 2 years and decreased slightly as the time between mammograms increased to be 0.91 (95% CI = 0.82 to 0.95) for mammograms taken 10 years apart.
BMI and being parous were negatively associated with DA asymptotes at the younger and older ages. Women with a family history of breast cancer had on average a slightly higher DA at younger ages (by an average of 2 cm2), though 92% of the mammograms before age 45 came from the ABCFR women and all had a family history of breast cancer.
The association of normalised PDA with age was similar to that above for DA (Table 3). Mean PDA was constant at 15% until age 40 years. From the age of 41 to 67 years, mean PDA decreased at a rate of 0.36%/year and from the age of 68 to 83 years it decreased at 0.03%/year. The correlation over time intervals between normalised and adjusted PDA measures decreased slightly as the time between mammograms increased and was 0.91 (95% CI = 0.80 to 0.95) for mammograms taken 10 years apart. Adjusting for BMI and the other confounders did not materially change the correlations. Higher BMI and parity were associated with lower PDA asymptotes at both the younger (i.e. 40 and younger) and older ages (i.e. older than 83). Later age at menarche was associated with a higher PDA asymptote at older ages and, similar to DA, women with family history had on average a higher PDA at younger ages.
Table 3. Estimates of the Gompertz mixed-effects model corresponding to normalised percent dense area.
| Unadjusted model | Model adjusted for BMI | Fully adjusted Modela | |
|---|---|---|---|
|
|
|||
| 1064 women and 4714 mammograms | 970 women and 4320 mammograms | 859 women and 3847 mammograms | |
| Fixed effect, estimate (95% CI) | |||
| Lower asymptote (l) | 3.58 (3.41, 3.74) | 5.82 (5.36, 6.28) | 5.93 (5.23, 6.64) |
| Upper asymptote (u) | 1.90 (1.76, 2.04) | 2.92 (2.53, 3.31) | 3.31 (2.71, 3.90) |
| Displacement along the age axis | 0.34 (0.28, 0.40) | 0.33 (0.27, 0.40) | 0.36 (0.29, 0.43) |
| Scale | 0.19 (0.22, 0.17) | 0.21 (0.24, 0.19) | 0.21 (0.25, 0.18) |
| BMI, kg/m2 | |||
| lower asymptote | -0.09 (-0.10, -0.07) | -0.08 (-0.09, -0.06) | |
| upper asymptote | -0.03 (-0.05, -0.02) | -0.03 (-0.05, -0.02) | |
| Menarche (13+ vs ≤ 12) | |||
| lower asymptote | -0.03 (-0.36, 0.29) | ||
| upper asymptote | 0.33 (0.05, 0.62) | ||
| Parity(1+ vs nulliparous) | |||
| lower asymptote | -0.82 (-1.29, -0.36) | ||
| upper asymptote | -0.87 (-1.31, -0.42) | ||
| Family history(Yes vs No) | |||
| lower asymptote | 0.71 (0.40, 1.02) | ||
| upper asymptote | 0.12 (-0.19, 0.44) | ||
| Random effect, estimate (95% CI) | |||
| SD(lower asymptote) | 2.06 (1.93, 2.20) | 1.87 (1.74, 2.00) | 1.86 (1.73, 2.00) |
| SD(upper asymptote) | 1.85 (1.75, 1.95) | 1.82 (1.72, 1.92) | 1.81 (1.71, 1.92) |
| Correlation(l, u) | 0.71 (0.64, 0.77) | 0.71 (0.63, 0.78) | 0.72 (0.64, 0.79) |
| Residuals, estimate (95% CI) | |||
| SD(Residual) | 0.52 (0.50, 0.53) | 0.52 (0.50, 0.53) | 0.52 (0.50, 0.53) |
| Correlation between mammograms taken within an individual woman (95% CI)b | |||
| 2 years apart | 0.94 (0.91, 0.94) | 0.94 (0.90, 0.93) | 0.94 (0.90, 0.93) |
| 4 years apart | 0.93 (0.90, 0.93) | 0.92 (0.88, 0.92) | 0.92 (0.88, 0.92) |
| 6 years apart | 0.92 (0.88, 0.93) | 0.91 (0.86, 0.92) | 0.91 (0.87, 0.92) |
| 8 years apart | 0.92 (0.89, 0.94) | 0.91 (0.87, 0.93) | 0.91 (0.87, 0.93) |
| 10 years apart | 0.91 (0.83, 0.95) | 0.90 (0.81, 0.94) | 0.91 (0.80, 0.95) |
Model is adjusted for BMI at each mammogram, age at menarche, parity and family history.
95% CIs are obtained using nonparametric bootstrapping. Number of bootstrap replicates that converged; 1036 for unadjusted model, 928 for model adjusted for BMI and 821 for fully adjusted model.
Figure 2 represents data for women who had the largest increase (> 17 %), largest decrease (> 35 %) and minimum change (0 to 0.01%) in PDA from their first to last mammograms. Only women with three mammograms or more were chosen. The figure shows the population mean curve and the individual predicted curve over time based on the fitted model. For these women, the individual predicted PDA measures over time based on the fitted model were close to the corresponding observed measures, regardless of a marked increase or decrease in PDA, or almost stable PDA.
Figure 2.
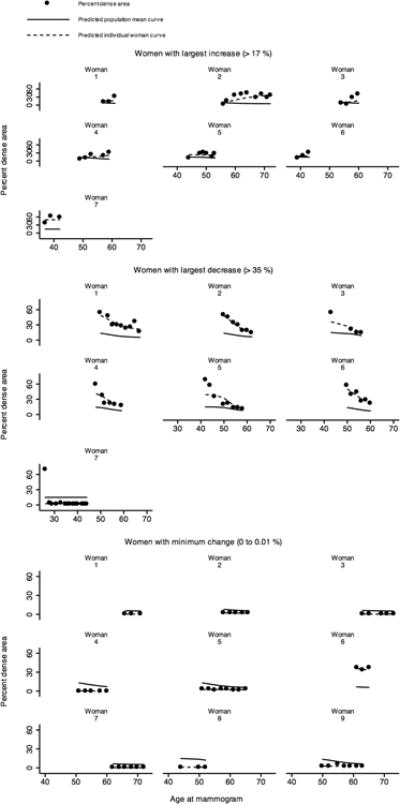
Observed, predicted population mean, and predicted individual percent dense area (PDA) as a function of age at mammogram for women with the largest increase (> 17%), largest decrease (> 35 %) and minimum change (0 to 0.01 %) in PDA from the first to the last mammogram and had 3 mammograms or more in total, plotted over the range of ages at mammograms relevant for each woman
For NDA, the pattern of association with age was generally in the opposite direction to that for DA and PDA (Table 4). Mean NDA was constant at 94 cm2 until 36 years of age, increased over the next four decades and slowly plateaued to be almost a constant of about 151 cm2 by the age of 84 years. From the age of 37 to 71 years, mean NDA increased at 1.54 cm2/year and from the age of 72 to 83 years it increased at 0.33 cm2/year. Mean NDA at the younger (i.e. mid 30s and younger) and older ages (i.e. older than 83) varied more than that of DA across women (SD for lower and upper asymptotes corresponding to normalised NDA: 3.54 and 3.19, respectively).
Table 4. Estimates of the Gompertz mixed-effects model corresponding to normalised non-dense area.
| Unadjusted model | Model adjusted for BMI | Modela | Modelb | |
|---|---|---|---|---|
|
|
||||
| 1064 w, 4714 m | 970 w, 4320 m | 859 w, 3847 m | 859 w, 3847 m | |
| Fixed effect, estimate (95% CI) | ||||
| Lower asymptote (l) | 12.88 (12.59, 13.16) | 7.82 (7.13, 8.51) | 7.64 (6.55, 8.73) | 7.57 (6.47, 8.67) |
| Upper asymptote (u) | 16.12 (15.87, 16.36) | 12.95 (12.31, 13.59) | 12.93 (11.96, 13.90) | 12.84 (11.87, 13.81) |
| Displacement along the age axis | 0.44 (0.38, 0.50) | 0.47 (0.40, 0.54) | 0.46 (0.39, 0.54) | 0.45 (0.38, 0.53) |
| Scale | 0.15 (0.16, 0.13) | 0.17 (0.19, 0.15) | 0.17 (0.19, 0.15) | 0.17 (0.19, 0.14) |
| BMI, kg/m2 | ||||
| lower asymptote | 0.20 (0.17, 0.22) | 0.19 (0.17, 0.22) | 0.20 (0.17, 0.22) | |
| upper asymptote | 0.11 (0.09, 0.13) | 0.11 (0.08, 0.13) | 0.11 (0.08, 0.13) | |
| Menarche (13+ vs ≤ 12) | ||||
| lower asymptote | -0.16 (-0.67, 0.34) | -0.17 (-0.68, 0.34) | ||
| upper asymptote | -0.68 (-1.14, -0.22) | -0.67 (-1.13, -0.21) | ||
| Parity (1+ vs nulliparous) | ||||
| lower asymptote | 0.71 (-0.03, 1.44) | 0.68 (-0.06, 1.42) | ||
| upper asymptote | 0.67 (-0.04, 1.39) | 0.76 (0.05, 1.48) | ||
| Family history(Yes vs No) | ||||
| lower asymptote | -0.41 (-0.91, 0.08) | -0.50 (-1.19, 0.19) | ||
| upper asymptote | -0.34 (-0.84, 0.16) | -0.03 (-0.60, 0.54) | ||
| Study(ABCFR vs MCCS) | ||||
| lower asymptote | 0.16 (-0.63, 0.94) | |||
| upper asymptote | -1.27 (-2.23, -0.30) | |||
| Random effect, estimate (95% CI) | ||||
| SD(lower asymptote) | 3.54 (3.34, 3.76) | 2.97 (2.79, 3.17) | 2.98 (2.78, 3.19) | 2.99 (2.79, 3.21) |
| SD(upper asymptote) | 3.19 (3.02, 3.38) | 2.88 (2.71, 3.07) | 2.86 (2.68, 3.05) | 2.84 (2.66, 3.04) |
| Correlation(l, u) | 0.67 (0.59, 0.73) | 0.67 (0.58, 0.74) | 0.68 (0.58, 0.75) | 0.70 (0.57, 0.75) |
| Residuals, estimate (95% CI) | ||||
| SD(Residual) | 0.75 (0.73, 0.77) | 0.75 (0.73, 0.77) | 0.75 (0.73, 0.77) | 0.75 (0.73, 0.77) |
| Correlation between mammograms taken within an individual woman (95% CI)c | ||||
| 2 years apart | 0.98 (0.97, 0.98) | 0.97 (0.96, 0.97) | 0.97 (0.96, 0.97) | 0.97 (0.96, 0.97) |
| 4 years apart | 0.98 (0.96, 0.98) | 0.97 (0.95, 0.97) | 0.97 (0.95, 0.97) | 0.97 (0.95, 0.97) |
| 6 years apart | 0.98 (0.97, 0.98) | 0.97 (0.96, 0.97) | 0.97 (0.96, 0.97) | 0.97 (0.96, 0.97) |
| 8 years apart | 0.98 (0.97, 0.98) | 0.97 (0.96, 0.97) | 0.97 (0.95, 0.97) | 0.97 (0.95, 0.97) |
| 10 years apart | 0.97 (0.94, 0.99) | 0.97 (0.93, 0.98) | 0.96 (0.93, 0.98) | 0.96 (0.93, 0.98) |
Model is adjusted for BMI at each mammogram, age at menarche, parity and family history.
Model is adjusted for BMI at each mammogram, age at menarche, parity, family history and study effect.
95% CIs are obtained using nonparametric bootstrapping. Number of bootstrap replicates that converged; 940 for unadjusted model, 641 for model adjusted for BMI, 410 for fully adjusted model and 305 for fully adjusted model including study effect.
The correlation over time intervals between mammograms for normalised NDA measures, adjusted for all the measured confounders, decreased slightly as the time between mammograms increased and was 0.96 (95% CI = 0.93 to 0.98) for mammograms taken 10 years apart.
BMI explained 30% and 18% of the variation across women in the NDA asymptotes at younger and older ages, respectively (SD for lower and upper asymptotes corresponding to normalised NDA dropped to 2.97 and 2.88, respectively, after adjusting for BMI). BMI was positively associated with the NDA asymptotes at the younger and older ages. Women whose age at menarche was earlier, and those who were parous, had higher NDA asymptotes at the older ages. There was no association between family history and NDA. Overall, the estimates of the parameters and the correlations over time intervals did not change considerably after adjusting for BMI and all the other confounders.
There was no evidence for heterogeneity of associations with age, or for correlations over time intervals, by study. Women in the ABCFR had lower NDA asymptotes at older ages than women in the MCCS. Restricting the analyses to controls did not change the results substantially.
Discussion
This study found that all of the three mammographic measures implicated in predicting breast cancer risk – DA, PDA and NDA adjusted for age and BMI - track strongly with age. The predicted correlations for mammograms taken 2 years apart were high, and the correlations attenuated only gradually as the time interval between measures increased, by about 0.4% per year, with correlations over 10 years intervals in excess of 0.9. If this rate of attenuation was maintained over 40 years, and under the Markov assumption that the changes over non-overlapping intervals are independent of one another, this would equate to a decrease of 15% to give a correlation in excess of 0.8 over that time interval. Given that the correlations do not differ across women of different ages, this means that the correlation between a woman's MD measures at age 30 and 70 years could be higher than the correlation between monozygotic twin pairs measured at the same time (22-24). This strong tracking raises the possibility that MD measures (adjusted for age and BMI) could be used to identify young adult women who are at increased absolute breast cancer risk in later life and subsequently offer risk-appropriate prevention and screening strategies that might reduce mortality.
Our mean MD measures are virtually constant with age up until the menopausal years. Previous studies of women from their 40s through to mid 60s and older have generally fitted a linear association. Figure 1 shows that, while this is not necessarily a poor description of the relationships over that age interval, the fitted straight line does not extrapolate well to younger (e.g. 40s or younger) or older (mid 60s or older) ages. Furthermore, this shape for the age relationship is unaltered after adjusting for BMI.
This is consistent with MD, as a breast cancer risk factor, being established at least by early adulthood. A cross-sectional study has shown that, after adjusting for age and BMI, other breast cancer risk factors explain little variance in the MD risk-predicting measures (24). These observations suggest that MD as a risk factor might not be consistent with the Pike's model of tissue ageing (9).
Strengths of our study are the inclusion of a substantial number of young women (74 women had at least one mammogram taken before age 40 years), the wide range in the ages of mammograms (24-83 years) and the high proportion of women with multiple mammograms (71% had three or more mammograms). Almost all the mammograms were craniocaudal views which means that NDA is a reliable measure of adipose tissue in the breast with minimal influence from body fat (4). There is also minimal chance of differences in mammographic measures due to laterality and view of the mammogram influencing the mammographic readings of each woman because, for all but four of the women, all mammograms were of the same breast and 99% of the mammograms were of CC view.
A limitation was that there were insufficient women with mammograms taken from the ages of 40s to 60s, the age range during which changes in MD occurred, to estimate random effects (or between-women variation) for d and scale. BMI was not available at the time of each mammogram so we assigned a value obtained from the linear interpolation/extrapolation of the measures available; this procedure was justified by the strong correlation of BMI with age: in MCCS, the spearman's rank correlation for BMI was 0.90 for measures taken at study entry and at the first follow-up 4 years later and 0.70 for measures taken at study entry and second follow-up occurring on average 11 years apart. In any case, any imprecision in interpolation/extrapolation would result in lower correlation estimates over time (i.e. weaker tracking), so the bias is if anything conservative. That is, if we had BMI measures at each mammogram the correlation estimates will only be higher. The mammogram machines may have varied over time and location, and this would only serve to weaken the correlations in mammographic measures of the breast over time. Therefore, the tracking could even be greater than we have estimated. The mammographic measures were also not adjusted for other potential variables that might have influenced the change in the measures, for example menopausal status and hormone replacement therapy. However, adjusting for these variables would likely make the tracking greater than observed.
Our results are consistent with a prospective Australian twin study (15) and a longitudinal UK study (9) that reported correlations of about 0.8 between the MD measures taken about 8 or 9 years apart. It has been speculated that the strong tracking with age may be because around 50% of the variance in MD and NDA appears to be explained by inherited genetic variants (22, 25, 26) that would have contributed to variation in MD measures before mid-life (15).
Most screening programs invite women from age 50 years onwards. Our data show that MD-based measures of risk track strongly with age, and from an age younger than when screening usually starts (such as before age 40 years). This has implications for etiologic research. It also raises the possibility that a mammogram taken early in adulthood could help identify women at increased risk of breast cancer later in life who might benefit from early prevention strategies or commencement of screening at a younger age.
Acknowledgments
We thank the Victorian Cancer Registry, BreastScreen Victoria and the Australian Mammographic Density Research Facility. K.K. is supported by the John and Allan Gilmour Research Award and May Stewart Bursary scholarships. J.L.H. is a Principal Research Fellow of the National Health and Medical Research Council. L.B. is supported by a Marie Curie International Incoming Fellowship within the 7th European Community Framework Programme. J.S. is supported by a Postdoctoral Research Fellowship from the National Breast Cancer Foundation.
Funding: The MCCS was supported by the Victorian Breast Cancer Research Consortium, the National Health and Medical Research Council (251533, 209057, and 504711), the Victorian Health Promotion Foundation and the National Breast Cancer Foundation and was further supported by infrastructure provided by the Cancer Council Victoria. The ABCFR was supported by grant UM1 CA164920 from the USA National Cancer Institute. The content of this manuscript does not necessarily reflect the views or policies of the National Cancer Institute or any of the collaborating centers in the Breast Cancer Family Registry (BCFR), nor does mention of trade names, commercial products, or organizations imply endorsement by the USA Government or the BCFR.
Footnotes
Conflict of interest: The authors declare that they have no conflict of interest.
References
- 1.Diggle JP, Heagerty P, Liang K, Zeger LS. Analysis of Longitudinal Data. 2nd. Oxford: Oxford University Press; 2002. [Google Scholar]
- 2.McCormack VA, dos Santos Silva I. Breast density and parenchymal patterns as markers of breast cancer risk: a meta-analysis. Cancer epidemiology, biomarkers & prevention : a publication of the American Association for Cancer Research, cosponsored by the American Society of Preventive Oncology. 2006;15:1159–69. doi: 10.1158/1055-9965.EPI-06-0034. [DOI] [PubMed] [Google Scholar]
- 3.Pettersson A, Graff RE, Ursin G, Santos Silva ID, McCormack V, Baglietto L, et al. Mammographic Density Phenotypes and Risk of Breast Cancer: A Meta-analysis. Journal of the National Cancer Institute. 2014;106 doi: 10.1093/jnci/dju078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Baglietto L, Krishnan K, Stone J, Apicella C, Southey MC, English DR, et al. Associations of mammographic dense and nondense areas and body mass index with risk of breast cancer. American journal of epidemiology. 2014;179:475–83. doi: 10.1093/aje/kwt260. [DOI] [PubMed] [Google Scholar]
- 5.Mariscotti G, Houssami N, Durando M, Bergamasco L, Campanino PP, Ruggieri C, et al. Accuracy of mammography, digital breast tomosynthesis, ultrasound and MR imaging in preoperative assessment of breast cancer. Anticancer research. 2014;34:1219–25. [PubMed] [Google Scholar]
- 6.Carney PA, Miglioretti DL, Yankaskas BC, Kerlikowske K, Rosenberg R, Rutter CM, et al. Individual and combined effects of age, breast density, and hormone replacement therapy use on the accuracy of screening mammography. Annals of internal medicine. 2003;138:168–75. doi: 10.7326/0003-4819-138-3-200302040-00008. [DOI] [PubMed] [Google Scholar]
- 7.Kerlikowske K, Grady D, Barclay J, Sickles EA, Ernster V. Effect of age, breast density, and family history on the sensitivity of first screening mammography. JAMA : the journal of the American Medical Association. 1996;276:33–8. [PubMed] [Google Scholar]
- 8.Kelemen LE, Pankratz VS, Sellers TA, Brandt KR, Wang A, Janney C, et al. Age-specific trends in mammographic density: the Minnesota Breast Cancer Family Study. American journal of epidemiology. 2008;167:1027–36. doi: 10.1093/aje/kwn063. [DOI] [PubMed] [Google Scholar]
- 9.McCormack VA, Perry NM, Vinnicombe SJ, Dos Santos Silva I. Changes and tracking of mammographic density in relation to Pike's model of breast tissue aging: a UK longitudinal study. International journal of cancer Journal international du cancer. 2010;127:452–61. doi: 10.1002/ijc.25053. [DOI] [PubMed] [Google Scholar]
- 10.Maskarinec G, Pagano I, Lurie G, Kolonel LN. A longitudinal investigation of mammographic density: the multiethnic cohort. Cancer epidemiology, biomarkers & prevention : a publication of the American Association for Cancer Research, cosponsored by the American Society of Preventive Oncology. 2006;15:732–9. doi: 10.1158/1055-9965.EPI-05-0798. [DOI] [PubMed] [Google Scholar]
- 11.Guthrie JR, Milne RL, Hopper JL, Cawson J, Dennerstein L, Burger HG. Menopause. Vol. 14. New York, NY: 2007. Mammographic densities during the menopausal transition: a longitudinal study of Australian-born women; pp. 208–15. [DOI] [PubMed] [Google Scholar]
- 12.Myles JP, Salmininen T, Duffy SW, Prevost TC, Day NE, Hakama M. Breast. Vol. 13. Edinburgh Scotland: 2004. Prospective estimation of rates of change in mammographic parenchymal patterns: influence of age and of hormone replacement therapy; pp. 56–60. [DOI] [PubMed] [Google Scholar]
- 13.Boyd N, Martin L, Stone J, Little L, Minkin S, Yaffe M. A longitudinal study of the effects of menopause on mammographic features. Cancer epidemiology, biomarkers & prevention : a publication of the American Association for Cancer Research, cosponsored by the American Society of Preventive Oncology. 2002;11:1048–53. [PubMed] [Google Scholar]
- 14.Reeves KW, Stone RA, Modugno F, Ness RB, Vogel VG, Weissfeld JL, et al. Longitudinal association of anthropometry with mammographic breast density in the Study of Women's Health Across the Nation. International journal of cancer Journal international du cancer. 2009;124:1169–77. doi: 10.1002/ijc.23996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Stone J, Dite GS, Giles GG, Cawson J, English DR, Hopper JL. Inference about causation from examination of familial confounding: application to longitudinal twin data on mammographic density measures that predict breast cancer risk. Cancer epidemiology, biomarkers & prevention : a publication of the American Association for Cancer Research, cosponsored by the American Society of Preventive Oncology. 2012;21:1149–55. doi: 10.1158/1055-9965.EPI-12-0051. [DOI] [PubMed] [Google Scholar]
- 16.Giles GG, English DR. The Melbourne Collaborative Cohort Study. IARC scientific publications. 2002;156:69–70. [PubMed] [Google Scholar]
- 17.Hopper JL, G G, McCredie MR, Boyle P. Breast. Vol. 3. Edinburgh Scotland: 1994. Background, rationale and protocol for a case-control-family study of breast cancer; pp. 79–86. [Google Scholar]
- 18.Hopper JL, Southey MC, Dite GS, Jolley DJ, Giles GG, McCredie MR, et al. Population-based estimate of the average age-specific cumulative risk of breast cancer for a defined set of protein-truncating mutations in BRCA1 and BRCA2. Australian Breast Cancer Family Study. Cancer epidemiology, biomarkers & prevention : a publication of the American Association for Cancer Research, cosponsored by the American Society of Preventive Oncology. 1999;8:741–7. [PubMed] [Google Scholar]
- 19.McCredie MR, Dite GS, Giles GG, Hopper JL. Breast cancer in Australian women under the age of 40. Cancer causes & control : CCC. 1998;9:189–98. doi: 10.1023/a:1008886328352. [DOI] [PubMed] [Google Scholar]
- 20.Box GEP, Cox DR. An Analysis of Transformations. Journal of the Royal Statistical Society Series B (Methodological) 1964;26:211–52. [Google Scholar]
- 21.Cleveland WS. Robust locally weighted regression and smoothing scatterplots. Journal of the American Statistical Association. 1979;74:829–36. [Google Scholar]
- 22.Boyd NF, Dite GS, Stone J, Gunasekara A, English DR, McCredie MR, et al. Heritability of mammographic density, a risk factor for breast cancer. The New England journal of medicine. 2002;347:886–94. doi: 10.1056/NEJMoa013390. [DOI] [PubMed] [Google Scholar]
- 23.Stone J, Dite GS, Gunasekara A, English DR, McCredie MR, Giles GG, et al. The heritability of mammographically dense and nondense breast tissue. Cancer epidemiology, biomarkers & prevention : a publication of the American Association for Cancer Research, cosponsored by the American Society of Preventive Oncology. 2006;15:612–7. doi: 10.1158/1055-9965.EPI-05-0127. [DOI] [PubMed] [Google Scholar]
- 24.Nguyen TL, Schmidt DF, Makalic E, Dite GS, Stone J, Apicella C, et al. Explaining variance in the cumulus mammographic measures that predict breast cancer risk: a twins and sisters study. Cancer epidemiology, biomarkers & prevention : a publication of the American Association for Cancer Research, cosponsored by the American Society of Preventive Oncology. 2013;22:2395–403. doi: 10.1158/1055-9965.EPI-13-0481. [DOI] [PubMed] [Google Scholar]
- 25.Ursin G, Lillie EO, Lee E, Cockburn M, Schork NJ, Cozen W, et al. The relative importance of genetics and environment on mammographic density. Cancer epidemiology, biomarkers & prevention : a publication of the American Association for Cancer Research, cosponsored by the American Society of Preventive Oncology. 2009;18:102–12. doi: 10.1158/1055-9965.EPI-07-2857. [DOI] [PubMed] [Google Scholar]
- 26.Sung J, Song YM, Stone J, Lee K, Jeong JI, Kim SS. Genetic influences on mammographic density in Korean twin and family: the Healthy Twin study. Breast cancer research and treatment. 2010;124:467–74. doi: 10.1007/s10549-010-0852-9. [DOI] [PubMed] [Google Scholar]


