Nonlinear effects of hyperpolarizing shifts in activation of mutant Na_v1.7 channels on resting membrane potential

Inherited erythromelalgia (IEM), the first human pain disorder linked to a sodium channel, is widely regarded as a genetic model of neuropathic pain. IEM is produced by Na_v1.7 mutations that hyperpolarize activation. These mutations produce a depolarization of resting membrane potential (RMP) in dorsal root ganglion neurons. Using dynamic clamp to explore the effect on RMP of the shift in activation, we demonstrate a nonlinear effect on RMP as the shift in activation voltage dependence becomes more hyperpolarized.

Abstract

The Na_v1.7 sodium channel is preferentially expressed within dorsal root ganglion (DRG) and sympathetic ganglion neurons. Gain-of-function mutations that cause the painful disorder inherited erythromelalgia (IEM) shift channel activation in a hyperpolarizing direction. When expressed within DRG neurons, these mutations produce a depolarization of resting membrane potential (RMP). The biophysical basis for the depolarized RMP has to date not been established. To explore the effect on RMP of the shift in activation associated with a prototypical IEM mutation (L858H), we used dynamic-clamp models that represent graded shifts that fractionate the effect of the mutation on activation voltage dependence. Dynamic-clamp recording from DRG neurons using a before-and-after protocol for each cell made it possible, even in the presence of cell-to-cell variation in starting RMP, to assess the effects of these graded mutant models. Our results demonstrate a nonlinear, progressively larger effect on RMP as the shift in activation voltage dependence becomes more hyperpolarized. The observed differences in RMP were predicted by the “late” current of each mutant model. Since the depolarization of RMP imposed by IEM mutant channels is known, in itself, to produce hyperexcitability of DRG neurons, the development of pharmacological agents that normalize or partially normalize activation voltage dependence of IEM mutant channels merits further study.

NEW & NOTEWORTHY Inherited erythromelalgia (IEM), the first human pain disorder linked to a sodium channel, is widely regarded as a genetic model of neuropathic pain. IEM is produced by Na_v1.7 mutations that hyperpolarize activation. These mutations produce a depolarization of resting membrane potential (RMP) in dorsal root ganglion neurons. Using dynamic clamp to explore the effect on RMP of the shift in activation, we demonstrate a nonlinear effect on RMP as the shift in activation voltage dependence becomes more hyperpolarized.

the na_v1.7 voltage-gated sodium channel, encoded by the SCN9A gene (Yang et al. 2004), is abundantly expressed in peripheral sensory (dorsal root ganglion; DRG) and sympathetic ganglion neurons (Persson et al. 2010; Rush et al. 2006, 2007). The biophysical properties of the Na_v1.7 channel allow it to activate at subthreshold membrane potentials and amplify small, slow-depolarizing stimuli (Ahn et al. 2013; Cummins et al. 1998; Herzog et al. 2003; Rush et al. 2007) and thus play a significant role in regulating sensory neuron excitability. Gain-of-function mutations of Na_v1.7 are known to cause inherited erythromelalgia (IEM), a painful syndrome in which intense sensations of burning of the hands and feet are precipitated by exposure to mild warmth (Cummins et al. 2004; Drenth and Waxman 2007; Rush et al. 2006; Waxman and Dib-Hajj 2005). The mutations causing IEM are notable in shifting activation in a hyperpolarizing direction (Cummins et al. 2004; Dib-Hajj et al. 2013).

Current-clamp studies have demonstrated that, when expressed within DRG neurons or sympathetic ganglion neurons, these IEM mutant channels depolarize resting membrane potential (RMP) and show that the depolarization of RMP, in itself, contributes substantially to altered excitability of these cells (Harty et al. 2006; Rush et al. 2006). To date, the mechanisms by which IEM mutant Na_v1.7 channels depolarize RMP have not been established. In this study, we wished to determine whether the hyperpolarizing shift of activation voltage dependence of an IEM mutant channel plays a role in determining RMP. One potential mechanism could be that hyperpolarizing shifts of activation voltage dependence could contribute to depolarizing RMP due to an increase of window current (Cregg et al. 2014; Frenz et al. 2014) as the overlap of the activation and fast-inactivation curves increases.

In this study we capitalized on recent advances that allow the elucidation of the contributions of an identified ion channel at all phases of neuronal activity via dynamic-clamp recording (Berecki et al. 2014; Chamorro et al. 2012; Clausen et al. 2013; Kullmann et al. 2004; Prinz et al. 2004; Sharp et al. 1993). Dynamic clamp employs a combination of hardware and software that can incorporate a computer model of the channel or channel variant of interest, calculate the current that the model would produce at each time point, and then apply that amount of current. A direct outcome of dynamic clamp is that the contribution of the modeled current can be directly measured as the current is added to, subtracted from, or altered within a single neuron, so that within-neuron comparisons can be made rather than neuron-to-neuron comparisons. When coupled to current-clamp recordings of DRG neurons, dynamic clamp can be used to document the hyperexcitability conferred by mutants of human Na_v1.7 channels (Ahn et al. 2013; Vasylyev et al. 2014) In addition to construction of models that faithfully reproduce actual ion channels, variants of actual ion channels can be constructed that explore parameter space in a systematic manner. To explore the effect on RMP of the shift in activation associated with a prototypical IEM Na_v1.7 mutation, we used dynamic-clamp models that represent variants of human (h)Na_v1.7 that fractionate the shift in activation voltage dependence produced by the L858H IEM Na_v1.7 mutation, which has been well studied by voltage clamp (Cummins et al. 2004) and current clamp (Rush et al. 2006). The starting points for this study were dynamic-clamp models for hNa_v1.7-wild-type (WT) and hNa_v1.7-L858H IEM mutant channels (Vasylyev et al. 2014). A previous study showed that the L858H model produces a depolarizing shift of RMP while the hNa_v1.7-WT model showed nearly no shift of RMP (Vasylyev et al. 2014). For the present study we constructed multiple additional dynamic-clamp models that have pure shifts of activation voltage dependence approximately equally spaced between hNa_v1.7-WT and hNa_v1.7-L858H values. Each of these models was implemented during dynamic-clamp recordings from DRG neurons. Dynamic-clamp recording, using a before-and-after protocol in each cell, made it possible, even in the presence of cell-to-cell variations in starting RMP, to assess the effects of these graded mutant models on RMP.

MATERIALS AND METHODS

Kinetic model of Na_v1.7 channel.

We developed our models of the Na_v1.7 channel and Na_v1.7 variant with Hodgkin-Huxley equations $\mathrm{d}\mathrm{m}\hspace{0.17em}\mathrm{/}\mathrm{d}\mathit{t}\mathrm{=}{\mathrm{\alpha }}_{\mathrm{m}}\mathrm{\left(}\mathrm{1}\mathrm{-}\mathrm{m}\mathrm{\right)}\mathrm{-}{\mathrm{\beta }}_{\mathrm{m}}\mathrm{m}$ and $\mathrm{d}\mathrm{h}\hspace{0.17em}\; /\mathrm{d}t={\alpha }_h\left(1-\mathrm{h}\right)-{\beta }_{\mathrm{h}}\mathrm{h}$, where m and h are channel activation and inactivation variables and α (β) are forward (backward) rate constants. Channel states were independent, with a first-order reaction between states. Thus channel activation and deactivation were considered as transitions between closed and open states, while channel inactivation and repriming were assumed to be transitions between primed and inactivated states, respectively. For models of WT and L858H mutant Na_v1.7 channels, steady-state parameters and kinetics obtained based on electrophysiological recordings were converted into appropriate rate constants at respective voltages with the following equations: $\alpha ={\mathrm{m}}_{\infty }\hspace{0.17em}\; /\tau$ and $\beta =(1-{\mathrm{m}}_{\infty })\; \hspace{0.17em}/\tau$. These reaction rate constants were fitted with Boltzmann equations of the form $y=A2+(A1-A2)\; \hspace{0.17em}/\left(1+\mathrm{e}\mathrm{x}\mathrm{p}\left[(V-V_{1/2})\; \hspace{0.17em}/k\right]\right)$, where V is membrane voltage, V_1/2 is voltage when reaction rate is half-maximal, and k is a slope coefficient. Fits were converted into steady-state inactivation (activation) variables and inactivation (activation) time constants according to the following equations: ${\mathrm{m}}_{\infty }=\alpha \hspace{0.17em}\; /\left(\alpha +\beta \right)$ and $\tau =1/\left(\alpha +\beta \right)$. The latter curves were overplayed on the experimental data to provide feedback to the rate constant fitting step. We obtained the following rate constants for the WT Na_v1.7 channel model as previously described (Vasylyev et al. 2014):

$${\alpha }_{\mathrm{m}}=10.22-10.22/\left(1+\mathrm{e}\mathrm{x}\mathrm{p}\left[\left(V+7.19\right)/15.43\right]\right),$$

$${\beta }_{\mathrm{m}}=23.76/(1+\mathrm{e}\mathrm{x}\mathrm{p}\left[\left(V+70.37\right)/14.53\right])\; ;$$

$${\alpha }_{\mathrm{h}}=0.0744/\left(1+\mathrm{e}\mathrm{x}\mathrm{p}\left[\left(V+99.76\right)/11.07\right]\right),$$

$${\beta }_{\mathrm{h}}=2.54-2.54/\left(1+\mathrm{e}\mathrm{x}\mathrm{p}\left[\left(V+7.8\right)/10.68\right]\right)$$

We modeled the L858H IEM Na_v1.7 mutation because it has been well studied at the voltage-clamp (Cummins et al. 2004) and current-clamp (Rush et al. 2006) levels and appeared to show a pure shift of activation with no alteration of inactivation. The L858H Na_v1.7 channel model was described by the following equations:

$${\alpha }_{\mathrm{m}}=9.1-9.1/(1+\mathrm{e}\mathrm{x}\mathrm{p}\left[\left(V+11.52\right)/22.49\right])\; ,$$

$${\beta }_{\mathrm{m}}=23.76/(1+\mathrm{e}\mathrm{x}\mathrm{p}\left[\left(V+87.6\right)/14.53\right])\; ;$$

$${\alpha }_{\mathrm{h}}=0.0744/(1+\mathrm{e}\mathrm{x}\mathrm{p}\left[\left(V+99.76\right)/11.07\right])\; ,$$

$${\beta }_{\mathrm{h}}=2.54-2.54/\left(1+\mathrm{e}\mathrm{x}\mathrm{p}\left[\left(V+7.8\right)/10.68\right]\right)$$

Sodium current was described by $I_{\mathrm{N}\mathrm{a}}=g_{\mathrm{m}\mathrm{a}\mathrm{x}}\hspace{0.17em}\; \times \; \hspace{0.17em}{m}^3\hspace{0.17em}\; \times \; \hspace{0.17em}h\hspace{0.17em}\; \times \; \hspace{0.17em}\left(V_{\mathrm{m}}-E_{\mathrm{N}\mathrm{a}}\right)$, where g_max is maximal conductance, V_m is membrane voltage, and E_Na = 65 mV is sodium reversal potential. Currents evoked by different voltage protocols were calculated at 10-μs precision with a custom program written in Origin8.5 LabTalk.

To generate Na_v1.7 models with approximately evenly spaced intermediate activation voltage dependence values, the hNa_v1.7-WT and hNa_v1.7-L858H models were adjusted to shift the voltage dependence of the m gate (α_m and β_m). These in silico models were run as simulations using LabTalk to create voltage-clamp activation sweeps, and the peaks were extracted and analyzed to determine the voltage dependence of the adjusted model. We constructed three additional models designated 25%-L858H, 50%-L858H, and 75%-L858H, which shifted activation approximately 25%, 50%, and 75% toward the L858H value. Each model was repeatedly adjusted to move the voltage dependence closer toward a target value until the models described below were obtained. The 25%-L858H model, as closest to the WT model, is a pure shift of the WT α_m and β_m values. The 75%-L858H model, as closest to the L858H model, is a pure shift of the L858H α_m and β_m values. The 50%-L858H model that transitions between the WT and L858H models was constructed by averaging all the α_m and β_m parameter values. All five models used identical α_h and β_h values. The values used for activation parameters of all five models are shown in Table 1.

Table 1.

Model activation parameters

	WT	25%-L858H	50%-L858H	75%-L858H	L858H
Kαm	10.22	10.22	9.66	9.10	9.10
Vαm	−7.19	−10.19	−9.36	−6.52	−11.52
Sαm	−15.43	−15.43	−18.22	−22.49	−22.49
Kβm	23.76	23.76	23.76	23.76	23.76
Vβm	−70.37	−73.37	−79.00	−82.60	−87.60
Sβm	14.53	14.53	14.53	14.53	14.53

${\mathrm{\alpha }}_{\mathrm{m}}\mathrm{=}{\mathrm{K}}_{\mathrm{\alpha }\mathrm{m}}\mathrm{-}{\mathrm{K}}_{\mathrm{\alpha }\mathrm{m}}\hspace{0.17em}\mathrm{/\; \hspace{0.17em}}\mathrm{\left(}\mathrm{1}\mathrm{+}\mathrm{e}\mathrm{x}\mathrm{p}\mathrm{\left[}\mathrm{(}\mathrm{V}\mathrm{+}{\mathrm{V}}_{\mathrm{\alpha }\mathrm{m}}\mathrm{)\; \hspace{0.17em}}\mathrm{/\; \hspace{0.17em}}{\mathrm{S}}_{\mathrm{\alpha }\mathrm{m}}\mathrm{\right]}\mathrm{\right)}$; ${\mathrm{\beta }}_{\mathrm{m}}\mathrm{=}{\mathrm{K}}_{\mathrm{\beta }\mathrm{m}}\hspace{0.17em}\mathrm{/\; \hspace{0.17em}}\mathrm{\left(}\mathrm{1}\mathrm{+}\mathrm{e}\mathrm{x}\mathrm{p}\mathrm{\left[}\mathrm{(}\mathrm{V}\mathrm{+}{\mathrm{V}}_{\mathrm{\beta }\mathrm{m}}\mathrm{)\; \hspace{0.17em}}\mathrm{/}{\mathrm{S}}_{\mathrm{\beta }\mathrm{m}}\mathrm{\right]}\mathrm{\right)}$.

All data are presented as means ± SE. Data were analyzed with pCLAMP 10 (Molecular Devices, Sunnyvale, CA) and Origin 8.5 (OriginLab, Northampton, MA) software.

Dynamic-clamp recording.

All animal experiments were approved by the Institutional Animal Care and Use Committee at the Department of Veterans Affairs Connecticut Healthcare System and conducted in accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals and the recommendations of the International Association for the Study of Pain.

DRG neurons with soma diameters between 20 and 25 μm obtained from neonatal P0–P5 Sprague-Dawley rats were dissociated and plated onto coverslips for use within 24 h (Ahn et al. 2013; Dib-Hajj et al. 2009). Small DRG neurons were dynamically clamped (Kemenes et al. 2011; Samu et al. 2012; Sharp et al. 1993) in whole cell configuration. Pipette resistance was 1.5–2 MΩ when filled with the intracellular solution (in mM): 140 KCl, 3 MgATP, 0.5 EGTA, 5 HEPES, 10 glucose, pH 7.3 with KOH (adjusted to 325 mosM with dextrose). The extracellular solution was (in mM) 140 NaCl, 3 KCl, 2 CaCl₂, 2 MgCl₂, 10 HEPES, pH 7.3 (adjusted to 325 mosM with dextrose). Liquid junction potential between pipette and bath solutions was not compensated. Membrane voltages and currents were recorded in dynamic clamp with a MultiClamp 700B amplifier (Molecular Devices, Sunnyvale, CA) interfaced with CED Power 1401 mk II DAI and Signal software (CED, Cambridge, UK), digitized by Digidata 1440A DAC, and stored on the hard disk using pCLAMP 10 software (Molecular Devices). Capacitance neutralization and bridge balance were employed to minimize the effect of electrode capacitance and series resistance on the dynamic-clamp recordings. Voltage and current traces were filtered at 10 kHz and digitized at 50 kHz. To compare the effects of the different models, equal conductances of each model were implemented and the level was chosen to match the average Na_v1.7 conductance of small DRG neurons (Vasylyev et al. 2014).

Recordings were made at room temperature (22–24°C). All data are presented as means ± SE. Data were analyzed with pCLAMP 10 (Molecular Devices), and Origin 8.5 (OriginLab) software. Unless specified otherwise, the hypothesis that population means are significantly different was checked by Mann-Whitney nonparametric test.

RESULTS

The dynamic clamp enables the functional testing of simulated conductances in real cells such as neurons. In many cases dynamic-clamp studies have utilized model conductances that faithfully mimic real channels such as our models of Na_v1.7-WT and Na_v1.7-L858H IEM mutant (Vasylyev et al. 2014). Dynamic clamp, however, provides the possibility to create artificial conductances with targeted biophysical properties, permitting evaluation of hypotheses that may not be possible with currently existing mutations. To determine whether there was a relationship between the size of the hyperpolarizing shift of activation voltage dependence and an observable shift of RMP in DRG neurons, we have utilized dynamic clamp to specifically compare artificial conductances with pure graded shifts of activation voltage dependence, comparing all these models in the same cells.

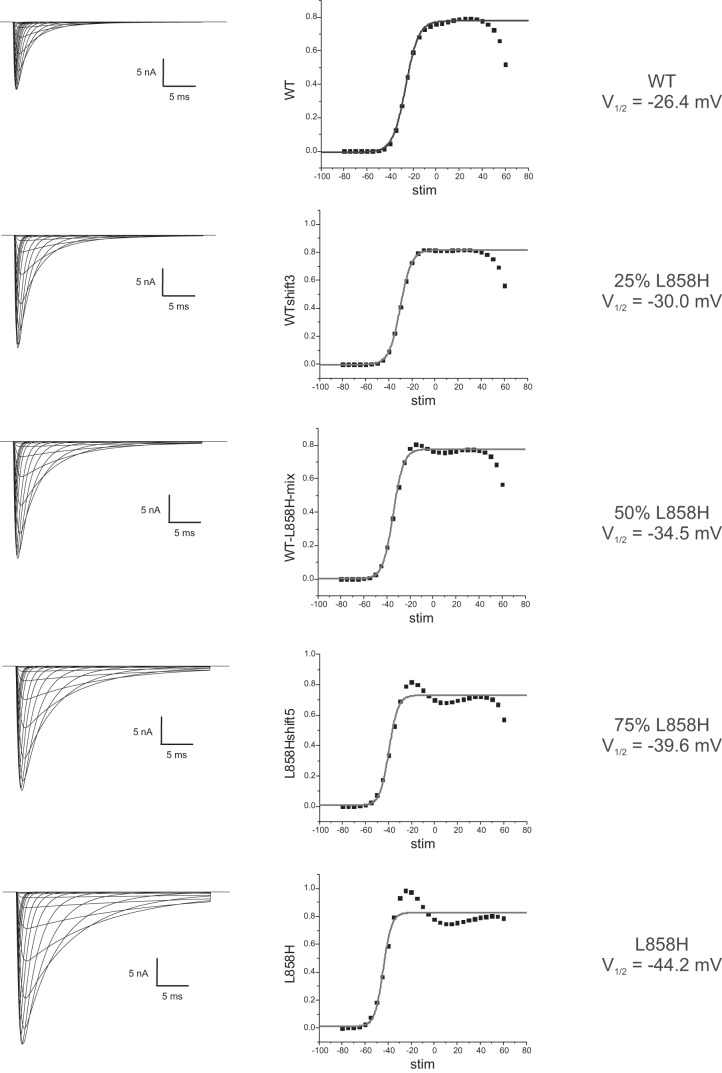
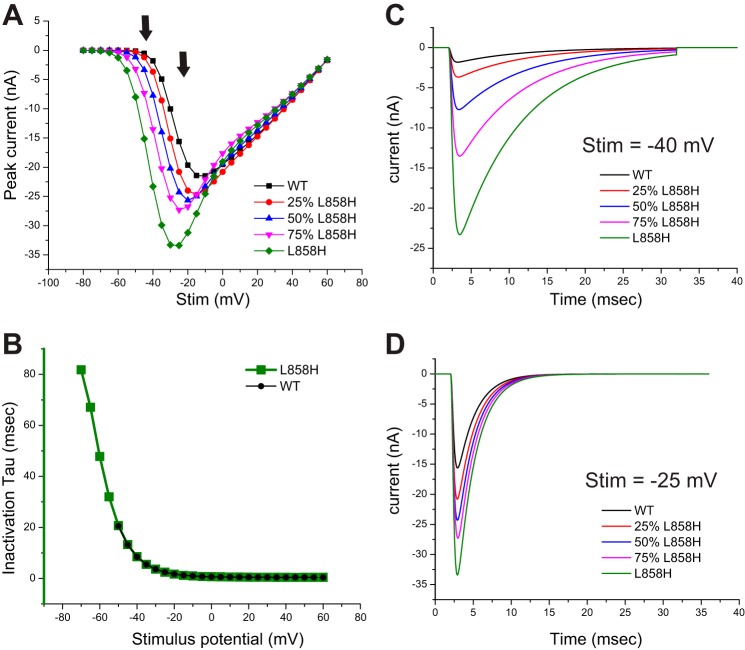
Since we had already created faithful models for Na_v1.7-WT and Na_v1.7-L858H, the present study only required the creation of artificial conductances that fill in intermediate values of activation voltage-dependence. As described in materials and methods, we created three additional conductances that represent Na_v1.7 channel variants with pure activation voltage dependence shifts spaced at ~4-mV increments. The simulated currents generated by the models evaluated in this study are illustrated in Fig. 1. The peak currents from each model were transformed into normalized conductance-voltage (G-V) values and then fit with a Boltzmann curve resulting in the activation V_1/2 parameters shown. The simulated traces in voltage clamp show typical inactivating inward currents. The scaling for all the models in Fig. 1 is the same, so it illustrates the trends that result from shifting activation voltage dependence. Shifting activation voltage dependence in a hyperpolarized direction results in a greater amount of peak current even though the total conductance specified was identical. The overlaid traces illustrated in Fig. 1 show an apparent gradual slowing of inactivation kinetics as the activation voltage dependence is shifted in the hyperpolarized direction. One likely contributor to this observation is that the hyperpolarized shifts of activation result in opening of a larger fraction of channels at membrane potentials at which the kinetics of inactivation are slower (Vasylyev et al. 2014). Consistent with this explanation, comparison of traces between models elicited with the same stimulus voltage, while varying in total peak current, still showed identical inactivation kinetics (Fig. 2B). We did observe that the various models showed increasing variations from the expected G_max plateau as activation was shifted toward the L858H values. In the I-V plots shown in Fig. 2A, it appears that each model converges to the same values as WT as the stimulation potential becomes strongly depolarized. Our models utilize the classical Hodgkin-Huxley formalism in which the activation and inactivation gates are independent, and since they all share the same inactivation gate parameters, this convergent behavior might be expected.

Fig. 1.

Simulated currents generated from the dynamic-clamp models used in this study. This figure illustrates traces obtained from each model in response to voltage steps from −80 mV to +50 mV in 5-mV increments from a starting potential of −120 mV. The simulations were set up with equal total conductances of each model, and the traces are plotted with identical axis scaling. The simulated traces were analyzed for peak inward currents, and the I-V data were transformed into normalized G-V data and plotted. The gray line represents a Boltzmann fit to the G-V data, and the midpoint of the fitted curve is shown for each model used in this study.

Fig. 2.

Overlay of traces from each model at selected stimulus values. This figure compares traces obtained from each model in response to selected stimulus values. A: the peak I-V curves generated from each model are plotted together to better illustrate the increased currents elicited in the stimulus range of −60 mV to −20 mV as the activation voltage dependence of each model was shifted. The arrows indicate the stimulus values chosen for sweep overlay comparisons. B: the inactivation kinetics were fitted with a single-exponential decay function, and the tau values derived from the Na_v1.7-WT and Na_v1.7-L858H model data are plotted. Fits were only performed on traces with at least 500 pA of peak current. C: traces computed from each model in response to a −40-mV stimulus are overlaid to illustrate that even though peak current is greatly increased, there is no difference in the inactivation kinetics for a shared stimulus potential. D: traces computed from each model in response to a −25-mV stimulus are overlaid. Again, even though there are differences in peak amplitude there is no difference in inactivation kinetics between the models.

After programming of the parameters that specify each of these models into the interface of the dynamic-clamp module of the Signal software, we systematically changed between each of the model conductances and reran the dynamic-clamp acquisition protocol while using the same neuron. To evaluate the effect of each model conductance on RMP, we created an acquisition protocol that acquired the membrane potential of the cell as well as the dynamic-clamp injected current for a period both before and after the active period of the dynamic-clamp amplifier. Example traces of a DRG neuron responding to addition of Na_v1.7-L858H conductance by dynamic clamp are illustrated in Fig. 3. The dynamic-clamp protocol runs 10 sweeps with an incrementing pulse to evaluate threshold for stimulated spiking, thus resulting in 10 repetitions of transitioning between before dynamic clamp (Pre) and during dynamic clamp (Post). Thus for each model, the change in RMP is the mean of 10 Pre and Post average membrane potentials as measured during the highlighted box regions (Fig. 3A). On occasion, and most likely when implementing the L858H model, the transition to active dynamic clamp resulted in the generation of spontaneous spiking, an example of which is illustrated in Fig. 3B. Model runs showing spontaneous activity were excluded from the analysis of shifts of RMP.

Fig. 3.

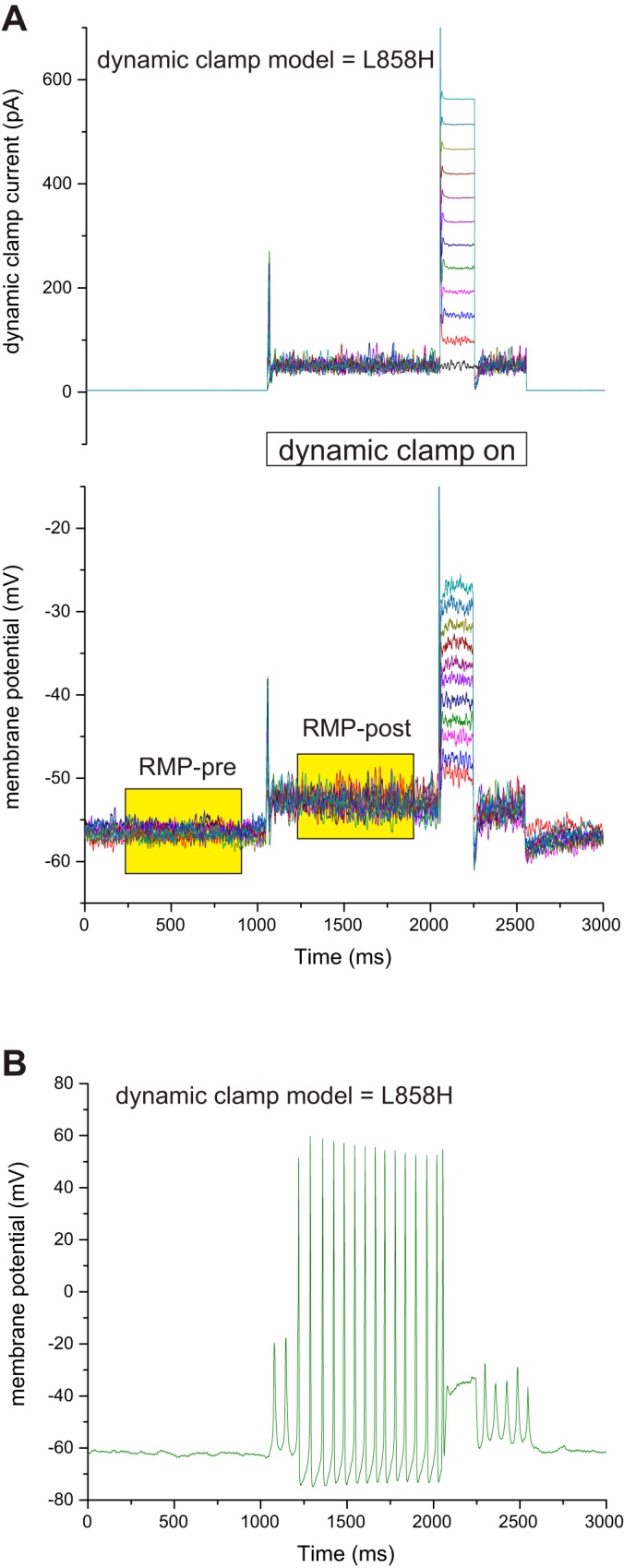
Measurement of change of RMP caused by turning on dynamic-clamp models. The dynamic-clamp models are implemented with a commercially available combination of CED Power 1401 mkII hardware and CED Signal software. The dynamic-clamp model is implemented during active data acquisition of the Signal software. To capture the transition of turning on the dynamic-clamp models, we used pCLAMP to acquire data both before and after triggering the data acquisition mode of Signal software. The protocol implemented in Signal software turns on the dynamic clamp for 1,000 ms before stimulating with an incrementing current injection pulse to evaluate threshold. The pCLAMP protocol passively records both the dynamic-clamp injected current as well as the cell’s membrane potential for a total of 3 s and triggers the Signal traces after a second of pre-dynamic clamp baseline. A: for each model, 10 sweeps of data are collected and each sweep is averaged for RMP both before and after dynamic clamp as illustrated by the yellow shaded boxes. Averaging over many hundreds of milliseconds filters out thermal fluctuations, and averaging over 10 repetitions reduces the influence of cellular fluctuations. B: in some cells the implementation of the L858H model caused the appearance of spontaneous spiking. Dynamic-clamp runs showing spontaneous spiking were removed from the analysis of shift of RMP.

Each run of a model generated an average RMP-Pre and RMP-Post, and thus the average change of RMP for a model measured using many different cells could be evaluated with paired t-test statistics. To compare between different models, the pair of numbers was transformed to a delta RMP that could then be compared with standard t-tests or other statistical tests as required. First we evaluated the relationship between the shift of RMP and the shift of activation voltage dependence for a series of added Na_v1.7 model conductances. Our results are plotted as a function of the activation V_1/2 of each model (Fig. 4A). The results show a progressively larger impact on RMP as the shift of activation voltage dependence becomes more hyperpolarized. In addition, we could replace the Na_v1.7-WT current with the Na_v1.7-mutant current by implementing two dynamic-clamp models in which the WT conductance is set negative to subtract the endogenous Na_v1.7 current and thus implement the mutant Na_v1.7 model in isolation (Fig. 4B). These results also showed a progressively larger impact on RMP as the shift of activation voltage dependence becomes more hyperpolarized.

Fig. 4.

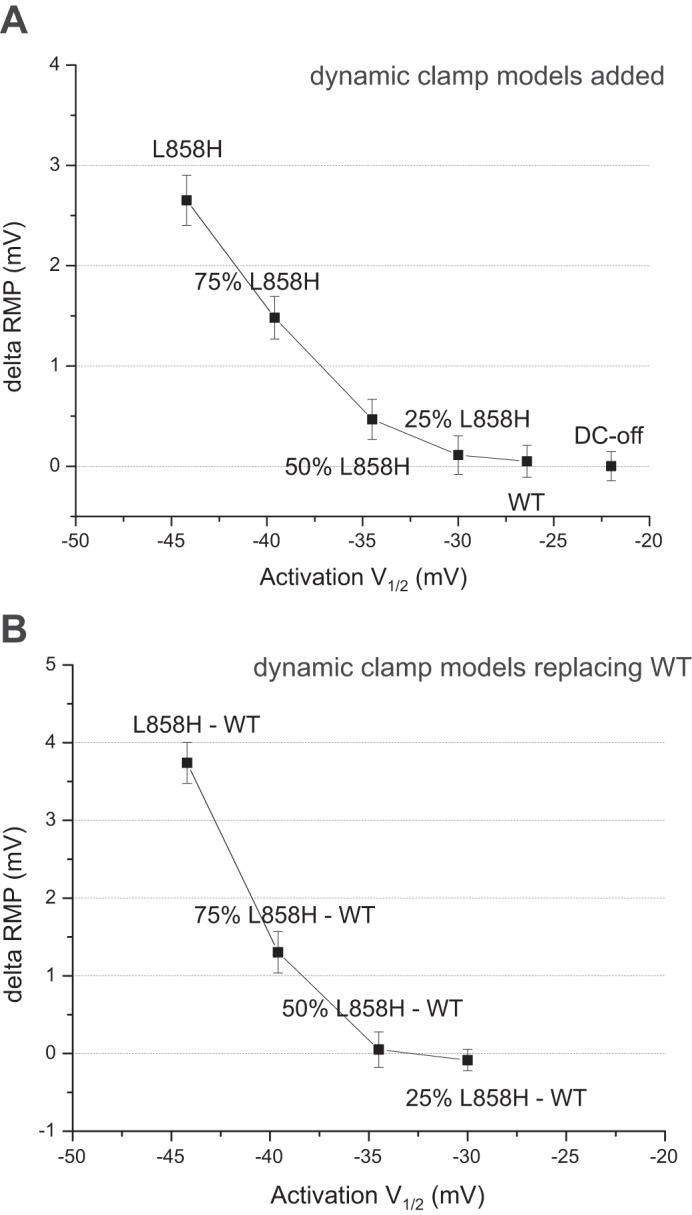
Shift of RMP observed by dynamic-clamp models. A: analysis of adding each dynamic-clamp conductance. To facilitate comparing the different dynamic-clamp models a fixed conductance was used, corresponding to an average reported conductance for small DRG neurons. The change of RMP was calculated, and the average results from many cells are plotted (n = 8–18). The average change of RMP is plotted as a function of the model’s activation V_1/2, which reveals a nonlinear relationship. B: analysis of replacing the WT-Na_v1.7 with mutant Na_v1.7. These data were obtained by implementing two models simultaneously and specifying a negative conductance for Na_v1.7-WT. As above, the data are averages from multiple cells (n = 4–8) and plotted using the mutant model’s activation V_1/2. Significance was evaluated by paired t-test.

One hypothesis for why hyperpolarizing shifts of activation voltage dependence result in progressively larger depolarizing shifts of RMP is that the predicted window current is increased as the activation voltage dependence is shifted. Figure 5A plots the activation and fast-inactivation G-V curves for the model conductances utilized in this study with the axes scaled to focus on the overlap regions. In the voltage range of typical RMP (between −55 mV and −60 mV) the overlap appears to get progressively larger. In addition, the window current hypothesis predicts that the size of the shift of RMP will depend upon the absolute value of the RMP-Pre, getting larger or smaller depending on the location of the RMP-Pre compared with the shape of the predicted window current. The actual size of the predicted window currents for each model was constructed by multiplying the activation and fast-inactivation G-V curves together and then scaling for total conductance and driving force to give the curves shown in Fig. 5B. To assess whether predicted window current underlies the shifts of RMP for each model, the measured dynamic-clamp currents for each model run, plotted as symbols using the same color scheme in Fig. 5B, were compared with the predicted values. As shown in Fig. 5B, the correspondence between the predicted lines and the observed data points, while showing similar trends, fell off at depolarized potentials.

Fig. 5.

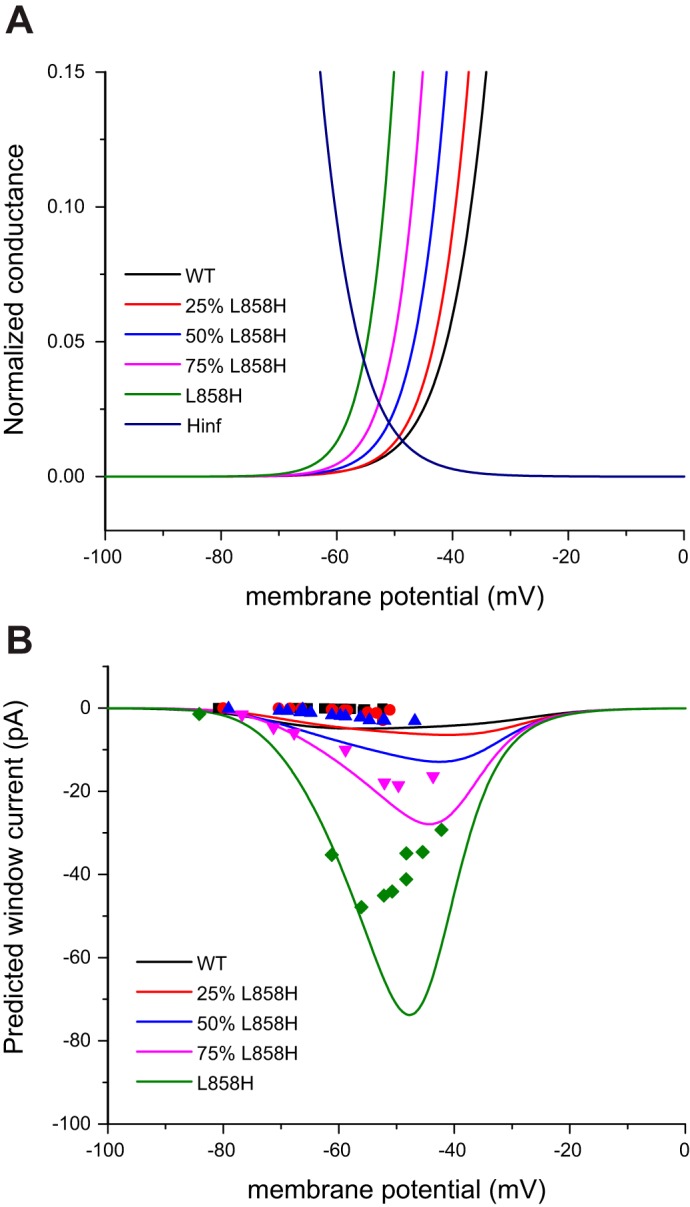
Observed RMP shifts for each model, as a function of starting RMP, are not predicted by window currents. A: activation and inactivation (Hinf) G-V curves for each of the dynamic-clamp models are overlaid and the axes scaled to focus on the “window current” regions. The crossing point of the activation and fast-inactivation curves shifts in the hyperpolarizing direction and occurs at an increased normalized conductance as the activation curves shift to the left. B: the predicted window currents for each model are obtained by calculating the combined conductance and then solving for current by scaling for total conductance and driving force. The “window current” hypothesis predicts that the magnitude of the current supplied by each model will vary as a function of the starting RMP. Symbols are plotted in the matching color and illustrate the dynamic-clamp currents generated by each model as a function of the starting RMP.

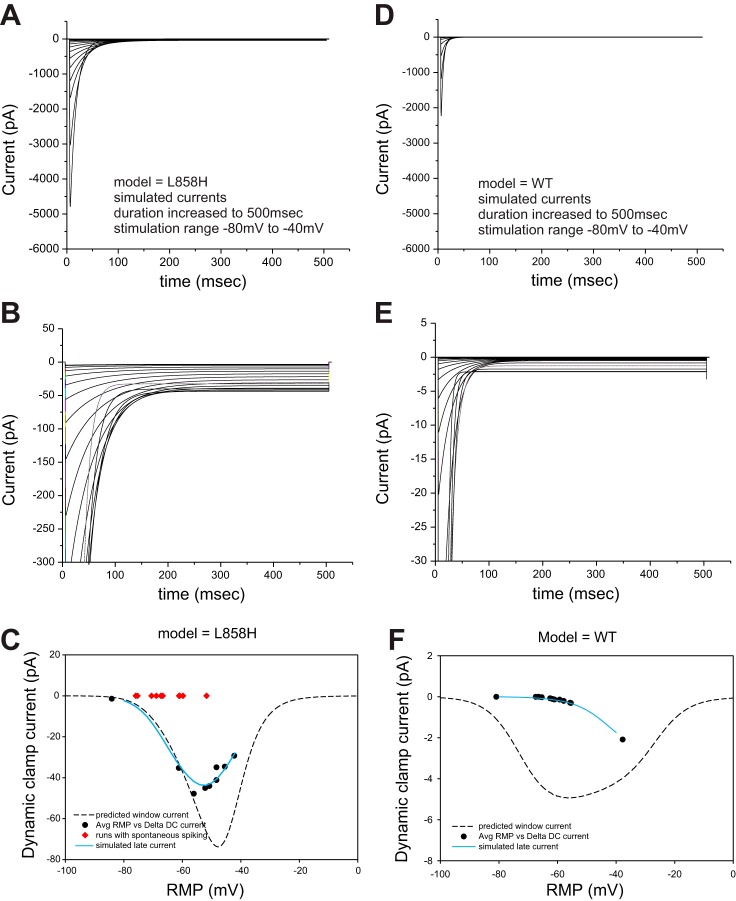
Because the activation and fast-inactivation G-V curves were constructed from peak responses, it might be expected that the predicted window currents might not reflect the steady-state equilibrium achieved by voltage-gated sodium currents in that particular voltage range. In fact, the apparent slowing of inactivation kinetics seen in the L858H model (Fig. 1, bottom) suggested an enhanced “late” or “persistent” current at voltages in the same range as predicted window current. Therefore an additional set of simulations of the L858H model in voltage-clamp mode were run in which the durations of the stimulation pulses were increased to 500 ms. Stimulation pulses of this duration were delivered from −80 mV to −40 mV in 2-mV increments to characterize in fine detail the behavior of our dynamic-clamp models in this voltage range. The traces generated from the L858H model are displayed in Fig. 6A and show typically inactivating sodium currents. As anticipated, expansion of the y-axis scaling (Fig. 6B) clearly demonstrates significant “late” current. The amount of late current as a function of stimulus voltage was determined from the final 100 ms of the simulated traces and plotted as a solid line in Fig. 6C; the predicted window current is also plotted as a dashed line. For comparison, the observed dynamic-clamp currents from each run of the L858H model from different cells are plotted. The dynamic-clamp currents track the “late” current line with very good fidelity.

Fig. 6.

The observed responses are better predicted by late current. A: the dynamic-clamp model for L858H was implemented with much longer pulse durations. Stimulation voltages examined span the subthreshold range of −80 mV to −40 mV. The currents showed clear late currents as displayed in B, where the y-axis is rescaled. The average late current of the last 100 ms is plotted as a solid line in C. For comparison, the predicted window current is plotted as a dashed line. The actual data obtained from dynamic-clamp runs in neurons are plotted with the black symbols showing the data from individual cells used for analysis and the red symbols showing cells not included because of spontaneous spiking. D–F show the same analysis using Na_v1.7-WT model and data. Note that the y-axis scaling is 10-fold lower compared with the L858H panels.

Even though the simulated traces of the Na_v1.7-WT model appear to inactivate completely, the WT model was also simulated for the longer durations over the stimulus voltage range of −80 mV to −40 mV. The WT traces are plotted in Fig. 6D and show typical inactivation behavior. Expansion of the y-axis in Fig. 6E, however, showed that even the WT model exhibits small but resolvable “late” current at certain stimulus voltage ranges. Note that the y-axis scaling for the WT model is 10-fold smaller than for the L858H model. In contrast to the L858H model, where the differences between the predicted window current and the simulated “late” current were within a factor of 2, the comparison of the predicted window current and simulated “late” current for the WT model shown in Fig. 6F shows very noticeable differences. When the observed dynamic-clamp data were plotted, there was nearly perfect correspondence with the “late” current curve and little correspondence to the predicted window current curve (Fig. 6C). The same analysis was also performed for the three intermediate models (data not shown), and all three again showed nearly perfect correspondence to the “late” current while the predicted window current curves poorly predicted the observed data.

The late current predicted by the dynamic-clamp models was nearly constant over the period of 200 ms to 500 ms and could arguably be defined as persistent current. We and others have examined sodium channel persistent current utilizing slow ramp protocols (Estacion and Waxman 2013; Fleidervish and Gutnick 1996; Kahlig et al. 2006). We recorded the responses to slow ramps starting at −100 mV to 20 mV over 600 ms (0.2 mV/ms ramp rate) from HEK cell lines stably expressing hNa_v1.7-WT or hNa_v1.7-L858H channels (Fig. 7A). When the dynamic-clamp currents recorded in response to activation of the L858H model on DRG neurons were scaled to approximately match the slow ramp traces, there was generally good correspondence between the two, especially in identifying the membrane potential range encompassing the greatest response. The dynamic-clamp currents recorded in response to activation of the hNa_v1.7-WT model also showed good correspondence after first scaling the same amount as the L858H model data and then scaling again to account for the difference in peak I-V relations between the WT and L858H models (Fig. 7A). To further demonstrate that the size of the dynamic clamp-induced shift of RMP depends upon the starting membrane potential, the dynamic-clamp responses were replotted assuming a fixed (shared) neuronal input resistance (Fig. 7B). The results suggest that the ramp current predicts, at any given starting membrane potential, the size of the depolarization produced by the mutant channel and that the resulting shift of RMP will peak at a similar voltage range as observed from a slow ramp recording.

Fig. 7.

Correspondence of late current to slow ramp current. A: traces represent currents recorded from HEK cells stably expressing either hNa_v1.7-WT (black line) or hNa_v1.7-L858H (green line) to a smoothly rising ramp protocol from −100 mV to +20 mV over 600 ms (0.2 mV/ms). The currents in response to this slow ramp protocol are normalized to the peak current measured from the I-V curve elicited by the cell. The dynamic-clamp hNa_v1.7-L858H model late current was transformed to approximately match the slow ramp trace and plotted with green squares. The dynamic-clamp hNa_v1.7-WT model late current was first scaled by the same amount as the L858H data and then further scaled to account for the smaller simulated peak I-V current compared with the L858H simulated peak I-V current (black squares). B: the shift of RMP predicted by the observed dynamic-clamp currents was calculated assuming an input resistance of 150 MΩ and plotted corresponding to the RMP observed just before activation of the dynamic clamp. Black symbols show hNa_v1.7-WT model data. and green symbols show hNa_v1.7-L858H model data.

DISCUSSION

In this study we examined the role that changes in activation voltage dependence play in modulating RMP of small-diameter DRG neurons. Our study was motivated by a growing number of variants of Na_v1.7 found in patients with the painful disorder IEM that have been shown by patch clamp to hyperpolarize activation voltage dependence (Dib-Hajj et al. 2008b, 2013; Estacion et al. 2008). Current-clamp studies show that these mutants depolarize neuronal resting potential (Han et al. 2012; Harty et al. 2006; Rush et al. 2006). Hyperpolarizing shifts of activation voltage dependence provide a biophysical substrate for an expanded predicted window current defined as the overlap region of the activation and fast-inactivation G-V curves. Window current defines a range of voltages that should support a sustained current through voltage-gated Na_v1.7 channels and thus modulate RMP. Utilizing dynamic clamp, we constructed models of Na_v1.7 that represent pure shifts of activation voltage dependence in graded increments between Na_v1.7-WT and Na_v1.7-L858H IEM mutant to directly test for an effect on small-diameter DRG neuron RMP. Using previously characterized dynamic-clamp models for hNa_v1.7-WT and Na_v1.7-L858H (Vasylyev et al. 2014) as starting points, we generated three additional dynamic-clamp models with shifted activation voltage dependence at ~25%-L858H, 50%-L858H, and 75%-of L858H values. Taken together, the inclusion of models that systematically explore changes in a single biophysical parameter in isolation illustrates the advantage of using dynamic clamp over comparing naturally occurring mutants that differ from each other in multiple biophysical parameters.

To quantify the impact of turning on each dynamic-clamp model, we utilized an independent data acquisition software that could capture the behavior of the DRG neuron both before and after the activation of the dynamic-clamp models. This before-and-after protocol made it possible to resolve statistically significant changes in RMP even in the presence of large variations of starting RMP. Here we report that both adding and replacing Na_v1.7-WT with our various dynamic-clamp Na_v1.7 models resulted in progressively larger shifts of RMP. Plots of the average shift of RMP as a function of the activation V_1/2 parameter for each model (Fig. 4) resulted in a relationship that is nonlinear and shows a progressively larger impact on RMP as the underlying shift of activation V_1/2 parameter shifts in the hyperpolarizing direction. Previous studies have reported mixed correlation between variants in Na_v1.7, with larger predicted window currents and an observed shift of RMP of DRG neurons expressing each variant (Ahn et al. 2013; Dib-Hajj et al. 2008b; Estacion et al. 2008; Faber et al. 2012). Based on the results reported here, the nonlinear impact of shifts of activation voltage dependence suggests that an activation voltage dependence shift of ~8 mV or greater may be required to significantly depolarize RMP. We have previously reported that Na_v1.7-Q10R with a 5-mV shift (Han et al. 2009) and Na_v1.7-S241T with an 8-mV shift (Yang et al. 2012) in activation, while showing a trend toward RMP depolarization, did not reach statistical significance. The Na_v1.7-S211P mutation with an 8-mV shift (Harty et al. 2006), however, did achieve a significant RMP depolarization. These multiple pain-associated variants, however, coexhibit additional biophysical properties such as fast and slow inactivation that were altered in addition to the voltage dependence of activation, which illustrates how difficult it is to tease out the contribution of any one biophysical parameter in isolation.

The dynamic-clamp method allowed a comparison of the effects of multiple mutant models in the same cell and thus circumvented the cell-to-cell variability that has previously been reported (Rizzo et al. 1994). This methodology revealed how the RMP changed and also captured the quantitative amount of current that each dynamic-clamp model injected to elicit the response. We also examined the voltage dependence of the actual amount of current injected by each model as a function of the RMP of each DRG neuron just before turning on the dynamic-clamp amplifier. If the window current hypothesis was correct, the amount of current that each dynamic-clamp model injected would be expected to depend upon the value of the RMP of the DRG neurons at the time that the dynamic-clamp model was activated (Fig. 5A). Since the activation and fast-inactivation G-V curves for each model were known and the total conductance was also known, the predicted window current could be calculated for each model and compared to actual currents injected into DRG neurons (Fig. 5B). Our results indicate that although the increasing window current predicted by each model qualitatively predicted a progressive impact on shifting RMP, the window current hypothesis did not quantitatively predict the RMP shifts observed. One possible source of the discrepancy could arise from construction of the activation and fast-inactivation G-V curves from peak responses while the shift of RMP represented steady-state behavior of the models (Agrawal et al. 2001; Estacion et al. 2008; Estacion and Waxman 2013).

We quantified the steady-state behavior of our dynamic-clamp models by running simulations with very long pulse durations and extracted the average “late” or “persistent” currents. In the absence of thermal noise, zooming in on the current axis clearly resolved an enhanced late current generated by the hNa_v1.7-L858H model compared with the hNa_v1.7-WT model (Fig. 6). Measured late current more closely matched the observed currents injected by the dynamic-clamp measurements in the DRG neurons for all five models. A commonly used protocol that uncovers late or persistent current in cells using a slow voltage-ramp stimulus in voltage-clamp mode (Estacion and Waxman 2013) revealed a good correspondence of both the relative amplitude and the voltage range between slow ramp responses measured from hNa_v1.7-WT- and -L858H-expressing cells with the dynamic-clamp currents generated by the hNa_v1.7-WT and -L858H models. This suggests that the shift of RMP will occur over a range of membrane potentials centered on the peak of the slow ramp response. In this study, we document that shifts of activation voltage dependence in our dynamic-clamp models both increased and shifted the steady-state current into the range typical of DRG neuron RMP. Consistent with earlier observations (Vasylyev et al. 2014), we found that the slow ramp peak of hNa_v1.7-WT channels is too depolarized and small to impact RMP whereas shifts of activation voltage dependence greater than ~8 mV result in a nonlinear progressively increasing depolarization of RMP as the peak slow ramp response is shifted in the hyperpolarized direction overlapping with the typical range of RMP in DRG neurons.

Since the underlying depolarizing current driving a shift of RMP is predicted by the slow ramp response, the resulting shift of RMP is not only dependent upon the total number of channels but also the starting RMP value and the input resistance at RMP. It can be expected that recordings from actual DRG neurons will show a variable range of RMP values and reduce the ability to achieve statistical significance to resolve smaller (<5 mV) shifts. In this study, the measured RMP shift to turning on the L858H model is also likely underestimated since some trials were excluded because of the generation of spontaneous spiking behavior. One corollary of this is that those trials showing spontaneous spiking had higher input resistance values and thus the underlying dynamic-clamp current resulted in depolarizations exceeding threshold. In our previous characterization of the Na_v1.7-L858H model by dynamic clamp, the DRG neurons did not show much spontaneous activity when the L858H model was applied and there was a shift of RMP up to 6 mV when the L858H model fully replaced the Na_v1.7-WT current (Vasylyev et al. 2014).

This study demonstrates that hyperpolarizing shifts of activation voltage dependence can modulate the RMP of DRG neurons in a nonlinear manner. Utilizing the advantages of the dynamic-clamp method, we could quantitate and compare the response to a series of models of hNa_v1.7, ranging from WT to the IEM mutant L858H, that change purely in terms of activation voltage dependence. This study found that the observed currents underlying the shifts of RMP arise from late or persistent currents. This study also documented that the observed persistent currents are only partially predicted by the window current derived from the overlap of the activation and fast-inactivation G-V curves but are more closely predicted by the slow ramp response. The ability of slow ramp current to contribute to RMP is also dependent upon the location along the voltage axis of the slow ramp peak. Thus simultaneous shifts of activation and fast inactivation can result in a larger window current and larger slow ramp current and yet for some mutations not result in a significant change of RMP (Dib-Hajj et al. 2008a; Estacion et al. 2008) since the peak of the slow ramp may be too far depolarized from DRG neuron RMP. Finally, we would note that a change of predicted window or slow ramp currents may not be the only biophysical parameter that can impact RMP. A number of variants of hNa_v1.7 that are associated with painful small-fiber neuropathy (Na_v1.7-I720K, Na_v1.7-D632N) exhibit only minor changes in the voltage dependence of activation and fast inactivation yet showed robust changes of RMP (Faber et al. 2012). A common biophysical change of those small-fiber neuropathy variants was an impairment of slow inactivation, allowing a greater fraction of channels to remain operable and contribute steady-state currents compared with hNa_v1.7-WT channels. Future studies utilizing the dynamic-clamp method will be needed to illuminate the relative contribution of each of the biophysical parameters found altered in pain-associated variants of voltage-gated sodium channels.

The results presented here demonstrate a nonlinear, progressively larger effect on RMP as the shift of Na_v1.7 activation voltage dependence becomes more hyperpolarized as a result of a prototypical IEM Na_v1.7 mutation and suggest that the differences in RMP are predicted by the “late” current of each mutant channel. It is now clear that the depolarization of RMP imposed by IEM mutant channels is, in itself, responsible for a substantial part of the hyperexcitability conferred on DRG neurons by these mutations. Thus the development of pharmacological agents that normalize activation voltage dependence of IEM mutant channels, as demonstrated in pharmacogenetic studies (Fischer et al. 2009; Yang et al. 2012), represents an additional approach to new drug development.

GRANTS

This work was supported in part by grants from the Rehabilitation Research Service and Medical Research Service, Department of Veterans Affairs to S. G. Waxman.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

M.E. and S.G.W. conceived and designed research; M.E. performed experiments; M.E. analyzed data; M.E. and S.G.W. interpreted results of experiments; M.E. prepared figures; M.E. drafted manuscript; M.E. and S.G.W. edited and revised manuscript; M.E. and S.G.W. approved final version of manuscript.