Determination of Original Infection Source of H7N9 Avian Influenza by Dynamical Model

Abstract

H7N9, a newly emerging virus in China, travels among poultry and human. Although H7N9 has not aroused massive outbreaks, recurrence in the second half of 2013 makes it essential to control the spread. It is believed that the most effective control measure is to locate the original infection source and cut off the source of infection from human. However, the original infection source and the internal transmission mechanism of the new virus are not totally clear. In order to determine the original infection source of H7N9, we establish a dynamical model with migratory bird, resident bird, domestic poultry and human population, and view migratory bird, resident bird, domestic poultry as original infection source respectively to fit the true dynamics during the 2013 pandemic. By comparing the date fitting results and corresponding Akaike Information Criterion (AIC) values, we conclude that migrant birds are most likely the original infection source. In addition, we obtain the basic reproduction number in poultry and carry out sensitivity analysis of some parameters.

In February 2013, a new type of avian influenza, H7N9, appeared in Mainland China. It was found in some kinds of domestic poultry, such as chickens, pigeons, and ducks¹,². In previous outbreaks of H7N9, it was only one of a subgroup of influenza viruses that normally circulated among birds. It is the first time that H7N9 virus begins to infect humans. H7N9 virus, as usually low pathogenic avian influenza virus which is not lethal among poultry, has become a highly pathogenic virus for the human species and can kill human beings who come in contact with birds or poultry carrying virus¹. That H7N9 virus transmissible between humans is scarce, since viruses tend to bind to the lower parts of the human lung¹.

The new type of influenza virus has propagated for more than one year since February 2013 in Yangtze River Delta region, including Shanghai, Anhui, Zhejiang and Jiangsu province. Yet, there is limited information about the scope of H7N9 influenza virus and the source of exposure. By analyzing gene sequences of H7N9 virus, it is known that the genes are primarily from East Asian duck origin, European wild duck and at least two H9N2 chicken viruses³,⁴,⁵,⁶, indicating that wild birds and domestic poultry are involved in the genetic reassortment of H7N9 virus. According to behavioral feature, wild birds can be divided into migratory and resident birds. The domestic poultry mainly refers to birds, chicken, geese, ducks, quail, pigeons in captivity and so on. Ríos-Soto⁷ pointed that mixing of bird populations plays an important role in the patterns of disease spread. The relationship between avian influenza outbreak and the migration of birds has also been discussed in detailed⁸,⁹. Chen et al.³ had determined that the virus isolated from the H7N9 patient was similar to that from a chicken in epidemiological live domestic poultry trading market where all kinds of domestic poultry are sold for human food. All viral gene segments of humans are of avian origin and the live poultry trading markets may be the direct source of infection of human bird influenza. However, for the prevalence of H7N9 virus in China, the original host species cannot be determined, which will transmit H7N9 virus to other host species by direct and indirect contact in coexistence environment. That is, original infection resource of H7N9 epidemic in China cannot be ascertained.

Robert and Juergen¹ pointed that animal and environmental scientists should turn to the following aspects: the identification of the original host species, its mode of transmission into intermediate host species including humans, and its ecology and survival in the environment. Locating the original infection source and cutting off the original infection from other species is the most effective control measure. Analysis of gene sequence only reveals that wild birds and domestic poultry participate in the formation and spread of H7N9 virus. Yet, which species would be the original host species of H7N9 virus is still under resolution. The purpose of this paper is to determine the original infection source of H7N9 influenza virus.

There have been lots of researches about avian influenza by various methods¹⁰,¹¹,¹². Dynamic method is an important tool in analyzing the epidemiological characteristics of infectious diseases, excavating internal transmission mechanism and assessing useful control measures. In this paper, we establish a dynamical model with migratory bird, resident bird, domestic poultry and human population to fit the true dynamics during the 2013 pandemic. Here, some assumptions in research are addressed. As is known to all, there is coexistence environment for migrant birds and resident birds, such as wetland, and for resident birds and domestic poultry, such as lakes¹³. So, interspecies transmission exists between either migrant birds and resident birds, or resident birds and domestic poultry, and there is no interspecies transmission between migrant birds and domestic poultry. Comparing with interspecies transmission, the role of intraspecies transmission is more important in epidemic spread. In order to distinguish the original infection source, it is assumed that if one of species is viewed as original infection source, it cannot be infected by other species, which can be interpreted as follows. Firstly, it is generally known that there exists a “host species barrier” between avian species which restricts the virus to only bind to a species¹⁴,¹⁵,¹⁶. Secondly, during the initial phase of the transmission of interspecies, the transfer of the influenza virus is generally unidirectional, from the original host species to others¹⁷. Thirdly, H7N9 virus that undergoes mutation and interspecies transmission may become more adapted to novel species and no longer adaptable to original species. If other species may transmit virus to the original host species and interspecies transmission rates are very small, it can be obtained that the original host species can only be located in wild birds (migrant birds or resident birds), which is shown in discussion section. The infection of human is only related to domestic poultry which transmit H7N9 virus to human by direct contact or by discharging virus to environment. For lack of solid evidence, human-to-human transmission of H7N9 is not considered here.

In the following sections, treating each kind of migratory bird, resident bird, domestic poultry as possible candidate of original infection source, three fitting results about H7N9 confirmed human cases and corresponding Akaike Information Criterion (AIC) values are obtained. By comparing these results, the most likely original host species is determined, and the most likely transmission situation is also given.

Results

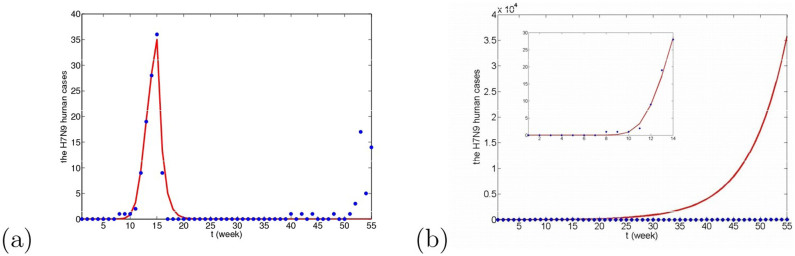
H7N9 human cases are first found in Shanghai and Anhui province, then the epidemic began to diffuse around. Most of the cases in China were confirmed in Shanghai, Anhui, Zhejiang and Jiangsu provinces, called “Yangtze River Delta region”. We apply the dynamical model (5) (see Method section) to fit the confirmed human cases in Yangtze River Delta region from January 1, 2013 to January 21, 2014 and take a week as the unit time, so the considered period is about 55 weeks. The unit of time is taken as a week. Due to lack of information about H7N9, some parameter values are unknown. So, before giving the fitting results, we need to carry out parameter estimation and further confirm the rationality of the range of parameter values.

Estimation of parameters

Apply the real situation and confirmed human cases to obtain parameter values in model (5).

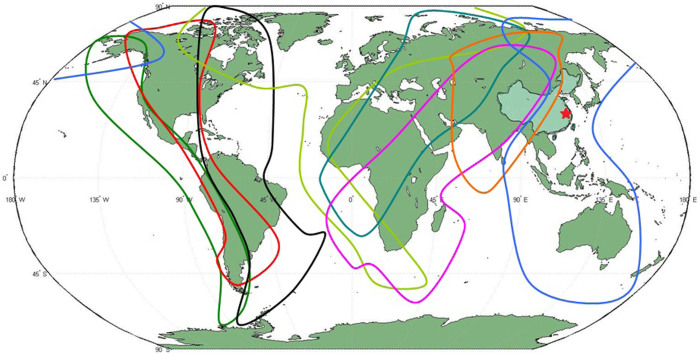
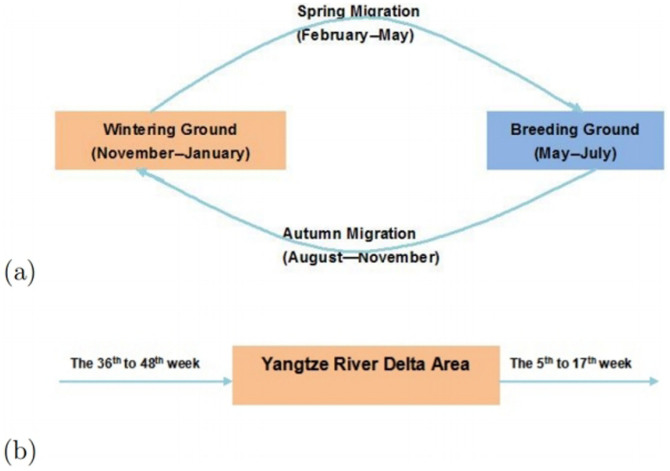
1. Parameters related to migrant birdsCurrently there are eight migratory routes for birds in the world¹⁹, see Fig. 1. Three of these routes pass through China: the west line (purple), the center line (orange) and the east line (blue). Among these three lines, the east route is closely related to the location of the 2013 outbreak of H7N9 bird flu, the Yangtze river delta area¹⁸ (the red star in Fig. 1). Due to bird migration, the behaviors of migrant birds among breeding, stopover and wintering grounds are different, see Fig. 2(a).The change of the number N_m(t) of migrant birds in Yangtze River Delta region can be described by the following differential equation.

   

   where A_m is the weekly immigration number and d_m is the weekly emigration number of migrant birds.To estimate d_m(t), assume the time of emigration obeys a normal distribution t ~ N(μ, σ²). From Fig. 2(b), the time of emigration in the Yangtze river delta area is from the 5th to the 17th week. It is easy to know that its peak time is the 11th week. Since there are 52 weeks in one year, the mean value μ of emigration time is 11 + 52 k, where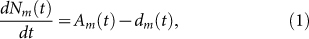 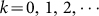. According to normal distribution diagram, the area in the range of the horizontal axis (μ − 3σ, μ + 3σ) accounts for 99.8% and the whole time of emigration of migrant birds in the Yangtze river delta area is about 12 weeks. So, 6σ = 12 and σ = 2. The time of immigration in the Yangtze river delta area is from the 36th to the 48th week. Similarly, the time of immigration obeys a normal distribution t ~ N(42 + 52 k, 2²), 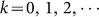. Therefore, A_m and d_m can be taken

   

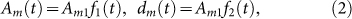
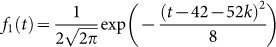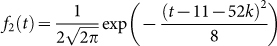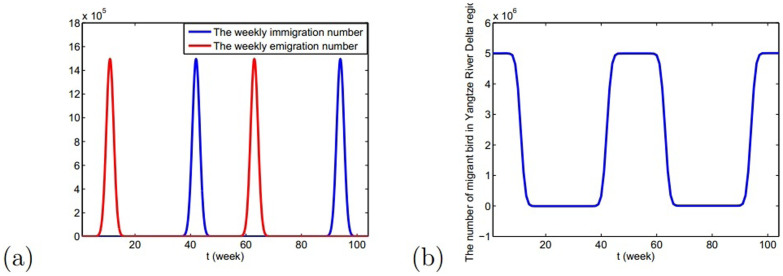
   where , , 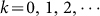and A_m1 is the annual number of migratory birds. Choose A_m1 = 5 × 10⁶, the medium value in Table 1(the description of parameters), the number of migrant birds can be seen in Fig. 3.
2. Parameters related to resident birdsSimilarly, the variation of the number of resident birds N_w(t) is

   

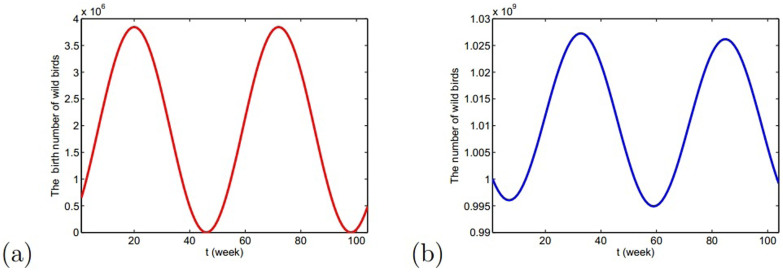
   where A_w(t) is the weekly birth number of resident birds and d_w is the weekly natural death rate. d_w is the reciprocal of the lifespan. Since the reproduction time of resident birds is cyclical and has only one peak time (about June) every year, the whole situation of weekly birth number is similar to the curve of sin function. So, the birth rate can be described by periodic function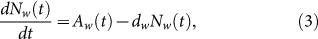 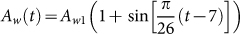. Choose A_w1 = 10⁹/520 and d_w = 1/520 from Table 1, we can show the birth number of resident birds in Fig. 4.

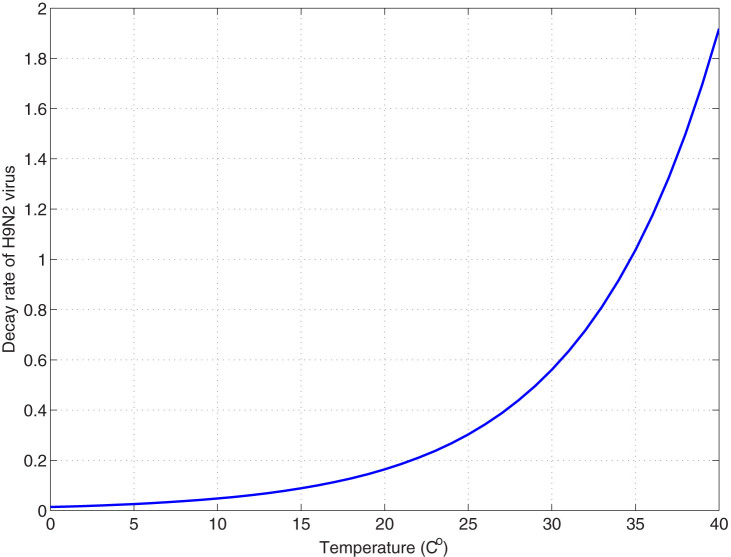
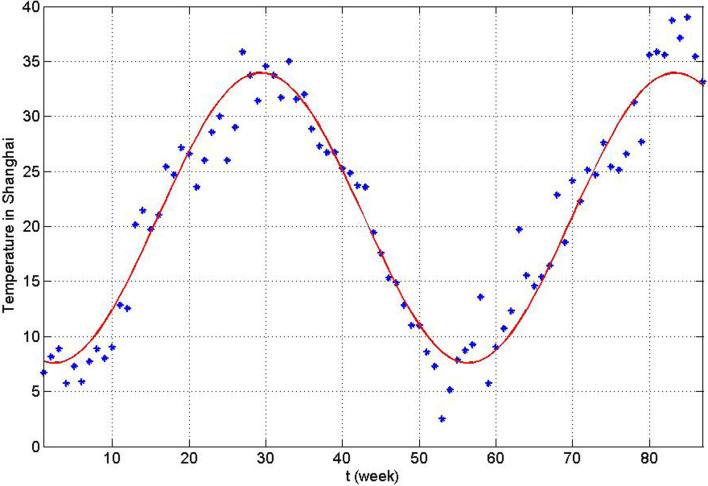
3. Parameters related to the decay rate of virus in the environmentIt is well known that the decay rate of most viruses depends on temperature: under different temperature, the influenza virus has different survival period. At high temperature, viruses may be more likely to die. Since dynamical model studies how the population evolves with time and the temperature is varying with time, we need to consider time-dependent decay rate δ(T(t)) of H7N9 virus. The change of the decay rate of influenza virus in the environment in term of temperature is described as δ(T) = α exp(γT)²⁰. Let α = 0.014, γ = 0.123, which is the situation of H9N2 virus²⁰, we can obtain Fig. 5. In addition, the change of temperature at Yangtze River Delta region with respect to time is periodic and can be described by a sine function. 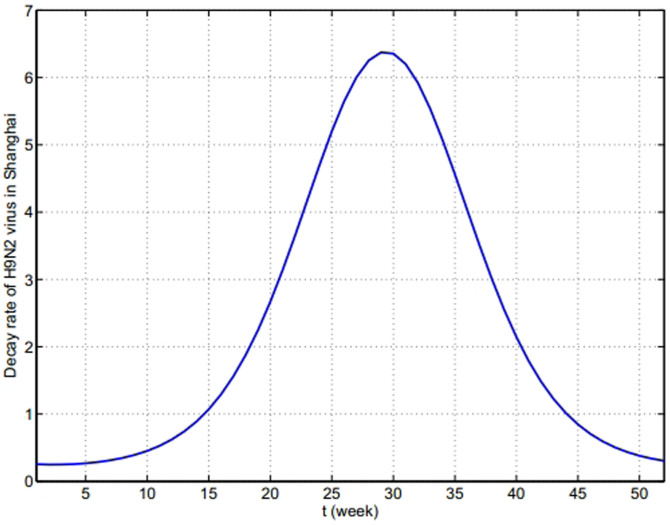Applying the least square fitting for the real historical temperatures in Yangtze River Delta region from related website, the sine function can be written as 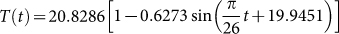, shown in Fig. 6. Combining Fig. 5 and Fig. 6, the general change of the decay rate of virus with time in Yangtze River Delta is portrayed in Fig. 7.

4. Other parametersNow, it is mainly to estimate confirmation rate p, transmission rates β_i and β_ij, i = m, w, p; j = m, w, p, h, in Table 1. The onset of the first human case was in February 19th, implying the epidemic had spread for a certain time in poultry before February. There is no any control measures to take until April 6(the 14th week). We apply data on the human cases from the first week to 14th week of 2013 to implement parameter estimation. Let Y(t) be theoretic confirmed human cases and 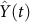be the actual reported confirmed human cases at week t. Then the least-square estimation is adopted here to find the parameter values to minimize the objective function

   

   where n is the number of reported data. This method is implemented by the command fminsearch, a part of the optimization toolbox in MATLAB. Combining model (5), Y (t) = X(t)− X(t−1),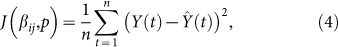 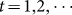, with Y(1) = X(1), where X(t) is the accumulated human cases and its change with time is described as 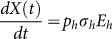. Viewing migrant birds, resident birds and domestic poultry as the original infection source, respectively, we obtain three estimation results as follows. The corresponding estimated parameter values and their corresponding Confidence Interval (CI) are given in Table 2.

Figure 1. The migration routes of migrant birds in all the world.

There are eight migratory routes for birds in the world. Three routes of them pass by China: purple line, orange line and blue line. Light green region represents China and Red star represents the location of H7N9 outbreak, which is the Yangtze river delta area. World map is drawn by Matlab R2009a. China map is drawn by ArcGIS 10. Lines and red star are added by Microsoft Office Word 2003.

Figure 2.

(a) The cycle of bird migration. (b) The migration time of birds in Yangtze river delta area. From November to January, migrant birds stay in wintering grounds. The northward migration of birds to breeding areas can be observed from February to April. From May to July, migrant birds stay in north areas to reproduce the next generation. From August to November, since the temperature in the northern region begins to decrease, migrant birds have to migrate to wintering grounds again. For Anseriformes related to H7N9 spread, Yangtze river delta area is the wintering ground. The time of emigration is from the 5th week to the 17th week and the time of immigration is from the 36th week to the 48th week.

Table 1. Description of parameters and variables in model (5).

Parameters	Value	Unit	Comments	resource
Am(t)		week−1	The immigration number of migratory bird
Am1	[3 × 106, 1 × 107]	year−1	The immigration number of migratory bird	Assumed
Aw1	[5 × 1010/520, 5 × 109/520]	week−1	The average birth number of resident bird.	Assumed
Ap	(1.0438 × 109)/8	week−1	The birth number of domestic fowl.	[a]
Ah	(2.269741 × 108)/70/52	week−1	The birth number of human.	24
dm(t)		week−1	The emigration rate of migratory bird.
dw	1/520	week−1	The natural mortality rate of resident bird.	[b]
dp	1/8	week−1	The sale rate of domestic fowl.	[c]
dh	1/70/52	week−1	The natural death rate of human.	[d]
βmm		week−1	Im(t)-to-Sm(t) transmission rate.
βm		week−1	Vm(t)-to-Sm(t) transmission rate.
βwm		week−1	Vw(t)-to-Sm(t) transmission rate.
βww		week−1	Iw(t)-to-Sw(t) transmission rate.
βw		week−1	Vw(t)-to-Sw(t) transmission rate.
βmw		week−1	Vm(t)-to-Sw(t) transmission rate.
βpw		week−1	Vp(t)-to-Sw(t) transmission rate.
βpp		week−1	Ip(t)-to-Sp(t) transmission rate.
βp		week−1	Vp(t)-to-Sp(t) transmission rate.
βwp		week−1	Vw(t)-to-Sp(t) transmission rate.
βph		week−1	Ip(t)-to-Sh(t) transmission rate.
βh		week−1	Vp(t)-to-Sh(t) transmission rate.
p		week−1	Confirmed rate of the infected population.
rm	[1, 10]	week−1	The discharging quantity of H7N9 virus by Im.	Assumed
rw	[1, 10]	week−1	The discharging quantity of H7N9 virus by Iw.	Assumed
rp	[1, 10]	week−1	The discharging quantity of H7N9 virus by Ip.	Assumed
δ(T(t))		week−1	The natural mortality rate of virus.
q	0.8 × 7	week−1	The effective disinfection rate.	[e]
σh	7/3.3	week−1	The reciprocal of the incubation period.	21
μh	0.36	week−1	The mortality rate of human caused by H7N9.	21
φm	[1/4, 2]	week−1	The recovery rate of migrant birds.	Assumed
φw	[1/4, 2]	week−1	The recovery rate of resident birds.	Assumed
φp	[1/4, 2]	week−1	The recovery rate of domestic poultry.	Assumed
φh		week−1	The recovery rate of human.
Sm(0)	Am1	individual	The initial number of the susceptible migratory bird.
Im(0)		individual	The initial number of the infective migratory bird.
Sw(0)	Aw1/dw	individual	The initial number of the susceptible resident bird.
Iw(0)		individual	The initial number of the infective resident bird.
Sp(0)	1.0483 × 109	individual	The initial number of the susceptible domestic fowl.	[a]
Ip(0)		individual	The initial number of the infective domestic fowl.
Sh(0)	2.269741 × 108	IU	The initial number of the susceptible human.	25
Eh(0)	0	individual	The initial number of the exposed human.
Ih(0)	0	individual	The initial number of the infected human.
Vm(0)	0	individual	The initial quantity of H7N9 virus in environment discharged by migrant birds.
Vw(0)	0	individual	The initial quantity of H7N9 virus in environment discharged by resident bird.
Vp(0)	0	individual	The initial quantity of H7N9 virus in environment discharged by poultry.

[a]The Laboratory of Animal Epidemiological Surveillance, China Animal Health & Epidemiology Center, Qingdao, Shandong, People's Republic of China.

[b]The lifetime of passerine birds, which will mature earlier, is only three or four years old. Large birds, such as eagle, eagle, etc., will need 8 to 11 years to arrive sexual maturity. In this paper, the average lifetime of resident birds is taken as 10 years.

[c]When domestic poultry grow to 8 weeks, they are the most flesh and will be sold by farmers. So, the sale coefficient is .

[d]d_h is the reciprocal of the lifetime of human and the lifetime of human is taken as 70 years.

[e]Assuming the effective disinfection rate in every disinfection is 80% and trading markets are disinfected every day, the disinfection rate every week is 7 × 0.8.

Figure 3.

(a) The number of emigration and immigration of migrant birds in Yangtze River Delta region in two years; (b) The number of migrant birds in Yangtze River Delta region with time in two years, where the starting time is the 1st week.

Figure 4.

(a) The birth number of resident birds during two years; (b) The number of resident birds during two years. The reproduction time of resident birds is generally from the 14th to the 26th week and the 20th week is the reproduction peak time, where the starting time is the 1st week.

Figure 5. The curve of temperature-dependent decay rate δ(T) = α exp(γT).

Figure 6. Temperature with time in Yangtze River Delta.

The blue dot is the real historical highest temperatures of Yangtze River Delta region from January 2012 to August 2013. The real line is the solution curve of the fitting function T(t).

Figure 7. The time-dependent decay rate δ(T(t)) with time in Yangtze River Delta in one year.

This figure starts from the 1st week.

Table 2. Values of estimated parameters and basic reproduction numbers in the fitting results from the 1st week to the 14th week.

Cases	p		β1		β2		R0
	mean value	CI	mean value	CI	mean value	CI	mean value	CI
I	0.0166	[0.0141, 0.0192]	4.505 × 10−10	[4.128 × 10−10, 4.882 × 10−10]	2.4645 × 10−15	[1.7581 × 10−15, 2.5649 × 10−15]	6.0185	[4.5965, 7.4435]
II	0.0228	[0.0149, 0.0308]	5.048 × 10−10	[4.565 × 10−10, 5.531 × 10−10]	6.5389 × 10−15	[0 × 10−15, 1.48923 × 10−14]	4.9407	[3.8712, 6.0101]
III	0.015	[0.0118, 0.0182]	7.755 × 10−10	[7.337 × 10−10, 8.174 × 10−10]	4.5531 × 10−15	[3.779 × 10−15, 5.3272 × 10−15]	4.11	[3.1832, 5.0368]

Case I. Viewing Migrant birds as the main original infectious source.

In this case, β_wm = 0. For simplicity, we choose β_m = β_mm = β_w = β_ww = β_mw = β_pw = β_p = β_pp = β_wp, denoted by β₁, and β_h = β_ph, denoted by β₂ to reduce the number of parameters. The corresponding fitting result is given in Fig. 8(a).

Figure 8. The fitting results under the three cases from the 1st week to the 14th week, where red dots are real confirmed human cases and the blue lines are solutions of our dynamical model under 50 times running.

(a) Case I, where I_w(0) ∈ [5, 500], I_m(0) = 0 and I_p(0) = 0; (b) Case II, where I_w(0) = 0, I_m(0) ∈ [5, 500] and I_p(0) = 0; (c) Case III, where I_w(0) = 0, I_m(0) = 0 and I_p(0) ∈ [5, 500]. Other parameter values can be seen in Table 2.

Case II. Viewing resident birds as the main original infectious source.

In this case, β_mw = β_pw = 0. In the same way, we choose β_m = β_mm = β_wm = β_w = β_ww = β_p = β_pp = β_wp, denoted by β₁, and β_h = β_ph, denoted by β₂. The corresponding fitting result is given in Fig. 8(b).

Case III. Viewing domestic poultry as the main original infectious source.

In this case, β_wp = 0. In the same way, we choose β_m = β_mm = β_wm = β_w = β_ww = β_mw = β_pw = β_p = β_pp, denoted by β₁, and β_h = β_ph, denoted by β₂. The corresponding fitting result is given in Fig. 8(c).

Fitting results

It is known that at the 14th week, three live poultry wholesale markets were closed and 111,122 live poultry were culled in Shanghai. Subsequently, the live poultry trading are partly suspended in Zhejiang, Jiangsu and Anhui province. During this closing period, all the markets were thoroughly disinfected. With the closure of trading markets, the epidemic has effectively been eased up. So, the corresponding control measures should be added into model. The transmission rates between domestic poultry and human, β_p, β_pp, β_wp, β_ph and β_h can reduce 93%²¹. However, closing markets is not a permanent solution, which had caused great economic loss. On June 19th (the 25th week), according to the press conference of Shanghai municipal government, the first batch of live poultry retail trading posts resumed business. At the same time, the trading markets in Jiangsu and Zhejiang province startes to work as well. Therefore, from the 25th week, the transmission rates are varied. However, after reopening trading markets, from November there appeared H7N9 human cases in Zhejiang province again. Thus, we investigate the H7N9 disease during a one-year period and predict the trend of the disease in the future, viewing different species as the original infection source in our model. The values of all parameters, A_m1, A_w1, q, r_m, r_w, r_p, φ_m, φ_w, φ_p, α, γ, I_w(0), I_m(0) and I_p(0), are fixed to be constants, see Table 3. Parameter values estimated can be seen in Tables 4. The fitting results corresponding to three cases can be seen in Figs. 9, 10 and 11.

Table 3. Values of parameters during fitting results.

Parameters	(FR I)	(FR II)	(FR III)
Im(0)	250	0	0
Iw(0)	0	250	0
Ip(0)	0	0	250
Am1		5 × 106
Aw1		1 × 109/520
rm		5
rw		5
rp		5
φm		1
φw		1
φp		1

Table 4. Values of parameters and the basic reproduction during fitting results.

	Before closing markets			After closing markets			After reopening markets
Parameters	Case I	Case II	Case III	Case I	Case II	Case III	Case I	Case II	Case III
p	0.0144	0.0259	0.0115	2.75 × 0.0144	2.65 × 0.0259	2.5 × 0.0159	2.75 × 0.0144	2.65 × 0.0259	2.5 × 0.0159
β1	4.545 × 10−10	5.653 × 10−10	6.805 × 10−10	7/100 × 4.545 × 10−10	7/100 × 5.653 × 10−10	7/100 × 6.85 × 10−10	10/100 × 4.545 × 10−10	10/100 × 5.653 × 10−10	6.85 × 10−10
β2	1.5954 × 10−15	9.934 × 10−16	2.2064 × 10−15	7/100 × 1.5954 × 10−15	7/100 × 9.934 × 10−16	7/100 × 2.2064 × 10−15	60/100 × 1.5954 × 10−15	60/100 × 9.934 × 10−16	2.2064 × 10−15
q		0			0.8 × 7			0.8 × 7

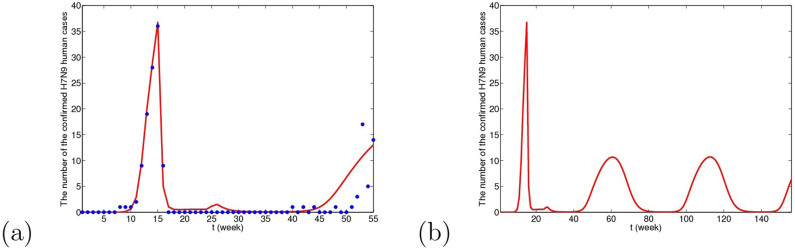
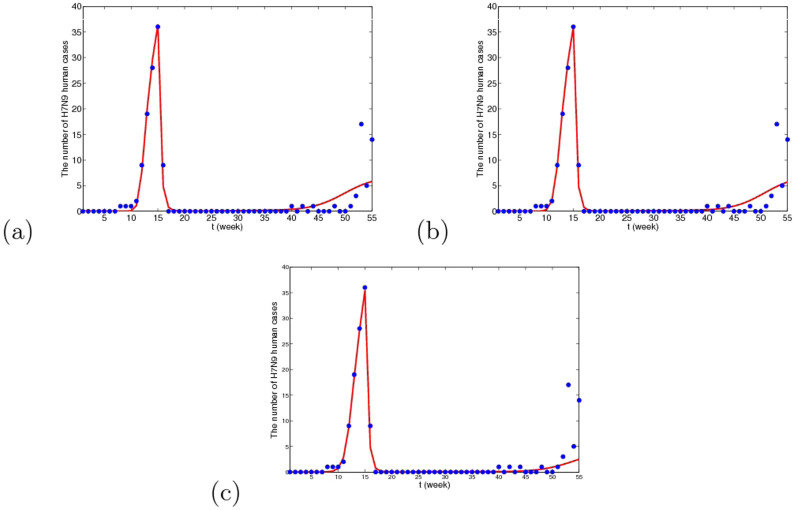
Figure 9. The simulative confirmed H7N9 human cases with time in Yangtze River Delta when migrant birds are viewed as the original source.

(a) The fitting result from the 1st week in 2013 to the 3rd week in 2014, where blue dots are reported confirmed human cases and the red line is solution of the dynamical model. (b) The prediction result for the next 2 years. It can be predicted that in winter and the next spring, there will be reappearance of H7N9 human cases and the peak time will be 61st week. The whole situation will not be very serious and the human cases will be cyclic occurrence.

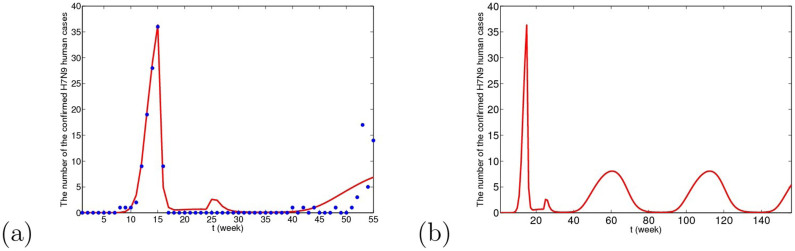
Figure 10. The simulative confirmed H7N9 human cases with time in Yangtze River Delta when resident birds are viewed as the original source.

(a) The fitting result from the 1st week in 2013 to the 3rd week in 2014, where blue dots are reported confirmed human cases and the red line is solution of the dynamical model. (b) The prediction result for the next 2 years. The predicted result is similar to Case I.

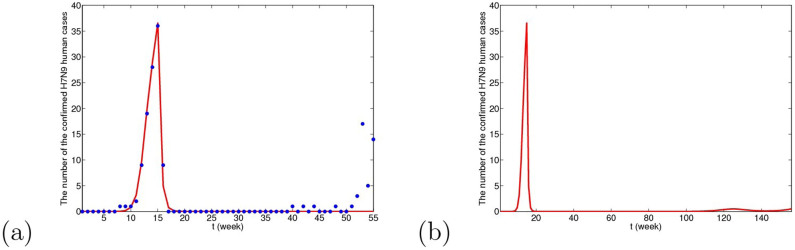
Figure 11. The simulative confirmed H7N9 human cases with time in Yangtze River Delta when domestic poultry are viewed as the original source.

(a) The fitting result from the 1st week in 2013 to the 3rd week in 2014, where blue dots are reported confirmed human cases and the red line is solution of the dynamical model. (b) The prediction result for the next 2 years. Under this case, the human cases will almost disappear and there may be several human cases occasionally after two or three year.

From Figs. 9, 10 and 11, we can conclude that in three cases, there is no obvious difference in the short-term fitting results. However, after undergoing closing live poultry trading markets and culling measure, the situations of epidemics among human under the three cases have some differences. According to the current situation, when the migrant birds or resident birds are the original infection source, there will reappear human cases in winter and next spring. Nevertheless, if the domestic poultry is the original source, the epidemic does not appear again in two years, even if the transmission rates returns to former levels before closing markets.

Akaike's information criterion values

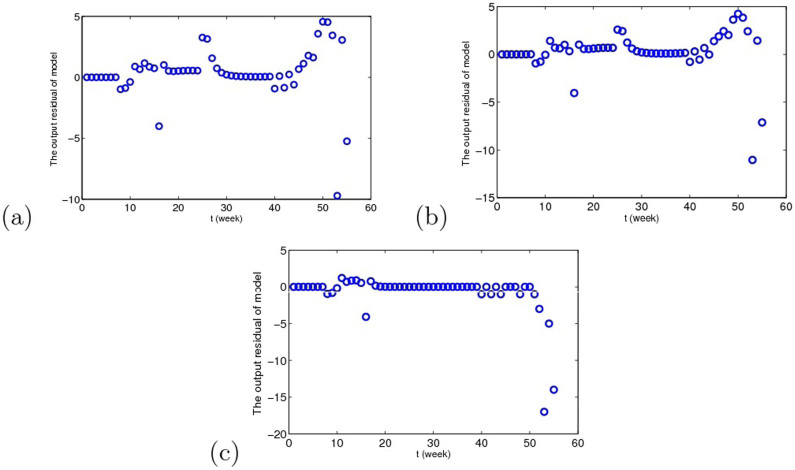
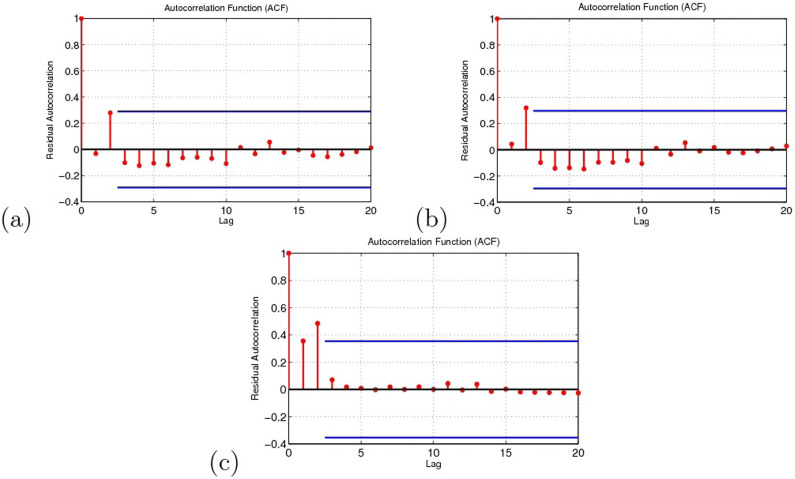
In order to check the adequacy of the model, we take a look at the residuals between theoretic and the real data under three cases, see Fig. 12, and autocorrelations of residuals are shown in Fig. 13. In Fig. 13, the areas between the two blue lines on the plots represent the regions within which residuals correlation are non-significant at the 95% level. Therefore, it is reasonable to conclude that the residuals are not correlated, which illustrates that we can apply Akaike's information criterion to compare the validity of the three results.

Figure 12. The residuals between theoretic and the real data under the three cases.

(a) Migrant birds as the original infection source. (b) Resident birds as the original infection source. (c) Domestic poultry as the original infection source.

Figure 13. The residual autocorrelations under the three cases.

(a) Migrant birds as the original infection source. (b) Resident birds as the original infection source. (c) Domestic poultry as the original infection source.

AIC_c values corresponding to three results in Figs. 9, 10 and 11 are AIC_cm = 160.246, AIC_cw = 168.7216, AIC_cp = 207.9282, and AIC_min = AIC_cm = 160.246. Moreover, Δ_w = 8.4756 > 4 and Δ_p = 47.6822 > 4, which imply that assumptions that residual birds and domestic poultry are considered as the original resource have less support. In a word, the possibility that migrant birds are viewed as the original infection source is the largest.

Sensitivity analysis

Sensitivity analysis are carried out by calculating correlation coefficients between input parameters and outcome variables. Here, we calculate correlation coefficients between some critical parameters and the two outcome variables: the basic reproduction number R₀ and the accumulated confirmed human cases X(52) during one year. The definition of R₀²² can be seen in supplementary material. The correlation coefficients between the input parameters r_m, r_w, r_p, β₁, q and R₀ under three cases are given in Table 5. From Table 5, it is can be easily known that the emissions coefficients and transmission rates have big effects on R₀. When the resident birds or domestic poultry is assumed to be the original infection source, the disinfection parameter q has little influence on R₀. The correlation coefficients between the input parameters r_m, r_w, r_p, β₁, q, β₂, α, γ and X(52) under three cases are given in the Table 6. From Table 6, we have that the transmission rates about human have the biggest effect on the accumulated human cases. The transmission rates between poultry and the emissions coefficients follow.

Table 5. Correlation coefficients (CCs) for the aggregate 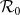and parameter variables.

	Case I		Case II		Case III
Parameters	PCC	p value	CC	p value	CC	p value
rm, rw, rp	1	0	1	0	1	0
β1	1	0	1	0	1	0
q	−0.9162	0.0002	0	1	0	1

Table 6. Correlation coefficients (CCs) for the aggregate X(14) and parameter variables.

	Case I		Case II		Case III
Parameters	PCC	p value	PCC	p value	PCC	p value
rm, rw, rp	0.9998	0	0.9998	0	0.9986	0
β1	0.9703	0	0.97	0	0.8796	0
β2	1	0	1	0	1	0
α	−0.5076	0.0042	−0.5889	0.0063	−0.3968	0.0043
γ	−0.8503	0	−0.8524	0	−0.8724	0
q	−0.8392	0	−0.8348	0	−0.4390	0

Table 7. Values of parameters and the basic reproduction during fitting results.

	Before closing markets			After closing markets			After reopening markets
Parameters	(FR I)	(FR II)	(FR III)	(FR I)	(FR II)	(FR III)	(FR I)	(FR II)	(FR III)
βb	1.3930 × 10−9	9.484 × 10−10	6.721 × 10−10	7/100 × 1.3930 × 10−9	7/100 × 9.484 × 10−10	7/100 × 6.721 × 10−10	55/100 × 1.3930 × 10−9	60/100 × 9.484 × 10−10	6.85 × 10−10
βc	1.3930 × 10−12	9.484 × 10−13	6.721 × 10−13	7/100 × 1.3930 × 10−12	7/100 × 9.484 × 10−13	7/100 × 6.721 × 10−13	55/100 × 1.3930 × 10−12	60/100 × 9.484 × 10−13	6.721 × 10−13
β2	1.4997 × 10−15	8.813 × 10−16	2.2064 × 10−15	7/100 × 1.4997 × 10−15	7/100 × 8.813 × 10−16	7/100 × 1.6632 × 10−15	55/100 × 1.4997 × 10−15	80/100 × 8.813 × 10−16	1.6632 × 10−15

Discussion

The analysis of genetic fragments tell us that H7N9 avian flu virus are traced to wild birds in east Asia area and poultry in Zhejiang, Jiangsu and Shanghai, which imply that migrant birds, resident birds and domestic poultry play important roles of appearance and prevalence of disease. As we know, the direct transmission source to human is live poultry trading markets. However, the original infection source, that is the original host species is not yet located. By taking migrant bird, resident birds, poultry and human into consideration, we establish a dynamical model and treat migrant bird, resident birds and poultry as candidate of the original infection source to fit the real confirmed human cases. There are two methods to determine the original infection source: graphic method and Akaike's information criterion. Using graphic method, we know that if the domestic poultry is the original infection resource, after reopening trading markets, the disease cannot reappear in two years. If the migrant birds or resident birds is the source, the disease can infect human again in winter and next spring. In fact, in November 2013, confirmed H7N9 human cases were reported again in the Yangtze River Delta region. So, from the fitting results, we conclude that the migrant birds or resident birds may be the original infection source. By calculating the values of Akaike's information criterion, we can obtain that the value under the case that migrant birds are viewed as the original infection source is the smallest. Thus, by applying two methods, it can be obtained that the probability that migrant birds are the original infection source is the largest.

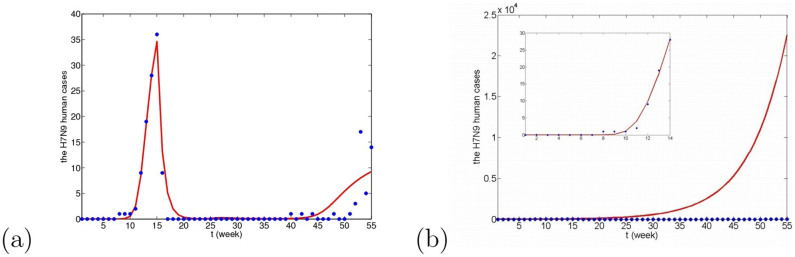
In this paper, there is an assumption addressed in introduction section that other host species infected by H7N9 virus cannot infect the original host species in turn. If the other host species can transmit virus to the original host species and interspecies transmission rates are very small, the fitting results are given in Fig. 14, which have small difference with the results in Figs. 9(a), 10(a) and 11(a). All corresponding AIC_c values are AIC_cm = 171.6606, AIC_cw = 170.0092, AIC_cp = 190.7212, and AIC_min = AIC_cw = 170.0092, which is the case that the residents birds are considered as the original resource. Δ_m = 1.6514 < 4 and Δ_p = 20.712 > 4, which means that migrant birds can also be the original resource, but domestic poultry cannot. So, the original host species can only be located in wild birds (migrant birds and resident birds). If there is no this assumption, the original host species cannot be precisely located. From Fig. 14(c), if the domestic poultry is the original transmission source, the human cases in winter would delay to appear.

Figure 14. The number of human cases with time under the situation that other host species can transmit virus to the original host species.

(a) Migrant birds are viewed as the original transmission source. (a) Resident birds are viewed as the original transmission source. (a) Domestic poultry are viewed as the original transmission source. The intraspecific transmission rates and the interspecific transmission rates are denoted by β_b and β_c, respectively. The changed parameter values can be seen in Table 7.

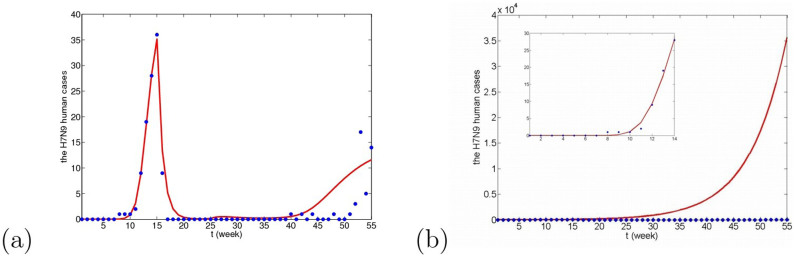
Although there is no solid evidence to confirm human-to-human transmission, it is happened in at least three families³,²⁶,²⁷. If human-to-human transmission, β_hh, is added in model (5), the new model (6) is obtained and fitting results are given in Figs. 15, 16 and 17. Applying the real confirmed human cases during the first 14 weeks, we can firstly estimate β₁, β₂ and β_hh and find that adding human-to-human transmission rate can lead to the decrease of β₁ and increase of β₂, which may enlarge the basic reproduction number. However, if human-to-human transmission rate is relatively small, there is no obvious difference between Figs. 15(a), 16(a), 17(a) and Figs. 9(a), 10(a), 11(a). On the contrary, if β_hh is relatively bigger, the prevalence situation of H7N9 may be serious and the number of the individual infected can reach thousands shown in Figs. 15(b), 16(b) and 17(b). So, according to real epidemic situation, even if human-to-human transmission exists, it must be very small.

Figure 15. The number of human cases with time under the situation that there exists human-to-human transmission when migrant birds are viewed as the original infection source.

(a) β_hh = 5 × 10⁻⁹, β₁ = 4.612 × 10⁻⁸, β₂ = 8.2 × 10⁻¹⁶; (b) β_hh = 10 × 10⁻⁹, β₁ = 5.728 × 10⁻⁸, β₂ = 1.2 × 10⁻¹⁶. p = 1.7.

Figure 16. The number of human cases with time under the situation that there exists human-to-human transmission when residual birds are viewed as the original infection source.

(a) β_hh = 5 × 10⁻⁹, β₁ = 5.769 × 10⁻⁸, β₂ = 4.969 × 10⁻¹⁶; (b) β_hh = 10 × 10⁻⁹, β₁ = 6.857 × 10⁻⁸, β₂ = 0.75 × 10⁻¹⁶. p = 1.7.

Figure 17. The number of human cases with time under the situation that there exists human-to-human transmission when domestic poultry are viewed as the original infection source.

(a) β_hh = 5 × 10⁻⁹, β₁ = 7.045 × 10⁻⁸, β₂ = 8 × 10⁻¹⁶; (b) β_hh = 10 × 10⁻⁹, β₁ = 7.969 × 10⁻⁸, β₂ = 1.45 × 10⁻¹⁶. p = 1.7.

In fact, due to the limitation of information now available, there exist some uncertain and roughness for this research. Firstly, the etiology about H7N9 virus is unclear, the decay rate of H7N9 virus in term of temperature obtained by applying the related information of H9N2 virus may be rough. Moreover, assumption of the viral load in environment is uncertain since it is very difficult to obtain the precise message. Control measures, such as closing and disinfecting live poultry trading markets, are considered in the fitting result of model (5). As we know, closing trading markets makes incidence rates decrease to 7%. However, after reopening markets, what extent to the transmission rates rise, and are they variational as human behaviour and mental process? All these cannot be quantified entirely and accurately. The values of transmission rates in Figs. 9, 10 and 11 may be the average values, so the fitting results of model (5) with real data after reopening markets are not very perfect.

Method

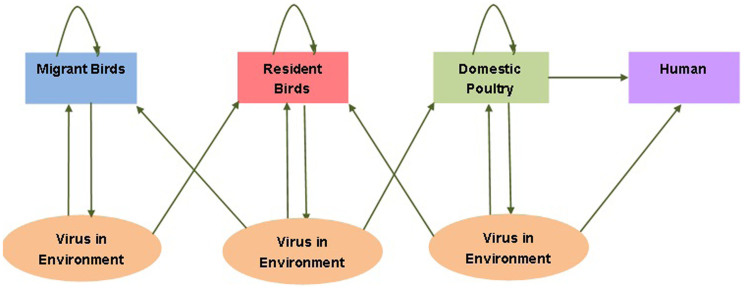
The populations we need to consider in dynamical model are migrant birds, resident birds, domestic fowl and human. Migrant birds and resident birds, resident birds and domestic birds, respectively, can possess common existence environment. Resident birds play an important intermediary role between migrant birds and domestic poultry. According to migrant birds, resident birds and domestic poultry, intraspecific transmission includes direct infection by contacting with each other or indirect transmission by environment containing H7N9 virus. Interspecific transmission only includes indirect transmission. Migratory birds, resident birds and domestic fowls can shed the virus to environment within the infected period. It is domestic poultry that brings virus to human. Human can be infected by H7N9 virus through the close contact with domestic poultry or by environment transmission and there exists no human-to-human transmission. All these connections are reflected in Fig. 18.

Figure 18. Transfer diagram on the dynamical transmission of H7N9 avian influenza among migrant birds, resident birds, domestic poultry and human.

Dynamical model

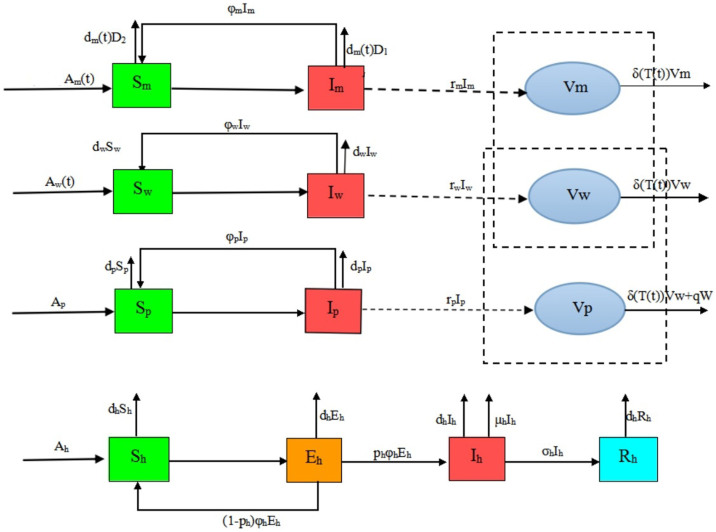
Let N_m(t), N_w(t), N_p(t), N_h(t) be the total number of migratory birds, resident birds, domestic poultry and human at time t, where N_m(t), N_w(t), N_p(t) are classified into two subclasses: the susceptible and virus carriers, denoted by S_m(t) and I_m(t), S_w(t) and I_w(t), S_p(t) and I_p(t) respectively. The quantity of virus in environment discharged by I_m(t), I_w(t) and I_p(t), are denoted by V_m(t), V_w(t) and V_p(t) whose unit can be the same as that of Hou et al²³. Since it is very difficult to determine the values of V_m(t), V_w(t) and V_p(t), the average number of virus that causes an H7N9 individual case is called an infectious unit (IU)²³. For human, once infected, he or she shows the clinical symptoms after a period of incubation. Some of the people may be killed by the influenza virus, and others can be cured. Thus, N_h(t) is divided into four subclasses: the susceptible, the infected, the confirmed and the recovered denoted by S_h(t), E_h(t), I_h(t) and R_h(t). The detailed description of dynamical transmission of H7N9 avian influenza is described in the following flowchart (Fig. 19). The corresponding dynamical model can be seen in equations (5), where the interpretation of the variables and parameters are shown in Table 1.

where 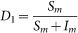and .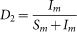

Figure 19. Detailed transfer diagram on the dynamical transmission of H7N9 avian influenza among migrant birds, resident bird, domestic poultry and human.

Adding human-to-human transmission rate β_hh to model (5), the following model is obtained.

Akaike's information criterion

Model validation is the most important step to examine the rationality of the model. We resort to Akaike's information criterion to seek a model that has the best fit to the actual data. Based on information theory, Akaike's information criterion (AIC)²⁸,²⁹,³⁰ provides a method for measuring model quality and a way of selecting a model from a set of models. The information criterion is defined as follows.

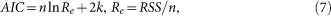where RSS is the residual sum of squares, n is the number of the real data and k is the total number of estimated parameters in the model equation plus 1.

Taking into account small sample, an improved information criterion is proposed,

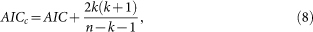which increases the relative penalty for model complexity with small data sets. When different models are tested on the same data set for both model estimation and validation, the model that has the smallest AIC_c is the most accurate.

Moreover, Define AIC difference as Δ_i = AIC_i − AIC_min, where AIC_min is AIC value for the best model. If 0 ≤ Δ_i ≤ 2, the ith model or result has substantial support. If 4 ≤ Δ_i ≤ 7, the ith model or result has considerable less support. If Δ_i ≥ 10, the ith model or result has essentially no support.

Supplementary Material

Supplementary Information

supplementary information pdf