Distinct perceptual rhythms for feature and conjunction searches

Abstract

Feature and conjunction searches are widely used to study attentional deployment. However, the spatiotemporal behavior of attention integration in these tasks remains under debate. Are multiple search stimuli processed in parallel or sequentially? Does sampling of visual information and attentional deployment differ between these two types of search? If so, how? We used an innovative methodology to estimate the distribution of attention on a single-trial basis for feature and conjunction searches. Observers performed feature- and conjunction-search tasks. They had to detect and discriminate a tilted low-spatial-frequency grating among three low-spatial-frequency vertical gratings (feature search) or low-spatial-frequency vertical gratings and high-spatial-frequency tilted gratings (conjunction search). After a variable delay, two probes were flashed at random locations. Performance in reporting the probes was used to infer attentional deployment to those locations. By solving a second-degree equation, we determined the probability of probe report at the most (P1) and least (P2) attended locations on a given trial. Were P1 and P2 equal, we would conclude that attention had been uniformly distributed across all four locations. Otherwise, we would conclude that visual information sampling and attentional deployment had been nonuniformly distributed. Our results show that processing was nonuniformly distributed across the four locations in both searches, and was modulated periodically over time at ∼5 Hz for the conjunction search and ∼12 Hz for the feature search. We argue that the former corresponds to the periodicity of attentional deployment during the search, whereas the latter corresponds to ongoing sampling of visual information. Because different locations were not simultaneously processed, this study rules out a strict parallel model for both search types.

Introduction

Visual search tasks, in which observers look for a target embedded among distractors, have long been used to study attentional deployment (for reviews, see Eckstein, 2011; Nakayama & Martini, 2011). There are two main categories of search. In feature search, the target differs from the distractors in a single dimension (e.g., color, shape, orientation). In this case, typically reaction time and accuracy are independent of the set size—that is, the number of distractors in the search array (near-zero slope). In conjunction search, the target is a combination of at least two features of different dimensions (e.g., color and shape). In such a case, typically the more stimuli, the longer the time required to find the target (positive slope) and the lower the accuracy (negative slope). The original view for these findings relied on an explanation based on processing speed: Feature search is preattentive and parallel, whereas conjunction search is attentive and sequential (Treisman & Gelade, 1980; Wolfe, Cave, & Franzel, 1989). However, many findings have questioned this two-stage assumption. For instance, in multiple studies conjunction searches have not yielded serial functions (e.g., Carrasco, Evert, Chang, & Katz, 1995; Egeth, Virzi, & Garbart, 1984; McLeod, Driver, & Crisp, 1988; Nakayama & Silverman, 1986); in conjunction tasks, search slopes have been shown to progress from steep (serial) to flat (parallel) within an experimental session (Carrasco, Ponte, Rechea, & Sampedro, 1998b); in feature searches with increasing set size, performance has diminished (as assessed by speed–accuracy trade-off methods; e.g., Carrasco, Giordano, & McElree, 2006; Carrasco & McElree, 2001; Dosher, Han, & Lu, 2004; McElree & Carrasco, 1999) and reaction times have decreased (e.g., Bravo & Nakayama, 1992; Buetti, Cronin, Madison, Wang, & Lleras, 2016; Carrasco et al., 1995; Carrasco & Chang, 1995). Even though these studies—and others, such as a recent one showing that slopes differ as a function of response method (yes/no detection vs. go/no-go)—provide evidence against this two-stage assumption, it is still very influential (Kristjánsson, 2015).

Over the years, several alternative explanations have been proposed. For example, some studies have shown the precueing the target location improves performance in feature “parallel” searches that would have been considered “preattentive” (Carrasco & McElree, 2001; Carrasco & Yeshurun, 1998) across eccentricity and isoeccentric locations in the visual field (Carrasco et al., 2004, 2006), and that a concurrent task impairs performance (Joseph, Chun, & Nakayama, 1997). These studies indicate that parallel search (i.e., near-zero slope, <10 ms; Wolfe & Horowitz, 2004) does not necessarily imply a preattentive search. For conjunction searches, the search pattern could result from parallel limited resources: The more numerous the stimuli, the more limited resources are, resulting in lower accuracy (e.g., McElree & Carrasco, 1999; Townsend, 1990). Thus, simply looking at performance, even trial by trial, does not allow one to disentangle parallel versus sequential search strategies. Moreover, for both feature and conjunction search, discriminability matters (Carrasco et al., 1995; Carrasco & Frieder, 1997; Carrasco, McLean, Katz, & Frieder, 1998a; Palmer, Ames, & Lindsey, 1993; Verghese & Nakayama, 1994). For example, target eccentricity affects the search: the larger the set size, the higher the probability that the target is at farther eccentricity, and given lower spatial resolution at the periphery, reaction time increases and accuracy diminishes. Consequently, the set-size effect can also be explained by the decrease of spatial resolution with eccentricity (Carrasco et al., 1995; Carrasco et al., 1998a; Carrasco & Frieder, 1997; Palmer et al., 1993; Verghese & Nakayama, 1994). Finally, many studies have shown that signal-detection theory can explain visual-search performance in a variety of detection, discrimination, and localization tasks in feature and conjunction searches (e.g., Cameron, Tai, Eckstein, & Carrasco, 2004; Dosher et al., 2010; Eckstein, 1998; Eckstein, Thomas, Palmer, & Shimozaki, 2000; Palmer et al., 1993; Verghese, 2001).

To date there is still no clear picture regarding the spatial deployment of attention during either feature- or conjunction-search tasks. Are multiple search stimuli processed in parallel or sequentially? Does sampling of visual information and attentional deployment differ between these two types of search? If so, how? Recently, using an innovative methodology (Dubois, Hamker, & VanRullen, 2009), Dugué, McLelland, Lajous, and VanRullen (2015b) showed that in a conjunction-search task, attentional resources are nonuniformly distributed in space—that is, some stimulus locations receive more attentional resources than others—and this pattern is periodically modulated in time, at the theta frequency (∼7 Hz).

A recent line of research concerning the temporal dynamics of visual information processing has posited that visual information is periodically sampled at low frequencies, theta (5–7 Hz) and alpha (8–12 Hz), in detection and discrimination tasks (Dugué et al., 2015b; Dugué, Marque, & VanRullen, 2015a; Dugué, Roberts, & Carrasco, 2016; Dugué & VanRullen, 2014; Fiebelkorn, Saalmann, & Kastner, 2013; Huang, Chen, & Luo, 2015; Landau & Fries, 2012; Landau, Schreyer, van Pelt, & Fries, 2015). Regarding visual-search studies, periodic sampling is considered to be compatible with a nonuniform spatial distribution of attention, with the periodicity reflecting sequential switching among stimulus locations. Conversely, a uniform spatial distribution of attention is considered to be compatible with continuous processing of information. However, periodic sampling may emerge for different reasons. VanRullen (2016) has recently proposed that periodicities peaking at ∼7 Hz reflect attentional sampling rhythm, whereas those peaking at ∼11 Hz reflect a sensory rhythm, underlying the sampling of visual information in a spontaneous, ongoing manner.

In this study, we assess the spatiotemporal dynamics of information processing during feature- and conjunction-search tasks. At various delays after search-array onset, we probed two of four stimulus locations and computed the performance of the observer in reporting both or none of the probes correctly. Then, using a second-degree equation, we estimated the amount of attention allocated to stimulus locations in the search array. We found that both the feature- and conjunction-search tasks led to a nonuniform distribution of resources, periodically modulated over time: ∼5 Hz for the conjunction search and ∼12 Hz for the feature search. We argue that the ∼5-Hz component observed in the conjunction task, consistent with findings of Dugué et al. (2015b), corresponds to the periodicity of attentional deployment during the search, whereas the ∼12-Hz periodicity revealed by the probes in the feature task corresponds to the ongoing sampling of visual information.

Materials and method

Observers

Sixteen observers participated in the main experiment (M ± SD = 23.7 ± 3.8 years old) and the cueing-task experiment (M ± SD = 24.7 ± 4.2 years old). The main experiment was accompanied by a control experiment, which was used as training beforehand and also run afterwards. One observer from the main experiment did not participate in the control experiment conducted after the main experiment. Thirteen of the observers in the main experiment also participated in the cueing-task experiment. All participants had normal or corrected-to-normal vision, and all gave written informed consent. The institutional review board of New York University approved the experiment.

Apparatus and stimuli

Observers sat in a dark room during the experiment, 57.5 cm from the screen (1280 × 1024 pixels, 85-Hz refresh rate). Stimuli were generated using MATLAB (The MathWorks, Natick, MA) and the MGL toolbox (http://gru.stanford.edu/doku.php/mgl/overview) on a Macintosh computer.

The search display, in both the control and the main experiment, was composed of sinusoidal gratings windowed by a raised cosine. They had a 5% contrast and were presented at 8° eccentricity on a gray background. The grating stimuli were either vertical, tilted 45° clockwise, or tilted 45° counterclockwise relative to the vertical. In both the feature and conjunction conditions, the target was a tilted low-spatial-frequency stimulus. The low-spatial-frequency stimuli were 2 c/°, and the high-spatial-frequency stimuli (distractors) were 3 c/°. In the control experiment, there were either four or eight stimuli, whereas in the main experiment, only four were presented.

The feature- and conjunction-search tasks had the same target but different types of distractors. In the feature condition, the distractors differed from the target in only a single attribute—that is, all of the stimuli were at low spatial frequency, but only the target was tilted (45° clockwise or counterclockwise from vertical). In the conjunction condition, the distractors differed from the target in one or two attributes—that is, they could be at high or low spatial frequency. All of the high-spatial-frequency stimuli were tilted, and all of the low-spatial-frequency stimuli were vertical except for the target (Figure 1B).

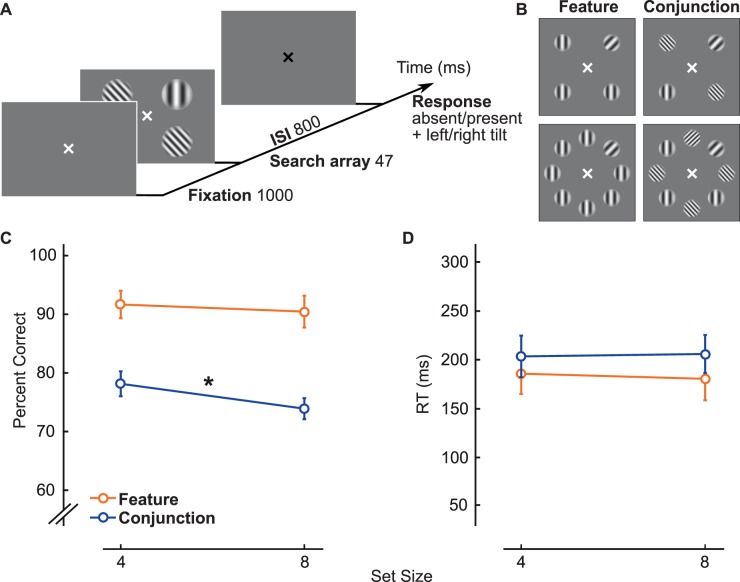
Figure 1.

(A) Procedure for control experiment. (B) There were four different search displays in the control. The search displays were of set size 4 or 8 and for either feature or conjunction search. (C) Percent accuracy in detection of the presence or absence of the target. The slope for conjunction performance is significantly negative (p < 0.01). (D) Reaction time in detection of the presence or absence of the target. Note: For illustration purposes, the stimuli shown in this figure are of higher contrast than those used in the experiment.

Experimental procedure

Before we assessed attentional deployment in the visual search, observers performed a control experiment. With set sizes of 4 and 8 in the control experiment, search slopes were calculated to ensure that the data were consistent with this typical way of analyzing the data (see Results). The entire experiment was conducted in 7 days (1-hr session for each of the first 6 days and a 30-min session for the seventh day). The control experiment was conducted merely as training on the first day, and to assess search accuracy on the last day. For 3 days observers participated in the feature-search task, and for the other 3 days they participated in the conjunction-search task. The order was counterbalanced across observers.

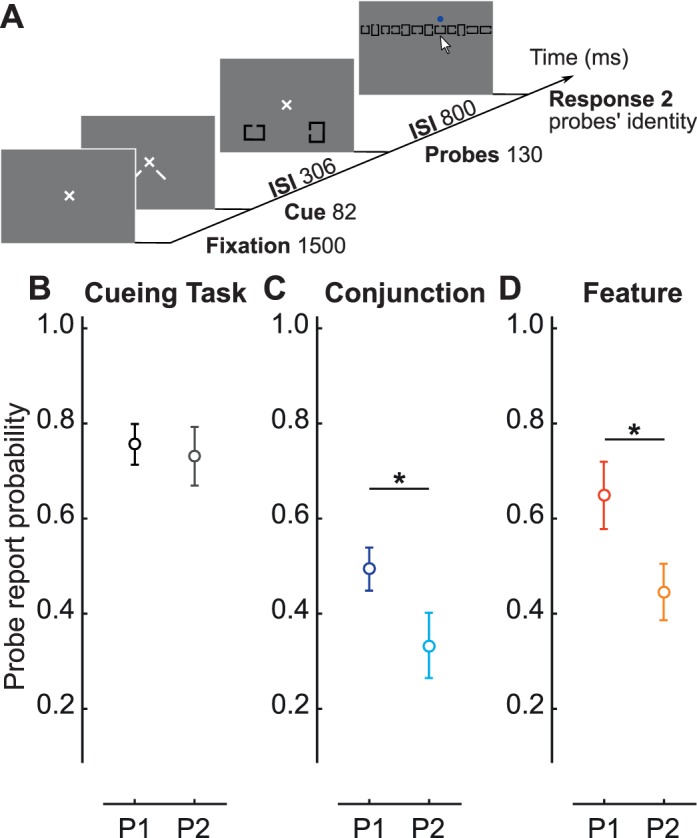
In the control experiment, observers were instructed to fixate on a white cross at the center of the screen. Eye position was monitored using an infrared video-camera system (EyeLink 1000, SR Research, Ottawa, Canada) to ensure that all observers maintained fixation throughout each trial. Stimulus presentation was contingent upon fixation; any trials in which observers broke fixation (defined as an eye movement ≥1° from the center of the fixation cross or if the observer blinked; M = 5.3% ± 4.7% in feature trials and M = 6.9% ± 9% in conjunction trials) was canceled and then repeated at the end of each experimental block. The stimuli of the search display were then presented for 47 ms (Figure 1A). There were either four or eight stimuli presented, and set size was chosen at random for each trial. When only four stimuli were presented, they could be presented as either a square or a diamond array. After 800 ms of the search-display offset, a response tone prompted observers to indicate, within a limited time window of 1000 ms, whether the target had been tilted counterclockwise or clockwise from vertical or absent, by pressing with their left hand the response key 1, 2, or 3, respectively. Feedback was provided at the end of each trial; a high tone was played when the answer was correct, and a low tone when the answer was incorrect or when the observers did not respond within the allotted time. The observers were instructed that there was a relatively long time window to respond, but that they should try to maintain steady response timing between trials. This enabled us to measure accuracy as our main dependent variable. We measured reaction times from the onset of the response window as a secondary dependent variable to be able to rule out any speed–accuracy trade-offs. We thus evaluated the slope on accuracy as a function of set size while the reaction times remained constant.

After observers performed the control experiment, they proceeded to perform the main experiment (Figure 2A). In the main experiment, after observers had fixated on the cross for 1500 ms, the search display was presented for 47 ms. The search display was identical to that of the control experiment, but there were always four grating stimuli. Two Landolt Cs, squares or rectangles with an aperture on one of the sides, were presented after one of 13 possible delays after search-display offset (interstimulus interval [ISI] = 106–526 ms, in increments of 35 ms). These probes, presented for 130 ms at two randomly chosen locations where the stimuli were previously presented, were used to measure attentional deployment (see Probability estimates). To ensure that identification of each probe was independent, the two probes could be identical. Upon offset of the probes, the fixation cross turned black to indicate the beginning of the response window during which observers could report the tilt orientation or absence of the target (note that no tone was used in this case to indicate the onset of the 1-s window). The response keys and auditory feedback were the same as in the control experiment. The fixation cross disappeared after the observers gave their answer, and a horizontally aligned array of 12 different probes appeared on the upper half of the screen. The order of the probes in the array was randomized between trials. Observers used a mouse with their right hand to click on the two probes they had seen after the search display. A blue dot briefly appeared above each clicked probe, indicating that it had been selected. When two identical probes were presented during the trial, the observer had to click twice on the same probe; the blue dot would then reappear above the same location. There was no feedback for performance on the probe task. The main dependent variables were accuracy in the search and probe tasks. To ensure that observers deployed attention in the search task, they were instructed to respond as accurately as possible. Reaction times, measured from the onset of the response window, were our secondary dependent variable to be able to rule out any speed–accuracy trade-offs.

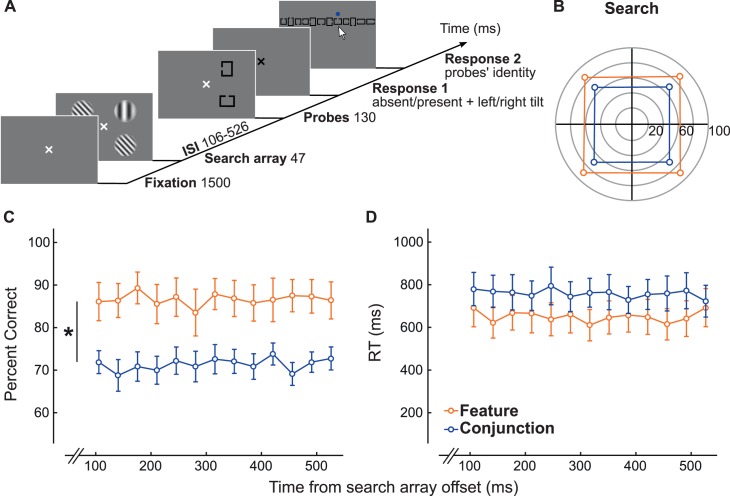
Figure 2.

(A) Experimental procedure. (B) Accuracy in detecting the target when the search display is a square array. (C) Performance in detecting the absence of the target for the search task. (D) Reaction time in detecting the absence of the target for the search task. There is a main effect of the feature and conjunction conditions on performance (p < 0.01). Note: For illustration purposes, the stimuli shown in this figure are of higher contrast than those used in the experiment.

Probability estimates

A strict parallel theory would predict that both items start to be processed simultaneously and at the same rate over time, whereas a strict serial model would predict that one stimulus is processed at a time (Palmer et al., 1993; Treisman & Gelade, 1980; Wolfe et al., 1989). General performance in search tasks is not informative regarding attentional deployment because accuracy would decrease with increasing set size for both sequential and limited-resource parallel models of attentional deployment. Overall probe accuracy is not informative about whether and how attention is deployed to each location in the visual search either. Even a trial-by-trial binary response (correct/incorrect) would not reflect whether attention is at one or the other or both locations.

To determine whether or not attention was divided among the stimuli uniformly, we calculated the independent probabilities of attending to each probe location by implementing the mathematical method used by Dubois et al. (2009) and Dugué et al. (2015b). The probabilities of attending to each of the probed locations, which were called P1 and P2, were determined using the probabilities of reporting both probes correctly (PBOTH) and reporting both probes incorrectly (PNONE).

The relation among PBOTH, PNONE, P1, and P2 can be defined as follows:

Equations (1) and (2) can be rearranged to isolate P1 and P2:

Given the product and sum of two unknowns (P1 and P2), the two unknown values can be solved for using quadratic theory. The product and sum of the two unknown values can be defined as follows:

From quadratic theory, P1 and P2 would be the roots of the following quadratic equation:

The discriminant Δ of Equation 7 is then

From the quadratic formula, Equation 8 has the following two solutions:

.

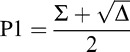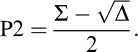The difference of P1 and P2, as can be seen here, is 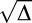. Because P1 and P2 are probabilities, they should theoretically be real numbers, and their difference should also be real. However, due to noise in responses and performance and a relatively low number of trials per condition, negative values of Δ were sometimes obtained (M = 3.4/13 trials in the feature task; M = 4.2/13 trials in the conjunction task). This is problematic because if 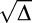is not real, there are no real solutions for P1 and P2. To resolve this issue, |Δ| was used as the discriminant and the sign of Δ was used as the sign of 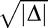, so that real values of P1 and P2 could be obtained:

.

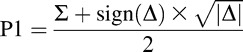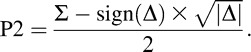This is a more conservative solution than solutions such as assigning a zero value to Δ or taking the absolute value of Δ, which would artificially lead to larger difference between P1 and P2 (see also Dugué et al., 2015b). By construction, the value of P1 should be greater than the value of P2, so P1 is considered the report probability at the most attended location and P2 at the least attended location. Although the probabilities of attending to each of the probed locations can be obtained, the specific locations that P1 and P2 refer to cannot be identified with this method.

Temporal analysis

We analyzed the temporal dynamics of attentional deployment during the search task by performing fast Fourier transforms (FFTs) on the probability estimates. We performed an FFT for each observer on the difference between P1 and P2 across all possible delays between search-display onset and probe onset (ISIs). The difference between P1 and P2 represents attentional deployment over time. We then averaged the obtained amplitude spectra, which allowed us to estimate the frequency component present in each observer's data, regardless of whether the data align across observers. We used bootstrapping to assess the significance of each frequency component obtained from the averaged amplitude spectra. Based on the null hypothesis that P1 and P2 were independent of delay, we shuffled the ISI labels to obtain surrogate amplitude spectra. We did 10⁵ iterations of shuffling and ranked the 100,000 surrogate amplitude spectra for each delay in ascending order. The limit of the 95% confidence interval (CI) was determined based on the 95,000th value, and we considered a peak significant if p < 0.001 (after Bonferroni correction for multiple comparisons—i.e., six comparisons for the six frequency components, 2.38, 4.76, 7.14, 9.52, 11.90, and 14.29 Hz; note that when an FFT is performed on a temporal signal that has 13 points, the returned amplitude spectrum contains 13 points as well, with the first point corresponding to the direct current (DC) and thus being disregarded and the last six points corresponding to the mirror image of the previous six points).

Cueing-task experiment

For the probability estimates described previously, it is important to ensure that the computation can lead to P1 and P2 being equal. To that end, we conducted a cueing-task experiment in which observers performed a task involving distributed resources, for which it was likely we could obtain P1 equal to P2. Observers had 1,500 ms to fixate on a white cross at the center of the screen. After fixation, two neutral cues were presented toward the lower half of the screen. The cues were presented for 80 ms, followed by a 300-ms ISI (necessary time to deploy voluntary attention; Busse, Katzner, & Treue, 2008; Cheal & Lyon, 1991; Liu, Stevens, & Carrasco, 2007; Müller & Rabbitt, 1989; Nakayama & Mackeben, 1989; Pestilli, Ling, & Carrasco, 2009; for a review, see Carrasco, 2011). Two black square or rectangular Landolt C probes were then presented at 8° eccentricity for 130 ms. The probes were presented at fixed locations so that there was no spatial uncertainty. The location of the probes was identical to the location of the probes in the main experiment in the lower half of the square array. After the offset of the probes, there was an 800-ms ISI and then the 12 possible probes were presented horizontally on the screen. The order of the probes was randomized between trials, and a blue dot appeared above each probe when selected. Observers had unlimited time to report the probes. As in the main experiment, it was possible for both probes to be identical, in which case the observers had to click twice on the same probe. Observers were instructed to attend equally the two locations indicated by the cues and were encouraged to report the identity of both probes as accurately as possible.

Results

We first examined search slopes for the control experiment, computed as accuracy (main dependent variable; Figure 1C) and reaction time (Figure 1D) as a function of set size. Accuracy was determined as correct detection of the presence or absence of the target. As expected, the performance slope for feature search was not significantly different from zero (−0.30% ± 0.06% per element), t(14) = −1.23, p = 0.24, 95% CI [−0.84, 0.23]. For conjunction search, however, the performance slope was significantly negative (−1.06% ± 0.13% per element), t(14) = −3.73, p < 0.01, 95% CI [−1.67, −0.45], indicating that the search involved attentional resources. These results are consistent with the expected search slopes for feature and conjunction searches. In addition, as expected given our response window encouraging observers to respond in a constant, steady manner, slopes for reaction time (the secondary dependent variable) were not significantly different from zero for either the feature search (−1.31 ± 0.17 ms per element), t(14) = −1.99, p = 0.07, 95% CI [−2.73, 0.10], or the conjunction search (0.62 ± 0.42 ms per element), t(14) = 0.37, p = 0.72, 95% CI [−2.95, 4.18].

We then assessed whether the results of the search task in the main experiment were consistent with the expected behavior of feature- and conjunction-search tasks. In the main experiment, observers performed a search task followed by a probe-identification task (Figure 2A). To ensure that attentional distribution was not affected by the target detection per se, we analyzed only trials in which the target was absent (see later and Figure 3), which enabled us to assess search strategy. We found that performance in detecting the absence of the target was significantly lower in the conjunction-search task than in the feature-search task (FIG. 2C; two-way repeated-measures analysis of variance [ANOVA]), F(1, 15) = 38.23, p < 0.01, η² = 71.82. There was no effect of the delay at which the probes appeared (two-way repeated-measures ANOVA), F(12, 180) = 0.86, p = 0.58, η² = 5.45, nor was there an interaction between the conditions and delays (two-way repeated-measures ANOVA), F(12, 180) = 0.74, p = 0.71. Furthermore, there was no significant difference in reaction time between the conjunction- and feature-search tasks (Figure 2D). Performance in the conjunction-search task was lower than in the feature-search task regardless of the delay at which the probe appeared, indicating that the conjunction search requires more resources.

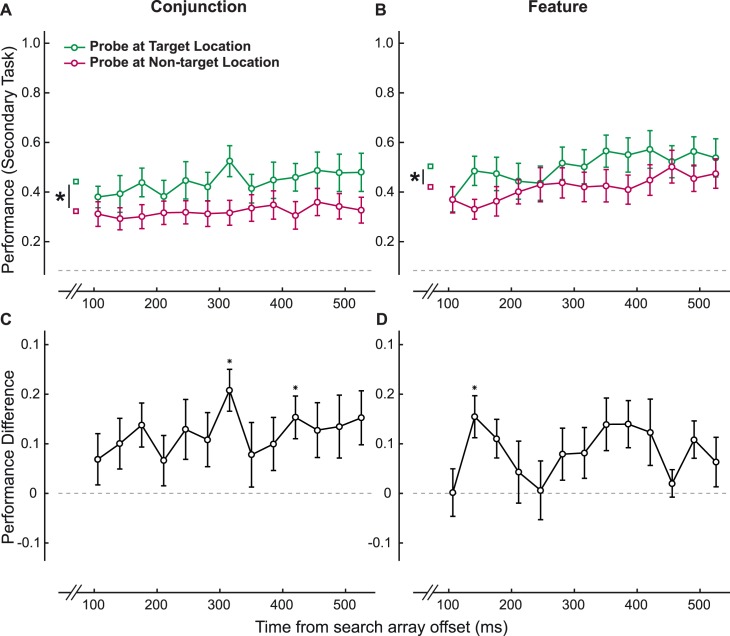
Figure 3.

(A–B) Performance in target-present square-array trials (see Figure 2A) for reporting the probe at target and nontarget locations in (A) the conjunction condition and (B) the feature condition. (C–D) The difference in performance for reporting the probe at target and nontarget locations for square-array trials in (C) the conjunction condition and (D) the feature condition. * indicates that the difference at that time point is significant after Bonferroni correction for multiple comparisons.

Two types of search arrays were used in the main experiment for each condition: a square array and a diamond array of stimuli. To assess whether the type of search array affects probe detection and probe-report probability, we calculated performance in detecting the target's presence at each location. We observed a main effect of the target location on detection performance when the search display was a diamond array for conjunction search (one-way repeated-measures ANOVA), F(3, 45) = 4.41, p < 0.01, η² = 22.73, but not for feature search, F(3, 45) = 1.61, p = 0.20, η² = 9.68. This performance asymmetry could influence probe detection as well as probe-report probability, which could lead to an erroneous conclusion that attention was focused. We also examined reaction time when the search display was a diamond array, and found a main effect of the target location for both conjunction search, F(3, 45) = 8.55, p < 0.001, η² = 36.31, and feature search, F(3, 45) = 4.30, p < 0.01, η² = 22.26. To avoid including the effects of this performance asymmetry on probe-report probability in our analysis of attentional deployment, we excluded all of the trials in which the search display was a diamond array. This asymmetry is consistent with canonical performance fields (better performance along horizontal than vertical meridian; e.g., Abrams, Nizam, & Carrasco, 2012; Carrasco, Talgar, & Cameron, 2001).

The same analysis was conducted on the square-array trials. We observed no main effect of the target location on target-detection accuracy (Figure 2B). This was true for both the conjunction task (one-way repeated-measures ANOVA), F(3, 45) = 0.10, p = 0.96, η² = 0.63, and the feature task, F(3, 45) = 1.71, p = 0.18, η² = 10.23. Likewise, for reaction time there was no significant effect of target location in conjunction search, F(3, 45) = 0.25, p = 0.86, η² = 1.62, or feature search, F(3, 45) = 1.76, p = 0.17, η² = 10.51. Because there were no performance asymmetries in the search task when the display was a square array, any effects observed in probe-report probability would not be due to perceptual differences and would be considered attentional rather than sensory.

For the secondary task, we first analyzed the effect of the target's presence on probe-report accuracy. We took the target-present trials when the search display was a square array and separately analyzed performance in identifying probes at the target and the nontarget location (Figure 3A, B). We observed a main effect of probe location for conjunction search (two-way repeated-measures ANOVA), F(1, 15) = 20.27, p < 0.01, η² = 57.41, and for feature search, F(1, 15) = 10.67, p < 0.01, η² = 41.57. There was also a main effect of delay for feature search, F(12, 180) = 2.19, p < 0.02, η² = 12.74. There was a significant interaction between probe location and delay for both conjunction tasks, F(25, 375) = 2.08, p = 0.02, and feature tasks, F(25, 375) = 4.20, p < 0.01. As expected, probe performance was greater at the target location at most delays (Figure 3C, D). Indeed, when the target was present, attention would have been focused at that location, not only allowing the observer to perform the orientation-discrimination task but also facilitating performance on the subsequent task of reporting the probe at the target location.

From the difference between probe-report performance at target and nontarget locations (Figure 3C, D), we observed that target detection took longer in conjunction search (316 ms after search-array offset), t(15) = 4.92, p < 0.0001, 95% CI [0.12, 0.30], than in feature search (141 ms after search-array offset), t(15) = 3.65, p < 0.01, 95% CI [0.06, 0.25]—both still significant after Bonferroni corrections for multiple comparisons. Note that the difference in the temporal dynamics between the results presented in Figure 3 and the results from the main experiment presented later (Figures 4 and 5) presumably arise from the fact that we analyzed target-present trials for the former and target-absent trials for the latter.

Figure 4.

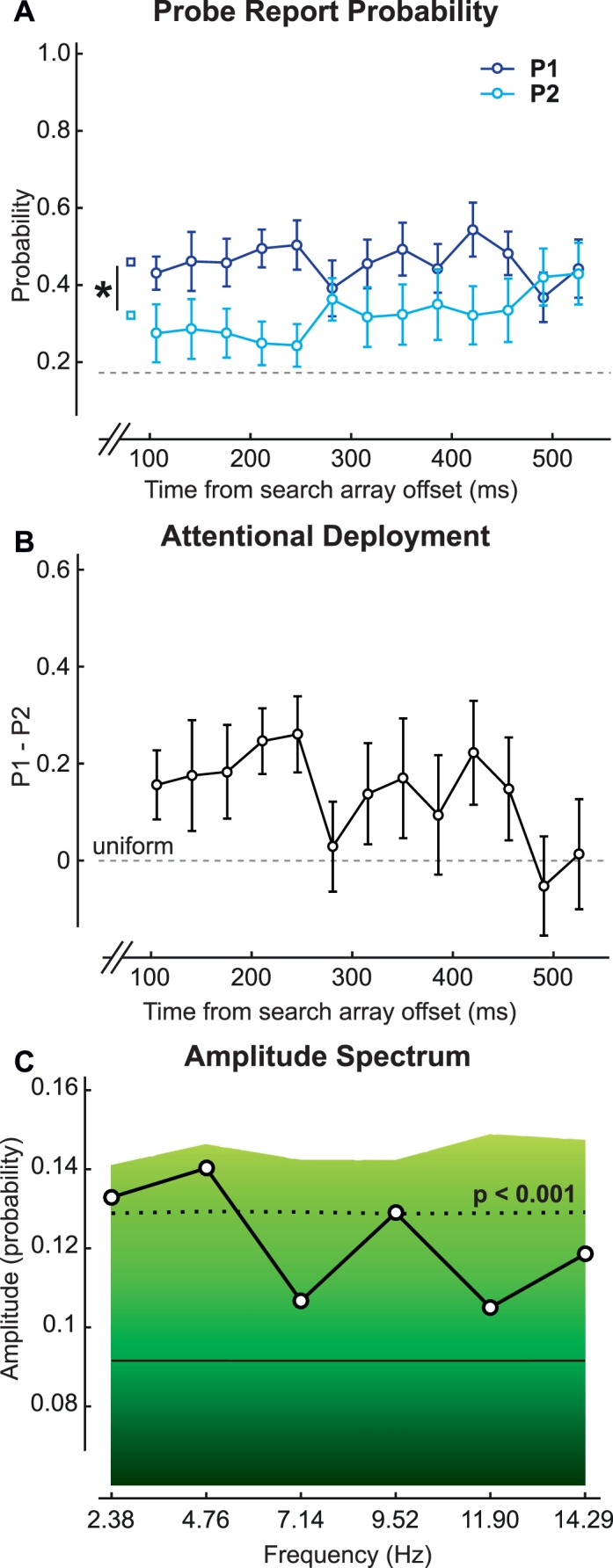
(A) P1 and P2 for the conjunction condition of the main experiment; the dotted gray line represents chance level for each event (0.083). (B) The difference of P1 and P2. (C) The amplitude spectrum obtained from the average of fast Fourier transforms on individual differences of P1 and P2 for each observer. The background colors indicate a bootstrap statistical test. The solid black line represents the average amplitude spectrum for the bootstrapped values. The dotted black line represents the boundary for p = 0.001.

Figure 5.

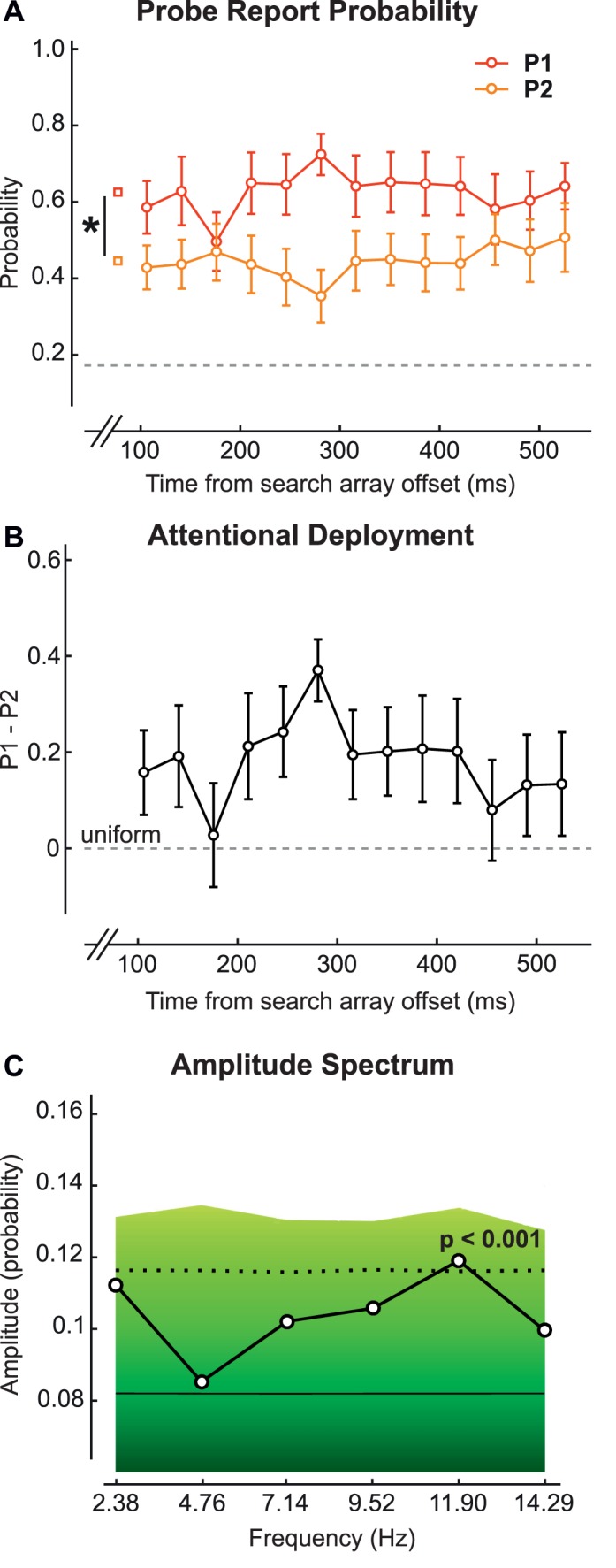
(A) P1 and P2 for the feature condition of the main experiment. (B) The difference of P1 and P2. (C) The amplitude spectrum obtained from the average of fast Fourier transforms on individual differences of P1 and P2 for each observer. The background colors indicate a bootstrap statistical test. The solid black line represents the average amplitude spectrum for the bootstrapped values. The dotted black line represents the boundary for p = 0.001.

After removing target-present trials and diamond-array trials from our analysis (18 trials per delay per observer remained), we recorded accuracy in the secondary task in reporting both probes (PBOTH) and none of the probes (PNONE) correctly. We used PBOTH and PNONE to estimate the probe-report probabilities (P1 and P2) (see Probability estimates, earlier) and found that P1 significantly differed from P2 in both the conjunction search (two-way repeated-measures ANOVA), F(1, 15) = 8.47, p < 0.02, η² = 36.09 (Figure 4A), and the feature search (two-way repeated-measures ANOVA), F(1, 15) = 10.06, p < 0.01, η² = 40.13 (Figure 5A). We argue that attentional deployment is nonuniform in both of these searches—that is, attention is not equally distributed on all four locations.

To assess the temporal behavior of attentional deployment, we plotted the difference between P1 and P2 (Figures 4B and 5B) and observed that attentional deployment was modulated over time between more and less uniform modes. To determine whether this modulation is periodic, we conducted an FFT on the difference between P1 and P2 for each observer and averaged the resulting amplitude spectra (see Temporal analysis, earlier). For the conjunction condition, we found three peaks significant after Bonferroni correction for multiple comparisons (Figure 4C): at 2.38, 4.76, and 9.52 Hz. A primary oscillatory peak exists at 4.76 Hz; a secondary oscillatory peak, at 9.52 Hz, may represent the harmonic frequency of 4.76 Hz. A significant peak is also present at 2.38 Hz, but because this is the lowest frequency limit (and frequency resolution) we could test (1/0.42 s, the total duration analyzed), we cannot determine whether it reflects a true spectral peak (and thus periodic activity). Moreover, this component could also reflect a slow drift over time toward zero of the difference between P1 and P2 (Dugué et al., 2015b; Dugué & VanRullen, 2014). We conclude that the difference between P1 and P2 in the conjunction search is modulated at 4.76 Hz (theta frequency). In the feature condition, there was one peak at 11.90 Hz that was significant after Bonferroni correction for multiple comparisons (Figure 5C).

We can conclude that the conjunction search is modulated periodically at ∼5 Hz, whereas the feature search is modulated periodically at ∼12 Hz. Note that although the peak at 11.9 Hz in the feature search is not at the upper limit established by the Nyquist frequency (half the sampling rate; i.e., half of 1/0.035 s = 14.29 Hz), it could still be affected by aliasing artifacts, which are more likely for higher frequencies, complicating the calculation of this frequency component. Further research should confirm this feature periodicity.

The amplitude spectra depicted in Figures 4C and 5C were obtained by computing an FFT on the data of each individual observer and then averaging the resulting amplitude spectra. Thus, the observed peaks at ∼5 Hz for the conjunction task and ∼12 Hz for the feature task correspond to frequency components observed for each individual, but not necessarily in phase across observers. Note that in the feature condition (Figure 5B) the ∼12-Hz component is not apparent on the average difference between P1 and P2, which suggests that this component is present for most observers but not in phase across observers. In Figure 6, we depict the amplitude of the 4.76- and 11.9-Hz components for individual observers. A two-way repeated-measures ANOVA performed on these data shows main effects of neither condition, F(1, 15) < 1, nor frequency component, F(1, 15) < 1, but reveals a significant interaction between these two factors, F(3, 45) = 6.04, p < 0.01. This interaction indicates that the two frequency components between the conjunction and feature conditions differ in opposite directions—that is, 4.76 Hz dominates in the conjunction condition and 11.9 Hz in the feature condition.

Figure 6.

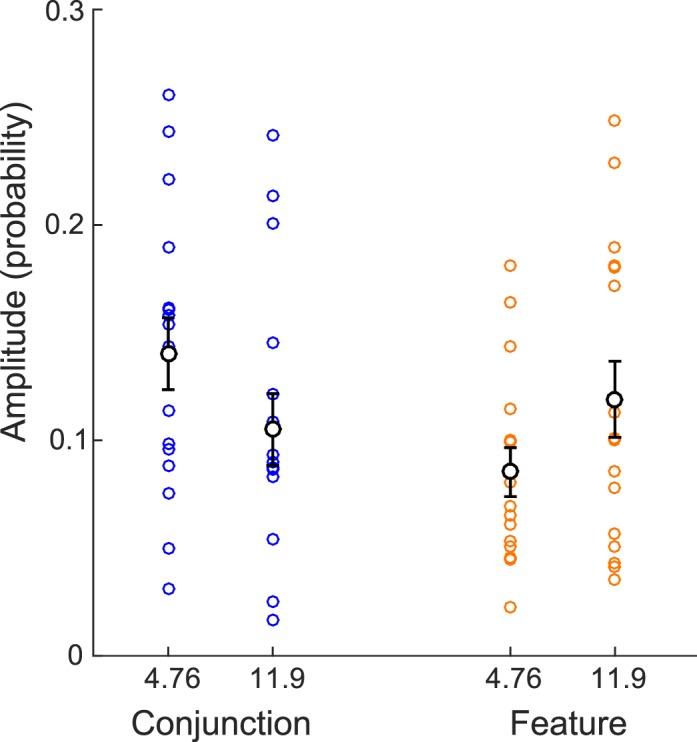
Amplitudes of the 4.76- and 11.9-Hz components, obtained from the average of fast Fourier transforms on individual differences of P1 and P2, compared for the conjunction and feature conditions. The data for each observer are represented with colored dots. The mean and standard error of the mean are represented in black.

In both conjunction and feature search, we found that attention was nonuniformly distributed. We conducted a cueing-task experiment to assess whether attention would be uniformly distributed—that is, P1 not different from P2—when attentional resources were experimentally manipulated to be uniformly allocated to the two probed locations. In this experiment, two identical precues encouraged observers to distribute attention equally to two locations that were then probed (see Materials and method and Figure 7A). As expected, P1 and P2 did not significantly differ, t(15) = 0.40, p = 0.69, 95% CI [−0.11, 0.16] (Figure 7B). Probe performance in the cueing task was higher than in the main experiment, but still challenging (cueing: 75.1% ± 4.3%; feature search: 51.8% ± 5.3%; conjunction search: 38.3% ± 4.4%; all well above chance, 8.3%). These results show that attentional deployment is uniform when resources are distributed. Probe onset in the cueing-task experiment was 388 ms after fixation, and we compared this to the average in the main experiment when the probes were presented 351, 386, and 421 ms after search-display onset. In the cueing-task experiment, P1 was significantly higher than P2 for both the conjunction task (one-tailed t test), t(15) = 2.07, p < 0.03 (Figure 7C), and the feature task (one-tailed t test), t(15) = 2.6, p < 0.02 (Figure 7D). Given that P1 and P2 did not differ when attention was distributed to the probed locations, we can conclude that the main effect of P1 and P2 in the main experiment for the conjunction and feature tasks was indicative of nonuniform attentional deployment during both types of search tasks, not a mere effect of the method used to estimate probability.

Figure 7.

(A) Cueing-task procedure. (B) The average of P1 and P2 across observers from the cueing task. The probes in the cueing task are presented 388 ms after fixation. (C–D) P1 and P2 averaged across observers for the average of the probe presentation at 351, 386, and 421 ms after search-display onset, in target-absent square-array trials for (C) the conjunction condition and (D) the feature condition.

Discussion

In this study, we compared the spatiotemporal behavior of attention in conjunction and feature search. First, consistent with previous studies (McElree & Carrasco, 1999; Treisman & Gelade, 1980; Wolfe et al., 1989), the control experiment revealed that feature search was more accurate and faster than conjunction search. In the main experiment, observers performed a visual-search task followed by a probe task after varying delays. Using the accuracy in reporting both and none of the probes correctly, we estimated the probabilities of reporting the individual probes. We used these probabilities to infer visual information sampling and attentional deployment in the visual search. The estimates of probe-report probabilities at the most and least attended locations of the two probed locations could have been equal or different. Had we observed the former, we would have concluded that attention was distributed uniformly. However, having observed the latter, we conclude that processing was nonuniform in either space or time in both the conjunction- and, remarkably, feature-search tasks. The cueing-task experiment (Figure 6) illustrates that the methodology we used can yield uniform estimates—that is, when we enforced attentional distribution to both cued locations, attention was indeed uniformly distributed to both probe locations (P1 was equal to P2). This demonstration is important for mathematical and methodological concerns; it is necessary to demonstrate that the procedure is able to yield the null hypothesis—that is, P1 = P2—when attentional distribution is uniform. However, this task does not inform the process by which attention exerts its effect at the probed location. In future experiments, we will address this point directly.

Both conjunction- and feature-search tasks have been widely used for the study of visual search and attention. In previous studies, overall accuracy and reaction time have been used to characterize the spatiotemporal behavior of attention in visual searches. Search slopes were originally interpreted to suggest that conjunction searches are attentive and sequential, whereas feature searches are preattentive and parallel (e.g., Treisman & Gelade, 1980; Wolfe et al., 1989). However, these measures can be subject to multiple interpretations, because both the parallel and sequential models of attention predict that with more stimuli, reaction time increases and accuracy decreases (e.g., Buetti et al., 2016; Kristjánsson, 2015; McElree & Carrasco, 1999). Thus, other explanations have provided alternate interpretations of those search slopes characteristic of conjunction and feature searches (e.g., Cameron et al., 2004; Eckstein, 1998; Eckstein et al., 2000; Hulleman & Olivers, 2015; Kristjánsson, 2015; McElree & Carrasco, 1999; Verghese, 2001). Recently, Buetti et al. (2016) have also challenged the original, strict parallel view of feature-search tasks and proposed that whereas all items in the search display start to be processed simultaneously, parallel search tends—because of the stochastic nature of processing—to produce logarithmic functions of reaction time with large set size.¹ In this study we characterize the nonuniformity in attentional allocation as well as its temporal dynamics; future work should identify the source of such nonuniformity. We note that stochastic noise would produce P1 > P2. Nevertheless, we speculate that if the nonuniformity observed in our study were due to stochastic noise, the difference between P1 and P2 would progressively increase over time. Instead, we observe that this difference is modulated periodically. To our knowledge, there is no reason to predict that a stochastic process would yield such a periodicity.

The methodology used in this study enables a more directly informative measure of attentional deployment during the search process. Briefly flashed probes after conjunction- and feature-search tasks revealed that stimuli were processed nonuniformly in both search tasks. In this experiment we could not determine the number of stimuli in the attentional focus but we could conclude that the focus did not contain all four stimuli—that is, attention was not uniformly distributed on the search array in either the feature- or the conjunction-search task. We can speculate three possible ways attention is deployed on the scene: It could focus on a single item and then be reoriented to another item sequentially until all the stimuli are processed; it could focus on two items sequentially; or it could focus on three items and, given the probe-report probabilities we obtained, there would not be a need to explore the last item to enable the observers to make a decision (for a mathematical demonstration of these three possibilities, see Dugué et al., 2015b; for discussion, see Hulleman & Olivers, 2015). Nonuniformity in conjunction search is consistent with the results of Dugué et al. (2015b), in which nonuniform, periodic (theta frequency, 5–8 Hz) attention allocation was found in a letter conjunction search. Such periodicity in attentional distribution is consistent with recent literature arguing that attention samples visual information periodically at the theta frequency when involved in a demanding visual-search task (Dugué et al., 2015a; Dugué et al., 2015b; Dugué et al., 2016).

In feature search, information was processed more efficiently and faster, but stimuli were also processed nonuniformly, even though search slopes were flat (accuracy did not decrease as a function of set size). Additionally, this process was modulated periodically at ∼14 Hz (alpha frequency). Thus, we argue that such periodicity reflects a sensory, ongoing sampling of visual information in the search display rather than periodicity of attentional deployment during the search. This suggestion is consistent with VanRullen's recent proposal (2016) that perceptual rhythms can correspond to the attentional sampling rhythm (theta frequency, 5–7 Hz) or a sensory rhythm underlying the sampling of visual information in a spontaneous, ongoing manner (alpha frequency, 8–14 Hz). This proposal is primarily based on observations in the visual domain (e.g., Dugué et al., 2011; Dugué & VanRullen, 2014; Fiebelkorn et al., 2013; Huang et al., 2015; Landau et al., 2015; Landau & Fries, 2012; Song, Meng, Chen, Zhou, & Luo, 2014), but evidence has also accumulated in the auditory (Giraud & Poeppel, 2012; Gross et al., 2013) and somatosensory (Ai & Ro, 2014; Baumgarten, Schnitzler, & Lange, 2015) domains as well as across auditory and visual dimensions (Lakatos et al., 2009; Romei, Gross, & Thut, 2012).

In conclusion, both conjunction- and feature-search tasks are nonuniform in space and time. We argue that in our conjunction search, attention was deployed nonuniformly within the theta-frequency range, whereas our feature search revealed ongoing sampling of information within the alpha-frequency range. Critically, both perceptual rhythms may coexist (VanRullen, 2016), but the specific demands of each task are more likely to yield either the attention or sensory rhythm. Because different locations were not simultaneously processed, this study rules out a strict parallel model for both search types.