Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2017 Apr 5.
Published in final edited form as: Phys Med Biol. 2016 May 25;61(12):4390–4401. doi: 10.1088/0031-9155/61/12/4390

Functionalized Anatomical Models for EM-Neuron Interaction Modeling

Esra Neufeld 1, Antonino Mario Cassará 1, Hazael Montanaro 1,2, Niels Kuster 1,2, Wolfgang Kainz 3
PMCID: PMC5381388  NIHMSID: NIHMS851272  PMID: 27224508

Abstract

The understanding of interactions between electromagnetic (EM) fields and nerves are crucial in contexts ranging from therapeutic neurostimulation to low frequency EM exposure safety. To properly consider the impact of in-vivo induced field inhomogeneity on non-linear neuronal dynamics, coupled EM-neuronal dynamics modeling is required. For that purpose, novel functionalized computable human phantoms have been developed. Their implementation and the systematic verification of the integrated anisotropic quasi-static EM solver and neuronal dynamics modeling functionality, based on the method of manufactured solutions and numerical reference data, is described. Electric and magnetic stimulation of the ulnar and sciatic nerve were modeled to help understanding a range of controversial issues related to the magnitude and optimal determination of strength-duration (SD) time constants. The results indicate the importance of considering the stimulation-specific inhomogeneous field distributions (especially at tissue interfaces), realistic models of non-linear neuronal dynamics, very short pulses, and suitable SD extrapolation models. These results and the functionalized computable phantom will influence and support the development of safe and effective neuroprosthetic devices and novel electroceuticals. Furthermore they will assist the evaluation of existing low frequency exposure standards for the entire population under all exposure conditions.

1. Introduction

Interaction between electromagnetic (EM) fields and neurons are important in many situations. EM field can affect axonal, neuronal, or neural network activity and be excitatory, inhibitory, or synchronizing. Neuroprosthetic devices for instance directly activate neurons using EM fields to compensate for lost sensory or motoric functionality in case of blindness, paralysis, hearing deficiencies, etc. Neuro-stimulating devices such as deep brain, spinal cord, and vagus nerve stimulators in turn are used to treat diseases such as chronic pain, depression, epilepsy, movement disorders, and Parkinson’s disease, while neuromuscular incapacitation devices stimulate nerves in view of disrupting voluntary muscle control. Besides intentional EM-neuron interactions, unwanted stimulation occurs as a result of strong low-frequency exposure, potentially resulting in pain or significant hazard.

The ability to realistically and reliably model EM-neuron interactions allows establishing improved safety criteria, optimizing device safety and efficacy, and improving mechanism comprehension. Stimulation thresholds, locations of high risk, the impact of pulse shape, and the selectivity of activation can be studied by coupled EM-neuronal dynamics modeling, provided the model properly accounts for the complexity of neurons (morphology that can include, e.g., large dendritic trees; channel dynamics and distribution) and the inhomogeneous EM field distribution inside the human body. The latter is even exacerbated in the presence of implants. As the field inhomogeneity has an impact on neuronal dynamics, coupled EM-neuronal dynamics modeling is required. It has been demonstrated (Neufeld et al 2015) that a series of simplifying assumptions underlying current low frequency (LF) safety and standards (IEEE 2002a, IEC 2010) appear questionable when considering coupled EM-neuronal dynamics modeling in realistic anatomical environments.

This study introduces novel computable, functionalized anatomical phantoms for the realistic modeling of coupled EM-(temperature)-neuronal dynamics interactions within the full complexity of the human body. The goals of this paper are:

  • to present the computable, functionalized anatomical phantoms and the underlying technology,

  • to discuss the associated verification efforts,

  • to demonstrate the applicability of the functionalized phantoms by investigating the influence of the exposure type on chronaxie (respectively the strength-duration (SD) time constant, τ; Figure 1).

Figure 1.

Figure 1

Open in a new tab

Theoretical SD-plots assuming both the hyperbolic and the exponential model (τ: 0.1 ms) for normalized current threshold I(t)/I0 (log-log plot) and charge threshold Q(t)/Q0 (lin-lin plot) as a function of pulse duration t.

The application example choice is motivated by a series of controversial issues concerning the dynamics of neural stimulation (Recoskie et al 2009, Reilly 2010, Recoskie et al 2010), namely: 1. the optimal τ for a neuronal dynamics model reproducing experimental data, 2. the differences in τ observed for electric- and magnetic-type stimulation, 3. the suitable analytical approximation of SD relationships, and 4. the optimal extraction of τ. Both, a hyperbolic ( I(t)=I0·(1+τt) and Q(t)=Q0·(1+tτ), where I(t) and Q(t) are threshold stimulation current and charge for a pulse duration t, with the rheobase I0) and an exponential ( I(t)=I0/(1-exp(-tτ)) and Q(t)=Q0·tτ/(1-exp(-tτ))) model have been proposed. The E-field threshold for electric stimulation and the switching rate threshold dB/dt are proportional to I and show the same behavior, while the total change in B (ΔB) follows the behavior of Q. If the hyperbolic model applies, τ can be estimated by measuring Q or ΔB thresholds for different t, performing a linear fit, and calculating the ratio between intercept and slope (Irnich and Schmitt 1995). Evidently, linear fitting of Q(t) is not appropriate when assuming the validity of the exponential SD model, and the more generally applicable formula τ = Q0/I0 (or ΔB0/(dB/dt)0) can be used, where Q0 and I0 are obtained from the short- and long-pulse asymptotic behaviors in strength-duration plots.

The τ of the Spatially Extended Nonlinear Node (SENN) model (Reilly et al 1985, Reilly and Diamant 2011a), which is important for exposure safety standards, has been determined using electric stimulation and has been reported to be in the order of 0.12 ms - with known dependence on, e.g., electrode distance. While this is in agreement with some experimental data (Reilly and Diamant 2011b), the important early magnetic resonance imaging (MRI)-related work by (McRobbie and Foster 1984) suggested a magnetic stimulation τ in the order of 0.47 ms. In their experiments and by reviewing literature data (Recoskie et al 2010) have found widely varying τ with typical electric peripheral nerve stimulation τ in the order of 0.04 ms and magnetic stimulation τ in the order of 0.5 ms, and with significant differences between sensory or motoric activation (e.g., factor two for electric stimulation determined using electromyography). This paper investigates the effect of field inhomogeneity in the human body and the applied neuron model on τ predictions.

2. Methods

2.1. Computable Phantoms

The computable anatomical human phantoms are highly detailed virtual human models that have been functionalized with integrated multi-physics solvers, tissue models, and functions such as posing and morphing. The phantom are based on the Virtual Population 3.0 (ViP3.0) anatomical models (IT’IS 2015), a set of high resolution anatomical models generated based on MRI data from healthy volunteers (Christ et al 2010, Gosselin et al 2014) who were chosen to optimally represent the Caucasian population. The models distinguish over 300 different tissues and organs for which dielectric and thermal properties are available in a synchronized tissue properties database (Hasgall et al 2014). The values are based on extensive literature review and consist of tissue-specific averages and variability information. The ViP3.0 model surfaces consist of conformal, non-self-intersecting, high quality triangle meshes suitable for structured (rectilinear) and unstructured (tetrahedral) discretization. The functionalized phantoms combined with an advanced and modern graphical user interface (GUI) are the center of the Sim4Life simulation platform (ZMT Zurich MedTech AG, Switzerland).

New solvers, including neuronal tissue models, have been developed as part of a government-funded project conducted by the IT’IS Foundation (Switzerland), Ecole Polytechnique Federale de Lausanne (EPFL, Switzerland), ZMT, and the US Food and Drug Administration, Center for Devices and Radiological Health. The high performance computing enabled solvers are optimized for the simulation of physical, biological, and physiological processes in living tissue.

Within the anatomical models, a range of nerves have been segmented. For the purpose of this study, the Virtual Family model Ella has been functionalized with an ulnar and a sciatic nerve (Figure 2).

Figure 2.

Figure 2

Open in a new tab

ViP3.0 Ella model functionalized with ulnar and sciatic nerves.

EM Modeling

A range of EM solvers were already available: a hardware-accelerated finite-differences time-domain (FDTD) solver (Taflove and Hagness 2005) and various voxel-based electro- and magneto-(quasi)-static solvers. All of these solvers have been optimized for inhomogeneous material distributions, which are typical of the human body. Through the use of hardware acceleration and Message Passing Interface (MPI) parallelization large, finely discretized models can be simulated.

However, none of the existing solvers of the computable phantoms was capable of handling anisotropic tissue properties, which have an important impact on the field distribution in neural tissues at low frequencies (Hasgall et al 2014, Chaturvedi et al 2010). Thus a real-valued unstructured mesh FEM (Finite Element Method) electro-quasi-static solver has been developed. This solver supports inhomogeneous, anisotropic tissue conductivity distributions such as those obtained from diffusion tensor (DTI) imaging (Iacono et al 2015).

As neuronal dynamics is typically temperature-dependent, knowledge about local tissue temperature is a prerequisite. The functionalized anatomical models also include thermal and blood perfusion properties as well as a range of thermal tissue models and solvers optimized for the modeling of in vivo thermal processes in the presence of perfusion and thermoregulation (Murbach et al 2014).

Neuronal Dynamics

For neuronal dynamics modeling, the NEURON software (Carnevale and Hines 2006) was integrated into the computable phantoms. Coupling to EM-fields is achieved by calculating the electric potential distribution along the neuron geometry and using the ‘extracellular mechanism’ of NEURON. The potential distribution along the neuron trajectory is directly computed by trilinear interpolation of the electro-quasistatic solver results. For the FDTD and the magneto-quasistatic solvers, the interpolated E-fields are extracted and the tangential part is integrated along the neuron trajectory to obtain potential values. For temperature-dependent neuronal dynamics, the local temperature is determined by trilinear interpolation of the temperature simulation results. Detailed neuron models, as available in the ModelDB (Hines et al 2004), can be imported (morphology and distributed channel mechanisms) or modeled inside Sim4Life. Transient scaling of the stimulating EM fields (‘pulse shape’) can be specified, which scales the external potential applied to the neuronal dynamics model at each time-step. Functionality to automatically perform titration to identify stimulation thresholds was implemented for this study along with postprocessing functionality to analyze, for instance, transmembrane potential variations in time and space, and spike propagation.

Additional functionality includes the possibility to trace splines and assign them predefined neuronal dynamics behavior. Currently the SENN (Reilly et al 1985, Reilly and Diamant 2011a), because of its importance for exposure safety standards, as well as a more detailed mammalian motor-neuron model based on McIntyre et al (2002) (MOTOR) are supported for that purpose by the computable phantom. The latter features a double cable structure, finite impedance myelin sheets, paranodal segments and terminal attachments, fast and slow sodium channels, and produces the experimentally observed, typical after potentials and recovery cycle behavior. The splines are automatically discretized into the corresponding nodal, paranodal, and internodal sections. The SENN model consists of alternating node and internode (myelinated) segments. While the nodes show a dynamics derived from the Frankenhaeuser-Huxley model of myelinated neurons (Frankenhauser and Huxley 1964), the internodes only perform resistive coupling between nodes. Coupling to the external potential occurs at all segments. Q10 values characterizing the temperature dependence of the dynamics have been determined by (Waxman et al 1995). A basic SENN model has been implemented within Sim4Life/NEURON, where temperature is defined only as a global parameter without spatial variation. To facilitate modeling of local temperature-dependent neuronal dynamics, a novel SENN(T) model was created by compiling a Frankenhaeuser-Huxley mechanism in NEURON which accepts local temperature as an additional distributed parameter to adjust the neuronal dynamics accordingly. A similar approach was also used to create MOTOR(T), i.e., a temperature dependent version of the MOTOR model.

2.2. Verification

Verification is the process of ascertaining that the intended model is correctly implemented, while validation ascertains that the model reproduces critical features of reality within the intended context of use. Verification can be performed by comparing against analytically or numerically derived reference solutions. The FDTD and structured grid electro- and magneto-(quasi)-static EM solvers have been extensively verified (e.g., the FDTD solver was verified according to the IEC/IEEE 62704-1 standard proposal (IEEE 2002b)) and their verification documented in the Sim4Life V2.0 Manual. Here we concentrate on verifying the new anisotropic LF FEM solver and the neuronal dynamics modeling.

Anisotropic LF FEM Solver

Solver features that require verification are: i) the correct solving of the underlying equation (∇·σ̿(x) ∇ϕ(x) = 0, where σ̿ is the conductivity tensor and ϕ is the electric potential from which the electric field is obtained as E = −∇ϕ), ii) the convergence to the precise solution with increasing refinement and stricter convergence tolerance criteria, iii) the correct handling of sharp dielectic interfaces, and iv) proper implementation of boundary conditions (Dirichlet and Neumann). To verify i) and ii) the method of manufactured solutions (MMS) is used: a σ̿ distribution and a reference solution ϕref (x) are defined, allowing the analytical determination of a source distribution S(x) := ∇·σ̿(x) ∇ϕref (x). Subsequently the equation ∇·σ̿(x) ∇ϕ(x) = S(x) is solved using the LF FEM solver and the obtained ϕ (x) can be compared to ϕref (x). Three MMS cases with spatially varying sources were created: isotropic σ̿ (CaseIa), homogeneous anisotropic σ̿ (CaseIb), and inhomogeneous, anisotropic σ̿ (CaseIc). In all cases, a cube with 1 mm edge length is simulated. Care was taken in CaseIc to ensure that both the orientation of the conductivity tensor Eigenvectors and the corresponding eigenvalues vary spatially, while the latter remain larger than zero. To verify iii), and iv) a discontinuous case (CaseII) with scalar σ is implemented so that the left cube half has a three times larger conductivity than the right half. The left side is fixed (Dirichlet) to 0 V, the right to 1 V, and the other four sides are treated as insulating (Neumann). The reference solution has 0.75 V at the interface with linear variation from there to the left and right sides. In all cases, simulations have been performed using second order tetrahedral meshes at four resolutions ranging from 0.05–0.3 mm (200–24’000 elements; in some cases also 0.02 mm, 300’000 elements) to ascertain convergence. The error is quantified as maximal deviation from the reference solution.

Neuronal Dynamics

Neuronal dynamics modeling features that require validation are: i) the integration of NEURON, ii) the coupling to EM fields, iii) the implementation of pulsing, iv) loading of models from the ModelDB, iv) implementation of SENN and MOTOR, and v) implementation of the titration procedure for threshold determination. CaseIII tests i) and iv) by reproducing in Sim4Life a pyramidal neuron cell model (ModelDB reference: 106551, Figure 3) from the CA1 region of the hippocampus (Migliore et al 2005, Cassara et al 2008) performed in the NEURON environment. 33 stimulating clamps are placed at different dendrites to represent synaptic connections. The geometry, channel distribution, dynamics, environmental conditions, and spatio-temporal discretization information can be found in the ModelDB. Transient transmembrane potential was monitored at the soma and three apical dendrites. CaseIV tests i), ii), iii), iv), and v) by determining stimulation thresholds for straight splines fitted with SENN dynamics (at 22 °C) and comparing against values reported in (Reilly and Diamant 2011b). Over 20 different configurations were simulated using monopolar and bipolar stimulation with pulse durations ranging from 0.1–2.5 ms, homogeneous and point electrode (at 1 and 2 cm distance) field exposure, and parameters corresponding to 10 and 20 μm fiber diameter. Using homogeneous and localized exposure conditions ensures that both end-node and center-type stimulation mechanisms are checked. CaseV verifies in addition the MOTOR model by assigning corresponding dynamics (at 37 °C) to a spline exposed to the field of a point electrode in an anisotropic medium at varying distances (0.2–0.8 mm), fiber diameter (10 and 14 μm), and stimulation durations (0.1–10 ms) for a total of 24 configurations and comparing stimulation thresholds, strength-duration plots, and pulse shapes with those reported in (McIntyre et al 2004).

Figure 3.

Figure 3

Open in a new tab

Pyramidal neuron cell model used for verification (left), snapshot of transmembrane voltage potential (center), comparison of transient transmembrane potential monitored at the soma and three apical dendrites (right) calculated with NEURON (dashed, shifted by −15 mV for visualization purposes) and Sim4Life (continuous).

2.3. Application

The experimental setup described in (Recoskie et al 2010) was mimicked by placing alternatively two electrodes (diameter: 8 mm, distance 30 mm) or a ‘square figure-eight’ coil modeled on the geometries and locations from (Recoskie et al 2010) near the ulnar nerve of the functionalized Ella ViP3.0 model (Figure 4). In addition, stimulation of the sciatic nerve with similar field sources was also modeled. Electric stimulation was simulated by applying Dirichlet boundary conditions on the electrodes and using the ohmic-current dominated electro-quasi-static solver, while magnetic stimulation was simulated using the magneto-quasi-static solver with prescribed current in the coils. Both of these exposures generate a primary E-field component aligned with the nerve. The tissue conductivities were assigned using the data from (Hasgall et al 2014). Simulations were also performed for a simplified homogeneous cylinder model (σ: 0.333 S/m, diameter: 100 mm, length: 400 mm, Figure 5) with straight neuron trajectories at different depths (10–25 mm). The neurons were modeled with SENN (at 22 °C and 37 °C; 20 μm fibers – the worst-case considered in the standard based on the largest fibers expected in the human peripheral nervous system (PNS)) and MOTOR (37 °C; 16 μm fibers – the largest diameter characterized in (McIntyre et al 2002)) dynamics. To determine τ, stimulation thresholds I(t) were determined by titration for pulse durations varying from 0.01 ms to 5 ms in 22 logarithmically spaced steps. τ was then evaluated according to three approaches: τ1 = Q(0.01ms)/I(5ms), τ2 = Intercept(Q(t))/Slope(Q(t)) with (y-)Intercept and Slope evaluated by linear fitting of Q(t), and τ3 = InterceptReduced(Q(t))/I(5ms), where InterceptReduced(Q(t)) is the intercept obtained by linear fitting the data in the reduced range 0.01ms ≤ t ≤ 0.08ms to estimate Q0 instead of using Q(0.01ms).

Figure 4.

Figure 4

Open in a new tab

Model of ulnar (left) and sciatic (right) nerve stimulation. Setup (top), electric field distribution from electric and magnetic distribution (below), and tissue distribution (bottom right) with location of nerve transition from muscle into fat where spiking is initiated highlighted by arrow.

Figure 5.

Figure 5

Open in a new tab

Simplified homogeneous cylinder setup with straight neurons at different depths, electrodes for electric stimulation, and coil for magnetic stimulation (left). Depth dependence of τ1 for different neuronal dynamics models (SENN at 22 °C and 37 °C, MOTOR) and stimulation types (electric/magnetic) (right).

3. Results

3.1. Verification

Anisotropic LF FEM Solver

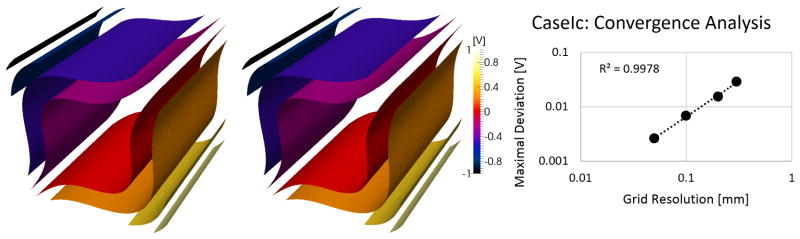
CaseIa-c all showed the expected exponential convergence to the reference solution as evident in log-log plots of maximum deviation against resolution that can be fitted linearly with an R2 > 0.994 in all cases (Figure 6 shows this for CaseIc). All resolutions of CaseII result in maximum deviations <3e-7 V, limited by the adaptable solver convergence tolerance criterion.

Figure 6.

Figure 6

Open in a new tab

Isosurfaces of reference solution and solution obtained using anisotropic LF FEM solver (left). Exponential reduction of error due to solution convergence with increasing mesh refinement, shown for CaseIc (right).

Neuronal Dynamics

No difference between the NEURON and Sim4Life results could be observed in CaseIII (Fig. 3). The SENN stimulation thresholds results of CaseIV show a maximal deviation of 12 % when compared to (Reilly and Diamant 2011b) which can be explained by the different numerical approaches of the temporal neuronal dynamics integration and the different discretization of the neuron. All the CaseV results obtained using MOTOR agree with those of (McIntyre et al 2002) within the variability specified in that paper.

3.2. Application

In the simplified cylindrical models the values obtained for τ1 as a function of the neuron depth for electric and magnetic stimulation and the three neuronal dynamics models can be seen in Figure 5. The values of τ1 obtained for sciatic and ulnar nerve stimulation using the functionalized anatomical model can be found in Table 1. τ1 is always (simplified and anatomical model) 10–34 % higher than τ2 for the SENN model at 22 °C, 76–107 % higher than τ2 for the SENN model at 37 °C, and between 25 % lower and 5 % higher than τ2 for the MOTOR model. τ3 is always similar to τ1 - between 1–12 % lower. Field distributions obtained in the functionalized anatomical models can be seen in Figure 4.

Table 1.

τ1 values obtained when applying electric or magnetic stimulation to the functionalized anatomical models.

τ1 [ms] SENN 22 °C SENN 37 °C MOTOR 37 °C
stimulation el. mag. el. mag. el. mag.
ulnar 0.16 0.13 0.11 0.085 0.45 0.38
sciatic 0.072 0.084 0.049 0.048 0.11 0.19
Open in a new tab

4. Discussion

The verification demonstrates the correctness of the anisotropic LF FEM solver implementation and the neuronal dynamics modeling.

When looking at the neuron-depth-dependence of the simplified, homogeneous cylindrical model (Figure 5), it is apparent that while magnetic stimulation produces constant τ, electric stimulation produces lower τ that approach the magnetic stimulation τ with increasing source distance. This is in agreement with the expected dependence on how localized the exposure is (Reilly and Diamant 2011b). τ1 for SENN at 22 °C and magnetic stimulation is 0.17 ms (τ2 is 0.13 ms, similar to the value reported in (Reilly and Diamant 2011b)). However, when a more realistic body temperature of 37 °C is used, τ1 decreases to 0.12 ms. And with MOTOR one obtains 0.5 ms which is closer to the mean reported measurements for magnetic stimulation in (Recoskie et al 2010) and very similar to the original data from (McRobbie and Foster 1984), while the MOTOR electric stimulation time constant is much higher than the measured one. The τ1 values obtained for electrical stimulation of the ulnar nerve in the anatomical model are very similar in magnitude to those observed in the cylindrical model (Table 1). The magnetic stimulation values are 30 % lower than those obtained in the homogeneous cylindrical model, which can be explained by the field inhomogeneity introduced by the body, by the curved trajectory, and by the varying nerve depth. However, the τ1 values obtained for the sciatic nerve are much shorter - in most cases about half of the τ1 values obtained for the ulnar nerve and only a quarter for electric stimulation with MOTOR dynamics (0.11 ms, much shorter than the magnetic stimulation τ1). Those sciatic τ values are closer to the ones reported for electric stimulation in (Recoskie et al 2010); and the difference between electric and magnetic stimulation τ observed for the sciatic nerve using MOTOR, while less pronounced, is also reminiscent of the difference observed in (Recoskie et al 2010). The important decrease in τ observed in the sciatic nerve model could be explained by a strong field inhomogeneity at the location where the nerve transitions from fat to muscle, marked by an arrow in Figure 4, which is also where spike initiation is observed. This indicates that anatomy-induced field inhomogeneity could be important for the observed behavior of τ and that functionalized, computable anatomical models play a valuable role for the investigation of these mechanisms. Incorporating these models into safety standards would improve the technical basis and reliability upon which safety criteria are established.

The important differences between τ1 and τ2 observed for the SENN model are due to the behavior of Q(t) for small t, which does not follow the linear relationship expected by the hyperbolic model, but starts flattening, though not as pronouncedly as expected by the exponential model (Fig. 7). This lowers the estimation of Q0 obtained from the intercept of the linear _t compared to using Q(0.01ms). With the MOTOR model, the flattening trend is also observed, but starts to reverse again for very short t below 0.1 ms, which compensates the effect, eliminating the difference between τ1 and τ2. The slightly lower τ3 compared to τ1 is a result of the modified approach to extrapolating the Q(t) behavior below t = 0.01 ms to obtain Q0. These results suggest that using τ2 is problematic when Q(t) does not follow exactly the hyperbolic model, and that the behavior for very short t must be carefully assessed when determining Q0.

Figure 7.

Figure 7

Open in a new tab

Q(t) for the SENN and MOTOR models (ulnar nerve, electric stimulation, 37 °C) over the full pulse duration range (left) and zoom to short pulse durations (right). The linear fits are shown, and the deviation for short pulse durations from the ideal linearity of the hyperbolic model is apparent.

5. Conclusions

This study describes the development and verification of computable, functionalized anatomical models for the investigation of coupled EM-neuronal dynamics within the high-fidelity anatomical environment of the Virtual Population. An anisotropic LF FEM solver has been developed and extensively verified using the method of manufactured solutions to ascertain correct handling of discontinuities, anisotropy, inhomogeneity, and boundary conditions. The full integration of NEURON permits modeling of neurons with complex morphologies and channel dynamics. This integration as well as the implementation of SENN and MOTOR models for peripheral nervous system modeling have been verified against published results obtained using different numerical implementations.

The computable, functionalized anatomical models can be used to study the combined effect of inhomogeneous in vivo fields and detailed neuronal dynamics. In this study, electric and magnetic stimulation of the ulnar and sciatic nerve were modeled to help resolve a range of controversial issues related to the strength-duration time constant. The results indicate that field inhomogeneities introduced for example at locations where the nerve transitions between muscle and fat, in combination with the stimulation-specific field distribution and the detailed neuronal dynamics model help explain the observed variation in time constants. The optimal approach of determining τ is affected by the Q(t) behavior for short duration pulses, and unless the hyperbolic model is strictly applicable, the linear fitting approach from (Irnich and Schmitt 1995) (τ2) should be employed with care, knowing that the obtained value of τ will depend on the measured pulse duration range.

The computable, functionalized anatomical models offer a new way of investigating applications ranging from electrical and magnetic stimulation (brain, spine, PNS, etc.) to low frequency exposure safety assessment, and the investigation of neuromotoric incapacitation. The functionalized computable phantom will influence and support the development of safe and effective neuroprosthetic devices and novel electroceuticals. Furthermore they will assist the evaluation of existing low frequency exposure standards for the entire population under all exposure conditions. Future work will include functionalization of the models with a large number of PNS nerve trajectories and neurons and experimental validation of the coupled EM-neuronal dynamics modeling.

Acknowledgments

This study was supported by the project CAPITALIS (14930.1 PFLS-LS) of the Swiss Commission for Innovation and Technology (CTI) and FDA’s Critical Path Initiative.

Footnotes

Disclaimer

The mention of commercial products, their sources, or their use in connection with material reported herein is not to be construed as either an actual or implied endorsement of such products by the Department of Health and Human Services.

References

  1. Carnevale NT, Hines ML. The NEURON Book. Cambridge University Press; 2006. [Google Scholar]
  2. Cassara A, Hagberg G, Bianciardi M, Migliore M, Maraviglia B. NeuroImage. 2008;39(1):87–106. doi: 10.1016/j.neuroimage.2007.08.048. [DOI] [PubMed] [Google Scholar]
  3. Chaturvedi A, Butson CR, Lempka SF, Cooper SE CMC. Brain Stimulation. 2010;3(2):65–77. doi: 10.1016/j.brs.2010.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Christ A, Kainz W, Hahn EG, Honegger K, Zefferer M, Neufeld E, Rascher W, Janka R, Bautz W, Chen J, Kiefer B, Schmitt P, Hollenbach H, Shen J, Oberle J, Szczerba D, Kam A, Guag JW, Kuster N. Physics in Medicine and Biology. 2010;55(2):N23–N38. doi: 10.1088/0031-9155/55/2/N01. [DOI] [PubMed] [Google Scholar]
  5. Frankenhauser B, Huxley AF. Journal of Physiology. 1964;171(2):302–315. doi: 10.1113/jphysiol.1964.sp007378. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Gosselin M, Neufeld E, Moser H, Huber E, Farcito S, Gerber L, Jedensjo M, Hilber I, Di Gennaro F, Lloyd B, Cherubini E, Szczerba D, Kainz W, Kuster N. Physics in Medicine and Biology. 2014;59(18):5287–5303. doi: 10.1088/0031-9155/59/18/5287. [DOI] [PubMed] [Google Scholar]
  7. Hasgall P, Neufeld E, Gosselin M, Di Gennaro F, Baumgartner C, Klingenbock A, NK IT’IS database for thermal and electromagnetic parameters of biological tissues, version 2.5. 2014 http://www.itis.ethz.ch/database.
  8. Hines ML, Morse T, Migliore M, Carnevale NT, Shepherd GM. Journal of Computational Neurosciences. 2004;17(1):7–11. doi: 10.1023/B:JCNS.0000023869.22017.2e. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Iacono MI, Neufeld E, Akinnagbe E, Bower K, Wolf J, Oikonomidis IV, Sharma D, Lloyd B, Wilm BJ, Wyss M, et al. PloS one. 2015;10(4) doi: 10.1371/journal.pone.0124126. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. IEC. Medical electrical equipment - particular requirements for the basic safety and essential performance of magnetic resonance. International Electrotechnical Commission; Geneva, Switzerland: 2010. [Google Scholar]
  11. IEEE. C95.6-2002, IEEE Standard for Safety Levels with Respect to Human Exposure to Electromagnetic Fields, 0–3 kHz. The Institute of Electrical and Electronic Engineers; New York, USA: 2002a. [Google Scholar]
  12. IEEE. IEC/IEEE Draft Standard for Determining the Peak Spatial Average Specific Absorption Rate (SAR) in the Human Body from Wireless Communications Devices, 30 MHz - 6 GHz. Part 1: General Requirements for using the Finite Difference Time Domain (FDTD) Method for SAR Calculations. The Institute of Electrical and Electronic Engineers; New York, USA: 2002b. [Google Scholar]
  13. Irnich W, Schmitt F. Magnetic resonance in medicine. 1995;33(5):619–623. doi: 10.1002/mrm.1910330506. [DOI] [PubMed] [Google Scholar]
  14. IT’IS. Virtual population version 3.0. 2015 http://www.itis.ethz.ch/virtual-population/
  15. McIntyre CC, Grill WM, Sherman DL, Thakor NV. Journal of Neurophysiology. 2004;91(4):1457– 1469. doi: 10.1152/jn.00989.2003. [DOI] [PubMed] [Google Scholar]
  16. McIntyre CC, Richardson AG, Grill WM. Journal of Neurophysiology. 2002;87(2):995–1006. doi: 10.1152/jn.00353.2001. [DOI] [PubMed] [Google Scholar]
  17. McRobbie D, Foster MA. Clinical Physics and Physiological Measurement. 1984;5(2):67–78. doi: 10.1088/0143-0815/5/2/002. [DOI] [PubMed] [Google Scholar]
  18. Migliore M, Ferrante M, Ascoli GA. Journal of neurophysiology. 2005;94(6):4145–4155. doi: 10.1152/jn.00521.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Murbach M, Neufeld E, Capstick M, Kainz W, Brunner DO, Samaras T, Pruessmann KP, Kuster N. Magnetic Resonance in Medicine. 2014;71(10):421–431. doi: 10.1002/mrm.24671. [DOI] [PubMed] [Google Scholar]
  20. Neufeld E, Vogiatzis Oikominidis I, Iacono MI, Angelone LM, Kainz W, Kuster N. Physics in Medicine and Biology. 2015 doi: 10.1088/0031-9155/61/12/4466. (submitted) [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Recoskie BJ, Scholl TJ, Chronik BA. Physics in medicine and biology. 2009;54(19):5965. doi: 10.1088/0031-9155/54/19/020. [DOI] [PubMed] [Google Scholar]
  22. Recoskie BJ, Scholl TJ, Zinke-Allmang M, Chronik BA. Magnetic Resonance in Medicine. 2010;64(6):1567–1579. doi: 10.1002/mrm.22505. [DOI] [PubMed] [Google Scholar]
  23. Reilly J, Diamant AM. Spatially extended nonlinear node (SENN) model of electrostimulation of myelinated nerve. 2011a http://www.artechhouse.com/static/reslib/reilly/reilly.html.
  24. Reilly JP. Physics in medicine and biology. 2010;55(4):L5. doi: 10.1088/0031-9155/55/4/L01. [DOI] [PubMed] [Google Scholar]
  25. Reilly JP, Diamant AM. Electrostimualtion Theory, Applications, and Computational Model. Artech House; 2011b. [Google Scholar]
  26. Reilly JP, Freeman VT, Larkin WD. IEEE Transactions on Biomedical Engineering. 1985;32(12):1001–1011. doi: 10.1109/TBME.1985.325509. [DOI] [PubMed] [Google Scholar]
  27. Taflove A, Hagness SC. Computational electrodynamics. Artech house; 2005. [Google Scholar]
  28. Waxman SG, Kocsis JD, Stys PK. The Axon: Structure, Function, and Pathophysiology. Oxford University Press; 1995. [Google Scholar]

RESOURCES