Mechanisms underlying the volume regulation of interstitial fluid by capillaries: a simulation study

Abstract

Background

Control of the extracellular fluid volume is one of the most indispensable issues for homeostasis of the internal milieu. However, complex interdependence of the pressures involved in determination of fluid exchange makes it difficult to predict a steady-state tissue volume under various physiological conditions without mathematical approaches.

Methods

Here, we developed a capillary model based on the Starling's principle, which allowed us to clarify the mechanisms of the interstitial-fluid volume regulation. Three well known safety factors against edema: (1) low tissue compliance in negative pressure ranges; (2) lymphatic flow driven by the tissue pressure; and (3) protein washout by the lymph, were incorporated into the model in sequence.

Results

An increase in blood pressure at the venous end of the capillary induced an interstitial-fluid volume increase, which, in turn, reduced negative tissue pressure to prevent edema. The lymphatic flow alleviated the edema by both carrying fluid away from the tissue and decreasing the colloidal osmotic pressure. From the model incorporating all three factors, we found that the interstitial-fluid volume changed quickly after the blood pressure change, and that the protein movement towards a certain equilibrium point followed the volume change.

Conclusion

Mathematical analyses revealed that the system of the capillary is stable near the equilibrium point at steady state and normal physiological capillary pressure. The time course of the tissue-volume change was determined by two kinetic mechanisms: rapid fluid exchange and slow protein fluxes.

1. Introduction

Quantitative analysis of microcirculation at the capillary bed is indispensable when studying systemic circulation. Fluids that circulate through the vessels filter in and out through the membrane at the capillary bed in organ tissues. In order to comprehend the dynamics of complex fluid regulation, it is important to estimate the amount of fluid exchanged at the capillaries quantitatively.

Volume regulation, which includes fluid filtration, reabsorption, and formation of lymph, had been discussed using analogue computer simulations in the 1970s and 1980s.1, 2, 3 They succeeded in simulating steady-state levels and transient responses of the essential physiological parameters involved in volume regulation, such as plasma volume, interstitial volume, and lymphatic flow (LF). However, such system analyses put emphasis on understanding the fluid balance in the whole body, and detailed analysis of the volume change and protein flux at the level of capillary was not feasible in those analyses due to the lack of computational capacity.

At a single capillary level, Curry and Michel⁴ suggested the fibre-matrix theory of capillary permeability in 1980. This theory led to the revision of Starling's principle (1886) after a centennial of belief (see Levick's⁵ review article). In line with the revision, Adamson et al⁶ introduced the idea of subglycocalyx fluid oncotic pressure (Π_g) instead of Π_isf in calculating effective filtration pressure. In this revised theory, they estimated that, in case of steady-state filtration, a subglycocalyx protein concentration was lower than the interstitial protein concentration, and there were smaller gradients between Π_isf and Π_g, which was assumed to be 70–90% of Π_isf. However, in case of steady-state absorption, they confirmed that the reversed flow of the interstitial fluid caused reflected protein to accumulate in the subglycocalyx space, and Π_g became larger than Π_isf to cease the absorption within a few minutes. Although a thorough revision of the hypothesis was a landmark study to look into the detailed function of the capillaries, it is also widely accepted that continuous vasomotion with a cycle time of ∼15 seconds keeps all of the parameters in the system in a transient state. Therefore, in the first stage of our single capillary model, we adopted the classical Starling's principle consisting of four primary forces to move fluids across the capillary membrane: the capillary plasma pressure (P_pl), the interstitial fluid pressure (P_isf), the capillary plasma colloidal osmotic pressure (Π_pl), and the interstitial fluid osmotic pressure (Π_isf), to evaluate the averaged function of multiple capillaries within tissue. There is also a tissue specific nonlinear relationship between P_isf and the interstitial fluid volume (V_isf), which plays a key role in preventing edema. Additionally, the LF, which is regulated by interstitial fluid pressure, carries protein as well as fluid away from the tissue.

In this study, we aimed to construct a realistic and versatile model of fluid exchange based on Starling's principle and included general features of tissue, such as the nonlinear relationship between P_isf and V_isf (tissue compliance) and the P_isf dependency of the LF. Then we applied mathematical analyses to the models to understand the mechanisms of the fluid volume regulation, quantitatively.

2. Methods

2.1. Governing equations for capillary filtration

In the present study, the involvement of the crystalloid osmotic pressure is entirely excluded, and the fluid filtration (J) across the capillary is determined by the following equation based on Starling's principle:

$$J=K\times P_E\cdot (\text{mL}/\text{ms}/\text{mm})$$ (1)

K (mL/ms/mmHg/mm) is the endothelial hydraulic conductance, which is a measure of the capacity of the capillary membrane to filter water per unit capillary length. P_E is the effective net filtration pressure that is the sum of four primary forces to move fluids across the membrane, P_pl, P_isf, Π_pl and Π_isf;

$$P_E=\left(P_{pl}-P_{isf}\right)-\left({\Pi }_{pl}-{\Pi }_{isf}\right)(\text{mmHg})$$ (2)

When P_E is positive, there will be a fluid filtration across the capillary membrane. Inversely, if P_E is negative, there will be a fluid absorption from the interstitial space into the capillary. Standard pressure values used in calculating P_E in the model are listed in Table 1.

Table 1.

Pressures used for calculating fluid effective filtration pressure

	Arterial end (mmHg)	Venous end (mmHg)
Capillary blood pressure (Ppl)	25	15
Plasma colloidal-osmotic pressure (πpl)	28
Tissue interstitial-fluid pressure (Pisf)	−3
Tissue interstitial-fluid colloidal osmotic pressure (πisf)	8
Effective filtration pressure (PE)	13	−7

2.2. Structure of the model

2.2.1. A capillary vessel model

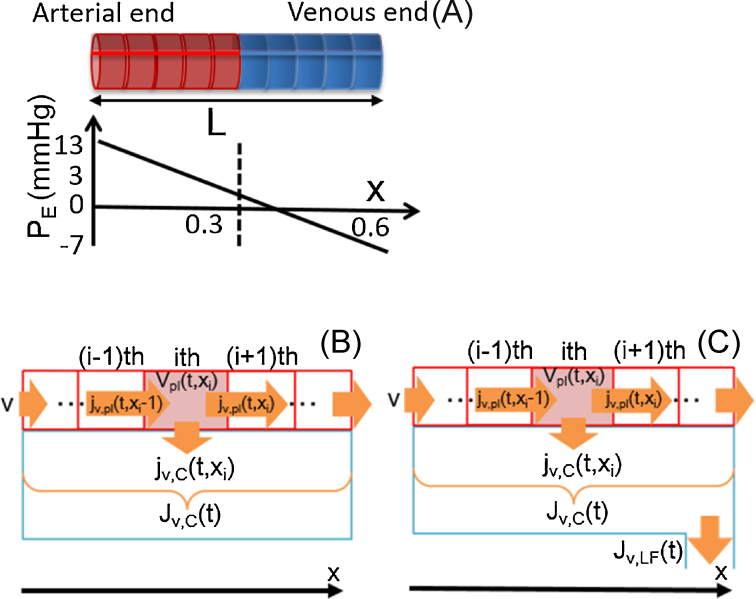
The conformation of the capillary is assumed to be a cylinder (Fig. 1A). Parameters used in the capillary model are listed in Table 2. The internal radius of the capillary model (r) is 5 μm, and the length of the vessel from the arterial end to venous end (L) is 0.6 mm. It is well known that blood flow through each capillary is intermittent because of vasomotion, which is caused by intermittent contraction of metarterioles and precapillary sphincters. There are so many capillaries present in living tissue that their overall function becomes averaged. Therefore, in the present model, the average function of the capillary will be discussed.

Fig. 1.

Schematic representation of a single capillary. (A) Effective filtration pressure along the capillary. (B, C) Compartmentalization of a single capillary model and interstitial fluid facing to the capillary. Lymph drains from the interstitial space.

Table 2.

Parameter values for the capillary model

Symbol	Definition	Value	Unit
t	Time		ms
Δx	Length of a capillary compartment (= L/N)	0.01	mm
xi	Axial position of ith compartment in the capillary		mm
N	Number of compartment	60
K	Serum conductivity	1.26 × 10−10	μL/mmHg/ms/mm
Hc	Hematocrit	0.4
Gp	Protein permeability of large pore system	1.13 × 10−11	μL/ms/mm
L	Capillary length	0.6	mm
r	Capillary radius	0.004	mm
rK	Radius of the Krough muscle cylinder	18	μm
vflow	Flow rate of capillary plasma	1.0 × 10−3	mm/ms
PE	Effective net filtration pressure		mmHg
Ppl,a	Blood hydrostatic pressure at the arterial end of the capillary	25	mmHg
Ppl,v	Blood hydrostatic pressure at the venous end of the capillary	15	mmHg
ppl(xi)	Blood hydrostatic pressure at axial position (xi)		mmHg
${\overline{p}}_{pl}$	Averaged value of hydrostatic pressure in capillary		mmHg
$P_{isf}^0$	Original interstitial fluid pressure	−3	mmHg
Pisf(t)	Interstitial fluid pressure at time (t)		mmHg
$V_C^0$	Original capillary volume	3.02 × 10−5	μL
$V_{pl}^0$	Original initial capillary volume at each compartment	3.02 × 10−5	μL/mm
vpl(t, xi)	Capillary compartment volume at axial position (xi) and time (t)		μL
$V_{isf}^0$	Original interstitial fluid volume	6.0 × 10−5	μL
Visf(t)	Interstitial fluid volume at time (t)		μL
Visf,L(t)	Instantaneous equilibrium point of interstitial fluid volume at time (t)		μL
${\Pi }_{pl}^0$	Initial plasma colloidal osmotic pressure in each capillary compartment	25	mmHg
πpl(t, xi)	Plasma colloidal osmotic pressure in capillary compartment at axial position (xi) and time (t)		mmHg
${\overline{\Pi }}_{pl}(t)$	Averaged value of colloidal osmotic pressure at time (t)		mmHg
${\Pi }_{isf}^0$	Initial interstitial fluid colloidal osmotic pressure	3	mmHg
Πisf(t)	Colloidal osmotic pressure in interstitial fluid at time (t)		mmHg
s	Proportional factor for lymphatic flow	9.79 × 10−12	μL/ms
R	Contamination ratio of protein in the serum filtrate	0.01555
Jv(t)	The volume change of interstitial fluid		μL/ms/mm
Jv,C(t)	Total transcapillary fluid flux		μL/ms/mm
jv,C(t, xi)	Transcapillary fluid flux at axial position (xi) and time (t)		μL/ms/mm
jv,pl(t, xi)	Plasma flux from ith compartment to (i + 1)th compartment at time (t)		μL/ms/mm
Jv,LF(t)	Lymphatic flow at time (t)		μL/ms/mm
Jq,C(t)	Total protein flux carried by large pore system by diffusion and fluid convection at time (t)		μg/ms/mm
jq,C(t, xi)	Protein flux carried by large pore system by diffusion and fluid convection at axial position (xi) and time (t)		μg/ms/mm
jq,pl(t, xi)	Protein flux carried by blood flow from ith compartment to (i + 1)th compartment		μg/ms/mm
Jq,LF(t)	Protein flux carried by lymph flow at time (t)		μg/ms/mm
qpl(t, xi)	Amount of protein in capillary compartment at axial position (xi) and time (t)		μg
Qisf(t)	Amount of protein in interstitial fluid at time (t)		μg
cpl(t, xi)	Concentration of serum protein in capillary compartment at axial position (xi) and time (t)		μg/μL
Cisf(t)	Concentration of serum protein in interstitial fluid at time (t)		μg/μL

2.2.2. Determination of the permeability for capillary

On the capillary wall, there are intercellular clefts at the junction between adjacent endothelial cells. The size of the clefts, or the pore size of the glycocalyx sieve, is large enough for the H₂O molecules and most small water-soluble substances, but is obviously too small for plasma proteins to permeate. In our model, this permeability of the capillary is represented as K, and is estimated by assuming that 8-mmHg filtration pressure causes, on average, ∼1/200 of plasma of flowing blood to filter out of the arterial ends of the capillary and into the interstitial spaces each time the blood passes through the capillaries.⁷ It is also assumed that one half of the capillary (L/2) is the arterial end, 60% of the blood is plasma (H_c = 0.4; Fig. 1A), and the velocity of capillary blood flow is v (1.0 × 10⁻³ mm/ms). K is determined as follows:

$$K=\frac{V_C\times (1-H_C)\times \frac{1}{200}}{\frac{L}{2\times v}\times 8}\times \frac{2}{L}=1.26\times {10}^{-10}(\mu \text{L}/\text{ms}/\text{mmHg}/\text{mm})\text{.}$$

2.2.3. Estimation of the interstitial fluid volume in relation to blood volume for a single cylinder capillary model

We introduced the idea of the Krogh muscle cylinder to estimate the interstitial fluid volume supplied by a single capillary.⁸ The radius of the Krough muscle cylinder (rK) varies between 18 μm and 36 μm, depending on the metabolic demand of the tissue. Here, we assumed the most perfused condition having the smallest rK value of 18 μm. The radius (r) and the length of the capillary (L) is 4 μm and 600 μm, respectively. Considering that 89% of the muscle is occupied by cells and the rest by the extracellular fluid, the interstitial fluid volume could be calculated by the following equation:

$$600\times \pi \times ({\text{rk}}^2-r^2)\times 0.11=6.3862(m{m}^3)\approx 6.0(\mu L)\text{.}$$

We used this value as the initial interstitial fluid volume, $V_{isf}^0$.

2.3. Mathematical formulations for simulation

We developed four models sequentially by introducing three safety factors in preventing edema: (1) low tissue compliance in negative pressure range; (2) increased LF; and (3) protein washout by the LF, and clarified the involvement of these factors in the interstitial-fluid volume regulation. In Model 1, there were two volumes with different hydrostatic and colloidal osmotic pressures, capillary, and the interstitial fluid. They exchanged fluid across the membrane, but not for the protein. Then, the nonlinear compliance of the tissue was implemented in Model 2 to determine the effect of the small tissue compliance in the range slightly negative to the atmospheric pressure. In order to clarify the effect of LF, we firstly assumed that the lymph carried only fluid in Model 3. Based on Model 3, we finally developed a full capillary model with the protein dynamics in Model 4. Equations corresponding to the sequential development from Model 1 to Model 4 are listed in Table 3.

Table 3.

Correspondence of equations used in Models 1–4

Model no.	Model features	Modifications in the model
Model 1	Base model
Model 2	Base model + nonlinear tissue compliance	Eq. (9) → qEq. (9′)
Model 3	Model 2 + lymphatic flow	Eq. (7) → qEq. (7′)
Model 4	Model 3 + protein dynamics	Eq. (10) → qEq. (10′) Eq. (11) → qEq. (11′)

2.3.1. Model 1

2.3.1.1. Calculation of plasma flow in a capillary and fluid flux across the capillary membrane

The capillary model is divided into N (60 in our model) compartments along the x-axis as in Fig. 1B to calculate plasma flow within a capillary in a discretized manner.

The plasma flux between the ith and the (i + 1)th compartment is expressed as $j_{v,pl}(t,x_i)$ and calculated by the following equation:

$$j_{v,pl}(t,x_i)=\frac{v_{pl}(t,x_i)}{\Delta x}\times v_{flow}\times \frac{1}{L}\text{,}$$ (3)

where $v_{pl}(t,x_i)$, Δx, and $v_{flow}$ are the plasma volume of the ith compartment, the length of each compartment, and the velocity of capillary plasma flow in the capillary, respectively.

Now we assume that the capillary wall is facing the interstitial-fluid space of the tissue, which has different P and Π, and the pressure difference across the wall forces fluids to permeate between the capillary and the tissue. From the governing equations, Eqs. (1), (2), the trans-capillary fluid flux at the ith compartment [$j_{v,C}(t,x_i)$ (μL/ms/mm)] is calculated from the fluid hydrostatic pressure and colloidal osmotic pressure differences between plasma and interstitial fluid [p_pl(x_i), P_isf, π_pl(t, x_i), and Π_isf(t) (mmHg)], as a function of axial position in the capillary [x_i (mm)) and time (t (ms)] as follows:

$$j_{v,C}(t,x_i)=K\times \left\{(p_{pl}(x_i)-P_{isf})-({\pi }_{pl}(t,x_i)-{\Pi }_{isf}(t))\right\}$$ (4)

Taken together, the inflow and outflow of the plasma volume in the ith compartment, the change in $v_{pl}(t,x_i)$ (μL) is calculated as:

$$\begin{array}{c}\hfill \frac{\partial v_{pl}(t,x_i)}{\partial t}=j_{v,pl}(t,x_{i-1})-j_{v,pl}(t,x_i)-j_{v,C}(t,x_i)\hfill \\ \hfill =-\frac{v_{pl}(t,x_i)-v_{pl}(t,x_{i-1})}{\Delta x}\times v_{flow}-j_{v,C}(t,x_i)\hfill \end{array}$$ (5)

It is known that the red blood cell size is similar to that of the capillary diameter. Therefore, the plasma flow in our capillary model is assumed to be similar to plug flow rather than laminar flow, assuming rapid radial diffusion. The fluid flux between each capillary compartment and the interstitial fluid space accumulates and changes the interstitial fluid volume, V_isf(t). The integration of the fluxes is calculated by the following discretized equation using the term, $J_{v,c}(t)$ (μL/ms/mm; Fig. 1B):

$$J_{v,C}(t)=\frac{1}{L}\times {\sum }_{i=1}^N\{j_{v,C}(t,x_i)\times \Delta x\}$$ (6)

$$\frac{\partial V_{isf}}{\partial t}=J_{v,C}(t)$$ (7)

2.3.1.2. Equations for calculating hydrostatic pressure of the capillary plasma and the interstitial fluid

In our capillary model, the plasma hydrostatic pressure, P_pl(x_i) (mmHg), is given by a linear function of axial distance of the ith compartment, x_i (mm), along the capillary of length L (0.6 mm), which is independent of time [t (s)].

$$p_{pl}(x_i)=P_{pl,a}+(P_{pl,v}-P_{pl,a})\times \frac{x_i}{L}\text{,}$$ (8)

where P_pl,a and $P_{pl,v}$ are the plasma hydrostatic pressures at the arterial and venous ends of the capillary, respectively. In Model 1, P_isf is fixed to a given value:

$$P_{isf}=P_{isf}^0(=-3)(\text{mmHg})\text{.}$$ (9)

2.3.1.3. Equations for calculating colloidal osmotic pressure in plasma and interstitial fluid

As the serum proteins are not assumed to move across the capillary membrane in Model 1, the amount of protein stays constant. Therefore, the colloidal osmotic pressures for plasma π_pl(t, x_i) (mmHg) and interstitial fluid Π_isf(t) (mmHg) are given by the following equations, respectively:

$${\pi }_{pl}(t,x_i)={\Pi }_{pl}^0\times \frac{V_{pl}^0}{v_{pl}(t,x_i)}\text{,}$$ (10)

$${\Pi }_{isf}(t)={\Pi }_{isf}^0\times \frac{V_{isf}^0}{V_{isf}(t)}\text{.}$$ (11)

2.3.2. Model 2

2.3.2.1. Calculating interstitial fluid pressure using a nonlinear compliance equation

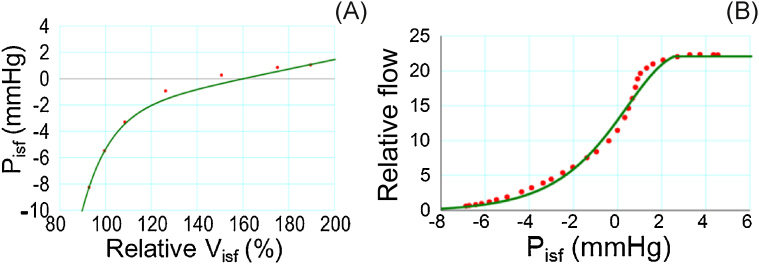
A nonlinear relationship is well-known between the interstitial fluid pressure and its volume from experiments on living tissue (Fig. 2A):

$$P_{isf}(t)=f_1\left(V_{isf}(t)\right)=-3.139\times e^{\frac{1-\frac{V_{isf}(t)}{V_{isf}^0}}{0.12}}+3.61\times \frac{V_{isf}(t)}{V_{isf}^0}-5.6964$$ (9′)

where f₁ represents an equation fitted to the experimental data.⁹

Fig. 2.

Nonlinear relationship used in models. (A) Relationship between V_isf and P_isf introduced in Models 2–4. (B) Relationship between P_isf and relative lymph flow introduced in Models 3 and 4.

2.3.3. Model 3

2.3.3.1. Estimation of the LF

LF is known to increase as the interstitial fluid pressure rises, but it reaches an upper limit when the interstitial fluid pressure rises above a certain level (Fig. 2B):

$$\begin{array}{c}\hfill J_{v,LF}(t)=f_2\left(P_{isf}(t)\right)\hfill \\ \hfill =\frac{s}{0.06\times e^{\frac{P_{isf}(t)}{2.16}}+0.015\times e^{\frac{P_{isf}(t)}{4.5}}}\times \frac{1}{L}\hfill \end{array}$$ (12)

where f₂ is obtained by fitting an equation to the relationship given by Taylor et al¹⁰ and rescaled by multiplying the scaling factor, s = 9.7922 × 10⁻¹² (μL/ms), to balance with the net filtration at the capillary.

As the LF carries fluid from the interstitial space to the lymphatic capillaries (Fig. 1C), the volume change of the interstitial fluid is expressed as:

$$\frac{\partial V_{isf}(t)}{\partial t}=J_{v,C}(t)-J_{v,LF}(t)\text{.}$$ (7′)

2.3.4. Model 4

2.3.4.1. Equations for calculating colloidal osmotic pressure in plasma and interstitial fluid

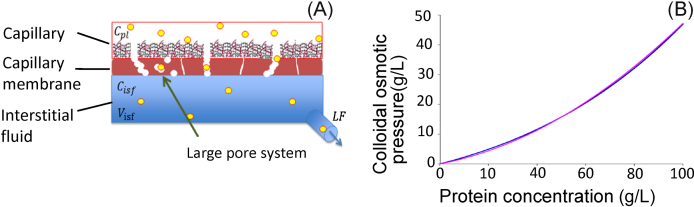
Lastly, protein concentration is taken into account to refine the model of fluid-volume regulation. It is known that there is a ‘large pore system’ that transports plasma proteins through the membrane (Fig. 3A). Additionally, a small amount of protein dissolved in plasma or interstitial fluid leaks through the membrane in the process of fluid convection. Therefore, the protein flux carried out by blood flow through capillary vessels [j_q,pl(t, x_i)] and the sum of the protein flux carried by the large pore system by diffusion and fluid convection across the capillary membrane [$j_{q,C}\left(t,x_i\right)$] are calculated for each compartment as follows:

$$J_{q,pl}(t,x_i)=\frac{q_{pl}(t,x_i)}{\Delta x}\times v_{flow}\times \frac{1}{L}$$ (13)

$$\begin{array}{c}\hfill \frac{\partial q_{pl}(t,x_i)}{\partial t}=j_{q,pl}(t,x_{i-1})-j_{q,pl}(t,x_i)-j_{q,C}(t,x_i)\hfill \\ \hfill =-\frac{q_{pl}(t,x_i)-q_{pl}(t,x_{i-1})}{\Delta x}\times v_{flow}-j_{q,C}(t,x_i)\hfill \end{array}$$ (14)

$$\left\{\begin{array}{c}\hfill j_{q,C}(t,x_i)=G_p\times \left(c_{pl}(t,x_i)-C_{isf}(t)\right)+j_{v,C}(t,x_i)\times c_{pl}(t,x_i)\times R(\text{in}\text{case}\text{of}\text{filtration})\hfill \\ \hfill j_{q,C}(t,x_i)=G_p\times \left(c_{pl}(t,x_i)-C_{isf}(t)\right)+j_{v,C}(t,x_i)\times C_{isf}(t)\times R(\text{in}\text{case}\text{of}\text{reabsorption})\hfill \end{array}\right)$$ (15)

where j_q,pl(t, x_i) or j_q,C(t, x_i), q_pl(t, x_i), G_p, c_pl(t, x_i) or C_isf(t), and R are protein fluxes along the capillary or across the capillary membrane, the quantity of protein in plasma, protein permeability through the large pore system, protein concentration in plasma or interstitial fluid, and relative protein permeability of the membrane to water, respectively. Then, similar to $J_{v,C}(t)$, integrated fluxes for the protein are calculated by the following discretized equation using the term J_q,C(t) (μg/ms/mm):

$$J_{q,C}(t)=\frac{1}{L}\times {\sum }_{i=1}^N\{j_{q,C}(t,x_i)\times \Delta x\}$$ (16)

Fig. 3.

Implementation of protein dynamics into Model 4. (A) Cross-section of capillary membrane showing transmembrane protein transport. (B) Relationship between protein concentration and colloidal osmotic pressure. An equation (pink) was fitted to a curve from a textbook⁸ (blue).

The removal of plasma proteins by LF is given by:

$$J_{q,LF}(t)=J_{v,LF}(t)\times C_{isf}(t)$$ (17)

$$\frac{\partial Q_{isf}(t)}{\partial t}=J_{q,C}(t)-J_{q,LF}(t)$$ (18)

The concentrations of protein [c_pl(t, x_i) and C_isf(t)] are calculated from the amounts of protein [q_pl(t, x_i) and Q_isf(t)] and the fluid volumes [$v_{pl}(t,x_i)$ and V_isf(t)].

$$c_{pl}(t,x_i)=\frac{q_{pl}(t,x_i)}{v_{pl}(t,x_i)}$$ (19)

$$C_{isf}(t)=\frac{Q_{isf}(t)}{V_{isf}(t)}$$ (20)

The relationship between plasma protein concentration and colloidal osmotic pressure was given by a cubic equation (Fig. 3B) in the literature.⁸ We fitted a secondary equation to the relationship as f₃ (Fig. 3B) and calculated the colloidal osmotic pressures for the plasma and the interstitial fluid [π_pl(t, x_i) and π_isf(t)] as follows:

$$\begin{array}{c}\hfill {\pi }_{pl}(t,x_i)=f_3\left(c_{pl}(t,x_i)\right)\hfill \\ \hfill =f_3\left(q_{pl}(t,x_i)/v_{pl}(t,x_i)\right)\hfill \\ \hfill =0.157\times \frac{q_{pl}(t,x_i)}{v_{pl}(t,x_i)}+3.2\times {10}^{-3}\times {\left(\frac{q_{pl}(t,x_i)}{v_{pl}(t,x_i)}\right)}^2\hfill \end{array}$$ (10′)

$$\begin{array}{c}\hfill {\Pi }_{isf}(t)=f_3\left(C_{isf}(t)\right)\hfill \\ \hfill =f_3\left(Q_{isf}(t)/V_{isf}(t)\right)\hfill \\ \hfill =0.157\times \frac{Q_{isf}(t)}{V_{isf}(t)}+3.2\times {10}^{-3}\times {\left(\frac{Q_{isf}(t)}{V_{isf}(t)}\right)}^2\hfill \end{array}$$ (11′)

2.4. An experimental protocol and the pressure balance analysis

All models were examined by applying a common perturbation to the capillary pressure, namely, $P_{pl,v}$ was changed in a stepwise manner as $P_{pl,v}=15\to 17\to 15\to 13\to 15\text{mmHg}$, with a 100-minute interval. In Model 4, the LF could be modified by changing the scaling factor, s, in Eq. (12). We reduced s to 10% of the original value for the simulation of the lymphatic obstruction.

Contributions of each component to tissue-volume regulation in the simulation experiment was demonstrated by piling inward and outward driving forces separately with positive and negative signs, respectively, referring to the direction towards the tissue space (Fig. 4, Fig. 5, Fig. 6, Fig. 7, Fig. 8B). In this analysis, the hydrostatic and colloidal osmotic pressure of individual capillary spaces were averaged as ${\overline{P}}_{pl}$, and ${\overline{\Pi }}_{pl}(t)$.

$${\overline{P}}_{pl}=\frac{1}{N}\times {\sum }_{i=1}^N{p}_{pl}(x_i)$$ (21)

and

$${\overline{\Pi }}_{pl}\left(t\right)=\frac{1}{N}\times {\sum }_{i=1}^N{\pi }_{pl}(t,x_i)$$ (22)

Fig. 4.

(A) V_isf, V_isf,L, and Π_isf change and (B) pressure-balance diagram in Model 1 in experiment changing P_pl,v.

Fig. 5.

(A) V_isf, V_isf,L, P_isf, and Π_isf change and (B) pressure-balance diagram in Model 2 in experiment changing P_plv.

Fig. 6.

(A) V_isf, V_isf,L, P_isf, and Π_isf change and (B) pressure-balance diagram in Model 3 in experiment changing P_pl,v.

Fig. 7.

(A) V_isf, V_isf,L, Q_isf, P_isf, and Π_isf change and (B) pressure-balance diagram in Model 4 in experiment changing P_pl,v.

Fig. 8.

(A) V_isf, V_isf,L, Q_isf, Q_isf,L, P_isf, and Π_isf change and (B) pressure-balance diagram in Model 4 in lymphatic obstruction experiment.

In case of Models 3 and 4, the LF $\left(J_{v,LF}(t)\right)$ makes small but significant contributions to $\frac{d{V}_{isf}(t)}{dt}$. $J_{v,LF}\left(t\right)$ is divided by K to calculate a pseudo pressure in order to evaluate the contribution of LF to $\frac{d{V}_{isf}(t)}{dt}$, and then added to the diagram.

2.5. Instantaneous equilibrium points and eigenvalue analyses

We derive an instantaneous equilibrium value of V_isf(t) as ${\text{V}}_{isf,L}\left(t\right)$, to which ${\text{V}}_{isf}\left(t\right)$ tends to approach at a given time. ${\text{V}}_{isf,L}\left(t\right)$ can be obtained by solving $\frac{\partial V_{isf}(t)}{\partial t}=J_v(t)=0$. To solve the equation, we have slightly modified the calculation method proposed by Shimayoshi et al.¹¹ We applied Newton's method to obtain an x-intercept of a tangential line of $\text{y}=J_v\left(V_{isf}(t)\right)$ iteratively by changing ${\text{V}}_{isf}\left(t\right)$, and detected a point at which $J_v({\text{V}}_{isf}(t))$ becomes <10⁻⁴.

In order to understand the dynamics of the system around the steady-state point, a phase plane was plotted around the steady-state point (V_isf = 6.305 × 10⁻⁵ μL, Q_isf = 1.997 × 10⁻⁴ μg) at a control condition of $P_{pl,v}=15$ mmHg in Model 4.

When we define a Jacobian matrix, A, for the system at the steady-state point at a control condition of $P_{pl,v}=15$ mmHg in Model 4, eigenvalues, λ₁ and λ₂, and corresponding eigenvectors, x₁ and x₂, are obtained. Then, ${\tau }_1=-\frac{1}{{\lambda }_1}$ and ${\tau }_2=-\frac{1}{{\lambda }_2}$ are calculated as the time constants, which determine the dynamics of the system. V_isf(t) and Q_isf(t) change their values in the direction of eigenvectors, x₁ and x₂, with the time constants, τ₁ and τ₂, respectively.

3. Results

3.1. A simple capillary base model (Model 1)

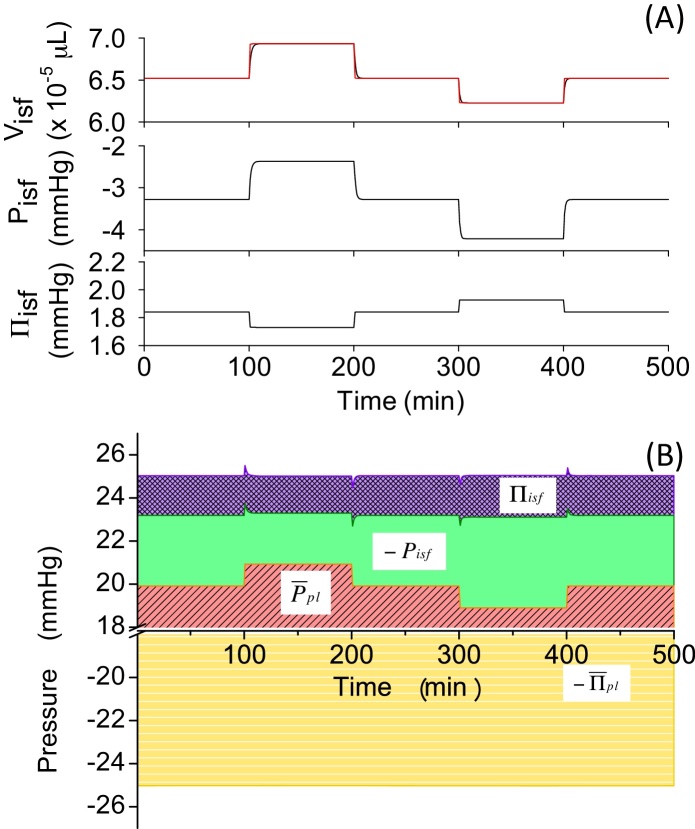
First, in Models 1–3, we assumed that the capillary membrane was only permeable to water. Fig. 4A shows the time course in V_isf(t), V_isf,L(t) and Π_isf(t) in Model 1 induced by perturbations changing $P_{pl,v}$ as indicated in Section 2. When $P_{pl,v}$ was increased by 2 mmHg from a control value of 15 mmHg at t = 100 minutes, P_E, calculated by Eq. (2), became positive and the fluid filtered out from the capillary. As a result, V_isf(t) increased by 81% within 100 minutes (Fig. 4A, ∼100–200 minutes; Table 4). Switching $P_{pl,v}$ back to the original level of 15 mmHg allowed V_isf(t) to return to the basal level of $V_{isf}^0$. Next, $P_{pl,v}$ decreased by 2 mmHg from the original level and switched back to the original level of 15 mmHg. This 2 mmHg decrease, which was the same in size as the P_pl,v-step increase, induced a smaller (∼-25%) decrease in V_isf(t), and reached a steady-state level (Fig. 4A, ∼300–400 minutes) and returned to the basal level of $V_{isf}^0$ with a relatively rapid time course (∼400–500 minutes). To identify the cause-effect relationship, we calculated an instantaneous equilibrium point, V_isf,L(t), and plotted this with a red line (Fig. 4A). It was clearly shown that, after $P_{pl,v}$ change, V_isf(t) gradually approached V_isf,L(t) as fluid filtration or absorption proceeded until it reached a new steady state. Π_isf(t) changed according to the V_isf(t) change by Eq. (11). The deviation of Π_isf(t) from the initial value at each steady state after changing $P_{pl,v}$ positively and negatively by 2 mmHg was approximately equal to the change in ${\overline{P}}_{pl}$.

Table 4.

Steady state numerical values obtained at steady-state level in Models 1–4

Model 1
	17 mmHg	15 mmHg	13 mmHg
Visf (μL)	1.02 × 10−4 (+80.98%)	5.62 × 10−5	3.86 × 10−5 (−31.28%)
Pisf (mmHg)	−3	−3	−3
Πisf (mmHg)	1.18	2.14	3.11

Model 2
Visf (μL)	6.91 × 10−5 (+5.96%)	6.52 × 10−5	6.24 × 10−5 (−4.28%)
Pisf (mmHg)	−2.43	−3.30	−4.19
Πisf (mmHg)	1.74	1.84	1.92

Model 3
Visf (μL)	6.57 × 10−5 (+3.71%)	6.34 × 10−5	6.14 × 10−5 (−3.12%)
Pisf (mmHg)	−3.16	−3.85	−4.59
Πisf (mmHg)	1.83	1.89	1.95

Model 4
Visf (μL)	6.77 × 10−5 (+2.89%)	6.58 × 10−5	6.44 × 10−5 (−2.13%)
Qisf (μg)	7.24 × 10−4	8.42 × 10−4	9.69 × 10−4
Pisf (mmHg)	−2.71	−3.14	−3.54
Πisf (mmHg)	2.04	2.53	3.09

In order to obtain further insights into the mechanisms underlying the volume change, we applied the pressure-balance analysis as shown in Fig. 4B. As $P_{pl,v}$ was changed manually in a stepwise manner, ${\overline{P}}_{pl}$ was changed accordingly (red area). Since P_isf is fixed to −3 mmHg in Model 1, Π_isf(t) is the only parameter in the pressure balance that can be actively changed by fluid movement to reach a new steady state after $P_{pl,v}$ change. According to the diagram, ±2 mmHg $P_{pl,v}$ change at t = 100, 200, 300, and 400 minutes broke the balance between positive and negative pressures in P_E, and the resultant filtered or absorbed fluid flux calculated by Eqs. (6), (7) induced V_isf(t) change towards V_isf,L(t), which, in turn, changed Π_isf(t) to cancel the pressure imbalance.

3.2. Effects of the nonlinear tissue compliance on the model (Model 2)

Compliance is one of the fundamental properties of the tissue and specifies characteristic behaviour of the tissue in relation to volume change. The relationship between the interstitial fluid pressure and the volume was obtained from an experiment performed on dogs,¹² and P_isf = 3 mmHg [Eq. (9)] in Model 1 was substituted with P_isf(t) = f₁[V_isf(t)] [Eq. (9′)] in Model 2. The same stepwise change of $P_{pl,v}$ as in Fig. 4 induced smaller changes compared to Model 1 (Table 4). The steep slope of the fitted equation, f₁, in the range slightly negative to atmospheric pressure meant that slight changes in V_isf(t) effectively changes P_isf(t) to resist volume change and induces a strong negative feedback in the V_isf(t) change. V_isf,L(t) in Model 2 (red line in Fig. 5A) was more closely followed by V_isf(t), and its deviation from the original level induced by $P_{pl,v}$ change was much smaller as compared to that seen in Model 1, suggesting that the volume regulation by nonlinear tissue compliance was more efficient at preventing the swelling of the tissue in this model. In Fig. 5B, it is evident that the perturbation in ${\overline{P}}_{pl}$ was almost totally balanced by P_isf(t).

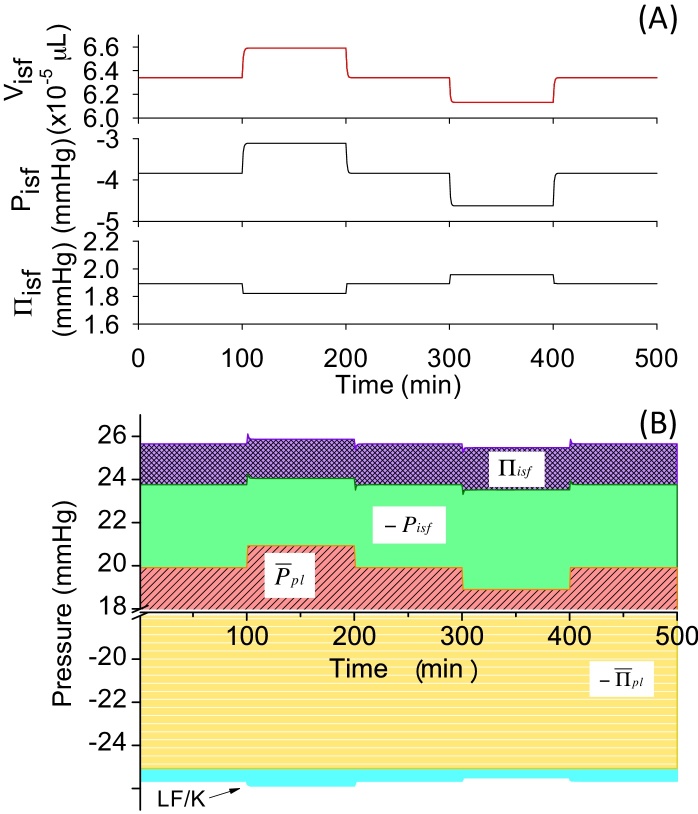
3.3. Draining excess interstitial fluid as lymph (Model 3)

The introduction of the drainage by LF induced much smaller deviations in V_isf(t) as compared to Models 1 and 2 when positive and negative changes were applied to $P_{pl,v}$ in Model 3 (Table 4). V_isf,L(t) was almost superimposable over V_isf(t), suggesting that the control of the interstitial fluid volume was effectively accomplished by the change in the LF. The contribution of the lymph drainage to interstitial-fluid volume regulation was then analyzed by the pressure balance diagram in Fig. 6. The lymph pumped interstitial fluid away from the tissue, therefore, contribution of LF divided by K to the pressure balance was negative, as shown at the bottom of the diagram (Fig. 6B). As this negative contribution of LF increased the net negative pressure, $\left|-P_{isf}(t)\right|$, the pressure-balance diagram became larger to balance with the negativity. The same ±2 mmHg change in $P_{pl,v}$ induced smaller changes in −P_isf(t) and −Π_isf(t) as compared to the changes in Model 2, because LF played a role in offsetting the stepwise changes in $P_{pl,v}$ instead of changing −P_isf(t) and −Π_isf(t). V_isf,L(t) in Model 3 was almost superimposable over V_isf(t), indicating that, due to the contribution of LF, P_E became zero immediately after the stepwise change in $P_{pl,v}$.

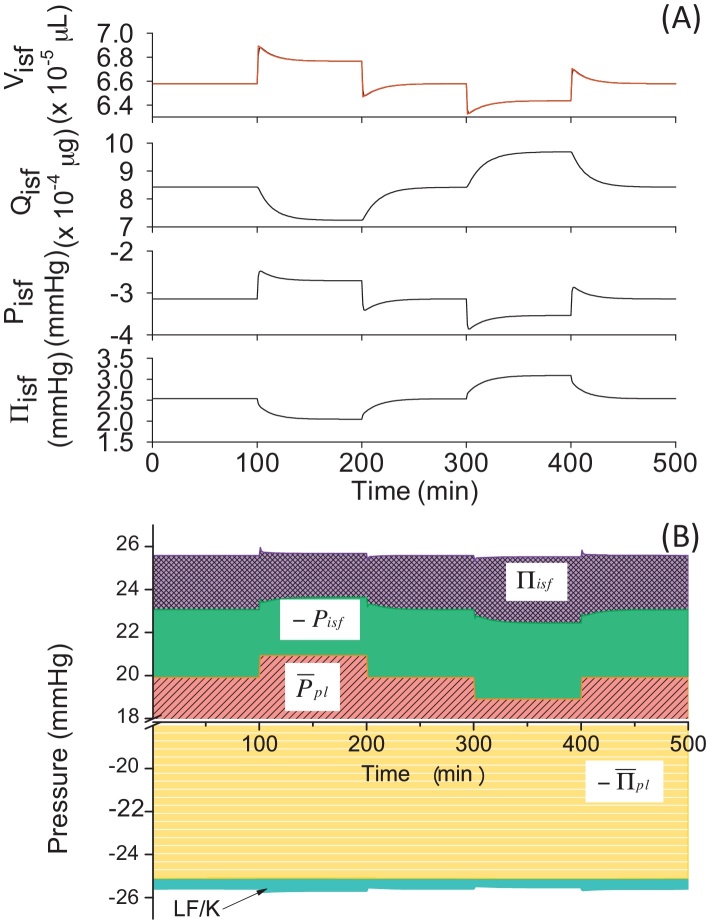
3.4. Lymphatic flow carries protein away from the tissue (Model 4)

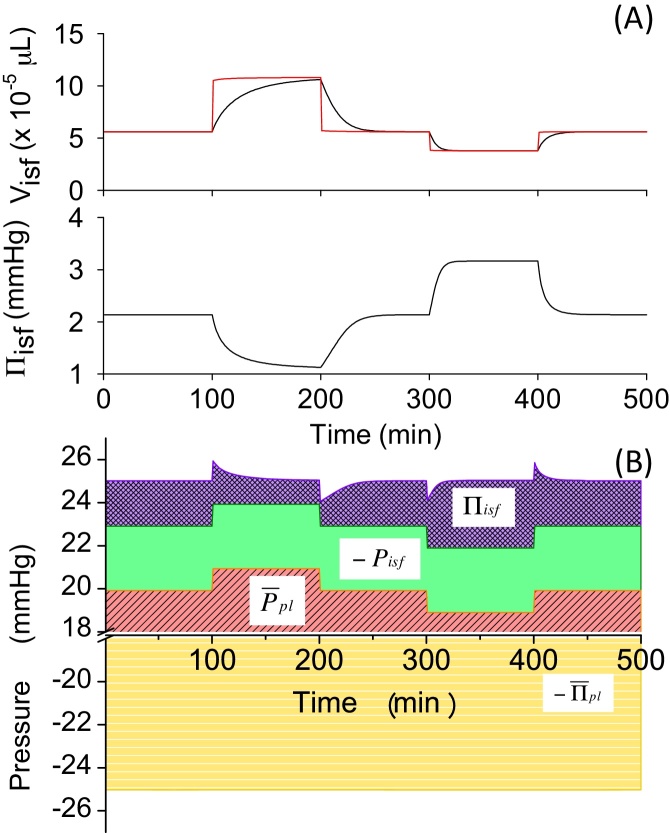
We implemented protein permeation across the capillary membrane and wash out by lymph into Model 3 to develop Model 4 (see Table 3 for the modifications in equations). When positive and negative changes were applied to $P_{pl,v}$ in the model, fluid moved to the interstitium from the capillary and made a jump in V_isf(t). After the initial jump, V_isf,L(t) kept changing and influenced V_isf(t) until it reached a steady state, which was closer to a value obtained at $P_{pl,v}=15$ mmHg in control conditions as compared to Models 1–3 (values are compared in Table 4). It should be noted that the change in V_isf,L(t) was biphasic in Model 4, which was different from the monophasic simple time courses observed in those of Models 1–3. The late gradual change in V_isf,L(t) seemed to coincide with that in Q_isf(t). Therefore, we calculated Q_isf,L(t) and plotted the results together with Q_isf(t) in Fig. 7A. The results revealed that the jump in V_isf,L(t) induced a large driving force in Q_isf,L(t) in the initial phase after the perturbation, which led Q_isf(t) to keep changing in the later phase.

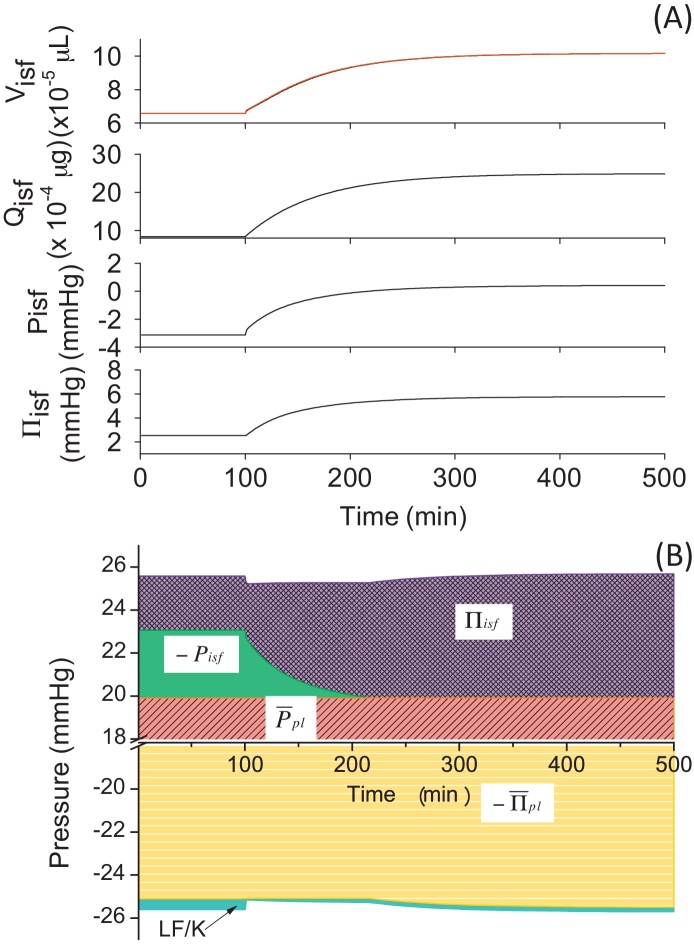
3.5. Simulated swelling induced by lymphatic obstruction

In order to understand the mechanisms associated with pathophysiological swelling, we performed a simulation experiment using our model (Model 4) to reproduce the effect of lymphatic obstruction. In this experiment, the amplitude of LF was scaled down to 10% of its original value. After the obstruction at the time of 100 minutes, V_isf,L(t) increased continuously and did not reach a steady state within 400 minutes (Fig. 8A). From the pressure-balance diagram in Fig. 8B, it is evident that Π_isf(t) increased dramatically after the obstruction, whereas P_isf(t) reduced its contribution complementarily. It was surprising that the reduction in the contribution of the LF at the bottom of the pressure-balance diagram was rather small compared to the change in Π_isf(t) and P_isf(t). This result suggested that the major effect of the lymphatic obstruction occurred through the change in Q_isf(t), which, in turn, increased Π_isf(t) and reduced $\left|-P_{isf}(t)\right|$ dramatically favouring increases in the positive pressure in P_E to cause swelling effectively. In case of edema in pathophysiological conditions, it is known that interstitial compliance becomes higher and less effective to prevent swelling.12, 13 This effect could be implemented simply by introducing a pathological compliance curve into the model.

4. Discussion

We showed that the same positive and negative stepwise change in $P_{pl,v}$ induced various impacts on four different models developed sequentially. To obtain further insight into the mechanisms underlying V_isf(t) and Q_isf(t) changes in the full model comprising nonlinear tissue compliance, lymphatic flow, and protein wash out (Model 4), we performed three mathematical analyses: 1) phase-plane analysis, 2) calculating instantaneous equilibrium points, and 3) calculating eigenvectors and eigenvalues from a Jacobian matrix.

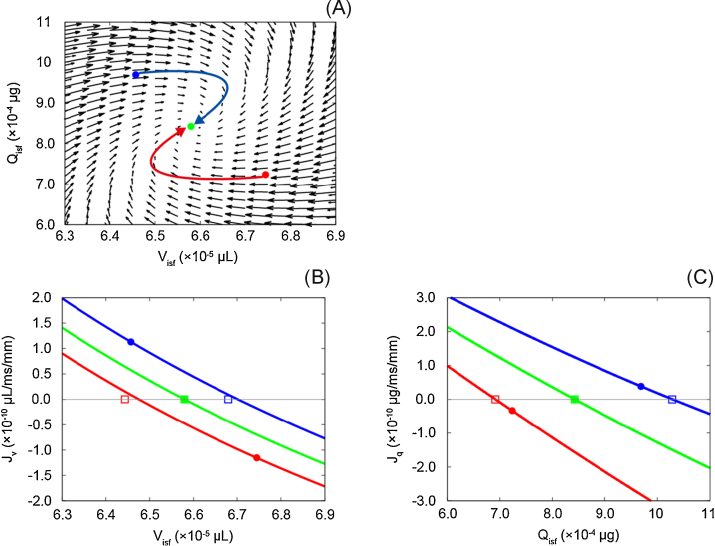
In the phase-plane analysis in Fig. 9A, the flow vectors of V_isf(t) and Q_isf(t), which correspond to $J_v(t)$ and J_q(t), are plotted. Two bent arrows indicate the trajectories of V_isf(t) and Q_isf(t) obtained when the venous pressure was returned to 15 mmHg (green circle) from 17 mmHg (red circle) or 13 mmHg (blue circle). In both cases, it was confirmed that first, V_isf(t) changed to compensate the ±2 mmHg change in the pressure at the venous end of the capillary. Then, Q_isf(t) gradually changed and V_isf(t) reversed the direction of its change. Here, it should be noted that the phase plane was calculated at an instant when the system was in the steady state and might be valid only in the area near the steady-state point of the figure. In order to determine whether the model behaviour was stable in the surrounding area near the steady state, we calculated instantaneous equilibrium points for both $J_v(t)$ and J_q(t) in a range used in our simulation experiment in this study and plotted in Fig. 9A.

Fig. 9.

(A) Phase-plane diagram in steady state at $P_{pl,v}=15$ mmHg and (B, C) instantaneous equilibrium point for $J_v$ and J_q. Arrows in A and B represent the trajectories for V_isf and Q_isf. $J_v$ and J_q were multiplied by 3.0 × 10³ and 6.0 × 10⁴, respectively, to visualize vectors in the diagram in A. Red and blue circles in A, Ba, and Bb indicate V_isf and Q_isf values obtained when $P_{pl,v}$ was switched back to 15 mmHg from 17 mmHg and 13 mmHg, respectively. Green circles in panels A, Ba, and Bb indicate values obtained at steady state at $P_{pl,v}=15$ mmHg. Red, green, and blue squares indicate equilibrium points, to which the circles with corresponding colours tended to approach at a given time.

From the result of the instantaneous equilibrium points, we confirmed that $J_v(t)$ and $J_q\left(t\right)$ had negative slopes and crossed each abscissa axis only once, even when $P_{pl,v}$ was changed, suggesting that the behaviour of the system would not be changed significantly after changing $P_{pl,v}$ from 17 mmHg or 13 mmHg to 15 mmHg. Then, $J_v(t)$ and J_q(t) in the instantaneous equilibrium point in Fig. 9B and 9C were reviewed in relation with the phase plane (Fig. 9A). At the x-intercept (V_isf = 6.58 × 10⁻⁵ μL) in the instantaneous equilibrium point diagram for $J_v(t)$, the flow vector of V_isf(t), $J_v(t)$, in the phase plane changed its direction when Q_isf(t) was at the steady state, J_q(t) = 0. The red and blue lines in Fig. 9B were obtained at the red and blue points in the phase-plane diagram in Fig. 9A when $P_{pl,v}$ was switched to 15 mmHg from 17 mmHg or 13 mmHg. Both red and blue lines tended to approach the green lines when the transient changes in V_isf(t) and Q_isf(t) proceeded after switching $P_{pl,v}$, and converged with the green line at the steady state in Fig. 9B. Similarly, in the instantaneous equilibrium-point diagram for J_q(t), the Q_isf(t) component of the vectors, J_q(t), in the phase plane changed its direction at the x-intercept (Q_isf(t) = 8.42 × 10⁻⁴ μg) V_isf(t) was at the steady state, $J_v=0$. Red and blue lines also converged with the green line at the steady state in J_q(t) in Fig. 9C. Taken together, we confirmed that the system was stable and did not change its behaviour significantly when $P_{pl,v}$ was changed by ±2 mmHg.

Finally, we obtained a Jacobian matrix from differential equations at $P_{pl,v}=15\text{mmHg}$ and derived eigenvectors and eigenvalues of the system at the steady state.

$$A=\left[\begin{array}{cc}\hfill \frac{\partial J_v}{\partial V_{isf}}\hfill & \hfill \frac{\partial J_v}{\partial Q_{isf}}\hfill \\ \hfill \frac{\partial J_q}{\partial V_{isf}}\hfill & \hfill \frac{\partial J_q}{\partial Q_{isf}}\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill -4.48\times {10}^{-5}\hfill & \hfill 4.56\times {10}^{-7}\hfill \\ \hfill -1.00\times {10}^{-4}\hfill & \hfill -8.36\times {10}^{-7}\hfill \end{array}\right]$$

$$x_1=\left[\begin{array}{c}\hfill -0.394\hfill \\ \hfill -0.919\hfill \end{array}\right],{\lambda }_1=-4.37\times {10}^{-5},{\tau }_1=-\frac{1}{{\lambda }_1}=2.29\times {10}^4(=0.381\min )$$

$$x_2=\left[\begin{array}{c}\hfill -0.0106\hfill \\ \hfill -1.00\hfill \end{array}\right],{\lambda }_2=-1.90\times {10}^{-6},{\tau }_2=-\frac{1}{{\lambda }_2}=5.26\times {10}^5(=8.77\min )$$

We determined that the values along the trajectory of V_isf(t) and Q_isf(t) after switching $P_{pl,v}$ to 15 mmHg from 17 mmHg or 13 mmHg were not largely different from those obtained at the steady state (Table 5). Both eigenvalues, λ₁ and λ₂, were negative, suggesting that the equilibrium point was stable. τ₂ was almost 22-fold larger than τ₁, suggesting that the change in the direction of x₂, which was determined mostly by the Q_isf(t) component, was 22-fold lower compared to that of x₁, which was determined by the V_isf(t) component and a smaller Q_isf(t) component. These results could explain why the changes in V_isf(t) and Q_isf(t) after the change in $P_{pl,v}$ were asynchronous.

Table 5.

Eigenvalues and time constants for the eigenvectors in the capillary model

Condition (mmHg)	Time (min)	τ1 (min)	τ2 (min)	τ2/τ1
Ppl,v 15 (steady state)	0	0.381	8.77	23.0
Ppl,v 17 → 15	0.05	0.445	8.52	19.1
	30	0.377	8.96	23.8
	90	0.381	8.77	23.0
Ppl,v 13 → 15	0.05	0.336	8.88	26.4
	30	0.386	8.59	22.3
	90	0.381	8.76	23.0

The more a mathematical model becomes integrative, the more difficult it becomes to investigate the mechanisms underlying the behaviour of the system. In this study, we tried to understand the mechanisms of the interstitial fluid volume regulation by sequentially adding three components of the system to the basal model of capillary (Model 1), nonlinear tissue compliance (Model 2), LF (Model 3), and protein washout (Model 4), and applying mathematical analyses to each model. As to Models 1–3, in which only fluid, but not protein, was allowed to move, it was shown that the fluid flux across the capillary membrane and through the lymph led V_isf(t) to follow the change in V_isf,L(t). Both the nonlinear compliance of the tissue and the LF added in Models 2 and 3 accelerated the volume change reaching a steady state. In Model 4, there was characteristic behaviour of the system, where the change in V_isf,L(t) was biphasic. To investigate the mechanisms of the biphasic change, we calculated the eigenvalues and time constants of the system in order to understand the model behaviour. The obtained eigenvalues offered us a quantitative insight that there were two different tendencies for the movement within the system; fast and slow movement. The fast component was mainly influenced by the fluid that changed V_isf(t), and the slow component was influenced by the protein that changed Q_isf(t). Given the higher mobility of the fluid compared to that of the protein into account, it was reasonable to think that the pressure imbalance induced externally was minimized by the quick fluid movement first, and then in the later phase, the contribution of the hydrostatic pressure and the colloidal osmotic pressure within the pressure balance were adjusted by the movement of the protein.

Conflicts of interest

The authors declare no conflicts of interest.