Triadic motifs in the dependence networks of virtual societies

Abstract

In friendship networks, individuals have different numbers of friends, and the closeness or intimacy between an individual and her friends is heterogeneous. Using a statistical filtering method to identify relationships about who depends on whom, we construct dependence networks (which are directed) from weighted friendship networks of avatars in more than two hundred virtual societies of a massively multiplayer online role-playing game (MMORPG). We investigate the evolution of triadic motifs in dependence networks. Several metrics show that the virtual societies evolved through a transient stage in the first two to three weeks and reached a relatively stable stage. We find that the unidirectional loop motif (M₉) is underrepresented and does not appear, open motifs are also underrepresented, while other close motifs are overrepresented. We also find that, for most motifs, the overall level difference of the three avatars in the same motif is significantly lower than average, whereas the sum of ranks is only slightly larger than average. Our findings show that avatars' social status plays an important role in the formation of triadic motifs.

The structure and social function of friendship networks formed of individuals with friendship ties, are of crucial importance in relation to our understanding of the evolution and behaviors of complex social systems. Conventionally, the construction of friendship networks are implemented by interviews or questionnaires¹,²,³. Usually, the sizes of these networks are not large and the samples are biased. Modern technology provides us alternative ways for the collection of data on social relationships. For instance, the wide use of mobile phones leaves footprints of human's social activities, making it possible to record and analyze very large social networks⁴,⁵,⁶,⁷,⁸,⁹,¹⁰. Another important source comes from the virtual worlds resided in computer servers running massively multiplayer online role-playing games (MMORPGs). The availability of big data recorded from MMORPGs potentially enables us to test social and economic hypotheses and theories in large-scale virtual populations¹¹. In recent years, such kind of data has been investigated from different angles of view¹²,¹³,¹⁴,¹⁵,¹⁶. In particular, studies on the structure and dynamic evolution of social networks in virtual worlds have unveiled intriguing results¹⁷,¹⁸,¹⁹,²⁰.

In virtual worlds, avatars (virtual characters in MMORPGs) interact with each other through their social and economic activities. An avatar can propose to another avatar to make friends when they encounter. If the later accepts the proposal, they become friends and their names appear in their friend lists. Hence, the friendship is reciprocal. We will investigate the friend lists of all avatars in 248 virtual societies of a popular MMORPG (for more information about the data sets, see Methods). In this MMORPG, the closeness of two avatars that are friends is measured and recorded, which is termed as intimacy. If two friends finish social or economic tasks together, their intimacy will increase. Therefore, the friendship networks are weighted. Just like almost all other social networks, these friendship networks are very heterogeneous in the sense that they have broad degree distributions and that each avatar has diverse intimacies. Indeed, we find that a large proportion of friendship ties have zero intimacy, while many other ties have very large intimacy. It suggests that some friendship ties are more important and significant than others. It is thus necessary to remove insignificant ties from the friendship networks.

The simplest and natural way is to set a threshold for the intimacy. If the intimacy of two friends is less than the threshold, the two avatars are not treated as friends. Another approach is to statistically validate the edges²¹,²², which has been applied to diverse fields, including organism networks²¹, stock networks²¹, movie networks²¹,²², paper networks²², stock trading networks²³,²⁴ and mobile phone communications²⁵,²⁶. In this work, we adopt an alternative and more systematic way of filtering proposed by Serrano et al²⁷. The idea is to statistically validate the links of each avatar by identifying which of her links carry disproportionate fraction of the weights. Links that deviate significantly a preset null model are kept to form the “multiscale backbone” of the original network. A significant link between an avatar i and her friend j means that the link plays an important role among all her links and we can argue that avatar i depends on her friend j. This results in a directed link from i to j. We call the resulting network as dependence network, which is directed.

In this work, we investigate the evolution of triadic motifs in the dependence networks among virtual societies. We find that some motifs occur more than random while other motifs appear less than random. We also find that the avatars forming these triadic motifs often have similar levels. These features are related to the evolution of the virtual societies.

Results

Illustration of dependence networks, degree distributions and distribution of level differences

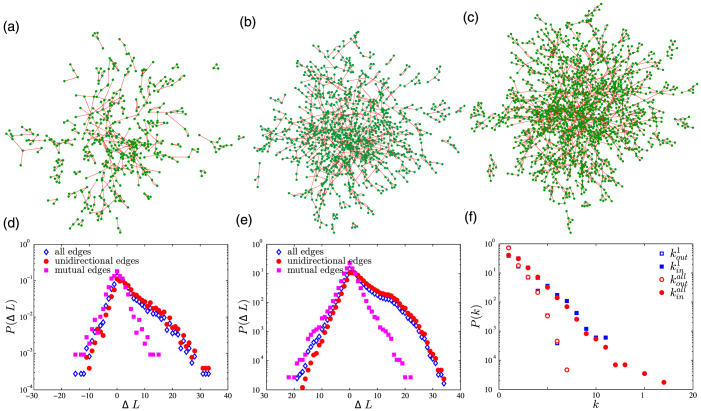
For each network (a society on a given day), we construct its dependence network (see Methods). In Fig. 1(a) to (c), we illustrate the evolution of the dependence network in a virtual society on three days. On the second day, the number of edges is low and hence the number of triadic motifs is also low. It is consistent with the fact that significant and stable friendship relations are still infant and under development. Such dependence relationship increases with the evolution of the virtual society because collaborations among avatars increase as well as their intimacies. In addition, a link present in an early dependence network may disappear in the later network.

Figure 1. Illustration of dependence networks, degree distributions and distribution of level differences.

(a) The dependence network of a virtual society on day 2. (b) The dependence network of the same virtual society on day 5. (c) The dependence network of the same virtual society on day 30. (d) Distributions of ΔL_ij for all links, for nonreciprocal links (link i → j exists while link j → i does not exist), and for reciprocal links (both links i → j and j → i exist) on day 30 for the same virtual society. (e) Distributions of ΔL_ij for all links, for nonreciprocal links, and for reciprocal links on day 30 for all virtual society. (f) In-degree distribution and out-degree distribution for the same virtual society and for all societies.

For a link i → j, we define the difference of levels of the two avatars as follows

where L_i and L_j are the levels of avatars i and j. Figure 1(d) plots the distribution of ΔL for all links, as well as nonreciprocal links and reciprocal links on day 30 for the same virtual society as in Fig. 1(a–c), while Fig. 1(e) shows the distributions for all societies. The most intriguing feature is that the probability maximizes at ΔL = 0 and decreases when |ΔL| increase on both the left and right parts of the distribution, which is consistent with empirical findings in real society that “collaboration is easiest when both partners share the same social status, and the probability of partnership formation decreases significantly as the status gap between the partners increases”²⁸. We also find that the left part of each distribution can be approximated by an exponential distribution. The distribution for reciprocal links is symmetric in reference to ΔL = 0 as expected because both ΔL_ij and ΔL_ji are counted. The average proportion of reciprocal links increases from 10% to 23%. However, for nonreciprocal links, the right tail of the distribution is much fatter than the left tail. On average, about 85% of the nonreciprocal links run from low-level avatars to high-level avatars and this ratio increases along time from about 82% to 86%.

Figure 1(f) shows the distributions of in-degrees and out-degrees of the dependence network in Fig. 1(c). The in-degree distribution decays exponentially, while the out-degree distribution decays faster than an exponential. It is intriguing to observe that the in-degree distribution is much fatter than the out-degree distribution. This observation is rational and can be explained in a mechanical way. Usually, a powerful avatar is able to help many less powerful avatars and play a relative important role in the friendship lists of those less powerful avatars. However, it is difficult for an avatar to have relatively similar intimacies from many different friends.

We also computed the correlation coefficients between in-degree and out-degree of avatars in individual societies. The average correlation coefficient on the first day is ρ(k_in, k_out) = −0.17 ± 0.21. Then ρ(k_in, k_out)(t) increases monotonically from ρ = −0.38 ± 0.20 on the second day (t = 2) to ρ = 0.27 ± 0.09 along time t and equals zero at around t = 11. We find that about 50% avatars have k_in = 0 and k_out = 1, which are leaf nodes in the dependence networks (see Fig. 1(a–c)). For small t, the social structure is flat and the proportion of avatars with k_in ≈ k_out > 1 is relatively small, resulting negative correlations between in-degree and out-degree. With the evolution of virtual societies, the structure of dependence networks becomes more complicated and more and more avatars depend on several avatars and are depended by several other avatars, which leads to increasing positive correlations between in-degree and out-degree.

Distribution and evolution of motif occurrence frequency

Let N_i,s,t denote the number of motif i in society s on day t. The relative occurrence frequency of motif i in virtual society s on day t is

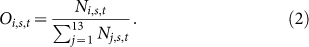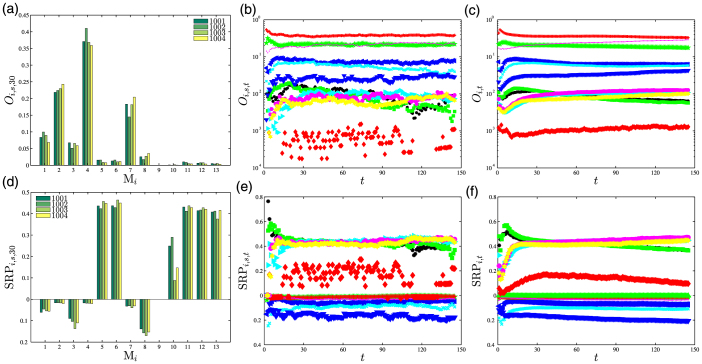
Figure 2(a) shows the distribution of relative occurrence frequencies of the 13 motifs on day 30, O_i,s,30, for four typical virtual societies. We find that the distributions are quite similar for different societies and open motifs (M₁, M₂, M₃, M₄, M₇ and M₈) have higher occurrence frequency than close motifs. We also find that the occurrence frequency of motif 9 is O_9,s,30 = 0. It suggests that the situation in which avatar a depends on avatar b, avatar b depends on avatar c, and avatar c depends on avatar a is unlikely to appear. These results are also observed for other virtual societies on other days, as shown in Fig. 2(b) for a typical society. It is found that the occurrence frequency experienced a transient stage in the first one or two weeks and then became relatively stable. For instance, the curve for M₄ on the top of the plot decreases fast in the first few days and becomes almost horizontal, while many other curves exhibit an increasing trend in the first few days and then decrease slowly or become almost horizontal. We also show in Fig. 2(c) the evolution of the average occurrence frequency over all societies on day t:

We confirm that there is no M₉ in all dependence networks.

Figure 2. Distribution of triadic motifs.

(a) Occurrence frequencies O_i,s,30 of the 13 motifs on the 30th day (t = 30) for four virtual societies. (b) Evolution of occurrence frequencies O_i,s,t of the 13 triadic motifs for a typical virtual society s. The occurrence frequency of motif 9 is zero along time, that is O_9,s,t = 0. (c) Evolution of average occurrence frequencies 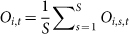of the 13 triadic motifs over all virtual society. The average occurrence frequency of motif 9 is zero along time, that is O_9,t = 0. (d) Significance SRP_i,s,30 of the 13 motifs on the 30th day (t = 30) for four virtual societies. (e) Evolution of significance SRP_i,s,t of the 13 triadic motifs for a typical virtual society s. (f) Evolution of average significance 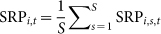of the 13 triadic motifs over all virtual society. The correspondence between the colourful symbols in plots (b), (c), (e) and (f) and motifs are given in Fig. 5.

Significance of motif occurrences

Some motifs are more likely to appear than other motifs in networks, even if there are no social factors in the formation of networks. Hence, we determine the occurrence significance of motifs by the z-score

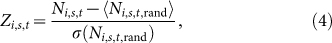where N_i,rand is the occurrence number of M_i in a randomized network from the dependence network of society s on day t, and 〈N_i,rand,s,t〉 and σ(N_i,rand,s,t) are the mean and standard deviation of N_i,rand,s,t over 100 randomized networks²⁹,³⁰.

The results of the dependence network in a typical virtual society on day 30 are shown in Table 1. Again, we find that the 13 motifs can be classified into three groups. The first group contains M₉, where N_{i = 9,s,t} = 0. Although M₉ was not detected in real networks, it appears occasionally in random networks. The second group contains all open motifs M₁, M₂, M₃, M₄, M₇ and M₈, where N_i,s,t < 〈N_i,s,t,rand〉. The third group contains other close motifs M₅, M₆, M₁₀, M₁₁, M₁₂ and M₁₃, where N_i,s,t > 〈N_i,s,t,rand〉. It is worthy stressing that M₁₃ appears in real networks but not in random networks. We find that all the standard deviations are less than 1 and the z-scores are significantly different from zero. Therefore, when compared with random networks, open motifs are less likely to occur while close motifs (except M₉) are more likely to appear in real dependent networks. For close motifs except M₁₃, the standard deviation is greater than the mean. In addition, there are five close motifs (M₆, M₉, M₁₀, M₁₁, M₁₂) having 〈N_i,rand,s,t〉 = 0.10 and σ(N_i,rand,s,t) = 0.30. It can be understood due to the fact that, for each motif i (i = 6, 9, 10, 11, 12), there are 10 random networks (out of 100) having N_i,rand,s,t = 1.

Table 1. Statistical significance of motif occurrences for a typical virtual society on day 30. Without loss of clarity, we have dropped the subscripts s and t in the variables. The motifs can be classified into three groups: (1) M₉ with zero occuurence; (2) Open motifs M₁, M₂, M₃, M₄, M₇ and M₈ that appear significantly less than random. (3) Close motifs M₅, M₆, M₁₀, M₁₁, M₁₂ and M₁₃ that appear significantly more than random.

i	Mi	Oi	Ni,real	〈Ni,rand〉	σ(Ni,rand)	Zi	p-value
9		0.00000	0	0.10	0.30	−0.27	1.00
1		0.08358	477	622.60	0.50	−273.78	1.00
2		0.21850	1247	1339.41	0.00	−95.85	1.00
3		0.06746	385	571.70	0.80	−247.95	1.00
4		0.37112	2118	2278.60	0.60	−265.61	1.00
7		0.18311	1045	1201.70	0.60	−254.97	1.00
8		0.02541	145	270.90	0.30	−461.82	1.00
5		0.01542	88	0.30	0.50	171.89	0.00
6		0.01279	73	0.10	0.30	227.26	0.00
10		0.00088	5	0.10	0.30	19.23	0.00
11		0.01016	58	0.10	0.30	212.43	0.00
12		0.00631	36	0.10	0.30	131.74	0.00
13		0.00526	30	0.00	0.00	0.00	0.00

Because the standard deviation can be very small or even zero when a subgraph is unlikely to occur in a network, the estimated z-score fluctuates a lot and may diverge. An alternative measure can be adopted to assess the occurrence significance of motifs²⁹. We calculate the abundance of M_i relative to random networks as follows

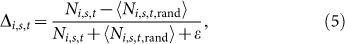where ε = 4 is to ensure that |Δ_i| is not too large when M_i appears very few times in both real and random networks, i.e., both N_i,s,t and 〈N_i,s,t,rand〉 are close to zero²⁹. This special case happens for M₉. We then compute the normalized abundance as follows

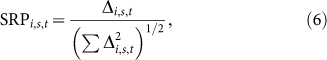which is called the subgraph ratio profile (SRP)²⁹. We can also calculate the average SRP over all virtual societies:

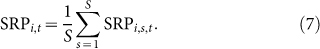The average procedure is meaningful because different societies exhibit similar motif profiles.

In Fig. 2(d), we show the subgraph ratio profile SRP_i,s,t for the four societies in Fig. 2(a) on day 30. The three groups identified in Table 1 are also observed. For the first group, we have SRP_{i = 9,s,t} = 0. For the second group, we have SRP_i,s,t < 0. For the third group, we have SRP_i,s,t > 0. We further find that the absolute SRPs for the open motifs in the second group are less than that for the close motifs in the third group. In Fig. 2(e) and (f), we also show the evolution of subgraph ratio profiles SRP_i,s,t for the same society as in Fig. 2(b) and the average subgraph ratio profiles SRP_i,t over all societies. Again, we observe a transient stage and a relative stable stage.

Correlation between motif counts

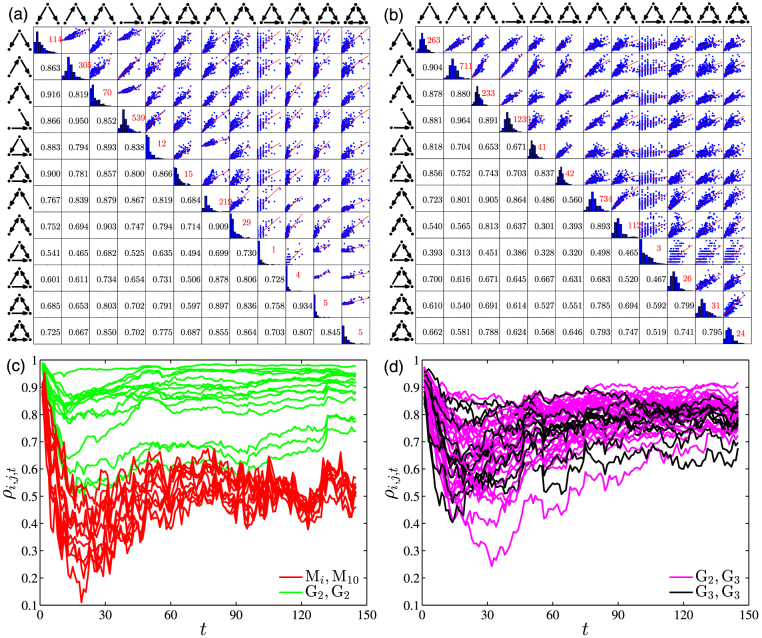
We perform motif count analysis to study the correlation between motif counts in dependence networks, similar as in human cell-specific transcription factor regulatory networks³¹. Specifically, for a given day t, we plot N_i,s,t against N_j,s,t for different society s, where each s gives a point. Panels (a) and (b) of Fig. 3 show the correlation plots for t = 7 and t = 30, respectively, where M₉ is not included because N_{i = 9,s,t} = 0. For each motif, the distribution of the motif count in the diagonal is unimodal with the peak close to the mean value. We find that the motif counts exhibit linear correlations. On average, the correlation coefficients ρ_ij between M₁₀ and other motifs are relatively small, due to the fact that the average count of M₁₀ is small with relatively large fluctuations.

Figure 3. Correlation of motif counts in 248 dependence networks.

(a) The panels in the upper triangle are scatter plots of motif counts between 13 motif counts on day 7. There are no M₉ motifs detected in the dependence networks. The correlation coefficients of motifs counts are presented in the lower triangular panels. Each diagonal panel shows the count distribution of these motifs and also the average motif count. (b) Same as (a) for day 30. (c) Evolution of motif count correlation coefficient ρ_i,j,t between M₁0 and other motifs (red curves) and between open motifs in the second group (green curves). (d) Evolution of motif count correlation coefficient ρ_i,j,t between close motifs in the third group (black curves) and between open motifs in the second group and close motifs in the third group (magenta curves).

In Fig. 3(c) and (d), we plot the evolution of correlation coefficient ρ_i,j,t for all the pairs of motifs. The correlation coefficient ρ_i,j,t decreases in the first two or three weeks and then increases to a relatively stable state. The count correlations between open motifs are relatively the strongest for most pairs, while the correlations between M₁₀ and other motifs are relatively the weakest.

The characteristics of these correlations are closely related to the results in Fig. 2(a)–(c). It suggests that the local structure of dependence networks in diverse virtual societies exhibits universal evolution patterns. The relative ratio of motif counts N_i,s,t/N_j,s,t between M_i and M_j converges to certain constant along the evolution of virtual societies.

Avatar levels in motifs

Abnormal occurrence of motifs is often in relation to certain features of the involving individuals in complex social networks¹⁰,²⁹,³²,³³,³⁴. We now investigate the levels of avatars in triadic motifs. Many social and economic activities of an avatar are converted to her experience point and her level promotes when her experience point reaches certain value. The levels of avatars are the most important trait, because levels reflect the power of attack, defence, and production of avatars.

Denote the levels of the three avatars in M_i by L_i,1, L_i,2 and L_i,3. The sum of avatar levels is

The mean value of level sums of the N_i,s,t motifs in society s on day t can be calculated as follows,

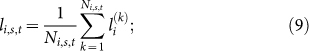Similarly, we define the difference of avatar levels as

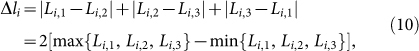and calculate its mean as follows

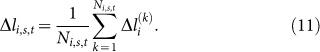To estimate if the sum and difference of avatar levels are significantly different from random networks (see Methods), we calculate the means of these two metrics for random networks, which are denoted by 〈l_i,s,t,rand〉 for level sums and 〈Δl_i,s,t,rand〉 for level difference. The z-scores of the two metrics can be obtained as follows

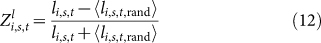and

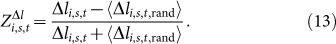The averaged z-scores over all virtual societies are computed as follows

and

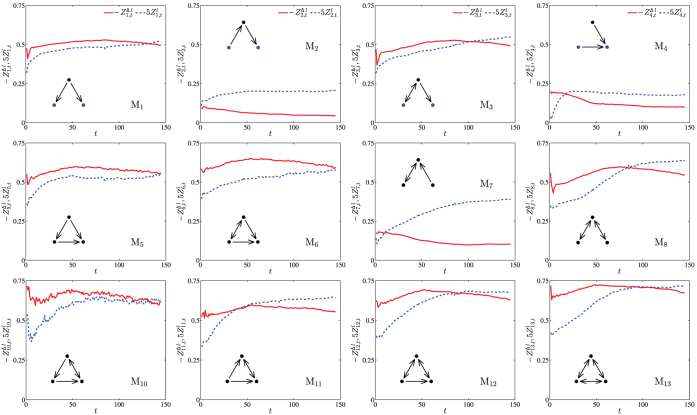
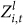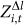Figure 4 shows the evolution of average z-scores and for all motifs excluding M₉.

Figure 4. Evolution of z-scores of the average level sum and level difference of avatars in motifs.

Each plot corresponds to a motif. For clarity, the 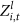values has been multiplied by a factor of 5.

It is found that the 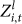values are positive. It indicates that the average level sum among avatars in the motifs is larger than the average level of all avatars. This observation can be explained by the fact that avatars in motifs often have relatively large intimacies and thus are more active in virtual societies. More activities may result in a relatively faster increase of levels. The 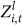curves have an overall increasing trend. Most curves increase relatively rapid in the first few weeks and then slow down, while some curves (say, M₁ and M₃) exhibit a continuous increase. It again indicates that, with the evolution of virtual societies, avatars in the motifs are even more active than other avatars. However, we notice that all the 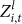values are less than 0.15, suggesting that the average level of avatars is not a determining factor in the formation of dependence motifs.

On the contrary, all the 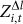values are negative, indicating that the average level difference among avatars in the motifs is smaller than that of all avatars. We can identify two groups of motifs with distinct behaviors. Three motifs (M₂, M₄ and M₇) have relative small absolute 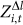values and the absolute z-scores decrease along time. These motifs are less significant than others, as shown by the SRP profiles in Fig. 2(d). Nine other motifs exhibit large absolute 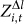values and the absolute z-scores increase first and then decrease. In the early stage of the virtual societies, avatars are more enthusiastic to collaborate in their implementation of tasks. Although avatars are apt to make friends and collaborate with higher-level avatars, such kind of imbalanced teams with high level differences are not common unless that the higher-level avatars are very altruistic. Even such imbalanced teams form, the level difference among avatars will decrease because low-level avatars benefit more in such collaborations. This results in the increase of the absolute 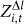values. Several months after the generation of a virtual society, many avatars become less active or even inactive such that their levels increase relatively slowly, whereas the dependence motifs are persistent. The absolute 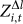values decrease.

Discussion

We have studied the friendship networks of hundreds of virtual societies. In friendship networks, the distributions of degree and weight (measuring the closeness or intimacy between two friends) are heterogeneous. For a given avatar i, it is often true that some friends are more helpful than others. If the intimacy between i and her friend j is significantly larger than the intimacies between i and her other friends, we argue that i depends on j. Based on a filtering method²⁷, we construct dependence networks as the “multiscale backbone” of the original friendship networks. The dependence networks allow us to study the reciprocal and altruistic behaviors among avatars by ignoring insignificant ties that bear marginal social information.

We focused on the evolution of triadic motifs in dependence networks. Our findings show that the occurrences of motifs evolved to a stable state and are persistent. We found that the unidirectional loop motif and open motifs are underrepresented, while other closed motifs are overrepresented. A very interesting result is that the level difference of avatars in motifs is an important factor in the formation of dependence networks, whereas the level sum of avatars are not. This finding is the same as the friendship networks of US students³. It suggests that virtual societies share certain common dynamics as our real society.

More generally, virtual societies can serve as a promising source of big data for understanding many key aspects of real human societies, such as the evolution of cooperation, homophily and the management of public goods, because time-resolved data of avatars' social and economic activities are recorded. Research in these directions has been flourishing in the past two decades³⁵,³⁶. For instance, the MMORPG data enable us to identify different forms of reciprocity³⁷ and test possible correlations between positive and negative reciprocity³⁸. Our work thus highlights the scientific potential of virtual societies in the study of human behaviors¹¹.

Methods

Data description

We use a huge database recorded from K = 124 servers of a popular Massively Multiplayer Online Role-Playing Game (MMORPG) in China. In a virtual world residing in a server there are two opposing societies. Two avatars i and j can make friends, and a measure of closeness I_ij called intimacy is assigned to the friendship link. The intimacy I_ij can increase according to the collaborative activities of i and j if they belong to a same society; Otherwise, I_ij remains zero if i and j belong to two different societies. Hence the friendship networks of the two camps are essentially separate. Each avatar can maintain a friendship list, denoted as 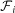for avatar i. The friendship relation is symmetric: if 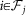, then .

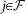Construction of dependence network

For a friendship network, we can construct a dependent network by filtering out insignificant edges based on a method proposed by Serrano et al²⁷. We can construct a directed weighted network W whose element w_ij is the relative intimacy of avatar j in reference to all friends of avatar i:

where w_ij ≠ w_ji. Following Ref. [27], a directed link i → j is significant at the level of α if

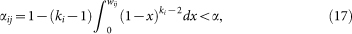where k_i is the number of friends avatar i has. We use α = 0.05 and remove all the insignificant links, resulting a directed network. If link i → j is significant, it means that j is relatively important to i in i's friends. Speaking differently, i depends on j and the directed network can be termed as a dependence network.

Definition and identification of triadic motifs

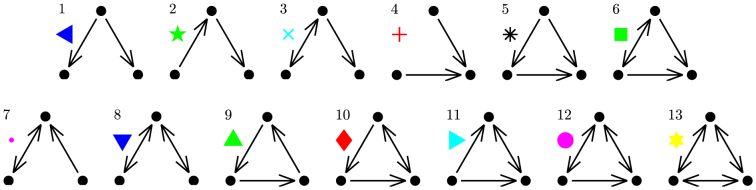
We consider directed triadic motifs for the dependence networks, each of which contains three connected nodes. As shown in Fig. 5, there are 13 directed triadic motifs. These motifs represent different dependence structure among avatars at the microscopic level. For instance, motif 1 stands for the situation that one avatar depends on two other avatars, while motif 2 means that one avatar depends on another avatar which in turn depends on the third avatar. To identify motifs, we adopt a widely used method proposed in Ref. [32].

Figure 5. List of triadic dependence motifs.

A unidirectional arrow from i to j means that avatar i depends on avatar j, while a bidirectional arrow indicates that the two avatars are mutually dependent.

Null model

The specification of null models is very important in the assessment of certain statistic and the difference between the real networks and the reference randomized networks should focus on the factor under consideration¹⁰. Because we investigate the possible distinctions of the level sum and level difference of avatars in dependence motifs, we shuffle the levels of all avatars in dependence networks. Specifically, the topological structure of the dependence networks remains unchanged, while the levels of avatars are randomized by repeatedly exchange the levels of two arbitrarily chosen avatars.