Abstract
The high-pressure behavior of zinc carbonate ZnCO3 has been investigated using universal structure prediction method together with the density functional theory. In order to explore all possible structures under pressure, separate calculations at high pressure are done here with increasing number of formula units in the unit cell. Two pressures induced phase transitions were considered. The first one occurs at 78 GPa and the second one at 121 GPa. The most stable ZnCO3 at ambient condition corresponds to the space group R-3c (phase I), which is in favorable agreement with experiment. The structure with C2/m space group (phase II) becomes stable between 78 GPa and 121 GPa. Finally, the structure with the space group P212121 (phase III) becomes the most stable when the pressure achieves 121 GPa. Some mechanical properties of R-3c structure were –additionally- calculated and compared with the experimental and previous theoretical data. The resulting behaviors support our findings and confirm the obtained phase transition. Besides, from the analysis of the electronic charge density it comes that at 78 GPa, new bond between oxygen and zinc is formed, what is likely the main cause behind the phase transition.
High-pressure polymorphs of carbon-bearing minerals are important to understand the circulation of carbon in the Earth's interior. Carbonates have been, for a long time, considered as important reservoirs of carbon in deep Earth. High-pressure phases of carbonates are probably among the host minerals for carbon that are present deeply in the mantle. For these reasons, phase transitions and physical properties of high-pressure phases related to carbonates have been subject of intense investigations1,2,3,4,5. Interesting crystal chemical changes that occur in carbonates under pressure, such as increase of coordination numbers and polymerization of carbonate-ions, may result on new useful materials.
Previous theoretical and experimental studies have focus on common carbonates such as magnesite (MgCO3)6,7,8,9 and calcite (CaCO3)10,11,12,13. For instance, it has been proved that the magnesite is stable at pressure up to 80 GPa6 and the calcite up to 3.3 GPa10. Magnesite goes through two phases transition, from magnesite phase I to magnesite phase II; and from phase II to phase III at 82 and 138 GPa respectively as reported by Oganov et al.7. In another work of Oganov et al.11, calcite was found to go through three phase transitions at pressures up to 150 GPa from calcite to aragonite at 4 GPa; from aragonite to post-aragonite at 42 GPa, and then to the C2221 phase at 137 GPa7.
ZnCO3 is one of carbon-bearing phases known at the surface at the Earth. This mineral has the same structure type as calcite. However, the knowledge of this zinc carbonate at high pressure remains still very limited. Only few experimental studies of smithsonite have been reported in the literature14,15. Graf14 has presented and defined the structure of ZnCO3. Zhang and Reeder15 performed experimentally the structural properties of smithsonite and they have also determined the bulk modulus. Recently, Bouibes et al.16 determined the ground state properties of smithsonite including structural, mechanical, electronic and bonding properties. Even if there is no clear study indicating the direct importance of zinc carbonate on interior earth, this mineral belongs to group II of carbonates such as MgCO3, MnCO3, FeCO317. Group II contains the most solid minerals needing a high pressure to crystallize. Several studies were performed on FeCO3 and MgCO3 because of their importance for earth science at high pressure. On the other hand, further study shows that high CO2 (g) partial pressure results in zinc carbonate being stable and potentially limit zinc mobility18.
The main goal here is to shed light on the structural evolution of ZnCO3 at high-pressure. To this end, high-pressure phase transitions will be investigated using the USPEX method/code19,20. This method has shown great success in numerous applications, including carbonates19.
Results
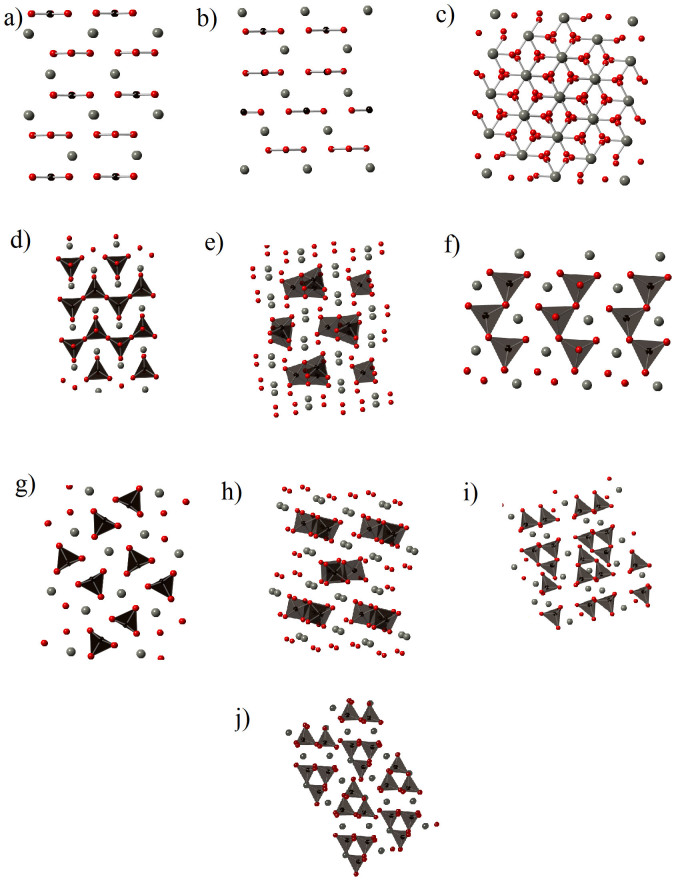
In Fig. 1, we display some ZnCO3 structures with lowest enthalpy. The obtained lattice parameters as well as bulk modulus and its pressure derivative for the most stable structure (R-3c) are summarized in Table 1.
Figure 1. Lowest-enthalpy structures for ZnCO3: P-31c (a); P3 (b); R-3c (Phase I) (c); Pbcm (d); P212121 (Phase III) (e); Pca21 (f); Pnma (g); Pna21 (h); C2/m (Phase II) (i); P21 (j).
Table 1. Stable ZnCO3 structure (Phase I) between 0 GPa and 78 GPa.
| Lattice parameters | ||||
| a (Å) = 5.71; | ||||
| α(°) = 48.92; | ||||
| V (Å3) = 97.21 | ||||
| Atomic coordinates (space group R-3c) | ||||
| Atom | X | Y | Z | |
| Zn | 0.00 | 0.00 | 0.00 | |
| C | 0.25 | 0.25 | 0.25 | |
| O | 0.97 | 0.52 | 0.25 | |
| Bond length (Å): | ||||
| Zn--O = 2.14 | ||||
| C--O = 1.29 | ||||
| Third-order Birch–Murnaghan equation of state (fitted between 0 and 150 GPa) | ||||
| B0 (GPa) = 126.45 (±1.6) | ||||
| B′0 = 4.00 (±0) | ||||
| V0 (Å3) = 98.11(±0.23) | ||||
Three structures corresponding to the space groups R-3c, P-31c and P3, contain triangular (CO3)2− ions, which are flat and coplanar. However, two structures with C2/m and P21 space group (30 atoms in the primitive cell), are characterized by a three-membered ring (C3O9)6− of corner-sharing carbonate tetrahedra. These latter structures were previously found as magnesium carbonate MgCO3 stable structure7. The structure with C2/m space group corresponds to MgCO3 structure that is stable between 82 GPa and 138 GPa and it is called magnesite phase II. In addition, the structure with P21 space group, called magnesite phase III, is the structure of MgCO3 above 138 GPa. The structure with space group Pnma is composed of a serial pentaedra carbonate. All the remaining structures contain carbonates (CO4)4− tetrahedra.
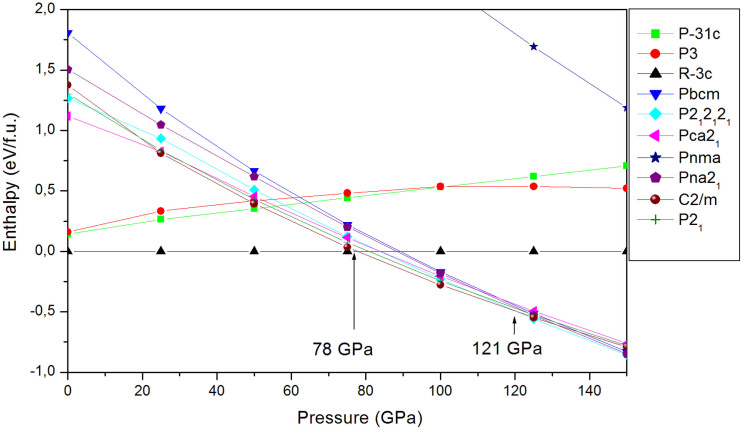
Having determined the most promising structures, we optimized them with very strict computational conditions at pressures ranging from 0 GPa to 150 GPa. Fig. 2 shows the enthalpy as a function of pressure. The most stable structure of ZnCO3 at ambient conditions is the R-3c space group structure (calcite structure), which fits perfectly the experiment15. The first phase transition occurs at 78 GPa. Under increasing pressure, the second phase transition occurs at 121 GPa. Between 78 GPa and 121 GPa the most stable structure has a space group C2/m with 30 atoms in the primitive cell. This structure is detailed in Table 2. Above 121 GPa, the structure of P212121 space group becomes more stable, as presented in Table 3.
Figure 2. Enthalpies of the best structures vs pressure at 78 GPa (C2/m: Phase II) and at 121 GPa (P212121: Phase III).
Table 2. Stable ZnCO3 structure (Phase II) between 78 GPa and 121 GPa.
| Lattice parameters | ||||
| a (Å) = 9.27; | b (Å) = 7.08; | c (Å) = 8.17 | ||
| β(°) = 104.83; | ||||
| V (Å3) = 519.13 | ||||
| Atomic coordinates (space group C 2/m) | ||||
| Atom | X | Y | Z | |
| Zn1 | 0.53 | 0.00 | 0.19 | |
| Zn2 | 0.50 | 0.27 | 0.50 | |
| Zn3 | 0.34 | 0.50 | 0.14 | |
| C1 | 0.86 | 0.83 | 0.79 | |
| C2 | 0.74 | 0.00 | 0.53 | |
| O1 | 0.85 | 0.00 | 0.45 | |
| O2 | 0.85 | 0.00 | 0.88 | |
| O3 | 0.60 | 0.00 | 0.43 | |
| O4 | 0.74 | 0.84 | 0.64 | |
| O5 | 0.83 | 0.68 | 0.88 | |
| O6 | 0.99 | 0.80 | 0.76 | |
| Bond length (Å): | ||||
| Zn1--O1 = 2.05; Zn1--O2 = 2.04; Zn1--O5 = 2.22; Zn1--O6 = 2.22 | ||||
| Zn2--O1 = 2.16; Zn2--O3 = 2.07; Zn2--O4 = 2.10; Zn2--O6 = 2.04 | ||||
| Zn3--O2 = 2.10; Zn3--O6 = 2.05 | ||||
| C1--O2 = 1.34; C1--O3 = 1.41; C1--O5 = 1.43; C1--O6 = 1.39 | ||||
| C2--O4 = 1.31 | ||||
| Third-order Birch–Murnaghan equation of state (fitted between 0 and 150 GPa) | ||||
| B0(GPa) = 180.8(±1.6) | ||||
| B′0 = 3.94 (±0.05) | ||||
| V0 (Å3) = 488.61 (±0.29) | ||||
Table 3. Stable ZnCO3 structure (Phase III) above 121 GPa.
| Lattice parameters | ||||
| a (Å) = 8.67; | b (Å) = 3.62; | c (Å) = 5.63 | ||
| α(°) = 90.00; | β(°) = 90.00; | γ(°) = 90.00 | ||
| V (Å3) = 176.7 | ||||
| Atomic coordinates (space group P212121) | ||||
| Atom | X | Y | Z | |
| Zn | 0.15 | 0.66 | 0.19 | |
| C | 0.03 | 0.54 | 0.61 | |
| O1 | 0.05 | 0.17 | 0.08 | |
| O2 | 0.34 | 0.60 | 0.02 | |
| O3 | 0.07 | 0.80 | 0.78 | |
| Bond length (Å): | ||||
| Zn--O1 = 1.9; Zn--O2 = 2.03; Zn--O3 = 2.12 | ||||
| C--O1 = 1.35; C--O2 = 1.39; C--O3 = 1.42 | ||||
| Third-order Birch–Murnaghan equation of state (fitted between 0 and 150 GPa) | ||||
| B0 (GPa) = 119.15 (±3.2) | ||||
| B′0 = 4.36 (±0.07) | ||||
| V0 (Å3) = 170.92 (±0.33) | ||||
Discussion
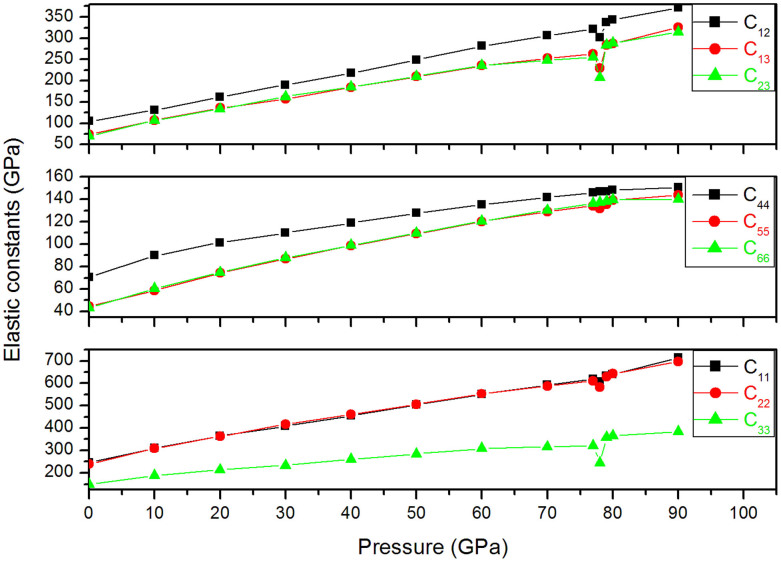
Remarkably, the results found confirm that smithsonite belongs to the group of calcite, since calcite structure is the most stable structure that ZnCO3 may adopt at ambient conditions. In order to assess the reliability of our simulation, the mechanical properties of ZnCO3 structure-phase I (R-3c space group) are evaluated. The obtained data are fitted to the Birch-Murnaghan equation of state25 in order to obtain the bulk modulus, which is in good agreement with the experimental15 and previous theoretical results16. The set calculated data are listed in Table 4. The dependence of the elastic constants of ZnCO3-phase I as a function of pressure variation is calculated from 0 to 90 GPa. Fig. 3 shows that elastic constants increase proportionally with the applied pressure until 78 GPa where a clear discontinuity is noticed, especially for C11, C22, C33, C12, C13 and C23 curves. This continuity supports our prediction regarding the structural transition at this pressure.
Table 4. Mechanical properties of ZnCO3 structure (Phase I), at ambient conditions.
| Experimenta | This work | Theoryb | |
|---|---|---|---|
| C11 | 244.97 | 243.51 | |
| C22 | 240.29 | 240.24 | |
| C33 | 148.79 | 145.36 | |
| C44 | 70.09 | 69.34 | |
| C55 | 44.33 | 41.31 | |
| C66 | 43.25 | 41.62 | |
| C12 | 104.41 | 103.75 | |
| C13 | 73.54 | 71.13 | |
| C23 | 70.49 | 68.58 | |
| B | 124 | 126.45c | 124.19c |
| 126.86d | 124.93d | ||
| B′ | 4.00 | 3.99 | |
| A | 1.00 | 0.99 | |
| G | 45.34 | 44.39 | |
| E | 121.54 | 118.98 | |
| ν | 0.34 | 0.34 | |
| Vs | 3.20 | 3.17 | |
| Vp | 6.50 | 6.43 |
Figure 3. Variation of the elastic constants C11, C22 and C33; C44, C55 and C66; and C12, C13 and C23 vs pressure for ZnCO3-Phase I.
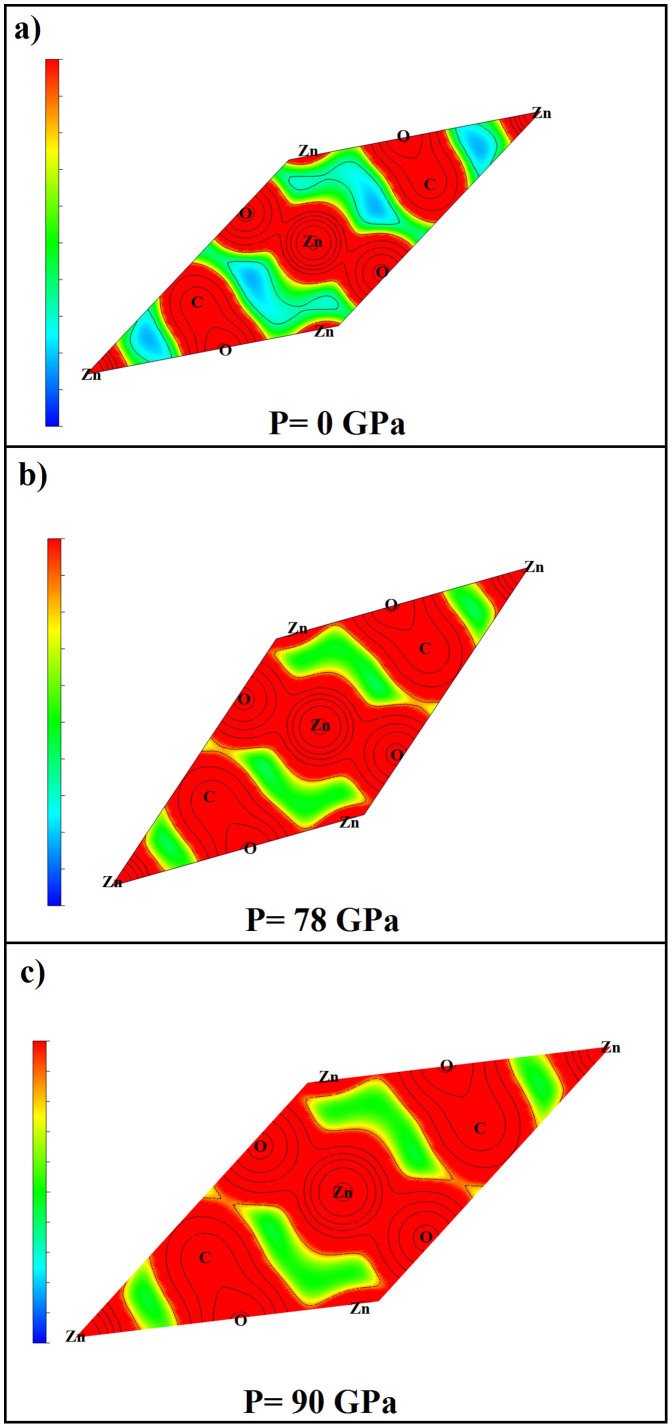
In order to understand the main reasons for the first phase transition, we will analyze - in the following - the electronic charge density. Fig. 4 represents the electronic charge density at 0 GPa (a), 78 GPa (b) and 90 GPa (c) in the (-3 2 1) plane, which includes the three constituents atoms of ZnCO3. At zero pressure (Fig. 4.a) there is a maximum of charge transfer between zinc and oxygen and also between oxygen and carbon. Fig. 4.b shows the electronic charge density at 78 GPa, where a maximum of charge is transferred between oxygen and two zinc atoms as well as together between oxygen and carbon-zinc atoms. Consequently, a new bond between oxygen and zinc is formed at that pressure. However at 90 GPa (Fig. 4.c), we notice only a slight new bond between oxygen and carbon.
Figure 4. Valence charge density of ZnCO3-phase I along the (-3 2 1) plane at zero pressure (a), 78 GPa (b) and 90 GPa (c).
On the other hand, a Bader charge analysis26 of the obtained charge densities is carried out from the present first principles calculations. The charge at the atom is obtained by subtracting the Bader charge from the number of valence electrons considered for that particular atom in the density functional theory (DFT) calculations27. The charges at Zn, C and O atoms at different pressures are given in Table 5. Our Bader charge analysis shows that the positive charge at Zn and C decreases by ~0.035e and ~0.084e respectively, from 1.3839e at ambient pressure to 1.3489e at 90 GPa for Zn atoms and from 2.1478e at ambient pressure to 2.0632e at 90 GPa for C atoms. However, the negative charge of O atoms increases by 0.04e from −1.1773e at ambient pressure to −1.1373e at 90 GPa. Therefore, our Bader charge analysis shows a partial electronic charge transfer only from the Zn to O atoms and C to O atoms.
Table 5. Atomic charge densities (e) from Bader charge analysis of Zn, C and O atoms at different pressures.
| Atomic charge (e) from Bader charge analysis | |||
|---|---|---|---|
| Pressure (GPa) | Zn | C | O |
| 0 | 1.3839 | 2.1478 | −1.1773 |
| 50 | 1.3626 | 2.1184 | −1.1603 |
| 70 | 1.3577 | 2.0656 | −1.1411 |
| 78 | 1.3544 | 2.0639 | −1.1394 |
| 90 | 1.3489 | 2.0632 | −1.1373 |
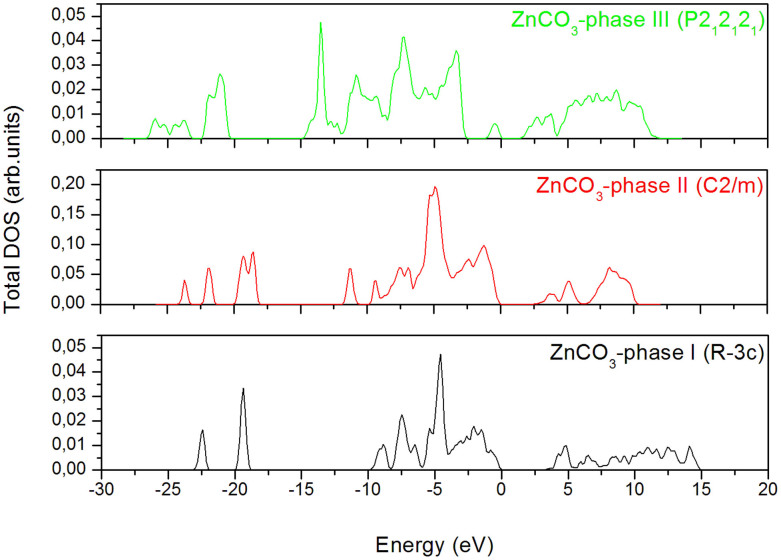
In order to complete the ground state properties of the obtained phases under pressure, we have – additionally – performed the total density of state for the three phases of ZnCO3, as presented in Fig. 5. The obtained band gap value of ZnCO3-phase I corresponds to ~3.34 eV, which is slightly higher than the one of the ground state phase II (~2.64 eV), and than the one of the phase III (~1.45 eV). Bouibes et al.16 found that the band gap value at the ground state of phase I is around 3.4 eV. The latter is in good agreement with the band gap value of phase I. However, it can be underlined here that the band gap of smithsonite remains closer to some semiconductors, such as ZnO (~3.4 eV), than carbonates such as CaCO3 (~6.0 eV), which is rather considered as insulator7.
Figure 5. Total density of states (DOS) for each predicted phase of ZnCO3.
The Fermi level is set to zero.
In summary, different phases of ZnCO3 were predicted here by means of USPEX method together with DFT. We mainly conclude that below 78 GPa, ZnCO3 stable structure has R-3c space group (calcite structure); and between 78 GPa and 121 GPa, ZnCO3 takes up a more complex structure (magnesite phase II7) with C2/m space group and containing (C3O9)6− rings of carbonate. Above 121 GPa, the structure of P212121 space group becomes more stable. The predicted structure is, remarkably, in perfect agreement with the experiment at ambient condition. In addition the computed mechanical quantities at the ground state of phase I agree well with experimental and previous theoretical data. Their behaviors under pressure support our prediction of structural transition of ZnCO3 at 78 GPa. Finally, an analysis from electronic charge density and Bader charge was developed to explain the charge transfer that is behind the phase transition.
Methods
In order to find the stable high-pressure structures of ZnCO3, an ab initio evolutionary algorithm (EA), as implemented in the “Universal Structure Predictor: Evolutionary Xtallography” (USPEX) code, is employed19,20,21. In this work, the structure prediction runs for ZnCO3 were performed at 10 GPa, 20 GPa, 40 GPa, 60 GPa, 90 GPa and 120 GPa, all at zero Kelvin. In these variable-cell simulations, we consider the system with 10, 15 and 20 atoms in the unit cell. The population size is fixed between 20 and 35 number of structures. The first generation is then created randomly. However, in the calculations including 20 atoms/cell, we fix the first generation from the known structures among the other carbonate systems such as calcite, aragonite, post-aragonite, and other structures obtained during the simulations. Magnesite II and magnesite III with 30 atoms in unit cell were added to the resulting structures.
The underlying ab initio structure relaxations and enthalpy calculations were carried out using a plane-wave method and the local density approximation (LDA) for the exchange-correlation22, as implemented in the Vienna Ab-initio Simulation Package (VASP)23,24. In addition, in order to investigate the fundamental properties of Smithsonite calculations, the exchange and correlation function was treated by means of generalized gradient approximation (GGA). Among the available GGA functional28, we selected AM0529 functional, which is particularly appropriate for calculating the properties of ZnCO316. The electron-ion interaction was described by the all-electron projector augmented wave (PAW) scheme30 and the electron configurations 4s2, 2s22p2 and 2s22p4 were treated as valence for Zn, C, and O, respectively. During structural relaxation an energy cutoff of 500 eV was used for the plane wave basis sets, and a k-point resolution of 0.08 Å−1 in the reciprocal space was used for all structures in order to minimize the error from the k-point meshes. The atomic positions, lattice parameters, and cell volume were fully relaxed until the force on each atom is less than 1 meV/Å, and stresses deviate from the desired hydrostatic pressure by less than 1 GPa.
Acknowledgments
Computer Resource Center of Lille1 (CRI) is gratefully acknowledged.
Footnotes
The authors declare no competing financial interests.
Author Contributions A.Z. conceived and designed the study. A.B. performed the theoretical studies and simulations. A.Z. and A.B. analysed and discussed the results. A.B. and A.Z. wrote the manuscript. All authors discussed the conceptual and practical implications of the method at all stages.
References
- Ono S. Synergy Between First-Principles Computation and Experiment in Study of Earth Science. In: Some Applications of Quantum Mechanics (ed Pahlavani, M. R.) 91–108 (Vienna-Austria, 2012). [Google Scholar]
- Sekkal W., Taleb N., Zaoui A. & Shahrour I. A lattice dynamical study of the aragonite and post-aragonite phases of calcium carbonate rock. Am. Mineral. 93, 1608–1612 (2008). [Google Scholar]
- Sekkal W. & Zaoui A. Nanoscale analysis of the morphology and surface stability of calcium carbonate polymorphs. Sci. Rep. 3, 1587 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaoui A. & Shahrour I. Molecular dynamics study of high-pressure polymorphs of BaCO3. Philos. Mag. Lett. 90, 689–697 (2010). [Google Scholar]
- Bakri Z. & Zaoui A. Structural and mechanical properties of dolomite rock under high pressure conditions: A first-principles study. Phys. Status Solidi B 248, 1894–1900 (2011). [Google Scholar]
- Fiquet G., Guyot F., Kunz M., Matas J., Andrault D. & Hanfland M. Structural refinements of magnesite at very high pressure. Am. Mineral. 87, 1261–1265 (2002). [Google Scholar]
- Oganov A. R., Ono S., Ma Y., Glass C. W. & Garcia A. Novel high-pressure structures of MgCO3, CaCO3 and CO2 and their role in Earth's lower mantle. Earth. Planet. Sci. Lett. 273, 38–47 (2008). [Google Scholar]
- Isshiki M. et al. Stability of magnesite and its high-pressure form in the lowermost mantle. Nature 427, 60–63 (2004). [DOI] [PubMed] [Google Scholar]
- Boulard E. et al. New host for carbon in the deep Earth. Proc. Natl. Acad. Sci. 108, 5184–5187 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ayoub A., Zaoui A. & Berghout A. High-pressure structural phase transitions and mechanical properties of calcite rock. Comput. Mater. Sci. 50, 852–857 (2011). [Google Scholar]
- Oganov A. R., Glass C. W. & Ono S. High-pressure phases of CaCO3: Crystal structure prediction and experiment. Earth. Planet. Sci. Lett. 241, 95–103 (2006). [Google Scholar]
- Ono S., Kikegawa T., Ohishi Y. & Tsuchiya J. Post-aragonite phase transformation in CaCO3 at 40 GPa. Am. Mineral. 90, 667–671 (2005). [Google Scholar]
- Merlini M., Hanfland M. & Crichton W. A. CaCO3-III and CaCO3-VI, high-pressure polymorphs of calcite: Possible host structures for carbon in the Earth's mantle. Earth. Planet. Sci. Lett. 333, 265–271 (2012). [Google Scholar]
- Graf D. L. Crystallographic tables for the rhombohedral carbonates. Am. Mineral. 46, 1283–1316 (1961). [Google Scholar]
- Zhang J. & Reeder R. J. Comparative compressibilities of calcite-structure carbonates: Deviations from empirical relations. Am. Mineral. 84, 861–870 (1999). [Google Scholar]
- Bouibes A., Zaoui A. & Tunega D. Bonds, bands and elasticity of smithsonite rock. Solid State Commun. 166, 76–82 (2013). [Google Scholar]
- Goldin D. M. & Kulikova G. V. On the dissociation mechanism of carbonates and their isomorphous mixture. J. Therm. Anal. 29, 139–145 (1984). [Google Scholar]
- McPhail D. C., Summerhayes E., Welch S. & Brugger J. The geochemistry and mobility of zinc in the regolith. Adv. Regolith, 287–291 (2003). [Google Scholar]
- Glass C. W., Oganov A. R. & Hansen N. USPEX–evolutionary crystal structure prediction. Comput. Phys. Commun. 175, 713–720 (2006). [Google Scholar]
- Oganov A. R., Lyakhov A. O. & Valle M. How Evolutionary Crystal Structure Prediction Works- and Why. Acc. Chem. Res. 44, 227–237 (2011). [DOI] [PubMed] [Google Scholar]
- Lyakhov A. O., Oganov A. R., Stokes H. T. & Zhu Q. New developments in evolutionary structure prediction algorithm USPEX. Comput. Phys. Commun. 184, 1172–1182 (2013). [Google Scholar]
- Van Leeuwen R. & Baerends E. J. Exchange-correlation potential with correct asymptotic behavior. Phys. Rev. A 49, 2421 (1994). [DOI] [PubMed] [Google Scholar]
- Kresse G. & Furthmüller J. Software VASP, vienna (1999). Phys. Rev. B 54, 169 (1996). [Google Scholar]
- Kresse G. & Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996). [DOI] [PubMed] [Google Scholar]
- Birch F. Finite elastic strain of cubic crystals. Phys. Rev. 71, 809 (1947). [Google Scholar]
- Bader R. F. Atoms in molecules- A Quantum Theory (Oxford Univ. Press, 1990). [Google Scholar]
- Pandey K. K., Poswal H. K., Kumar R. & Sharma S. M. High pressure iso-structural phase transition in BiMn2O5. J. Phys.: Condens. Matter 25, 325401 (2013). [DOI] [PubMed] [Google Scholar]
- Perdew J. P., Burke K. & Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996). [DOI] [PubMed] [Google Scholar]
- Mattsson A. E., Armiento R., Paier J., Kresse G., Wills J. M. & Mattsson T. R. The AM05 density functional applied to solids. J. Chem. Phys. 128, 084714 (2008). [DOI] [PubMed] [Google Scholar]
- Kresse G. & Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999). [Google Scholar]