Support for Lungfish as the Closest Relative of Tetrapods by Using Slowly Evolving Ray-Finned Fish as the Outgroup

Abstract

In a previous analysis of the phylogenetic relationships of coelacanths, lungfishes and tetrapods, using cartilaginous fish (CF) as the outgroup, the sister relationship of lungfishes and tetrapods was constructed with high statistical support. However, using as the outgroup ray-finned fish (RF), which are more taxonomically closely related to the three lineages than CF, the sister relationship of coelacanths and tetrapods was most often constructed depending on the methods and the data sets, but the statistical support was generally low except in the cases in which the data set including a small number of species was analyzed. In this study, instead of the fast evolving ray-finned fish, teleost fish (TF), in the previous data sets, by using two slowly evolving RF, gar and bowfin, as the outgroup, we showed that the sister relationship of lungfishes and tetrapods was reconstructed with high statistical support. In our analysis the evolutionary rates of gar and bowfin were similar to each other and one third to one half of TF. The difference of the amino acid frequencies of the two species with other lineages was larger than those of TF. This study provides a strong support for lungfishes as the closest relative of tetrapods and indicates the importance of using an appropriate outgroup with small divergence in phylogenetic construction.

Introduction

In phylogenetic trees of coelacanths, lungfishes and tetrapods, these lineages are connected by short branches and coelacanth and lungfish have long branches in constructed phylogenetic trees (e.g., Amemiya et al. 2013; Liang et al. 2013; Braasch et al. 2016; Takezaki and Nishihara 2016). In such cases the relationships of the taxa become vulnerable to the effect of long branch attraction (LBA) (Felsenstein 1978) and the relationship is likely to be estimated incorrectly in phylogeny construction (Philippe et al. 2011). Two studies using the coelacanth genome data showed the sister relationship of lungfish and tetrapods with high statistical support (Amemiya et al. 2013; Liang et al. 2013). Although the use of a large amount of data reduces sampling error (Hillis and Huelsenbeck 1992; Goldman 1998; Massingham and Goldman 2000; Townsend et al. 2012), it may increase bias in phylogeny construction due to a heterogeneous substitution pattern among genes and lineages (Goldman 1998; Lockhart and Steel 2005; Geuten et al. 2007; Su and Townsend 2015; Susko 2015) and the constructed phylogenetic trees may not be free from the effect of LBA (Philippe et al. 2011).

Therefore, we carried out an analysis of the phylogenetic relationship of coelacanths, lungfishes, and tetrapods using the data sets from the previous two studies and our own data set (Takezaki and Nishihara 2016). The relationships of the three lineages in the constructed phylogenetic trees were most strongly affected by the outgroup used, irrespective of the data sets with the variable number of species and genes and extent of missing data, tree construction methods, substitution models and whether concatenated sequences or individual genes were used.

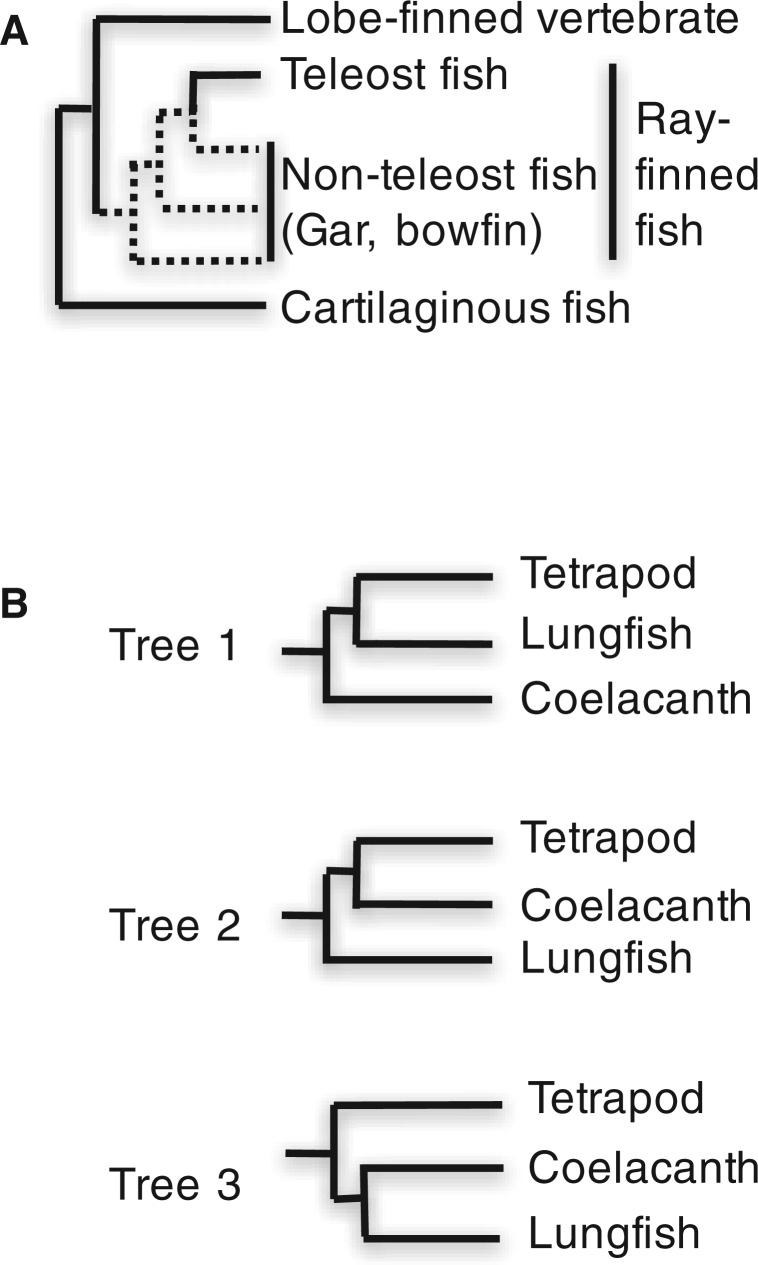
When cartilaginous fish (CF) and ray-finned fish (RF) were both included as the outgroup as in the two previous studies (Amemiya et al. 2013; Liang et al. 2013) or only CF were used as the outgroup, the sister relationship of lungfishes and tetrapods (Tree 1, fig. 1B ) was constructed with high statistical support. However, when only RF were used as the outgroup, the sister relationship of coelacanths and tetrapods was most often constructed (Tree 2, fig. 1B ), though all the possible relationships of the three lineages were generated depending on the data sets and the methods used (Trees 1–3, fig. 1B ). However, the statistical support tended to be low except in the cases in which the data set including a small number of species was used. Coelacanths and lungfishes are two extant lineages of lobe-finned fish. RF are taxonomically more closely related to lobe-finned fish and tetrapods (lobe-finned vertebrates) than CF (fig. 1A ). However, sequence data of RF was more divergent than that of CF, having long branches and different amino acid frequencies. Our study showed that the tree topologies were likely to be distorted in the case where RF were used as the outgroup because of the large divergence of the RF sequences. It should be noted that in our study the effect of choosing genes with large lengths, slow rates or small amino acid frequency differences with other lineages in RF on the constructed phylogenetic relationship of the three lineages was relatively small and that the tree topologies and the statistical support largely remained the same (Takezaki and Nishihara 2016).

Fig. 1.—

Phylogenetic relationships of major lineages of jawed vertebrates. (A) The relationships among lobe-finned vertebrates, RF, and CF. The lobe-finned vertebrates include lobe-finned fish (coelacanths and lungfishes) and tetrapods. (B) The possible phylogenetic relationships of coelacanths, lungfishes, and tetrapods.

RF in the data sets analyzed in our previous study were all teleost fish (TF) (fig. 1A ). It is known that the common ancestor of TF underwent whole genome duplication (e.g., Taylor et al. 2003; Crow et al. 2006) and that TF evolve in a faster rate than other vertebrate lineages (Brunet et al. 2006; Amemiya et al. 2013; Venkatesh et al. 2014). However, RF such as gar and bowfin, which separated from the TF lineage before the whole genome duplication appear to evolve in a slower rate than TF (Braasch et al. 2016). It was suggested that increasing taxon sampling generally improves the accuracy of phylogenetic construction (e.g., Graybeal 1998; Rannala et al. 1998; Pollock et al. 2002; Townsend and Lopez-Giraldez 2010; Nabhan and Sarkar 2011; Townsend and Leuenberger 2011). However, it was shown that addition of distantly related taxa can decrease the accuracy of phylogeny reconstruction (Rannala et al. 1998; Zwickl and Hillis 2002; see for the review in Nabhan and Sarkar 2011) and that deletion of fast-evolving taxa can be beneficial for the reconstruction of the correct phylogeny (Susko and Roger 2012). Therefore, the use of the slowly evolving non-teleost RF as the outgroup is likely to mitigate the effect of LBA and to provide a strong support for the phylogenetic relationship of coelacanths, lungfishes and tetrapods. In this study, we added the spotted gar and the bowfin (Braasch et al. 2016) to our previously compiled data of 26 species (Takezaki and Nishihara 2016) and investigated the effect of the outgroups on the phylogeny of the three lineages.

Results and Discussion

Analysis of Data Set with Gar

The data set to which the gar sequence was added consisted of 702 genes in total of 242,475 sites with no missing data (data set I). Maximum likelihood (ML) trees were constructed for the concatenated sequences with Jones et al. (1992) model + F (amino acid frequencies estimated from the data) + G (gamma distribution of substitution rate across sites) (JTTFG) (see fig. 2A–D ) and GTR (general time reversible) model + G (GTRG) (table 1). The result by the Bayesian method is shown only in a supplementary table S1, Supplementary Material online because the tree topologies of the Bayesian trees were always the same as those by the ML method when the same substitution model was used. The statistical support by the Bayesian method was higher than that by the ML method. However, it is known that the Bayesian method often gives much higher posterior probabilities (PPs) than bootstrap probabilities (BPs) of the ML methods in computer simulation studies (e.g., Buckley 2002; Alfaro et al. 2003; Cummings et al. 2003; Douady, Delsuc, et al. 2003) and analyses of actual data (e.g., Murphy et al. 2001; Whittingham et al. 2002; Douady, Catzeflis, et al. 2003). Theoretical studies showed that it can give a high PP even in cases of polytomy with a large number of sites (Suzuki et al. 2002; Holder and Lewis 2003; Huelsenbeck and Rannala 2004; Lewis et al. 2005; Steel and Matsen 2007; Yang 2007).

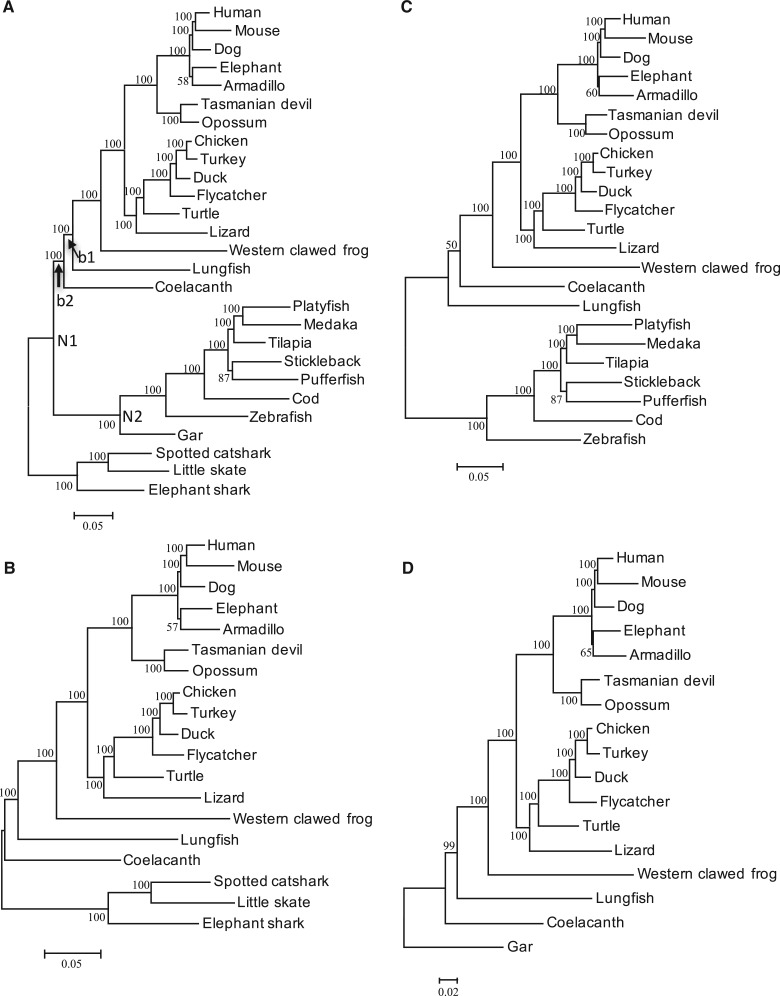
Fig. 2.—

The ML trees constructed for data set I. JTTFG model was used. (A) All species were included. (B–D) show the trees with CF, TF and gar as the outgroup, respectively. N1: the common ancestral node of lobe-finned vertebrates and RF. N2: the common ancestral node of TF and gar. b1: the branch connecting coelacanth with lungfish and tetrapods. b2: the branch connecting the common ancestral node of the lobe-finned vertebrates and N1.

Table 1.

Summary of Tree Topologies and the Statistical Supports

Data set	Outgroup	ML method												Multispecies gene tree based method
		Concatenated sequence								Partitioned
		JTTFG		GTRG		LG4XG		LG4MG		BIC		AICc		JTTFG		GTRG
		Tree	BP	Tree	BP	Tree	BP	Tree	BP	Tree	BP	Tree	BP	Tree	BP	Tree	BP
I	Gar + TF + CF	1	100	1	100	1	100	1	100	1	100	1	100	1	100	1	100
	Gar	1	99	1	100	1	100	1	99	1	100	1	100	1	97	1	100
	TF	2	50	1	63	2	66	2	73	1	51	1	50	1	47	1	53.6
														2	45
	CF	1	100	1	100	1	100	1	100	1	100	1	100	1	98	1	99.2
II	Gar + bowfin + TF + CF	1	100	1	100	1	100	1	100	1	100	1	100	1	100	1	100
	Gar	1	100	1	100	1	100	1	100	1	100	1	100	1	97.4	1	98.8
	Bowfin	1	100	1	100	1	100	1	100	1	100	1	100	1	97.4	1	98.8
	TF	1	58	1	72	2	53	2	63	1	62	1	61	1	50.4	1	58.2
														2	35.8
	CF	1	99	1	98	1	97	1	97	1	100	1	99	1	96.8	1	97.2

Note.—BP, bootstrap probability in percent. BIC and AICc were criteria used in the search of the optimal partition scheme by PartitionFinder.

As in our previous result, Tree 1 was constructed with high statistical support (BP = 100%) with CF and RF (CF + RF) or only CF as the outgroup. When only TF were used as the outgroup, Tree 2 was constructed for JTTFG and Tree 1 for GTRG model. But the statistical support was low in both cases (BP ≤ 60%). As we expected, when gar was used as the outgroup, Tree 1 was constructed with high statistical support (BP ≥ 99%).

The result of AU test (Shimodaira and Hasegawa 2001) was consistent with the constructed ML trees (supplementary tables S2 and S3, Supplementary Material online). With CF + RF, CF or gar as the outgroup, Tree 1 had the highest likelihood and Trees 2 and 3 were significantly rejected (P ≤ 0.003). With TF as the outgroup, Tree 2 had the highest likelihood for JTTFG and Tree 1 for GTRG, but the difference between the likelihoods of Trees 1 and 2 was small and none of Trees 1–3 were significantly rejected (P ≥ 0.077).

In addition we constructed ML trees and carried out AU test with LG4X and LG4M substitution models (Le et al. 2012), in which four different pre-estimated substitution matrices were used depending on the evolutionary rates of sites for the concatenated sequences and by making partitions in the alignment of sequences, using PartitionFinder (Lanfear et al. 2012) (see supplementary tables S4–S6, Supplementary Material online and “Materials and Methods” section for the details of the partitions).

The results of these analyses remained similar to those with JTTFG and GTRG (table 1, supplementary tables S2 and S3, Supplementary Material online). With CF + RF, only CF, or gar as the outgroup Tree 1 was constructed with high statistical support (BP ≥ 99%) and Trees 2 and 3 were significantly rejected by AU test (P ≤ 0.013). With TF as the outgroup Tree 2 was constructed with LG4XG and LG4MG and Tree 1 with the partitioned data, but the statistical supports were low (BP ≤ 73%) and AU test rejected none of Trees 1–3 (P ≥ 0.092).

The AICc value that penalizes the log-likelihood (L) with the number of parameters estimated (k) (AICc $=2k-2L+2k\left(k+1\right)/(n-k-1)$ where n is the number of sites examined) of the tree topologies for concatenated sequence with GTRG were smaller than those with JTTFG (supplementary table S3, Supplementary Material online), indicating a better fit of the substitution matrix estimated from the data used with GTRG than the JTT model. The AICc values with LG4XG and LG4MG were higher than those with JTTFG, even though different substitution matrices were used for categories of sites with different rates. Thus, JTTFG appears to fit better to the data used in this study than LG4XG and LG4MG.

Compared with the AICc values for concatenated sequence with the JTTFG, the AICc values for the partitioned data by the BIC criterion were smaller, but those for the partitioned data by the AIC criterion were larger. In the analysis of the partitioned data JTTG or JTTFG was assumed for most of the partitions (20 out of 28 partitions in total in the scheme searched by BIC criterion and 245 out of 286 partitions by AICc criterion; see supplementary tables S5 and S6, Supplementary Material online). Therefore, the L values with the partitioned data mainly improved by estimation of branch lengths for different partitions. The L values with the larger number of the partitions by the AICc criterion were higher than those by the BIC criterion. However, because AICc penalizes L value with the number of parameters estimated and branch lengths and substitution parameters are estimated for each partition, the AICc values for the partitioned data by the AIC criterion with a large number of partitions became larger than those by the BIC criterion.

The AICc values for concatenated sequences with the GTRG were smaller than those for the partitioned data. The L values with GTRG were higher than those for the partitioned data (supplementary tables S3, Supplementary Material online). Note that the number of parameters estimated for the GTRG was smaller than those for the partitioned data, because only one set of branch lengths were estimated for the whole concatenated sequence, though the substitution matrix was estimated from the data. Therefore, it appears that estimation of the substitution matrix from the data with GTRG had a greater effect on the fit to the data rather than the partitioning.

In the analysis of individual genes the highest numbers of genes supported Tree 1 with CF + RF, CF or gar as the outgroup and Tree 2 with TF as the outgroup (supplementary table S7, Supplementary Material online). The phylogenetic trees estimated by the multispecies gene tree-based method (Mirarab et al. 2014) for ML trees constructed for each gene were also consistent with the ML trees constructed for concatenated sequences and the partitioned data (table 1). With CF + RF, CF or gar as the outgroup, Tree 1 was constructed with high statistical support (BP ≥ 97%), whereas with TF as the outgroup Tree 1 or Tree 2 was constructed with low BPs (≤53.6%).

Properties of Gar Sequence

Table 2 shows the average branch lengths from the common ancestral node of RF and lobe-finned vertebrates (N1 in fig. 2A ) to the five taxonomic groups: tetrapods, lungfish, coelacanth, TF, gar, and CF. The branch length to gar (0.145) was about half of that to TF (0.297) and shorter than that to CF (0.179). Note that from the common ancestral node of gar and TF (N2 in fig. 2A ) the branch length to gar (0.066) was about one third of that to TF (0.176). These values of the branch lengths indicated a much slower rate of evolution of gar than that of TF. The branch lengths from N1 to coelacanth (0.104) and lungfish (0.141) were shorter than that to gar, though in Braasch et al. (2016) only coelacanth had a slower rate than gar. Note, however, in data set II (see below) the branch length to lungfish was as long as or longer than those to gar and bowfin. The length of the branch connecting coelacanth with lungfish and tetrapods (b1) (0.009) was about 10–20% of the branch lengths to coelacanth, lungfish and tetrapods (0.104–0.170), and two-thirds of the length of the branch between the common ancestral node of the lobe-finned vertebrates and N1 (b2), similarly to our previous study.

Table 2.

Average Branch Lengths to the Taxonomic Groups

Branch	Data set I		Data set II
	N1	N2	N1	N2
Tetrapod	0.170	—	0.167	—
Lungfish	0.141	—	0.149	—
Coelacanth	0.104	—	0.104	—
TF	0.255	0.176	0.216	0.137
Gar	0.145	0.066	0.149	0.070
Bowfin	—	—	0.148	0.068
CF	0.179	—	0.178	—
b1	0.009	—	0.009	—
b2	0.014	—	0.014	—

Note.—The lengths from the common ancestral node of lobe-finned vertebrates and RF (N1) and that of TF and gar or bowfin (N2) (figs. 2A and 3A) are shown. b1: the branch connecting coelacanth with lungfish and tetrapods. b2: the branch connecting the common ancestral node of the lobe-finned vertebrates and N1.

In accord with the slow rate of gar, δ score, a measure of the extent of incompatibilities of tree topologies (Holland et al. 2002) of gar (0.047) was smaller than those of TF (0.050–0.086) and of CF (0.057–0.068) (supplementary table S8, Supplementary Material online).

The shorter branch lengths to gar from the ancestral nodes and the smaller δ score compared with those for TF and CF suggest that gar is more relevant as the outgroup to have a higher probability to estimate the phylogeny of coelacanths, lungfishes and tetrapods correctly than CF and TF.

We examined the difference of amino acid frequencies among the five taxonomic groups (table 3). As in our previous study, amino acid frequencies of TF were all significantly different from those of the other lineages (P < 0.01 by chi-square test), whereas the differences of CF with coelacanth, lungfish, and tetrapods were not significant (table 3). Unexpectedly, despite the slow rate, the differences of amino acid frequencies between gar and the other lineages were all significant and larger than those of TF except that with CF.

Table 3.

Differences in Amino Acid Frequencies among the Taxonomic Groups

Taxomonic group	Tetrapod	Lungfish	Coelacanth	TF	Gar	Bowfin	CF
Tetrapod	—	16.4	13.5	38.9*	44.1*	—	16.5
Lungfish	14.8	—	5.4	55.2*	81.9*	—	7.9
Coelacanth	11.8	5.1	—	60.1*	84.7*	—	10
TF	35.1*	49.6*	54.1*	—	41.0*	—	127.8*
Gar	38.9*	71.1*	73.5*	38.6*	—	—	65.3*
Bowfin	37.9*	67.2*	71.0*	38.5*	4.9	—	—
CF	15.7	7.9	10.1	117.5*	59.5*	49.6*	—

Note.—Chi-square values are shown. Upper and lower diagonals are those for data sets I and II, respectively. An asterisk indicates that the value is significant at 1% level.

Data Set with Gar and Bowfin

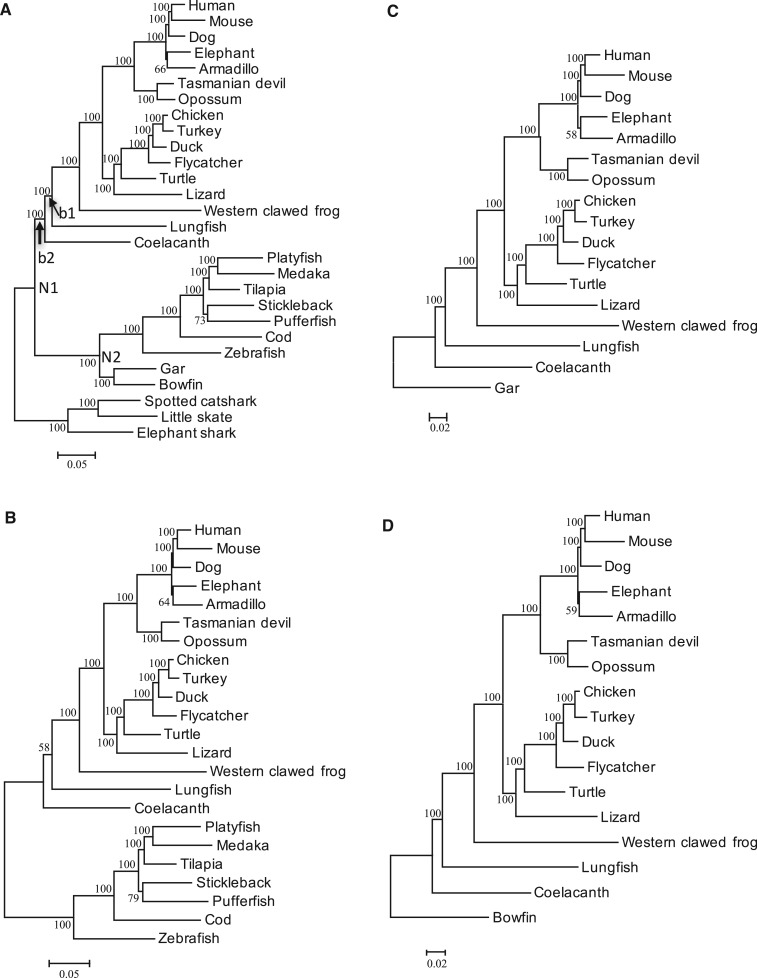
With addition of bowfin (Braasch et al. 2016), the data set became slightly smaller, consisting of 651 genes in total of 185,280 sites (data set II). However, the constructed phylogenetic trees with CF + RF, CF, TF, or gar as the outgroup were essentially the same as those for data set I (fig. 3; table 1 and supplementary fig. S1 and supplementary tables S1, S2, and S7, Supplementary Material online). In this data set, with bowfin as the outgroup, Tree 1 was constructed with high statistical support, as in the case with gar as the outgroup.

Fig. 3.—

The ML trees constructed for data set II. JTTFG model was used. (A) All species were included. (B–D) show the trees with TF, gar, and bowfin as the outgroup, respectively. The ML tree with CF as the outgroup is shown in supplementary fig. S1, Supplementary Material online. N1: the common ancestral node of lobe-finned vertebrates and RF. N2: the common ancestral node of TF, gar and bowfin. b1: the branch connecting coelacanth with lungfish and tetrapods. b2: the branch connecting the common ancestral node of the lobe-finned vertebrates and N1.

The branch lengths to bowfin and gar were virtually identical (0.148 and 0.149 from N1 and 0.068 and 0.070 from N2 to bowfin and gar, respectively) (table 2). Because in this data set the branch lengths to TF were shorter than those in data set I (0.253 from N1 and 0.137 from N2), the difference of the rate between TF and gar or bowfin became smaller and branch lengths to gar and bowfin were about 60% and a half of those to TF from N1 and N2, respectively.

Amino acid frequencies of gar and bowfin were similar to each other and there was no significant difference. The differences of amino acid frequencies between bowfin and the other taxonomic groups were all significant as those with gar, but slightly smaller for bowfin than for gar (table 3). δ score of bowfin (0.041) was also slightly smaller than that of gar (0.045) (table S8). This suggests that bowfin may be more relevant as the outgroup than gar, though the difference is small.

In this study, we examined the phylogenetic relationship of coelacanths, lungfishes, and tetrapods using gar and bowfin as the outgroup. With gar and bowfin that have a much smaller divergence than TF as the outgroup, the sister relationship between lungfishes and tetrapods was constructed with high statistical support, in contrast to the case in which with TF as the outgroup the sister relationship of coelacanths and tetrapods was often constructed and the statistical support was low. This study provides a strong support for lungfishes as the closest relative of tetrapods and indicates the importance of the use of appropriate outgroups with a small extent of divergence in phylogeny construction.

Materials and Methods

We first added the spotted gar (Lepisosteus oculatus) (Braasch et al. 2016) to the 831 gene dataset of 26 species used in our previous study (Takezaki and Nishihara 2016) (data set I). Orthologs of the spotted gar were collected according to one-to-one ortholog annotation with zebrafish genes in Ensembl release 76 (Cunningham et al. 2015). The amino acid sequences of each gene were aligned using MAFFT (Katoh and Standley 2013) with the settings of –maxiterate 1000 and –localpair and subsequently checked visually. Sites with ambiguity or gaps were excluded. Genes of short length (<100 amino acids) were discarded.

Next bowfin (Amia calva) data was added to data set I. The transcriptome data of the bowfin (Braasch et al. 2016) was obtained from the PhyloFish database (http://phylofish.sigenae.org/). A Nucleotide BLAST search (r = 2, G = 2, E = 2, e-value cutoff of 1 × 10^{− 10}) was performed with the bowfin contigs as the queries against the human (GRCh38) and zebrafish (Zv9) cDNA data in Ensembl. If the human and zebrafish best-hit sequences were annotated as one-to-one orthologs in Ensembl, the bowfin query sequence was considered as the ortholog. Amino acid sequences of each gene were aligned in the same way as described earlier. We decided to add the gar genome first and then the bowfin transcriptome data to our previously compiled data. Because the gene content of the transcriptome data appeared to be limited compared with the genome data, addition of the gar genome data, for which the one-to-one ortholog annotation at ENSEMBL is available, first would make the generation of alignment data and maintain the quality easier than addition of the bowfin data first.

ML trees were constructed with Jones et al. (1992) + FG model using PhyML 3.1 (Guindon et al. 2010). The JTTFG was used because JTT model gave the higher likelihood than other empirical substitution matrices LG (Le and Gascuel 2008), WAG (Whelan and Goldman 2001), and Dayhoff (Dayhoff et al. 1978), and the setting of F and G increased the likelihood considerably in our previous study (Takezaki and Nishihara 2016). ML trees were also constructed with GTRG in which the substitution matrix was estimated from the data and LG4XG and LG4MG (Le et al. 2012) in which the four different substitution matrices were used depending on the evolutionary rates of sites, and by partitioning data (see the details below), using RAxML 8.1.16 (Stamatakis 2014). The rate across sites (setting of G) was approximated by the discrete gamma distribution with four categories. 500 bootstrap replications were carried out.

We searched the optimal partition scheme using PartitionFinder 1.1 (Lanfear et al. 2012). In the preliminary analysis we carried out the search with the “all-protein” option to find the best substitution model in the wide variety of models for 200 genes of data set I dividing them into groups of 10 genes. In the result JTT model was suggested as the best substitution model for most of the partitions except in a few cases where JTTF and MTMAM (Yang et al. 1998) +F was suggested as the best model. As stated earlier, in our previous study JTT model produced the highest likelihood for majority of genes, but LG, WAG, Dayhoff gave the highest likelihood for the remaining of the genes. Therefore, we compared the likelihood values of JTT, LG, WAG, Dayhoff, and MTMAM models for each gene and divided the genes into two groups, one consisting of genes that JTT provided the highest likelihood (600 and 558 genes in data sets I and II, respectively) (JTT group) and one with the remaining genes (102 and 93 genes in data sets I and II, respectively) (Other group) (supplementary table S4, Supplementary Material online). For the JTT group of the genes we carried out the search of the optimal partition scheme by limiting the substitution models to JTTG and JTTFG and for the Other group LG, WAG, Dayhoff, and MTMAM (+G for all the models) with or without F. The algorithms “rcluster” and “greedy” were used in the search of the JTT group and the Other group, respectively. Twenty and eight partitions were generated for the JTT and the other group, respectively, by BIC criterion and 245 and 41 partitions by AICc criterion in the case of data set I (supplementary table S5, Supplementary Material online). It should be noted that BIC $=-2L+k\mathit{ln}\left(n\right)$ and AICc $=2k-2L+2k\left(k+1\right)/(n-k-1)$ where L is the log-likelihood estimated for a tree toplogy, k is the number of parameters, and n is the number of data (sites in this case). The numbers of partitions generated for data set II were 16 and eight for the JTT and the other groups, respectively, by BIC criterion and 227 and 38 by AICc criterion (supplementary table S6, Supplementary Material online). In all the searches by the PartitionFinder the tree topology was fixed to Tree 1 (topology 10 in supplementary table S9, Supplementary Material online).

Likelihoods were computed for the possible tree topologies taking into the ambiguities of the relationships among armadillo, elephant and the other eutherian mammals and those among stickleback, pufferfish and the other TF in addition to the relationship among coelacanth, lungfish and tetrapods using RAxML 8.1.16 (supplementary table S9, Supplementary Material online). AU test was carried out by CONSEL (Shimodaira and Hasegawa 2001). Bayesian trees were constructed using MrBayes 3.2.2 (Altekar et al. 2004). The number of generations and the burn-in fraction were set to 500,000 and 0.2 for JTTFG and 4,000,000 and 0.5 for GTRG. The species tree was estimated by the multispecies gene tree-based method using ASTRAL 4.7.12 (Mirarab et al. 2014) with the ML trees constructed for individual genes assuming JTTFG. A heuristic search was carried out. The statistical support was obtained by the multilocus bootstrap approach (Seo 2008) with 500 replications. δ scores (Holland et al. 2002) were computed by SplitsTree 4.14.2 (Huson and Bryant 2006) using JTTG distance.

Supplementary Material

Supplementary data are available at Genome Biology and Evolution online.

Acknowledgments

This work was supported by the Japan Society for the Promotion of Science KAKENHI (grant number 15K08187 to N.T. and 26106004 to H.N). Computations were partially performed on the NIG supercomputer at the ROIS National Institute of Genetics and the supercomputer system of the Institute of Statistical Mathematics.