Differential responses to thermal variation between fitness metrics

Abstract

Temperature is a major factor affecting population abundance and individual performance. Net reproductive rate (R₀) and intrinsic rate of increase (r) differ in their response to different temperature regimes, and much of the difference is mediated by generation time (Tg). Here, we evaluate the effects of thermal mean and variability on R₀, r and Tg, at four population densities in Drosophila melanogaster. The results show that R₀, r and Tg present differential responses to thermal variation. Although temperature effects on R₀ and Tg are non-linear, r response was negligible. R₀ and Tg comprise a generational time scale, while r is at a chronological time scale. Thus, we argue that individuals growing under different thermal environments perform similarly on a chronological scale, but differently on a generational scale.

Environmental temperature varies in time and space at different scales and its influence is complex, involving interactions between mechanisms and processes at different levels of ecological organization¹. Physiology, behavior, population dynamics, and interactions with other species depend, to different degrees, on the thermal environment surrounding the organism². In this context, the effect of temperature on several demographic parameters of ectotherms is well known²,³,⁴,⁵,⁶, as well as how their combined effects impact population dynamics and viability (i.e.⁷,⁸,⁹).

The relationship between environmental temperature and performance has been commonly described as a unimodal and asymmetric function, with a gradual increase as temperature reaches a maximum (the optimal temperature, T_opt), and then an abrupt decay beyond this peak¹,²,⁴,¹⁰,¹¹. Nevertheless, some studies have proposed that the effects of mean temperature and thermal variance may lead to more complex responses in performance curves. In this regard, Estay et al.¹¹ have suggested that performance could be affected either positively or negatively by temperature, depending on the specific thermal mean. Different measures of performance are available, but demographic parameters deserve special attention. They allow us to establish a direct link between individual performance and population properties, such as viability, equilibrium density¹²,¹³ or the expected pattern of fluctuations⁶,¹¹. The most common demographic parameters used as proxies of fitness or performance are R₀ and r. R₀ is the average number of offspring produced by an individual during its lifetime. The intrinsic rate of natural increase, r, is the rate at which the population increases by time step. As can be observed, the main difference between these two measurements is time scale, generational and chronological, respectively. This difference is contained in a third measurement, the generation time (Tg), which is estimated as the average time between the birth of a female and the birth of her first female offspring. Despite their applicability as measurements of fitness, Pásztor, et al.¹⁴ and Kozłowski¹⁵ pointed out that the use of demographic parameters in life history studies needs to be taken with caution, because each parameter must be interpreted in its own context and is constrained by its own assumptions. Thus, these parameters must be used under limited conditions. For instance, R₀ must be used when the state of the trait under study, o, is fixed along an individual's lifetime. Contrarily, r is an accurate measure of fitness when the state of an individual changes from year to year¹⁴. These restrictions have profound consequences in the design of experiments, the interpretation of results obtained in the laboratory, and their extrapolation to field conditions.

In a comprehensive study, Huey and Berrigan³ showed that net reproductive rate (R₀) and intrinsic rate of increase (r) differed in their response to different constant temperature regimes, and that much of this difference was mediated by generation time (Tg). For instance, among ectotherms, the optimal temperature for r is generally higher than that for R₀. Despite these advances, there are at least two important factors that need to be included in further analyses to increase the accuracy of experimental treatments and to improve the predictive ability of laboratory models. The first factor is the incorporation of thermal variability in laboratory experiments as a way to better mimic field conditions. The importance of mean temperatures is widely recognized, but thermal variability could be a factor as important as average values, and could also be a strong selection force acting on organisms in the wild²,¹⁶,¹⁷. Previous efforts have focused on the effects of temperature and variability through short and repeated exposures to stressful temperatures²,¹⁹. Thus, the effect of thermal variability over longer periods of time has received less attention (but see20,21). The second factor is population density and its potential interaction with environmental variables, which could generate a combined effect on demographic parameters (see²²). Environmental factors such as temperature may influence population parameters in different ways, and the net effect could be mediated by density. According to Royama²², temperature could modify population parameters through nonlinear changes in both fecundity and mortality.

We attempt to go beyond current efforts and address the combined impact of mean temperature, thermal variability and population density on demographic parameters of Drosophila melanogaster. This species constitutes a good model to test hypotheses on the impacts of thermal change because its responses to environmental temperature are well known²³,²⁴,²⁵. To this end, we experimentally investigated the effects of these factors on the fecundity and survival of adult fruit flies during their entire life cycle.

Results

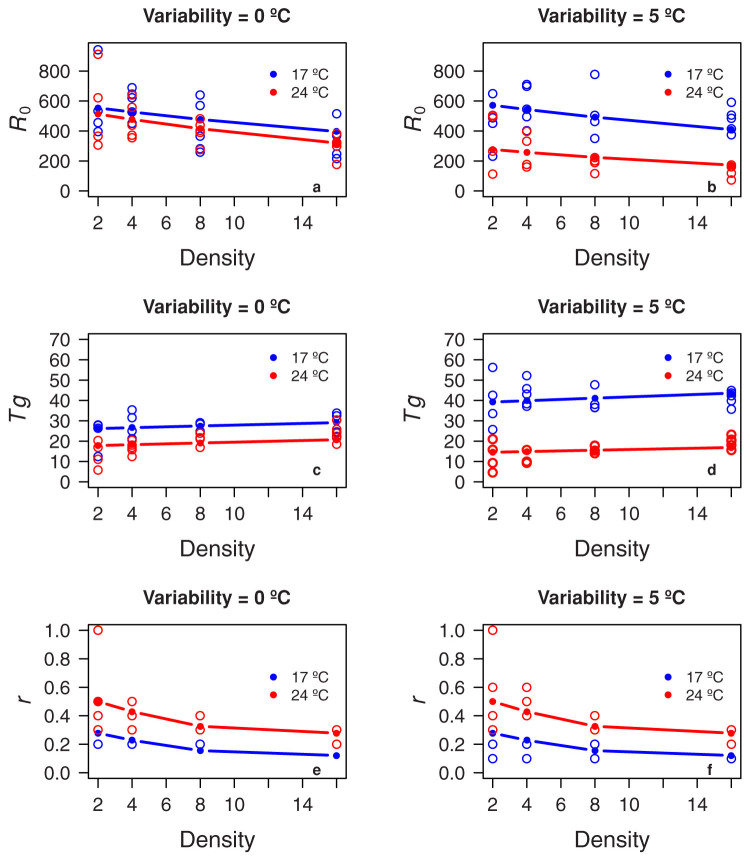
Our experimental results show that mean temperature, variability, and population density all had clear effects on demographic parameters. Values of R₀ showed a decrement with increasing temperature, and this reduction was greater when we incorporated a ±5°C in variability (Figure 1, top panels). The effect of density is also clear: R₀ values were lower at high population density (Figure 1, top panels). In the case of generation time, a decrease in Tg with increasing temperature was also the pattern, and again the reduction was larger in the scenario of ±5°C (Figure 1, panels C and D). On the other hand, population density caused a slight increment on Tg at both 17°C and 24°C treatments (Figure 1, panels C and D). Finally, r values increased with temperature, but variability did not have an effect on the magnitude of change (Table 1). Here, the effect of density was quite similar between both treatments, with a clear decrease in the magnitude of r with an increasing density (Figure 1, panels E and F).

Figure 1.

(A and B) Plot of the best model for R₀ fitted to experimental data. (C and D) Plot of the best model for Tg fitted to experimental data. (E and F) Plot of the best model for r fitted to experimental data. Predicted and observed values for mean treatment temperatures are shown in red and blue for 24°C and 17°C, respectively. Population densities are expressed as individuals per treatment. Left, model considering no thermal variability. Right, the same model considering ±5°C of thermal variability. Note that several points are overlapped.

Table 1. Results of the GAM fitted for each response variable.

Models for R0	loglik	sum edf	BIC	BICw	R2
Ln (R0) = 6.48 + s1(D, df = 1.11) − 0.02 × Tm + 0.32 × Tv − 0.02 × Tm × Tv	−463,40	5,11	952,94	0,16	0,43
Ln (R0) = 7.15 + s1(D, df = 1.10) − 0.05 × Tm − 0.03 × Tv	−469,90	4,10	961,64	0,00	0,33
Ln (R0) = 7.23 + s1(D, by = Tv, df = 0.46) − 0.06 × Tm + 0.02 × Tv	−475,60	3,46	970,35	0,00	0,22
Ln (R0) = 7.18 +s1(D, by = Tm, df = 1.02) − 0.05 × Tm + 0.03 × Tv	−469,00	4,02	959,58	0,01	0,35
Ln (R0) = 6.50 + s1(D, by = Tm, df = 1.03) − 0.01 × Tm + 0.32 × Tv − 0.02 × Tm × Tv	−462,20	5,03	950,68	0,51	0,45
Ln (R0) = 6.51 + s1(D, by = Tv, df = 0.22) − 0.02 × Tm + 0.34 × Tv − 0.02 × Tm × Tv	−470,10	4,22	962,56	0,00	0,33
Ln (R0) = 6.51 +s1(D, by = Tm, df = 1.15) + s2(D, by = Tv, df = 0.68) − 0.01 × Tm + 0.31 × Tv − 0.02 × Tm × Tv	−461,20	5,83	951,66	0,31	0,46
Ln (R0) = 7.19 + s1(D, by = Tm, df = 1.15) + s2(D, by = Tv, df = 0.58) − 0.05 × Tm − 0.04 × Tv	−468,10	4,72	960,77	0,00	0,36
Ln (R0) = 7.07 + s1(D, by = Tm, df = 2.78) + s2(D, by = Tv, df = 1.79)	−467,90	5,56	964,03	0,00	0,35
Ln (R0) = 7.06 + s1(D, by = Tm, df = 2.83)	−471,00	3,83	962,73	0,00	0,31

*D is population density, Tm is mean temperature, and Tv is thermal variability. s_irepresents the cubic regression spline for this variables and df are the effective degrees of freedom for each term. Loglik is log likelihood values, sum edf is the sum of effective degrees of freedom, BIC is the Bayesian information criterion for the model, BICw is the weight of this model (see methods), and R² is the determination coefficient. Note that GAM BIC is calculated using the sum of the edf as an equivalent to the traditional number of parameters.

*D is population density, Tm is mean temperature, and Tv is thermal variability. s_irepresents the cubic regression spline for this variables and df are the effective degrees of freedom for each term. Loglik is log likelihood values, sum edf is the sum of effective degrees of freedom, BIC is the Bayesian information criterion for the model, BICw is the weight of this model (see methods), and R² is the determination coefficient. Note that GAM BIC is calculated using the sum of the edf as an equivalent to the traditional number of parameters.

*D is population density, Tm is mean temperature, and Tv is thermal variability. s_irepresents the cubic regression spline for this variables and df are the effective degrees of freedom for each term. Loglik is log likelihood values, sum edf is the sum of effective degrees of freedom, BIC is the Bayesian information criterion for the model, BICw is the weight of this model (see methods), and R² is the determination coefficient. Note that GAM BIC is calculated using the sum of the edf as an equivalent to the traditional number of parameters.

The best model (higher BIC weight) for R₀ included effects of mean temperature (Tm), thermal variability (Tv) and interactions between Tm and Tv, and between population density (D) and Tm (Table 1). This model explained >45% of the variance in the experimental data (Table 1). D and Tm showed a negative relationship with R₀, which was intensified by variability (Figure 1, panels A and B). Temperature variability per se showed a complex effect on R₀. Below a mean temperature of 17°C the effect was negligible or positive (see blue lines in Figure 1B), while at 24°C, the effect was negative (see red lines in Figure 1B).

In the case of Tg, the model with the highest BCI weight included effects of Tm, Tv and interactions between Tm and Tv, and between D and Tm (Table 1 and Supplementary information). This model explained a large proportion of the variance (76%). Tg showed a positive relationship with D, but a negative one with Tm (Figure 1, panels C and D). On the other hand, thermal variability had an effect on Tg quite similar to the effect on R₀: below a mean temperature of 20°C the effect was positive, but it was negative above this value (Table 1 and Supplementary information).

Finally, the best models for r showed a different structure from other population parameters. These models only contained interactions between Tm and Tv with D, and explained 49% of the variance (Supplementary information and Table 1). No effect of either Tm or Tv alone was retained in the model (Table 1). The effect of the interaction between D and Tm was strongly nonlinear as can be seen from the high value of the apparent degrees of freedom (Figure 1E and F, and Supplementary Information). However, the effect of the interaction between D and Tv was so weak that it was almost undetectable, while removing this term from the model did not improve the results (no changes in BIC, see Table 1). Overall, the relationship between r and D was negative, and positive between r and Tm. Tv had no significant effects on r values according to the best models (Figure 1E and F, and Supplementary information).

Discussion

Our results show how the complex interaction between mean temperature, thermal variability, and population density determine observed values in demographic parameters. Specifically, our results show that r and R₀ not only respond differently to the average thermal environment, but that the magnitude and directionality of this difference is modulated by thermal variability and population density (Table 1 and Supplementary information).

The response of R₀ is nonlinear due to D and Tm – Tv interactions (see the best model in Table 1). Our model shows that at 17–18°C there is a pivotal point where thermal variability has no effect, but that below and above this value, thermal variability causes falls and rises in fitness, respectively. Individuals or populations living in thermal environments with mean temperature below the pivotal point increase the number of their progeny as thermal variability increases, whereas above this point, the number of progeny decreases with thermal variability.

Regarding Tg, there is also a pivotal point around 20–22°C, depending on density, where variability above and below that point causes rises and falls in performance; a similar pattern with respect to R₀ (Supplementary information). According to the best model (Table 1), the average age of reproduction, Tg, in thermal environments above the pivotal point comes earlier in the lifetime of individuals at higher levels of thermal variability; but below this point it is delayed if variability in temperature increases.

The above results are in line with the predictions of Estay, et al.¹¹ and Bozinovic, et al.². These authors showed that the inflexion point in the thermal performance curve -- slightly below the thermal optimum -- is where the expected effect of variability is nil. Considering that the ranges of pivotal points are slightly below the thermal optimum for D. melanogaster²,²⁵,²⁶, they could be close to the predicted inflexion point in the thermal performance curve¹¹.

The results concerning r were surprising. According to the best model, the effect of thermal variability is negligible, despite the strong non-linear effect of density. This suggests that changes in R₀ and Tg caused by thermal variability cancel each other out, resulting in a similar daily rate of increase under either scenario of variability. Considering that r is a measure of the mean rate of increase at a chronological scale and that r ≈ Ln(R₀)/Tg, the best model suggests that D. melanogaster individuals with similar r values could show larger (shorter) Tg and more (less) numerous progeny, depending on the stability of the thermal environment. The endresult is that individuals growing under different thermal environments, in terms of variability, could perform similarly at a chronological scale, but differently at a generational scale. That is, reinforcing the conclusions of Pásztor, et al.¹⁴ and Kozłowski¹⁵ about the different uses of each parameter and their interpretation.

Nevertheless, this last statement is contrary to results obtained in previous studies or the theoretical explanations for the interplay between these three parameters¹¹,²⁶. It has been suggested that in stochastic environments species tend to maximize r to take advantage of short, unpredictable opportunities for reproduction. Due to this, it is expected that species follow the least expensive route to fitness maximization, and theory predicts that a reduction in average age of reproduction is more efficient than producing more offspring²⁷,²⁸. The reason behind this difference with theoretical predictions could lie in our experimental design, the restricted range of temperatures used, or our assumption of linearity in evaluating temperature effects.

New questions arise from our results, such as what are the expected changes at an evolutionary scale in a variable thermal scenario? In this regard, and despite having neither direct evidence of individual plastic responses nor heritability of this trait, we may speculate that, considering the genetic homogeneity of this Drosophila strain, an important part of the observed response could be linked to phenotypic plasticity. However, this assumption should be taken with caution until new evidence is available, supported by adequate experiments.

Evolutionary biology and theoretical demography have provided insights into the potential effects of environmental variability on individual fitness and population dynamics, respectively²⁹. The main message is that physiological performance and population dynamics in variable environments may be substantially different compared to those obtained from experiments or models that assume constant environments²,¹¹,³⁰,³¹,³²,³³,³⁴.

Methods

We used Oregon RC strain fruit flies from a laboratory stock that was reared at 24°C in 250 mL bottles with 30 mL of Burdick³⁵ culture medium. The aim of this study was to analyze the interaction between population density and environment temperature, and its effects over fitness. Species-specific response to temperature has been widely addressed in the literature¹⁸,³⁶,³⁷. This strain of D. melanogaster was cultured for several generations under laboratory conditions, and it was selected to describe the effects of the factors of interest (population density and environmental temperature) over fitness without strong influence of genetic variability. After CO₂ anesthesia, newly emerged adults were collected from the stock, and were immediately sexed and acclimated for 15 days in 47 mL sterilized glass vials in their respective treatment (see below) on a 12 L: 12 D photoperiod regime. During the acclimation period, males and females were kept in different vials to avoid reproduction. R₀ estimates may be biased because the reproductive peak in Drosophila happens during the first days after hatching. However, Dillon et al.³⁸ showed that this peak occurs during the first three days and thereafter oviposition is stabilized. The total number of eggs during the entire peak was less than 100 at 25°C and 50 at 18°C³⁸. Considering this information, it is difficult to think that missing this peak in fecundity could affect an R₀ estimation at the level of hundreds. Once the acclimation period ended, four different population densities were established according to Estay, et al.⁵, namely: 2, 4, 8, and 16 individuals per treatment. Thermal treatments were: 17 ± 0°C, 17 ± 5°C, 24 ± 0°C and 24 ± 5°C. Selection of these temperatures was based on the assumption that populations of D. melanogaster grow fastest at or near 24°C, as reported by Siddiqui and Barlow²⁶. In addition, the same thermal treatments have been used in previous studies². We prepared five glass vials (cohorts) with 11 g of culture medium per density and thermal treatment with the same number of virgin females and males (sex ratio 1:1). Photoperiod regime was 12 L: 12 D. Every three days, the vials were checked to determine the number of dead flies and to replace the culture medium until complete mortality of the cohort. To estimate fecundity, we counted the number of eggs (hatched and non-hatched) from the removed medium. In some cases, when we removed the medium from some vials, larvae and buried eggs could be seen in the medium. For this reason, and in order to ensure an accurate estimation of fecundity, we completely disaggregated the medium to count all eggs.

Statistical analysis

A Lotka life table (sensu Carey³⁹) was constructed for each replicate to estimate net reproductive rate per generation (R₀), generation time or average age of reproduction (Tg), and intrinsic rate of increase (r) using standard procedures (described by Carey¹²). Specifically, we constructed the life table for each cohort by using fecundity (m_x) and the proportion of the surviving individuals at stage x (l_x) from the original number of individuals. Thus, we estimated R₀, r and Tg as R₀ = ∑ l_x m_x, by Tg = ∑ × l_x m_x/R₀, and r ≈ Ln(R₀)/Tg. This last equation is an approximation of r, the intrinsic rate of natural increase, that works acceptably when R₀ ≈ 1 or when Tg shows little variation⁴⁰. These three variables were analyzed separately to obtain the effect of thermal regime on each life-history trait.

To obtain the global response of each variable to density, mean temperature, and variability, we performed a nonparametric regression analysis using a generalized additive model (GAM) incorporating population density (D), mean temperature (Tm), and thermal variability (Tv) as predictors. We chose to use GAM because this method does not make a-priori assumptions about the shape of the relationship between the variables of interest, which is key in our evaluation of the effect of population density. Moreover, the main difference between GAMs and linear models is that linear functions of the variables in GAM are replaced by unknown smooth functions, giving additional flexibility to the modeling process⁴². Considering our experimental design and to avoid over-parameterization, we used linear predictors for mean temperature (Tm) and thermal variability (Tv); however, for population density a partial cubic spline function was used, since it is well known that density-dependence functions exhibit nonlinear forms²². The complexity of the curve (the number of degrees of freedom) and the smoothing terms were determined by penalized regression splines and generalized cross-validation (GCV⁴¹,⁴²,⁴³,⁴⁴) to avoid overfitting⁴³. Also, we permitted shrinkage of the smoothers. This technique allows for extra penalty to be added in the model, and if the penalty is high enough, it will shrink all smoothing coefficients to zero. In simple words, the effect of the variable is removed from the model (a procedure similar to the stepwise variable selection)⁴³.

Regarding the response variables, for R₀ and Tg we used Gaussian error distribution with natural logarithm as the link function during the model fitting process, while for r we used the identity function as link. Several models with and without interactions between predictor variables were evaluated. Models were fitted in the R environment (R Development Core Team, 2013. R: A language and environment for statistical computing) using packages stats and mgcv⁴², and ranked according to the Bayesian Information Criterion (BIC or Schwarz Criterion⁴⁵). For clarity, BIC weights were also included in the results. BIC weights are the probability of each model being the best, given the set of models.

Supplementary Material

Supplementary Information

Supplementary video

Supplementary Information

Supplementary dataset