Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Jun 27;4:5470. doi: 10.1038/srep05470

Highly Sensitive and Wide-Band Tunable Terahertz Response of Plasma Waves Based on Graphene Field Effect Transistors

Lin Wang 1, Xiaoshuang Chen 1,2,a, Anqi Yu 1, Yang Zhang 1, Jiayi Ding 1, Wei Lu 1,2
PMCID: PMC5381543  PMID: 24969065

Abstract

Terahertz (THz) technology is becoming a spotlight of scientific interest due to its promising myriad applications including imaging, spectroscopy, industry control and communication. However, one of the major bottlenecks for advancing this field is due to lack of well-developed solid-state sources and detectors operating at THz gap which serves to mark the boundary between electronics and photonics. Here, we demonstrate exceptionally wide tunable terahertz plasma-wave excitation can be realized in the channel of micrometer-level graphene field effect transistors (FET). Owing to the intrinsic high propagation velocity of plasma waves (>~108 cm/s) and Dirac band structure, the plasma-wave graphene-FETs yield promising prospects for fast sensing, THz detection, etc. The results indicate that the multiple guide-wave resonances in the graphene sheets can lead to the deep sub-wavelength confinement of terahertz wave and with Q-factor orders of magnitude higher than that of conventional 2DEG system at room temperature. Rooted in this understanding, the performance trade-off among signal attenuation, broadband operation, on-chip integrability can be avoided in future THz smart photonic network system by merging photonics and electronics. The unique properties presented can open up the exciting routes to compact solid state tunable THz detectors, filters, and wide band subwavelength imaging based on the graphene-FETs.

The terahertz (THz) region of the electromagnetic spectrum contains almost half of all the photons emitted in the Universe1,2. Because of this, the terahertz technology has recently emerged as a highly sought-after and versatile scientific tool in wide spectrum of applications, including medical diagnose, biological sensing and wireless communications3,4. However, due to the lack of easy-to-use sources and detectors in this frequency range, the scientific progress historically lags behind microwave and infrared edges, which is known as “terahertz gap”5,6,7. To satisfy the terahertz frequency, making metal-oxide-semiconductor field-effect-transistor (FET) smaller is continuously anticipated8. The state-of-art high-frequency performance including cut-off frequency fT ~600 GHz for Si, InP and GaAs devices with gate length shorter than 30 nm has been achieved8,9, while it will be increasing difficulty to raise the frequency above 1 THz when the device arrives its ballistic limit. A more recent approach for exploiting FETs such as III–V high electron mobility transistors (HEMT) or Si complementary metal oxide semiconductor transistors relies on the excitation of plasma waves in the channel10 (see Supplementary Information). It has been predicted that the hydrodynamic nonlinearity of plasma waves can lead to the multiplication and detection of THz radiation11,12,13,14. A strong resonant photoresponse of plasma waves in 50 nm InAlAs/InGaAs HEMT with voltage tuned from 1.8 to 3.1 THz has been observed at 10 K15. However, the dissipative damping caused by the scattering of impurities or phonons, and the strong reflection at Restralen-band, limit the maximum available THz photon absorption and range of working frequency (e. g. GaAs ~ 2.5 THz, GaN ~ 10 THz) at room temperature16,17.

To this regard, graphene, a two-dimensional crystal of carbon atoms packed in honeycomb lattice, may offer efficient platform for strong light-matter interaction, due to its intrinsic high mobility and chiral electronic spectrum18,19,20. From the first large-scale patterning of graphene FETs18, performance has improved at a rapid pace. Graphene, synthesized by various techniques including exfoliation of highly ordered pyrolitic graphite18, chemical vapor deposition21, epitaxial growth on silicon carbide22,23 exhibits prominent advantage for high-frequency applications. Recent progress on either back-gated or top-gated graphene FETs integration with high-k dielectric such as Al2O3, has achieved mobility over 8000 cm2/Vs at high charge density and and 40000 cm2/Vs at low charge density22, making graphene a potential candidate for THz nanoelectronics. In principle, the free carrier density in graphene can be tuned by several orders of magnitude (1011 ~ 1014 cm−2). Such unique property allows one to control strongly the plasma waves from far-infrared to terahertz frequencies. However, there are still limited investigations on the ac dynamics of Dirac fermions in FETs at THz frequency, and the efficient excitation of plasma waves in graphene-FETs is imposed as a key step towards future resonant detectors. Motivated by such awareness, in this work, we deal with the plasma wave excitation in the channel-cavity of graphene-FETs. In the meantime, the screening effects of metallic grating-gates/cooperative electric vibrators on the plasma wave are explored for opto-electronic interconnect. The strong change of optical transmission with wide voltage-tunability is observed at the resonant frequency of plasma waves. These results allow one to explore electro-optic properties of plasma waves based on the configuration of graphene FETs, and can be used to build both the ultra-fast THz modulators and the tunable detectors.

Results and discussions

The plasma wave and its quality factor Q in FET-based THz-detectors is commonly limited by the scattering of impurities and phonons during the propagation of plasma waves. When the resonant conditions is satisfied, the plasma waves excited by the incident radiation reflect at boundary between gated and ungated part of channel and create standing wave oscillation with enhanced amplitude. Here the Q factor is ideally be determined by the product ω0τ(where ω0 is the plasma wave frequency, τ is the momentum relaxation time), it evaluates the sharpness of plasma wave resonance in relative to the background absorption (see Materials and Methods) or the frequency selectivity for tunable resonant detection. In addition, the inverse of τ determines the linewidth of plasma wave resonance, and the propagation distance of plasma waves is evaluated by ~sτ (s denotes the plasma wave velocity). Therefore, samples with higher momentum relaxation time τ are desirable for THz detection or modulation. Even though the carrier mobility of graphene film reported in the literature exhibits extreme variability from ~3000 cm2/Vs to 20000 cm2/Vs under different growing conditions, recent studies demonstrate that the intrinsic mobility can exceed 100000 cm2/Vs in both single and bilayer graphene systems after eliminating the scattering in the substrate, as shown in Table I. For a moderate room-temperature mobility of 10000 cm2/Vs at Fermi energy EF ~ 0.4 eV, the momentum relaxation time τ of the Dirac fermions is 0.4 ps larger than that of III–V semiconductor, such as GaN24,25. In the non-ballistic regime (e. g. longer channel length), the decay of plasma waves along the propagation direction is exponential, with 1/e characteristic length lch ~ 2 sτ (4 μm at EF = 0.1 eV). In the graphene FETs for terahertz detection, the channel of 2DEG serves as a cavity, the standing plasma wave oscillation can be established when the half-wavelength of plasma waves is commensurate with the length of channel22,23,24,25,26,27,28,29. Therefore, the resonant detection with frequency tunability and selectivity can be easily realized if the channel length L is much less than the characteristic length. In III–V semiconductors such as GaAs, InGaAs, such resonant condition requires the gate length shrinking down to 100 nm, in order to reach plasma resonance over 1 THz (seeing Table II). However, one of the major bottlenecks limits the room-temperature operation of THz detection is the resonant broadening caused by the scattering between gated and ungated plasma waves due to the long access region in the architecture of FET17,24. During the every reflection at the boundary of channel cavity, the amplitude of plasma wave deteriorates so that the quality factor Q is much smaller than that predicted by the theory. Therefore, the graphene-based plasma-wave FETs will potentially eliminate these deficiencies due to both the highly tunable electron density (higher plasma velocity s) and high mobility.

Table 1. Experimental mobility (cm2/Vs) of monolayer, bilayer and multilayer graphene on different substrates.

  SiO2 BN SiC
Monolayer graphene 9 000–30 00030 55 000–125 00031 18 10032
Bilayer graphene33 3 000–12 000 40 000 6 000–10 00028
Multilayer graphene ~10 00034   1 000–3 00035
Open in a new tab

Table 2. Quality factors of various III–V FETs (experimental) and the proposed one in this work.

Materials Room temperature mobility (cm2/Vs) Cyclotron mass (m0) Quality Factor (Q) Gate Length (μm)
Monolayer Graphene   10 000 0.069 ~15.5 (6.39 THz) 2.4
0.104 ~29 (11.89 THz)        
Bilayer Graphene (AB stacking)   10 000 0.037 ~7.5 (6.85 THz)  
0.059 ~20 (9.84 THz)        
AlGaN/GaN25 ~1200 0.22 ~1 (1.1 THz) 1.15
InGaAs/InAlAs ~7000 0.04230 ~2.5 (2.5 THz) 0.05
AlGaAs/GaAs38 7480 0.063 ~5.5 (2.5 THz) 0.16
Open in a new tab

Excitation of plasma waves and electrostatic screening effect in FETs

Here, we employ the grating-gate to facile the excitation of plasma waves and Fermi level modulation, and thus the grating-gate serves both as the polarizer and electrode, as shown in Fig. 1(c), where all the graphene sheets are connected to the same voltage sources. Although various prototypes of graphene plasmonic devices has been proposed at mid-infrared frequency, the Dirac plasma waves in FETs and the screening effect of the metallic gate has rarely been investigated. Here, we demonstrate that the effect can be a key factor in developing high tunable plasma wave THz detector or modulator. For normally incident THz radiation, the plasma wave resonances are developed with the filling factor (f) of the grating acts as an important parameter. When f ≪ 1, i. e. in the limit of single gate, the resonance take places when the wavelength of plasma wave is commensurate with gate length (L). On the other hand, the wavelength of plasma waves can occupy the entire period (Λ) of the grating if f ~ 1. Due to the screening of the metallic grating-gates, the effective permittivity ε* is determined by the thickness d of dielectric layer separating the graphene from electrodes and the period Λ or the plasma wavelength (seeing Material and Methods). Thus, the propagation of plasma waves in the gated and ungated channels follows different dispersion relationship36.

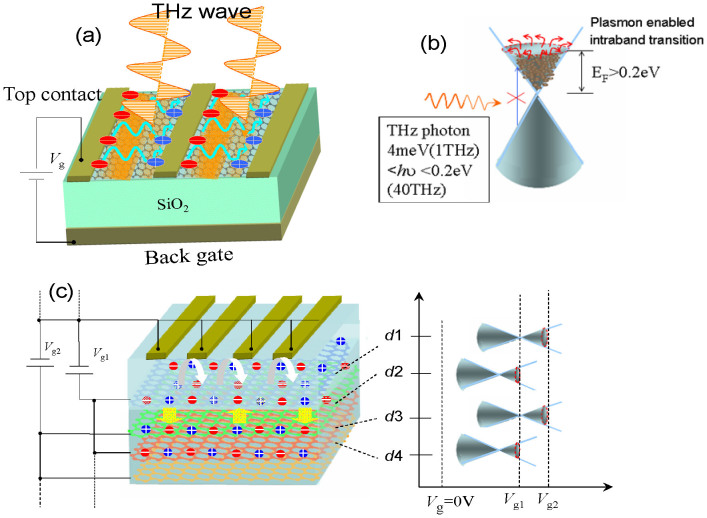
Figure 1. Illustration of plasma waves in graphene FETs for terahertz detection and modulation.

Figure 1

Open in a new tab

(a) The formation of plasmonic cavity with electric vibrator at top contact monitoring the conductivity of graphene channel, the bottom gate is used to tune the Fermi level, and the cascade cooperative plasma oscillation is formed, leading to the rectify and detection of THz radiation (seeing Materials and Methods). (b) The conical band structure and the optical process are shown. The plasmon enabled intraband electron transition is dominant due to the Pauli blocking and low density of states at Dirac point. (see Supplementary Information). (c) Left column: the proposed MGL-FETs with the stacked graphene sheets being connected to different or same voltage sources if needed, the grating contacts at the top side act both as electrodes and couplers. Right column: with an applied bias, the shift of Hartree band and the Fermi level accommodate the carriers' distributions.

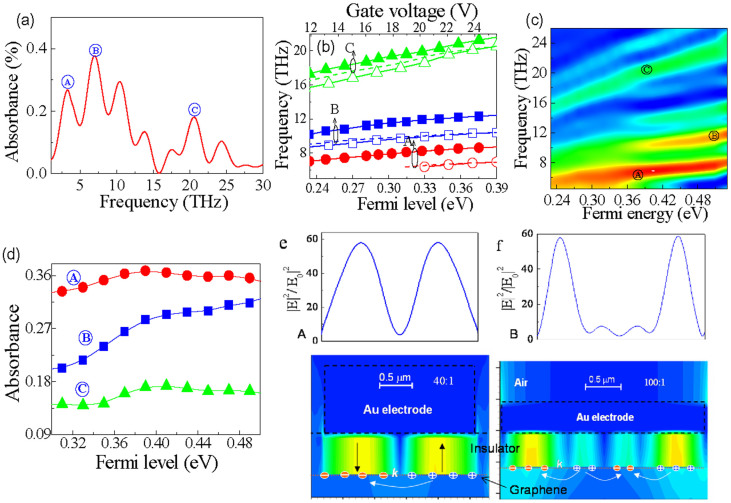
We tune the Fermi level from Dirac point electrically. Fig. 2 (a) shows the plasma wave-induced THz optical absorption in graphene-FETs when the Fermi energy is 0.39 eV above the CNP (charge neutral point). There are rich veins of sharp resonances with frequency ranging from 2.5 THz to 30 THz are induced in the near-field zone of the electrodes (seeing Figs. 2(e) and (f)). It is shown that the quality factor (Q) of ~15 can be order of magnitudes larger than that of previous GaAs or GaN heterojunction FETs37 with the same dimensions (seeing Table II), and the absorption strength approaches to the maximum available value ~40% (seeing Material and Methods), which is remarkable since the active device is only one-single layer. It is worth noting that period Λ of the present device is about two times and order of magnitude longer than that of AlGaN/GaN and InAlAs/InGaAs, therefore the quality factor presented here is a conservative estimation. Moreover, the resonances up to seventh order can be discernable from Fig. 2(a), which can be engineered to facile wider tunable THz detection or modulation beyond other available ones. Such results benefit from the potential highly tunable electron density from 1011 cm−2 at CNP up to 1014 cm−2 or above and higher carrier's mobility.

Figure 2. The plasma wave resonance in monolayer and double-layer FETs with grating coupler (Fig. 1(c)), period Λ = 2.8 μm, gate length L = 2.4 μm (corresponding to the filling factor f = 0.86), the thickness of dielectric tunneling junction d = 50 nm.

Figure 2

Open in a new tab

(a) All kinds of resonances have higher Q value than other conventional 2DEG system like GaN. (b) The shift of plasma wave resonance frequency after electrically tuning the Fermi level, solid symbols indicate the frequency dependence of plasma waves in double-layer FETs on the gate voltage, and the dashed line is that of monolayer FETs, both of these device exhibit approximately Vg1/4 relationship. Open symbols is the frequency dependence of plasma waves in monolayer FETs on Fermi level relative to the CNP. (c) and (d) are the contour map of plasma wave resonance in monolayer FETs. It is found that there is the non-monotonous dependence of resonance on Fermi level. (e)The near-field enhancement caused by the screening of the electrodes is related to the first two resonances A and B.

However, due to the relativistic electron transport properties caused by the linear dispersion, the plasma waves in graphene-FETs exhibit properties different from those in conventional 2DEG system with parabolic dispersions. Fig. 2(b) displays the scaling of graphene plasma waves under different gate voltages or Fermi levels. Unlike the conventional 2DEG, the plasma wave in graphene-FETs can not be simply described by employing the parallel plate capacitor model. The quantum capacitance effects in the graphene-channel are notable even with 50 nm thick dielectric layer due to its low density of state near Dirac point. Such effects cannot be neglected at higher order plasmon resonance (seeing dashed line in Fig. 2(b)), and thus may play an important role in the near infrared or visible light region. The sub-linear frequency dependences of these resonances on Fermi energy and gate voltage are in consistent with theoretical predictions and experimental observations recently39. In parallel-plate capacitor model26,39, the frequency of plasma waves is approximately proportional to Vg1/4 (Vg is the gate voltage) in theory, which is in contrast to the Vg1/2 relation in 2DEG with parabolic dispersion21. However, in actual graphene device, the deviation from Vg1/4 relation may take place if the quantum capacitance dominates over geometrical capacitance or the device has long ungated part of channel weakening the cavity confinement of plasma waves. Such phenomenon is slightly exhibited in Fig. 2b, where the voltage-induced frequency-shift of higher plasma waves (dashed line) departures from those at different Fermi levels (open symbols).

To understand better the intrinsic physical mechanism, Figs. 2 (e) and (f) display the induced field distributions of resonances a and b along the channnel of graphene-FETs. Due to the capacitive coupling between grating-gate and graphene, the intensity of optical-field is strengthened by more than 200 times. These figures also indicate that resonances A and B in the channel have two and four antinodes of field amplitude under the metal gate. The results also indicate that resonance B is the higher order mode of resonance A (fB:fA = 2:1). In addition, the half-wavelength of plasma wave is approximately in commensurate with the length of gate finger, in consistent with the above discussions. For plasma waves in the pristine graphene, the propagation constant, length and field-localization depend strongly on the dielectric environment ε*(seeing Materials and Methods), the value of which can be tuned efficiently with the implementation of electrostatic-gating. Also, the tunability of dielectric environment can be explored to realize highly tunable THz waveguide. The resonance C of Fig. 2(a) occurring at higher frequency is actually due to the ungated plasma wave with the similar in-plane dipole distribution along the channel. Fig. 2(c) displays the color plot of the resonant spectra with the change of Fermi energy or gate voltage. We find that higher order modes are growing up alternatively at higher Fermi energy or gate voltage. The results indicate the potential of graphene-FETs for wide-band THz applications. For more clarity, the transformations of resonances A, B and C are shown in Fig. 2(d), and non-monotonous dependence of resonant strength on the Fermi energy or gate voltage is observed. Interestingly, we find that both fundamental plasma mode A and C experiencing the process of resonant enhancement and damping near the critical Fermi energy EF ~ 0.4 eV, and higher order mode B is growing up continuously. The behavior has not yet been observed in conventional 2DEG system, which may be concealed by the lower mobility and finite tunable range of electron density. In graphene, the plasma wave resonance is mainly determined by three phenomenological parameters (radiative loss, electron relaxation loss and nonradiative loss), among which the radiative loss can exceed the electron relaxation if the samples have higher mobility and higher Fermi energy (seeing Materials and Methods). Following such a way, the higher order plasma waves would be growing up alternatively as depicted in Fig. 2d.

Plasma wave resonances in MGL-FETs and tunable dispersions

Based upon the above results, it is known that the tunability of double-layer graphene FETs can be limited by the screening of carriers in the top-graphene channel and is poorer than that of the single-layer ones. The behavior can be understood intuitively after taking into account the fact that the top and bottom graphene layers share the same amount of carriers Q0 as the electrodes. The frequency of the combined resonance in double-layer devices is obviously lower than that in single-layer ones with the same electron number Q0 (seeing also the following discussions). In order to eliminate these drawbacks, we proceed to exploit the modification of plasma wave resonance in MGL-FETs with dielectric barrier-layers separating different graphene sheets as shown in Fig. 1(c), and the dielectric layer thickness is sufficient large that only the Coulomb interactions between those graphene layers are presented (seeing Supplementary Informations).

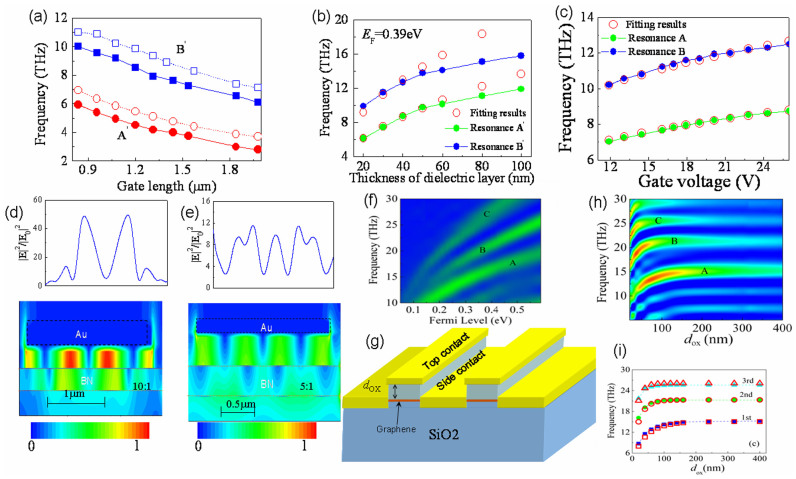
Fig. 3 illustrates the scaling behavior of plasma wave resonances in monolayer and strong coupling double-layer system. Unlike other results on graphene-dielectric grating system from where the frequency of plasma wave resonance depends on the period Λ only, the frequency of plasma waves propagating in graphene-FETs is inversely proportional to the gate length ~1/L, which may originate from the screening caused by the electrodes (seeing Materials and Methods). In strong coupling multi-layer graphene system (Fig. 3(e)), the screening between graphene-layer can not be neglected and the “virtual gate” effect should be taken into account40. In such cases, the graphene layer not only supports the plasma waves but also behaves like another electrode to tune the frequency. Therefore, the resonance frequency of plasma waves in the strong coupling limit should be modified as 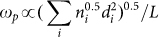Inline graphic, i is the layer index, di is the separation between graphene layers, and ni is sheet charge density in the ith graphene layer. The results indicate that tunability of detector or modulator can be improved in separately electrical-controlled layers. The scaling scheme of frequency dispersion in the multilayer-FETs (five graphene sheets in Fig. 3(f)) is in good agreement with the assumption. Rewriting the law as, ωp = C EF1/2, one can see that multilayer graphene has larger coefficient C than monolayer graphene, leading to the better electrical tunability. Meanwhile, the non-monotonous change of plasma wave resonance can also be resolved, and the intensity of the fundamental mode A is starting to decline around Fermi energy EF ~ 0.45 eV. As discussed above, it is expected that the intensity of higher order mode can be strengthened alternatively. Compared with the similar structure using the single graphene-layer, the fundamental mode of multilayer graphene can be tuned from 10 THz to 19 THz when the Fermi level increases from 0.15 eV to 0.59 eV, but the monolayer graphene can just be tuned only from 4 THz to 8 THz.

Figure 3. Illustration of the scaling of plasma wave resonance and screening effect in MGL-FETs (Fig. 1(c) under different controllable parameters.

Figure 3

Open in a new tab

(a) The frequency dependence of plasma waves in strong coupling double-layer device (Fig. 1(c)) with interlayer spacing d ~ 50 nm is proportional to the inverse of gate length L, the solid and open symbols are the first two resonances at EF ~ 0.21 eV and EF ~ 0.29 eV, respectively. (b) The screening (virtual-gate effect) between two graphene sheets affect obviously the dispersion of plasma wave resonance in the strong coupling limit (d < 60 nm), where the virtual gate effect dominates (Fig. 3(d)), and the tunability degrades to the monolayer plasma wave resonance if the interlayer spacing exceeds 60 nm, in the meantime, a sharp contrast in near-field strength is seen between Figs. 3(d) and (e). Also, the good agreement between “virtual gate” model and obtained data in Fig. 2(b) corroborates again the dominated role of screening (Fig. 3 (c)). By increasing the number of graphene sheets, the plasma wave resonance can be tuned in wider frequency band (f). (g) is the schematic of the multi-waveguide-like FETs as proposed for nano-photonics making use of the strong screening effect and confinement of plasma wave in graphene. (i) Indicating the good agreement between effective medium model (seeing Materials and Methods) (open symbols) and obtained results (solid symbols). We find the sensitive tunable resonance and propagation constant or absorption in deep subwavelength regime from 0 nm to 200 nm (i. e. λ2/d2 ~ 104) (h), enabling the flexible design of monolithic THz photonic network system.

Furthermore, the above mentioned screening behavior can be clearly discernable in double-layer graphene device (Figs. 3(b) and (c)) when the separation d between them is smaller than 60 nm. On the contrary, when the thickness d exceeds 60 nm, the modified formula deviates obviously from the obtained results and the tunability of plasma wave is deteriorated arising from the poor coupling between these two graphene sheets. Furthermore, in Fig. 3(d), we can indeed see that the formation of “virtual gate” causes strong screening of electric-field spreading from the two channels in the device with 40 nm dielectric layer. The screening leads to the out of phase dipole oscillation of plasma waves between the two channels. However, the effect can be neglected in Fig. 3(e) with dielectric layer thicker than 100 nm, and obviously, the device behaves like that with only single-layer. Meanwhile, with only 60 nm thickness separation, the coupling strength between graphene sheets is decreased by more than four times. The results also demonstrate the strong field confinement of graphene plasma waves in deep-subwavelength regime. Other interesting findings in Fig. 3 (e) is that the propagation of plasma waves in lower channel is very similar to the ones in pristine graphene waveguide (seeing the following sections).

Furthermore, the multiple-waveguide-like FET structure with monolayer graphene serves as a transmission medium can be formed (Fig. 3(g)). The resonant frequencies in such configuration exhibit blue shift when the thickness dox of the insulating layer increases, as shown in Figs. 3(h) and (i), due to the fact that the effective permittivity (seeing Materials and Methods) is in strongly correlation with the screening of electrodes. It is also clear that the resonant peaks scale vary rapidly with the changing of dox in submicrometer range (0 ~ 200 nm) and can be well fitted by the effective medium model (Fig. 3(i)). Except for the shift of the resonances, the intensities also depend strongly on the thickness of the insulator from 0 nm ~ 200 nm. It is indicated that the propagation length Lp ~ 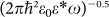Inline graphicof plasma wave can be optimized in deep subwavelength regime according to different purposes as expected. The result also inspires us to develop compact terahertz waveguide (seeing Supplementary Information) in more controllable ways and facile monolithic integration with existing solid-state terahertz sources, such as quantum cascade lasers, backward diodes etc.

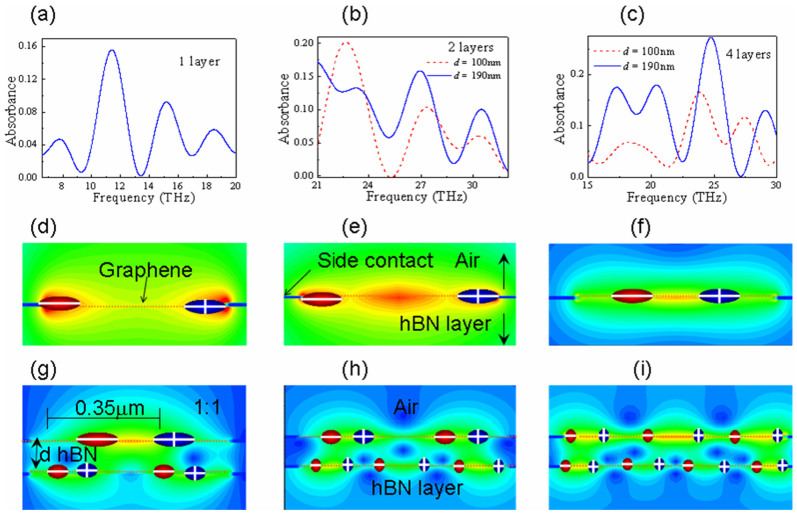
Fig. 4 presents the oscillations of plasma waves in monolayer and multi-layer graphene devices in the absence of metallic screening. The side contacts of devices serve both as electrodes/electric-vibrators for photon detection or slot-line for THz plasma waveguide (Fig. 1(a)). In monolayer device, three kinds of guide mode resonances can be excited independently with similar modal characteristics as the results reported above (Figs. 4(d)–(f)). We find that in the device with only single graphene sheet, two modes originate from the hybridization of edge-graphene-plasma waves (EGP)41. Due to the splitting, one of two modes with the field distribution being localized at the edge is similar to the even-parity edge mode (Fig. 4(d)) in freestanding graphene nanoribbon, and another is similar to the guided edge mode with odd parity (Fig. 4(e)). In addition to EGP, the so-called waveguide-graphene-plasma waves (WGP) with electric polarization extending over the entire ribbon width can also be excited (Fig. 4(f)). In similar to the aforementioned plasma waves, such WGP mode is activated when the half-wavelength is commensurate with the separating between side contacts. It should be noted that the near-field strength of WGP mode is an order of magnitude stronger than other two edge modes. The results indicate the potential of the graphene device for deep-subwavelength imaging. The hybridization of plasma waves has originally been investigated on GaN and AlGaAs/GaAs double quantum wells42,43. Here only OP (optical plasma) plasma waves can be observed in double-layer graphene FETs due to the small net dipole of AP (acoustic plasma) mode. The reduced symmetry between upper and lower graphene channel is reflected in the combination of different plasma waves in the two channels (Figs. 4(g)–(i)), which can be inferred from the dielectric structure above and below the individual graphene sheet. In these figures, more node-number of plasma waves can be seen in the lower channel. It is indicated that there is larger effective dielectric polarization suppressing plasma wave oscillation of the FETs, in consistent with the above results. In addition, the multi-resonance can be developed by increasing the number of graphene layers or introducing the nonsymmetric structures into the graphene plane. For example, we find the splitting of plasma resonance in the device with four layers and resonance up to 7th order occurs in single-layer ones (Figs. 4(a)–(c)), and activation of AP mode when the channel length between upper and lower channel is different. All these results illustrate potentially wide tunable THz/far-infrared detection of graphene, meanwhile, the plasma wave will cause the modulation and control the polarization of incident waves (seeing Supplementary Information), and thus enabling the realization of monolithic THz spectrometer.

Figure 4.

Figure 4

Open in a new tab

The hybridization modes in monolayer and multi-layer graphene FETs, as shown in Fig. 1(a), (a)–(c) the spectral characteristics of plasma waves in monolayer (a), double-layer (b) and four-layer devices (c), in which the Fermi level can be tuned separately. We find the enhancement and splitting due to the interaction between Edge and Waveguide plasma waves. (d)–(f) displays elementary plasma waves in monolayer graphene-FETs, (d) and (e) illustrate the Edge-graphene-plasma waves (EGP), and (f) illustrates Waveguide-graphene-plasma waves (WGP). (g)–(i) demonstrate the interaction between WGP modes with different node numbers along the two channels of double-layer FETs. The oscillating charges are all extracted and shown along the channels.

Conclusions

In summary, we have introduced novel graphene-based FETs with the plasma waves acting as a new quasi-particle to transfer THz signal. Owing to its intrinsic high transport velocity and mechanical flexibility, the plasma wave devices yield very promising properties, including high sensitivity and wide-band tunability throughout the entire THz domain. The multiple guide-wave resonances in the graphene plane create deep sub-wavelength confinement of plasma wave and lead to Q-factor an order of magnitude higher than that of conventional 2DEG system at room temperature. Such unique properties enable the potentially application of graphene-based plasma wave device for compact solid state THz detectors. Most importantly, the screening effect of plasma waves in FETs can be explored both electrically with tuning the Fermi level and geometrically with changing the structural sizes. Rooted in the understanding, the performance trade-off among signal attenuation, broadband operation, on-chip integrability and structural complexity can be avoided in future THz smart photonic network system merging the photonic and electronic advantages of graphene. Besides the presented exciting results, the plasma wave FETs may offer sub-wavelength imaging for defects, adsorbents or surface morphology of epitaxial-grown layers by implanting recent IR nanoscopy technique44. To that end, the THz waves are unambiguously safer due to its lower energy and higher penetrability. During the nano-imaging, there would be no additional free-carriers generated in target materials through direct interband transition, and free-carrier absorption distorting available information. Moreover, since graphene is a two-dimensional conducting sheet with high electrical tunability, the signals can be transferred or amplified to other conventional electronic system, opening up the exciting routes to wide band subwavelength imaging.

Methods

The dispersion of 2D plasma waves in FETs

In the long wavelength limit, the Bohr radius of Dirac fermions is far less than the periodic perturbation of charge density and plasmon wavevector q is smaller the electron Fermi wavevector 2kF. Therefore, the carriers suffer from collisions with each other very rapidly under the action of terahertz field, and behave like a fluid, in which the validity of the hydrodynamic formalism can be established. Linearization the continuity and Euler's equation, the following expressions can be obtained,

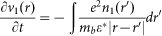graphic file with name srep05470-m3.jpg

and

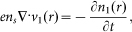graphic file with name srep05470-m4.jpg

where v1(r) and n1(r) are the first order perturbative quantities of electron velocity and density, ε* is the effective permittivity, the dispersion relation of plasma wave in the single-layer graphene sheet can be obtained as shown in the text. The Coulomb interaction or the restoring forces between carriers depend strongly on the dielectric environment. In metallic gated graphene structure the effective permittivity ε* = 1/2[εs + εbcoth(qd)] (εs andεb are the dielectric constants of the substrate and barrier layer, respectively) is determined by the plasma wave wavevector and the thickness of the dielectric barrier layer d separating the channel from electrodes. If qd ≫ 1, the effective permittivity is ~1/2(εs + εb), on the contrary it is reduced to εb/2qd. If the graphene layer is only covered by dielectric layer d, the permittivity ε* is ~1/2[εs + εb(1 + εbtanh(qd))/(εb + tanh(qd))], in consistent with the metallic screening one if qd ≫ 1, and depends strongly on the thickness d if qd ~ 1. The results also indicate that the screening effect of the gate decreases the plasma wave frequency evidently.

The hydrodynamic nonlinearity

The hydrodynamic nonlinearity of 2D electron fluid originates from its intrinsic correlation between electron velocity and density. To excite plasma waves in graphene plane, the frequency ω of the incident wave should satisfy the condition ωτ ≫ 1 or it can be overdamped. After linearizing the hydrodynamic equation, the following relationship of signal can be obtained δU = U(L) − U(0) = < Ek(v1(0))> − <Ek(v1(L))>, where U(L) and U(0) are the time-average potential at the two ends of the channel in FETs, and Ek is the electron's kinetic energy. Such relationship requires asymmetrical boundary condition between the two ends of the actual channel, being introduced by the direct current I0 through the channel. When the plasma wave is excited in the channel, the signal δU ~Σq,ωσ(ω,q) q|Eq|2 (where Eq is the total self-consistent electric field) can be resonantly enhanced by the plasma wave. At the plasma wave resonance, the Fourier amplitude of self-consistent field is |Eq| ~ Q|Eext| when compared with the external terahertz field with amplitude Eext. Here Q = ω(q)/Δω is the quality factor of plasma wave resonance, Δω is the full width at half maximum (FWHM) of the plasma wave resonance line. However in the regime of off-resonance, only the Drude absorption can be introduced, and leads to the broadband THz detection.

The surface resonant layer model

Such model45 treats the whole structure as a single plane with an analytic form of surface admittance Yeff(ω) = ΣnYn(ω) = −iσ0Σn2βn2ωγe(ω2 − ωpn2 − 2iωγe), where ωpn is the frequency of plasma waves, the βn describing the coupling strength between plasma wave and the incident ones, γe is the electron scattering loss, σ0 is the dc conductivity in the whole structure. The model can describe the energy transformation well in the electrostatic limit when the magnetic effect can be neglected. For the zeroth term in the model, Yeff reduces to the Drude form and only the background absorption exists. When the frequency of incident wave approaches that of plasma wave, the ωpn term in the series dominates. By applying the conventional Fresnel formula, the plasma wave absorption is An ~ γeγrn[(ω − ωpn)2 + (γe + γrn)2]−1, where γrn ~ βnσ0 is the contribution of radiative loss. If the plane is placed on the dielectric substrate, the absorption can be reduced due to the reflection. Therefore, the maximum available absorption is 50% of incident waves.

Supplementary Material

Supplementary Information

Highly Sensitive and Wide-Band Tunable Terahertz Response of Plasma Waves Based on Graphene Field Effect Transistors

srep05470-s1.pdf (1.1MB, pdf)

Acknowledgments

The authors acknowledge the support provided by the State Key Program for Basic Research of China (2013CB632705, 2011CB922004), the National Natural Science Foundation of China (11334008, 61290301), the Fund of Shanghai Science and Technology Foundation (13JC1408800).

Footnotes

The authors declare no competing financial interests.

Author Contributions L.W. performed major part of numerical experiments and written the paper. A.Y. performed simulation study of Fig. 3 and tunable graphene waveguide, filters in the Supplementary Information. Y.Z. and J.Y.D. performed numerical analysis of electrostatic effect. W.L. and X.S.C. developed the optical models of graphene plasma waves. All authors discussed the simulation results.

References

  1. Wei J. et al. Ultrasensitive hot-electron nanobolometers for terahertz astrophysics. Nature Nanotech. 3, 496–500 (2008). [DOI] [PubMed] [Google Scholar]
  2. Blain A. W., Smail I., Ivison R. J., Kneib J. -P. & Frayer D. T. Submillimeter galaxies. Phys. Rep. 369, 111–176 (2002). [Google Scholar]
  3. Tonouchi M. Cutting-edge terahertz technology. Nature Photon 1, 97–105 (2007). [Google Scholar]
  4. Zhang X. -C. & Xu J. Introduction to THz wave photonics (Springer-Verlag, New York, 2009). [Google Scholar]
  5. Sirtori C. Bridge for the terahertz gap. Nature 417, 132–133 (2002). [DOI] [PubMed] [Google Scholar]
  6. Williams G. P. Filling the THz gap-high power sources and applications. Rep. Prog. Phys. 69, 301–326 (2006). [Google Scholar]
  7. Nagatsuma T. Terahertz technologies: present and future. IEICE Electron. Expr. 8, 1127–1142 (2011). [Google Scholar]
  8. Schwierz F. Graphene transistors. Nature Nanotech. 5, 487–496 (2010). [DOI] [PubMed] [Google Scholar]
  9. Kim T.-W., Kim D. -H. & del Alamo J. A. InGaAs HEMT with InAs-rich InAlAs barrier spacer for reduced source resistance. Electron. Lett. 47, 406–407 (2011). [Google Scholar]
  10. Knap W. et al. Field effect transistors for terahertz detection and emission. J. Infrared Mill. Terahz. Waves. 32, 618–628 (2011). [Google Scholar]
  11. Dyakonov M. & Shur M. Detection, mixing and frequency multiplication of terahertz radiation by two-dimensional electronic fluid. IEEE Trans. Electr. Dev. 43, 380–387 (1996). [Google Scholar]
  12. Vicarelli L. et al. Graphene field-effect transistors as room-temperature terahertz detectors. Nat. Mater. 11, 865–871(2012). [DOI] [PubMed] [Google Scholar]
  13. Dyakonov M. & Shur M. S. Shallow water analogy for a ballistic field effect transistor: new mechanism of plasma wave generation by dc current. Phys. Rev. Lett. 71, 2465–2469 (1993). [DOI] [PubMed] [Google Scholar]
  14. Muraviev A. V. et al. Plasmonic and bolometric terahertz detection by graphene field-effect transistor. Appl. Phys. Lett. 103, 181114 (2013). [Google Scholar]
  15. Fatimy A. E. I. et al. Resonant and voltage-tunable terahertz detection in InGaAs/InP nanometer transistors. Appl. Phys. Lett. 89, 131926 (2006). [Google Scholar]
  16. Popov V. V., Polischuk O. V. & Shur M. S. Resonant excitation of plasma oscillations in a partially gated two-dimensional electron layer. J. Appl. Phys. 98, 033510-1-6 (2005). [Google Scholar]
  17. Popov V. V., Polischuk O. V., Knap W. & Fatimy A. E. I. Broadening of the plasmon resonance due to plasmon-plasmon intermode scattering in terahertz high-electron-mobility transistors. Appl. Phys. Lett. 93, 263503 (2008). [Google Scholar]
  18. Novoselov K. S. et al. Electric field effect in atomically thin carbon films. Science 306, 666–669 (2004). [DOI] [PubMed] [Google Scholar]
  19. Peres N. M. R. The transport properties of graphene: An introduction. Rev. Mod. Phys. 82, 2673–2700 (2010). [Google Scholar]
  20. Castro Neto A. H., Guinea F., Peres N. M. R., Novoselov K. S. & Geim A. K. The electronic properties of graphene. Rev. Mod. Phys. 81, 109–162 (2009). [Google Scholar]
  21. Smith C., Qaisi R., Liu Z., Yu Q. & Hussain M. M. Low-voltage back-gated atmospheric pressure chemical vapor deposition based graphene-striped channel transistor with high-k dielectric showing room-temperature mobility > 11000 cm2/Vs. ACS Nano. 7, 5818–5823 (2013). [DOI] [PubMed] [Google Scholar]
  22. Guo Z. et al. Record maximum oscillation frequency in C-face epitaxial graphene transistors. Nano. Lett. 13, 942–947 (2013). [DOI] [PubMed] [Google Scholar]
  23. Pallecchi E. et al. High electron mobility in epitaxial graphene on 4H-SiC (0001) via post-growth annealing under hydrogen. Sci. Rep. 4, 4558 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Wang L. et al. Plasmon resonant excitation in grating-gated AlN barrier transistors. Appl. Phys. Lett. 100, 123501-1-123501-5 (2012). [Google Scholar]
  25. Muravjov A. V. et al. Temperature dependence of plasmonic terahertz absorption in grating-gate gallium-nitride transistor structures. Appl. Phys. Lett. 96, 042105-1-042105-3 (2010). [Google Scholar]
  26. Ryzhii V. Terahertz plasma waves in gated graphene heterostructures. Jpn. J. Appl. Phys. 45, L923–L925 (2006). [Google Scholar]
  27. Fateev D. V., Popov V. V. & Shur M. S. Transformation of the plasmon spectrum in a grating-gate transistor structure with spatially modulated two-dimensional electron channel. Semiconductors. 44, 1406–1413 (2010). [Google Scholar]
  28. Stern F. Polarizability of a two-dimensional electron gas. Phys. Rev. Lett. 18, 546–548 (1967). [Google Scholar]
  29. Allen S. J. Jr, Tsui D. C. & Logan R. A. Observation of the two-dimensional plasmon in Silicon inversion layers. Phys. Rev. Lett. 38, 980–982 (1977). [Google Scholar]
  30. Shaner E. A., Grine A. D., Reno J. L., Wanke M. C. & Allen S. J. Next-generation detectors-Plasmon grating-gate devices have potential as tunable terahertz detectors. Laser Focus World. 44, 131–133 (2008). [Google Scholar]
  31. Zomer P. J., Guimarães M. H. D., Tombros N. & van Wees B. J. Long-distance spin transport in high-mobility graphene on hexagonal boron nitride. Phys. Rev. B 86, 161416(R) (2012). [Google Scholar]
  32. Robinson Joshua A. et al. Correlating Raman Spectral Signatures with Carrier Mobility in Epitaxial Graphene: A Guide to Achieving High Mobility on the Wafer Scale. Nano Lett. 9, 2873–2876 (2009). [DOI] [PubMed] [Google Scholar]
  33. Zou K., Hong X. & Zhu J. Effective mass of electrons and holes in bilayer graphene: Electron-hole asymmetry and electron-electron interaction. Phys. Rev. B 84, 085408 (2011). [Google Scholar]
  34. Dean C. R. et al. Boron nitride substrates for high-quality graphene electronics. Nature Nanotech. 5, 722–726 (2010). [DOI] [PubMed] [Google Scholar]
  35. Hong X., Posadas A., Zou K., Ahn C. H. & Zhu J. High-Mobility Few-Layer Graphene Field Effect Transistors Fabricated on Epitaxial Ferroelectric Gate Oxides. Phys. Rev. Lett. 102, 136808 (2009). [DOI] [PubMed] [Google Scholar]
  36. Popov V. V., Koudymov A. N., Shur M. & Polischuk O. V. Tuning of ungated plasmons by a gate in the field-effect transistor with two-dimensional electron channel. J. Appl. Phys. 104, 024508 (2008). [Google Scholar]
  37. Peale R. E. et al. Grating-gate tunable plasmon absorption in InP and GaN based HEMTs. Proc. of SPIE 7467, 74670Q (2009). [Google Scholar]
  38. Knap W. et al. Field Effect Transistors for Terahertz Detection: Physics and First Imaging Applications. J. Infrared Milli. Terahz. Waves. 30, 1319–1337 (2009). [Google Scholar]
  39. Yan H. et al. Tunable infrared plasmonic devices using graphene/insulator stacks. Nature Nanotech. 2012, 7, 330–334. [DOI] [PubMed] [Google Scholar]
  40. Wang L. et al. The plasmonic resonant absorption in GaN double-channel high electron mobility transistors. Appl. Phys. Lett. 2011, 99, 063502. [Google Scholar]
  41. Yu Nikitin A., Guinea F., García-Vidal F. J. & Martín-Moreno L. Edge and waveguide terahertz surface plasmon modes in graphene microribbons. Phys. Rev. B(R). 84, 161407 (2011). [Google Scholar]
  42. Kainth D. S. et al. Angle-resolved raman spectroscopy of the collective modes in an electron bilayer. Phys. Rev. B 59, 2095–2101 (1999). [Google Scholar]
  43. Wang L. et al. The resonant tunability, enhancement, and damping of plasma waves in the two-dimensional electron gas plasmonic crystals at terahertz frequencies. Appl. Phys. Lett. 102, 243507 (2013). [Google Scholar]
  44. Fei Z. et al. Gate-tuning of graphene plasmons revealed by infrared nano-imaging. Nature 487, 82–85 (2012). [DOI] [PubMed] [Google Scholar]
  45. Popov V. V. et al. Absorption of terahertz radiation by plasmon modes in a grid-gated double-quantum-well field-effect transistor. J. Appl. Phys. 94, 3556–3562 (2003). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Highly Sensitive and Wide-Band Tunable Terahertz Response of Plasma Waves Based on Graphene Field Effect Transistors

srep05470-s1.pdf (1.1MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES