Abstract
We develop and test two methods for distinguishing between recent admixture and ancestral population structure as explanations for greater similarity of one of two populations to an outgroup population. This problem arose when Neanderthals were found to be slightly more similar to nonAfrican than to African populations. The excess similarity is consistent with both recent admixture from Neanderthals into the ancestors of nonAfricans and subdivision in the ancestral population. Although later studies showed that there had been recent admixture, distinguishing between these two classes of models will be important in other situations, particularly when high-coverage genomes cannot be obtained for all populations. One of our two methods is based on the properties of the doubly conditioned frequency spectrum combined with the unconditional frequency spectrum. This method does not require a linkage map and can be used when there is relatively low coverage. The second method uses the extent of linkage disequilibrium among closely linked markers.
Keywords: admixture, population structure, population genetics
Introduction
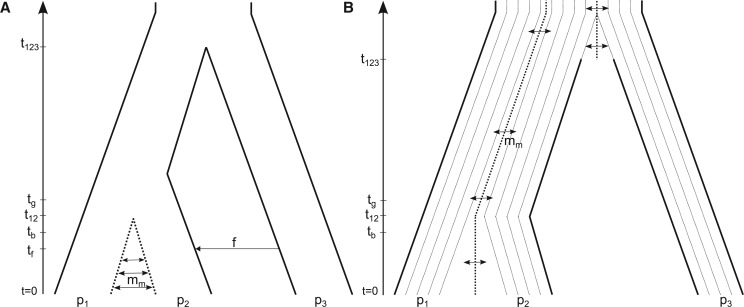
Admixture between previously isolated populations creates genetic similarity beyond what is attributable to common ancestry. But excess similarity does not require recent admixture. Persistent subdivision of an ancestral population can create similarity in the absence of recent admixture (Slatkin and Pollack 2008). That possibility is illustrated in figure 1B . Populations p 2 and p 3 will be more similar to each other than either is to p 1 because they both arose from the same side of a barrier to gene flow in the ancestral population. Many statistics that quantify population similarity, notably D-statistics that were introduced by Green et al. (2010) for the analysis of the draft Neanderthal genome, cannot distinguish between recent admixture and ancestral structure as causes of similarity (Durand et al. 2011). In the context of Neanderthals, p 1 represents a present-day African population, p 2 represents a present-day nonAfrican population, and p 3 represents Neanderthals. However, in general there is no reason that p 1 and p 2 be present-day populations and p 3 be archaic. It is important only that p 1 and p 2 are sister groups and p 3 be the outgroup.
Fig. 1.—
Demographic models relating three populations p 1, p 2, and p 3. Population size changes may happen at times tb and tg (see table 1). (A) Recent admixture model. p 1 and p 2 exchange migrants at rate mm. Assuming time going backward, at time p 3 admixed with p 2 at rate f. At time t 12 p 1 joined with p 2 and at time t 123 p 3 joined p 12. (B) Model of ancestral structure. Each population is made of up of nd demes (nd = 4 in the figure). Faint dotted lines represent separate demes in the same population which exchange migrants at rate mm. The thicker dotted lines indicate the separation of demes in adjacent populations. Solid lines represent barriers to gene flow. There are two periods during which p 1 and p 2 exchange migrants, between t = 0 and t 12 and between t 12 and TMRCA. p 2 and p 3 can exchange migrants between times t 123 and the TMRCA.
Although the possibility of ancestral structure was acknowledged by Green et al. (2010), they argued for recent admixture on the grounds of parsimony and biological plausibility. Later studies have confirmed that there was recent admixture between Neanderthals and the ancestors of nonAfrican populations. Patterns of linkage disequilibrium (Sankararaman et al. 2012) and the analysis of a 45,000-year-old modern human DNA sequence (Fu et al. 2014) provide independent lines of evidence. The theoretical question remains, however, of how can ancestral structure be distinguished from recent admixture, particularly in other groups for which abundant high-coverage genomes and additional archaic sequences cannot be obtained.
Yang et al. (2012) suggested one such method. They analyzed the model of ancestral structure illustrated in figure 1B and showed that the doubly conditioned frequency spectrum (dcfs), which is the frequency spectrum in a modern human population conditioned on the Neanderthal being derived and an African sequence being ancestral, could distinguish the two hypotheses. However, Eriksson and Manica (2012) simulated a more complex model of ancestral structure, one that allowed for range expansion and a stepping-stone pattern of subdivision, and showed that the dcfs did not necessarily distinguish between the two hypotheses.
In this paper, we revisit the problem. We confirm the conclusion of Eriksson and Manica (2012) and show that a stepping-stone model only in p 2 is necessary to create a dcfs similar to what is expected if there had been recent admixture. We show, however, for that model the unconditional frequency spectrum in p 2 is distorted by the ancestral population structure. Comparing the doubly conditioned and unconditioned frequency spectra can distinguish between ancestral structure and recent admixture under a wide variety of conditions.
Our second method is based on linkage disequilibrium (LD). Sankararaman et al. (2012) used the extent of LD to estimate the time of admixture between nonAfrican modern humans and Neanderthals. Sankararaman et al. analyzed the rate of LD decay at sites in the genome that carry the derived allele in Neanderthals (p 3) and in the tested population (p 2) at a frequency of . This ascertainment scheme increases the number of sites informative about the time of admixture. Sankararaman et al. (2012) used this method to support a model of recent admixture between Neanderthals and nonAfrican modern humans as they expanded out of Africa.
Summarizing, starting with models of recent admixture and ancestral population structure that represent extremes in population structure and produce the same output for dcfs from Yang et al. (2012) and D from Green et al. (2010), we ask whether there are additional approaches to distinguish between them. We further investigate the behavior of the decay of LD from Sankararaman et al. (2012) under a more complex representation of ancestral structure. Finally, we introduce two ways of analyzing the data, the unconditional site frequency spectrum and the ratio of LD decay that can both be used to distinguish between the models.
Materials and Methods
Recent Admixture Model
Figure 1A shows the model of recent admixture for three populations. Assuming time going backward, modern gene flow occurs at a rate mm between the present day (t = 0) and the divergence time of p 1 and p 2 (denoted t 12). This model also assumes a single episode of admixture of rate f from p 3 into p 2 at time tf. The parameter f is the probability that a lineage from p 2 is descended from p 3. Likewise, the divergence time of p 12 and p 3 is denoted by t 123. This model is similar to the model of recent admixture used in Yang et al. (2012), Durand et al. (2011), and Sankararaman et al. (2012). A most recent common ancestor (MRCA) of all three populations is present before t 123.
To study the potential admixture from Denisovans into ancestors of Melanesian (PAP) individuals from Papua New Guinea, we simulated a more complex model including three admixture events; (1) from a sister group of Denisovans into the ancestors of Melanesians, (2) from Neanderthals into nonAfrican modern humans, and (3) from a different unknown archaic population into the ancestors of Denisovans. The reason for assuming admixture comes from a sister group of the Denisovan is that Prüfer et al. (2014) inferred a deep divergence between the sequenced Denisovan and the population that admixed with Melanesians. A graphical representation of this model (denoted BS2) can be found in supplementary information 17 figure 1 and table 3 of Prüfer et al. (2014).
Model of Ancestral Structure
This model is different from the ones used in Yang et al. (2012), Durand et al. (2011), Slatkin and Pollack (2008), and Sankararaman et al. (2012) to model population subdivision and is similar to the model analyzed by Eriksson and Manica (2014). Each population is subdivided into randomly mating demes. As shown in figure 1B , symmetrical migration between adjacent demes occurs at rate mm. This migration represents gene flow between demes within p 1 and p 2 and later within demes of p 3 and p 2. The MRCA is present after t 123, when all lineages are able to migrate to any other deme. The model used in Eriksson and Manica (2014) is slightly different; we are not using sequential founder events to simulate a range expansion.
In our model, each population can be subdivided into nd demes and the degree of subdivision can be different in different populations. In addition, ancestral barriers to gene flow between neighboring populations can be partly removed. The model of ancestral structure for the Melanesian individuals is similar to the one used for recent admixture (BS2) without the admixture events but with nd = 15 demes per population.
Simulations
The coalescent software ms (Hudson 2002) was used to simulate samples from the two demographic models of figure 1. Unless otherwise stated, a generation time of 25 years and an effective population size of per population is assumed. Parameter values and ranges that are used to explore the recent admixture model are to some extent similar to the ones used in table 1 of Yang et al. (2012). However, for the model of ancestral structure, we vary the number of demes per population nd, and the ancestral populations are not joined, but demes persist until the MRCA of the sample is found (see fig. 1b in Yang et al. [2012] for a direct comparison). We have chosen parameter values to be consistent with the history of modern African and nonAfrican humans and Neanderthals and their observed D statistics (Durand et al. 2011). A summary of parameter values and ranges can be found in table 1. For each parameter combination, a total of 1 million ms replicates were simulated. Recombination and mutation rates were assumed to be constant. We simulated 50 chromosomes each sampled from p 1 and p 2 and one chromosome from p 3.
Table 1.
Parameters Used for the Models of Recent Admixture and Ancestral Structure
| Parameter | Recent Admixture | Ancestral Structure |
|---|---|---|
| (4N) | 20 | 20 |
| (4Nr) | 100 | 100 |
| Admixture rate f | — | |
| Admixture time | 0.05 | — |
| coalescence time | 0.1125 | — |
| coalescence time | 0.3 | — |
| End time of ancient migration between | — | 0.1125 |
| End time of ancient migration between | — | 0.3 |
| Modern gene flow () between | — | |
| () between adjacent demes | — | |
| Bottleneck time () | ||
| Bottleneck strength (b) | 0.01 | 0.01 |
| Time of population growth () | 0.115 | 0.115 |
| Number of demes per population nd | 1 |
To study the potential admixture from Denisovans into ancestors of Melanesians, we simulated 50 chromosomes for the model BS2 which is represented together with the point estimates of times of admixture events, admixture proportions, and split times in supplementary information 17 figure 1 and table 3 of Prüfer et al. (2014).
Data Processing
In addition to the simulated data, we analyzed data from the 1000 Genomes Project Phase3 from which we randomly sampled 25 diploid European (CEU) and 25 diploid African (Yoruba, YRI) individuals (1000 Genomes Project Consortium et al. 2015). We calculated statistics for chromosomes 14, 16, and 22 and saw no significant differences in results. We restricted our analyses to polymorphic SNPs that passed the basic 1000 Genomes Project filtering criteria and for which ancestral allele information was available in the two modern populations and in the Altai Neanderthal genome (Prüfer et al. 2014). The ancestral state in the Altai individual was determined by using information from the Chimpanzee ancestor at each site. We filtered sites with a Map20 <1 (Duke uniqueness tracks of 20bp), and we removed deletions and insertions.
We also analyzed data from 25 diploid Melanesian individuals from Papua New Guinea (PAP) recently published in Vernot et al. (2016) (data source dbGAP phs001085.v1.p1). Data filtering was done as described in the supplementary materials of Vernot et al. (2016). For this analysis, we used sites for which ancestral allele information was available in the Melanesia and Yoruba population and in the Denisova genome (Meyer et al. 2012). Data filtering is similar as described before.
Site Frequency Spectrum Statistics
D is calculated by sampling one chromosome each from the two sister populations p 1 and p 2 and one chromosome from p 3 and another chromosome from an outgroup population denoted O. This test is also known as the “ABBA BABA” test as the calculation is restricted to biallelic sites in the genome where p 1 has either the ancestral allele “A” (state at outgroup O) or the derived (alternative) allele “B,” p 1 differs from p 2 and “B” is seen in p 3. These conditions result in site configurations “ABBA” or “BABA.” The ratio of the difference to the total number of these configurations indicates how much more similar p 1 is to p 3. For a more detailed review see Durand et al. (2011) and Green et al. (2010).
The dcfs is calculated by sampling one chromosome at random each from p 1 and p 3 and multiple chromosomes from p 2. One then counts the number of derived alleles in p 2 for sites at which p 1 is ancestral and p 3 is derived (see Yang et al. (2012) for details). The unconditional spectrum is calculated for p 2 without conditioning on the allelic states in p 1 and p 3 (table 2).
Table 2.
Explanation of Statistics
| Statistic | Samples | Allele Conditions | Pattern |
|---|---|---|---|
| D | 1 sample each from , O | ABBA or BABA | |
| dcfs | 1 sample each from | =A, =B, =B, | ABBA |
| n samples from | |||
| SFS | 1 sample each from | , f() | -BBA |
| n samples from | |||
| LD | 1 sample each from | , f() | -BBA or B-BA |
| n samples each from |
SFS is the unconditional spectrum. are the two present day populations, is the archaic population, O is denoted the outgroup. Alleles “A” and “B” are the ancestral (state at O) and derived alleles, respectively.
Linkage Disequilibrium
For the set of ascertained SNPs, we calculated r 2 as a function of physical distance. We restricted the analyses to SNPs that are not more than 300 kbp apart and that have the derived allele in p 3 and a derived allele frequency of in p 1 and p 2. This approach is similar to the ascertainment scheme in Sankararaman et al. (2012) (see Sankararaman et al. [2012, p. 3] for a more detailed explanation). r 2 was calculated between all pairs of ascertained SNPs i,j at physical distance y:
| (1) |
P(y) denotes all pairs of ascertained SNPs at a physical distance y and therefore is the mean r 2 over all pairs of SNPs at distance y. We also clustered LD based on physical distance because, for species other than humans, a genetic map might not be available.
In addition, we explored the ratio of r 2 between different populations:
| (2) |
This ratio was computed separately for sites that are either derived or ancestral in the p 3 individual but had a derived allele frequency of in p 1 and p 2.
Statistical Model Fit
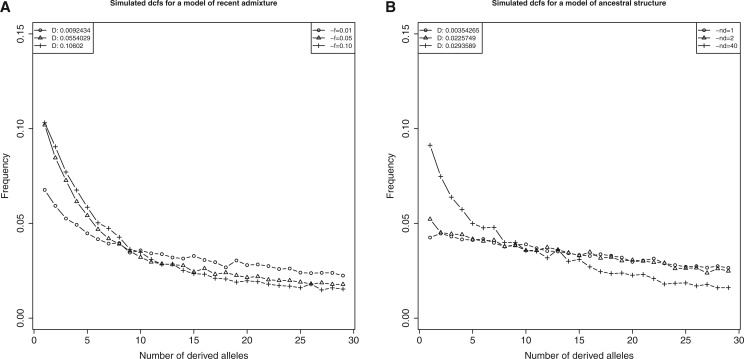
In addition to visually examining how different two statistics from different models are we calculated the root–mean–square error (rmse) between each single statistic from a certain model and 50 replicates of a contrasting model. We present the results of this approach in supplementary table 1, Supplementary Material online, for details. For example, in figure 2 the RMSE between the single representation of dcfs for the admixture model f = 0.01 from figure 2A and 50 replicates of the ancestral structure model nd = 1 from figure 2B is rmse = 0.006672129. The comparisons between models can either be admixture–admixture, structure–structure, or admixture–structure.
Fig. 2.—
Simulated dcfs for models of constant Ne, n = 50 chromosomes (number of alleles only shown up to n = 30). (A) Model of recent admixture and no ongoing gene flow for three different values of admixture rate f. (B) Similar setting for the model of ancestral structure, shown for three different values of nd with mm = 6. Values of D statistics are given in the upper left corner.
Results
Effects of Admixture and Ancestral Structure on the Simulated SFS
First, we studied the effects on the site frequency spectrum using data simulated under the models shown in figure 1 (see Materials and Methods for further details). Figure 1A shows the model of recent admixture for three populations. We were able to confirm the results from Yang et al. (2012) for the effects of recent admixture on the dcfs for various parameter values. In the simplest case of constant Ne, no ongoing gene flow between p 1 and p 2 and no recombination, figure 2A shows the effect of different admixture rates on the shape of the dcfs, where a higher f results in a more pronounced L-shape. Figure 2B shows the dcfs for a model of ancestral structure with different numbers of demes nd. Only population p 2 is structured and the ancestral population p 12 has nd + 1 demes. The higher the degree of subdivision, the more the dcfs differs from the case of nd = 1. Interestingly, population structure in the remaining populations p 1 and p 3 is not necessary to produce the L-shaped dcfs similar to the model of recent admixture. Simulations are filtered to be consistent with observed D statistics of between 1% and 10%. Results shown are based on sampling one chromosome each from population p 1 and p 3 and 50 chromosomes from p 2. Chromosomes were sampled from the first deme of each population. The results of introducing variation in population size (growth and bottleneck), time of admixture and time and rate of gene flow agree well with results from Yang et al. (2012) and do not significantly change the patterns observed from the simple cases mentioned above (see supplementary fig. SF1, Supplementary Material online, for details). Hence, we were able to reproduce results from Yang et al. (2012) and Eriksson and Manica (2014) and additionally show that only population structure in p 2 and p 12 is sufficient to generate a pattern that cannot be distinguished by means of D statistic or dcfs. We also calculated the root–mean–square error (rmse) between the simulation results from the different models (see supplementary table 1, Supplementary Material online, for details and Materials and Methods for further details). As can be seen for figure 2 the smallest rmse is between the admixture model with f = 0.01 and the ancestral structure model with nd = 1. However, what we intend to show in this figure is the increase in low frequency dcfs (which was taken as evidence for a model of admixture in Yang et al. (2012)) under a model of ancestral structure rather than a perfect match between the model of ancestral structure and the different models of admixture.
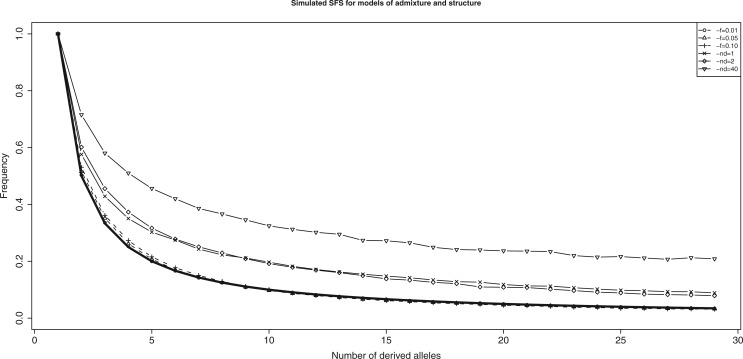
We then focused on these parameter combinations to determine whether there is additional information that will allow us to distinguish between the two demographic hypotheses. The expected allele frequency spectrum for a sample of n neutral alleles in a population of constant size without population structure is , where Fu (1995). Therefore, under the model of recent admixture and no population structure, the unconditional frequency spectrum for p 2 should be proportional to . As shown in figure 3, comparing the simulated derived allele frequency spectrum from the admixture and ancestral structure models yields expected results. There are clear differences between the two classes of simulations. The SFS from ancestral structure lies consistently above the line, whereas the SFS from recent admixture lies consistently on the line. The number of demes per population for the model of population structure has a stronger effect on the SFS than the rate or time of admixture for the recent admixture model, as there is a clear difference between cases with nd = 1 and nd = 40, but almost no difference between the simulations of admixture. Interestingly, nd = 40 is the only case that was able to mimic the dcfs shape of recent admixture and also showed the strongest deviation from the line (see supplementary fig. SF2, Supplementary Material online, for details for models including population size changes). The skewing of the site frequency spectrum in an isolation-by-distance model towards more intermediate and high frequency derived alleles was also shown by De and Durrett (2007). Therefore the SFS is useful to detect isolation by distance when the average time to the MRCA (TMRCA) is increased. Population size variation has a more pronounced effect on simulations under the recent admixture model, with the SFS being further below the expectation when introducing population bottlenecks and growth (see supplementary fig. SF2, Supplementary Material online, for details).
Fig. 3.—
Simulated derived allele SFS (normalized by the frequency of singletons) for sites in p 2 not being dependent on the allelic state in p 3 for a model of constant Ne, n = 50 chromosomes and no ongoing gene flow (number of alleles only shown up to n = 30). Thick solid line is the expected SFS . Solid lines denoted by parameter nd represent the SFS for sites simulated under the model of ancestral structure, dotted lines denoted by parameter f represent the SFS for sites simulated under the model of recent admixture.
To study the potential admixture from Denisovans into ancestors of Melanesian individuals from Papua New Guinea (PAP), we simulated a more complex model including three different admixture events (see Materials and Methods for further details). Results from this model show dcfs and SFS patterns under admixture and ancestral structure similar to the results from the three population models described before (see supplementary fig. SF3, Supplementary Material online, for details).
Effects of Admixture and Ancestral Structure on Simulated LD
In order to compare LD between different populations, we simulated data for the models shown in figure 1 with populations p 1 and p 2 both being structured into nd demes under the model of ancestral structure and 50 chromosomes each. A similar approach of calculating LD under a model of recent admixture and ancestral structure with nd = 1 has previously been applied in Sankararaman et al. (2012). The authors showed that LD for sites that have the derived allele in Neanderthals and a derived allele frequency of in Europeans decays more slowly, producing more long range LD than under a model of ancestral structure. This result was verified by computer simulations and observed in data from the 1000 Genomes Project. This observation indicates that a recent admixture event introduces derived alleles into the population p 2 that are younger than in a model without admixture. In that case derived alleles are older and LD has had more time to break down (for further results showing the differences between the effects of island, stepping stone and homogeneously mixing models on LD see De and Durrett (2007)). However, in Sankararaman et al. (2012) the model of ancestral structure used as the alternative to the admixture model did not allow for a variable number of demes per population and it remains unclear to what extent this might affect the power to differentiate between them.
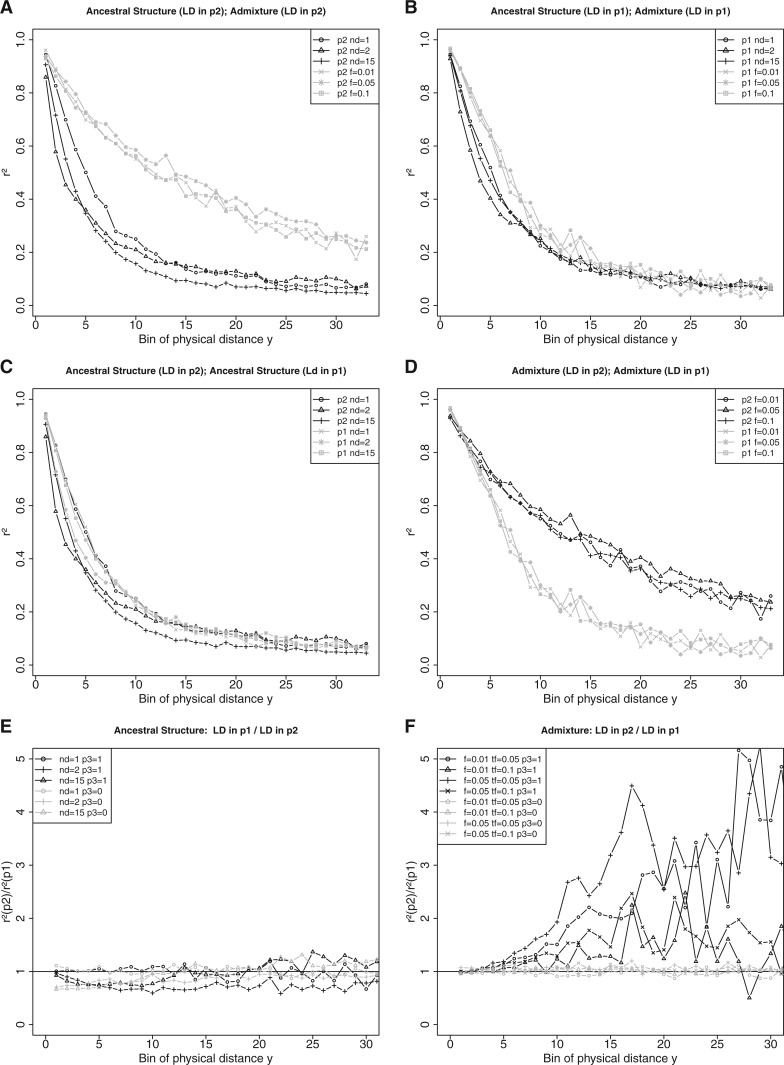
We calculated r 2 for sites from p 1 and p 2 that have the derived allele in p 3. Figure 4A shows the decay of LD for simulated sites in p 2 under separate models of recent admixture and ancestral structure (different lines show different values for parameters f and nd). As expected LD decays more slowly when derived alleles are introduced into p 2 through admixture. The degree of subdivision nd does influence the rate of decay of LD, with an increase in subdivision reducing the amount of LD, a result that might have implications for the accuracy of methods for dating admixture events. Overall there is a clear difference between LD calculated from sites in p 2 generated under the two different models. Figure 4B shows the same statistic but for LD calculated for sites from p 1. As expected, LD decay for the two models does not show a clear separation as p 1 did not receive alleles from p 3 through admixture. Therefore, derived alleles are on average older as they must have arisen from mutations that originated in the ancestral population p 123. Figure 4C presents LD for sites from p 1 and p 2 generated only under the model of ancestral structure. We do not observe any clear difference between the two models, as the age of derived alleles should be similar under both models. Panel D shows the comparison similar to figure 4C but for sites calculated only under the model of recent admixture. In contrast, these effects are not observed when calculating LD for sites that show the ancestral allele in p 3 (see supplementary fig. SF4, Supplementary Material online, for details).
Fig. 4.—
Panels (A–D) simulated pairwise r 2 for populations p 1 and p 2, calculated as the mean over pairs of sites in bins of physical distance y. Sites have a derived allele frequency in both p 1 and p 2 and show the derived allele in p 3. Lines denoted by parameters nd and f show r 2 for separate models of ancestral structure and admixture, respectively. Simulated sequence length is 106 bp, divided into 100 bins, first 35 bins are shown. The recombination rate was constant (see table 1). Panels A–D show the results for the two models and the two populations that were used to calculate LD. Panels (E, F) show the ratio of pairwise r 2 calculated as in A–D. The ratios are calculated for LD from populations p 2 and p 1 for sites that show the derived allele in p 3 (p 3 = 1) or the ancestral allele in p 3 (p 3 = 0). Lines denoted by parameters nd and (f, tf) represent r 2 ratio for models of ancestral structure and admixture, respectively.
The difference seen in LD is visually more striking when computing the ratio of LD between p 1 and p 2. Figure 4E and F presents this ratio for several scenarios. Summarizing, the strong signal is observed only when calculating LD for sites that show the derived allele in p 3 under the model of recent admixture (see fig. 4F ). The time and strength of admixture affect this signal, because older or weaker admixture makes it more similar to LD calculated from p 1. There is no clear signal when calculating LD for sites that show the ancestral allele in p 3. Introducing a population bottleneck in p 2 that reduces the size of the population by a factor of 100 does not have a strong effect on this ratio (see supplementary fig. SF5, Supplementary Material online, for details). Allowing for symmetrical modern gene flow between p 2 and p 1, however, does influence the decay of LD and weakens the signal (see supplementary fig. SF6, Supplementary Material online, for details). A similar effect is observed when using sites from p 1 and p 2 that have a derived allele frequency of instead of (see supplementary fig. SF7, Supplementary Material online, for details). In these cases, LD for the two populations is very similar and the effects of modern symmetrical gene flow and population bottlenecks weaken the signal (see supplementary figs. SF8 and SF9, Supplementary Material online, for details). This observation supports the utility of the ascertainment scheme of from Sankararaman et al. (2012) to amplify the admixture signal.
Results from the simulated model including Melanesians and one Denisovan individual show very similar LD patterns to those found above. The r 2 ratio for sites that show the derived allele in Denisova shows an even stronger signal under this model (see supplementary fig. SF10, Supplementary Material online, for details).
Observations from Real Data
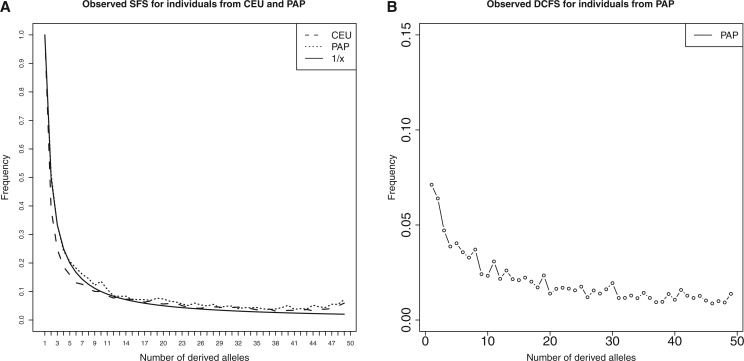
We applied our approach to data from the 1000 Genomes Project Phase3 and randomly sampled 25 individuals each from the African (YRI) and nonAfrican (CEU) populations and to data from 25 Melanesian individuals from Papua New Guinea (PAP) (see Materials and Methods for further details). Figure 5A shows the unconditional spectrum for sites that are not conditioned on Altai (or Denisova in the case of Melanesians) being ancestral or derived in comparison with the neutral expectation of . We do not observe a skew of the SFS towards intermediate and high frequency derived alleles. In addition we calculated the dcfs for the 25 Melanesian individuals as shown in figure 5B . The increase in low frequency derived alleles for the dcfs looks similar to what we observed in our simulations for models of recent admixture (e.g., fig. 2A ). However, as the demographic history of nonAfricans is the product of various demographic events that we did not attempt to model in detail, the only conclusion we can draw is that there seems to be evidence against a model of ancestral structure as indicated by our simulations (see figs. 2, 3, and supplementary figs. SF1 and SF2, Supplementary Material online, for details) and not necessarily evidence for admixture.
Fig. 5.—
Panel (A) observed SFS from the 1000 Genomes Project phase 3 data set and Melanesian individuals. Unconditional SFS (normalized by the frequency of singletons) calculated for sites from 25 CEU and 25 Melanesian (PAP) individuals (dotted lines). Thick solid line is the expected SFS . Panel (B) shows the calculated dcfs from 25 Melanesian individuals.
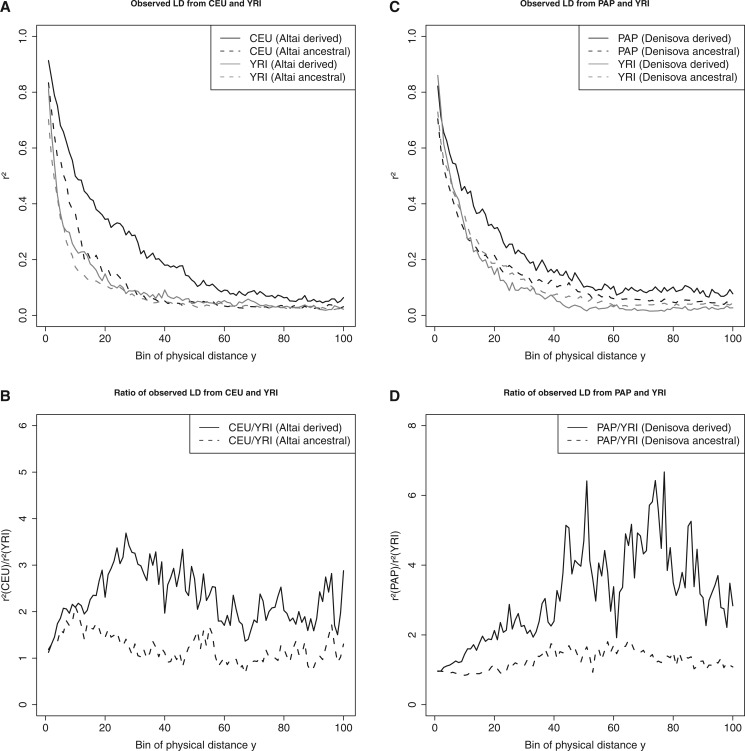
The results from the LD analyses in figure 6A confirm what has previously been observed and what was shown by our simulations (see fig. 4). The LD calculated for sites that show the derived allele in Altai decays more slowly in Europeans, hence producing longer range LD than observed in Yorubans. There is less of a difference between the two populations when calculating LD for sites that show the ancestral allele in the Altai individual. Visualizing the ratio of r 2 in figure 6B shows a shape similar to obtained by simulating a model of recent admixture (see fig. 4F ). Similar results are observed when calculating LD for the Melanesian individuals (PAP) depending on the allelic state in Denisova (see fig. 6C and D ). However, we noticed that the r 2 ratio calculated between PAP and YRI shows the strongest signal at more long range LD. Further work needs to be done to determine the underlying causes for this observation.
Fig. 6.—
Observed r 2 from the 1000 Genomes Project phase 3 data set and Melanesian individuals. (A) Pairwise r 2 calculated in the same way as in figure 4A–D for sites from 25 CEU and 25 YRI individuals. Distance between sites was , divided into 100 bins. Panel (B) shows the ratio of r 2 between CEU and YRI. Solid and dotted lines represent r 2 for sites that show the derived and ancestral allele in the Altai individual, respectively. Panels (C, D) show the same analyses but based on 25 Melanesian (PAP), 25 YRI and one Denisova (archaic) individuals, respectively.
Conclusion
In this study, we analyzed the effects of representing population structure as a one dimensional model of isolation by distance on methods aiming to distinguish patterns generated under recent admixture and ancestral structure. Although it has been shown by several past studies that the more realistic model of isolation by distance affects statistics calculated from LD and the SFS, a direct comparison for the purpose of contrasting the two models has been lacking. By means of coalescent simulations, we tested the statistics D, dcfs, r2, and SFS known to be able to detect a signal of recent admixture. Our observations agree well with results from previous studies. We show that even a small number of demes in population p 2 and the ancestral population p 12 is sufficient to reduce the power of methods based on the SFS to distinguish between admixture and population structure (see fig. 2). However, in cases where the dcfs and D signals were indistinguishable, the unconditional spectrum in p 2 did still show a difference between cases of admixture and population structure, with the SFS skewed towards intermediate and high frequency derived variants (see fig. 3). All of the tested parameter combinations showed a distinction between SFS patterns from population structure and recent admixture when previous SFS-based methods did not show distinct results (see figs. 2, 3, and supplementary fig. SF2, Supplementary Material online, for details).
Furthermore, we studied the decay of r 2 under both models and confirmed that admixture can create a signal that can be visualized by calculating the ratio of LD between p 1 and p 2 for sites that show the derived allele in p 3 and have a derived allele frequency of in p 1 and p 2. No combination of parameters in the model of ancestral structure showed a pattern similar to that observed in 1000 Genomes data and data from the Melanesian individuals. The extent of ancestral structure influences the decay of LD and might therefore affect inference of dating the admixture events.
To summarize our conclusions, we recommend computing both statistics if possible. Each reinforces the conclusion from the other. However, if the data quality is not sufficient, for example, if phased chromosomes are not available, LD cannot be calculated. Or if the polymorphic markers are too sparse to detect short range LD it can be problematic to apply the LD method because the differences in LD between admixture and ancestral structure models are only visible for very closely linked sites. A small sample size can also reduce the reliability of LD. These factors could make it difficult to use LD to distinguish between the models. In such cases the site frequency spectrum statistics should be more powerful. We see no benefit of statistically combining LD with the SFS results into one measure. The SFS and LD statistics are partly independent because one depends on a linkage map and the others do not. We believe it is a more powerful approach to use both of them to test for model support.
Finally, we note that we investigate two simple representations of recent admixture and ancestral structure models and studied the behavior of certain summary statistics to distinguish between them. We did not attempt to explore the large variety of intermediate models (including bidirectional gene flow, admixture, population structure, size changes, etc.) that most likely cannot be distinguished using the approaches presented here. Instead, we review existing methods and suggest two independent ways of analyzing the data to obtain further evidence for either of the competing models.
Supplementary Material
Supplementary data are available at Genome Biology and Evolution online.
Acknowledgments
The authors gratefully acknowledge the help of Janet Kelso for providing the data for the Melanesian individuals. This work was supported in part by the Max Planck Society (as a salary for C.T.) and in part by a US National Institutes of Health grant (R01-GM40282 to M.S.).
Literature Cited
- 1000 Genomes Project Consortium, et al. 2015. A global reference for human genetic variation. Nature 526(7571):68–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De A, Durrett R. 2007. Stepping-stone spatial structure causes slow decay of linkage disequilibrium and shifts the site frequency spectrum. Genetics 176(2):969–981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durand EY, Patterson N, Reich D, Slatkin M. 2011. Testing for ancient admixture between closely related populations. Mol Biol Evol. 28(8):2239–2252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eriksson A, Manica A. 2012. Effect of ancient population structure on the degree of polymorphism shared between modern human populations and ancient hominins. Proc Natl Acad Sci U S A. 109(35):13956–13960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eriksson A, Manica A. 2014. The doubly conditioned frequency spectrum does not distinguish between ancient population structure and hybridization. Mol Biol Evol. 31(6):1618–1621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu Q, et al. 2014. Genome sequence of a 45,000-year-old modern human from western Siberia. Nature 514(7523):445–449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu YX. 1995. Statistical properties of segregating sites. Theor Popul Biol. 48(2):172–197. [DOI] [PubMed] [Google Scholar]
- Green RE, et al. 2010. A draft sequence of the neandertal genome. Science 328(5979):710–722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson RR. 2002. Generating samples under a Wright-Fisher neutral model of genetic variation. Bioinformatics 18(2):337–338. [DOI] [PubMed] [Google Scholar]
- Meyer M, et al. 2012. A high-coverage genome sequence from an archaic Denisovan individual. Science 338(6104):222–226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prüfer K, et al. 2014. The complete genome sequence of a Neanderthal from the Altai Mountains. Nature 505(7481):43–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sankararaman S, Patterson N, Li H, Pääbo S, Reich D. 2012. The date of interbreeding between neandertals and modern humans. PLoS Genet. 8(10):1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slatkin M, Pollack JL. 2008. Subdivision in an ancestral species creates asymmetry in gene trees. Mol Biol Evol. 25(10):2241–2246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vernot B, et al. 2016. Excavating Neandertal and Denisovan DNA from the genomes of Melanesian individuals. Science 352(6282):235–239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang MA, Malaspinas AS, Durand EY, Slatkin M. 2012. Ancient structure in Africa unlikely to explain neanderthal and non-african genetic similarity. Mol Biol Evol. 29(10):2987–2995. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.