Preliminary Experiments with a Unified Controller for a Powered Knee-Ankle Prosthetic Leg Across Walking Speeds

Abstract

This paper presents the experimental validation of a novel control strategy that unifies the entire gait cycle of a powered knee-ankle prosthetic leg without the need to switch between controllers for different periods of gait. Current control methods divide the gait cycle into several sequential periods each with independent controllers, resulting in many patient-specific control parameters and switching rules that must be tuned for a specific walking speed. The single controller presented is speed-invariant with a minimal number of control parameters to be tuned. A single, periodic virtual constraint is derived that exactly characterizes the desired actuated joint motion as a function of a mechanical phase variable across walking cycles. A single sensor was used to compute a phase variable related to the residual thigh angle’s phase plane, which was recently shown to robustly represent the phase of non-steady human gait. This phase variable allows the prosthesis to synchronize naturally with the human user for intuitive, biomimetic behavior. A custom powered knee-ankle prosthesis was designed and built to implement the control strategy and validate its performance. A human subject experiment was conducted across multiple walking speeds (1 to 3 miles/hour) in a continuous sequence with the single phase-based controller, demonstrating its adaptability to the user’s intended speed.

I. INTRODUCTION

One in 190 Americans have experienced limb-loss, primarily due to complications from vascular diseases [1]. The vast majority of prosthetic legs on the market are mechanically passive, which dissipate energy rather than inject energy in the walking gait. A lower-limb prosthesis that provides input power at the joints from a powered actuation system could potentially restore the biomechanical function of the missing leg muscles. This could enable improved amputee gait for a variety of daily activities, such as walking at variable speeds more efficiently.

Powered lower-limb prostheses are currently in development with a variety of control methods to allow amputees to ambulate in a natural and safe manner [2]. The study of biomechanics classifies human gait into specific intervals over the gait stride (e.g., heel strike, toe off, etc.) [3]. Generally, powered prosthesis controllers mimic this ideology by using different controllers over sequential periods of gait based on predefined transition criteria. For example, a finite state machine is implemented with jointed impedance controllers for each discrete state/period in [4], [5]. This requires tuning of the Proportional-Derivative (PD) gains for each period of the gait cycle. This control strategy is further implemented for other ambulation modes, such as slope ascent/descent [6] or running [7], which require more control parameters to be tuned for each subject [8]. Furthermore, issues can arise when the prosthesis is perturbed, as controllers of this type could end up in the wrong state, thus increasing an amputee’s risk of falling.

The prosthetic control method presented in this paper unifies the different periods of gait through virtual kinematic constraints that are driven by a human-inspired phase variable. Often used to control bipedal walking robots [9]–[17], virtual constraints define desired joint trajectories as functions of a monotonically increasing mechanical signal called a phase variable. The phase variable is a time-invariant quantity that captures the motion of an unactuated degree of freedom. The progression through the stride, either moving forward or backward, is driven by the phase variable. The proposed controller enslaves the prosthetic joints to adjust and react based on the progression of the phase variable.

The choice of phase variable makes a difference in how the prosthetic leg responds to human movement or perturbations. A recent study identified the thigh phase angle as a robust representation of the phase of human gait across perturbations [18]. Using this human-inspired phase variable could allow the prosthesis to respond naturally as a biological leg would to the amputee’s residual thigh motion or perturbations. This could allow the amputee to have greater control over the prosthesis (e.g., directly controlling walking speed through the rate of thigh motion) and thus a stronger embodiment of the prosthesis. The proposed controller parameterizes the entire gait cycle with measurements of this human-inspired phase variable from a single sensor on the residual thigh.

We parameterize periodic virtual constraints with the thigh phase angle in order to define continuous joint kinematics across gait cycles. In particular, virtual constraints defined with the Discrete Fourier Transform (DFT) encapsulate the property of periodicity [19], which respects the repetitive nature of the gait cycle. The conceptual design of DFT virtual constraints was studied in simulations of an amputee biped model in [20], demonstrating that the unified controller can produce stable walking across various walking speeds.

Previous work in a parameterized phase-based control scheme for wearable robots has only considered one actuated degree of freedom rather than coordinated control of multi-joint kinematics. The powered ankle prosthesis in [21] is controlled by the tibia phase angle, which is not as well correlated with a phase oscillator as the thigh phase angle [18]. The hip exoskeleton in [22] uses the thigh angle in a phase oscillator to determine when to inject or dissipate energy, which may not be sufficient to replicate joint kinematics in a prosthesis application. In our work, virtual constraints produce the desired kinematics in the absence of biological limb motion. Both [21] and [22] use angular velocity in the computation of the phase angle, which presents a few challenges for real-time control. Angular velocity is more susceptible to noise from impacts, and it makes the phase variable only one derivative away from the equations of motion, i.e., relative degree-one [23], which prevents the use of derivative error corrections in the controller [24]. In this paper we utilize a relative degree-two version of the thigh phase angle based on angular position and its integral.

A powered knee-ankle prosthesis was designed and manufactured as an experimental test platform to validate the proposed control strategy. The prosthesis was designed to meet the range of motion and torque requirements of an able-bodied knee and ankle during walking. The linear ball screw actuator and electronic sensing for each joint are located onboard the leg, whereas the power source and embedded system processing are located offboard the leg for control prototyping purposes.

This paper presents experimental results with the powered knee-ankle prosthesis with an able-bodied subject wearing a bypass adapter to demonstrate the unified control method. A single sensor was used to measure the phase variable from the human thigh, thus capturing the human phase through the gait cycle and promoting biomimetic responses to speed changes. The experimental results show that a single controller for a powered knee-ankle prosthesis can provide natural gait across various walking speeds. Only two control parameters were tuned per joint, whereas other control methods can have over a dozen parameters per joint to tune for a specific walking speed [2], [8]. No adjustments were required in the proposed controller or its parameters while the subject varied walking speed.

II. CONTROL METHOD

A. Control Law

The proposed controller coordinates the knee and ankle patterns of the prosthetic leg by enforcing virtual constraints. Virtual constraints encode the desired motions of actuated variables in output functions to be zeroed through the control action [9]:

$$y_i=q_i-h_i^d(s_h),$$ (1)

where q_i is the measured angular position of joint i (with i = k for the knee or i = a for the ankle), and $h_i^d$ is the desired joint angle trajectory as a function of the phase variable s_h (often normalized between 0 and 1). We will design $h_k^d$ and $h_a^d$ in Section II-B and s_h in Section II-C for application to a powered knee-ankle prosthesis.

Eq. 1 is considered the tracking error of the control system. Various torque control methods can be utilized to regulate this error. Bipedal robots typically enforce virtual constraints using partial (i.e., input-output) feedback linearization [9]–[16], which has appealing theoretical properties including exponential convergence [23], reduced-order stability analysis [9], and robustness to model errors [11]. However, to apply feedback linearization to a powered prosthesis, the dynamics of the prosthesis and the interaction forces with the human user must be known [25], [26]. Identifying a sufficiently accurate model of the prosthetic leg is very difficult, and measuring interaction forces requires expensive multi-axis load cells. Therefore, we utilize a model-free torque control method in this application, specifically output PD control [20], [25].

The PD controller implemented in the powered prosthesis has the following form:

$$u_i=-K_{\mathrm{p}i}{y}_i-K_{\mathrm{d}i}{\dot{q}}_i,$$ (2)

where q̇_i is the measured angular velocity of the i^th joint, K_pi > 0 is the proportional gain affecting the stiffness of joint i, and K_di > 0 is the derivative gain behaving as the viscosity of joint i. This PD controller determines the desired torques at the prosthetic joints. We now design a unified virtual constraint and a human-inspired phase variable that will be used in the PD controller.

B. Virtual Constraint Design by DFT

In general, virtual constraints are time-invariant and depend on a phase variable that is monotonic and unactuated [9]. If the phase variable is monotonic over the complete gait cycle (as designed in Section II-C), then a single output function can represent one joint’s motion over the entire gait. Taking advantage of the periodic kinematics observed in human gait [27], the method of DFT can be used to parameterize periodic virtual constraints for a powered prosthesis.

Consider a desired joint trajectory expressed as a function of a phase variable. Let the discrete signal x[n] represent this trajectory sampled over N evenly distributed points. The DFT is a linear transformation of the signal x[n] that produces a sequence of complex numbers across a spectrum of discrete frequency components X[k]:

$$X[k]=\sum _{n=0}^{N-1}x[n]W_N^{kn},\hspace{1em}k=0,1,\dots ,K,$$ (3)

where N is the finite number of samples, K is the running index for the finite sequence of k (up to N − 1), and W_N = e^−j(2π/N) is the complex quantity [28]. Because the time-domain signal x[n] is periodic, there are a finite number of discrete frequencies X[k].

After obtaining the frequency content terms X[k], the original signal can be reconstructed using Fourier Interpolation:

$$x[n]=\frac{1}{N}\sum _{k=0}^{K}X[k]W_N^{-kn},\hspace{1em}n=0,1,\dots ,N-1,$$ (4)

where X[k] = Re{X[k]} + j Im{X[k]} and $W_N^{-kn}=\text{Re}\{W_N^{-kn}\}+j\text{ Im}\{W_N^{-kn}\}$ in standard complex form. Since the joint kinematic signals are real numbers, only the real part of x[n] remains in Eq. 4 (see [28]).

Eq. 4 can then be decomposed as a summation of sinusoids using Euler’s relationship e^±jΩ = cos Ω±j sin Ω, Ω ∈ ℝ, for W_N within the DFT. From this we finally obtain the desired joint angle function

$$h^d(s_h)=\frac{1}{2}{\rho }_0+\frac{1}{2}{\rho }_{\frac{N}{2}}\text{ cos}(\pi N{s}_h)+\sum _{k=1}^{\frac{N}{2}-1}[{\rho }_k\text{ cos}({\mathrm{\Omega }}_k{s}_h)-{\psi }_k\text{ sin}({\mathrm{\Omega }}_k{s}_h)],$$ (5)

where Ω_k = 2πk, and ρ_k and ψ_k are the computed coefficients from the real and imaginary terms of X[k] from Eq. 4. The phase variable is normalized between 0 and 1 using

$$s_h(\vartheta )=\frac{\vartheta -{\vartheta }^{+}}{{\vartheta }^{-}-{\vartheta }^{+}},$$ (6)

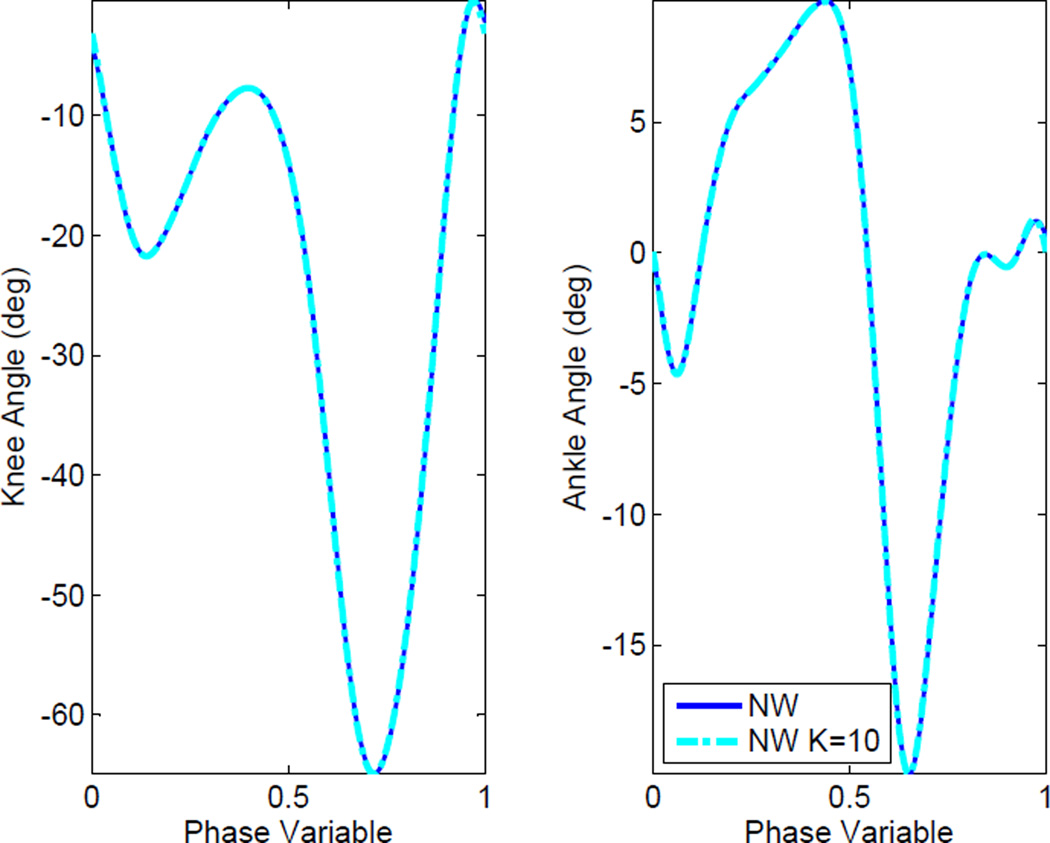
where ϑ represents the unnormalized phase variable (to be determined), ‘+’ signifies the value at the start of the stance period for the prosthetic leg, and ‘−’ indicates the value at the end of its swing period. Eq. 5 is inserted into an output function (Eq. 1) to generate the prosthesis virtual constraints. Because the desired joint angle function (Eq. 5) is composed of sine and cosine functions, the resulting virtual constraints are bounded and inherently periodic across the phase variable with a period of one. For the experiments, the DFT virtual constraints in Fig. 1 were designed from able-bodied human data for normal walking speed [27].

Fig. 1.

The desired joint trajectory and the virtual constraint by DFT with K = 10 for the knee (left) and ankle (right) with normal walking (NW) speed for an entire gait cycle. The reference data from [27] is indicated with solid lines and the virtual constraint is indicated with broken lines. Note, the knee angle is defined from the thigh to the shank and the ankle angle is defined from the shank to the foot (minus 90 deg). Both angles follow the right-hand rule.

C. Human-Inspired Phase Variable Design

The proposed phase variable s_h is based on previous work [18] that found a robust parameterization of human leg joint kinematics based on the thigh phase angle, which is monotonic and bounded even across perturbations (e.g., [29]). This choice of phase variable also has connections to biology, as hip motion is known to be a major contributor to synchronizing the leg joint kinematics in mammals [30].

Although the thigh phase angle can be easily computed offline from post-processed kinematic data [18], real-time computation is a challenge to implementation in a prosthetic control system. In particular, the phase angle is typically computed with the angular position and velocity [21], [22], but angular velocity is prone to noise and makes the control system relative degree-one [24]. We instead compute a phase angle utilizing angular position and its integral:

$$\vartheta (t)=\mathrm{a}\text{tan}2(-z(\mathrm{\Phi }(t)+\mathrm{\Gamma }),-(\varphi (t)+\gamma )),$$ (7)

where

$$z=\frac{|{\varphi }_{\mathit{\text{max}}}-{\varphi }_{\mathit{\text{min}}}|}{|{\mathrm{\Phi }}_{\mathit{\text{max}}}-{\mathrm{\Phi }}_{\mathit{\text{min}}}|},$$

$$\gamma =-(\frac{{\varphi }_{\mathit{\text{max}}}+{\varphi }_{\mathit{\text{min}}}}{2}),\hspace{1em}\mathrm{\Gamma }=-(\frac{{\mathrm{\Phi }}_{\mathit{\text{max}}}+{\mathrm{\Phi }}_{\mathit{\text{min}}}}{2}).$$

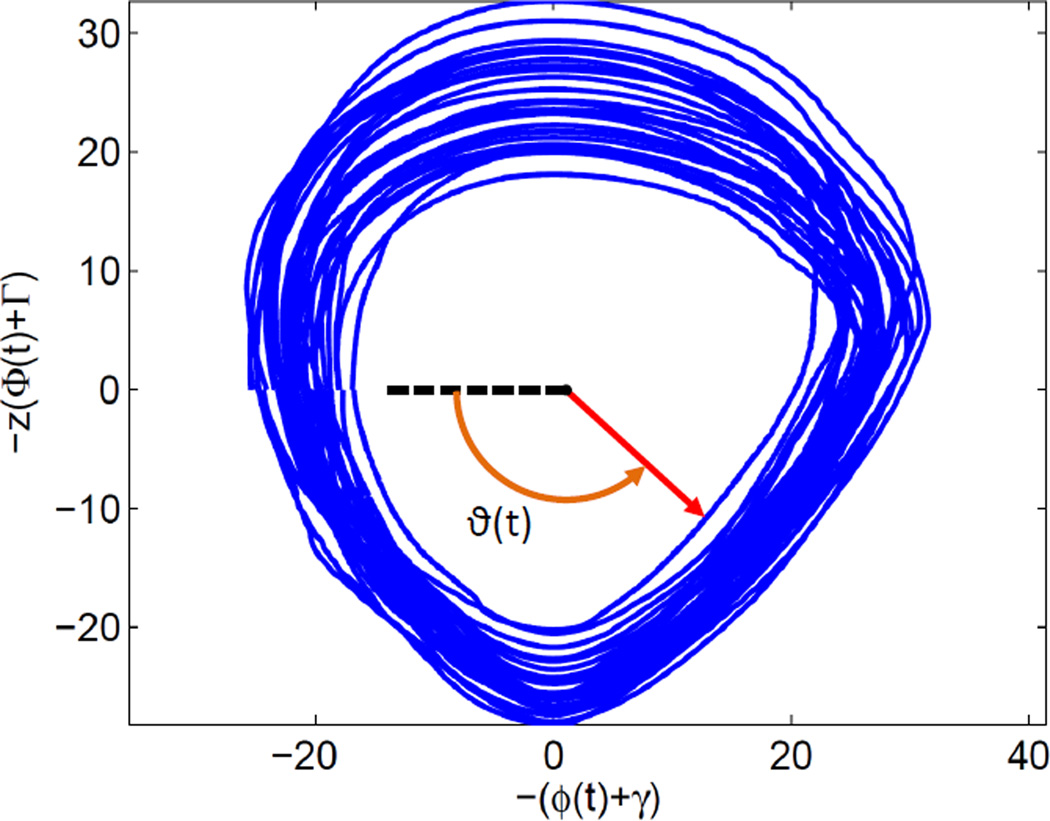
The variable ϕ(t) is the thigh angle with respect to the vertical gravity vector (i.e., the global thigh angle), and the variable $\mathrm{\Phi }(t)={\int }_0^t\varphi (\tau )$ dτ is the time integral of the thigh angle. The integral was reset every gait cycle to prevent the accumulation of drift due to variation in thigh kinematics. The constant z is referred to as the scale factor, and the constants γ and Γ are known as the shift parameters for the thigh angle and its integral, respectively. These parameters improve the linearity of the phase variable by centering the thigh’s orbit around the origin (0, 0) and scaling it to a constant radius within each quadrant to provide an approximately circular orbit. The scale and shift of a particular quadrant axis was recalculated during each crossing of (ϕ, Φ). Because these updates occurred when the phase angle radius was collinear with the axis, the phase angle calculation remained continuous. Fig. 2 shows the scaled/shifted orbit in the thigh phase plane over several steps. Changes in circular orbit diameter are associated with changes in walking speed per stride. Finally, the phase angle from Eq. 7 is normalized according to Eq. 6, where the constants ϑ⁺ = 0 and ϑ⁻ = 2π are the phase angle values at the start and end of the gait cycle.

Fig. 2.

Phase plane of the thigh angle ϕ(t) vs. its integral Φ(t) during prosthetic leg experiments (Section IV). The phase plane has been scaled by z and shifted by (γ, Γ) to achieve a circular orbit across the stride, which improves the linearity of the phase variable ϑ(t).

III. HARDWARE SETUP

A. Powered Prosthesis Actuation Design

An experimental robotic leg platform was designed and built at the University of Texas at Dallas (UTD) to implement the proposed control strategy. The design requirements of the powered prosthesis were based on the joint kinematics and kinetics of able-bodied walking [27]. The knee and ankle joints were designed for a maximum torque of 40 Nm and 120 Nm, respectively, based on a user weight of 75 kg.

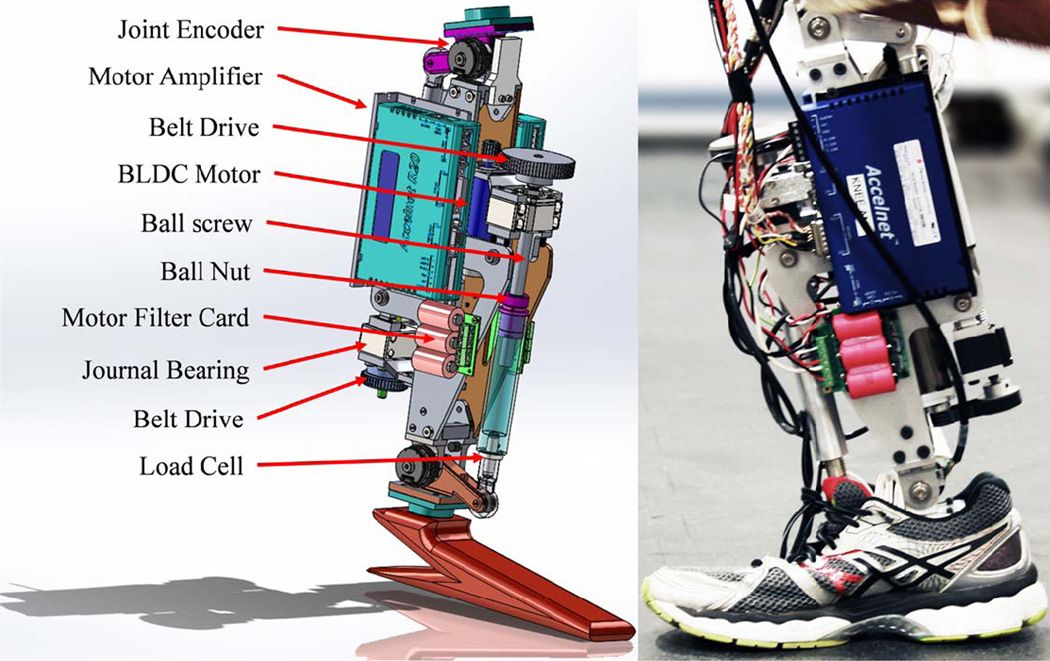
The proper selection of motors and transmission design are an important and critical design step to meet the large demand in joint torque and power while limiting overall weight. A linear ball screw actuator with a lever arm at each joint was chosen for this purpose. A high power-to-weight ratio Maxon EC-4pole 30, 200 Watt, three phase Brushless DC (BLDC) Motor provided input power to actuate each joint transmission for joint torque output. A timing belt drive is attached between the motor output shaft and the linear ball screw, giving a transmission ratio of 2:1 at the knee and 4:1 at the ankle. The ball screw for both the knee and ankle was a Nook 12 mm diameter, 2 mm lead ball screw. This transmission converts the rotary motion from the motor with a belt drive to linear motion of the ball nut, therefore driving the lever arm attached to the joint in generating torque output. The ball screw was supported axially and radially by a Nook double bearing support journal bearing. To obtain the full range of motion at each joint, a motor mount with a rotational pivot point was designed to eliminate buckling of the ball screw and increase its linear motion as it travels upward/downward and rotates the joint at the lever arm. Fig. 3 displays key design components of the actuation system for the powered prosthesis. Overall the mass of the leg is 4.8 kg, which is comparable with other powered knee-ankle legs in the literature [6], [7], [31].

Fig. 3.

The UTD Prosthetic Leg actuation design (left) using computer-aided design software SolidWorks and the manufactured version of the experimental leg (right). Each joint actuator consists of a motor with timing belt producing rotary motion that is converted to translational motion from a linear ball screw driving a lever arm to achieve torque at the joint.

B. Embedded Systems & Sensing

An offboard microcontroller received signals from onboard sensors and transmitted commands to onboard motor drivers through a tether. The microcontroller was a dSPACE DS1007 Freescale OorIQ P5020, dual-core, 2 GHz processor, where the control algorithms were programmed for real-time control of the powered prosthesis and real-time data acquisition for performance monitoring. The motors were controlled using a motor amplifier (Copley Controls, ADP-090-36) programmed with three phase sinusoidal commutation for low-level current loop control. Due to the low inductance design of the BLDC motor an inductance filter card with 0.200 mH inductors per phase was embedded inline between the motor phase lines and the motor amplifier. At the joints, an assembled high resolution optical encoder (US Digital, EC35) was mounted on the output shaft to measure joint angular position for feedback to the high-level control algorithms programmed in the microcontroller. Joint velocities were computed numerically with a second-order low-pass Butterworth filter (20 Hz cutoff for the knee and 35 Hz cutoff for the ankle).

Uniaxial force sensors (Measurement Specialties, ELHST1E-5KN-AC) with offboard analog amplifiers (Measurement Specialties, ARD154) were installed along each linear ball screw to measure the amount of force applied to the lever arm at each joint. The input voltage for powering the motor amplifiers and sensors were tethered from a power supply to the leg. An Inertial Measurement Unit (IMU) (LORD MicroStrain, 3DM-GX4-25) containing triaxial accelerometer, gyroscope, and magnetometer is placed along the human thigh in the sagittal plane. This sensor is critical in computing the thigh phase angle to serve as the phase variable in the prosthesis controller (see Section II-C).

IV. EXPERIMENTAL TESTING

A. Experimental Setup & Protocol

Benchtop experiments were first performed to tune the two control parameters (K_pi, K_di) per joint (Eq. 2) in order to determine starting parameters for walking experiments. The parameters were tuned with the prosthesis attached to the bench while an able-bodied subject walked on a treadmill at their comfortable walking speed (2.0 miles/hour (mph)) with the IMU sensor mounted fixed to their thigh along the sagittal plane to compute the phase variable. The leg was controlled by the virtual constraints as the subject walked continuously. Control parameters were then tuned until tracking error was reduced while observing the prosthesis as it synchronized with the subject’s leg during walking. After the initial control parameters were determined, the leg was mounted onto the bypass adapter for the able-bodied subject experiments.

The experimental protocol was reviewed and approved by the Institutional Review Board (IRB) at the University of Texas at Dallas. Experiments were conducted with an able-bodied subject wearing the powered prosthesis through a leg-bypass adapter while walking on a treadmill (Fig. 4). Prior to recording data, the subject was given time to acclimate to the prosthetic leg. During this time only one parameter was adjusted for the comfort of the human subject. Specifically, the knee joint’s proportional gain K_pk was lowered for less forceful interaction with the subject. A smaller knee proportional gain was required during walking because of the thigh motion produced by the human, which created an aiding moment at the prosthetic knee joint. Note that the subject’s comfortable walking speed during initial testing with the powered prosthesis was 1.5 mph.

Fig. 4.

Photo of able-bodied human subject walking on the powered prosthesis through a leg-bypass adapter during treadmill experiment. The IMU can be seen attached to a red mount on the bypass adapter.

The experiment with variable walking speeds began with the subject at rest on a treadmill. Walking was initiated by setting the treadmill speed to 1.0 mph. The treadmill speed was increased by increments of 0.5 mph after about 15 seconds of comfortable, steady walking at each speed. The highest walking speed reached was 3.0 mph. After walking at the fastest speed, the subject lowered speed to 2.0 mph and then 1.0 mph before settling back to rest. The same controller was used for all walking speeds.

B. Experimental Results

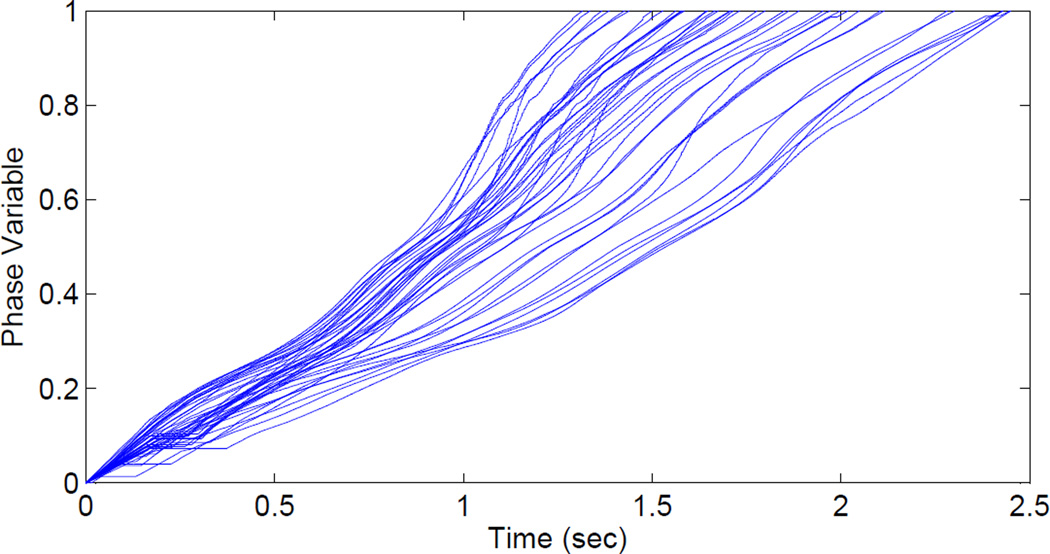
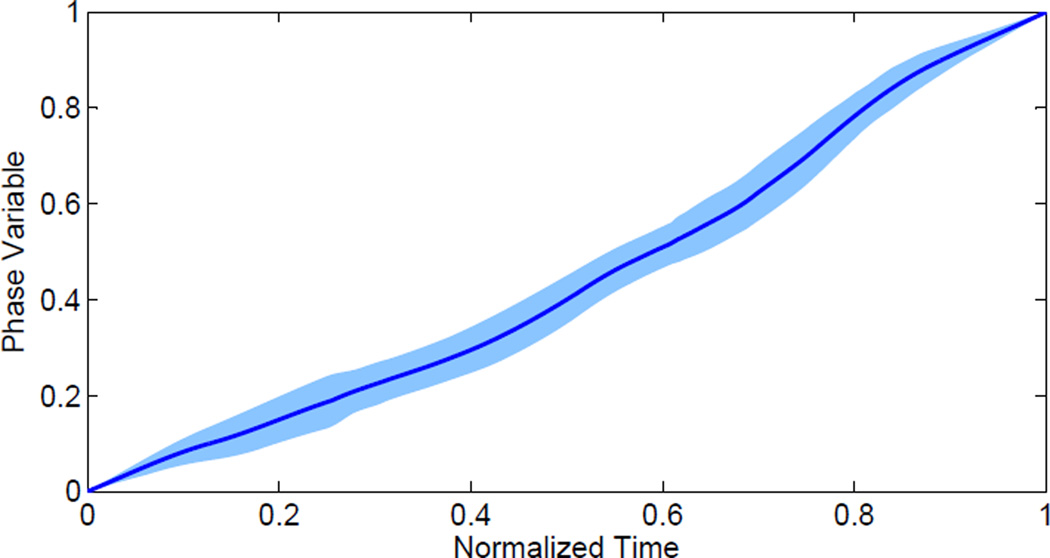
A supplemental video of the experiment is available for download. The video demonstrates the subject’s control over the prosthetic joints through their thigh motion. Fig. 5 shows the phase variable (computed from the phase plane in Fig. 2) over time for 40 continuous strides between 1.0 to 3.0 mph. The trajectories with shallower slopes over a longer time period correspond to slower walking, whereas the steeper slopes over a shorter time period correspond to faster walking. The slope of the phase variable trajectory influenced the speed of the commanded joint trajectory through Eq. 1, by which the prosthetic leg adapted its kinematics to the user’s walking speed. The mean and standard deviation of the phase variable are shown over normalized time in Fig. 6. Overall, the phase variable exhibited a consistent, linear trajectory, which enabled consistent, smooth behavior for the prosthetic leg. The small variability about the mean can be attributed to transient changes in speed between treadmill settings and normal variability between the durations of stance vs. swing. For example, gait cycles with a longer stance period and shorter swing period would account for shallower slopes between 0 and 0.6 normalized seconds in Fig. 6.

Fig. 5.

The normalized phase variable over raw time per stride for 40 continuous strides at various walking speeds (1 to 3 mph). The phase variable is monotonic and approximately linear for all strides, where the slope of the trajectory depends on the walking speed. Flat regions can be observed between 0 and 0.4 sec in a few trajectories, which are the result of a zero-order hold to enforce monotonicity during non-steady walking motions (i.e., the first few steps after starting from rest).

Fig. 6.

The normalized phase variable over normalized time per stride at various walking speeds (1 to 3 mph). The average trajectory (blue solid line) and ±1 standard deviation (shaded region) are computed across 40 continuous strides. The phase variable is strictly monotonic and approximately linear across the gait cycle.

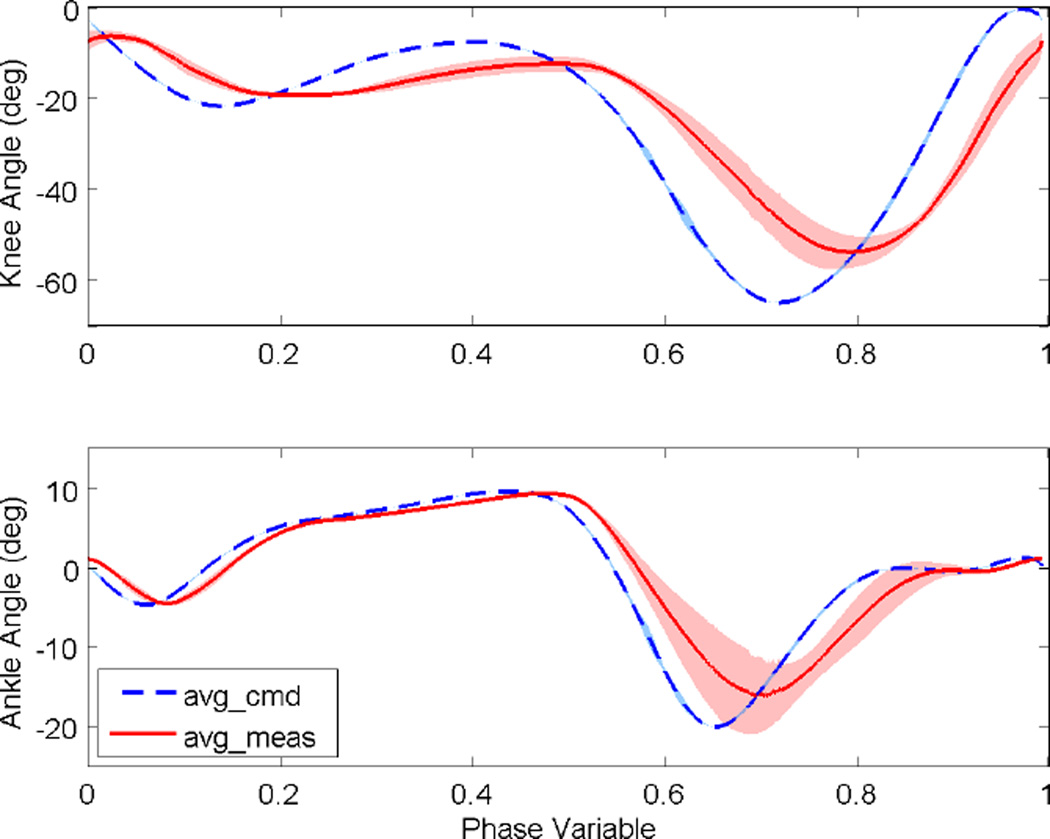
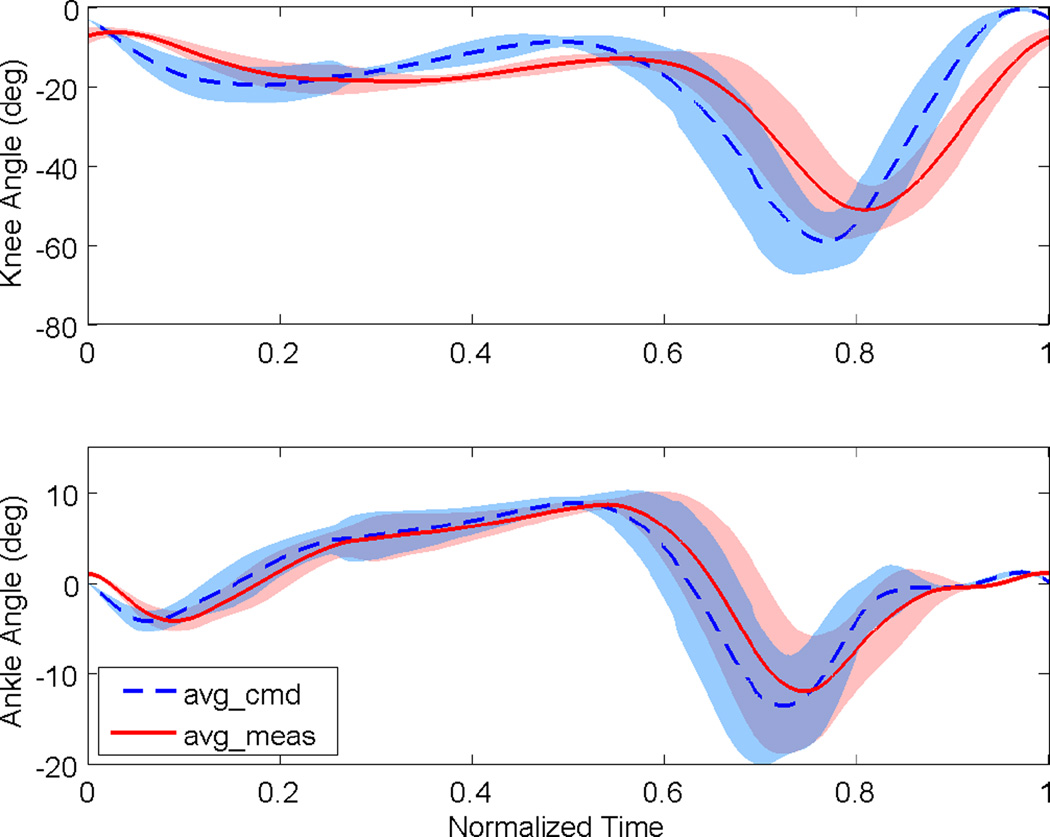
Fig. 7 displays the mean and standard deviation of the commanded and measured joint angles over the phase variable. The commanded signals exhibit negligible variance, which was expected from the definition of virtual constraints as functions of the phase variable (the x-axis of Fig. 7). The larger variations of the measured joint angles demonstrate the flexibility afforded by the controller as external forces change with speed. Some phase delay can be observed in tracking the commanded signal, which we hope to address in future work by implementing output derivative corrections (instead of joint viscosity) in the PD control law of Eq. 2. Efforts at shifting the phase variable to compensate for this phase delay did not prove beneficial in these experiments. For a different perspective, the joint kinematics are shown over normalized time in Fig. 8. The variations in the commanded signals are associated with variations of the measured phase variable within gait cycles (Fig. 6).

Fig. 7.

Joint kinematics of the prosthetic knee (top) and ankle (bottom) over the phase variable at various walking speeds (1.0 to 3.0 mph). The black dashed line is the average commanded angle for each joint. The red solid line is the average measured angle for each joint. The shaded regions represent ±1 standard deviation about the mean. The averages and standard deviations are taken over 40 continuous strides. The control system reasonably tracked the commanded angles from the virtual constraints, which were designed from healthy human data in Fig. 1.

Fig. 8.

Joint kinematics of the prosthetic knee (top) and ankle (bottom) over normalized time at various walking speeds (1.0 to 3.0 mph). The black dashed line is the average commanded angle for each joint. The red solid line is the average measured angle for each joint. The shaded regions represent ±1 standard deviation about the mean. The averages and standard deviations are taken over 40 continuous strides.

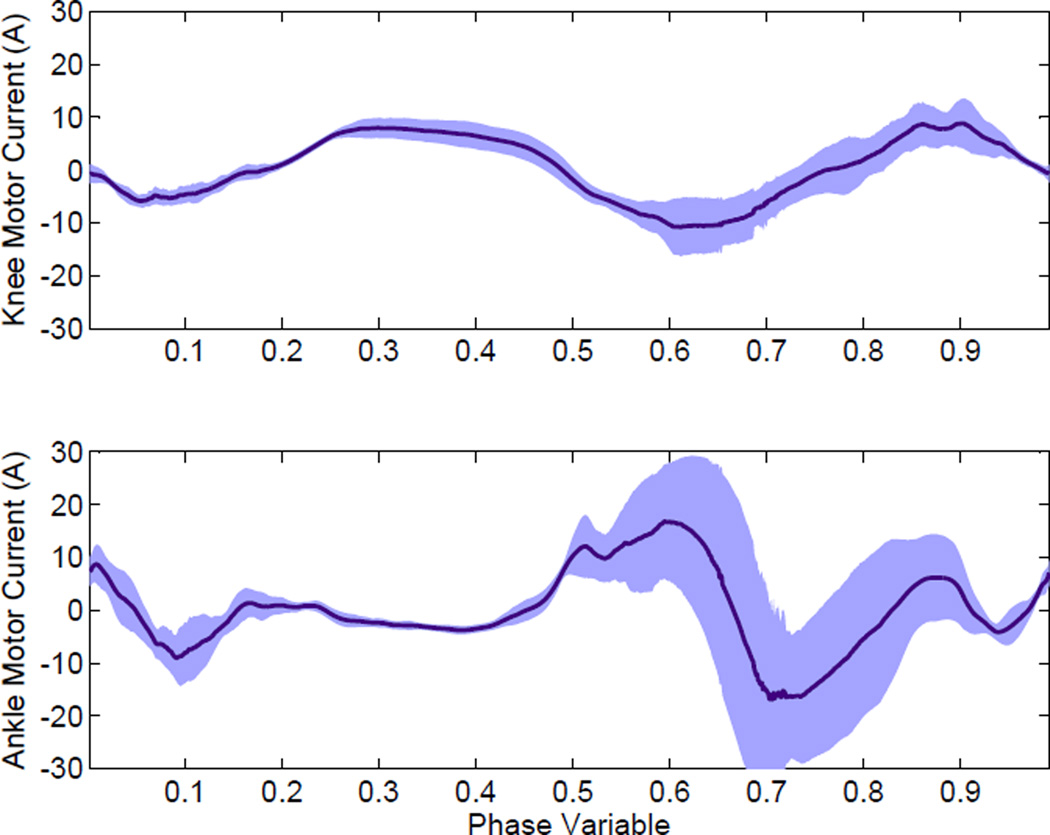
The motor current commands sent to the motor drivers were measured across the various walking speeds (Fig. 9). These motor commands roughly correspond to output torque at the joints through a nonlinear mapping based on the dynamics and kinematics of the actuator transmission. The ankle demanded the highest torque during a noticeable powered push off (phase variable between 0.5 to 0.6) at the end of stance. The knee required the most torque during late stance (knee flexion) and late swing (knee extension).

Fig. 9.

The commanded motor currents from the controller for the knee (top) and ankle (bottom) over the phase variable at various walking speeds (1.0 to 3.0 mph). The knee requires the most current during the swing period (phase variable between 0.6 to 1.0), and the ankle current peaks during late stance (phase variable between 0.5 to 0.6) as powered push off injects energy to propel the prosthetic leg into swing motion. Note, push off occurs around phase variable of 0.6.

V. DISCUSSION & CONCLUSION

We developed a single, unified prosthesis controller that captures the entire gait cycle using a periodic virtual constraint driven by a human-inspired phase variable. The unified controller eliminates the need to divide the gait into different periods with independent controllers, reducing the control parameters to tune for each individual subject and walking speed. This could significantly reduce the clinical time and effort to configure a powered knee-ankle prosthesis for an individual subject. The controller was implemented in a powered prosthesis and tested with an able-bodied subject using a bypass adapter to evaluate walking at variable speeds.

The same controller was used for all walking speeds, demonstrating adaptability as the human user initiated, accelerated, decelerated, and terminated walking with their thigh motion. Although the controller used fixed virtual constraints based on able-bodied joint kinematics for a specific walking speed, the human subject naturally forced desirable changes in the prosthetic knee and ankle kinematics as the walking speed changed (Fig. 7). This behavior approximates the slight variations observed in able-bodied joint kinematics across different walking speeds [27], though updates to the commanded trajectory based on walking speed (as in [21]) could also be beneficial. The combination of the flexible controller and the subject’s intact hip joint enabled appropriate changes in step length as the walking speed changed to achieve a comfortable walking gait.

The maximum speed achieved in these experiments is on par with the fastest walking speed currently reported in the literature [32] for a powered knee-ankle prosthesis, but our results were achieved with a single controller. This walking speed is substantially faster than typical finite state machine approaches for walking (e.g., [31]), but not as fast as the running-only controller in [7]. To our knowledge, no other controller has been reported for a knee-ankle prosthesis that can vary across such a wide range of walking speeds without adjusting any control parameters. Future efforts include additional control loops, such as closed-loop torque control, which can potentially provide better tracking that may enable faster walking. Preliminary experiments also suggest that comfortable walking can be achieved without retuning control parameters for different human subjects, which will be the topic of future investigation.

The proposed control approach can be applied equally well to other locomotion activities with well-characterized joint kinematics from able-bodied data, such as walking on slopes or stairs [27]. Clinicians could graphically tune the joint trajectories in this control framework, as opposed to iteratively guessing several impedance parameters in a state machine to achieve the intended effect. Future experiments will involve transfemoral amputee subjects to further validate the performance of the powered prosthesis using the unified controller.