RELATING ACCUMULATOR MODEL PARAMETERS AND NEURAL DYNAMICS

Abstract

Accumulator models explain decision-making as an accumulation of evidence to a response threshold. Specific model parameters are associated with specific model mechanisms, such as the time when accumulation begins, the average rate of evidence accumulation, and the threshold. These mechanisms determine both the within-trial dynamics of evidence accumulation and the predicted behavior. Cognitive modelers usually infer what mechanisms vary during decision-making by seeing what parameters vary when a model is fitted to observed behavior. The recent identification of neural activity with evidence accumulation suggests that it may be possible to directly infer what mechanisms vary from an analysis of how neural dynamics vary. However, evidence accumulation is often noisy, and noise complicates the relationship between accumulator dynamics and the underlying mechanisms leading to those dynamics. To understand what kinds of inferences can be made about decision-making mechanisms based on measures of neural dynamics, we measured simulated accumulator model dynamics while systematically varying model parameters. In some cases, decision- making mechanisms can be directly inferred from dynamics, allowing us to distinguish between models that make identical behavioral predictions. In other cases, however, different parameterized mechanisms produce surprisingly similar dynamics, limiting the inferences that can be made based on measuring dynamics alone. Analyzing neural dynamics can provide a powerful tool to resolve model mimicry at the behavioral level, but we caution against drawing inferences based solely on neural analyses. Instead, simultaneous modeling of behavior and neural dynamics provides the most powerful approach to understand decision-making and likely other aspects of cognition and perception.

Cognitive modeling allows us to infer the mechanisms underlying perception, action, and cognition based on observed behavior (Busemeyer & Diederich, 2009; Farrell & Lewandowsky, 2010; Townsend & Ashby, 1983). In the domain of decision-making, accumulator models (also called sequential-sampling models) provide the most complete account of behavior for many different types of decisions (Bogacz, Brown, Moehlis, Holmes, & Cohen, 2006; Brown & Heathcote, 2005; Brown & Heathcote, 2008; Laming, 1968; Link & Heath, 1975; Link, 1992; Nosofsky & Palmeri, 1997; Palmer, Huk, & Shadlen, 2005; Ratcliff & McKoon, 2008; Ratcliff & Smith, 2004; Reddi & Carpenter, 2000; Shadlen, Hanks, Churchland, Kiani, & Yang, 2006; Smith & Vickers, 1988; Usher & McClelland, 2001; Vickers, 1979). These models assume that evidence for a particular response is integrated over time by one or more accumulators. A response is selected when evidence reaches a response threshold. Variability in the time it takes for accumulated evidence to reach threshold accounts for variability in choice probabilities and response times observed in a broad range of decision-making tasks.

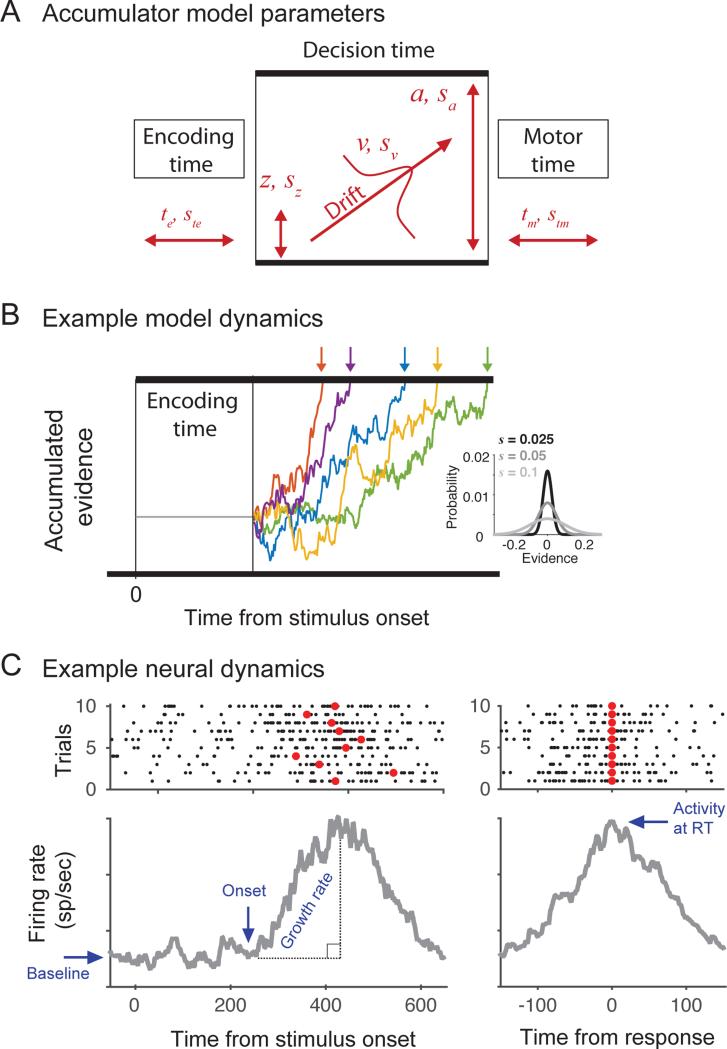
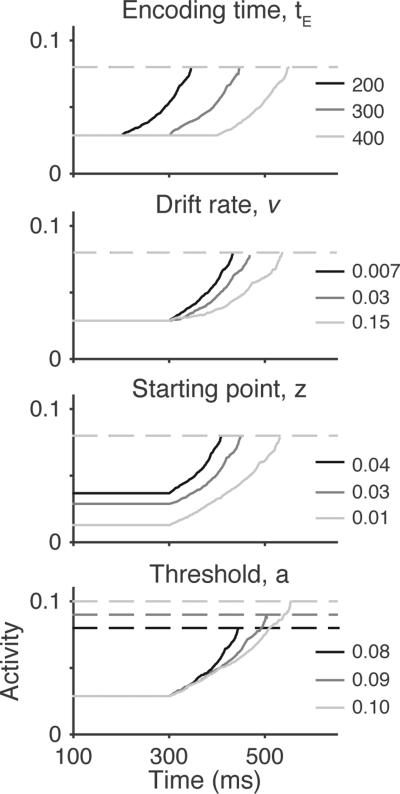
Particular accumulator model parameters represent distinct decision-making mechanisms (Figure 1). An encoding time (t_e) parameter defines the time for sensory and perceptual processing, a drift rate parameter (v) defines the mean rate of evidence accumulation, a starting point parameter (z) determines the initial state of an accumulator, a threshold parameter (a) defines the level of evidence that must be reached before a response is initiated, and a motor response time (t_m) parameter defines the time to execute a response (Figure 1A). By identifying parameter values that maximize the match between observed and predicted behavior (e.g., Vandekerckhove & Tuerlinckx, 2007), the models can reveal the mechanisms underlying variation in decision-making behavior across different experimental conditions. For example, manipulations of speed versus accuracy instructions affect the response threshold (Brown & Heathcote, 2008) (Wagenmakers, Ratcliff, Gomez, & McKoon, 2008), manipulations of experience (Nosofsky & Palmeri, 1997; Palmeri, 1997; Petrov, Van Horn, & Ratcliff, 2011; Ratcliff, Thapar, & McKoon, 2006) or stimulus strength (Palmer et al., 2005; Ratcliff & McKoon, 2008; Ratcliff & Rouder, 1998) affect drift rate, and manipulation of dynamic stimulus noise prolong encoding time (Ratcliff & Smith, 2010). In addition, many accumulator models assume that some of these mechanisms can vary over trials to explain within-condition variability in behavior, with additional parameters defining the degree of variability in other parameters.

Figure 1.

Expected relationships between accumulator model parameters, model dynamics, and neural dynamics. A: Illustration of accumulator model parameters. Four primary parameters determine the decision-making mechanisms: encoding time (t_e) defines the time for perceptual processing preceding evidence accumulation, drift rate (v) defines the mean rate of accumulation, starting point (z) determines the initial state, threshold (a) defines the level of evidence that must be reached before a response is initiated, and motor response time (t_m) defines the time to execute a response. Four corresponding stochastic parameters (s with subscript) define the across-trial variability for each parameter (see General Simulation Methods). In these simulations, motor time was always assumed to be zero. B: Example model dynamics for five simulated trials using identical parameters. During encoding time, the model activity is fixed at the starting point. Following encoding time, evidence is sampled from a distribution with mean v and standard deviation s (within-trial noise, inset) and accumulated over time. Response times (RTs, arrows) are the sum of encoding time, the time needed for accumulated evidence to reach threshold (i.e., decision time). Due to within-trial noise, even the same set of parameters produces variability in both RT and the evidence accumulation trajectory. C: Example simulated single-unit activity and measures of neural dynamics. Top panels show that neural activity on individual trials given by the spike discharge times (black dots) aligned on stimulus onset (left) or RT (right; red circles). Individual spike trains are highly noisy, but the average firing rate over trials reveals underlying structure in the dynamics (grey lines, bottom). Four measures of neural dynamics are commonly applied to make inferences about model parameters. The onset is hypothesized to correspond to the encoding time, the growth rate is hypothesized to correspond to the drift rate, the baseline is hypothesized to correspond to the starting point, and the activity at RT is hypothesized to correspond to the threshold. Dashed black lines illustrate the computation of growth rate based on the slope of the line connecting the activity at onset to activity at RT. Neural spike times were simulated according to a time inhomogenous Poisson process with a rate parameter determined by simulated accumulator model dynamics.

Recent neurophysiological and neuroimaging studies have identified potential linking propositions (Schall, 2004; Teller, 1984) between accumulator models and measures of brain activity (Forstmann, Ratcliff, & Wagenmakers, 2015; Forstmann, Wagenmakers, Eichele, Brown, & Serences, 2011; Gold & Shadlen, 2007; Palmeri, Schall, & Logan, 2014; Shadlen & Kiani, 2013; Smith & Ratcliff, 2004). Different approaches have established different kinds of connections between models and neural measures (Turner, Forstmann, Love, Palmeri, & Van Maanen, in press). One approach has been to fit a model to behavior, and use the fitted parameters as a tool for interpreting or identifying neural signals. Correlating model parameters and neural signals across subjects and conditions can provide insight into what brain regions might be involved in determining the model threshold, drift rate, and non-decision time (Forstmann et al., 2008; Heekeren, Marrett, Bandettini, & Ungerleider, 2004; van Maanen et al., 2011; White, Mumford, & Poldrack, 2012). Another approach has been to jointly model behavioral data and neural responses together, significantly constraining parameter estimates (Cassey, Gaunt, Steyvers, & Brown, in press; Turner, van Maanen, & Forstmann, 2015).

Another line of work suggests that the firing rates of certain neural populations directly represent the evidence accumulation process proposed in the accumulator model framework. In these studies, animals are trained to perform perceptual decision-making tasks and neural activity is recorded from one or more intracranial electrodes simultaneously while animals perform the task. Neural responses can then be analyzed aligned to the timing of task events (e.g., stimulus onset) or the behavior of the animal (e.g., response initiation). Specifically, the firing rates of neurons within a distributed network of areas including pre-frontal cortex (Ding & Gold, 2012; Hanes & Schall, 1996; Heitz & Schall, 2012; Kiani, Cueva, Reppas, & Newsome, 2014; Kim & Shadlen, 1999; Mante, Sussillo, Shenoy, & Newsome, 2013; Purcell et al., 2010; Purcell, Schall, Logan, & Palmeri, 2012), superior colliculus (Horwitz & Newsome, 1999; Ratcliff, Cherian, & Segraves, 2003; Ratcliff, Hasegawa, Hasegawa, Smith, & Segraves, 2007), posterior parietal cortex (Churchland, Kiani, & Shadlen, 2008; de Lafuente, Jazayeri, & Shadlen, 2015; Mazurek, Roitman, Ditterich, & Shadlen, 2003; Roitman & Shadlen, 2002), premotor cortex (Cisek, 2006; Thura & Cisek, 2014; Thura, Cos, Trung, & Cisek, 2014), and basal ganglia (Ding & Gold, 2010) exhibit dynamics consistent with accumulation of perceptual evidence. Following the onset of a stimulus, the firing rates of these neurons gradually rise over time depending on the animal's upcoming choice. Consistent with expected accumulator model dynamics, the rate of rise depends on stimulus strength and RT. Importantly, activity converges to a fixed firing rate shortly before the response is initiated regardless of the stimulus and RT, consistent with a threshold mechanism for decision termination (Hanes & Schall, 1996). The finding that certain neural populations might be implementing the computations proposed by accumulator models suggests that neural activity from these populations can provide a window onto the dynamics of evidence accumulation in the brain.

The proposed link between accumulator model dynamics and neural dynamics suggests that we could infer the parameters of the decision-making process directly from analyses of neural dynamics. Conversely, the best-fitting parameters of model fits to behavioral data could be used to directly generate predictions about expected neural dynamics. For example, one straightforward mapping for accumulator models associates the encoding time parameter with the measured onset of accumulation when neural activity first begins to rise from baseline, the starting point parameter with measured baseline activity before the stimulus turns on and before accumulation begins to rise, the drift rate parameter with measured growth rate of accumulation, and the response threshold parameter with measured activity prior to the onset of the observed motor response (Figure 1C). If we observe changes in the measured neural onset, then without ever fitting a model to data, we might assert that differences in the encoding time parameter in the accumulator model explains why people or animals are slow in one condition and fast in another. We could also choose to constrain an accumulator model by setting the encoding time parameter equal to the measured neural onset time across conditions. Working in the other direction, suppose that an accumulator model fitted to behavior required that there be changes in the encoding time parameter across conditions. This model could be tested by examining whether there are concomitant changes in the measured neural onset.

Of course, both of these approaches are valid only if the mapping between model parameters and neural dynamics is one-to-one. A one-to-one mapping between parameters and dynamics is indicated when variation in a certain parameter corresponds to variation in a unique measure of dynamics. For example, that variation in the onset time is only associated with variation in the encoding time parameter (Figure 1C), and not the drift rate, starting point, or threshold. A direct mapping between model parameters and dynamics may seem almost self-evident, but several factors can make things more complicated than intuition might suggest. To begin with, noise is ubiquitous in neural activity (Faisal, Selen, & Wolpert, 2008) and many accumulator models assume that evidence is noisy (e.g., Ratcliff & Smith, 2004). As we will see, within-trial noise introduces additional sources of variability such that qualitatively different model parameters can sometimes predict very similar dynamics. The mapping between accumulator model parameters and neural dynamics can also be obscured because of averaging over trials that resulted in different RTs, which is often necessary to combat noise in analyses of neural data (Figure 1C). If not done properly, this averaging can further obscure the mapping between model parameters and neural dynamics.

To understand how variation in accumulator model parameters relates to variation in neural dynamics, we quantified how variation in accumulator model parameters relates to variation in model dynamics (i.e., the trajectory of accumulated evidence). To do this, we applied commonly used neurophysiological analyses to characterize model dynamics generated from known sets of parameters. In the following section, we describe the accumulator models that were simulated, the parameters of those models that were varied, the measures of accumulator dynamics that were made, and how relationships between model parameters and dynamics were assessed.

General Simulation Methods

Model Overview

Researchers have proposed various accumulator model architectures that make specific assumptions about the form of evidence accumulation (e.g., the diffusion model, Ratcliff, 1978; Ratcliff & Rouder, 1998; linear ballistic accumulator (LBA), Brown & Heathcote 2008; leaky-competing accumulator (LCA), Usher & McClelland, 2001; linear approach to threshold with ergotic rate (LATER), Reddi & Carpenter, 2000). Our goal here was not to evaluate a specific architecture per se, but to evaluate the dynamics produced by different parameterized model mechanisms that can be shared across architectures. Therefore, we adopted a general modeling framework that included a broad range of decision-making mechanisms. We first provide a broad overview of the framework followed by a formal description of the model.

For biological plausibility, we modeled the decision process as accumulation of perceptual evidence to a positive response threshold (Figure 1B). For our purposes, the model activation can be identified with the firing rates of neurons that increase their activity in support of a particular response (Mazurek et al., 2003; Purcell et al., 2010; Ratcliff et al., 2007). Note that this approach is compatible with accumulator models, like the diffusion model (Ratcliff, 1978), that represent the decision process using a single accumulator with positive and negative response thresholds because these models can usually be reformulated using multiple accumulators (Bogacz et al., 2006; Ratcliff et al., 2007; Usher & McClelland, 2001). For simplicity, we modeled only a single accumulator, but the framework can be naturally extended to explain choice behavior with the addition of more accumulators (e.g., LBA, LATER, LCA). To maintain focus on the decision making mechanisms and their resulting dynamics, we did not explore models that included competition among accumulators or leakage of accumulated information (Smith, 1995; Usher & McClelland, 2001); analyses of model dynamics may help to distinguish between these mechanism as well (Bollimunta & Ditterich, 2012; Boucher, Palmeri, Logan, & Schall, 2007; Purcell et al., 2010; Purcell, Schall, et al., 2012).

Recall that four primary parameters determine how accumulator-model mechanisms can vary across experimental conditions (Figure 1A). The encoding time (T_e) determines the delay between the onset of a stimulus and the start of accumulation. Neurally, this parameter can be associated with afferent conduction delays, including the time needed to encode a stimulus with respect to potential responses. Typically, encoding time and post-decision motor time (T_m) are combined into a single “non-decision time” parameter (often denoted T_r or T_er) because the two parameters are indistinguishable using only behavior. However, because they can be distinguished in model and neural dynamics, we distinguish between them here, focusing specifically on encoding time because the motor time is relatively short and invariable for neurophysiological signals identified with some motor responses like saccadic eye movement (Scudder, Kaneko, & Fuchs, 2002). The drift or drift rate (V) determines the mean of perceptual evidence for a particular response, and therefore the rate of accumulation. The starting point (Z) determines the initial state of evidence at the start of the accumulation process. The threshold (A) determines the amount of evidence that must be accumulated before a motor response is initiated, and determines the tradeoff between accuracy and speed.

Each primary parameter is associated with stochastic parameters that can produce across-trial variability in behavior. Following common conventions (e.g., Brown & Heathcote, 2008; Ratcliff & Rouder, 1998), we assumed that encoding time varied according to a uniform distribution with range s_T ; drift rate varied according to a Gaussian distribution with standard deviation s_V; starting point varied according to a uniform distribution with range s_Z; threshold varied according to a uniform distribution with range s_A (some previous models have assumed normally-distributed thresholds (e.g., Grice, 1968; Grice, 1972), but we used a uniform to eliminate the possibility that the threshold could be placed below the starting point). In other words, primary parameters determine the mean of parameter distributions, and stochastic parameters determine the variability. We adopt the convention of using upper-case variables to refer to primary parameters that define a fixed parameter distribution over trials, and lower-case variables to refer to a sample from the distribution on an individual trial. To be clear, a model assuming all four sources of across-trial variability would be non-identifiable based on behavioral data alone, but variability in the four mechanisms can possibly be distinguishable based on analysis of accumulator dynamics.

The other major source of variability is within-trial noise. Many accumulator models assume that evidence is noisy (Figure 1B, inset; Ratcliff, 1978; Usher & McClelland, 2001), perhaps because of some combination of within-trial stimulus noise, momentary variation of the evaluation of a percept, or intrinsic variability in the brain; other models do not assume within-trial variability (Brown & Heathcote, 2005; Brown & Heathcote, 2008; Reddi & Carpenter, 2000). Here, we explored different levels of within-trial noise to understand what impact this noise might have on measures of model dynamics. Following common convention (e.g., Link & Heath, 1975), we assumed that within-trial variability in drift rate is normally distributed with standard deviation s (but see Jones & Dzhafarov, 2014; Ratcliff, 2013).

If we assume that the evidence in the accumulator maps onto the firing rate of a neuron, then the translation from rate to spikes will introduce an additional source of noise in any measure of neural dynamics (Figure 1C; Churchland et al., 2011; Nawrot et al., 2008; Smith, 2010, 2015). This additional source of variability can be added to the model dynamics by assuming that the neural activity is a doubly-stochastic process reflecting both rate variability (trial-by-trial variation in accumulated evidence) and point-process variability (Poisson-like spiking noise). This point-process variability has the potential to further obscure the relationship between model parameters and dynamics. However, because separate trials are generally recorded sequentially, the spiking noise is independent across trials and can be reduced by averaging. For the analyses reported in this paper, we reached the same conclusions regardless of whether we directly analyzed the model trajectories directly or used the model trajectories to drive a Poisson process and then analyzed the resulting spike count histograms (Figure 1C; Purcell et al., 2010; 2012), at least so long as the number of trials was ~20 or more (most neurophysiological studies record many more). Here, we report direct analyses of the model trajectories to demonstrate that our conclusions about the relationship between model parameters and dynamics are not an artifact of the conversion from spike rates to spike times, nor are they a consequence of limited statistical power. In practice, when comparing neural and model dynamics, one should always take spiking variability into account to ensure that differences between model and neural dynamics are not explained by differences in statistical power.

Simulation Details

At the start of a simulated trial, model activation, x(t), is fixed at starting point, z, which is sampled for that trial from a uniform distribution with range $[Z-\frac{s_Z}{2},Z+\frac{s_Z}{2}]$. Activation remains at z throughout the encoding time, t_e, which is sampled for that trial from a uniform distribution with range $[T_e-\frac{s_T}{2},T_e+\frac{s_T}{2}]$. After the encoding time, model dynamics are governed by the following stochastic differential equation (see Bogacz et al., 2006; Usher & McClelland, 2001):

$$dx=\frac{\mathrm{dt}}{\tau }v+\sqrt{\frac{\mathrm{dt}}{\tau }}\xi$$

where x is the model activation (accumulated evidence), v is the drift rate, which is sampled for that trial from the Gaussian distribution with mean V and standard deviation s_V, and ξ is a within-trial Gaussian noise term with mean zero and standard deviation s. The process terminates when model activation exceeds a threshold, a, which is sampled for that trial from a uniform distribution with range $[A-\frac{s_A}{2},A+\frac{s_A}{2}]$.

The predicted response time, RT, is the sum of the encoding time (t_e), the decision time – the time for the activation to reach threshold – and the motor time (t_m; here, set to zero). Because firing rates cannot drop below zero, we initially explored versions of the model that included a lower reflecting bound at zero. However, we found that our results were qualitatively similar with or without such a lower bound, so we report results from a model that does not include a lower reflecting bound to be clear that this is not a crucial factor influencing our findings and conclusions.

By analyzing the relationship between model dynamics and model parameters, we hoped to inform the types of inferences that can be made by analyzing real neural signals. We therefore adopted simulation and analysis methods designed to mimic the type of data and analyses seen in actual neurophysiological experiments. Although closed-form solutions are available for expected behavior, simulations are needed to study the dynamics at the level of individual simulated trials. We used Monte-Carlo simulations to generate expected single-trial model dynamics (e.g., Tuerlinckx, Maris, Ratcliff, & De Boeck, 2001). All simulations used a simulation time step dtτ = 0.1 ms, and model trajectories were downsampled to 1 ms resolution to match the resolution of typical neural recordings.

We simulated different parameter sets to represent different experimental conditions. For each parameter set, we generated 5000 simulated trials, with each trial providing one RT and one model activation trajectory, x(t). In some cases, we chose parameter sets by systematically varying individual parameters to understand the selective influence these parameters have on accumulator dynamics. In other cases, we randomly sampled parameters from specified ranges to ensure that our results were not specific to a particular parameter set. For those simulations, we sampled 2500 parameter sets from the following ranges: T_e: 0.15 - 0.5; V: 0.01 - 0.15; Z: 0.001 - 0.1; A: 0 - 0.15; s_Te: 0 – 0.2; s_V: 0 – 0.1 ; s_Z: 0 – 0.1; s_A: 0 – 0.1). These parameters generated a diversity of RT distributions that spanned the range of RTs observed in typical decision-making experiments with humans and non-human primates. To ensure that each parameter set produced realistic behavior and dynamics, we also imposed several criteria. We required that Z < A so that the model produced non-zero decision times. In addition, we required that the leading edge (5^th percentile) of the decision time distribution must be at least 50 ms to ensure a sufficiently long time interval over which to measure accumulator dynamics. Finally, we required that at least 90% of trials reached the threshold within 2.0 seconds of decision time (our maximum simulation time) to prevent excessively long decision times and reduce computational demands.

Measures of Model Dynamics

We applied several measures of model dynamics to identify the parameters underlying variability in RT. We considered two types of RT variability. First, we asked whether we could identify the parameters underlying within-condition variability in RT (i.e., random, across-trial variability). Here, the goal is to infer which stochastic parameters are greater than zero given the observed model trajectories. Second, we asked whether we could use model dynamics to identify mechanisms underlying across-condition variability in RT – for example, variation due to an experimental manipulation. Here, each set of primary parameters can be identified with a simulated experimental condition and the goal is to infer which primary parameters have changed given the observed changes in the model trajectories. In both cases, the problem is not trivial because within-trial noise contributes to all variability in RT.

Both neural and model trajectories are very noisy at the level of individual trials (Figure 1), which makes it difficult to extract meaningful insights about model parameters based on single trials alone. Signal averaging is the most common method of noise reduction in analyses of neural data. Individual trials are first binned according to the condition or behavior of interest and then averaged in order to eliminate across-trial noise and reveal common underlying structure. To mirror this approach for our model dynamics, we will bin and average our model trajectories before analyzing the pattern of dynamics. Each measure of model dynamics (described below) will applied to the average trajectory for individual bins.

To understand sources of within-condition variability in RT, we analyzed the activation trajectories that produced different RTs for a single parameter set. We divided the 5000 simulated trials for each condition into bins based on the predicted RT and averaged trajectories within each bin. We choose a bin size of 20 because it was large enough to average out some across-trial noise, but small enough to limit the range of RTs within a single bin, and also approximated the values used in physiological studies (e.g., Purcell et al., 2010; Purcell, Schall, et al., 2012; Woodman, Kang, Thompson, & Schall, 2008).

To understand sources of across-condition variability in RT, we evaluated several different approaches to binning trials that have been employed by previous neurophysiological studies. First, one could simply group all trials from a condition into a single bin and average. Alternatively, one could analyze response dynamics in small RT bins as described above and then averaging the resulting measurements over bins. Ultimately, we will show that both of these methods are problematic for inferring model parameters from dynamics, but focusing on the subset of trials that result in moderately fast RTs (e.g., 30^th – 50^th percentile) produces better results for the set of neural measured that we evaluated.

We adapted four measures of model dynamics that were developed to analyze observed neural responses (Figure 1C; Pouget et al., 2011; Purcell et al., 2010; Purcell, Schall, et al., 2012; Woodman et al., 2008). Each measure was originally defined and developed to correspond conceptually to a particular accumulator model parameter in the absence of any sensory noise. We can then ask how effective is each measure once noise is introduced.

First, we measured the onset time of accumulation when activity first increased above the pre-stimulus baseline levels. To quantify the onset time, we used a sliding-window algorithm (+/−50 ms) that moves backward in 1 ms increments beginning at RT. The onset of activation was determined as the time when the following criteria are met: (1) activity no longer increases according to a Spearman correlation (alpha = 0.05) within the window around the current time; (2) activity at that time was lower than 50% of the maximum; and (3), as the window was moved backwards in time, the correlation remains nonsignificant for 30ms. Our results were unchanged when we instead computed the onset as the time at which activation first exceeds 10% of the distance from baseline to threshold.

Second, we measured the baseline of accumulation. This is the initial level of activation immediately following stimulus onset. To quantify the baseline, we computed the average activation in the initial 100ms of each simulated trial, which was always less than the minimum encoding time assumed by our choice of parameters.

Third, we measured the activity at RT. This is the level of activation near the time when the response was initiated. To quantify the activity at RT, we first aligned all simulated trials to the time of the initiated response. The activity at RT was then computed as the average activation in the 5ms window centered on response time.

Fourth, we measured the growth rate of accumulation to threshold. This is the average rate of accumulation from the time when activity first began increasing (onset time) until the threshold was reached. To quantify the growth rate, we estimated the slope of model activation from the onset time until RT. This was computed as the activity at RT minus the baseline, divided by the RT minus the onset time (see Figure 1C).

Simulation Results

Variability in accumulator model parameters causes variability in predicted behavior and model dynamics. We asked whether the source of variability could be inferred not by fitting parameterized models to behavioral data, as in cognitive modeling work, but by measuring accumulator dynamics directly, as in neurophysiological work. To do this, we simulated a general accumulator model architecture while introducing variability in particular parameterized mechanisms. We then measured accumulator dynamics in ways analogous to how neurons are analyzed in order to determine how variability in those dynamics relate to the variability we introduced via model parameters.

Within-Condition Variability in Parameters and Dynamics

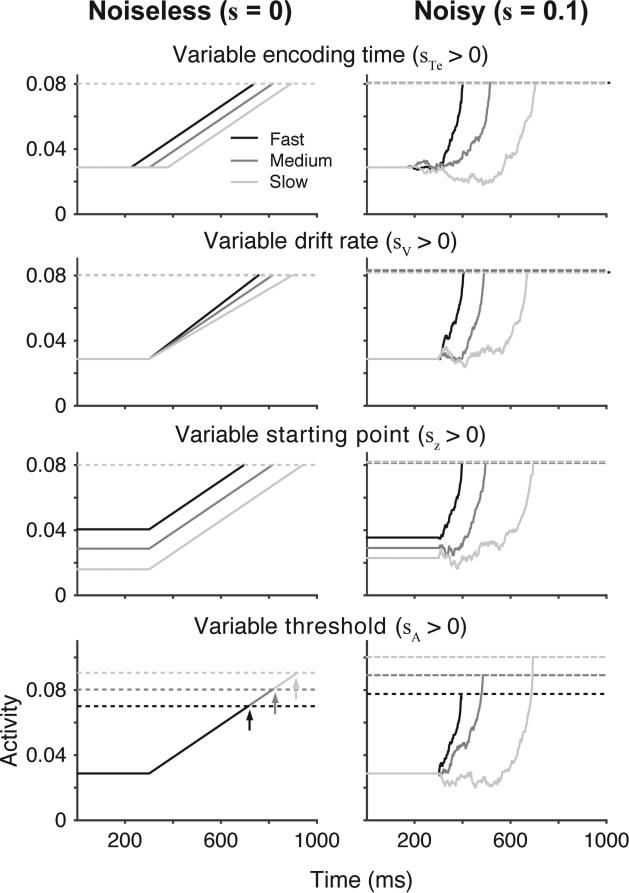
To understand sources of within-condition variability in RT, we analyzed the model trajectories that produced different RTs given a set of parameters. We first examined a model architecture assuming no within-trial noise (“Noiseless”, s = 0) to validate our measures of neural dynamics and provide a baseline for comparison to noisy models. We started by simulating four versions of the model assuming across-trial variability in only one of the four primary parameterized mechanisms (encoding time, drift rate, starting point, threshold); in other words, in each of the four model versions, only one of the stochastic parameters, s_Te, s_V, s_Z, or s_A, were non-zero and all the rest were equal to zero. The left column of Figure 2 illustrates model dynamics for each version of the model using a representative set of primary parameter values; later, we generalize beyond this particular parameter set. In the absence of within-trial noise, there is a clear one-to-one mapping between variability in manipulated parameters and variability in measured dynamics. As anticipated by our earlier discussion, variability in encoding time (T_e) maps onto variability in measured onset, variability in drift (V) maps onto variability in measured rate, variability in starting point (Z) maps onto variability in measured baseline, and variability in threshold (A) maps onto variability in activity at RT.

Figure 2.

Inferring sources of within-condition variability from model dynamics. Each panel shows the average model trajectories divided by RT for different sets of parameters. For each row, one stochastic parameter was set to a positive value, and the remaining stochastic parameters were set to zero (row 1 – encoding time, s_Te = 0.3; row 2 – drift rate, s_V = 0.02; row 3 – starting point, s_Z = 0.05; row 4 - threshold, s_A = 0.04). Model trajectories shown in the left column included no within-trial noise (s = 0, “Noiseless”) and model trajectories shown in the right column included conventional levels of within-trial noise (s = 0.1, “Noisy”). For all panels, primary parameters were fixed at the following values: T_er = 0.3, V = 0.1, Z = 0.029, A = 0.08. Following standard neurophysiological approaches, model trajectories for each set of parameters were grouped by RT and averaged in bins of size 20 (see General Simulation Methods). Fast, medium, and slow refers to the average trajectory for the RT bins at the 25^th, 50^th, and 75^th percentile, respectively. Dashed lines indicate the model threshold for each RT group. Arrows, when shown, highlight the time when the threshold is crossed for each RT group.

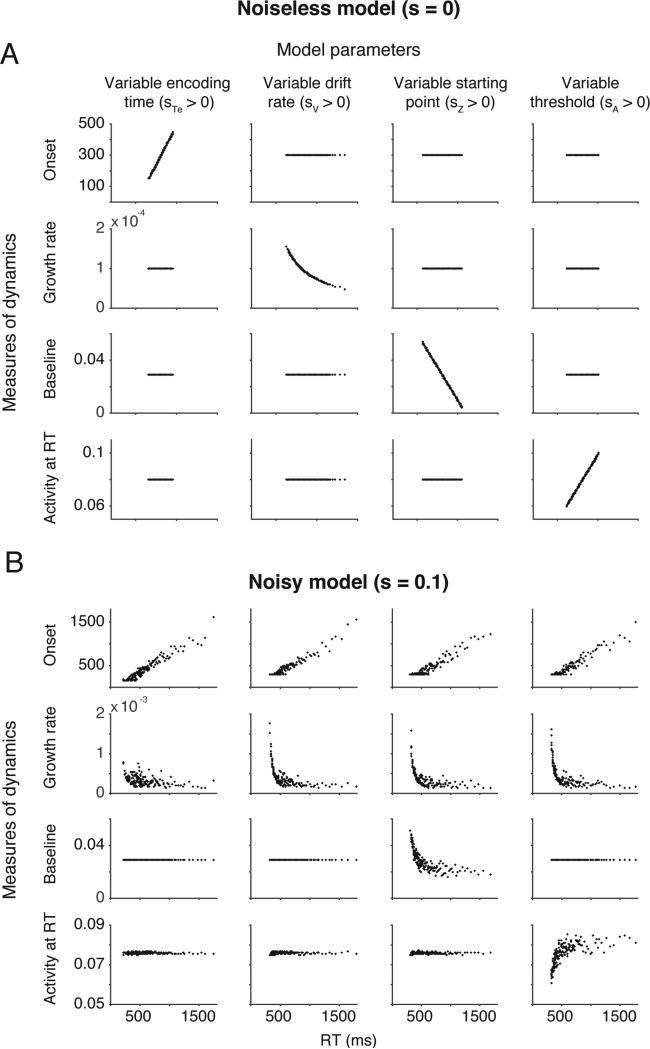
To quantify this, following typical neural analyses, we grouped trials into bins of size 20 and plotted each measure of model dynamics as a function of the mean RT for all bins (Figure 3A). A particular measure of model dynamics correlated with RT only for a single stochastic parameter in the model. This is illustrated in Figure 3A by the fact that only the diagonal panels show any relationship between manipulated model parameters and measured dynamics. Without within-trial noise (s = 0), the measured dynamics of accumulation and variability in the resulting behavior are exclusively determined by variability in a particular accumulator model parameter. In that case, the relationship between model dynamics and model parameters is one to one, straightforward and intuitive.

Figure 3.

Correlations between accumulator model parameters and measures of model dynamics for example model simulations without noise (A, Noiseless) and with convention levels of noise (B, Noisy). For each column, one stochastic parameter was set to a positive value, and the remaining stochastic parameters were set to zero. Parameter values were identical to the simulations shown in Figure 2. Each row shows one measure of model dynamics (onset time, growth rate, baseline, activity at RT) applied to the average trajectories of individual RT bins as a function of the average RT that bin. When evidence accumulation is noiseless, each stochastic parameters produces correlations between RT and a single measure of neural dynamics (a one-to-one mapping). When evidence accumulation is noisy, multiple measures of neural dynamics correlate with RT for each stochastic parameter (a many-to-one mapping).

The relationship between variability in accumulator model parameters and measured model dynamics is more complicated with the addition of within-trial noise. The right column of Figure 2 illustrates variability in accumulator dynamics generated with the same set of parameters, but now with the addition of within-trial noise (Noisy, s = 0.1). All four parameter sets, regardless of the underlying source of variability, produce variation in the measured onset and growth rate with RT. This was clearly evident in the correlation between the measured onset and growth rate and RT for all four models. As shown in Figure 3B, there is a relationship between onset and RT (first row) and between growth rate and RT (second row) even when a seemingly incommensurate parameter was varied. This means that simply observing changes in the onset or growth rate of neural signals as a function of RT is not sufficient to draw conclusions about parameterized sources of variability in the decision process. Changes in the measured baseline and activity at RT can be somewhat diagnostic, but changes in the onset and growth rate could well reflect accumulator noise.

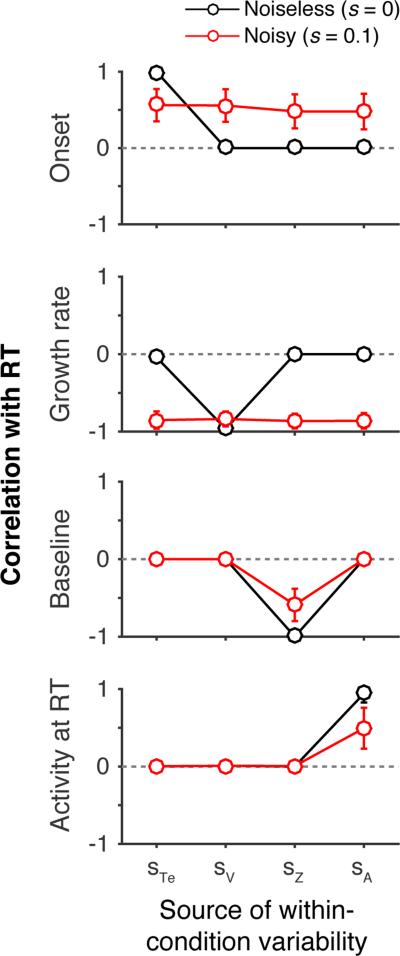
This “one-to-many” relationship between measured dynamics and manipulated parameters was not unique to the particular set of parameters we used in the above illustrations, but was observed across a broad range of parameter sets. To demonstrate this, we again simulated four model variants in which a single stochastic parameter (st, sv, sz, or sa) took on a value greater than zero. But instead of evaluating just a single set of parameters, we sampled from a broad range of values resulting in diverse RT distributions (see Methods). Across 2500 sampled parameters sets, Figure 4 displays the average correlation between measured dynamic and RT for each of the manipulated stochastic parameters. As shown in the figure, without any within-trial noise (Noiseless, s = 0), there is a clear one-to-one mapping between the measures of model dynamics and stochastic parameters. However, within-trial noise of a standard magnitude (Noisy, s = 0.1) produces strong correlations between the measured onset of activity and RT and between the measured growth rate of activity and RT.

Figure 4.

Average correlations between measures of model dynamics and RT. When evidence is noiseless (black), correlations between RT and measures of model dynamics (onset, growth rate, baseline, and activity at RT) indicate a single source of within-condition variability (stochastic parameters, x-axis). When evidence is noisy (red), correlations between RT and measured onset and growth rate are observed regardless of stochastic parameters. For a given set of simulations, one stochastic parameter (x-axis) and all primary parameters were randomly sampled from a range of values (see Simulation Methods); the other stochastic parameters were set to zero. The sampled parameter values were used to generate 5000 simulated trials. The simulated trials were divided into RT bins of size 20, and the Pearson correlation coefficient was computed between each measure of model dynamics and the mean of each RT bin (see Figure 3). This process was repeated 2500 times for each stochastic parameter and each value of within-trial noise. Panels show the mean and standard deviation of the resulting correlations.

Figure 5 provides some intuition about why the dynamics under cases of within-trial noise take this form. The left panels illustrate example trajectories sampled from different ranges of RTs (fast, medium, and slow), while the right column shows the probability distribution of accumulated evidence at each time step conditional on the same RT range. Fast RTs result from positive samples of noise that elevate the observed growth rate, even if the underlying mean rate of growth is invariable. Slow RTs occur when accumulated evidence meanders around the starting point, only rising immediately prior to reaching the threshold. As a result, the actual end of encoding time (start of evidence accumulation) may have occurred long before activity first begins rising toward threshold.

Figure 5.

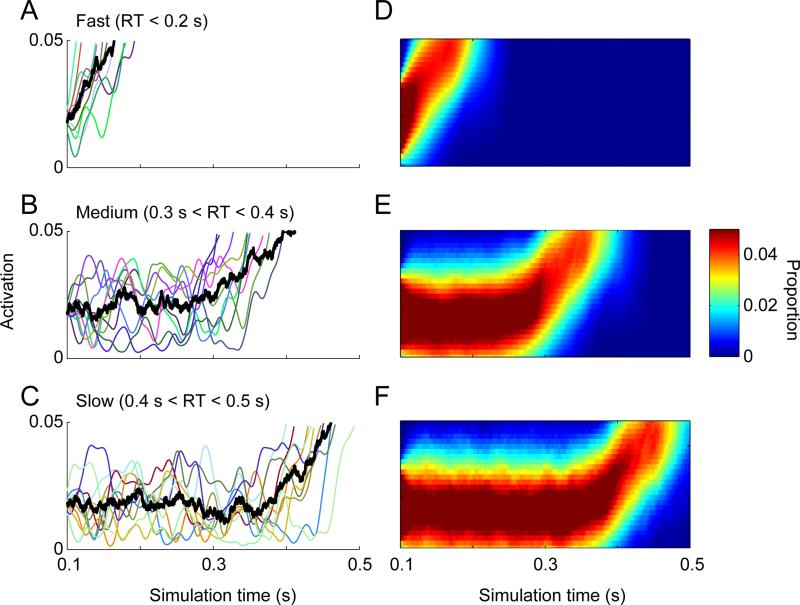
Example single-trial trajectories and probability distribution of accumulated evidence conditional on RT. Grouping noisy model trajectories by RT produces delays in the measured onset. All stochastic parameters were set to zero and within-trial noise was set to 0.1. (A-C) Example single-trial trajectories (colored lines) and average (black line) for simulated trials that resulted in fast (A, 0 - 0.2 s), medium (B, 0.3 – 0.4 s), or slow (0.4 – 0.5 s) RTs. (D-F) Probability distribution for accumulated evidence conditional on RTs terminating with the specified fast, medium, and slow ranges. Individual trajectories and probabilities were smoothed with a Gaussian filter for illustration purposes only; no other analysis or figure used smoothed trajectories.

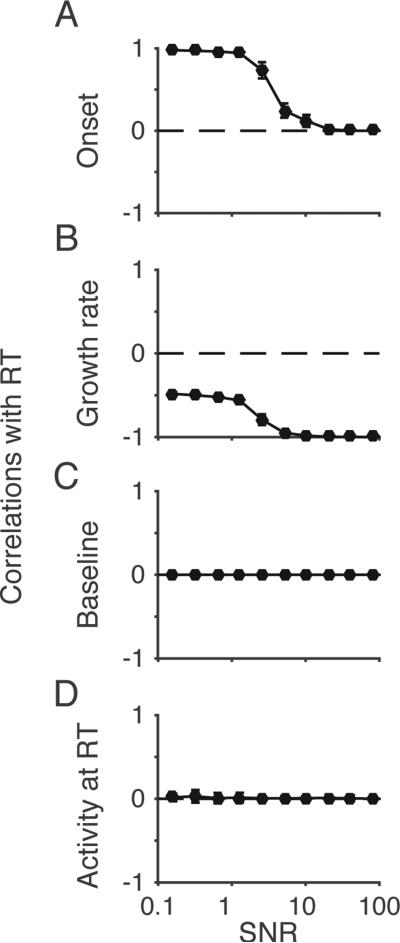
We found that the signal-to-noise ratio (SNR) of incoming evidence is a key factor influencing the correlation between measured onset and RT, and between measured growth rate and RT. In the accumulator model framework, SNR is defined by the ratio of the mean drift rate (V) over within-trial noise (s). To study the influence of SNR on model dynamics, we simulated a model in which within-trial noise was the only source of variability; in other words, all other stochastic parameters were set equal to zero. We varied the SNR, while all other primary parameters were randomly sampled as described above. The relationship between onset and RT is highly dependent on SNR. When SNR is high (≥10), the model trajectories are more likely to rise directly to threshold, and so measured onset does not correlate with RT (Figure 6A). However, when the SNR is low (roughly <5), the onset correlates strongly with RT. In this case, the growth rate correlates with RT irrespective of SNR because the within-trial noise is the only source of variability in the model. In contrast, the measured baseline and threshold are unaffected by SNR.

Figure 6.

Correlations between RT and measured onset depend on the signal-to-noise ratio (SNR, v/s). Primary parameters were randomly sampled from a range of values and the level of within-trial noise was chosen to systematically vary the SNR. Stochastic parameters were fixed at zero. For each parameter set, the correlation between RT and measures of model dynamics were computed as in Figure 4.

Across-Condition Variability in Parameters and Dynamics

The analyses above focused on within-condition variability in model dynamics and stochastic parameters, but accumulator models are also frequently used to infer changes in decision making across experimental conditions (e.g., variation in stimulus strength, speed-accuracy instructions, etc.). To understand whether measuring neural dynamics can be used to directly identify changes in decision-making mechanisms across conditions, we also tested how variation in measured accumulator dynamics are related to manipulated variation in primary model parameters.

Quantifying changes in model dynamics and neural dynamics across experimental conditions raises a challenge of how to summarize dynamics across multiple trials. For speeded decision-making tasks in which a subject determines when to make their response, the total trial duration will vary substantially over trials. While it is straightforward to average RTs of different durations since those are simply point observations, there is no clear way to average trajectories of different durations because those are extended time series. Neurophysiological studies have dealt with this variability in different ways, but the choice of how to average and bin trials can have a marked influence on the form of resulting measured dynamics that can help or hinder inferences about underlying parameters.

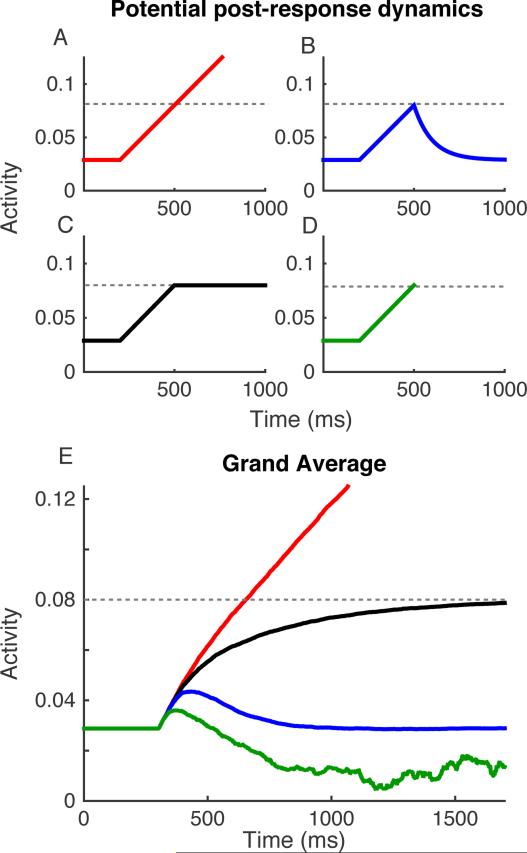
One seemingly straightforward approach is to simply average across all trials regardless of their RT. A critical limitation of this approach is that it requires some explicit assumption about how to treat post-response accumulator activity (Figure 7A-D). For early time points, all of the model or neural trajectories can be averaged together at every time step, but at progressively later time points, increasingly more of the trajectories will have hit threshold and triggered a response. Once a trajectory has resulted in an RT and exited the process, how should it contribute to the average trajectory? Most accumulator models do not define the state of accumulated evidence after the response (but see Moran, Teodorescu, & Usher, 2015; Pleskac & Busemeyer, 2010; Resulaj, Kiani, Wolpert, & Shadlen, 2009). Following the response, activity might continue to accumulate above the threshold after the decision is made (Figure 7a), decay back to baseline (Figure 7b), or remain at the threshold (Figure 7c). Alternatively, we may exclude all post-response activity from the analysis of neural trajectories by clipping the trajectories after each response (Figure 7e).

Figure 7.

Different assumptions about post-response activity can strongly influence average model dynamics. (A-C) Four illustrations of potential post-response dynamics on single trials. (A, red) Evidence accumulation continues after the threshold is reached, (B, blue) evidence decays back to starting point, (C, black) evidence remains at the threshold levels, and (D, green) evidence is clipped when the threshold is reached. (E) Average dynamics over 5000 simulated trials for the same set of model parameters, but assuming different forms of post-response dynamics. Parameter values are identical to those used for Figure 2. Colors indicate post-response dynamics illustrated in A-D. The green line in which activity on individual trials is clipped at RT becomes noisier as time progresses because fewer trials contribute to the average.

Unfortunately, we do not know which assumption about post-response activity is correct in actual neural data and different assumptions about post-response activity can produce very different dynamics when averaged across trials. Figure 7e illustrates this point by showing the grand average model trajectories from the same set of parameters used in Figures 2-3, but differing only in the assumptions about post-response dynamics. The average trajectory is dramatically different depending on whether activity continues to accumulate (red), decays to baseline (blue) or remains at threshold (black). Simply dropping post-response activity and averaging across trials is also problematic for several reasons. As time progresses, the composition of RTs contributing to the average changes. As more trials drop out over time, the signal becomes progressively noisier as fewer trials contribute to the average and the dynamics are dictated by the sensory noise of individual trials. As a result, earlier and later time points may be associated with very different dynamics (e.g., higher growth rate early, lower drift rates later), resulting in a grand average that is nonlinear and non-representative of individual trials (Figure 7e, green curve).

An alternative approach is to first group trials into small RT bins as in the preceding section, compute the measures of model dynamics for each RT bin, and then simply average the resulting measures over all bins (i.e., imagine averaging all data points in each panel of Figure 3). This approach will minimize the contribution of post-response activity, but it is susceptible to the same influences of within-trial noise highlighted in the previous section. Figure 8 illustrates the problem for an example set of parameters in which across-condition variability is explained solely through different values of the drift rate, all stochastic parameters were fixed at zero, and there was accumulator noise (s = 0.1). For the faster RTs, the measured onset closely matches the actual end of encoding time because evidence rises directly from baseline to the threshold on those trials (Figure 8A). For moderate and slow RTs, however, the measured onset is often later than the actual end of encoding time (Figure 8B,C). Because V (signal) is decreasing and s (noise) remains fixed, the SNR drops across conditions, resulting in increased correlations between onset and RT even though the encoding time parameter remains fixed (Figure 8D). To summarize, under this approach, conditions in which the SNR is different across conditions as a result of fixing within-trial noise and varying drift may result in non-selective influences on the measured onset.

Figure 8.

Across-condition variation of drift rate can produce variation in measured onset. (A-C) Simulated model dynamics for three values of drift rate divided into fast RTs (A, 25^th percentile), medium RTs (B, 50^th percentile), and slow RTs (C, 75^th percentile). For slow RTs, the onset appears to increase with drift rate, although the encoding time parameter was unchanged. (D) Each measure of model dynamics was computed for individual RT bins of size 20, and the resulting measures were averaged over all RT bins for a given set of parameters. The average onset decreases with drift rate due to changes in the SNR.

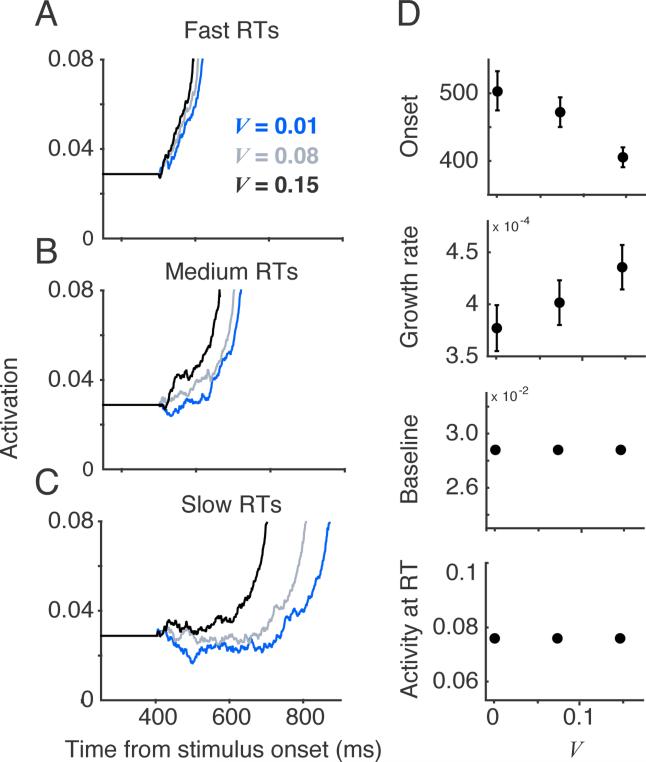
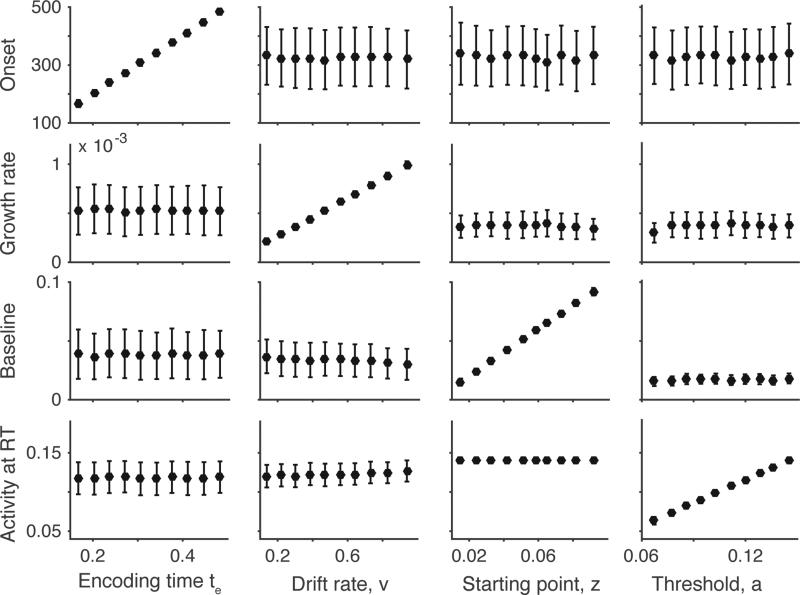
One simple solution is to focus on a relatively small range of fast to moderate RTs (e.g., 30^th to 50^th percentile). This range of RTs is small enough to limit the influence of post-response activity and early enough to allow a good estimate of the true encoding time. Figure 9 shows the average model trajectories for the 30^th-50^th RT percentile generated from different sets of primary parameters; for each set of simulations, one primary parameter was varied across conditions (encoding time, starting point, drift rate, or threshold), while the other primary parameters were held fixed, within-trial noise was fixed at 0.1, and stochastic parameters were fixed at zero. In each case, the model dynamics qualitatively reflect the primary parameter that was varied. We applied this approach to a broad range of randomly sampled parameter sets that included within trial noise (s = 0.1; see Methods), and found that it captured variation in primary parameters reasonably well even with the inclusion of within-trial noise (Figure 10). Other solutions such as examining the full distribution onset, growth rate, baseline, and threshold across all RT bins or developing alternative measures of neural dynamics may work as well. The critical point is that the link between model parameters and neural dynamics is not assumed, but is directly tested through analysis of model dynamics.

Figure 9.

Averaging model trajectories for the 30^th to 50^th percentile of the RT distribution produces qualitative changes in dynamics that match model parameters. For each set of simulations one primary parameter was varied (rows) while the rest were held constant. All stochastic parameters were fixed at zero and within-trial noise was set to 0.1.

Figure 10.

Measures of model dynamics can track changes in primary parameters when model trajectories are averaged for the 30^th to 50^th percentile of the RT distributions. Primary parameters were randomly sampled from a range of values (see Simulation Methods), stochastic parameters were fixed at zero, and within-trial noise was fixed at 0.1. Panels show the mean and standard deviation for each measure of model dynamics (rows) grouped into deciles by primary parameter values (columns). Each measure of model dynamics captures variation in one primary parameter when only a restricted range of RTs is averaged. Note that it was possible for our inclusion criteria to induce spurious correlations between parameters and measure of model dynamics; for example, because the starting point must be lower than the threshold, increasing the threshold could produce increased baseline simply because the possible range of starting points increased. To eliminate these spurious correlations, we used a limited range of parameter values for starting point and threshold.

General Discussion

The discovery that certain neural signals represent accumulated evidence has raised exciting new possibilities to constrain model parameters with measures of neural dynamics and predict neural dynamics based on parameters values fitted to behavior. To understand the relationship between accumulator model parameters and neural dynamics, we examined the relationship between accumulator model parameters and model dynamics. We systematically varied model parameter values over large ranges and quantified model dynamics by adapting established neurophysiological methods. Our simulations revealed both advantages and potential pitfalls of directly relating accumulator model parameters to measured neural dynamics. On the one hand, our results provide a simple example of using neural dynamics to distinguish alternative models that make identical behavioral predictions. On the other hand, our results show how within-trial noise and trial averaging can potentially obscure the relationship between model parameters and dynamics in misleading ways. In the following discussion, we review advantages and challenges of analyzing neural dynamics as a model selection tool. Methods that attempt to simultaneously explain both behavioral and neural data provide the strongest constraints on inferences about underlying mechanisms. We emphasize that, when possible, model and neural dynamics should be directly compared to avoid incorrect assumptions about links between measures of neural dynamics and model parameters.

Potential Pitfalls of Inferring Parameters from Model and Neural Dynamics

The discoveries that link accumulator models and neural dynamics (Hanes & Schall, 1996; Roitman & Shadlen, 2002) might seems to suggest that we can bypass fitting models to behavior altogether and simply “read out” the underlying parameters from the neural dynamics. Our simulations highlight some of the significant dangers of inferring parameters from dynamics in the absence of behavioral model fitting.

Our simulations show that the onset of neural activity does not necessarily reflect the end of encoding time, a component of the T_er parameter in accumulator models; introducing variability in the drift rate, starting point, and threshold parameters all manifest as variability in measured onset. This result has important implications for the interpretation of neural signals in decision-making experiments. During a variety of perceptual decision-making tasks, the onset time when firing rate increases correlates strongly with stimulus strength and RT in pre-frontal cortex (DiCarlo & Maunsell, 2005; Pouget et al., 2011; Purcell et al., 2010; Purcell, Schall, et al., 2012; Woodman et al., 2008) and superior colliculus (Ratcliff et al., 2003; Ratcliff et al., 2007). Similar increases in the onset time with RT are sometimes observed in parietal neurons (Cook & Maunsell, 2002). It is tempting to interpret these increases in the onset activity as delays in the start of evidence accumulation, but our results indicate that this may simply reflect a signature of noisy evidence accumulation.

The observation that the onset of neural activity may vary without explicit variation in encoding time has important implications for inferences about the nature of information flow across processing stages (Meyer, Osman, Irwin, & Yantis, 1988; Miller, 1982). Previous studies have used the onset of motor-related neural signals as a proxy for the start of a discrete stage of motor processing (Miller, 1998; Miller, Ulrich, & Rinkenauer, 1999; Osman et al., 2000; Smulders, Kok, Kenemans, & Bashore, 1995; Woodman et al., 2008). Experimental manipulations that prolong onset time have been interpreted as delays in the start of motor processing. Our simulations show that the measured onset of neural responses may be substantially different from the actual start time of evidence accumulation. Even a continuous flow of information to the accumulator network can produce correlations between the onset and RT or variation of onset with stimulus strength.

We found that the relationship between the encoding time parameter and the measured onset depends critically on SNR. If the SNR is low (roughly less than 5; see Figure 6), then one can expect reasonably strong correlations between onset and RT even in the absence of any explicit encoding time variability. SNR is tightly linked to stimulus strength, which is often manipulated in psychophysical studies (e.g., Palmer et al., 2005), meaning that the relationship between model parameters and dynamics may differ across conditions of the same experiment. Strong correlations between onset and RT may be observed for weaker, but not stronger stimuli, even with a fixed unvarying encoding time (Figure 8). In the absence of behavioral model fits, changes in the onset time alone are not conclusively diagnostic about the underlying cause of behavioral variability.

Our simulations highlight how methods of binning and averaging over trials can dramatically influence the resulting form of the measured dynamics. Simply averaging trajectories for all trials, as is common in many neural analyses, produces average trajectories that are highly dependent on assumptions about the form of post-response activity. Unless the behavioral state of the subject after the response is carefully controlled during an experiment and the model makes clear predictions about the form of post-response dynamics (e.g., Moran et al., 2015; Pleskac & Busemeyer, 2010; Resulaj et al., 2009), then it is risky to draw strong conclusions that depend heavily on unchecked assumptions about post-response activity. Binning and averaging by small groups of RTs before applying measures of dynamics is one way to exclude post-response activity, but simply averaging over all RT bins can produce misleading results because the relationship between the measured onset and RT changes with SNR (Figures 6A and 8). One possible solution is to examine changes in measures of model dynamics over the full distribution of RT bins; for example, as drift rate increases, how does the measured onset change for every single RT bin? However, we found that simpler method may suffice. Binning over a limited subset of trials that produced fast to moderate RTs (~30^th to 50^th percentile) seems to provide a simple and reliable method for tracking across-condition parameter variability, at least in the subset of model architectures and model parameterizations that we explored here.

Of course, the analyses of model and neural dynamics that we applied here are not exhaustive. We selected four measures (onset, growth rate, baseline, and activity at RT) to inform the interpretation of past and future neurophysiological studies that used similar approaches (e.g., Woodman et al., 2008). Alternative methods for quantifying dynamics could potentially provide additional insights about the underlying parameters. For example, although our analyses focused specifically on analyses of mean activity, the trial-to-trial variance and covariance of neural trajectories over time can reveal important insights about the underlying parameters (Churchland et al., 2011). For example, Churchland et al. (2011) showed that the trial-to-trial variance of LIP neurons exhibited signatures of noisy evidence accumulation. Similar responses have been observed in FEF movement neurons (Purcell, Heitz, Cohen, & Schall, 2012).

Neural Dynamics as a Model Selection Tool

Our simulations demonstrate a simple illustration of how neural dynamics might be used to resolve behavioral model mimicry. In many accumulator model frameworks, variation in the starting point and variation in threshold make indistinguishable predictions about variation in behavior because they both change the total evidence that must be accumulated for a choice. But these parameters have very different implications for the underlying neural mechanisms. For example, adjustments in neural activity at the time of RT are associated with changes in the strength of cortico-striatal connections (Lo & Wang, 2006), whereas adjustments of the baseline may be implemented through background excitation and inhibition (Lo, Wang, & Wang, 2015). Although the measured onset time and growth rate of neural dynamics appear to be less diagnostic about specific underlying parameters, variation in measured neural baseline and neural activity at RT can be associated more directly with variation in the starting point and threshold parameters of accumulator models. Examining neural dynamics can reveal underlying mechanisms that can be invisible based on fits of models to behavioral data alone.

A number of recent studies have provided further illustrations of the power of neural dynamics as a model selection tool in diverse experimental paradigms. For example, behavior in stop-signal tasks, in which subjects must withhold a preplanned response following an infrequent cue to stop, have traditionally been explained as a race between independent processes representing going and stopping (Logan & Cowan, 1984). Boucher et al. (2007) implemented the stop and go processes as either independent racing accumulators or interactive racing accumulators that inhibit one another (Boucher et al., 2007). Both models explained behavior equally well, but the interactive model provided a better account of neural responses from FEF movement neurons. More recently, Logan et al. (2015) showed that models in which stopping inhibition is not direct, but instead acts as a gating mechanism on the input to the go unit, provide an even better account of the neural dynamics (Logan, Yamaguchi, Schall, & Palmeri, 2015).

As another example, in the domain of visual search, Purcell et al. (2010, 2012) evaluated different accumulator models based on their ability to explain not only behavior (RT and accuracy), but also the dynamics of FEF movement neurons thought to implement the evidence accumulation process for this task. Models in which evidence was not integrated at all or integrated perfectly could be ruled out based on poor fits to behavior alone. Models that assumed leaky evidence accumulation provided an excellent account of behavior, but failed to explain the observed neural dynamics. The failure of the leaky models motivated a novel gating mechanism in which evidence accumulation begins only after the evidence exceeds some constant level. In addition to providing an excellent fit to behavior, the gated model also predicted the observed neural dynamics.

Analyses of neural dynamics have also revealed crucial insights about the mechanisms underlying strategic adjustments of speed and accuracy. Traditionally, accumulator models explain tradeoffs between speed and accuracy through adjustments in the model threshold (e.g., Brown & Heathcote, 2008; Palmer et al., 2005; Wagenmakers et al., 2008). Surprisingly, recent experiments in which monkeys were trained to emphasize speed or accuracy in different blocks did not show the expected changes in the firing rates of LIP and FEF neurons around the time of the response (Hanks, Kiani, & Shadlen, 2014; Heitz & Schall, 2012). Instead, neurons in both areas showed changes in the baseline activity and in the dynamics of the evidence accumulation process; when speed was emphasized, the growth rate of neural responses was stronger irrespective of the subject's choice. One way to reconcile the model and the FEF data was to extend the model with a second stage of accumulation (Heitz & Schall, 2012). Alternatively, the LIP data were explained by assuming that adjustments in threshold are implemented through an evidence-independent urgency signal (Churchland et al., 2008; Hanks et al., 2014; Thura et al., 2014). Increasing urgency causes responses to rise faster irrespective of incoming evidence, leading to faster but more error-prone responses, whereas decreasing urgency allows more time for evidence accumulation, leading to slower and more accurate responses. Similar analyses of neural dynamics suggest that urgency signals may implement adjustments of response threshold following errors (Purcell & Kiani, 2016). Recent behavioral modeling suggests that the strength of urgency may vary considerably over subjects and experiments (Hawkins, Forstmann, Wagenmakers, Ratcliff, & Brown, 2015), but this model mechanism currently provides the most parsimonious explanation for both behavioral and neural data.

Modeling Behavioral and Neural Dynamics

While neural dynamics can provide a powerful tool to select among competing models, analysis of dynamics alone can produce misleading inferences about the underlying mechanisms. We recommend a modeling approach in which both behavioral and neural data are jointly considered; several approaches to doing so have been implemented (Turner et al., in press).

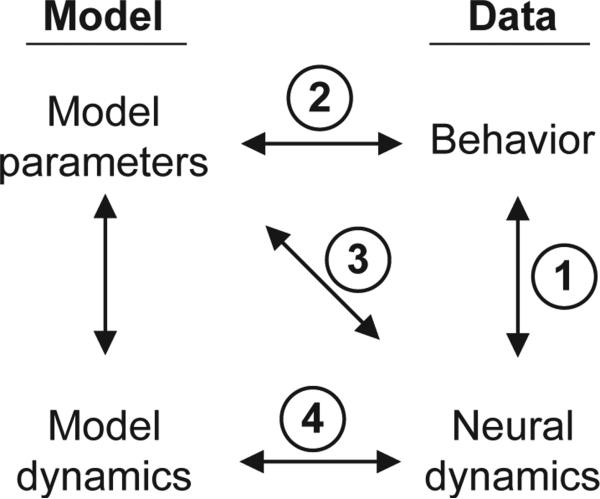
Figure 11 summarizes some different approaches that have been used to understand behavioral and neural data. Traditional neurophysiological approaches involve directly analyzing neural dynamics to infer the mechanisms that give rise to behavior (arrow 1). For examples, correlations between neural responses and behavior are taken as evidence that the neural population is somehow involved in generating the behavior; direct manipulations such as electrical microstimulation and pharmacological inactivation can help infer a causal role of a particular brain region in the behavior (Fetsch, Kiani, Newsome, & Shadlen, 2014; Gold & Shadlen, 2000; Hanks, Ditterich, & Shadlen, 2006; Monosov & Thompson, 2009; Stuphorn & Schall, 2006). However, without the aid of formal models, the precise mechanisms linking neural responses to observed behavior often remains murky.

Figure 11.

Illustration of different approaches to relating cognitive models, behavior, and neural dynamics. We assume that the behavior and neural dynamics were observed simultaneously in the context of some task, and neural dynamics may be analyzed in relation to task events or observed behavior. Arrow 1: Traditional neurophysiological approaches relate neural dynamics directly to behavior (e.g., how do neural responses change under task conditions in which choices are more or less accurate?). Arrow 2: Traditional cognitive modeling infers model parameters based on fits to behavior (e.g., how do model parameters change when fitted to behavioral from conditions associated with higher or lower accuracy?). Arrow 3: One approach to model-based cognitive neuroscience relates model parameters directly to observed neural dynamics (e.g., how do BOLD responses in a particular brain region correlate with model parameters fitted to behavior?). Arrow 4: An alternative approach to model-based cognitive neuroscience involves a direct comparisons between model dynamics and neural dynamics (e.g., how well does the model replicate both behavioral and neural dynamics across different conditions?).

Traditional cognitive modeling involves making inferences about mechanisms by optimizing model parameters to maximize the correspondence between predicted and observed behavior (arrow 2 in Figure 11). This approach makes assumptions about the underlying cognitive mechanisms explicit and facilitates rigorous comparison of alternative models through evaluation of quantitative predictions. In the absence of neural data, however, these models make no explicit predictions for where and how these cognitive mechanisms are implemented in the brain. Additionally, as noted above, behavior alone may be inadequate to distinguish competing models.

Model-based cognitive neuroscience aims to combine the power of cognitive modeling with measures of neural activity. One approach involves directly relating model parameter values to observed neural dynamics (arrow 3 in Figure 11). A researcher might first fit a model to behavioral data and then identify correlations between fitted model parameters values and observed neural measures (Mulder, van Maanen, & Forstmann, 2014). For example, subject-to-subject variation in the magnitude of the response threshold parameter is correlated with variation in the strength of BOLD responses in striatum and pre-supplementary motor area (Forstmann et al., 2008). This approach can identify particular brain areas that are somehow related to the mechanisms controlled by model parameters (O’Reilly & Mars, 2011), providing a useful tool for interpreting neural data.

A potentially more powerful approach is to simultaneously fit the neural and behavioral data by jointly maximizing the likelihood of behavior and dynamics. For example, Turner and colleagues developed a method to simultaneously fit model parameters to behavior while also constraining parameter estimates based on patterns of BOLD activation in cortex (Turner et al., 2015). An important advantage of this approach is that it incorporates constraints from the neural data as part of the fitting process, allowing one to identify whether a subset of parameter space can jointly explain both the behavioral and neural data. Still, it is common that the link that is established is one between model parameters and neural measures (arrow 3 in Figure 11).

Our simulations suggest, at least when appropriate forms of neural data are available, that best practices may be to establish links not between model parameters and neural dynamics (arrow 3) but between model dynamics and neural dynamics directly (arrow 4). One example is a “two-stage” approach, in which behavioral data are first fitted and then model dynamics are generated by the best fitting parameters (Boucher et al., 2007; Mazurek et al., 2003; Purcell et al., 2010; Purcell, Schall, et al., 2012; Ratcliff et al., 2007). The key is that rather than directly comparing neural dynamics to the best-fitting model parameters, the neural dynamics are compared to the simulated model dynamics. Simulation methods should be chosen to match the statistical power of the neural analyses; for example, matching the number of simulated and observed trials, matching the simulated and observed firing rates, and simulating spiking noise based on observed model trajectories. Identical measures should then be applied to the model dynamics to allow for a direct comparison to observed neural dynamics. This approach avoids many potential pitfalls highlighted by our simulations; for example, incorrect assumptions about the direct relationships – or lack thereof – between model parameters and neural dynamics. One advantage of this two-stage approach is that the model dynamics represent a true prediction (not a fit) to the neural data. If the same parameter values that maximize the quality of fit to the behavior also provide a good a priori account of the underlying neural dynamics without any additional fitting, this provides compelling validation of the model fits and guards against overfitting.

A complementary approach to link accumulator models to neural data is to replace model mechanisms specified by free parameters with actual neural data. Purcell et al. (2010; 2012) used the observed firing rates of visually-responsive FEF neurons during a visual search task as the input to a network of model accumulators in place of the mechanisms instantiated via the encoding time, starting point, and drift rate parameter. This neurally-constrained model provided a good fit to behavior, indicating that variability in the responses of the visually-responsive neurons were sufficient to explain behavioral variability for this task. Note that this approach is distinct from the method described above because there is no comparison of neural and model dynamics; instead, the observed neural dynamics replace the parameterized model mechanisms.

Complementing Purcell et al. (2010, 2012), Cassey and colleagues (Cassey et al., in press) recently developed a joint modeling approach that simultaneously fitted the neural dynamics and used the model specification of those dynamics to drive an accumulation of evidence. With this approach, the influence of different parameters on the expected dynamics are directly incorporated into the fitting process, obviating the need for proposing and validating connections between specific measures of dynamics and model parameters.

Linking propositions

We have primarily made connections to work using single-unit recordings from individual neurons in awake and behaving non-human primates because these responses have been most strongly identified with a representation of the evidence accumulation process. To date, most neurophysiological studies of this type are limited to recordings within a single region of the brain, raising the question of whether it is valid to draw conclusions about the decision-making process based on analyses of a limited population of cells. It is highly doubtful that any one region implements the evidence accumulation process alone. Rather, neurophysiological evidence suggests that the evidence accumulation process is represented by a network of brain regions distributed throughout cortical and subcortical regions (Schall, 2013; Shadlen & Kiani, 2013). When different regions of the network are observed during the same decision making tasks, neural responses exhibit remarkably similar dynamics in relation to common task events and behaviors. For example, during a visual search task with eye movement responses, visual and motor neurons distributed throughout parietal cortex (Thomas & Pare, 2007), prefrontal cortex (Bichot & Schall, 1999; Thompson, Hanes, Bichot, & Schall, 1996), and superior colliculus (McPeek & Keller, 2002; White & Munoz, 2011) exhibit response properties consistent with a representation of perceptual evidence or the accumulation of evidence to a response threshold. During a motion-discrimination task, neurons throughout the same network of structures exhibit dynamics consistent with gradual accumulation of sensory evidence to a threshold (Ding & Gold, 2012; Horwitz & Newsome, 1999; Kim & Shadlen, 1999; Purcell & Kiani, 2016; Roitman & Shadlen, 2002). Therefore, while the strongest conclusion about the decision making process would need to include recordings from multiple brain regions, even recordings from a single regions can provide critical insights about activity that is likely taking place throughout the network.

Other studies have suggested that a representation of evidence accumulation may be monitored noninvasively through extracranial electroencephalogram (EEG). During certain perceptual decisions, extracranial voltage potentials can be analyzed to extract an evolving signal that demonstrates dynamics consistent with evidence accumulation (Kelly & O'Connell, 2013; O'Connell, Dockree, & Kelly, 2012). The lateralized readiness potential, an event-related potential associated with motor preparation, also exhibits dynamics similar to accumulation to a threshold (De Jong, Coles, Logan, & Gratton, 1990; Gratton, Coles, Sirevaag, Eriksen, & Donchin, 1988; Schurger, Sitt, & Dehaene, 2012). Our conclusions regarding the relationship between model and neural dynamics should apply equally to these higher-level representations of the decision process. The major limitation of larger-scale representations of evidence accumulation is that they will reflect the combined activity of cortical areas not directly involved in evidence accumulation as well as aggregating over neurons representing distinct choices. It is not clear how these additional signals might distort the resulting dynamics.

An essential goal for future research is to understand how the representation of evidence in individual neurons scales up to larger populations of neurons within and across multiple areas. Going from individual neurons to larger populations raises important questions about how evidence accumulation is coordinated over neurons and how these different neurons reach a consensus to terminate the decision process. Spiking neural network models have demonstrated how large pools of neurons with recurrent and competitive dynamics could implement the evidence accumulation process proposed by these models (Furman & Wang, 2008; Wang, 2002), but the complexity of these models can make it difficult to contrast competing hypotheses about neuronal cooperation and decision termination. To address this problem, Zandbelt et al. (2014) used simulations to explore how large ensembles of redundant accumulators (multiple accumulators representing a single choice) could produce both RT distributions and neural dynamics consistent with single-unit recordings. They found that a very broad range of mechanisms by which the accumulators coordinate and terminate their response could produce RTs and neural responses consistent with observed behavioral and neural data. On the one hand, these results indicate that redundant stochastic accumulators represent a very robust method to produce realistic RT distributions and single-unit activity. On the other hand, these results suggest that single-unit recordings and behavior alone are not adequate to identify the precise mechanisms by which large networks of accumulators coordinate and terminate upon a choice.

Distinguishing alternative mechanisms for evidence accumulation in large populations requires simultaneous recordings from many individual neurons during ongoing decision making. Exciting new technological advances in multielectrode arrays have made it more common to record simultaneously from tens to hundreds of neurons in awake behaving animals (Churchland, Yu, Sahani, & Shenoy, 2007). Thus far, these techniques have primarily been applied to the study of motor control (e.g., Churchland et al., 2012) and neural prosthetics (e.g., Sadtler et al., 2014), but are just starting to be applied in awake behaving animals during more complex decision-making tasks (Cohen & Maunsell, 2009; Kiani et al., 2014). In one notable example, Kiani et al. (2014) trained a linear classifier to decode animal's choices from a large population of ~90 neurons recorded simultaneously from dorsolateral prefrontal cortex while animals performed a motion direction discrimination task. The accuracy of the classifier gradually increased throughout the trial at a rate that depended on the strength of sensory evidence, consistent with a population-wide representation of evidence accumulation. The population activity revealed “changes of mind” in which the accumulated evidence flipped from favoring one choice to another, consistent with predictions of an existing behavioral model (Resulaj et al., 2009). As more large-scale data sets become available, these approaches can be further extended to constrain potential sources of behavioral variability at the level of individual trials.

Conclusions

Neural dynamics have proven to be a powerful tool to evaluate alternative hypotheses about decision making mechanisms, but the connections between model parameters and neural dynamics often go untested. We systematically varied model parameter values and applied established neurophysiological measures to model dynamics to test for selective influences of model parameters on expected neural dynamics. In some cases, model parameters could be successfully inferred from model dynamics, but in other cases measures of dynamics alone could provide a misleading picture about the underlying sources of behavioral variability. Altogether, we argue for a modeling approach in which both behavioral and neural data are jointly considered, and model dynamics are directly compared to neural dynamics.

Highlights.

• Neural analyses are used to quantify changes in accumulator model dynamics.

• Accumulator model dynamics distinguish models that behavior alone cannot.

• However, analysis of dynamics alone cannot pinpoint underlying model parameters.

• Joint consideration of behavior and neural dynamics provides maximal constraint.