Classification of biodegradable materials using QSAR modeling with uncertainty estimation

Abstract

The ability to determine the biodegradability of chemicals without resorting to expensive tests is ecologically and economically desirable. Models based on quantitative structure-activity relations (QSAR) provide some promise in this direction. However, QSAR models in the literature rarely provide uncertainty estimates in more detail than aggregated statistics such as the sensitivity and specificity of the model’s predictions. Almost never is there a means of assessing the uncertainty in an individual prediction. Without an uncertainty estimate, it is impossible to assess the trustworthiness of any particular prediction, which leaves the model with a low utility for regulatory purposes. In the present work, a QSAR model with uncertainty estimates is used to predict biodegradability for a set of substances from a publicly available data set. Separation was performed using a partial least squares discriminant analysis model, and the uncertainty was estimated using bootstrapping. The uncertainty prediction allows for confidence intervals to be assigned to any of the model’s predictions, allowing for a more complete assessment of the model that would be possible through a traditional statistical analysis. The results presented here are broadly applicable to other areas of modeling as well, because the calculation of the uncertainty will clearly demonstrate where additional tests are needed.

1 Introduction

In recent years, several countries around the world have recognized the need to reduce the amount of non-biodegradable materials used to intensify measures for the environment and encourage the recycling of materials. An example was the signing of the Treaty of Paris by 175 countries in April 2016 for the reduction of carbon dioxide emissions and other greenhouse gases. By this initiative, countries compromise to establish their own targets for the reduction of greenhouse gases which implies indirectly the reduction of the consumption of non-biodegradable materials. This is because the decrease provides a smaller amount of material sent to landfills, which reduces the production of greenhouse gases [1–5]. Another factor that contributes to it is the increasing use of biodegradable materials due to the results of research related to discovery and production of new materials [1, 6–11], as well as the use of alternative non-toxic and biodegradable source of energy as biodiesel [12–15].

Several countries in the world have agencies and regulations responsible for the use of chemical substances and evaluation of their potential impacts on both human health and the environment, including the Environmental Protection Agency (EPA), National Health Surveillance Agency (ANVISA), and the Registration, Evaluation, Authorisation and Restriction of Chemicals (REACH). REACH, a regulation of the European Chemicals Agency of the European Union, is particularly notable because it promotes alternative methods for the hazard assessment of substances in order to reduce the number of tests on animals. Such alternative methods include the biodegradability predictions of chemicals from quantitative structure-activity relationship (QSAR) models.

Biodegradability is fundamental to the assessment of environmental exposure and risk from chemical products. QSAR models can be used to pursue both regulatory and chemical design goals. In the literature, various QSAR models have been investigated that are intended to predict the ready biodegradability of different substances [16–22]. Other authors have examined different methods of selecting molecular descriptors [23, 24] and the use of different machine learning algorithms [22, 25]. In all cases, the model’s performance was quantified using aggregate statistics such as sensitivity, specificity, and correlation coefficients [26]. However, it is rarely reported by what method, if indeed at all, uncertainty in an individual model output is quantified. Uncertainty in this context means the range of values that can be reasonably attributed to an analytical result, considering the level of confidence [27–30]. Without an estimate of the individual prediction uncertainty, the results of these models are not complete.

The objective of this work is to calculate the uncertainty of the predictions of the classification of a QSAR model using the residual bootstrap method to predict the ready biodegradability of chemicals using literature data [31]. The uncertainty then provides an estimate of the reliability of the PLS model’s predictions.

2 Theoretical Background

2.1 Partial least squares discriminant analysis estimation of a QSAR model

Partial least squares regression discriminant (PLS-DA) is a classification method in multivariate analyses that combines the properties of partial least squares regression with the discrimination power of classification techniques [32]. This method searches for latent variables that are a linear combination of the independent variables X which have the maximum covariance with the dependent variables Y [33–37].

The general underlying PLS-DA model is given by

$$\mathbf{X}=\mathbf{T}{\mathbf{P}}^{\mathrm{T}}+\mathbf{E},$$ (1)

and

$$\mathbf{Y}=\mathbf{U}{\mathbf{Q}}^{\mathrm{T}}+\mathbf{F},$$ (2)

where X is the matrix of independent variables, in this case the molecular descriptors; Y is the matrix of dependent variables, which has values of either 0 or 1 to indicate to which class the corresponding sample belongs. T and U are orthogonal score matrices of X and Y respectively. P and Q are the corresponding loadings matrices that describe the latent variables, and E and F are the residual terms.

The T scores are orthogonal and estimated as a linear combination of the X variables [38, 39] with weighting coefficients W* which are obtained by successive optimizations. Then, the T matrix can be determined using

$$\mathbf{T}={\mathbf{XW}}^{\ast }.$$ (3)

The T scores are then a set of latent variables within X that are good predictors of Y, assuming that Y and X are well-described by the same latent variables. Using Equation (3), Equation (2) can be rewritten as

$$\mathbf{Y}={\mathbf{XW}}^{\ast }{\mathbf{Q}}^{\mathrm{T}}+\mathbf{F}=\mathbf{X}\mathbf{\beta }+\mathbf{F}.$$ (4)

A full description of the PLS-DA regression is given by Wold et al. [39].

The classification values obtained by the PLS-DA model are real numbers given by Eq. 4, not reading exactly 0 or 1. The results are scattered in a range of values for each class. Thus, it is necessary to establish a threshold value, y_bound, to define the class limits. There are several ways to set the threshold, for example, such as Bayes’ theorem [40], receiver-operating characteristic (ROC) curves [41], threshold-based classification rule [42, 43] or by establishing confidence limits for each sample classified. These confidence intervals can be calculated by re-sampling techniques, such as bootstrap.

2.2 Bootstrap-based uncertainty estimation

Bootstrap is a test based random sampling with replacement [44, 45] which allows confidence intervals to be placed on a model’s predictions based on uncertainties in the input data. In this case, it provides confidence interval of the classification results of substances in a given class.

In this paper, residual bootstrap was used to calculate the uncertainties in the biodegradability prediction of the PLS-DA model. The procedure was originally presented by Almeida et al. [33] and will be briefly described.

According to Almeida et al., [33] it is necessary to calculate the residuals of the PLS-DA model using

$${\mathbf{F}}^{\ast }=\frac{\mathbf{F}}{\sqrt{1-D_f/N}},$$ (5)

where F* is the weighted residual of the model, F is the residual term from Equation (2) given by F = Y − Xβ, D_f is the number of pseudo degrees of freedom (see [46]), and N is the number of calibration samples (substances, in this case).

Once the residual calculations are complete, the bootstrapping procedure is as follows. First, the substance a whose uncertainty is being calculated is removed from the model. A new dependent variable matrix Y* is then generated by replacing the remaining Y values with the model predicted Y_PLSDA = Xβ values. The residuals are assumed to be representative of the uncertainty in the model, and so a new random residual vector ${\mathbf{F}}_{\text{boot}}^{\ast }$ is generated by bootstrapping. The Y_PLSDA values are perturbed by adding the bootstrapped residual F*,

$${\mathbf{Y}}^{\ast }={\mathbf{Y}}_{\text{PLSDA}}+{\mathbf{F}}_{\text{boot}}^{\ast }.$$ (6)

Then, a new PLS-DA model can be calculated from Y*, with a new corresponding regression coefficient (β*) and new predictions ${\widehat{\mathbf{Y}}}^{\ast }={\mathbf{X}\mathbf{\beta }}^{\ast }$. The confidence interval for substance a is estimated based on the difference between the bootstrap predicted values for substance a, ${\widehat{Y}}_a={\mathbf{X}}_a{\mathbf{\beta }}^{\ast }$, and the PLS predicted value, Y_a,PLSDA according to

$${\widehat{F}}_a^{\ast }=Y_{a,\text{PLSDA}}-{\widehat{Y}}_a.$$ (7)

In the case of a 95% confidence interval, the lower bound, denoted c_low, is the 2.5 percentile of ${\widehat{F}}_a^{\ast }$ and the upper bound, c_up, is the 97.5 percentile. More details about bootstrap can be found in the literature [47].

2.3 Uncertainty application and misclassification probability

Calculating the misclassification probability proceeds as follows. First, the classifications Y_a,pred are treated as being normally distributed random variables with mean equal to Y_a,PLSDA and standard deviation ${\sigma }_a=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.\left(c_{\text{low}}-c_{\text{up}}\right)$. The confidence intervals here are not symmetric but they are close enough for this to be a reasonable approximation. As stated earlier, a given sample a is identified as class 0 if its Y_a,PLSDA value is less than the threshold value y_bound. The probability that sample a is class 0, denoted P₀, is equivalent to the probability that Y_a,pred is less than y_bound. That probability is then given by the cumulative distribution function for the normal distribution, that is,

$$P_0=P\left(Y_{a,\text{pred}}\le y_{\text{bound}}\right)=\frac{1}{2}\left[1+\text{erf}\left(\frac{y_{\text{bound}}-Y_{a,\text{PLSDA}}}{\sqrt{2}{\sigma }_a}\right)\right].$$ (8)

Likewise, the probability that sample a is class 1, denoted P₁, is equal to 1 − P₀. The probability of a misclassification, P_misclass, can then be determined based on the actual classification of the sample, Y_a, using

$$P_{\text{misclass}}=P_{1-Y_a}.$$ (9)

The misclassification probabilities can then be used to assess the trustworthiness of the model. If a model has large P_misclass for the misidentified samples, then using the model would mean that we would likely make incorrect claims with a high degree of false assurance. Such a model would not be very useful in a regulatory context. Likewise, if the model has large P_misclass for the correctly-identified samples, our correct claims would be assigned a low degree of assurance, which is also undesirable for regulation.

3 Implementation

3.1 Data Sets

In the present work, QSAR models with estimation of uncertainty were explored to discriminate chemicals into two classes: RB (readily biodegradable) and NRB (not readily biodegradable). The data used in this study can be obtained from the publicly-available QSAR biodegradation data set described by Mansouri, et al. [31]. A version of the data set is included in the supplementary information.

The data are of three sets of substances: 837 substances used for the calibration stage (284 RB and 553 NRB), 218 substances for the validation stage (72 RB and 146 NRB) and 670 substances for the external validation stage (479 RB and 191 NRB). All the data have 41 molecular descriptors. According to Mansouri, et al. [31], using only 23 descriptors among the 41 descriptors it is possible to improve the performance of the model. Thus, only these 23 recommended molecular descriptors were used to generate the model (Table 1).

Table 1.

List of molecular descriptors used for the QSAR PLS-DA Model

Symbol	Description	DRAGON block
B01[C-Br]	presence/absence of C–Br at topological distance 1	2D atom pairs
B03[C-Cl]	presence/absence of C–Cl at topological distance 3	2D atom pairs
B04[C-Br]	presence/absence of C–Br at topological distance 4	2D atom pairs
C%	percentage of C atoms	constitutional indices
F03[C-O]	frequency of C–O at topological distance 3	2D atom pairs
F04[C-N]	frequency of C–N at topological distance 4	2D atom pairs
HyWi_B(m)	hyper-Wiener-like index (log function) from Burden matrix weighted by mass	2D matrix-based
LOC	lopping centric index	topological indices
Me	mean atomic Sanderson electronegativity (scaled on Carbon atom)	constitutional indices
Mi	mean first ionization potential (scaled on carbon atom)	constitutional indices
N-073	Ar2NH/Ar3N/Ar2N–Al/R⋯N⋯R	atom centered fragments
nArNO2	number of nitro groups (aromatic)	functional group counts
nCIR	number of circuits	ring descriptors
nCRX3	number of CRX3	functional group counts
nN-N	number of N hydrazines	functional group counts
nO	number of oxygen atoms	constitutional indices
Psi_i_1d	intrinsic state pseudoconnectivity index–type 1d	topological indices
SdO	sum of dO E-states	atom-type E-state indices
SM6_L	spectral moment of order 6 from Laplace matrix	2D matrix-based
SpMax_A	leading eigenvalue from adjacency matrix (Lovasz–Pelikan index)	2D matrix-based
SpMax_L	leading eigenvalue from Laplace matrix	2D matrix-based
SpPosA_B(p)	normalized spectral positive sum from Burden matrix weighted by polarizability	2D matrix-based
TI2_L	second Mohar index from Laplace matrix	2D matrix-based

3.2 Procedure and Software

The PLS-DA models from PLS Toolbox 8.0 and from scikit-learn 0.17 were used to analyze the data. Uncertainty in the PLS model predictions was estimated by the residual bootstrap technique. 10⁴ bootstrap evaluations were used and the analysis was repeated 15 times to ensure the reliability of the bootstrap results.

A dummy matrix Y was created with 0 for readily biodegradable and 1 for not readily biodegradable substances. The optimal number of latent variables for the PLS-DA model was determined by cross-validation using the leave-one-out criterion [40] in order to avoid overfitting or lack of fit. The threshold for the class was calculated using the plsthres function from PLS Toolbox [40] and a similar function in Python. The confidence interval estimations for each sample were obtained with residual bootstrap, according Almeida et al. [33] and as described in Section 2.

The structural data were preprocessed through autoscaling [40], because the units on each descriptor are different and have different ranges of variation. Calculations were performed in Anaconda Python 4.0.0 and in Matlab R2015b. The results presented here are from Anaconda, but the Matlab results were largely similar. The Python code to conduct the analysis and generate the figures has been included in the supplementary information.

4 Results and Discussion

The performance of the PLS-DA model was rated using the following standard statistical parameters (Table 2): root mean squared error (RMSE), Pearson’s correlation coefficient, sensitivity (percentage of true positives, i.e., samples were correctly assigned to the RB class), specificity (percentage of true negatives, i.e., samples that were correctly assigned to the NRB class) and misclassification error, ME, defined as

$$ME=\frac{Y_a-Y_{a,\text{PLSDA}}}{Y_a}.$$ (10)

where Y_a,PLSDA represents the PLS-DA predicted class observed, and Y_a denotes the reference class.

Table 2.

Statistical metrics for the QSAR PLS-DA model

	CALIBRATION		VALIDATION		EXTERNAL VALIDATION
CLASS	RB	NRB	RB	NRB	RB	NRB
N	284	553	72	146	479	191
NMISCLASS	34	93	12	19	69	38
ME (%)	11.97	16.81	16.67	13.01	14.405	19.89
TP	0.88028	0.83183	0.8333	0.86986	0.80105	0.85595
FP	0.16817	0.11972	0.13014	0.16667	0.14405	0.19895
TN	0.83183	0.88028	0.86986	0.83333	0.85595	0.80105
FN	0.11972	0.16817	0.16667	0.13014	0.19895	0.14405
SENS	0.880	0.832	0.833	0.870	0.801	0.856
SPEC	0.832	0.880	0.870	0.833	0.856	0.801
R	0.6457		0.6530		0.6063
RMSE	0.361516		0.356293		0.3676

N: number of substances in each class.

N_misclass: number of misclassifed substances.

ME (%): misclassification error;

TP: true positive;

FP: false positive;

TN: true negative;

FN: false negative;

Sens: sensitivity;

Spec: specificity.

R: Pearson’s correlation coefficient for calibration, validation, and external validation.

RMSE: root mean square error for calibration, validation, and external validation.

The model developed can be said that to be accurate, based on the aggregate statistics (Table 2). In particular, it has Pearson’s correlation coefficient values considered high for this dataset (near 0.65) and low error values (represented by RMSE and ME (%) values). The model presented specificity and sensitivity close to 0.8, meaning that the majority of substances were classified according to their correct class.

In addition to the global statistics of the model, we examine the scores and loadings of the PLS-DA model developed (Figure 1). The scores for the first two latent variables of the PLS-DA model show how the calibration and validation sets are separated by the model (Figure 1a) and the loadings shows the influence of each descriptor in the separation of substances (Figure 1b). Most RB substances are in the region of the scores plot where the first and second latent variable are both negative (Figure 1a), while the majority of NRB substances are in other regions. Through the analysis of the graph of loadings plot in Figure 1b, it is possible to explain this separation.

Figure 1.

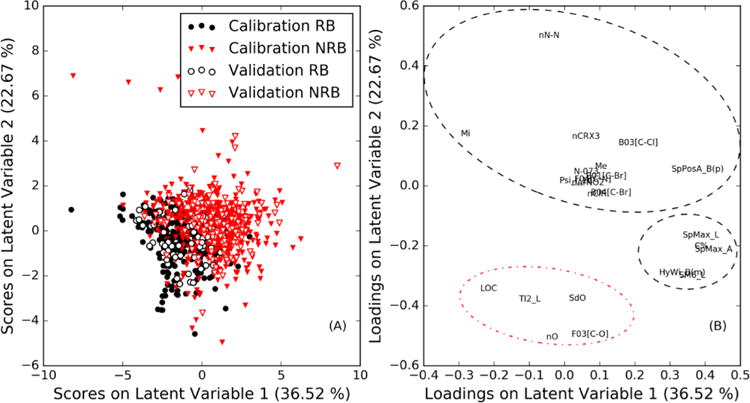
Scores plot (A) and loadings plot (B) with respect to the first and second latent variables of the PLSDA model. Molecular descriptors refer to symbols listed in Table 1. Descriptors responsible for identifying NRB substances are circled with the dashed line and those responsible for identifying RB substances are circles with the dash-dot line.

The molecular descriptors related to the presence of oxygen (nO, F03 [C-O], and SDO), LOC, and TI2_L have negative loadings with respect to the second latent variable (Figure 1b), which corresponds to the scores of the RB substances (Figure 1a). These descriptors are therefore likely responsible for the separation of RB substances. Descriptors involving cycles, halogens, and nitrogen have positive loadings with respect to the second latent variable, and the molecular matrix-based descriptors have loadings above a value of about 0.2 with respect to the first latent variable. These descriptors are therefore likely responsible for the separation of the NRB substances, as the NRB substances have scores similar to these descriptors’ loadings. The results shown here are consistent with the literature [48, 49], where it has been shown that materials which have functional groups with oxygen atoms increase biodegradation. On the other hand, the presence of atoms such as nitrogen and halogens decrease biodegradation.

The scores of the external validation set follow the same trend as the separation found for the set of calibration and validation substances (Figure 2), i.e. the RB substances are mainly located on the negative region of the first and second latent variable.

Figure 2.

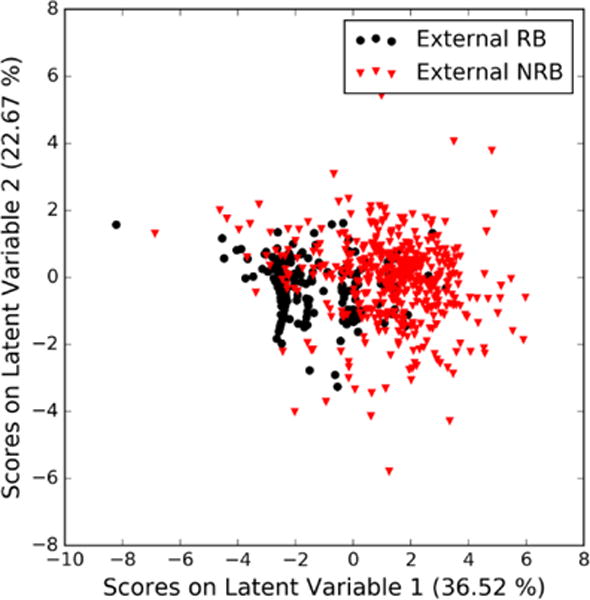
Scores plot with respect to the first and second latent variables of the PLS-DA model for external validation substances.

Through analysis of the detailed results of the PLS-DA model (Figure 1 and Figure 2), it is possible to have a general vision of the performance of the model developed according to Mansouri [31]; however it is not possible to estimate the uncertainty of the classification of each sample individually. That is, most substances were classified according to their respective class and some substances were misclassified, but the reliability of that classification is not known. This is the motivation behind the use of residual bootstrapping to calculate the individual classification uncertainties.

The bootstrapping process allows us to attach classification uncertainties and misclassification probabilities to the PLS-DA model results. The PLS-DA-predicted classifications, Y_PLSDA, can be plotted along with the corresponding confidence intervals and compared the threshold value, y_bound, (Figure 3). In particular, the samples are ordered by the probability of classification as NRB, P₀, (Equation 8). This information is used to calculate the misclassification probabilities P_misclass (Equation 9), plotted with respect to the Y_PLSDA values and also including y_bound (Figure 4). Substances with confidence intervals above y_bound were classified as RB, which corresponds to P₀ << 1. Those substances with confidence intervals below y_bound were classified as NRB, corresponding to 1 − P₀ << 1. Likewise, these are the substances that have P_misclass close to either 0 or 1, because the model allows us to make confident assertions about how these substances should be classified. Those substances with confidence intervals that include y_bound could not be confidently classified in either group. Such substances have a P₀ and therefore a P_misclass approaching 0.5. In these cases, the model does not permit a confident assertion about the classification of the substance. Here we have a new type of results caused by the uncertainty of calculation, that is, substances that are not possible to classify into any of the two classes.

Figure 3.

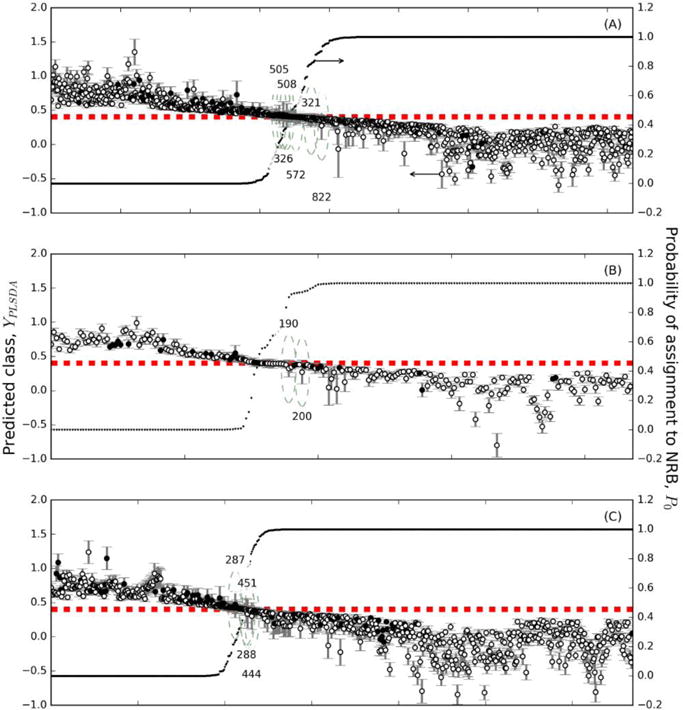
Classes predicted by the PLS-DA model for the calibration, validation, and external validation sets, with confidence intervals for all substances as estimated by the residual bootstrap method. The class boundary y_bound is shown with a dashed line and the probability of assignment to the NRB class is shown with dots. Predicted RB substances have confidence intervals above y_bound and predicted NRB substances have confidence intervals below y_bound. Substances that are correctly classified are shown with open circles and those that are incorrectly classified are shown with filled circles. (A) Calibration substances, (B) Validation substances, and (C) External Validation substances.

Figure 4.

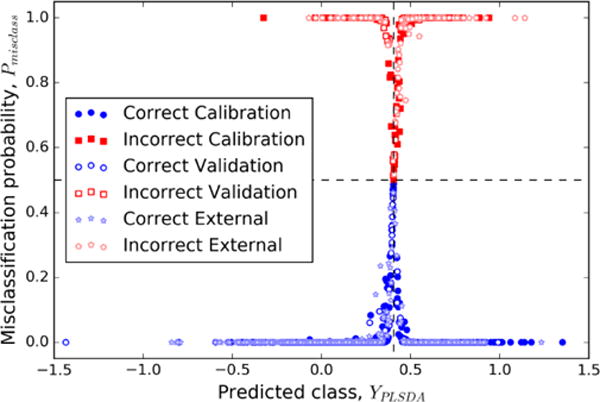
Misclassification probabilities with respect to classifications predicted by the PLS-DA model. The vertical dashed line indicates y_bound, with RB substances to the right and NRB substances to the left. The horizontal dashed line indicates P_misclass = 0.5, corresponding to the boundary between correctly-classified and misclassified substances.

Through the uncertainty calculation, it is possible to question the classification of a particular substance. An example of this is the classification of the substance 200 belonging to the validation set in the NRB class (Figure 3b). If the prediction the uncertainty had not been calculated, this substance would be considered to belong to the NRB class, however due to the greater rigor imposed by the uncertainty calculation, this substance cannot be classified in any of the two classes, because of its uncertainty intersects with limit between the classes.

Similar results can also be seen, for example, with the validation substance 190 (Figure 3b) and the external validation substances 287, 288, 444, and 451 (Figure 3c), which likewise cannot be classified in either of the two classes. This type of result provides a more rigorous classification of substances. Indeed, when the uncertainty of the result of classification is not calculated, there are only two types of classifications possible: correctly classified substances and incorrectly classified substances.

5 Conclusions

A partial least squares discriminant analysis (PLS-DA) model was used to determine the biodegradability of substances based on quantitative structure-activity relations (QSAR). In addition, the classification uncertainty for this model was estimated using bootstrapping. Traditional modeling allows the substances to be distinguished into two classes (readily and not readily biodegradable). Considering the uncertainty in classification allows for a third classification, those substances about which no confident statement can be made.

The uncertainty analysis methodology used here permits a more in-depth evaluation of the QSAR model that would be possible using the standard statistical parameters. A standard analysis would allow some conclusion about the accuracy of the model as a whole, but it would not allow any statement about the reliability of any particular prediction. The uncertainty analysis, by contrast, allows for an evaluation of the precision of the model’s predictions, thereby allowing us to say that the model cannot confidently classify certain substances. Estimating the uncertainty makes it possible to obtain a conclusion that is more reliable and complete. These results highlight the challenges associated with developing reliable and easily applied acceptability criteria for the regulatory use of QSAR models, and it is hoped that a more widespread adoption of uncertainty analysis in these models will help to address some of these challenges.