Atomic Force Microscopy Mechanical Mapping of Micropatterned Cells Shows Adhesion Geometry-Dependent Mechanical Response on Local and Global Scales

Abstract

In multicellular organisms cell shape and organization are dictated by cell-cell or cell-extracellular matrix adhesion interactions. Adhesion complexes crosstalk with the cytoskeleton enabling cells to sense their mechanical environment. Unfortunately, most of cell biology studies, and cell mechanics studies in particular, are conducted on cultured cells adhering to a hard, homogeneous and unconstrained substrate with non-specific adhesion sites – thus far from physiological and reproducible conditions. Here, we grew cells on three different fibronectin patterns with identical overall dimensions but different geometries (▽, T and Y), and investigated their topography and mechanics by atomic force microscopy (AFM). The obtained mechanical maps were reproducible for cells grown on patterns of the same geometry, revealing pattern-specific subcellular differences. We found that local Young’s moduli variations are related to the cell adhesion geometry. Additionally, we detected local changes of cell mechanical properties induced by cytoskeletal drugs. We thus provide a method to quantitatively and systematically investigate cell mechanics and their variations, and present further evidence for a tight relation between cell adhesion and mechanics.

Tissue development and maintenance relies on a continuous interplay between each cell and its environment, through both biochemical signals and physical cues. Through cell-cell and cell-extracellular matrix contacts and interactions, cells are able to sense external forces and geometrical constraints.^1–4 Such signals are fundamental to regulate cellular processes such as differentiation, growth, division and even cell death.^3,5–7 A quantitative characterization of cell mechanics, and elasticity in particular, is thus fundamental to understand how structural and functional integrity of cells and tissues are maintained.^6,8 The major contribution to cell elasticity is provided by the cytoskeleton, and by actin filaments in particular.^9,10 Several techniques have been developed in the last decades to investigate cell mechanics,¹¹ such as magnetic (MT)^12–14 and optical tweezers (OT),^15,16 the optical stretcher (OS),¹⁷ magnetic twisting cytometry (MTC),^12,16,18 particle tracking microrheology (PTM),^19–22 traction force microscopy (TFM),^23,24 real-time deformability cytometry (RTDC),²⁵ atomic force microscopy (AFM)^26,27 and others. Despite its low through-put compared to MT, OS, MTC or RTDC, AFM offers high spatial and force resolution over a wide range of forces and a controlled contact geometry. Additionally, AFM provides simultaneous topographical and mechanical characterization of living cells.^28–30 Unlike MT, MTC or PTM, no probe binding or injection into the sample are needed and measurements are thus performed in physiological conditions. Moreover, AFM is suitable for both adherent and non-adherent cells.^31,32

Improvements of AFM elasticity measurements, better understanding of contact geometry, as well as models accounting for the influence of sample thickness, set the standards in the field of cell mechanics.^33–40 Although quantification of the elasticity by one single value measured in the central region of cells has proven to give useful information, for example in the comparison of cancer and normal cells,^41–43 local elasticity variations could not be detected in such experiments and important information about the mechanics of subcellular structures was missed.⁴⁴ Such information is provided by AFM mechanical mapping, i.e. acquiring force-distance curves on each pixel of the image, thus allowing to identify subcellular regions characterized by specific stiffness associated with local structures.^{29,30,26,45,46} For example, nuclear versus peripheral regions, or actin-rich versus actin-poor areas show differences in elasticity of up to four orders of magnitude, from tens of Pa to some hundreds of kPa.^{19,45,47–49} Moreover, local mechanical characteristics have been attributed to specific cellular structures as tested by drug treatments.^10,48,50,51 These may affect some cell areas (i.e. the structures present in these areas), but leave others unaltered revealing structural and mechanical heterogeneity.

A major problem in the quantification of mechanical maps on cells is the lack of reproducible morphology in standard culture conditions. In fact, culture dishes represent an infinite, homogeneous surface on which cells undergo continuous structural and morphological rearrangements and never attain a defined state. The mechanical properties of cells reflect such variability, preventing a quantitative description of cell mechanics that takes into account subcellular differences in a systematic manner.

By growing cells on adhesive micropatterns, a well-defined and confined environment is imposed that drives cells to adopt regular shapes and cytoskeletal organization.^4,52–55 Such regularity allows us to investigate single cells, but also to average maps acquired on different cells, providing information on constant and reproducible cell features. Moreover, specific cellular processes such as division or migration could be controlled by defining the cell adhesion geometry, mimicking the spatial constraints that a cell is exposed to inside a tissue.^{53,54,56–58} Indeed, the combination of patterning techniques with mechanical mapping has provided new insights in the identification of local mechanical heterogeneities of cells. Park et al. investigated local cell stiffness in relation to the remodeling rate of the CSK actin density and prestress, and provided evidence for a linear correlation between cell stiffness and prestress.⁵⁹ Other groups used AFM mechanical mapping to study cell elasticity dependence on parameters like cell spread area, substrate stiffness or actin distributions.^60,61 Although important findings have been achieved, a systematic method is still lacking which allows identifying preserved mechanical features and their precise location within the cell in relation to the adhesion geometry. The aim of this work was to show how cell mechanics are determined on a global and local level by the adhesive cell environment. This has been achieved through establishing a combined method of AFM-based mechanical mapping and averaging of elasticity maps of living cells confined on adhesive micro-patterns. This strategy allows a more quantitative and reproducible way of probing local mechanics of cells. By computing average elasticity maps of cells plated on three different patterns, we identified specific mechanical responses that depend on the adhesion geometry, on both global and local scales. Importantly, averaging mechanical maps allows us to distinguish local elasticity variations present at repetitive cell locations on each adhesion pattern, separating them from non-reproducible variations due to the intrinsic heterogeneity of cells. As a proof of concept, we perturbed the acto-myosin cytoskeleton of patterned cells with specific drugs and mapped their elasticity.

Results

Cell adhesion determines cell elasticity

To investigate how the adhesion geometry influences cell global and local elasticity, RPE1 cells were plated on micropatterned glass-bottom culture dishes. The three micropatterns, ▽, T and Y (Figure 1A), impose similar overall cell shapes, but provide different adhesion geometries. As a consequence, adhesion structures formed by the cells differ and the actin cytoskeleton is in turn reorganized in a pattern-dependent manner (Figure 1B). Thick actin fibers and curved membrane borders are formed at concave pattern edges, as occur on the T- and Y-shaped patterns. On fully adhesive edges (▽ and top side of T) thinner fibers and straight membrane borders are formed.

Figure 1. Example of individual RPE1 cells plated on ▽-, T-, Y-shaped Y fibronectin micropatterns (left to right).

Horizontal scale bar is 10 μm, vertical scale bar in C is 5 μm.

A. Fibronectin-fibrinogen-GFP ▽-, T- and Y-shaped micropatterns.

B. Fluorescence microscopy image of individual actin-labeled (mCherry-lifeAct) RPE1 cells plated on the micropatterns shown in A. In the three cases, actin-rich regions are visible at the vertices. Thick actin stress fibers are present at the concave, non-adhering borders of T- and Y-shape micropatterns, while thinner structures are visible along the straight, adhering borders of ▽-micropatterned cells.

C. AFM topography images of the same individual RPE1 cells showed in B and, at the bottom, cross-section along the vertical axis (dotted line) The cell plated on the Y-pattern is slightly shorter (~37 μm) than those on the ▽- and T-patterns (~40 μm), as expected because of the concavity of its top border. Interestingly, the Y-cell is higher (~5 μm) than the ▽-cell (~ 4.5), suggesting that cell volume is independent from the pattern shape.

AFM was operated in peak force quantitative nanomechanical mapping (PF-QNM) mode using cantilevers with nominal spring constant of ~ 0.1 N/m featuring a conical tip of 15 μm in height and half open angle of 11°. Single cell topography and elasticity maps were acquired of RPE1 cells plated on ▽-, T-, and Y-shaped fibronectin micropatterns (referred to as ▽-, T- or Y-cells, n=16, 14, 18 respectively). Figure 1C reports cell topography images and vertical cross sections of single ▽-, T- and Y- cells. The latter appear slightly shorter ~37 μm along the vertical axis compared to T- and ▽-cells ~40 μm, as expected b ecause of the concavity of the top border.

Two different strategies were applied for the characterization of the mechanics of micropatterned cells. On the one hand, we computed average maps (Figure 2A and B), which were obtained by calculating the mean value of each pixel after aligning single elasticity and topographical maps. Such average maps highlighted local elasticity features resulting from specific and reproducible responses of cells to a given adhesion pattern, and not due to single cells’ differences. On the other hand, we evaluated mechanical heterogeneity within each pattern group by calculating average elasticity histograms and coefficient of variation (CV) maps (Figure 3). These take into account both cell-to-cell and single cell intracellular heterogeneities. From average elasticity maps, histograms were plotted to evaluate average elasticity distributions (Figure 2C). Cells plated on a ▽ were overall softer (median at 32 kPa, 4.52 log (Pa)) than cells plated on T (34 kPa, 4.54 log (Pa)) while cells plated on Y were the stiffest (41 kPa, 4.61 log (Pa)) (the observed differences of the three distributions were statistically significant according to Mann-Whitney U-test at 0.05% confidence level. Figure SI1 shows overlapped distributions and box plots). Other than presenting different median values, two regions could be identified in the histograms, which were not superposed in the three cases. In particular, the histogram of the average ▽ presented a unique region in the interval 25 – 32 kPa (4.4–4.5 log (Pa)) and average Y histogram showed a characteristic region between 40 and 63 kPa (4.6 and 4.8 kPa). The average T histogram did not show unique features and compared to the ▽ and the Y, as expected because of its ‘mixed’ adhesion geometry (i.e. it includes both adherent and non-adherent borders). A superposition of the three distributions and a boxplot are reported in Figure SI1. On a local scale, average maps revealed patterned-specific mechanical features, as well as common features shared by the three cell groups. In the three cases high elasticity values (40 to 100 kPa) were found at the cell corners – i.e. where anchoring structures are located - and in the nuclear region. The remaining regions of the cells were soft on ▽-cells, while T- and Y- cells presented additional stiff areas. In particular, high elastic moduli were measured at concave cell borders. Such stiff regions coincide with thick actin fibers (Figure 1B). T-cells showed higher elasticity on the upper periphery and along the vertical axis, while we measured two softer regions on the left and right interstices of the T along the concave edges. Y-cells presented only small soft regions localized along the three borders but not at their extreme peripheries, with values between 25 and 35 kPa. Along cell edges, at corners, in the central region and along the three arms of the Y, values span from 40 to 65 kPa. These results suggest a colocalization of stiff regions with the fibronectin patterns. To verify such correlation, we separately analyzed the elasticity contributions of adherent and non-adherent cell areas (Figure 2D). In the case of T- and Y-cells, the elasticity distributions of the cell regions above the patterns and of non-adhering areas are significantly separated. Non-adherent cell areas were generally softer than attached ones, except for the very high values found in colocalization with the thick fibers found at concave cell edges. ▽-cells presented less separated distributions, with both adherent and non-adherent regions showing values between 25–40 kPa (4.4 and 4.6 log (Pa)). A tail at higher values in the elasticity histogram of the adherent region was observed representing the contribution of the cell corners, while high elasticity of the non-adherent portion was attributed to the nuclear region. To rule out the hypothesis that these results were biased by the location of the nucleus on top of the pattern in T- and Y-cells and in the non-adherent region in ▽-cells, we plotted separately the histograms of cell borders, corners and central region (Figure SI2). For all regions considered, we observed the same trend as the average distribution, with the ▽-cells being the softest and the Y-cells the stiffest. The corners showed quite a large range of elasticity values in all three cases, with two main broad peaks, the one at stiffer values being more intense in the case of Y-cells. The central region, i.e. the area including the nucleus, showed a similar elasticity distribution as the whole-cell, slightly shifted to higher values in the case of ▽-cells, and with a tail only at low values. Interestingly, the histogram of the edge regions presented the lowest values in all three cases, and a tail in the highest elasticity range (> 4.7 log (Pa), 50 kPa) in the case of T- and Y-cells.

Figure 2. Average Young’s moduli of RPE1 cells.

A. Average topography of RPE1 cells plated respectively on a ▽ (n=16), T (n=14), Y (n=18)-shaped fibronectin micropatterns. Scale bar is 10 μm.

B. Average stiffness maps in log (Pa) of RPE1 cells plated respectively on a ▽ (n=16), T (n=14), Y (n=18)-shaped fibronectin micropatterns. Maps were obtained by aligning and averaging pixel-by-pixel single-cell maps obtained in Peak Force mode. The color scale corresponds to the values of the histograms shown in b (black= 4.2 log (Pa), yellow= 5 log (Pa)).

C. Histograms of the average maps shown in a.

D. Histograms of the average of the whole average stiffness map (black line), cell area adherent to the fibronectin pattern (purple line), and non-adherent cell area (yellow line).

Scale bar = 10 μm.

Figure 3. Evaluation of elasticity heterogeneity within cells plated on ▽- (n=16), T- (n=14), Y- (n=18) shaped fibronectin micropatterns.

A. Averaged elasticity histograms calculated by averaging the bin values of each single-cell elasticity histogram. Error bars correspond to the standard error of the mean. The distributions show that cells plated on a ▽ present the lowest variability, while the ones plated on a Y the highest. B. Coefficient of variation maps of log (E) maps shown in Fig. 2 of RPE1 cells plated on ▽ (n=16), T (n=14), Y (n=18)-shaped fibronectin micropatterns. Coefficient of variation (CV) maps were calculated by dividing the standard deviation of each pixel by its corresponding average value. The medians of CV maps were 0.10, 0.13, and 0.15 for ▽-, T - and Y-cells respectively.

Average elasticity histograms were obtained by averaging the bin values of the elasticity histograms of each individual cell map (Figure 3A). As all possible sources of elasticity variation, inter- and intracellular, are taken into account, large distributions are observed, spanning from a few kPa of softest regions to hundreds of kPa of actin-rich cell areas (Figure 3A). A narrower distribution compared to T- and Y- cells was observed for ▽-cells, with one single peak at ~ 40 kPa. Two peaks (16 kPa and 79 kPa) were found in the case of T-cells, and three (13, 40 and 250 kPa) in the case of Y-cells. This observation suggests that ▽-cells have lower variability than T- and Y-cells. To further investigate the origin of this heterogeneity, coefficient of variation (CV) maps were calculated (Figure 3B). In the three cases, all CV values were below 0.25 with the highest CV values found at cell peripheries. Thus, average histograms and CV maps together provide information about the mechanical and structural cell-cell variability of the cells for each micro-pattern shape, as well as about the origin of local variations.

Perturbation of the acto-myosin cytoskeleton by Latrunculin-A

Latrunculin-A disrupts actin filaments and causes cell softening.⁶² We used 1 μM Latrunculin-A to determine which subcellular regions are more sensitive to its action. Mechanical mapping of single patterned cells before and after drug addition to the imaging medium illustrated dramatic changes of the cell mechanics (Figure 4). As expected, cells become softer as a consequence of the disruption of the actin skeleton (the experiment was performed on 3 cells per pattern, all reporting cell softening), but this change in the elastic properties did not involve the entire cell body. In fact, the mechanical properties of the nuclear region, as well as the adhesive regions, remained unaltered. On the contrary, as the actin cortex was disrupted, non-adherent peripheral regions underwent drastic changes. In particular, the thick stress fibers present at concave edges in the case of T- and Y-cells were depolymerized, and the cells lost their shape and retracted to the adhesive surfaces only (Figure SI3). These morphological changes were accompanied by cell softening by a factor of about 10 in the peripheral regions. In detail, non-adhering edges of T- and Y-cells (with initial stiffness around 100 kPa) collapsed, and their elasticity contribution shifted from 100 to 10 kPa, while the peak elasticity corresponding to the nucleus remained constant at ~40 kPa. ▽-cells showed similar changes in the mechanical properties, with the nuclear region maintaining its characteristic elasticity, while the surrounding regions presented drastic softening. Morphological changes were also less pronounced because the adhesion structures were present all along the adhesive ▽-pattern. T-cells presented similar behavior to Y-cells at concave edges and similar to ▽-cells at the straight edge.

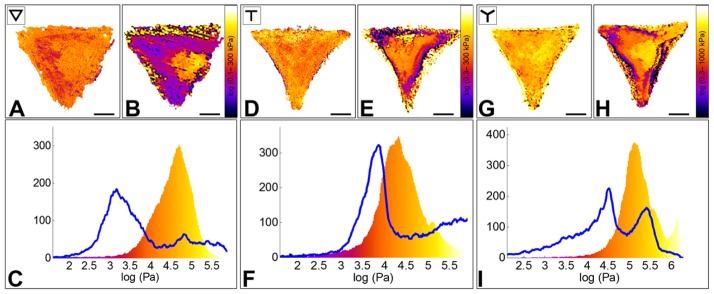
Figure 4. Effect of Latrunculin-A on the Young’s modulus of RPE1 cells plated on ▽ -, T - and Y micropatterns.

A, D, G. Elasticity maps of single cells plated, respectively, on a ▽-, T- and Y- shaped micropatterns before Latrunculin A addition.

B, E, H. Elasticity maps of the same cells ~20 minutes after drug addition.

C, F, I. Elasticity distribution of the same cells before (color-coded histogram) and after drug addition (blue line). In the three cases, the cells show a 10-fold Young’s modulus decrease, which involves mostly peripheral regions of the cells. On the contrary, the nuclear area seems less affected by actin disruption.

Perturbation of the acto-myosin cytoskeleton by Blebbistatin

Blebbistatin binds to Myosin II and blocks it in a conformation with low affinity for actin, which results in a reduction of crosslinking of actin filaments.⁶³ As a consequence, intracellular tension is released, the cell retracts and its elastic modulus decreases.¹⁰ We treated cells with 20 μM Blebbistatin, and monitored the change of the elastic modulus by mechanical mapping before and after drug addition (Figure 5). We observed a retraction of non-attached cell borders, and a 5-fold overall softening. Again, while the nuclear region maintained its elasticity value, stronger effects were found for peripheral regions, with an elasticity decrease of about 10 times.

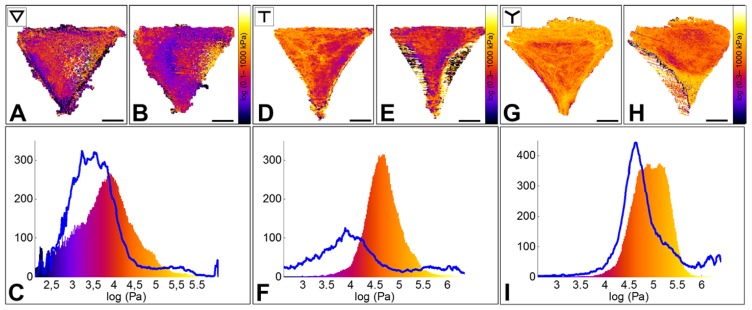
Figure 5. Effect of Blebbistatin (−) on the Young’s modulus of RPE1 cells plated on ▽ -, T - and Y micropatterns.

A, D, G. Elasticity maps of single cells plated, respectively, on a ▽-, T- and Y- shaped micropatterns before Blebbistatin addition.

B, E, H. Elasticity maps of the same cells ~40 min after drug addition.

C, F, I. Elasticity distribution of the same cells before (color-coded histogram) and after drug addition (blue line). Cells show a 5 to 10-fold decrease of the Young’s modulus. Such decrease is observed in the peripheral regions, but not on the nucleus, which appears to maintain its elastic properties after the disruption of acto-myosin fibers, similarly to what observe after Latrunculin A injection.

Discussion

By growing cells on adhesive micropatterns and mapping their mechanical properties by AFM, we show that adhesion geometry triggers specific mechanical properties at both local and global scales. In particular, by using ▽-, T- and Y-shaped fibronectin micropatterns, which share the distance between the extremities but differ in the adhesive geometry, we show that the mechanical response of cells varies driven by the localization of their adhesion sites. We performed PF-QNM AFM to obtain mechanical maps on single micropatterned cells. It is important to note that the thickness of the patterns themselves does not affect the mechanics of the cells: as measured with the AFM, the fibronectin layer is only a few nanometers thick (Figure SI4). All measurements were performed using a rectangular cantilever with a nominal spring constant of 0.1 N/m and a 15 μm high conical tip (Figure SI5). These features combine good lateral resolution with well-defined tip geometry. Moreover, using such a very high tip reduces the influence of the viscous drag on the measurements. In PF-QNM AFM the average indentation velocity at which force curves are acquired (~1200 μm/s) is higher than conventional force curves (in the μm/s range). This leads to measured Young’s moduli in the tens-of-kPa range, slightly higher than at slower velocity due to the viscoelastic response of living cells.^{45,47,48,64–67} To corroborate this, we performed elasticity measurements at varying velocities (Figure SI6), in agreement with previous reports.^64,67 Measurements on the central part of ▽ cells at 5, 25, 50 and 100 μm/s yielded Young’s moduli of 9.6 ± 3.0, 9.7 ± 2.9, 14.7 ± 1.5 and 16.1 ± 0.5 kPa (geometric mean ± standard deviation), respectively, while the value obtained in Peak Force is of 32 ± 1.5 kPa (mean value obtained from the log-scale average).

Importantly, the mechanical response of cells on a given pattern was reproducible, with local variability below 25%, as shown in the CV maps of the average log (E), and average variations below 15% in all three cases (Figure 3B). The medians of the Young’s modulus distributions of the average maps (Figure 2) were 32 kPa, 34 kPa and 41 kPa, for ▽-, T- and Y- respectively. Interestingly, previous studies on cells patterned on adhesive disks and squares reported increasing Young’s moduli with increased adhesion areas.^60,61 This is a direct consequence of the cell spreading on larger patterns and in agreement with our measurements of non-patterned RPE1 cells, which are free to spread on very large areas and present Young’s moduli 10-times higher than our patterned cells (Figure SI7). Our measurements show highest Young’s moduli in the case of Y-cells, and lowest in the case of ▽-cells, though the Y-pattern provides an adhesive area of ~400 μm² and the ▽- pattern ~800 μm². In our experiments the cells have constant size, and the adhesion geometry - not variable spreading - is at the origin of the mechanical differences. In general, decreasing the peripheral adhesion area leads to a decrease of focal adhesions at the cell borders, resulting in the appearance of concave cell edges.⁶⁸ Such concavity is the result of a membrane-cortex-induced inward pulling force that is counterbalanced by thick actin fibers, which appeared as high Young’s modulus regions in our mechanical maps. The tensegrity model and the prestress hypothesis are in accordance with our observation,^18,69–72 as they predict a higher overall stiffness of the cells in response to the high tension created by acto-myosin fibers. Such tension is inversely dependent on the number of available anchoring points^59,73,74, which is consistent with the stiffness order ▽ < T < Y obtained from our measurements. Since elasticity variations of a group of cells are due to intracellular and intercellular differences, we investigated heterogeneities by two different approaches. Average histograms reported in Figure 3A show the broadest distributions for cells plated on Y-patterns, and the narrowest for cells grown on ▽-patterns. Similarly, CV maps (Figure 3B) present higher variations both locally and globally for Y-, and lower for ▽-cells. Nevertheless, CVs were small in the three cases. Thus, combining the results of such analysis suggests that the higher variability observed for Y and T-cells is mainly due to cell-to-cell mechanical heterogeneity. In particular, highest CVs are found at concave borders of T- and Y-cells, which are also the stiffest regions and probably where local cytoskeletal organization is more uneven. In agreement with these results, a high variability of actin bundle strength, (i.e. variability of the curvature radius) at concave cell borders was shown.⁷⁵ In contrast, peripheral adhesion sites provided by ▽ patterns counterbalance acto-myosin tension, and exhibit a more controlled and reproducible structure and mechanical response. Namely, it is easier and more reproducible to regulate the prestress if the perimeter of the cell is adhering.

The tensegrity and prestress models apply well also to the results we obtained from the Latrunculin-A and Blebbistatin addition experiments. When disrupting actin fibers with Latrunculin-A (Figure 4), we measured an overall ~10-fold decrease of the Young’s modulus, and a drastic collapse of the cell structure. The most dramatic effect was observed at concave borders of Y- and T-cells, where the line tension keeping the cell shape at borders was released, thus leaving membrane tension and adhesive forces alone as cell shape determinants. This results in the reduction of the area covered by the cell exclusively to the adhesive areas. ▽-cells show less dramatic effect on their morphology, i.e. cell edges remain attached to the pattern border, but show a softening of comparable magnitude. Similarly, Myosin II inhibition with Blebbistatin lead to the release of tension in the acto-myosin fibers (Figure 5), which resulted in a dramatic increase of edge concavity in T- and Y- cells, along with a 5-fold decrease of cell elasticity. Interestingly, softening induced by both Latrunculin-A and Blebbistatin concerned peripheral areas but not as much the nuclear region. These observations suggest that the mechanical properties of the nucleus do not dependent on the actin cytoskeleton. Moreover, in non-patterned cells, overall much stiffer than patterned cells, the nucleus presented Young’s moduli close to that of patterned cells (Figure SI7). Previous works showed no significant alteration of the nuclear shape after actin filament disruption by Cytochalasin D⁷⁶ corroborating the hypothesis that the physical properties of the nucleus are mainly determined by the nuclear lamina.⁷⁷ These results suggest that conventional cell elasticity measurements should be performed on areas near but not on the nucleus, especially if a difference is to be probed after drug treatment. They further highlight the usefulness of the presented approach to precisely control the cell morphology and where the measurements are performed.

Conclusion

In this work we perform AFM-based mechanical mapping on cells plated on micropatterns and we show that these yield a pattern-specific reproducible mechanical response. A fundamental advantage of the proposed method is the possibility of obtaining average elasticity maps. These average maps allow us to specifically locate intracellular elasticity differences, which are maintained among cells and to identify regions characterized by higher or lower mechanical stability. Our data show that cells adapt the mechanical properties of subcellular regions according to the adhesion geometry, providing unique information about the relation of cells’ mechanical properties to their adhesive environment. Our results showed that adhesive cell borders provide mechanical stability and homogeneity within the cell. On the contrary, concave cell shapes, due to a lack of peripheral adhesion, induce high tension in the cytoskeleton and higher mechanical heterogeneity. Three general rules can thus be formulated: 1) at locations where cells adhere to the patterns, high Young’s moduli are to be expected, due to the higher concentration of actin structures; 2) in the absence of adhesive borders, the cell is obliged to form thick and tensed actin fibers to cover a sufficient spread area. Such fibers result in mechanical maps as very stiff regions. 3) In non-adherent cell areas, no cytoskeletal structure can be anchored, thus intracellular tension is low and, consequently, low elasticity values are found in these regions. Importantly, our findings suggest that cell stiffness is not always higher, the larger the adhesive area. We also showed that perturbation of specific cytoskeletal components affects cell mechanics in different ways depending on the local actin structure and adhesive geometry, suggesting that tension is concentrated on concave cell borders. This deepens our understanding of the role of specific cytoskeletal components, as well as the interdependence of intracellular elements, in the maintenance of cell morphological and mechanical integrity. Therefore, the combination of micropatterns, AFM mechanical mapping and image averaging constitutes a promising approach to investigate the mechanical heterogeneity of individual cells and the mechanics of subcellular components.

Material and Methods

Microcontact printing

PDMS stamps were washed in milliQ water and sonicated 15 min in pure ethanol, let dry and incubated with 50 μM Fibronectin (Sigma-Aldrich F1141), 5 μM Fibrinogen-A488 (green, Invitrogen) in 100 mM NaHCO₃ (pH 8.6) for 45 min at room temperature. The solution was then aspired and the stamps let dry for 10 sec under the hood, placed on glass-bottom culture dishes (GWSt-5040, Willcowells), gently pressed and removed after 10 min. Non-printed areas were then passivated by 1h incubation with 1 ml PEG-poly-L-Lysine (Surface Solutions) 0.1 mg/ml in 10 mM HEPES (pH 7.4). The dishes were then repeatedly washed in PBS ⁷⁸.

Cell culture

hTERT-RPE1 cells (infinity telomerase-immortalized Retinal Pigment Epithelial human cell line) were cultured in Dulbecco’s modified Eagle’s medium (DMEM, GIBCO) supplemented with 10% fetal calf serum (FBS, GIBCO). Cells were cultured at 37 °C in a 5% CO₂ incubator. For plating on the micropatterns, cells where detached with 0.02% EDTA, centrifuged, resuspended in warm culture medium and plated on the patterned culture dishes at a concentration of 50000 cells/ml. Unattached cells were washed after 15–20 min with equilibrated medium.

Atomic force microscopy

All experiments were conducted using a Bioscope Catalyst (Bruker, Santa Barbara, CA, USA) mounted on an inverted optical microscope (Olympus, Japan). Trace and retrace images of topography and Young’s modulus were acquired in peak force tapping (PFt) mode with a setpoint peak force of 750 pN and an oscillation frequency of 0.5 kHz. Rectangular cantilevers with a nominal spring constant of 0.1 N/m and a 15 μm high conical tip with 60 nm tip radius and 32° open angle (CSG11, NT-MDT, Moscow, Russia) (Figure SI7) were used for all measurements. Cantilever spring constant and sensitivity were calibrated before each experiment using the thermal fluctuation method ^79,80. Tip height, radius and angle where verified by scanning electron microscopy (Figure SI8). For mechanical mapping, typical acquisition time was of about 10 min per image, using a scan rate of 0.45 Hz and an image size of 256 × 256 pixels (scan size: 55 μm). We report 256 × 256 pixels mechanical maps with elasticity values computed by the AFM control software. Young’s moduli were calculated according to the elastic contact model for conical indenters (named Sneddon in the software):

$$F=\frac{2}{\pi }·\frac{E·tan\alpha }{1-v^2}·{\delta }^2,$$ (1)

where F is the measured force, E the elastic modulus, α the half-opening angle of the tip, δ the indentation and ν the sample’s Poisson’s ratio, assumed to be 0.5. 30% and 90% of the maximum force were set as force fit boundaries. Elasticity map values were corrected for the bottom effect (see Image analysis section). To confirm the accuracy of the software in the determination of the elasticity values, we acquired mechanical maps at 128 × 128 pixels, allowing simultaneous recording of each force curve. Young’s moduli obtained with a custom algorithm based on Matlab (Mathworks, Natick, MA), but with the same parameters used by the software, were in good agreement with the moduli obtained by the software (Figure SI9). For drug time–lapse experiments, the image size was reduced to 128 × 128 pixels, to allow faster acquisition times (5–6 min at a scan rate of 0.3–0.35 Hz).

Elasticity values from mechanical maps were also compared to conventional force-distance curves at 1, 5, 10, 20 Hz, with a ramp size of 2.5 μm and a maximum deflection threshold of 3 nm for 1 and 5 Hz, 10 nm for 10 and 20 Hz (Figure SI6).

All measurements were conducted in CO₂-indipendent Leibovitz-L15 medium supplied with 10% FBS. To account for evaporation, medium was regularly replaced.

Latrunculin-A and Blebbistatin addition

Drugs directed against the actin cytoskeleton (Latrunculin-A, Blebbistatin) were used to investigate the contribution to cell elasticity provided by actin and myosin II, respectively. Drugs were solubilized in DMSO to a mother solution, then diluted to a volume of 500 μl in warm medium, added to the culture dish to obtain the desired final concentration (1 μM for Latrunculin-A, 20 μM for Blebbistatin). To avoid concentration gradients due to slow diffusion of the drug, the medium was mixed several times after drug addition. To exclude non-specific effects due to DMSO toxicity, control experiments with DMSO alone were conducted (Figure SI10).

Image analysis

All images were analyzed using self-written programs in Matlab (The MathWorks, Natick, MA). In brief, a black and white mask was obtained for each set of images by applying the hysteresis threshold algorithm to the topography image, an edge detection method that sets the cell border where neighboring pixels values deviate from the values of the flat sample support. Masked topography images were used to rotate all images and align them by cross-correlation. The mask was equally applied to the elasticity maps to calculate the individual stiffness histograms. The average images were then calculated from the rotated and translated images without excluding background pixels and considering both trace and retrace data. An average mask was then calculated on the average height image in the same way as for individual images and the histograms of the average image calculated. Stiffness maps were corrected for the bottom effect according to the model by Chadwick and Gavara ³⁷:

$$F=\frac{2E·tan\alpha }{\pi ·(1-v^2)}{\delta }^2·\left\{1+1.7795\frac{2\mathit{tan}\alpha }{{\pi }^2}\frac{\delta }{h}+16{(1.7795)}^2{\mathit{tan}}^2\alpha \frac{{\delta }^2}{h^2}+O\left(\frac{{\delta }^3}{h^3}\right)\right\},$$ (2)

where h was the height at each pixel of the topography image. As previously shown, this effect is relevant only for thin regions of the cells, in our case at the cell borders ^34,81. Average elasticity histograms (Figure 3A) where obtained by first calculating each single cell’s histogram, and then averaging the bin heights of all single-histograms, previously normalized on the number of pixels. This procedure differs from simply pooling all pixels values from all cells in that bin height averaging and normalization allow to represent the data independently of the sample size (number of cells) and on single cells’ spread area (number of pixels). The latter is negligible in the case of patterned cells, but relevant in the case of non-patterned cells.

Force curve analysis

Conventional force-distance curves were analyzed using self-written programs in Matlab. The contact elastic model for conical indenters was used to determine the Young’s modulus (Eq. 1). No bottom-effect correction was applied in this case as measurements were performed on the top of the cell, where the deformation/height ratio is small (~10%). The values reported in Figure SI6 correspond to the geometric mean of the Young-s moduli obtained on four different cells, to allow the comparison with the Young’s modulus of the average log-scale map in Figure 2B.

Supplementary Material

1

Figure SI1. Elasticity distribution of averaged mechanical maps​

The box plot on top reports the medians and quartiles (25 and 75%), the circle corresponds to the mean value and the crosses the minimum and maximum values.

From the superposed histograms, a region at low values can be identified that is unique for ▽- cells, while the average Y-cell showed a unique region at high elasticity (above 4.7 log (Pa)). The average T-cell shared mechanical features of both Y- and ▽-cells.

Figure SI2. Elasticity repartition of cell areas.​

Elasticity histograms of whole cell (black line), cell edges (blue line), corners (yellow line) and central region (purple line) of ▽-, T- and Y- cells, from left to right.

Figure SI3. AFM topography of cells plated on ▽-, T-, and Y- shaped micropatterns, from left to right, before (A) and after (B) Latrunculin-A addition.​

Disruption of actin filaments by Latrunculin-A causes a collapse of the cell structure, with particular strong effects on non-adherent cell borders. These undergo an increase of their concavity due to the release of tension, which counterbalances inward pulling force of the cell membrane. The cell-substrate contact area is thus reduced to the adhesive area exclusively. The symmetry-breaking of forces results in some cases in the repositioning of the nucleus, e.g. from the center to one corner in the case of ▽-cells.

Figure SI4. Topography of fibronectin micropatterns obtained by AFM.​

Height profile correspond to the section indicated by the red bar in the images, averaged over 5 μm. Scale bars = 10 μm, color scales 0 – 20 nm.

Figure SI5. Main figure: bright-field image of RPE1 cells on Y-micropatterns and AFM probe. Scale bar = 50 μm. Inset: SEM image of a CSG11 AFM probe. Scale bar = 1 μm.

Figure SI6. Dependence of Young’s modulus measurements on the tip velocity.​

Main figure: Young’s modulus vs velocity plot. Values are obtained from conventional force-distance curves by averaging measurements performed on the nuclear region of 4 cells plated on ▽-pattern at 5, 25, 50, 100 μm/s (1, 5, 10, 20 Hz with 2.5 μm ramp size). The white dot corresponds to the average value obtained in Peak Force mode on the nucleus of ▽-cells. The PeakForce velocity of 1200 μm/s is the average velocity in the region of the oscillation cycle used for fitting the Young’s modulus, i.e. 30 to 90% of the maximum deflection.

Figure SI7. Young’s modulus of non-patterned RPE1 cells.​

Average histogram and single-cell mechanical map of RPE1 cells grown on a culture dish. Non-patterned cells present a great variability of shape and size and higher elasticity the patterned ones. Moreover, inversely than patterned cells, the nuclear region is the softest while cell peripheries the stiffest.

Figure SI8. SEM images of a CSG11 AFM probe.​

A. 6000x magnification, scale bar = 1 μm

B. 18000x magnification, scale bar = 1 μm

Figure SI9. Force-distance curves obtained on a Y-cell in PeakForce-QNM mode​

The three curves, from left to right, were acquired on a corner, on the nuclear region and on a soft region of the cell (between the cell nucleus and the border). Young’s moduli obtained from the AFM control software were of 20, 38 and 91 kPa, respectively. Such values are calculated fitting the conical contact elastic model to the curve region between the 30 and 90% of the maximum force. Young’s moduli obtained fitting the same curves with a custom algorithm based on Matlab were 24, 36, 88 kPa when fitting the whole force curve, and 30, 31, and 97 when fitting the range 30–90% of the maximum force.

Figure SI10. Control time-lapse experiment with DMSO.​

A. Young’s modulus maps of an RPE1 cell before (0 min) and after DMSO injection. Full image size is 50 μm.

B. Elasticity histogram of the maps reported in a.

No significant variation is observed during the 43 minutes following DMSO injection.