Robust Cell Segmentation for Histological Images of Glioblastoma

Abstract

Glioblastoma (GBM) is a malignant brain tumor with uniformly dismal prognosis. Quantitative analysis of GBM cells is an important avenue to extract latent histologic disease signatures to correlate with molecular underpinnings and clinical outcomes. As a prerequisite, a robust and accurate cell segmentation is required. In this paper, we present an automated cell segmentation method that can satisfactorily address segmentation of overlapped cells commonly seen in GBM histology specimens. This method first detects cells with seed connectivity, distance constraints, image edge map, and a shape-based voting image. Initialized by identified seeds, cell boundaries are deformed with an improved variational level set method that can handle clumped cells. We test our method on 40 histological images of GBM with human annotations. The validation results suggest that our cell segmentation method is promising and represents an advance in quantitative cancer research.

1. Introduction

Glioblastoma (GBM, WHO grade IV) is the most common astrocytoma [1], with an incidence of about 10,000 cases per year in the United States. In contrast to the lower grade gliomas, GBMs present with radial growth rates almost ten times as fast, yet underlying mechanisms are only partly explained [2]. Specific pathological hallmarks in GBM, such as highly anaplastic and pleomorphic tumor cells, pseudopalisading cells around necrosis and vascular proliferation are thought to be relevant to the drastically accelerated disease progression [3, 4].

To enhance investigation of GBM using histologic sections of human tissue samples, a robust and automated cell segmentation method is required. However, cell segmentation for histological imaging data is challenging because of the large variations in cell shape and appearance. In addition, it is quite common for groups of cells to clump together, presenting a barrier to accurate cell delineation. A large number of cell segmentation methods have been developed, including watershed [5], dynamic generalized Voronoi diagram [6], contour concavity detection [7], concave vertex graph [8], deformable models [9], and gradient flow analysis [10]. In contrast to these methods, a class of approaches involving seed detection has drawn special attention [11, 12, 24, 14]. The final outputs of all these methods depend on a set of seeds for cell contour initialization. Therefore, the accuracy of seed detection for cell localization is important.

In this work, we develop a new cell segmentation system to automatically segment cells in digital histological images of GBM specimens. As illustrated in Figure 1, it consists of a new seed detection algorithm and a newly designed cell contour deformation method based on the variational level set framework. The cell seed detection algorithm draws joint information of spatial connectivity, distance constraint, image edge map, and a shape-based voting result derived from eigenvalue analysis of Hessian matrix across multiple scales. Thus, it produces robust and accurate seed detection results, especially for overlapped or occluded cells. With cell contours initialized from these seeds, we deform them with an improved variational level set method that can converge to true cell boundaries.

Fig. 1.

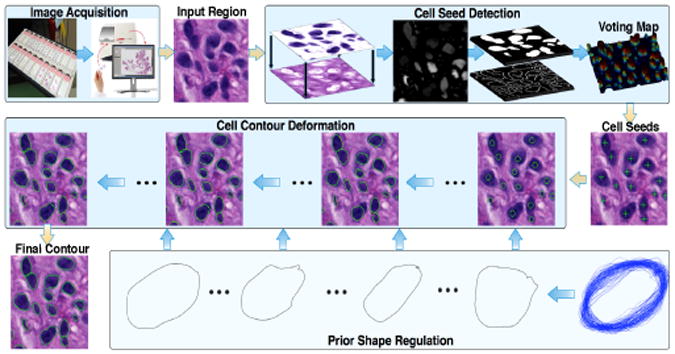
An overview of the proposed method is presented.

2. Method

Our workflow for cell segmentation in bright-field histological images of GBMs has two sequential steps, seed detection and cell contour deformation (Figure 1). Additionally, each step consists of a sequence of processing modules that are described below in detail.

2.1. Seed Detection

Seed detection identifies the number and location of cells presented in histological images. This is a critical step for robust cell analysis as histological images present a large number of overlapped cells with some parts occluded.

GBM tissue sections for analysis are stained with Hematoxylin and Eosin (H&E) stains. Hematoxylin is a dark blue or violet stain that positively binds to DNA/RNA in nucleus, whereas eosin binds to proteins in cytoplasm and intracellular membranes. In light of H&E staining mechanism, we first deconvolve each stain component from the original color image. Color deconvolution [15] can be realized by computing the Optical Density (OD): OD = − log(L_o/L_i), where L_i and L_o are intensity of light entering and exiting a specimen, respectively. The un-mixer U ≜ (u⃗₁ | u⃗₂ | u⃗₃) is defined as a 3 × 3 matrix with unit length columns that represent the OD values associated with the red, green, and blue channel for hematoxylin, eosin, and null stain. Denoting C(i, j)_3×1 as a vector representing three stain amounts at pixel (i, j), we can compute OD for red, green, and blue channel as Y = UC. This leads to an orthogonal representation of the stains as C = U⁻¹Y, where U⁻¹ is the color deconvolution matrix.

We next use image hues from hematoxylin channel for cell locations. Although the decoupled hematoxylin channel only reflects hematoxylin stain intensity, its background presents variable levels of noise due to imperfect staining process and heterogeneous responses of histological components to chemical stains. To remedy this problem, we “normalize” local image background noise with morphological reconstruction operation [16]. Two image morphological components, namely marker Φ and mask Ψ image, are involved in a morphological reconstruction operation, which can be written down as follows: ${\mathbf{R}}_{\mathrm{\Phi }}^{{\chi }_{\rho }}(\mathrm{\Psi })={\chi }_{(\rho ,\mathrm{\Psi })}^{n^{\ast }}(\mathrm{\Phi })$, where ${\chi }_{(\rho ,\mathrm{\Psi })}^n(\mathrm{\Phi })=min({\chi }_{(\rho ,\mathrm{\Psi })}^{n-1}(\mathrm{\Phi })\oplus \rho ,\mathrm{\Psi })$. Note n* is the smallest positive number such that ${\chi }_{(\rho ,\mathrm{\Psi })}^{n^{\ast }}(\mathrm{\Phi })={\chi }_{(\rho ,\mathrm{\Psi })}^{n^{\ast }+1}(\mathrm{\Phi })$; ρ represents the structural element with which marker image Φ is recursively dilated with. In addition, ⊕ represents morphological dilation. When subtracting the reconstructed image ${\mathbf{R}}_{\mathrm{\Phi }}^{{\chi }_{\rho }}(\mathrm{\Psi })$ from the mask image Ψ, the difference image $\mathrm{\Delta }(\mathrm{\Phi },\mathrm{\Psi },\rho )=\mathrm{\Psi }-{\mathbf{R}}_{\mathrm{\Phi }}^{{\chi }_{\rho }}(\mathrm{\Psi })$ consists of a near zero-level background, and a group of enhanced foreground peaks, each representing an object of interest. In our analysis, we use the complement of the decoupled hematoxylin channel image as the input to morphological reconstruction. In Figure 2 (A), we present a typical background normalization result with morphological reconstruction where the marker image is obtained by applying the image opening process to the mask image with a circular structural element ρ having a radius of r = 10 pixels.

Fig. 2.

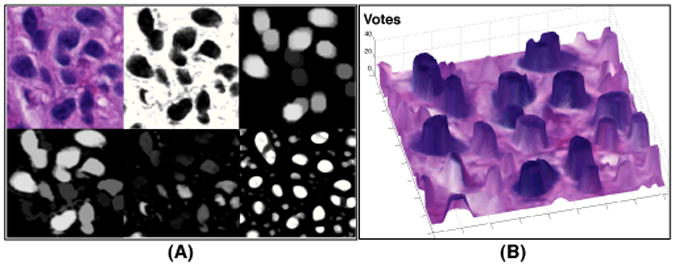
The voting map of a typical image region is demonstrated. (A) The original, deconvolved hematoxylin channel, marker image (top), reconstructed, difference, and voting image (bottom); (B) Voting map overlaid with original image.

Given the difference image Δ with a near zero-level background, we proceed with a voting process where we assume all cells are close to either a circle or an ellipse in shape. Note that image intensity Δ(x) at x in proximity to x* can be represented by Taylor series expansion: $\mathrm{\Delta }(\mathbf{x})\approx \mathrm{\Delta }({\mathbf{x}}^{\ast })+{(\mathbf{x}-{\mathbf{x}}^{\ast })}^T\nabla \mathrm{\Delta }({\mathbf{x}}^{\ast })+\frac{1}{2!}{(\mathbf{x}-{\mathbf{x}}^{\ast })}^T\mathcal{H}\{\mathrm{\Delta }({\mathbf{x}}^{\ast })\}(\mathbf{x}-{\mathbf{x}}^{\ast })$ where x = (x₁, x₂)^T; ℋ(Δ(x)) is a 2 × 2 Hessian matrix with its entry H(i, j) = ∂²Δ/(∂x_i∂x_j) |_x. As Hessian matrix is symmetric, it is diagonalizable. We denote λ₁ and λ₂ (λ₁ ≤ λ₂) as two eigenvalues of ℋ(Δ(x)). Note that cell centers in Δ have larger intensity values than peripheral points, i.e. Δ(x*) > Δ(x). Therefore, both eigenvalues of the resulting Hessian matrix have negative sign [17]. As λ₁ ≤ λ₂, we only need to check sign of λ₂ to infer whether the associated pixel x belongs to a cell. As cells have variable sizes, we convolve Δ with a family of Gaussian filters with different scales G(x, s_i), i = 1, 2, …, N to reach scale invariant. For the voting process, we begin with a zero-valued voting map for all pixels in the image domain. As we check the sign of bigger eigenvalue of the Hessian matrix at all scales for each pixel, we incrementally increase the voting map V(x) at pixel x where the sign of bigger eigenvalue is negative at a given scale. In Figure 2 (B), we present a voting map overlaid with a typical histological image region where cell regions in dark exhibit high votes.

The vote at any given location on the voting map is an integer not larger than the number of scales N: V(x) ≤ N, ∀x ∈ Ω, where Ω is the voting map domain. If we consider the voting map as a surface in a three-dimensional space as shown in Figure 3 (A), those strong peaks on the voting surface can be detected as we move down an imaginary horizontal plane (e.g. from the green to magenta plane in Figure 3) intersecting with the voting surface. For each intersection plane P(v; x), we generate a binary image from the original voting map with threshold v. The resulting centroids of foreground objects satisfying all the following conditions are appended to the peak list L(v): (a) It does not exist in the peak list L(v + 1); (b) The object is valid with its size no less than area threshold A(α, β, v), where α and β are pre-defined scalars; (c) Its centroid is within the foreground region in the binary mask M(x) detected by Otusu's adaptive thresholding method. For all peaks in L(v), pairwise distances are computed. Centroids of adjacent centroids (p₁, p₂) departed less than distance threshold D₁ are then iteratively merged. Peak merging is necessary as typical large cells present a few dark spots representing nucleoli. One such example is shown in Figure 3 (B: top) where two green points are merged to a red one. Next, we conduct a second round of distance-based merging process with a more stringent threshold D₂ (D₁ < D₂). Iteratively, two peaks (p₁, p₂) are merged only if the following conditions are both true: (a) Distance between p₁ and p₂ is less than D₂; (b) The path $\overrightarrow{p_1,p_2}$ connecting p₁ and p₂ is not intersected with any canny edge point derived from the original image. We make use of information drawn from edge map to prevent centroids of closely clumped nuclei from being merged. The yellow arrow in Figure 3 (B:bottom) highlights the edge that blocks adjacent two seeds from merging. The complete algorithmic description is presented in Algorithm 1. The developed seed detection method can help localize clumped cells in histological images without tedious parameter tuning process, as it uses joint information from spatial connectivity, distance constraint, image edge map, and a shape-based voting map derived from eigenvalue analysis of Hessian matrix across multiple scales.

Fig. 3.

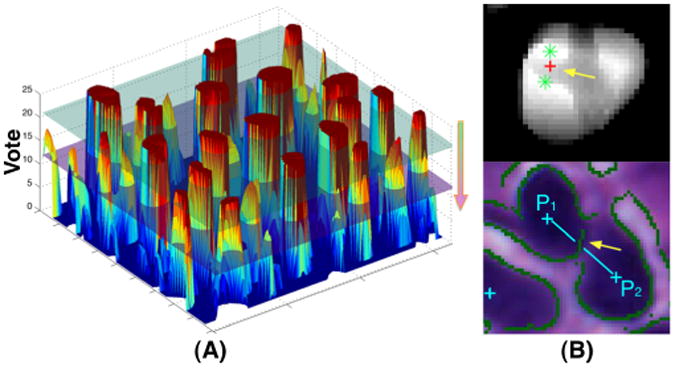
Illustration of (A) voting peak detection by sliding down an imaginary horizontal plane that intersects with the voting surface; (B) Distance-based Seed Merging (top) and Edge-based Seed Separation (bottom).

Algorithm 1 New Seed Detection Algorithm
Input: Icolor: original image; L ← Ø; V(x) ← 0, ∀x; parameters (ρ(r), {si}, α, β, D1, D2)
Output: L: a list of seeds for cells
1:	{Initialization Phase}
2:	Decouple Icolor into two stain channels: hematoxylin IH and eosin IE
3:	Construct mask image: Ψ ← complement(IH) and marker image: Φ ← IH ⊕ ρ
4:	Compute reconstructed image ${\mathbf{R}}_{\mathrm{\Phi }}^{{\chi }_{\rho }}(\mathrm{\Psi })\leftarrow \text{morphRecon}(\mathrm{\Phi },\mathrm{\Psi },\rho )$
5:	Compute difference image $\mathrm{\Delta }\leftarrow \mathrm{\Psi }-{\mathbf{R}}_{\mathrm{\Phi }}^{{\chi }_{\rho }}(\mathrm{\Psi })$
6:	Igray(x) ← rgb2Gray(Icolor); M(x) ← otusuThresholding(Igray(x))
7:	{Voting Map Construction}
8:	for all i ∈ (1, 2, …, N) do
9:	for all x ∈ Ω do
10:	λ2 (x) ← eigHessian(Δ(x), si)
11:	if sign(λ2(x))< 0 then
12:	V(x) ← V(x) + 1
13:	{Detecting and Merging Seeds}
14:	vsort ← descentSort(V(x)); v0→1 ← flip(normalize(vsort))
15:	Let vc and vp be the current and previous voting value in vsort
16:	for all vc and vp ∈ vsort, where vc ← vsort(i) do
17:	find objects 𝒪(vc) ← label(V(x) ≥ vc)
18:	for all o ∈ 𝒪(vc) do
19:	if size(o)≥ A(α, β, vi) = β + exp(αv0→1 (i)) && M(centroid(o)) = 1 && o ∩ L = Ø then
20:	L ← L ∪ {centroid(o)}
21:	while any(L.pairwiseDistance() ≤ D1)=true do
22:	find p ∈ L s.t. any(L.pairwiseDistance(p) ≤ D1) = true && sum(L.pairwiseDistance(p)) ≤ sum(L.pairwiseDistance(p′)) ∀p′ ∈ L
23:	find Q = {q| s.t. (L.pairwiseDistance(p, q) ≤ D1) = true}
24:	L ← L ∪ Mean({p} ∪ Q)
25:	L ← L \ ({p} ∪ Q)
26:	{Merging Seeds with Edge Information}
27:	while any(L.pairwiseDistance() ≤ D2 && !L.isBlockedByEdge()) = true do
28:	for all p ∈ L do
29:	find Q(p) = {q| s.t. (L.pairwiseDistance(p, q) ≤ D2 && !L.isBlockedByEdge(p, q)) = true}
30:	find p ∈ L s.t. Q(p) ∆ Ø && sum(L.pairwiseDistance(p, Q(p))) ≤ sum(L.pairwiseDistance(p′,Q(p′))) ∀p′ ∈ L
31:	L ← L ∪ Mean({p} ∪ Q(p))
32:	L ← L \ ({p} ∪ Q(p))

2.2. Cell Contour Deformation

We initialize cell contours as small circles centered around cell seeds and use active contour deformable models to converge them to true cell boundaries. By contrast to boundary-based deformable models highly dependent on image gradient strength, region-based methods work better when image gradients are weak. Therefore, they are more appropriate for occluded cell segmentation. Enlightened by the variational level set formulation [19, 9, 21], we modify this model with integration of shape prior knowledge and adaptive occlusion term to segment multiple objects with occlusion.

For a given image, we assume N Lipschitz functions ϕ_i : Ω → ℛ, where i = 1, 2, …, N. Their zero-level sets represent N cells {𝒪_i} with closed and bounded contours in the image domain Ω [19]. To drive cell contour deformation, we aim to minimize the following functional:

$$\begin{array}{c}E(C,\mathrm{\Phi },\mathrm{\Theta },T)={\lambda }_o\sum _{i=1}^N{\int }_{\mathrm{\Omega }}{(I-c_i)}^{2}H({\varphi }_i(\mathit{x}))d\mathit{x}\\ +{\lambda }_b{\int }_{\mathrm{\Omega }}{(I-c_b)}^2\prod _{i=1}^N(1-H({\varphi }_i(\mathit{x})))d\mathit{x}\\ +\omega {\int }_{\mathrm{\Omega }}(\sum _{i=1}^{N}H({\varphi }_i(\mathit{x}))-(1-\prod _{i=1}^N(1-H({\varphi }_i(\mathit{x})))))d\mathit{x}\\ +\nu \sum _{i=1}^N{\int }_{\mathrm{\Omega }}{\Vert \mathrm{\Gamma }({\varphi }_i(\mathit{x}))-\mathrm{\Psi }(T_i(\mathit{x})){\eta }_i\Vert }^{2}d\mathit{x}\\ +\mu \sum _{i=1}^N{\int }_{\mathrm{\Omega }}Q(\mathit{x})|\nabla H({\varphi }_i(\mathit{x}))|d\mathit{x}+\xi \sum _{i=1}^N{\int }_{\mathrm{\Omega }}R(|\nabla {\varphi }_i(\mathit{x})|)d\mathit{x}\end{array}$$ (1)

where C = {c_i, c_b} are constants for the cell i and background, respectively; H(x) is the Heaviside step function; Q(x) is an edge strength function approaching to zero, i.e. the smallest value, on edges; R(x) is a double-well potential function [20]; Γ is a distance vector derived from ϕ_i; T_i is a similarity transformation from cell i to shape priors; Ψ is a matrix consisting of distance vectors derived from training shapes; η_i is a sparse coefficient vector for the i-th cell, with each non-zero entry representing approximation weight of specific shape prior; {λ_o, λ_b, ω, ν, μ} is a set of weights.

First two terms in the functional represent intensity fitting errors with region-wise constants for cells and background. We design the third component as an adaptive occlusion term that dynamically penalizes overlapped contours based on overlapped contour number. With theory of sparse representation [22], we introduce to the variational model a shape reconstruction error by approximating the shape of interest with a sparse linear combination of manually extracted shape priors. All shape priors are aligned with generalized Procrustes analysis [23]. The last two terms regulate zero level set smoothness, drive contour to strong edges, and maintain the signed distance property for computation stability.

3. Experiments and Results

We test our method on a set of histological images of H&E stained GBM specimens captured at 40 × magnification. The whole image dataset consists of 40 image patches of interest, with 0.2265 micrometer per pixel. The total number of human annotated cells for seed detection and boundary segmentation is 5396 and 237, respectively. We apply the proposed seed detection method to GBM dataset with the following parameter setup: r = 10, S = {s_i|3, 3.3, 3.6, …, 10}, α = β = 10, D₁ = 15, D₂ = 25. Moderate variations to this set can lead to similar results.

For quantitative analysis, we assess performance of seed detection methods with reference to human annotations that serve as ground truth. Note that we evaluate our approach with non-touching and occluded cells in each image separately. Four metrics are computed from each image to show seed detection performance: Cell Number Error (C), Miss Detection (M), False Recognition (F), Over Segmentation (O), and Under Segmentation(U). Cell Number Error is used to demonstrate the absolute difference between the number of cells detected by machine and that reported by human expert. Miss and False Detection represent the number of missing and false recognition events when machine-based seed detection method is used to detect individual cells with no occluded neighbors. Meanwhile, we use Over and Under Segmentation to record events where the number of machine-identified cells from a cell clump is more and less than the true number marked by human expert, respectively. The resulting outputs are shown in Table 1. Additionally, we compare our method with an oriented kernel-based iterative voting method [24]. By contrast to our method, the iterative voting method tends to miss detecting cells. We illustrate seed detection results from both methods on two typical images in Figure 4. For cell contour deformation, we have λ_o = λ_b = 1, ω = 2000, ν = μ = 5000, and ξ = 2. Typical seed detection and final contour deformation results are shown in Figure 5 where cell boundaries are color coded. Importantly, our method can recognize occluded cells with seed detection method and successfully recover their overlapped boundaries. We validate the final cell boundaries using human annotations, with Jaccard coefficient J = 0.70 ± 0.14, Precision P = 0.96 ± 0.10, Recall R = 0.73 ± 0.15, and Hausdorff distance d = 5.97 ± 4.87.

Table 1.

Image-wise seed detection performance. The aggregated rates of these metrics in reference to the true number of cells are also shown in the last column.

Metric	Mean	Std	Med	Min	Max	Overall Rate
C	2.15	1.51	2.00	0.00	5.00	1.59%
M	2.85	1.99	2.00	0.00	7.00	2.11%
F	1.30	1.18	1.00	0.00	5.00	0.96%
O	0.33	0.66	0.00	0.00	3.00	0.24%
U	0.50	0.72	0.00	0.00	2.00	0.37%

Fig. 4.

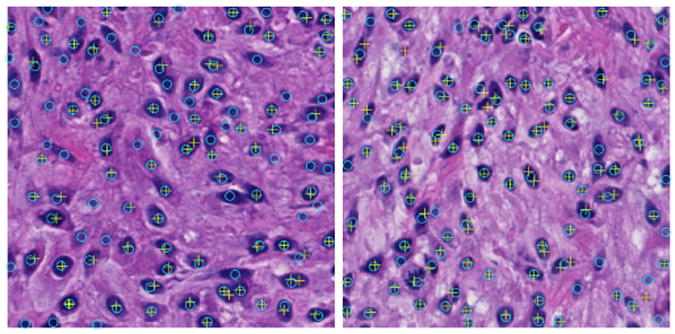
Comparisons of seed detection results between our method (cyan circle) and iterative voting [24] (yellow cross).

Fig. 5.

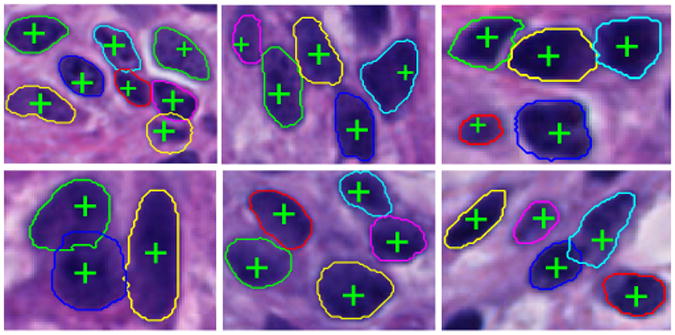
Typical results of cell seed detection and contour deformation by our modified variational level set method.

4. Conclusions

In this paper, we present a robust cell segmentation method for high-resolution histological imaging data, with capability to recover boundaries of occluded cells commonly seen in histology samples. This new method first detects cells with seed connectivity, distance constraints, image edge map, and a shape-based voting image. Next, it deforms cell boundaries with an improved variational level set method that can handle occluded cells. We apply our method to a histological image dataset of GBM specimens. Validation results suggest our method is promising for segmentation of touching cells and could prove important to cancer research.