Incorporating a Spatial Prior into Nonlinear D-Bar EIT Imaging for Complex Admittivities

Abstract

Electrical Impedance Tomography (EIT) aims to recover the internal conductivity and permittivity distributions of a body from electrical measurements taken on electrodes on the surface of the body. The reconstruction task is a severely ill-posed nonlinear inverse problem that is highly sensitive to measurement noise and modeling errors. Regularized D-bar methods have shown great promise in producing noise-robust algorithms by employing a low-pass filterin of nonlinear (nonphysical) Fourier transform data specifi to the EIT problem. Including prior data with the approximate locations of major organ boundaries in the scattering transform provides a means of extending the radius of the low-pass filte to include higher frequency components in the reconstruction, in particular, features that are known with high confidence This information is additionally included in the system of D-bar equations with an independent regularization parameter from that of the extended scattering transform. In this paper, this approach is used in the 2-D D-bar method for admittivity (conductivity as well as permittivity) EIT imaging. Noise-robust reconstructions are presented for simulated EIT data on chest-shaped phantoms with a simulated pneumothorax and pleural effusion. No assumption of the pathology is used in the construction of the prior, yet the method still produces significant enhancements of the underlying pathology (pneumothorax or pleural effusion) even in the presence of strong noise.

I. Introduction

Electrical Impedance Tomography (EIT) is a non-invasive radiation-free imaging modality in which low amplitude current is applied through electrodes placed on the surface of a body and the resulting voltages are measured. From these surface measurements, images of the interior conductivity and permittivity can be obtained. The severe ill-posedness of the inverse conductivity/permittivity problem limits the spatial resolution of the reconstructed images, which hinders their clinical applicability. Mathematical stability estimates for the problem can be found in [1], [2], [3], [4], for example. The use of spatial a priori information in the solution of the inverse problem provides a means of including anatomical information that is present with high confidence while still allowing unknown features such as lung pathologies to emerge in the reconstructed image without any assumption of their presence. In patients with serious respiratory illness, it is often the case that a CT scan is performed to obtain a diagnosis or for a regular exam in the case of a chronic illness, and the condition is monitored with one or more follow-up scans. The initial scan can provide basic a priori information for the reconstruction algorithm such as chest shape, approximate lung and heart sizes, and relative positions in the plane of the electrodes.

The state-of-the-art of EIT in critical care thoracic imaging is to image 2-D slices in the plane of a belt of electrodes placed around the thorax [5], [6], [7], [8], [9], [10]. Estimates of alveolar collapse and compliance can be determined from reconstructions of impedance changes in lung regions in these slices, and the gravitational vector inside the lung can be taken into account [11]. Ventilation and perfusion maps can also be created in these slices in real time, providing a method of monitoring PEEP titration [7].

A priori information has been used successfully in iterative reconstruction algorithms to enhance image quality (see, for example, [12], [13], [14], [15], [16], [17], [18], [19], [20], [21] for a partial list), and more recently in [22] in the direct 2-D D-bar method for (real-valued) conductivity reconstruction. In this paper, the method of [22] is extended to the 2-D D-bar algorithm for the reconstruction of complex admittivities [23], [24], [25]. The reconstruction algorithm for complex admittivities differs from the D-bar algorithm for real-valued conductivities in the construction of the complex geometrical optics (CGO) solutions. While the well-developed real-valued case [26], [27], [28], [29], [30] utilizes the familiar transformation of the generalized Laplace equation governing the physical EIT problem to a Schrödinger equation, the complex admittivity algorithm requires transforming the problem to a firs order elliptic system and constructing two sets of CGO solutions. The algorithm is described briefl in Section 2, and the reader is referred to [23], [24], [25] for further detail. In [22] a method of including a priori information in the 2-D D-bar algorithm for real-valued conductivities was proposed and proved to be a nonlinear regularization strategy. It was tested on simulated data on a circular domain. The 2-D D-bar algorithm for reconstructing complex admittivities differs from the algorithm in [22] in several ways. First, a 2 × 2 elliptic system of equations must be solved to recover the complex admittivity, and so the scattering transform becomes a scattering matrix, and a system of firs order PDEs in ∂_z and ∂_z̄ arises for the CGO solutions. In contrast to the method in [22], there are, in fact, two sets of CGO solutions to compute (described in SectionII-B). Second, in contrast to [22], determining the admittivity requires an additional computational step beyond evaluation of the CGO solution at complex frequency k = 0, as is the case for the methods based on [31]. In this work, the a priori information is included in the high-frequency component of the scattering matrix and in the appropriate CGO solution computations, which consist of two decoupled systems of integral equations. Thus, while the a priori information is in the analogous functions to those in [22], the overall algorithm contains some significan differences. The algorithm presented here is tested on realistic numerical phantoms on noncircular domains simulating a cross-sectional human chest. Similar phantoms have been used in, for example, [14], [32], and [33].

The method incorporates spatial a priori information about the admittivity distribution in the scattering transform, as well as in the system of D-bar equations, and includes regularization parameters in each place that can be adjusted to control the amount of influenc the prior has on the reconstruction. This approach does come at the cost of solving the forward problem once using the prior admittivity distribution. For the D-bar method, the forward problem that is solved using the prior is not the generalized Laplace equation with the complete electrode model that is typically solved at each iteration by, for example, the finit element method, but rather the equations that defin the CGO solutions. Also, depending upon how the prior is constructed, a preliminary reconstruction (that could be computed using the D-bar method with no prior, or a different method) may be required. In contrast, iterative methods include the prior in the cost functional in the regularization term, which does not come at additional computational cost. Both types of method run the risk of biasing the solution with the a priori information, and care must be taken in weighting such information. Depending upon the choice of weighting parameters, the segmented prior can be very strong or very weak. Post-processing methods also run the risk of introducing bias in the images.

The effectiveness of the method is tested here on simulated data with 0.1% and 1.0% added Gaussian relative noise for a 2-D phantom chest with a simulated pleural effusion and with a simulated pneumothorax. No a priori information about the presence of the effusion or the pneumothorax is used in the reconstruction, only a priori spatial information about the heart and lung boundaries. Nevertheless, both the effusion and pneumothorax become considerably sharper than in images computed without the a priori organ boundary information.

The organ boundaries of the “heart and lungs prior” are depicted in Figure 1(a). While the initial prior is piecewise constant, after conductivity and permittivity values have been assigned, the prior is mollifie to obtain a smooth function since the method of computing the scattering transform for the prior requires that it be differentiated. Assigning the initial admittivity values to the prior can be done in a number of ways, and the a priori reconstruction algorithm presented here is valid for any assignment method. In our tests, we computed an initial reconstruction with no prior from the noisy data (which we will refer to as a standard D-bar reconstruction), then computed the maximum conductivity/permittivity in the heart region, and minimum conductivity/permittivity in each lung region of the piecewise constant “heart and lungs prior” prior, and assigned those values to each respective region of the piecewise constant prior. Further implementation details are found in Section III-B.

Fig. 1.

The “heart and lungs” phantom (a) and the test examples studied to simulate two pathologies: (b) a pneumothorax in the ventral part of the left lung and (c) a pleural effusion in the dorsal part of the left lung. The black lines correspond to true boundaries in the simulations, and the superimposed red dots are the organ boundaries used in the construction of the admittivity prior γ_PR before smoothing.

The paper is organized as follows. The a priori method is presented in Section II, which firs provides a brief description of the forward model in Subsection II-A used to simulate the EIT data, followed by a summary of the D-bar method for complex admittivity imaging in Subsection II-B, with the modification for the a priori method described in Subsection II-C. The D-bar method for admittivity reconstruction is admittedly mathematically complicated, and the reader is referred to the papers [25], [24], [34] for further details. The numerical implementation and testing of the method is outlined in Section III, and the discussion and conclusions presented in Section IV.

II. Methods

A. The forward model

The electric potential u(x, y) inside the 2-D region Ω is modeled by the admittivity equation, a generalized Laplace equation,

$$\nabla ·\gamma (x,y)\nabla u(x,y)=0,$$ (1)

where γ(x, y) = σ(x, y)+iωε(x, y) denotes the complex valued admittivity, σ(x, y) the electrical conductivity (bounded away from zero 0 < σ(x, y) < C), ε(x, y) the electrical permittivity (assumed to be non-negative), and ω the angular frequency of the applied current. The boundary data for the inverse problem is the Dirichlet-to-Neumann (DN) map Λ_γ which maps a voltage at the boundary to the corresponding current density, i.e., ${{\mathrm{\Lambda }}_{\gamma }:u\mid }_{\partial \mathrm{\Omega }}\mapsto \gamma {\frac{\partial u}{\partial v}|}_{\partial \mathrm{\Omega }}$, where ν denotes the outward unit normal vector to the boundary ∂Ω. In practice, to dampen rather than amplify the noise in the measured data, currents are applied and the resulting voltages are measured. This corresponds to knowledge of the Neumann-to-Dirichlet ND map $R_{\gamma }:\gamma {\frac{\partial u}{\partial v}\mid }_{\partial \mathrm{\Omega }}\mapsto {u|}_{\partial \mathrm{\Omega }}$. Ensuring conservation of charge and specifying a ground, the ND map can be inverted to obtain the DN map Λ_γ = (R_γ)⁻¹.

For the simulation of the data, a finit element implementation of the complete electrode model (CEM) was used. The CEM [35] takes into account both the shunting effect of the electrodes and the contact impedances between the electrodes and tissue. The complete electrode model consists of the admittivity equation (1) and the following boundary conditions on L electrodes:

$$\begin{array}{ll}\hfill u+z_l\gamma \frac{\partial u}{\partial v}& =U_l,x\in e_l,l=1,2,\dots ,L\hfill \\ \hfill {\int }_{e_l}\gamma \frac{\partial u}{\partial v}dS& =J_l,x\in e_l,l=1,2,\dots ,L\hfill \\ \hfill \gamma \frac{\partial u}{\partial v}& =0,x\in \partial \mathrm{\Omega }\backslash {\cup }_{l=1}^L{e}_l,\hfill \end{array}$$

where z_l is the effective contact impedance between the l^th electrode e_l and the medium, J_l is the applied current, and U_l is the measured voltage. In addition, Kirchhoff’s Law and the choice of ground must be imposed to ensure existence and uniqueness of the result:

$$\sum _{l=1}^L{J}_l=0,\text{and}\sum _{l=1}^L{U}_l=0.$$

The uniqueness and existence of a solution to the CEM has been proven in [36].

Since the D-bar method, described below, relies on CGO solutions to equations that do not include the CEM, there is an inherent modeling error introduced in the reconstructions.

B. The D-bar method for complex admittivities

D-bar methods are named for the partial derivatives with respect to the complex conjugates that arise in the equations in the methods. The ∂̄ operator with respect to the complex variable z = x +iy and the related operator ∂_z are define by

$${\overline{\partial }}_z=\frac{1}{2}\left(\frac{\partial }{\partial x}+i\frac{\partial }{\partial y}\right),{\partial }_z=\frac{1}{2}\left(\frac{\partial }{\partial x}-i\frac{\partial }{\partial y}\right).$$

Throughout the paper, ℝ² is associated with ℂ via z = (x, y) ↦ x + iy.

The method described below is based on the uniqueness proof for the inverse admittivity problem [37], which was completed as a constructive proof in [24], [23]. The work [37] was based on the real-valued paper [38] in which a 2×2 elliptic system was introduced to reduce the smoothness required in the constructive uniqueness proof [31]. An implementation of [38] was described in [39] and [40].

With the introduction of a non-physical complex parameter k, the admittivity equation (1) admits solutions with special exponentially growing behavior known as CGO solutions. In particular, it was shown in [24] that there exist separate solutions u₁(z, k) and u₂(z, k) to (1) such that $u_1(z,k)~\frac{e^{\mathit{ikz}}}{ik}$ and $u_2(z,k)~-\frac{e^{-ik\overline{z}}}{ik}$ for large |k| or |z|.

Definin an operator vector 𝒟 = γ^1/2(∂_z, ∂̄_z)^T, the change of variables

$$Q(z)=\left[\begin{array}{cc}0& -\frac{1}{2}{\partial }_{\mathrm{z}}log\gamma (z)\\ -\frac{1}{2}{\overline{\partial }}_{\mathrm{z}}log\gamma (z)& 0\end{array}\right],$$ (2)

and

$${(M_{11},M_{21})}^T=e^{-\mathit{ikz}}\mathcal{D}{u}_1,{(M_{12},M_{22})}^T=e^{ik\overline{z}}\mathcal{D}{u}_2$$ (3)

transform the admittivity equation (1) into the firs order elliptic system [37]

$$D_{k}M(z,k)-Q(z)M(z,k)=0,$$ (4)

where

$$D_{k}M(z,k)=\left[\begin{array}{cc}{\overline{\partial }}_{\mathrm{z}}& 0\\ 0& {\partial }_{\mathrm{z}}\end{array}\right]M-ik\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]\left[\begin{array}{cc}0& M_{12}\\ M_{21}& 0\end{array}\right].$$

Equation (5) has a unique solution M(·, k) where each component of M(·, k) − I is in L^p(ℝ²) for some p > 2, where I denotes the 2×2 identity matrix.

D-bar methods follow the basic computational outline:

$$\mathbf{DN}\mathbf{map}\mapsto \underset{\mathbf{Data}}{\mathbf{Scattering}}\mapsto \underset{\mathbf{Solutions}}{\mathbf{CGO}}\mapsto \mathbf{Admittivity}.$$

The scattering data is a 2×2 matrix function S(k), not directly physically measurable from the data, with zero entries on the diagonal and off-diagonal entries given by

$$\begin{array}{l}{S}_{12}(k)=\frac{i}{\pi }{\int }_{\mathrm{\Omega }}{Q}_{12}(z)e(z,-\overline{k})M_{22}(z,k)\mathit{dxdy}\\ S_{21}(k)=-\frac{i}{\pi }{\int }_{\mathrm{\Omega }}{Q}_{21}(z)e(z,k)M_{11}(z,k)\mathit{dxdy}\end{array}$$ (5)

where e(z, k) ≡ e^i(kz+k̄z̄) and supp Q(z) ⊆ Ω̄ from (2).

The DN map Λ_γ uniquely determines the scattering data S(k), and the scattering data uniquely determines the admittivity γ(z) [37]. However, the relationship between the scattering data and the DN map relies on the intermediate computation of the CGO solutions u₁ and u₂ on the boundary of Ω as well as functions Ψ₁₂(z, k) ≡ e^−ikz̄ M₁₂(z, k) and Ψ₂₁(z, k) ≡ e^ikz M₂₁(z, k). This is described in Step 1 below.

Step 1: From Boundary Measurements to Scattering Data

For each |k| ≤ R, solve the following two boundary integral equations

$$\begin{array}{l}{u}_1(z,k)=\frac{e^{\mathit{ikz}}}{ik}=\underset{\partial \mathrm{\Omega }}{\int }{G}_k(z-\zeta )\left(\delta {\mathrm{\Lambda }}_{\gamma }\right)u_1(\zeta ,k)ds(\zeta )\\ u_2(z,k)=-\frac{e^{-ik\overline{z}}}{ik}-\underset{\partial \mathrm{\Omega }}{\int }{G}_k(\overline{\zeta }-\overline{z})\left(\delta {\mathrm{\Lambda }}_{\gamma }\right)u_2(\zeta ,k)ds(\zeta )\end{array}$$ (6)

for the traces of the CGO solutions u₁ and u₂ on the boundary. Here G_k (z) denotes the Faddeev Green’s function for the Laplace operator given by (see [41], [42]),

$$G_k(z)=e^{\mathit{ikz}}{\int }_{{ℝ}^2}\frac{e^{iz·\xi }}{\xi (\overline{\xi }+2k)}d\xi ,$$

and δΛ_γ = Λ_γ − Λ₁ where Λ₁ denotes the DN map corresponding to a constant admittivity 1 and γ = 1 near ∂Ω. Provided that γ is a constant γ_b near ∂Ω, the DN map can be scaled as in [28].

Next, compute the traces of the CGO solutions Ψ₁₂ and Ψ₂₁ from the second set of boundary integral equations

$$\begin{array}{l}{\mathrm{\Psi }}_{12}(z,k)=p.v.\underset{\partial \mathrm{\Omega }}{\int }\frac{e^{i\overline{k}(z-\zeta )}}{4\pi (z-\zeta )}\left(\delta {\mathrm{\Lambda }}_{\gamma }\right)u_2(\zeta ,k)ds(\zeta )\\ {\mathrm{\Psi }}_{21}(z,k)=p.v.\underset{\partial \mathrm{\Omega }}{\int }\overline{\left[\frac{e^{ik(z-\zeta )}}{4\pi (z-\zeta )}\right]}\left(\delta {\mathrm{\Lambda }}_{\gamma }\right)u_1(\zeta ,k)ds(\zeta ),\end{array}$$ (7)

where p.v. denotes the principal value of the integral.

Then, compute the scattering transforms S₁₂(k) and S₂₁(k):

$$\begin{array}{l}{S}_{12}(z,k)=\frac{i}{2\pi }\underset{\partial \mathrm{\Omega }}{\int }{e}^{-i\overline{k}z}{\mathrm{\Psi }}_{12}(z,k)\nu (z)ds(z)\\ S_{21}(z,k)=-\frac{i}{2\pi }\underset{\partial \mathrm{\Omega }}{\int }{e}^{i\overline{k}\overline{z}}{\mathrm{\Psi }}_{21}(z,k)\overline{\nu (z)}ds(z),\end{array}$$ (8)

where ν(z) = (ν₁(z), ν₂(z)) = ν₁(z) + iν₂(z) denotes the outward unit normal to ∂Ω at the point z, and $\overline{\nu (z)}$ denotes its complex conjugate. The parameter R acts as a low-pass cutoff radius of the scattering data used to stabilize the reconstruction method in the presence of noise. The scattering data is set to zero for |k| > R. This approach has been proved to be a nonlinear regularization strategy in the case of real-valued conductivities [43]. Parallel computing can be used to solve equations (7)–(9) since each of these equations is solved for each k independently. Further implementation details are found in Section III-B.

Step 2: Computation of CGO Solutions

Let $\overline{{\mathrm{\Omega }}^{+}}$ be a domain slightly larger than Ω. This will be needed to numerically compute the ∂_z and ∂̄_z derivatives of the CGO solutions M(z, 0) required to form the matrix potential Q(z) in Step 3. For each $z\in \overline{{\mathrm{\Omega }}^{+}}$, solve the ∂̄_k equation

$${\overline{\partial }}_{k}M(z,k)=M(z,\overline{k})\left[\begin{array}{cc}e(z,\overline{k})& 0\\ 0& e(z,-k)\end{array}\right]S(k),$$ (9)

using the fundamental solution $\frac{1}{\pi k}$ for the ∂̄_k operator, by solving the decoupled systems

$$\{\begin{array}{ll}{M}_{11}(z,k)\hfill & =1+\frac{1}{\pi k}\ast [M_{12}(z,\overline{k})e(z,-k)S_{21}(k)]\hfill \\ M_{12}(z,k)\hfill & =0+\frac{1}{\pi k}\ast [M_{11}(z,\overline{k})e(z,\overline{k})S_{12}(k)]\hfill \end{array}$$ (10)

$$\{\begin{array}{ll}{M}_{21}(z,k)\hfill & =0+\frac{1}{\pi k}\ast [M_{22}(z,\overline{k})e(z,-k)S_{21}(k)]\hfill \\ M_{22}(z,k)\hfill & =1+\frac{1}{\pi k}\ast [M_{21}(z,\overline{k})e(z,\overline{k})S_{12}(k)].\hfill \end{array}$$ (11)

The convolutions * take place in k over the disc of radius R as S_ij (k) now has compact support. The systems are solved numerically as in [44].

Step 3: From CGO Solutions to the Admittivity

Using the CGO solutions corresponding to k = 0, compute the potentials (only one is actually needed)

$$\begin{array}{l}{Q}_{12}(z)=\frac{{\partial }_{\mathrm{z}}[M_{11}(z,0)+M_{12}(z,0)]}{M_{22}(z,0)+M_{21}(z,0)}\\ Q_{21}(z)=\frac{{\overline{\partial }}_{\mathrm{z}}[M_{22}(z,0)+M_{21}(z,0)]}{M_{11}(z,0)+M_{12}(z,0)},\end{array}$$ (12)

and from these, compute the admittivity γ(z) using either

$$\gamma (z)=exp\left\{-\frac{2}{\pi \overline{z}}\ast Q_{12}(z)\right\}=exp\left\{-\frac{2}{\pi z}\ast Q_{21}(z)\right\},$$ (13)

where the convolution in z takes place over Ω̄ since Q has compact support.

The reader is referred to [25], [23], [34] for developments and implementations of numerical algorithms for complex D-bar EIT imaging.

C. Inclusion of a priori admittivity information

The low-pass filterin (setting S(k) = 0 for |k| > R) in the non-physical scattering domain has an effect similar to that of traditional low-pass filterin in the standard Fourier domain. As |k| → ∞, M(·, k) ~ I and thus the scattering data in (5) reduces to $S_{12}(k)\approx \frac{i}{\pi }\widehat{Q_{12}}(2k_1,2k_2)$ and $S_{21}(k)\approx -\frac{i}{\pi }\widehat{Q_{21}}(-2k_1,2k_2)$. Thus, for large |k| the scattering data are essentially shifted Fourier transforms of the potential Q(z). Hence, it is reasonable to expect a loss of sharp edges in reconstructions of γ(z) from the low-pass filtere scattering data.

In practice, the scattering data computed via the boundary integral equations (9) “blows up” in magnitude as |k| increases, sometimes as early as |k| = 3.5 due to the presence of noise. The relationship between blow-up in the scattering transform and noise was established for the real-valued D-bar method in [43], where a bound was established on the error in the scattering transform in a disk whose radius is a function of the noise level. In the absence of noise, the scattering transform can be computed with high fidelit in a disk of large radius [43], [30], [42]. This motivates the use of a scattering transform computed from the forward problem for the prior in an annulus outside the disk of the experimental scattering data. This approach differs significantl from the methods based on post-processing D-bar conductivity images [45], [46].

The original scattering data is augmented by the scattering data that corresponds to the prior outside the feasible region of computation of the true scattering data. Denoting the scattering data from the admittivity prior by S^PR, and the feasible region of computation by |k| ≤ R, we form the new extended scattering data via the formula

$$S_{R,R_2}(k):=\{\begin{array}{ll}S(k)\hfill & \mid k\mid \le R\hfill \\ {\mathrm{S}}^{\text{PR}}(k)\hfill & R<\mid k\mid \le R_2\hfill \\ 0\hfill & R_2<\mid k\mid ,\hfill \end{array}$$ (14)

where S(k) is computed from current and voltage measurements using (9) for |k| ≤ R. The truncation radius R₂ controls the amount of influenc the inclusion of S^PR has on the reconstruction. The larger R₂, the greater the influence When R₂ = R, there is no inclusion of S^PR. Note that since | S^PR| → 0 as |k| → ∞, the influenc of S^PR does not grow without bound as R₂ increases.

The second place that a priori information is included in the reconstruction method is in the integral forms of the D-bar equations, systems (11) and (12). The +1 and +0 terms in (11), (12) arise from terms of the form

$$\underset{R\to \infty }{lim}\frac{1}{\pi R^2}{\int }_{\mid k\mid \le R}{M}_{ij}(z,k)dk,i,j=1,2,$$ (15)

whose limits are 0 for M₁₂ and M₂₁ and 1 for M₁₁ and M₂₂. Analogously to [22], to include a priori information encoded in the CGO solutions, the terms in (16) are replaced by a weighted integral, which we will denote by

$${\mathrm{M}}_{\text{ij}}^{int}\equiv \{\begin{array}{l}\alpha +(1-\alpha ){\int }_{\mid k\mid \le R_2}{M}_{ij}^{\text{PR}}(z,k)dk,i=j,\hfill \\ 0+(1-\alpha ){\int }_{\mid k\mid \le R_2}{M}_{ij}^{\text{PR}}(z,k)dk,i\ne j\hfill \end{array}$$ (16)

Note, when α = 1 and R₂ = R the method reduces to the original D-bar method of Subsection II-B without a priori information. Using α = 0 corresponds to the heaviest weighting of (i.e. greatest trust in) the prior for the replacement of the asymptotic condition.

We summarize the steps of the a priori method. The fina approximation to the admittivity is denoted by γ_new.

Step 0: Setup

Compute the DN map Λ_γ from the voltage and current measurements and determine an admittivity prior γ_PR.

Step I: Computation of Scattering Data S_R,R2

Compute the extended scattering S_R,R2 via (15). This involves using Step 1 of Subsection II-B to compute the traditional scattering data S(k) for |k| ≤ R. To obtain S^PR computationally, the smoothed admittivity prior is firs used to compute the potential Q^PR via (3). Then, for |k| ≤ R₂, the system (5) is solved, and the resulting matrix of CGO solutions is denoted by M^PR(·, k). The scattering data S^PR(k) is then computed via (6) using Q^PR and M^PR in these equations.

Step II: Computation of CGO solutions

Using the extended scattering data S_R,R2, solve the systems (11) and (12) with (17) replacing the constant terms 0 and 1 to obtain CGO solutions M_ij (z, k), i, j = 1, 2, z ∈ Ω, where

$$\begin{array}{ll}{M}_{11}(z,k)\hfill & ={\mathrm{M}}_{11}^{int}+\frac{1}{\pi k}\ast [M_{12}(z,\overline{k})e(z,-k)S_{21}(k)]\hfill \\ M_{12}(z,k)\hfill & ={\mathrm{M}}_{12}^{int}+\frac{1}{\pi k}\ast [M_{11}(z,\overline{k})e(z,\overline{k})S_{12}(k)]\hfill \\ M_{21}(z,k)\hfill & ={\mathrm{M}}_{21}^{int}+\frac{1}{\pi k}\ast [M_{22}(z,\overline{k})e(z,-k)S_{21}(k)]\hfill \\ M_{22}(z,k)\hfill & ={\mathrm{M}}_{22}^{int}+\frac{1}{\pi k}\ast [M_{21}(z,\overline{k})e(z,\overline{k})S_{12}(k)].\hfill \end{array}$$ (17)

Step III: From CGO solutions to the Admittivity γ_new(z)

This is computed in the same manner as Step 3 in Subsection II-B to obtain γ_new(z) via (13) using M_ij (z, k), i, j = 1, 2, and subsequently (14).

III. Simulation and Implementation

A. Simulation of Voltage Data

The FEM was used to simulate voltages for each of the test problems using the Complete Electrode Model (CEM) on the chest-shaped domain in Figure 1 of perimeter 1016 mm, with L = 32 electrodes of length 22 mm and height 13.5 mm (area 297mm^2.) The contact impedance was set to 2.4×10⁻³ on all electrodes, and trigonometric current patterns with amplitude C = 1 mA were used. The trigonometric current patterns are given by

$$T_{\ell }^j:=\{\begin{array}{ll}C\text{cos}(j{\theta }_{\ell })\hfill & 1\le \ell ,1\le j\le \frac{L}{2}\hfill \\ Csin((\frac{L}{2}-j){\theta }_{\ell })\hfill & 1\le \ell ,\frac{L}{2}+1\le j\le L-1,\hfill \end{array}$$ (18)

where ${\theta }_{\ell }=\frac{2\pi \ell }{L}$ corresponds to the angle of the center point z_ℓ = R (θ_ℓ) e^iθ_ℓof the ℓ-th electrode e_ℓ. The quantity $T_{\ell }^j$ therefore represents the current applied on e_ℓ corresponding to the j-th current pattern. Note that L−1 linearly independent current patterns were applied since L electrodes were used in the simulations.

Zero mean Gaussian relative noise was added to each complex-valued vector of simulated voltages V^j in the same manner as [25] as follows. Let η denote the desired noise level and N^j a vector of Gaussian zero mean noise that is unique for each current pattern j (and each test scenario). Then, the real and imaginary parts of the noisy voltage data Ṽ^j were computed as

$$\begin{array}{ll}\mathfrak{R}\left({\stackrel{\sim }{V}}^j\right)\hfill & =\mathfrak{R}\left(V^j\right)+\eta max\left|\mathfrak{R}\left(V^j\right)\right|N^j\hfill \\ \mathfrak{J}\left({\stackrel{\sim }{V}}^j\right)\hfill & =\mathfrak{J}\left(V^j\right)+\eta max\left|\mathfrak{J}\left(V^j\right)\right|N^j.\hfill \end{array}$$ (19)

The discrete approximation ${\mathrm{\Lambda }}_{\gamma }^M$ to the D-N map was computed as in [27], [28], where it is formed from the inner product of the vectors of current and voltage, which are discrete approximations in ℂ^L−1 and ℂ^L, respectively. Denoting by $t_{\ell }^j$ the (ℓ, j)-th entry of the matrix of applied currents with each column normalized with respect to the l²-vector norm, $t_{\ell }^j=\frac{T^j}{{\Vert T^j\Vert }_2}$, let $v_{\ell }^j$ denote the entries of the j-th voltage vector normalized so that ${\sum }_{\ell =1}^L{v}_{\ell }^j=0$ and $v_{\ell }^j=\frac{V_{\ell }}{{\Vert T^j\Vert }_2}$. Let |e_ℓ| denote the area of the ℓ-th electrode. Then ${\mathrm{\Lambda }}_{\gamma }^M={(R_{\gamma }^M)}^{-1}$ where the (m, n)-th entry of $R_{\gamma }^M$ is given by

$$R_{\gamma }^M(m,n):=\frac{{\gamma }_b}{\mid e_{\ell }\mid }\sum _{\ell =1}^L{t}_{\ell }^m{v}_{\ell }^n,$$ (20)

where γ_b denotes the background admittivity near ∂Ω.

We consider two phantoms with simulated pathologies depicted in Figure 1: (b) a pneumothorax, (c) a pleural effusion. For both scenarios, the admittivity of the heart was 1.1+0.6i S/m, the lungs 0.5+0.4i S/m, and the background 0.8 + 0.4i S/m. The pneumothorax was set to 0.25 + 0i S/m and the pleural effusion to 1.1 + 0.6i S/m. All images are shown in DICOM orientation in which the left lung is on the viewer’s right, as if viewed from the subject’s feet.

B. Implementation of the a priori method

In this paper, the admittivity prior γ_PR was computed using a standard D-bar reconstruction γ_DB recovered using Steps 1–3 of Section II-B with the measured data Λ_γ. However, in practice, any initial prior γ_PR can be used, making the method easily adaptable to other approaches.

Step 0

The matrix approximation to the DN map Λ_γ was formed using the noisy voltages computed from the CEM. The admittivity prior γ_PR was formed as follows. First the standard D-bar reconstruction γ_DB was computed using Steps 1–3 of Section II-B (see [25] for details regarding the computation of γ_DB). Next, using the “heart and lungs prior” (see the red dots of Figure 1), the maximum value of the pixels in the heart region and minimum pixel value in each lung region were computed, and the corresponding value assigned to each region to form the admittivity prior γ_PR. Note that the spatial prior does not assume any pathology is present. The prior γ_PR was then mollifie to a C¹ smooth version and Q^PR computed using finit differences for the ∂_z and ∂̄_z derivatives of log (γ_PR(z)).

Step I

The extended scattering data S_R,R2 was computed via (15). Using the DN maps Λ_γ and Λ₁, the traditional scattering data S(k) for |k| ≤ R was determined via Step 1 of Section II-B. The reader is referred to [25] for the computational details of computing u₁ and u₂ and subsequently ψ₁₂ and ψ₂₁. Briefl, the Fredholm integral equations for u₁ and u₂ (7) are solved by a Galerkin method, and the integrals for evaluating ψ₁₂ and ψ₂₁ and scattering data S(k), |k| ≤ R in (9) are computed using a Simpson’s rule, with the 32 electrode centers on the boundary as the discretization points in the quadrature. This is suitable since these are the points in z for which Ψ₁₂ and Ψ₂₁ are known, and since the scattering transforms are not highly oscillatory at the values of k for which they are computed here. The scattering prior S^PR was determined as follows. First, the admittivity prior γ_PR is smoothed to compute the potential Q^PR via (3). Then, for |k| ≤ R₂, the system (5) was solved for M^PR using Fourier transforms on the following two decoupled systems:

$$\begin{array}{l}\{\begin{array}{ll}{M}_{11}^{\text{PR}}(z,k)\hfill & =1+\frac{1}{\pi z}\ast [Q_{12}^{\text{PR}}(z)M_{21}^{\text{PR}}(z,k)]\hfill \\ M_{21}^{\text{PR}}(z,k)\hfill & =0+\frac{e(z,-k)}{\pi \overline{z}}\ast [Q_{21}^{\text{PR}}(z)M_{11}^{\text{PR}}(z,k)]\hfill \end{array}\\ \{\begin{array}{ll}{M}_{12}^{\text{PR}}(z,k)\hfill & =0+\frac{e(z,\overline{k})}{\pi z}\ast [Q_{12}^{\text{PR}}(z)M_{22}^{\text{PR}}(z,k)]\hfill \\ M_{22}^{\text{PR}}(z,k)\hfill & =1+\frac{1}{\pi \overline{z}}\ast [Q_{21}^{\text{PR}}(z)M_{12}^{\text{PR}}(z,k)],\hfill \end{array}\end{array}$$ (21)

where the convolutions take place in z over Ω. Using a uniform z-grid of size 2^m × 2^m with stepsize h, convolutions such as $\frac{1}{\pi z}\ast f(z)$ can be implemented as

$$\frac{1}{\pi z}\ast f(z)=h^2\text{IFFT}2\left(\text{FFT}2\left(\frac{1}{\pi z}\right)\text{FFT}2(f(z))\right).$$

A matrix-free solution of the resulting system for each value of z was computed using GMRES with the parameters (RESTART=10, tol= 10⁻⁶, and MAXIT=50). The system can be solved in parallel for each z in Ω. The scattering prior is then evaluated via (6) using Simpson’s rule, and the combined scattering data S_R,R2 is subsequently formed via (15).

Step II

Choose a regularization weight α ∈ [0, 1]. Using the combined scattering data S_R,R2, the CGO solutions $M_{11}^{R_2,\alpha }$ and $M_{12}^{R_2,\alpha }$ were recovered using Fourier transforms to solve the modifie equations (23)

$$\{\begin{array}{ll}{M}_{11}^{R_2,\alpha }(z,k)\hfill & =M_{11}^{int}(z)+\frac{1}{\pi k}\ast \left[M_{12}^{R_2,\alpha }(z,\overline{k})e(z,-k)S_{R,R_2}^{21}(k)\right]\hfill \\ M_{12}^{R_2,\alpha }(z,k)\hfill & =M_{12}^{int}(z)+\frac{1}{\pi k}\ast \left[M_{11}^{R_2,\alpha }(z,\overline{k})e(z,\overline{k})S_{R,R_2}^{12}(k)\right]\hfill \end{array}$$ (22)

where the convolutions take place in k over |k| ≤ R₂ and $M_{ij}^{int}$ is computed from (17) using a Simpson’s rule. An analogous system is solved to recover $M_{21}^{R_2,\alpha }$ and $M_{22}^{R_2,\alpha }$.

Step III

The new admittivity is recovered in the same manner as Step 3 of Subsection II-B to obtain γ_new(z) via (13) using finit differences on $M_{ij}^{R_2,\alpha }(z,0)$, i, j = 1, 2, and subsequently Fourier transforms to solve (14).

C. Examples

In this work, two noise levels were considered: 0.1% added relative noise and 1.0% relative noise. For each example, we present results with three values of the truncation radius R₂ in the prior, and three regularization weights for the D-bar equation: α = 0, 0.5, 1. Recall that α = 0 corresponds to the strongest weight and α = 1 to no weight given (see (17)). Due to the ill-posedness of the inverse problem, the radii R of admissible scattering data is problem specific and the scattering transform will blow up in the presence of noise at a rate that is more rapid in some directions in the k-plane than others. The value chosen for each example was chosen empirically to be as large as possible without exhibiting blow up in the initial reconstruction without a priori information. The blow-up was more rapid in the case of 1% noise, and so in those examples a non-uniform truncation of the scattering transform was used. In such cases a threshold of the scattering data S(k) was enforced by setting S_ij (k) = 0 if |ℜ(S_ij)| > 0.15 or |ℑ(S_ij)| > 0.15, where the value 0.15 was chosen empirically to be the largest permissible value of the magnitude. Determining such a threshold is intuitive from a plot of the scattering data since the blowup rate is exponential.

The admittivity prior γ_PR consisted of approximate knowledge of the organ boundaries (see Figure 1) with no assumption of pathology in the lungs. The values used for the prior are given in Table I.

TABLE I.

Admittivity values used in the examples of a simulated pneumothorax and pleural effusion in the left lung.

	Background	Left Lung	Right Lung	Heart	Pneumo.
Truth	0.8 + 0.4i	0.5 + 0.2i	0.5 + 0.2i	1.1 + 0.6i	0.25 + 0i
Prior 0.1%	0.8 + 0.4i	0.54 + 0.16i	0.52 + 0.18i	1.04 + 0.63i	N/A
Prior 1.0%	0.8 + 0.4i	0.59 + 0.15i	0.55 + 0.20i	0.98 + 0.64i	N/A

	Background	Left Lung	Right Lung	Heart	Pl. Effusion
Truth	0.8 + 0.4i	0.5 + 0.2i	0.5 + 0.2i	1.1 + 0.6i	1.1 + 0.6i
Prior 0.1%	0.8 + 0.4i	0.64 + 0.25i	0.50 + 0.20i	1.08 + 0.62i	N/A
Prior 1.0%	0.8 + 0.4i	0.65 + 0.27i	0.46 + 0.23i	1.05 + 0.69i	N/A

1) Example 1: Simulated Pneumothorax

This test problem corresponds to phantom (b) in Figure 1. The preliminary reconstruction with no prior was computed for the 0.1% added noise case using a radius of R = 4.5, and for the 1% added noise case using a nonuniform truncation with a maximum radius of R = 4.0. Table I contains the values of the true admittivity in each region as well as the values assigned to the “heart and lungs prior” for 0.1% and 1% noise. We emphasize that we assume only approximate knowledge of the boundaries of the heart and lungs (see the red dots in Figure 1(b)), and no knowledge of the presence of a pneumothorax. Figure 2 compares the true phantom to the D-bar reconstruction with no prior, as well as to the reconstructed admittivity using the new method for the strongest use of the prior (α = 0 and R₂ = 9.0) for 0.1% noise. Additional reconstructions varying the truncation radii (R₂ = 4.5, 6.75, 9.0) for the prior as well as weights (α = 0, 0.5, 1) are found in Figure 3. Reconstructions for the 1% added relative noise case with truncation radii for the prior R₂ = 4, 6, 8 and weights α = 0, 0.5, 1 are shown in Figure 4. Table II compares the ℓ₂ relative errors in the heart, right lung, healthy portion of the left lung, as well as entire left lung region for each value of the parameters R₂ and α to the D-bar reconstruction with no prior. As the true value of the pneumothorax has zero permittivity, the absolute ℓ₂ errors are given for that region rather than relative errors. Additionally, the minimum pixel value for the reconstruction in the pneumothorax region is provided.

Fig. 2.

Reconstructions for the pneumothorax example with 0.1% noise plotted on the same scale. Left: the true admittivity. Middle: the initial D-bar reconstruction γ_DB. Right: the new admittivity γ_new with strongest prior R₂ = 9.0 and α = 0 all plotted on the same scale.

Fig. 3.

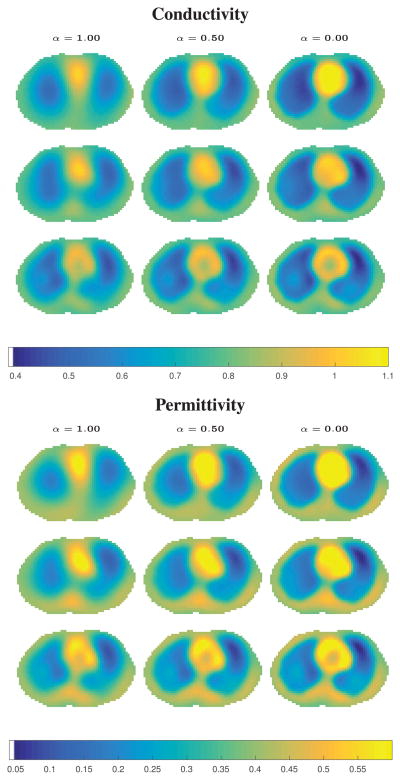
Reconstructions of simulated pneumothorax with 0.1% added noise. Regularization parameter α = 1, 0.5, 0 increases the influenc of ${\mathrm{M}}_{\text{ij}}^{int}$ as α decreases, and R₂ = 4.5, 6.75, 9.0 (rows) increases the influenc of S^PR as R₂ increases. No pneumothorax is assumed to be present in the prior. Max conductivity: 1.1608, max permittivity: 0.7983.

Fig. 4.

Reconstructions of simulated pneumothorax with 1.0% added noise. Regularization parameter α = 1, 0.5, 0 increases the influenc of ${\mathrm{M}}_{\text{ij}}^{int}$ as α decreases, and R₂ = 4, 6, 8 (rows) increases the influenc of S^PR as R₂ increases. No pneumothorax is assumed to be present in the prior. Max conductivity: 1.1187, max permittivity: 0.8820.

TABLE II.

Errors for the Pneumothorax Example: The ℓ₂ relative errors in the heart, right lung, healthy portion of the left lung, and entire left lung are listed. Additionally, for the pneumothorax region, the absolute ℓ₂ error is presented as well as the minimum pixel value in the region. Errors are listed as (Conductivity, Permittivity).

	D-bar Recon	R2 = 4.5			R2 = 6.75			R2 = 9
		α = 1	α = 0.5	α = 0	α = 1	α = 0.5	α = 0	α = 1	α = 0.5	α = 0
0.1% Noise
Heart	(22%, 29%)	(23%, 30%)	(18%, 22%)	(14%, 23%)	(22%, 28%)	(19%, 23%)	(16%, 18%)	(21%, 25%)	(19%, 21%)	(17%, 18%)
R. Lung	(29%, 52%)	(29%, 51%)	(19%, 34%)	(15%, 29%)	(26%, 43%)	(20%, 32%)	(16%, 27%)	(22%, 36%)	(19%, 31%)	(17%, 29%)
L. Lung (Healthy)	(45%, 67%)	(44%, 66%)	(32%, 45%)	(23%, 37%)	(36%, 53%)	(29%, 42%)	(23%, 36%)	(34%, 52%)	(30%, 45%)	(26%, 40%)
L. Lung (Entire)	(59%, 91%)	(58%, 90%)	(46%, 69%)	(37%, 58%)	(49%, 73%)	(42%, 63%)	(36%, 57%)	(47%, 72%)	(42%, 66%)	(39%, 62%)
Pneumo (abs ℓ2)	(3.02, 1.85)	(3.00, 1.83)	(2.61, 1.56)	(2.31, 1.35)	(2.66, 1.54)	(2.41, 1.41)	(2.21, 1.31)	(2.54, 1.50)	(2.38, 1.44)	(2.25, 1.40)
Pneumo (min)	(0.61, 0.19)	(0.61, 0.19)	(0.51, 0.12)	(0.44, 0.07)	(0.54, 0.13)	(0.47, 0.09)	(0.42, 0.06)	(0.49, 0.11)	(0.45, 0.08)	(0.41, 0.05)
1.0% Noise	D-bar	R2 = 4			R2 = 6			R2 = 8
Heart	(25%, 30%)	(25%, 30%)	(20%, 23%)	(17%, 28%)	(24%, 27%)	(21%, 23%)	(19%, 20%)	(23%, 24%)	(22%, 19%)	(20%, 16%)
R. Lung	(29%, 48%)	(28%, 48%)	(18%, 33%)	(13%, 30%)	(23%, 39%)	(17%, 29%)	(13%, 25%)	(21%, 33%)	(17%, 28%)	(15%, 25%)
L. Lung (Healthy)	(43%, 54%)	(42%, 53%)	(32%, 40%)	(24%, 48%)	(36%, 42%)	(30%, 39%)	(25%, 44%)	(33%, 41%)	(29%, 40%)	(26%, 41%)
L. Lung (Entire)	(59%, 88%)	(59%, 86%)	(49%, 67%)	(41%, 65%)	(53% 69%)	(46%, 61%)	(41%, 61%)	(50%, 67%)	(45%, 63%)	(42%, 62%)
Pneumo (abs ℓ2)	(3.25, 2.11)	(3.31, 2.05)	(2.93, 1.65)	(2.63, 1.35)	(3.02, 1.66)	(2.75, 1.43)	(2.53, 1.26)	(2.93, 1.60)	(2.74, 1.47)	(2.58, 1.37)
Pneumo (min)	(0.66, 0.20)	(0.67, 0.21)	(0.59, 0.14)	(0.51, 0.07)	(0.62, 0.16)	(0.55, 0.10)	(0.49, 0.05)	(0.58, 0.12)	(0.53, 0.08)	(0.49, 0.05)

2) Example 2: Simulated Pleural Effusion

This test problem corresponds to phantom (c) in Figure 1. The preliminary reconstruction with no prior was computed for the 0.1% added noise case using a radius of R = 5.5, and for the 1% added noise case using a nonuniform truncation with a maximum radius of R = 4.5. Table I presents the values used in the prior γ_PR for each noise level and Figure 5 compares the true phantom to reconstructions using the D-bar method with no prior and the new method for the strongest weight of the prior at 0.1% added noise. Reconstructions for additional truncation radii (R₂ = 5.5, 8.25, 11) and weights (α = 0, 0.5, 1) of the prior are found in Figure 6. Reconstructions for the 1% added relative noise case with truncation radii for the prior R₂ = 4.5, 6.75, 9.0 and weights α = 0, 0.5, 1 are shown in Figure 7. Table III compares the ℓ₂ relative errors of the D-bar reconstruction with no prior to those of the new method in each region, and also gives the maximum value in the pleural effusion region.

Fig. 5.

Reconstructions for the pleural effusion example with 0.1% noise plotted on the same scale. Left: the true admittivity. Middle: the initial D-bar reconstruction γ_DB. Right: the new admittivity γ_new with strongest prior R₂ = 11.0 and α = 0 all plotted on the same scale maxed out at 1.1 + 0.6i.

Fig. 6.

Reconstructions of simulated pleural effusion with 0.1% added noise. Regularization parameter α = 1, 0.5, 0 increases the influenc of ${\mathrm{M}}_{\text{ij}}^{int}$ as α decreases, and R₂ = 5.5, 8.25, 11 (rows) increases the influenc of S^PR as R₂ increases. No effusion is assumed to be present in the prior. Max conductivity: 1.1537, max permittivity 0.7416.

Fig. 7.

Reconstructions of simulated pleural effusion with 1.0% added noise. Regularization parameter α = 1, 0.5, 0 increases the influenc of ${\mathrm{M}}_{\text{ij}}^{int}$ as α decreases, and R₂ = 4.5, 6.75, 9.0 (rows) increases the influenc of S^PR as R₂ increases. No effusion is assumed to be present in the prior. Max conductivity: 1.2452, max permittivity: 0.9699.

TABLE III.

Errors for the Pleural Effusion Example: The ℓ₂ relative errors in each region as well as the maximum pixel value in the region containing the pleural effusion. Errors are listed as (Conductivity, Permittivity).

	D-bar Recon	R2 = 5.5			R2 = 8.25			R2 = 11
		α = 1	α = 0.5	α = 0	α = 1	α = 0.5	α = 0	α = 1	α = 0.5	α = 0
0.1% Noise
Heart	(20%, 28%)	(21%, 27%)	(17%, 22%)	(13%, 19%)	(20%, 24%)	(18%, 21%)	(15%, 18%)	(20%, 24%)	(18%, 22%)	(17%, 20%)
R. Lung	(26%, 51%)	(25%, 50%)	(18%, 37%)	(15%, 29%)	(20%, 41%)	(17%, 35%)	(15%, 31%)	(19%, 39%)	(17%, 36%)	(16%, 34%)
L. Lung (Healthy)	(44%, 71%)	(43%, 69%)	(36%, 55%)	(29%, 44%)	(39%, 64%)	(35%, 58%)	(31%, 52%)	(37%, 62%)	(34%, 58%)	(32%, 54%)
L. Lung (Entire)	(30%, 34%)	(30%, 34%)	(31%, 34%)	(32%, 37%)	(30%, 33%)	(31%, 34%)	(31%, 35%)	(30%, 33%)	(30%, 33%)	(30%, 34%)
Pl. Effusion	(25%, 25%)	(26%, 24%)	(29%, 30%)	(33%, 36%)	(28%, 26%)	(30%, 29%)	(31%, 32%)	(28%, 26%)	(29%, 28%)	(30%, 30%)
Pl. Effusion (max)	(0.92, 0.52)	(0.91, 0.53)	(0.87, 0.49)	(0.83, 0.45)	(0.91, 0.54)	(0.88, 0.51)	(0.85, 0.50)	(0.87, 0.53)	(0.86, 0.53)	(0.84, 0.54)
1.0% Noise	D-bar	R2 = 4.5			R2 = 6.75			R2 = 9
Heart	(20%, 22%)	(19%, 20%)	(15%, 22%)	(13%, 34%)	(19%, 21%)	(16%, 20%)	(14%, 22%)	(18%, 17%)	(16%, 17%)	(14%, 20%)
R. Lung	(23%, 60%)	(22%, 60%)	(16%, 45%)	(19%, 37%)	(18%, 53%)	(15%, 44%)	(15%, 38%)	(14%, 48%)	(14%, 43%)	(15%, 39%)
L. Lung (Healthy)	(41%, 76%)	(39%, 73%)	(31%, 56%)	(23%, 44%)	(35%, 67%)	(29%, 58%)	(25%, 51%)	(32%, 65%)	(29%, 60%)	(26%, 56%)
L. Lung (Entire)	(32%, 37%)	(33%, 38%)	(34%, 40%)	(37%, 44%)	(33%, 38%)	(34%, 39%)	(35%, 41%)	(33%, 38%)	(33%, 39%)	(34%, 40%)
Pl. Effusion	(29%, 26%)	(31%, 30%)	(35%, 37%)	(40%, 44%)	(33%, 32%)	(35%, 36%)	(38%, 40%)	(33%, 32%)	(35%, 35%)	(36%, 37%)
Pl. Effusion (max)	(0.83, 0.48)	(0.84, 0.45)	(0.80, 0.40)	(0.76, 0.37)	(0.86, 0.46)	(0.83, 0.43)	(0.79, 0.40)	(0.84, 0.46)	(0.81, 0.44)	(0.79, 0.44)

IV. Discussion and Conclusions

In Figures 3, 4, 6, and 7, the upper left figur corresponds to the weakest/no prior, and the weight of the prior increases to the right and down the columns. It is evident that the spatial resolution of the organ boundaries improves with the introduction of the prior and as the influenc of the prior increases. The colormaps are maxed out at 1.1 for the conductivity and 0.6 for the permittivity to allow easier comparative viewing. The maximum conductivity and permittivity values always occurred for the smallest R₂ and strongest weight α = 0. In the case of the pneumothorax, no pathology is evident without the inclusion of a prior, but as the influenc of the prior increases, even though the prior includes no assumption of pathology, the pneumothorax is clearly visible in the reconstructions. However, in both the conductivity and permittivity images, a lower conductivity and permittivity region becomes evident in the dorsal right lung as well, which is an artifact of the reconstruction, and it becomes stronger as the weighting of ${\mathrm{M}}_{\text{ij}}^{int}$ increases (α = 0.5 and 0). This artifact is less pronounced in the permittivity images, and is arguably not present in the 1.0% added noise case in the permittivity images. The error norms in Table II clearly demonstrate that the introduction of the prior decreases the ℓ₂ errors for all regions of interest, as well as the minimum value in the pneumothorax region.

The presence of the simulated pleural effusion, on the other hand, is clearly evident in the reconstructions with the weakest/no prior for both conductivity and permittivity and for both noise levels. The presence of the prior improves the spatial resolution of the organs and the region of the effusion, but since the regularization results in reconstructed conductivity and permittivity functions that are smooth, there is a smooth transition from the healthy ventral portion of the left lung to the effusion, and so the boundary is far from being as sharp as in the piecewise constant phantom. In practice, image segmentation is often used on reconstructed EIT images, which would likely improve the appearance of the reconstructed images. Alternatively, once a pathology is visible, an iterative method could then be invoked as in [22] which segments the prior in the region of a possible pathology potentially sharpening the pathology even more. Post-processing approaches are left for future work. The error norms in Table III show that employing the prior greatly decreases the ℓ₂ errors for the healthy portions of the phantom and do not have a large effect on the pleural effusion region even though the prior assumes the entire left lung has an admittivity (lower rather than higher) than the background.

Although the error norms are, on average, higher for reconstructions from the higher noise levels, they are reduced by the introduction of the prior. A stronger weighting may be required to achieve an equivalent accuracy to the lower noise level. For each given α and R₂, the algorithm took approximately 35 seconds to recover the updated admittivity γ_new. The implementation was not optimized for speed and thus further speedup is attainable.

It is clear from all of these images and error norms that this method is highly effective when organ boundaries are known with some confidenc for improving the reconstructions without any bias of prior knowledge of the pathology. The influence of various qualities of prior knowledge of the boundary and organ boundaries is left for future work, as are results from experimental data. In practice, this high quality knowledge of organ boundaries corresponds to electrodes placed in the same plane as a CT scan slice. This can be accomplished with careful use of fiducia markers, and averaging of several slices to account for the fact that EIT electrodes are typically much higher than a CT scan slice, resulting in an image that corresponds to a much thicker slice.