Modelling tumour volume variations in head and neck cancer: contribution of magnetic resonance imaging for patients undergoing induction chemotherapy

SUMMARY

Primary tumour volume evaluation has predictive value for estimating survival outcomes. Using volumetric data acquired by MRI in patients undergoing induction chemotherapy (IC) these outcomes were estimated before the radiotherapy course in head and neck cancer (HNC) patients. MRI performed before and after IC in 36 locally advanced HNC patients were analysed to measure primary tumour volume. The two volumes were correlated using the linear-log ratio (LLR) between the volume in the first MRI and the volume in the second. Cox's proportional hazards models (CPHM) were defined for loco-regional control (LRC), disease-free survival (DFS) and overall survival (OS). Strict evaluation of the influence of volume delineation uncertainties on prediction of final outcomes has been defined. LLR showed good predictive value for all survival outcomes in CPHM. Predictive models for LRC and DFS at 24 months showed optimal discrimination and prediction capability. Evaluation of primary tumour volume variations in HNC after IC provides an example of modelling that can be easily used even for other adaptive treatment approaches. A complete assessment of uncertainties in covariates required for running models is a prerequisite to create reliable clinically models.

Introduction

Treatment of head-and-neck cancer (HNC) now requires complex multi-specialistic management and HNC types are typically characterised by wide heterogeneity of anatomical sites, primary treatment approaches and diagnostic pitfalls, the latter increasingly connected with procedures of optimisation of radiotherapy treatment planning ^1-4. Treatment of HNC is mainly based on integrating a chemoradiation approach ^5-7, and in this context the use of induction chemotherapy (IC) has shown a consistent number of clinical responses before the start of radiotherapy ⁸. The role of this approach is still under debate because of unclear advantages in final survival outcomes after definitive radiochemotherapy (RTCT) compared to treatment based only on concurrent RTCT ⁹. The individualisation of cancer treatment is an increasingly important topic in the medical literature ¹⁰. Starting from this background, the use of IC provides the chance to analyse changes in tumour appearance, where imaging techniques can be evaluated moving towards adaptive radiotherapy strategies ¹¹. Traditional tumour evaluation approaches, such as tumour volume delineation on simulation computed tomography, have already proven to be consistent in terms of outcome correlations ¹². The aim of this study was to evaluate the feasibility and potential outcome classification for HNC patients undergoing IC, by using MRI based primary tumour volume shrinking evaluation after IC. After modelling, survival outcomes on imaging data a nomogram followed by strict model evaluation are assessed. This evaluation procedure is the main goal of this paper, being the base of further evaluations that can be extended to other adaptive treatment procedures.

Materials and methods

Patient characteristics

Thirty-six locally-advanced HNC patients were retrospectively analysed in our institution by selecting cases that underwent IC before the administration of definitive RTCT (34 patients) or before undergoing surgery (2 patients with oral cavity cancer, these latter underwent adjuvant RTCT after surgery). All patients gave informed consent for inclusion in the study. Main selection criteria were availability of complete on-site MRI diagnostics in patients with locally advanced HNC (stage III or IV, without distant metastases). Patient staging, chemotherapy and radiotherapy details are summarised in Table I. All patients were evaluated using MRI before and after IC. After RTCT patients were evaluated by MRI at 1^st followup time to assess response to treatment. Subsequently, follow-up was routinely performed using CT, MRI and PET-CT to detect loco-regional or distant failures.

Table I.

Summary of patient characteristics and RTCT treatment.

Patient characteristics		Number	(%)
Primary tumour site	Oropharynx	15	(41.7)
	Nasopharynx	14	(38.9)
	Larynx	3	(8.3)
	Oral cavity	2	(5.5)
	Hypopharynx	1	(2.8)
	Nasal cavity	1	(2.8)
Stage	IV*	34	(94.4)
	III	2	(5.6)
	Dose [Gy]
PTV1 (primary + margin)	70.2	33	(91.6)
	68.4	1	(2.8)
	64.8	1	(2.8)
	50.4†	1	(2.8)
PTV2 (positive lymphatic compartment)	64.8	15	(41.6)
	61.2	2	(5.6)
	59.4	16	(44.4)
	50.4†	2	(5.6)
	36	1	(2.8)
PTV3 (elective lymph nodes)	64.8	2	(5.6)
	59.4	23	(63.8)
	50.4	9	(25)
	36	1	(2.8)
	30.6	1	(2.8)
RT technique	IMRT	35	(97.2)
	3D CRT	1	(2.8)
Concomitant chemotherapy	CDDP	35	(97.2)
	Cetuximab	1	(2.8)

^*No distant metastases at diagnosis.

^†One of the two post-operative patients was treated using a two volumes approach in CTV delineation, with maximum delivered dose 50.4 Gy. All treatments were delivered at 1.8 Gy per fraction.

Treatment details

IC was administered using a TPF chemotherapy regimen: taxotere 75 mg/m² (day 1), cisplatin 75 mg/m² (day 1) and 5-flurouracil 750 mg/m² in continuous infusion (days 1-4) every three weeks for 3 cycles. Radiotherapy was delivered using a linear accelerator, and the dose and technique are summarised in Table 1. Lymphatic target volumes for radiation treatment were delineated according to Gregoire's indications for neck-positive and post-operative necks ¹³. Concurrent cisplatin based chemotherapy (2 cycles at 100 mg/ m2 at the beginning of radiotherapy and after 3 weeks) was administered in 35 patients, while 1 patient received concurrent cetuximab at 250 mg/m². The outcomes evaluated were loco-regional control (LRC), disease-free survival (DFS) and overall survival (OS).

Magnetic resonance evaluation

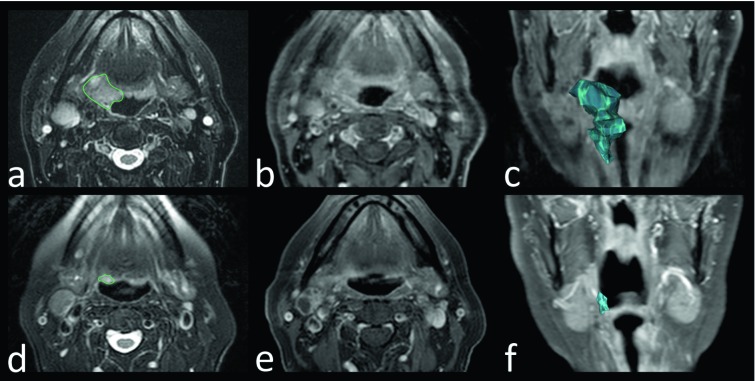
Volumetric evaluation of primary tumours was performed using OsiriX Imaging Software (http://www.osirix-viewer.com): contours of primary lesions were manually outlined by two different radiologists who are expert in HNC imaging, in order to evaluate the impact of inter-observer differences in delineation. Volumes were delineated on axial T2w images, also using other sequences, mostly T1w images, before and after intravenous contrast injection, to better refine the delineation (Fig. 1). When both radiologists were satisfied with the outlines, tumour volumes were finally calculated.

Fig. 1.

Volumetric assessment of primary tumour volume. Squamous cell carcinoma of the oropharynx in a 73-year-old man. (a,d) Axial fat-saturated T2-weighted MR images. (b,e) Axial post-contrast T1-weighted fat-saturated MR images. (c,f) Coronal post-contrast T1-weighted fat-saturated MR images with 3D volumetric tumour reconstructions. Before induction chemotherapy (a,b,c): MR images show expansive/infiltrative tissue centred on the right glossopharyngeal fold, hyper-intense on T2- weighted image (a) with slight and faint enhancement on post-contrast T1-weighted fat-saturated MR image (b). The lesion was manually outlined (green closed line in a) to obtain a volumetric reconstruction of the tumour (blue volume in c). After induction chemotherapy (d,e,f) MR images show significant volumetric reduction of the lesion.

Statistical analysis

Statistical analysis was performed using R Statistical Software (R Core Team 2013. http://www.R-project.org/). All statistical tests considered an alpha level of 5% to indicate statistical significance. The series of volumes delineated by each radiologist (labelled 'a' and 'b') before (V₁a, V₁b) and after (V₂a, V₂b) IC were analysed to detect normal distribution of values. Correlation between volumes measured at each step by each radiologist (V₁a vs. V₁b, V₂a vs V₂b) was calculated to assess homogeneity in delineation between the operators. Afterwards, two series of mean values of volumes for each diagnostic step were calculated

$$m{V}_1=\frac{V_{1}a+V_{1}b}{2}$$

,

$$m{V}_2=\frac{V_{2}a+V_{2}b}{2}$$

and used to divide patients in subsets to calculate stratified log-rank tests for survival outcomes. To define the relationship between volumes in the two diagnostic steps, two regression models were calculated, the first using linear regression between mV₂ over mV₁, and the second between mV₂ over log(mV₁). Considering the higher predictive power of the log-linear regression in describing the relationship between mV₂ and mV₁ (see results) a new score was calculated (Linear-Log-Ratio, LLR):

$$\text{LLR}=\frac{m{V}_2}{\text{log}\left(m{V}_1\right)}$$

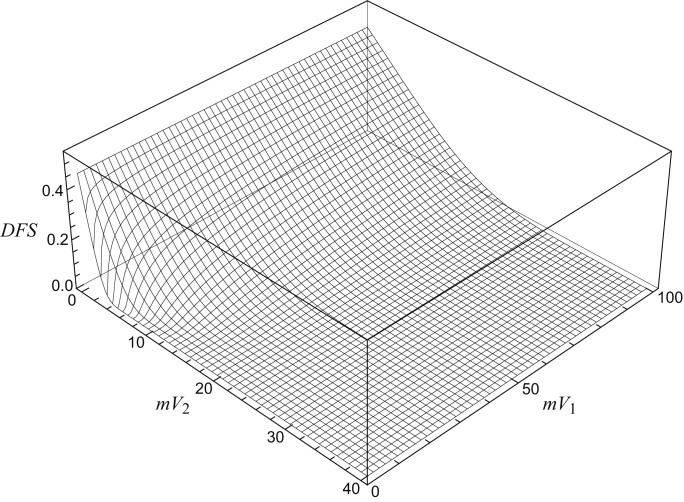
and used in Cox's proportional hazards model (CPHM) regression together with the values of mV₁ and mV₂ to find the best significant predictor for survival outcomes. Backward elimination process was used for determining the entry and removal of variables from the models with significance levels, respectively, of 0.05 and 0.15. After calculation of CPHMs, we tested the discrimination ability of the models using Harrell's c-index ¹⁴ calculated by bootstrap analysis on 1000 of a randomly created dataset based on the first. The prediction power of the models was defined using calibration plots drawn by resampling 200 cases for each model and calculating the mean prediction error as difference between observed - predicted outcome in the series ¹⁴. Considering the problem of inter- subject (but also intra-subject) variations in volume delineation that arises from the literature in many anatomical sites and using different delineation procedures or imaging modalities ^15-24, a procedure to evaluate the susceptibility of the model to variations in the delineation was defined: we created a function of mV₁ and mV₂ that gives the value of punctual uncertainty using the concept of 'gradient' of a function in two variables. The chosen function for the analysis was DFS at 24 months, achieved by CPHM. Considering the appearance of the survival function at 24 months in a three-dimensional coordinates space (Fig. 2, DFS at 24 months) as a function of two variables (mV₁ and mV₂) linked by LLR, we can easily find portions of the surface where the slope of the function is higher, corresponding to values of survival prediction with high susceptibility to variability in volume delineation. In order to provide a quantification of the value of this susceptibility the gradient of survival function was calculated using mV₁ and mV₂ as parameters of the function. Being:

$$S\left(m{V}_1,m{V}_2\right)=\text{exp}\left\{-H_{0}t·\text{exp}\left[\beta ·m{V}_2/\text{log}\left(m{V}_1\right)\right]\right\}$$

(1) the value of survival function at time t (it can be used either for LRC or DFS) with H₀t the baseline hazard at chosen time (in our case 24 months), _ the coefficient of the covariate calculated with CPHM (see Table II), we first calculated the partial derivatives of S with respect to mV₁ and mV₂ and gave a first order estimate of the variation of S as a function of mV₁ and mV₂:

$$\Delta S\left(m{V}_1,m{V}_2\right)\cong \left|\left(\frac{\partial S}{\partial m{V}_1},\frac{\partial S}{\partial m{V}_2}\right)\right|=\sqrt{{\left(\frac{\partial S}{\partial m{V}_1}\right)}^2+{\left(\frac{\partial S}{\partial m{V}_2}\right)}^2}$$

(2) The result of this equation is function of mV₁ and mV₂ only, and can be used to assess the sensitivity to error in volume delineation: it corresponds to the punctual maximum variation that survival function can show by changing the values of mV₁ and mV₂; looking at the 3D graph of survival function it is the module of the vector in one point, tangent to the direction of the highest steepness of the surface in such point. Using this method it is possible to determine both the predicted survival result and the level of uncertainty that matches the prediction given by the model. This last analysis was performed using Wolfram Mathematica® 9.0.1.0 (©1988-2013 Wolfram- Research Inc. Champaign, IL). Finally, a nomogram for DFS to directly calculate the predicted outcome using the two measures of MRI tumour volume, before and after IC (mV₁ and mV₂), was created. It was delineated using Pynomo, a program to create nomograms using Python interpreter (http://www.pynomo.org).

Fig. 2.

Plot of 3D surface showing DFS at 24 months as a function of mean tumour volume before (mV₁) and after (mV₂) induction chemotherapy: the slope of the surface can vary according to the values of the two volumes, being steeper in the left corner of the plot, where the values of mV₁ and mV₂ are close to zero.

Table II.

Summary of Cox's proportional hazards models for the LLR (Linear-Log-Ratio) covariate. All models and single LLR covariates in each model are largely significant (P-Values < 0.05 in all cases). The bootstrap over 1000 resampled series for each model allowed to calculate Harrell's c-index decreased by the 'optimism' for preventing model overfitting in starting case series. The performance of models is very close to the original c-index in all cases, meaning high discriminating power. The evaluation of the mean error of prediction of survival outcomes at 24 months, through calibration on 200 resampled cases, is also provided.

Summary of Cox's Proportional Hazards Regression models with unique significant covariate
Outcome	Model P-value (Likelihood ratio test)	Standard error	P-value Pr(> |z|)	Standard error	Harrell's c-index (c)	Optimism (Op)	Corrected Harrell's c-index (c – Op/2)	Mean calibration error (24 months prediction)
LRC	0.0013060	0.4271	0.000788	0.1272	0.7668	0.0105	0.7615	0.073
DFS	0.0006376	0.3427	0.000234	0.0931	0.7546	0.0034	0.7529	0.056
OS	0.0008928	0.4905	0.000771	0.1458	0.8000	0.0155	0.7923	0.062

Results

The two volume series delineated by each radiologist (labelled 'a' and 'b') before (V₁a, V₁b) and after (V₂a, V₂b) IC analysed using D'Agostino-Pearson test showed non-normal distribution (in all four series P < 0.0001). Thus, non-parametric tests were used to assess correlation between V₁a vs V₁b and V₂a vs V₂b (Spearman's coefficient of rank correlation and Kendall's Tau P < 0.0001 in both cases). These tests showed an optimal consistence in contouring procedure, and were not biased by different operators. All subsequent statistical analyses were carried out using the mean value of volume measures before (mV₁,) and after (mV₂) IC. Each series of mean values was used to determine factors for performing stratified Kaplan Meier (KM) analysis for LRC, DFS and OS: using the median value of mV₁ and mV₂ as cut-off (thus dividing the population into equal subsets, each one with 18 patients).

The KM Logrank test for mV₁ (cut-off: median = 12.9744 cc, range: 2.209 to 96.7385 cc) was not significant in all tested outcomes, while the same test for mV₂ (cut-off: median = 4.2181 cc, range: 0 to 39.3675 cc) was always significant (LRC: P-value = 0.0003, HR = 8.9437, 95% CI = 2.9196 to 27.3972; DFS: P = 0.0011, HR = 5.9193, 95% CI = 2.1952 to 15.9613; OS: P = 0.0097, HR = 5.7386, 95% CI = 1.8458 to 17.8412). In order to detect a correlation between mV₁ and mV₂ two regression functions were calculated and compared: the first, using a straight linear regression (

$$m{V}_2=\beta ·m{V}_1+\epsilon$$

), showed a significant overall P < 0.0001, b P < 0.0001, e P = 0.402 (n.s.), adjusted R² = 0.3796; the second, using a regression with log-transformation of variable mV₁, (

$$m{V}_2=\beta ·\text{log}\left(m{V}_1\right)+\epsilon$$

), showed a significant overall P < 0.0001, b P < 0.0001 and also an e P = 0.00525 (meaning that there is a better regression fit using log transformation rather than the simple correlation shown with lacking significance in the e term for the linear model) and finally a higher predictive power shown by higher adjusted R² = 0.4329.

Starting from this evidence, which links the concept of tumour regression with the biological assumption of fractional killing due to chemotherapy administration ^{25 26}, an assumption proven for fractionated radiotherapy ²⁷, we considered the possibility to create three different CPHM using LRC, DFS and OS as outcome, and both values of the volumes (mV₁ and mV₂) together with the value of linear-log ratio (LLR) as covariates, being such covariates dependent each other from the regression. Using the process of backward elimination of covariates we found a consistent significance for LLR that measures volume shrinkage against all checked survival outcomes, while mV₁ and mV₂ were no longer significant.

The results of CPHM are summarised in Table II. In order to assess the reliability of the models Harrel's c-index ¹⁴ was calculated for each model. Using a bootstrapping procedure, over 1000 randomly resampled datasets, we prevented the effect of overfitting by decreasing the value of the c-index: the value of optimism as defined by Harrel, performance of fitted model compared to that expected by chance ¹⁴, was always very low (Table II), showing an overall good discrimination performance of initially fitted models. The calibration plots ²⁸ of the models showed a small underestimation of the predicted outcomes with respect to the observed outcomes (Table II).

Considering as sufficient the number of patients at risk ²⁹ at 24 months of survival (16 patients), with a median follow-up time of 27 months (range 6-46), we developed a nomogram for DFS, calculating predicted survival as a direct function of mV₁ and mV₂ at 24 months. For OS the median follow-up time was considered too short to ensure a clinically reliable model, despite the significance in the modelling procedure, while LRC was considered redundant respect to the DSF evaluation in our case series. No stratification of patients according tumour primary site was performed, because of lack of significance in Kaplan- Meier LRC, DFS and OS according to this factor.

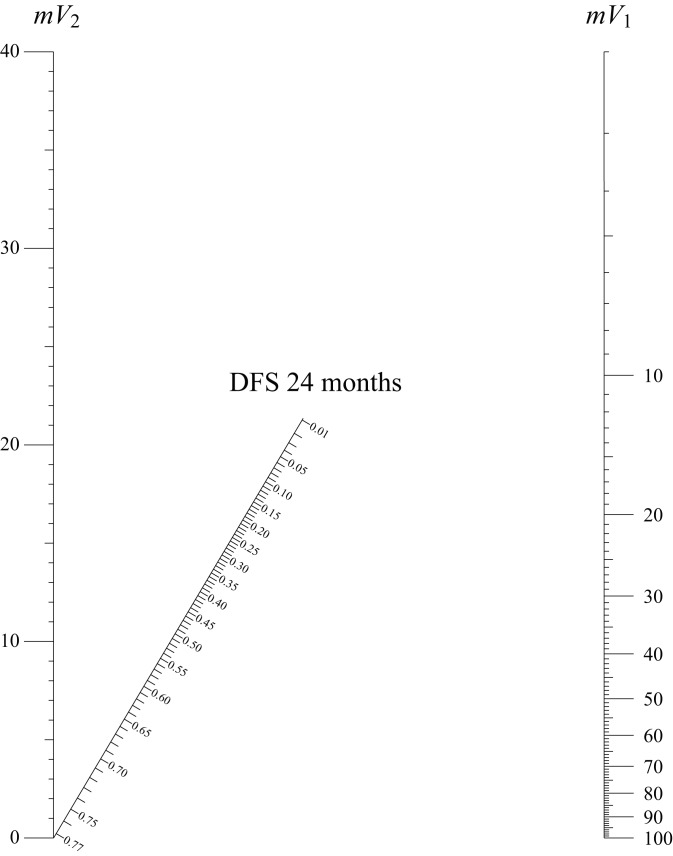
In Figure 3 the nomogram showing predicted DFS at 24months is shown. The use of this nomogram does not require calculating sums, but only placing a ruler connecting the value of the mV₁ on the right with the value of the mV₂ on the left. The predicted value of DFS at 24 months can be read on the oblique line showing the outcome prediction where the connection intersects this line. An aspect usually not analysed using current predictive models evaluation and nomogram drawing procedures ³⁰ is the need to assess the level of uncertainty (that is error) in measures of covariates put into the model. Covariates as sex, age and similar, used within predictive models, usually do not need to be evaluated for errors in detecting the value (especially when considering simple dummy variables). Indeed, when managing variables such as the value of delineated volume, as in our study, or similar measures subject to some kind of detection error, a verification of the variability in outcome prediction due to uncertainties in covariates should always be considered: as cited previously, there is much evidence for great variability in volume delineation procedures, that can vary to according anatomical site, imaging modality etc. ^{15-24 31}.

Fig. 3.

Nomogram for calculating disease-free survival (DFS) at 24 months. Two vertical lines show the values of mean tumour volume before (mV₁) and after (mV₂) induction chemotherapy. Using a ruler to draw a straight line connecting the values of the two volumes on the oblique outcome line the predicted survival probability can be directly read.

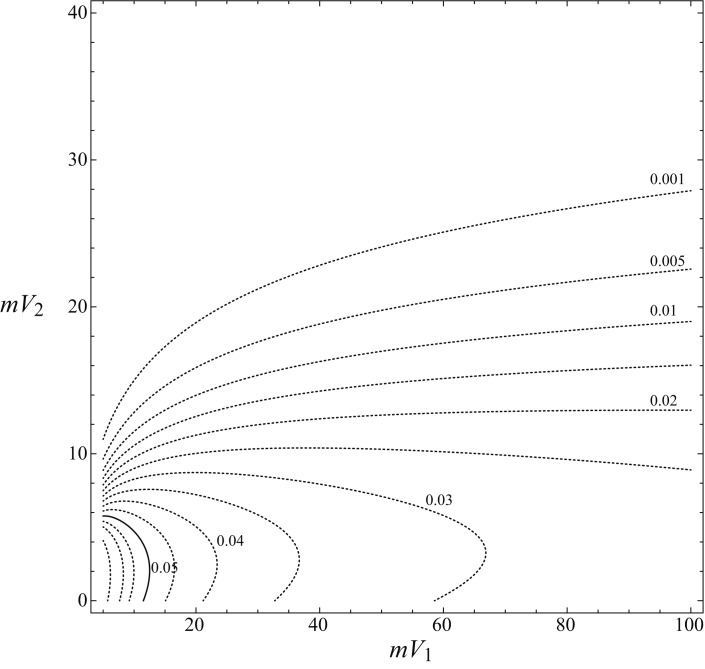
This situation led us to use the procedure described in the previous section to assess the susceptibility of the model to variations in volume delineation using the gradient function derived from the survival functions calculated by CPHMs. The values of the gradient as a function of mV₁ and mV₂ for DFS are shown in Figure 4. This plot directly shows the maximum variation of survival prediction for small changes in covariates. In every point of the plot, the error in the determination can be always considered lower than or equal to the value shown by curved lines. As shown in Figure 4, only for very small values of mV₁ (< 12.5 cc) and mV₂ (< 6 cc) did the amount of delineation error become significant in affecting the predicted outcome, a prediction that can vary more than 5% in a very small portion of the parameter space (area shown by the continuous line in the down-left corner).

Fig. 4.

Plot of gradient function. This plot shows the values of maximum variation in the outcome as a function of mV₁ and mV₂. It corresponds to maximum level of error for the survival function and can be used to assess the reliability of the prediction after survival calculation. In the down-left corner of the plot small variations of mV₁ and mV₂ can lead to outcome variations larger than 5% (continuous line). For most of the graph, the level of uncertainty can be considered reasonably low.

Discussion and conclusions

The evaluation of response in patients undergoing to treatment for different tumour types is one of the key-points in adaptive radiotherapy (ART), but the study of geometrical or volumetric changes in tumour volume and their subsequent impact on survival outcomes are still poor.

MR and CT are non-invasive imaging techniques that have an important role in assessing response to therapy, evaluating both morphological and "functional" parameters ³². These parameters, as described in the literature, can be useful tools in oncological management. In fact, it is possible to characterise tissue cellularity by evaluating the motion of water molecules on MR diffusion-weighted imaging (DWI) and to provide information regarding tumour perfusion and permeability with MR perfusion-weighted imaging (PWI) or perfusion-CT (PCT) studies. DWI is described to be a predictor of response to therapy and a good tool to differentiate between recurrent tumours from post-radiation changes ^{3 33-34}. PWI may play a role in detecting residual disease and predict patient outcomes ^{35 36}. PCT, as well, may be helpful to differentiate between post-therapeutic changes and tumour recurrence, to monitor patients after radiotherapy and/or chemotherapy and predict response after induction chemotherapy ^{37 38}. In this study, we highlight the meaningful contribution of morphological MRI through the assessment of changes in tumour volume before and after CI to predict survival outcomes of HNC patients undergoing definitive RTCT.

This approach can be considered an assumption to be addressed by other types of strict radiotherapy 'adaptive' approaches. Indeed, despite the relative small number of cases, the relationship between survival outcomes and changes in tumour volumes shown by this analysis is consistent in HNC patients undergoing CI.

The modelling of CPHM using a non-linear relationship between two observed volumes allows to overcome the problem of co-linearity ³⁹ when analysing parameters that are related each other, as the two volumes are. Furthermore, the use of LLR implies identification of the effect of treatment on tumour volume, as calculated by considering the possibility of tumour shrinkage rather than no change or enlargement in tumour volume. From a clinical point of view, this correlation has stronger predictive value than using the simple values of mV₁ and mV₂, because as a consequence of the assumptions of CPHM the two volumes should be independent in conditioning the outcome ⁴⁰, but this assumption cannot be considered feasible in this model. The possibility to obtain a consistent 'benchmark' to refer the outcome prediction in a single predictor, being the definition of the LLR based on biological and clinical assumptions, confirms the result despite the small number of cases and heterogeneity of the patient cohort. In the literature, there are already examples of correlations between survival outcomes and tumour volume assessment, but in HNC have been limited to diagnosis ^{12 41-43}. In cervical cancer, there is evidence of a semi-logarithmic relation between tumour volume at diagnosis and subsequent measures achieved by weekly MRI ⁴⁴, and this relation was confirmed in our study for HNC after CI. As stated before, the semi-logarithmic volume reduction is the mathematical translation of the fractional killing phenomenon ^25-27, due to constant proportion between the number of killed and surviving tumour cells for each therapeutic event that is the single radiotherapy fraction ⁴⁴ or the single chemotherapy administration as in our study. The real value of the modelling procedure described in this work is not in the predictive value of the model itself, which gives only the evaluation of the results for this single case series and not yet validated by any external dataset, but rather it is in the method chosen for data analysis and evaluation of the pitfalls hidden in the volume assessment.

In this case, considering the small number of patients, better performance could be achieved by increasing the number of cases or refitting the models by introducing other clinical covariates that can improve the predictive power of the survival functions. The results of this study imply that measurement of the tumour volume can be considered a good predictor for patients undergoing CI and the strong correlation among outcomes and LLR can be an helpful parameter to be evaluated in perspective studies with 'adaptive' approaches to treatment. Hopefully, a similar approach to evaluate measures achieved by different diagnostic procedures could be used to better refine the actual impact of survival models in describing outcomes based on imaging studies.