Efficient receptive field tiling in primate V1

Abstract

The primary visual cortex (V1) encodes a diverse set of visual features, including orientation, ocular dominance (OD) and spatial frequency (SF), whose joint organization must be precisely structured to optimize coverage within the retinotopic map. Prior experiments have only identified efficient coverage based on orthogonal maps. Here, we used two-photon calcium imaging to reveal an alternative arrangement for OD and SF maps in macaque V1; their gradients run parallel but with unique spatial periods, whereby low SF regions coincide with monocular regions. Next, we mapped receptive fields and find surprisingly precise micro-retinotopy that yields a smaller point-image and requires more efficient inter-map geometry, thus underscoring the significance of map relationships. While smooth retinotopy is constraining, studies suggest that it improves both wiring economy and the V1 population code read downstream. Altogether, these data indicate that connectivity within V1 is finely tuned and precise at the level of individual neurons.

Introduction

The sensory cortex of large mammals is organized into continuous maps, whereby adjacent neurons encode similar features and locations of the environment (Mountcastle et al., 1955). Although the benefits and mechanisms leading to this scheme are still debated (Chklovskii and Koulakov, 2004; Horton and Adams, 2005; Nauhaus and Nielsen, 2014), it is certain that functional continuity comes at a cost of reduced feature coverage that can be minimized by specific patterns of organization (Swindale, 1991; Swindale et al., 2000). For instance, Hubel and Wiesel’s ice-cube model demonstrates how orthogonal alignment between the gradients of orientation and ocular dominance maps (OD) can yield a full representation of two parameters for each retinotopic location (Hubel and Wiesel, 1974). Many studies have since validated the general notion that V1 maps can be efficiently combined via orthogonal gradients (Bartfeld and Grinvald, 1992; Hübener et al., 1997; Issa et al., 2000; Nauhaus et al., 2012; Obermayer and Blasdel, 1993; Yu et al., 2005), with those in the macaque having the strictest orthogonality between maps of orientation and OD, and between orientation and spatial frequency (SF). However, it is still uncertain how all three of the known periodic maps are aligned in the macaque. Furthermore, it is unclear how the cell-by-cell maps of receptive field (RF) location (i.e. the “micro-retinotopy”) tile the visual field within compartments of the periodic maps, yet this knowledge is required for a complete assessment of how the V1 functional architecture affects coding.

The micro-retinotopy helps define the V1 point-image, which is the cortical area devoted to processing a point of visual space. The size of the point-image increases with the standard deviation, or “scatter”, in RF position for a finite point in the cortex. If retinotopy remains perfectly smooth as we zoom into the map, then scatter equals zero. Some electrode studies in the primate have yielded a substantial degree of scatter (Hubel and Wiesel, 1974), whereas newer studies in the cat using more advanced electrodes and quantification have identified far less scatter (Hetherington and Swindale, 1999; Jin et al., 2011). Hubel and Wiesel estimated that the amount of scatter in primate V1 is comparable to RF size at a given eccentricity, which would double the area of the point-image relative to the baseline of zero scatter. More scatter in the retinotopic map would greatly relax restrictions placed on inter-map geometry for achieving feature coverage. In addition to scatter, local distortions may reside within the retinotopic map. One proposition is that large shifts in RF location coincide with local discontinuities in the orientation map (Das and Gilbert, 1999). An interdependence of this form would hamper coding efficiency, as a given point-image would be biased to cover a limited range of orientations. However, this result is disputed by other studies showing orientation and retinotopy maps to be independent (Bosking et al., 2002; Hetherington and Swindale, 1999).

Here, we used two-photon calcium imaging to answer multiple fundamental questions about functional architecture in the macaque that are directly relevant to V1’s coding capacity. In part 1, we used wide-field two-photon imaging to simultaneously map orientation, OD, and SF. Wide-field imaging was used to capture a full spatial period of these periodic maps. Similar to previous studies, we observed a strongly orthogonal relationship between orientation and OD maps (Bartfeld and Grinvald, 1992; Obermayer and Blasdel, 1993), as well as orientation and SF maps (Nauhaus et al., 2012). To complete the picture of how these classic stimulus properties are mapped, we demonstrate that OD and SF maps have gradients that progress in parallel, and that regions of low SF coincide with the center of OD columns. In other words, the maps have unique spatial periods, a valid strategy for achieving coverage (Swindale, 1991). This is in stark contrast to results in the carnivore suggesting that all three of the above mentioned maps have near orthogonal alignment, at most locations. In part 2 of this study, we examined the retinotopy down to the finest spatial scale in primate V1 by determining RF locations on a cell-by-cell basis across ~200 μm of V1. The retinotopy in each region was observed as systematic shifts of the RF centers that were much smaller than the RF widths (i.e. minimal scatter), thus placing greater constraints on the alignment between functional maps. This highlights the significance of the observed detailed inter-map alignment seen in part 1. Furthermore, we find substantial independence between orientation tuning curves that is uncorrelated with the minimal RF scatter, which should yield greater orientation discrimination at all visuotopic locations. In summary, our data show that primate V1 achieves efficient coverage of orientation, OD and SF using a combination of orthogonal and non-orthogonal gradients, and that it counterbalances smooth micro-retinotopy with efficient alignment of the three functional maps.

Results

The joint-organization of orientation, OD, and SF maps

Orientation, OD, and SF form continuous maps in primate V1. The orthogonal alignment between the orientation and the other two maps is well established in the primate (Bartfeld and Grinvald, 1992; Nauhaus et al., 2012; Obermayer and Blasdel, 1993), thus demonstrating an efficient alignment between two of the three map pairings. However, SF and OD maps cannot also be orthogonal at each location of the 2D surface. To complete the picture of how these three classic stimulus properties are mapped, we presented drifting gratings of different orientation and SF to either eye. Similar to our previous experiments, multiple injections of the calcium sensitive dye Oregon Green BAPTA-1AM (OGB) were made to cover a field-of-view that spanned at least one spatial period (> 500 μm) of the maps (Nauhaus et al., 2012). Using two-photon imaging of visual stimulus-evoked fluorescence changes, tuning curves for orientation, SF, and OD were generated for each pixel in each imaging region (Fig. 1). We first replicated the result that orientation maps are orthogonal to both OD (Bartfeld and Grinvald, 1992; Obermayer and Blasdel, 1993) and SF maps (Nauhaus et al., 2012) in macaque V1 (Fig. 2A, B; Table 1). Next, we performed the first direct comparison of SF and OD maps in macaque V1. We find that the two periodic maps are in phase such that regions of high SF (red patches in Fig. 2C) coincide with transition zones in the OD map (i.e. binocular regions, indicated by thick lines in Fig. 2C). We quantified this observation by computing the correlation coefficient between the binocularity map (binocularity map = 1−|OD map|) (Fig. 2D) and the logarithm of the SF map. There was a positive correlation in 5 of 6 imaging regions (p < 10⁻¹⁰ in 5 of 6; p > 0.05 in the remaining region; Table 1). This positive correlation implies that SF and binocularity maps have similar spatial periods. As the OD map has twice the spatial period as the binocularity map, it also implies that the OD map has a larger spatial scale than the SF map.

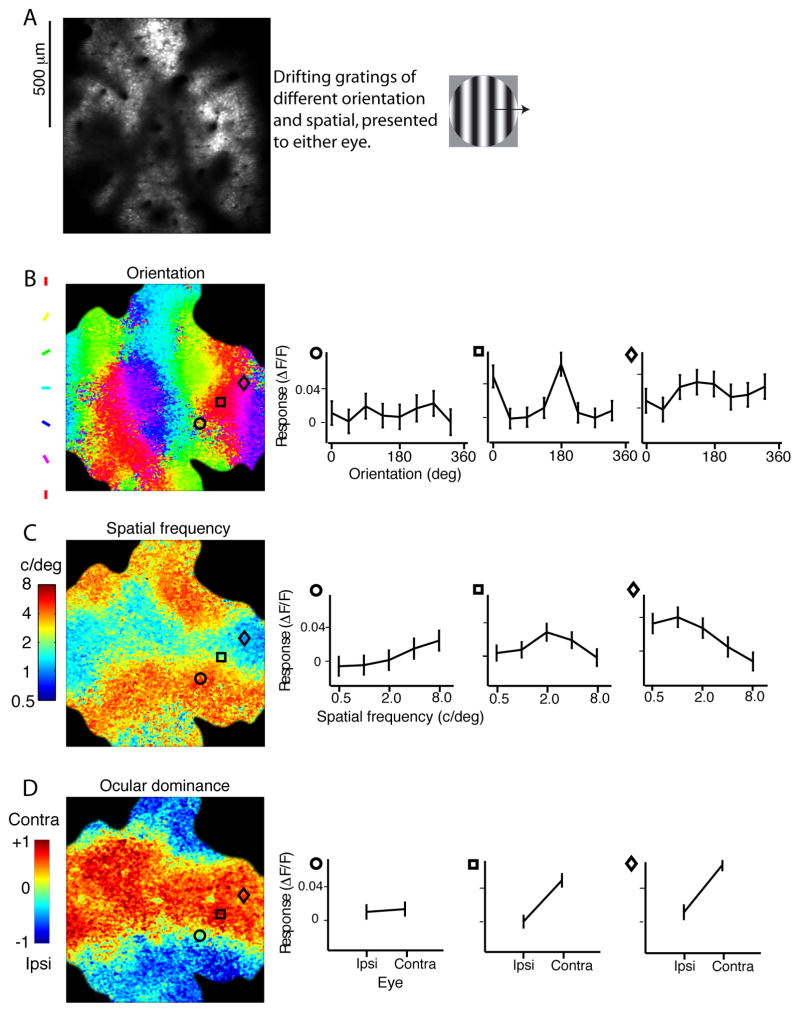
Figure 1. Computing the preferred orientation, SF, and OD at each pixel.

(A) The average image from a single trial. Cells can be clearly seen in the image, but pixels are too large to determine the response of each cell independently of neuropil contributions. Drifting gratings of different orientation and SF were shown over the receptive fields for each eye. (B) Orientation map. The preferred orientation at each pixel is computed from the tuning curves. The tuning curves from three pixel locations are shown to the right. Standard-error bars were computed from variability across stimulus presentations. (C) SF map. The color at each pixel represents the center-of-mass of the SF tuning curve. (D) OD map. Eye preference was computed by taking the response to the contralateral eye, minus the response to the ipsilateral eye, and dividing by the sum of both.

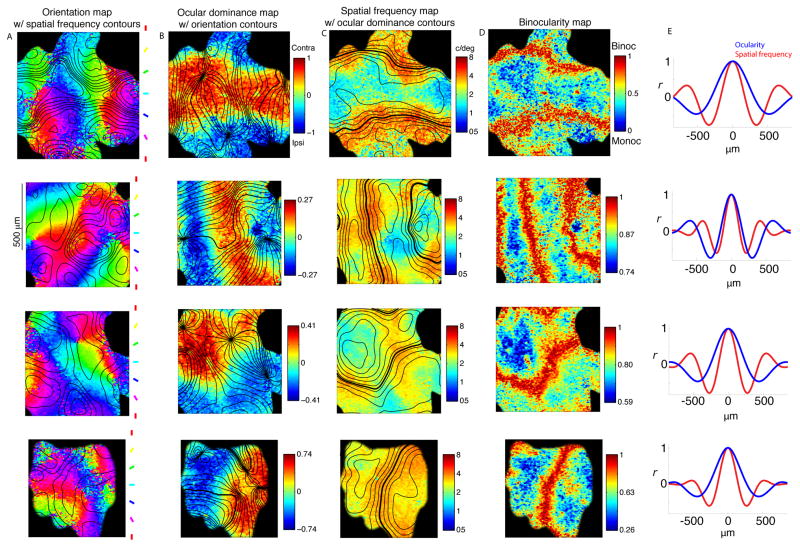
Figure 2. Relationships between functional maps.

Each row is data from a single imaging region. (A) Orientation maps, with the iso-contour lines of the SF map in black. The SF contours are spaced 0.17 octaves apart. (B) OD maps, with iso-contour lines of the orientation map in black. Contours are spaced 10 deg apart. (C) SF maps, with iso-contour lines of the OD map in black. The zero-crossing of the OD map is shown as a thicker contour line. (D) Binocularity map, computed as 1−|OD|. (E) Autocorrelation of OD and SF maps, projected perpendicular to the axis of maximum variance.

Table 1.

Summary of the alignment between orientation, OD, and SF maps. The first four (Regions u–v) are shown in Fig. 2, in the same order. 1^st column: Six patches of cortex were imaged, identified in each row as regions ‘u–z’. 2^nd column: Animal the region was recorded in. 3^rd column: The preferred intersection angle between the gradients of the orientation and SF map (0°–90°). This is computed from the pixel-by-pixel distribution of intersection values. 4^th column: The preferred intersection angle between the gradients of the orientation and OD map (0°–90°). 5th column: The preferred intersection angle between the gradients of the SF and OD map (0°–90°). 6^th column: Correlation coefficient between log(SF) and |∇OD| at each pixel. Asterisk indicates p<10⁻¹⁰. 7^th column: Correlation coefficient between log(SF) and 1−|OD| at each pixel. Only region ‘z’ was not significant (p>0.05). 8^th column: Spatial period of the SF map (μm). 9th column: Spatial period of the OD map (μm). Note that the computed spatial period of the OD map is likely underestimated in instances where the imaged regions were smaller than the period of the map, thus yielding an underestimate of the ratio between the maps. For instance, region ‘y’ had a ratio near unity, in spite of a significantly positive correlation between SF and the OD metrics.

Imaging region	Animal ID	Preferred Ori-SF intersection ∠	Preferred Ori-OD intersection ∠	Preferred SF-OD intersection ∠	r SF vs. |∇OD|	r SF vs. 1-|OD|	SF period (μm)	OD period (μm)
u	1	86°	82°	2°	0.50*	0.33*	690	1140
v	2	82°	62°	23°	0.28*	0.19*	430	630
w	2	63°	85°	16°	0.28*	0.43*	580	960
x	2	83°	78°	25°	0.18*	0.13*	590	990
y	3	81°	87°	14°	0.41*	0.31*	596	600
z	4	86°	89°	28°	0.19*	0.006	686	880

We quantified the spatial periods of OD and SF maps by computing the Fourier transform of their autocorrelation function (Fig. 2E) – i.e. we found the peak location of the power spectrum. Since most of the variance in the OD maps is contained along a single axis in each imaging region – perpendicular to the OD bands – the power spectrum in each imaging region was only computed along this axis. Furthermore, as we were interested in how the SF map gradients are interwoven with the parallel OD map gradients, the power spectrum of the SF map was computed along the same axis. In each imaging region, both maps produced a single peak in the power spectrum from which we determined the spatial period (Table 1). The average ratio of OD period to SF period across imaging regions was 1.42. Taken together, the data show that OD and SF maps have unique spatial periods and are aligned to make binocular regions encode the highest SFs.

This result closes a significant gap in our understanding of how stimulus features are jointly represented by cortical maps. A large angle of incidence between map gradients is the most commonly considered means of obtaining complete coverage and is the only form of interaction observed in other species where similar measurements have been made (Hübener et al., 1997; Issa et al., 2000; Yu et al., 2005). However, differences in spatial periods between maps could also be used to obtain coverage (Swindale, 1991). Indeed, our data demonstrate that maps in primate V1 exhibit orthogonally aligned map gradients, along with differences in periodicity. The level of intimacy between the three maps strongly suggests that they are built from common circuit mechanisms.

Micro-retinotopy in orientation maps

Previous electrode studies have indirectly assessed V1 micro-retinotopy by quantifying the degree of “scatter” in RF position for cells recorded during a given penetration (Dow et al., 1981; Hetherington and Swindale, 1999; Hubel and Wiesel, 1974; Van Essen et al., 1984). To directly characterize micro-retinotopy within maps of orientation preference, we used higher resolution two-photon imaging to measure responses of populations of individual neurons to a sparse-noise visual stimulus. The stimulus ensemble was parameterized for orientation and position (Fig. 3), allowing us to extract each cell’s orientation tuning curve width and peak, along with its RF width and X/Y location (see Supplemenatal Fig. 1 for additional raw RF data). In Figures 4A, B, X and Y maps are plotted for four of our six imaging regions. To detect a retinotopic gradient at this cortical scale, the retinotopy must be precise; the depth of the gradient is expected to be small given that V1 (~35 mm across) is much larger than the imaged regions (~0.2 mm across), but must nonetheless be greater than the magnitude of the positional scatter. From visual inspection, there appear to be detectable gradients. To quantify the retinotopic precision, we first fit 2D planes to the X and Y position maps, which accounted for a significant amount of the variance (F-test, p < 0.01). The slope parameters also provided a magnification factor for each imaging region (Methods, Eq. 1), which were 0.47 mm²/deg² and 5.90 mm²/deg² for the first two regions of Fig. 4, the minimum and maximum of our six imaging regions (Table 2). This range is comparable to values measured on a coarser scale in parafoveal V1 (Blasdel and Campbell, 2001; Daniel and Whitteridge, 1961; Dow et al., 1981; Hubel and Wiesel, 1974; Van Essen et al., 1984).

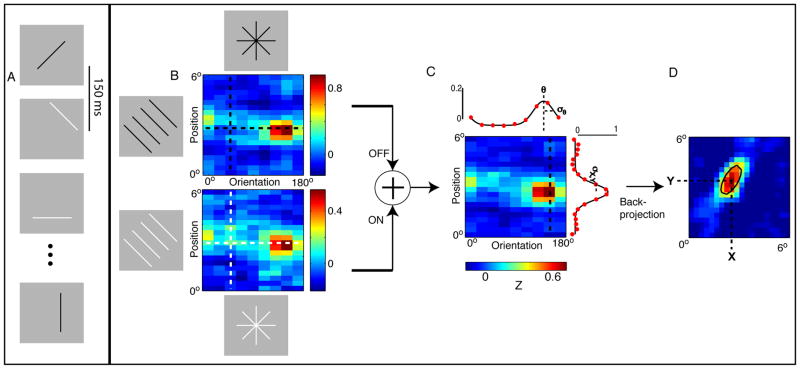
Figure 3. Constructing RFs from a modified sparse-noise stimulus.

Measuring RF properties from a sparse noise stimulus: (A) Each presentation consisted of a static bar, randomized for orientation, position, and luminance. (B) For each neuron, the expected response to each orientation and position was taken at the optimal delay from stimulus onset. The response matrix of a single neuron is shown for the black (top) and white (bottom) bars. A vertical slice in the position-orientation matrix, shown by the vertical dashed line, is a series of aligned bars with the same orientation (left). A horizontal slice in the position-orientation matrix, shown by the horizontal dashed line, is a series of bars with different orientations that are the same radial distance from the center of the stimulus space (bottom and top). (C) Next, the black bar and white bar response matrices were averaged together. Orientation tuning curves were computed by taking the average over the position dimension (top, red dots), and fit with a Gaussian. Orientation preference and bandwidth were computed from the fits (top, black curve). To compute RF width, we first took a slice in the response matrix at the optimal orientation, which yielded the RF projection along the preferred orientation’s axis (right, red dots). RF width was then quantified as 2σ from the Gaussian fit. (D) Lastly, the 2D RF profile was computed by performing back-projection on the orientation-position response matrix. After thresholding the kernel at half the maximum, we fit a 2D Gaussian to identify the RF location in visual space. A contour line of the fit is overlayed in black.

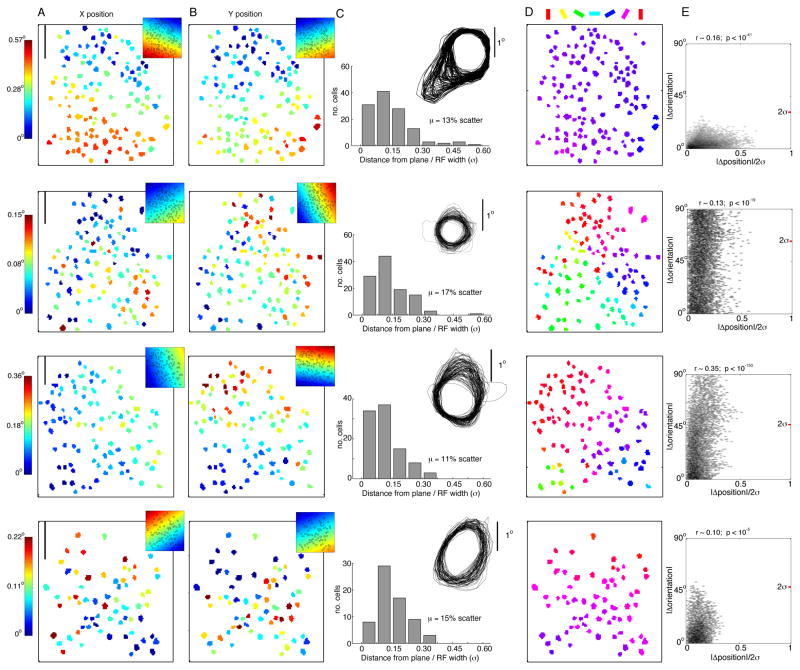
Figure 4. Micro-retinotopy within maps of orientation preference.

Each row is data from a single imaging region. (A) Relative X and (B) Y position of each neuron’s RF (in deg of visual angle) is color-coded, with the corresponding planar fit in the top right corner. Planar fits accounted for a significant amount of the variance (F-test, p < 0.01). Scale bar at top left is 50 μm. (C) To quantify RF scatter, the residual error from the planar fits was normalized by RF size. “Relative scatter” was computed as the mean of the normalized residual error distribution. Half-height contour lines are an overlay of the RF profiles of all neurons in an imaging region. (D) Color-coded orientation preference for each neuron. (E) Micro-retinotopy versus orientation map. Each data point is computed from a pair of neurons in the imaging region. The x-axis denotes the absolute distance between the two RFs, normalized by the sum of their widths. The y-axis denotes the absolute difference in preferred orientation. The red tick mark shows the average 2σ for the orientation tuning curves. A small but significant positive correlation is observed.

Table 2.

Retinotopy summary from 6 imaging regions. The first four (Regions a–d) are shown in Fig. 4, in the same order. 2^nd column: Animal the region was recorded in. 3^rd column: R² of the fit of a 2D plane to the X-position retinotopy map. Asterisk indicates F-test p-value < 0.01. 4^th column: Same, for Y-position retinotopy map. 5^th column: Average and standard deviation of RF width (2σ), computed from a Gaussian fit along the axis perpendicular to the orientation preference. 6^th column: Relative scatter, computed as the mean of the scatter distribution. Each point of the scatter distribution is the RF’s absolute distance from the X and Y planar fits, divided by the RF width (σ). 7^th column: The inverse of the maximum slope in the X-plane fit. 8^th column: The inverse of the maximum slope in the Y-plane fit. 9^th column: The angle of intersection between the gradients of the X and Y planar fits. 10^th column: Areal magnification factor by computing the inverse of the Jacobian from the X and Y planar fit gradients. 11^th column: Point-image size, computed from RF width, magnification factor, and absolute scatter. The double-asterisk indicates that magnification was computed only from the X-plane, as a significant fit was not identified for the Y-plane fit. 12^th column: Correlation coefficient between pairwise change in orientation preference and distance between RFs (normalized by sum of widths). Asterisk indicates p<0.01. 13^th column: Same pairwise comparison, but after subtracting the planar fits from the X and Y RF positions.

Imaging region	Animal ID	$R_{\widehat{X}}^2$	$R_{\widehat{Y}}^2$	RF width (deg) (2σ)	Scatter/σ	1/|∇X̄| (mm/deg)	1/|∇Ȳ| (mm/deg)	|∠∇X̄ − ∠∇Ȳ|	Mag. factor (mm2/deg2)	Point-image size (mm)	r (ΔOri vs. ΔPos/σ)	r (ΔOri vs. ΔPos/σ -Plane)
a	5	0.69*	0.64*	1.30 +/−0.10	0.13	0.49	0.60	39°	0.47	0.91	0.35*	0.01
b	6	0.18*	0.35*	0.54 +/−0.09	0.17	2.78	2.11	97°	5.90	1.35	0.10*	−0.0002
c	7	0.51*	0.66*	1.08 +/−0.13	0.11	1.37	0.77	53°	1.33	1.26	0.16*	0.009
d	6	0.34*	0.13	1.02 +/−0.12	0.15	1.05	-	-	-	1.07**	0.13*	−0.0007
e	6	0.20*	0.27*	0.80 +/−0.06	0.17	1.60	1.37	88°	2.20	1.22	0.08*	0.03
f	1	0.62*	0.34*	0.74 +/−0.07	0.16	0.85	2.63	126°	2.78	1.26	0.22*	0.06*

To visualize the degree of RF scatter, we overlaid the RF contours of all neurons in each imaging region (Fig. 4C). This qualitative assessment of the population is in stark contrast to previous studies (Dow et al., 1981; Hubel and Wiesel, 1974), as the RFs are quite closely aligned without individual scatter. Next, we computed a distribution of “relative scatter” for each imaging region as the deviation of a RF’s position from the fitted planes, normalized by the RF width (Methods, Eq. 2, Fig. 4C). Mean relative scatter was between 0.11 and 0.17 in the six imaging regions (Table 2). With bulk-loaded calcium indicators like OGB, contamination of the measured neuronal responses by contribution from the neuropil becomes a concern. We therefore assessed possible effects of neuropil contamination on the measurement of RF scatter, and find it insufficient to explain the low relative scatter observed in our experiments (see Supplement). Small relative scatter implies that the point-image size can be computed based on magnification factor and average RF width alone (Methods, Eq. 3). The computed point-image size (2σ) was between 0.91 and 1.26 mm in the six imaged regions (Table 2). This point-image size is approximately 2-fold smaller than if relative scatter had a ratio of ~1, as originally suggested (Hubel and Wiesel, 1974). For perspective, we note that the point-image is about 1/1200^th the total area of V1, yet its width is slightly greater than the 1D spatial period of the OD maps.

Next, we addressed the question of whether distortions in retinotopy, and thus distortions in the point-image, correlate with the orientation map. Previous studies disagree on whether changes in magnification factor correlate with transition zones in the orientation map (Bosking et al., 2002; Das and Gilbert, 1999; Hetherington and Swindale, 1999). To assess this relationship, we first computed a metric for “RF independence” between every pair of cells, defined as the distance between the two RF peaks divided by the sum of their widths (Methods, Eq. 4). RF independence was plotted against the absolute difference in orientation preference (Fig. 4E), which yielded weak but significant correlations. However, this correlation may be a trivial consequence of pooling over cell pairs separated by a range of cortical distances; i.e. cell pairs separated by greater cortical distances are also more separated across the gradients of orientation and retinotopy maps. In a second analysis, we accounted for the gradients by using RF scatter instead of absolute RF peak position. We recomputed the pairwise RF independence after subtracting the planar fits of X and Y retinotopy from each RF location. There was no significant correlation between the orientation map and scatter in 5 of 6 imaging regions (Table 2). In summary, the map gradients can account for the correlation between retinotopy and orientation, which is a testament to the precision of the maps at this spatial scale.

Also notable from each imaging region of Figure 4 is the finding that many neuron pairs have non-overlapping orientation tuning curves, yet highly overlapping RF envelopes. This is highlighted in the maps obtained near the centers of orientation pinwheels (Fig. 4, rows 2, 3); there are an abundance of neuron pairs that respond to largely independent orientations (e.g. the points above the red tick on the y-axis), yet these same pairs encode coincident retinotopic coordinates given that they are well below unity on the x-axis. This shows that neurons are able to discriminate across a broad range of orientations within a localized coverage of visual space, which translates to effective orientation coverage within the point-image.

In summary, our measurements on retinotopic precision establish a point-image that is as small as possible, given the baseline constraints of RF size and magnification factor. Nonetheless, a given point-image encompasses sharp transitions in the orientation map to encode all orientations at each point.

Discussion

Here, we have used multiple scales of two-photon calcium imaging to answer fundamental questions about functional architecture and coding capacity in macaque V1. Our data show that primate V1 contains a smooth micro-retinotopy, and achieves efficient coverage of orientation, OD and SF within the retinotopy using a combination of orthogonal and non-orthogonal map alignments. As expected from previous studies, OD and orientation maps were strongly orthogonal (Bartfeld and Grinvald, 1992; Obermayer and Blasdel, 1993), as were orientation and SF maps (Nauhaus et al., 2012). In contrast, we find that OD and SF maps have gradients that progress in parallel but have unique spatial periods such that low SF coincides with the center of OD columns and high SF with binocular regions. Furthermore, by precisely examining retinotopy across V1 on a cell by cell basis, we have observed systematic shifts of the RF centers that are much smaller than the RF widths. This imposes the need for the observed precise arrangement of functional maps to achieve efficient coverage of three different stimulus properties.

These observations have important implications for wiring precision within V1 and provide new insights into how V1 converts thalamic lateral geniculate nucleus (LGN) inputs into a systematic representation of novel features that are extracted and transmitted to higher cortical areas. Because thalamic afferents lack tuning for the combinations of features (orientation, SF, OD) that are represented and mapped within the more superficial cortico-cortical output layers, construction of the mapping relationships that we have observed must require cortical connections that are amazingly precise and highly organized. Consideration of how each of these features is represented and organized at each processing stage (thalamus, input layers, output layers) and where new features are extracted and combined, is therefore informative about how this is accomplished.

Cortical maps of parallel inputs

LGN inputs are monocular and un-oriented, so orientation selectively and binocular features such as disparity tuning must be constructed within V1 and organized de novo into systematic maps. In contrast, LGN neurons are well tuned for SF and the three main parallel pathways provide broad coverage across the range of SFs: parvocellular neurons are tuned to the highest SFs, koniocellular are intermediate, and magnocellular are tuned to the lowest SFs (Derrington and Lennie, 1984; Irvin et al., 1993; Kaplan and Shapley, 1982) Thus, over the range of SFs represented in the LGN population, the observed smooth, systematic representation of SF maps in V1 can be created by simply mixing these 3 channels. Considerable evidence strongly suggests that this is done by a combination of organized thalamocortical and intracortical connections. It also appears that the organization of thalamic input contributes to the observed relationship between OD and SF, with lower SFs represented within monocular regions. CO blobs tightly align with the center of OD bands (Horton, 1984) and receive a predominance of input from pathways that have larger receptive fields; koniocellular LGN afferents and magno-recipient layer 4Cα (Callaway, 1998; Yabuta and Callaway, 1998a). Furthermore, blobs were shown to align with low SF zones using electrophysiology (Born and Tootell, 1991; Edwards et al., 1995) and 2-[¹⁴C]deoxyglucose uptake (Silverman et al., 1989; Tootell et al., 1988). In contrast, the more binocular zones between CO blobs receive predominantly higher SF parvocellular inputs relayed from layer 4Cβ (Yabuta and Callaway, 1998a) While these studies point to differences between blob and inter-blob compartments, our data show that the transitions in both OD and SF tuning are gradual, consistent with anatomical evidence that long-distance connections linking columns treat transitions from blobs to interblobs as a continuum (Yabuta and Callaway, 1998b). Taken together, this study and others demonstrate a spatial coincidence between blobs centers, the center of OD bands, low SF zones, direct koniocellular input and indirect magnocellular input, while the interblob zones demonstrate a similar relationship between binocularity, high SF and parvocellular input.

Feedforward segregation of parallel inputs in macaque V1 helps explain the relationship between SF and OD maps, but it is less clear how parallel inputs might build orientation maps and their orthogonal alignment to SF and OD. The combined input from subcortical ON- and OFF-center pathways has long been recognized as the likely substrate for V1 orientation selectivity (Hubel and Wiesel, 1962). Studies in the carnivore have shown columnar biases of ON-OFF polarity in geniculate afferents (Jin et al., 2008; McConnell and LeVay, 1984; Norton et al., 1985; Smith et al., 2015; Zahs and Stryker, 1988) and V1 (Smith et al., 2015; Wang et al., 2015), which could be a scaffold for orientation maps (Jin et al., 2011; Kremkow et al., 2016; Lee et al., 2016; Miller, 1994; Paik and Ringach, 2011). It seems possible that OD and ON/OFF columnar biases are systematically aligned to produce the orthogonality between OD and orientation maps in the cat (Crair et al., 1997). Less is known about the horizontal organization of ON-OFF inputs to macaque V1, let alone the alignment between ON/OFF inputs and V1 maps of orientation and OD. However, blue-ON afferents have patchy terminations in superficial V1 (Chatterjee and Callaway, 2003), which are likely koniocellular in origin, and may thus align with the OD columns. With additional data and modeling, the seemingly complex interdependencies between maps and parallel inputs may begin to unfold and yield basic principles of connectivity. V1 maps provide a valuable constraint in addressing general questions about circuitry, regardless of their importance in cortical computation.

Binocular disparity tuning in V1

Binocular V1 neurons often exhibit “disparity tuning”, i.e. responses are maximized by a unique phase differential between images on the two retinas. Disparity tuning arises in V1 and is thought to represent the initial stage of depth perception in the visual cortex. SF selectivity and OD are particularly significant parameters in most models attempting to explain V1’s disparity tuning. For instance, the disparity energy model predicts that high SF preferring cells should be more sharply tuned for disparity since they are able to detect finer changes in visual space. Electrode recordings have shown this to be the case, but the dependence is not particularly strong (Ohzawa et al., 1997; Prince et al., 2002; Smith et al., 1997). The energy model also predicts that the most binocular cells should have the strongest disparity discrimination. However, most experiments have shown that so-called monocular cells are actually tuned for disparity with a similar strength to binocular cells (Kara and Boyd, 2009; Kato et al., 1981; LeVay and Voigt, 1988; Ohzawa and Freeman, 1986; Poggio and Fischer, 1977; Prince et al., 2002; Read and Cumming, 2004; Smith et al., 1997). Taken together, the high SF – binocular zones we observe are not necessarily subpopulations of disparity encoders with the highest fidelity, as might otherwise be intuited. Further two-photon imaging of how disparity tuning intermingles with maps of orientation, SF, and OD within layer 2/3 (Kara and Boyd, 2009) may help to reconcile discrepancies and refine models of how disparity tuning arises in V1.

Comparison with previous measurements of point-image parameters: RF size and scatter

The V1 point-image is directly relevant to V1’s coding capacity, so it is not surprising that studies have modeled its size using estimates of RF size, RF scatter, and magnification factor (Eq. 3). Our data indicate a smaller point-image than suggested by previous studies. The main source of discrepancy is the RF scatter – prior studies usually assume larger RF scatter based on more indirect measures. Also, the measured RF size (and thus relative scatter and point-image size) can depend on the chosen visual stimulus. These issues are discussed in more detail below

RF scatter has been the point-image dependency with the most uncertainty because of recording limitations. There are clear advantages of using two-photon imaging over electrodes to measure RF scatter. For one, many RFs can be measured at once, which provides statistical power and helps to account for changes in eye position that occur even in the anesthetized preparation. In other words, there is greater susceptibility to inflation of scatter from eye movements when single units are recorded successively over time. Second, relative cell locations can be determined precisely for all cells in the two-photon imaging region, which allowed us to account for the overall retinotopic gradient in estimating scatter. In summary, two-photon imaging yields parallel measurements of RFs of large populations, along with precise spatial localization of each cell. We believe these advantages have enabled our novel result of smooth micro-retinotopy in macaque V1.

Another potential source of contrast with prior studies is that scatter is greater in the deeper layers than what we have reported in layer 2/3. Although we are not aware of any studies that have examined laminar dependencies of scatter, we can look to previous studies on laminar dependencies of RF size to help address this issue. For example, cells within layers 4A, 4Cα, and 4Cβ have smaller RFs than cells in layers 4B, and 5 (Blasdel and Fitzpatrick, 1984). The former layers would have greater relative scatter for the same retinotopic positioning of the RFs. Other studies have shown less dependency of RF size on V1 depth, aside from a preponderance of somewhat larger RFs in deeper layers (Angelucci et al., 2002; Cavanaugh et al., 2002; Hubel and Wiesel, 1977; Levitt and Lund, 2002). A study in V1 of the awake primate also reported that the mean size of RFs in layer 2/3 tended to be smaller than most other layers (Gur et al., 2005). The overall evidence therefore suggests that the RFs we are measuring in layers 2/3 tend to be on the smaller end of the spectrum. Therefore, prior studies suggest that relative scatter is unlikely to be significantly greater in deeper layers. Yet, the size of the point-image in these layers could be somewhat larger, based on differences in RF size alone

Finally, it is important to consider that V1 RF sizes, and thus the point-image, are stimulus dependent. The stimulus used here – randomized presentation of elongated bars - was designed to quickly yield quantitative measurements of V1 RFs for all cells in an imaging region. Our RFs can be classified as a “minimum response field” (mRF) (Barlow et al., 1967) and had widths between 0.5 and 1.3 deg (Table 2). Earlier reports of mRF width tend to be smaller, between 0.2 and 1.0 deg at a similar eccentricity (Blasdel and Fitzpatrick, 1984; Gattass et al., 1981; Hubel and Wiesel, 1974; Van Essen et al., 1984). However, these prior studies typically identified mRF qualitatively by periodically flashing small stimuli. Our more persistent presentation of oriented bars may put each cell in a response regime that is above the baseline average and thus more likely to drive the cell at the fringes of the RF. This effect would increase RF width, reduce relative scatter, and increase point-image size. Yet another method of measuring RF size is to determine the stimulus size, along a stimulus size tuning curve, at which firing rate no longer increases (Angelucci et al., 2002; Cavanaugh et al., 2002; Kapadia et al., 1999; Levitt and Lund, 2002; Sceniak et al., 1999). Using this method in parafoveal V1, reported averages of RF size are ~1.0 deg, which are more similar to our measurements (i.e. larger) than the early mRF measurements. Considering that the size–tuning experiments use larger, steady-state drifting gratings, they are also more likely to drive the RF border and yield greater estimates of the RF and point-image size.

Advantages of smooth micro-retinotopy

Why would the V1 circuitry enforce such precise retinotopy? For one, a retinotopically-organized circuit conserves space, time, and energy by performing local computations of the visual scene locally within the brain (Chklovskii and Koulakov, 2004). For instance, the RF overlap we have observed would allow the dense network of columnar connections to link neurons that process a localized region of the visual field. Next, RF scatter requires a complex untangling by downstream areas to fully decode V1’s output. With precise retinotopy, new tuning properties in the visual hierarchy could instead arise from simpler mechanisms, e.g. homogenous pooling from non-homogenous neighborhoods of the functional maps (Nandy et al., 2013; Nauhaus and Nielsen, 2014; Paik and Ringach, 2011). Lastly, smooth micro-retinotopy seems likely to enhance the perceptual discrimination of object shape and position by increasing spatial resolution: Multiple wide-field imaging studies have shown that shape and position discrimination are at least partly encoded within retinotopic coordinates of the V1 population response (Duncan and Boynton, 2003; Michel et al., 2013; Murray et al., 2006; Schwarzkopf et al., 2011). The resolution of this decoding mechanism would be limited by the size of the point-image.

Concluding remarks

Our two-photon imaging data demonstrate that the organization of the functional architecture in primate V1 is more rigid and stereotyped than previously thought, yet consistent with the original notion of the V1 hypercolumn. Primate behavior relies heavily on bottom-up visual information routed through superficial V1, a fact that has likely leveraged this organization. Future studies will need to assess exactly how the functional architecture, and thus neuronal tuning, is built from the similarly specific input and local V1 circuits (Callaway, 1998).

Methods

Animal preparation and surgery

All procedures were conducted in accordance with guidelines of the National Institutes of Health and were approved by the IACUC at the Salk Institute. We used a total of 7 juvenile macaque monkeys in these experiments. Data for the retinotopy experiments are from four of the seven (1 female M. mulatta, 2 male M. fascicularis, 1 male M. radiata); data for the wide-field mapping are also from four of the seven (2 male and 1 female M. radiata; 1 male M. fascicularis). Data from four of these animals was also used in a previous study (Nauhaus et al., 2012). Details of the experimental and surgical approach are given in (Nauhaus et al., 2012). Briefly, anesthesia was maintained throughout the experiment with sufentanil citrate (4 – 20 μg/kg/hr, i.v.), supplemented with isoflurane (0.5–2%) during surgeries. In a few cases, we additionally administered diazepam (50–100 μg/kg, i.v.) as needed. For two animals, we used low levels of isoflurane (0.3% to 0.5%) throughout the entire experiment. Animals were paralyzed with pancuronium bromide (0.1–0.2 mg kg⁻¹hr⁻¹, i.v.) and artificially ventilated. The EtCO2, EKG, EEG, SpO2, heart rate, and body temperature were monitored continuously to judge the animal’s health and maintain proper anesthesia levels. For imaging, we attached a custom–made well to the skull over V1. Eyes were dilated with 1% atropine, and corneas protected with contact lenses. External lenses refracted the eyes, with optimal refraction determined by the ability of V1 neurons to resolve fine spatial frequencies.

Multicell bolus dye loading and in vivo two-photon microscopy

Injection of a dye solution containing Oregon Green BAPTA-1AM and sulforhodamine 101 (both life technologies), as well as the imaging was performed as described previously (Nauhaus et al., 2012). Imaging was performed at 920 nm excitation, and at two different spatial scales for micro-retinotopy and other feature maps. A 40× objective lens (0.8 NA Olympus) was used to assess micro-retinotopy, and a 16× objective lens (0.8 NA Nikon) for imaging wide-field functional maps. Images were acquired at a frame rate of 16 Hz for the former, and between 2 and 8 Hz for the latter. Eccentricity was at 6 deg to 10 deg from the fovea, and depth was between 200 and 350 μm below the cortical surface. We estimate that imaging regions in the micro-retinotopy experiments were approximately between 8 and 12mm lateral (along the M-L axis) from the midline, and imaging regions in the wide-field experiments approximately between 10 and 15mm. Data were collected with ScanImage software (Pologruto et al., 2003).

Visual stimuli and computing tuning curves

Visual stimuli were generated using the Psychophysics Toolbox extensions for Matlab (Brainard, 1997; Pelli, 1997) on a 17″ CRT monitor (1024×768) with a refresh rate of 100 Hz. The monitor was gamma corrected using a Photo Research-701 spectroradiometer. The monitor was positioned at a distance of 60 – 80 cm from the animal.

Wide-field functional maps

To measure orientation, SF, and OD, we computed responses of individual pixels to drifting gratings. Sinewave gratings were presented to one eye at 8 directions (45 deg steps) and 5 spatial frequencies (0.5 to 8 cyc/deg spaced logarithmically) at full contrast. Stimulus size was approximately 30 deg wide. Gratings were shown for 3 sec on each trial, and a uniform gray screen was shown between trials. For 3 of the 6 imaged regions, the full set of sinewave gratings were randomly presented to either eye, from which OD could be assessed. For the 3 other imaging regions, the sinewave gratings were presented to only one eye. OD was assessed in a subsequent experiment, in which we presented square wave gratings fixed at 1.0 cyc/deg randomly interleaved across 8 orientations and the two eyes. Six to seven repeats of each stimulus condition were always shown.

The response time course of each pixel for each trial was first computed as [F(t)−F_o]/F_o, where F_o is the mean response to the grey screen prior to stimulus onset for the given trial. To compute each point of a pixel’s tuning curve, we computed the average of [F(t)−F_o]/F_o within the stimulus time window and across repeated presentations. Orientation preference was computed as $\frac{1}{2}\angle {\sum }_{\theta }{T}_{\theta }{e}^{i2\theta }$, where T_θ is the tuning curve as a function of orientation. SF preference was determined by first computing the center-of-mass (CoM) of the SF tuning curve in the logarithmic domain, CoM[T_log2(ϕ)], followed by taking 2^CoM to put the metric in units of cycles/deg. OD (contralateral vs. ipsilateral eye) was measured as (contra-ipsi)/(contra+ipsi). The mean of each OD map was subtracted.

For further analysis, the imaging region was cropped based on a signal-to-noise ratio (SNR) metric. The SNR of each pixel was computed at the time-to-peak of the average response to the best stimulus. SNR was measured as (μ_max−μ_min)/(SE_max+SE_min), where μ_max and μ_min are the mean responses to the best and worst stimulus, and SE_max and SE_min are the corresponding standard errors. Next, this “SNR image” was smoothed with a 2D Gaussian (σ = 25 μm). The cropped ROI used for analyses consisted of pixels with SNR > 2. Areas of the map with SNR < 2 are darkened in the images (Fig. 2)

Micro-retinotopy

To measure the micro-retinotopy, we computed responses of individual neurons to a sparse noise stimulus presented monocularly. Following off-line movement correction (Nauhaus et al., 2012), time courses were extracted from the pixels of each neuron. Time courses were filtered with a difference-of-Gaussians (σ_lowpass = 5 ms; σ_highpass = 5000 ms) and then Z-scored within each 60-second trial. The visual stimulus consisted of static bars varying in orientation, position, and luminance, shown in succession every 100-to-200 ms (Fig. 3). Prior to performing the additional computations described below, responses were averaged into 8 to 10 orientation bins and 20 to 30 position bins. Positional binning was spaced approximately at the bar’s width (0.2 deg to 0.3 deg) within the domain’s range of 6 deg to 7 deg. The bar’s length was between 5 deg and 7 deg. There were 2 luminances for each bar (black and white bars on a grey background). The average response kernel for orientation (θ), position (P), luminance (L), and time delay after stimulus onset (τ) is given as K(θ,P,L,τ). Each kernel was taken at the time slice of maximum response to give K(θ,P,L,τ_o), shown in Fig. 3B. Because ON and OFF subfields were overlapping for most cells (i.e. K(θ,P,white,τ_o) ~ K(θ,P,black,τ_o)), responses to black and white bars were averaged to give K(θ,P,τ_o) = K(θ,P) (Fig. 3C).

Multiple RF properties were then extracted from each neuron’s spatial response kernel, K(θ,P). For each orientation of the stimulus domain, position varied along the orthogonal axis. In turn, responses to a given orientation yielded a 1D projection of the 2D receptive field. RF width was computed by fitting a 1D Gaussian at the slice of optimal orientation, K(θ_o,P) (Fig. 3C, right). Next, an orientation tuning curve was produced by summing the kernel over position, Σ_P[K(θ,P)], from which orientation tuning width and preference were computed by fitting a 1D Gaussian (Fig. 3C, top). To compute the 2D location of the RF, we first performed back-projection on K(θ,P) to get the RF in Cartesian coordinates, R(x,y). R(x,y) was then thresholded at the median (Fig. 3D), and finally fit with a 2D Gaussian to obtain a robust estimate of RF position.

Neuron selection for further analysis was based on the quality of the Gaussian fits. The exclusion of neurons within two imaging regions can be explicitly seen in Fig. 4. The upper-right insets of Fig. 4A, B provide outlines for all neurons that were initially selected in the raw image; i.e. their selection was based solely on the anatomical identification of neuronal cell-bodies in an image that was the average of one trial. The larger retinotopy maps of Fig 4A,B show the subset of neurons selected to analyze micro-retinotopy and relative scatter; we only used RFs with 2D Gaussian fits that accounted for 50% of the variance. At least 98% of the RFs in each of the 6 imaging regions passed this criterion. Next, the analysis of orientation tuning vs. retinotopy (Fig 4E) only used fits to the orientation tuning curves that accounted for 50% of the variance. Compare the orientation preference maps in Figs D to the insets of Fig. 4A, B to see which cells were removed based on this criterion. At least 92% of the orientation tuning curves in each of the 6 imaging regions passed this criterion.

Analysis of wide-field functional maps

Computing autocorrelation and spatial period

First, the 2D autocorrelation of both log(SF) and OD maps was computed by taking the Pearson correlation coefficient (r) for each spatial shift. Only the pixels within the SNR defined imaging region (see above) were used to compute r. Next, we took a 1D projection of both SF and OD autocorrelation matrices along the axis that produced the maximum 1D variance in the OD map. Specifically, to identify the axis of maximum OD variance, we took the projection of the OD map along a discrete set of axes (i.e. we computed the Radon transform of the OD map), and the variance of the projected 1D waveform was computed for each axis. We then went back to the 2D autocorrelation functions of OD and SF and computed the 1D projection along the same axis that yielded maximum variance in the OD map. Lastly, power spectra were computed from the Fourier transforms of the “zero-padded” (spatial padding interpolates in the spectral domain) autocorrelation, and the peak locations provided spatial periods given in Table 1.

Gradient Intersection

The following steps were taken to compute the “preferred intersection angle” between map gradients (Table 1, columns 3–5): Orientation, SF, and OD maps were first smoothed with a 2D Gaussian (σ = 9 μm). Smoothing captures the trend of the gradient on the scale of the smoothing kernel. The gradient of the smoothed orientation map, ∇θ_x,y, was computed by taking the difference between values at adjacent pixels, followed by adding 180 to values <−90 and subtracting 180 from values >90°. The gradient of the smoothed SF map, ∇log(ϕ_x,y), and OD map, ∇O_x,y, were simply computed by taking differences between values at adjacent pixels.

Next, the intersection angle between OD and SF maps was taken from the following resultant vector: R̄ = Σ_ke^{i2[∡∇O_k−∡∇Φ_k]}. The sum is over all pixels that are within the SNR defined region-of-interest. Note that ∡ computes the “axis” of the gradient (i.e. yielding values in the range [0° 180°]). Finally, the preferred intersection angle equals $\mid \frac{1}{2}\angle \overrightarrow{R}\mid$, which gives a value in the range [0° 90°] when ∠R̄ is defined in the range [−180° 180°]. The intersection between orientation and SF, along with orientation and OD, was computed in the same manner.

Analysis of micro-retinotopy

The RF position, [X_i Y_i], for each cell (i) was obtained from a 2D Gaussian fit, as described above. X̂ and Ŷ planes were then fit to each imaging region by linear regression. The slopes of X̂ and Ŷ yield a magnification as follows:

$$\mathit{Cortical}\mathit{magnification}(\frac{{mm}^2}{{\mathit{deg}}^2})={\left|\begin{array}{cc}\frac{\partial \widehat{Y}}{\partial u}& \frac{\partial \widehat{Y}}{\partial v}\\ \frac{\partial \widehat{X}}{\partial u}& \frac{\partial \widehat{X}}{\partial v}\end{array}\right|}^{-1}$$ Eq. 1

which is the inverse of a determinant. u and v are the two dimensions on the cortical surface.

“Relative scatter” was computed for each imaging region as

$$\mathit{Relative}\mathit{scatter}={\langle \frac{\sqrt{{(X_i-{\widehat{X}}_i)}^2+{(Y_i-{\widehat{Y}}_i)}^2}}{{\sigma }_{W,i}}\rangle }_i$$ Eq. 2

where the numerator is the absolute deviation of the RF’s actual position from the fitted planes at the given cortical location (X̂_i and Ŷ_i), the denominator is the RF’s width at the preferred orientation (Fig 3C), and the brackets indicate that the ratio was averaged over all neurons.

By assuming that the RF envelope and the distribution of scatter are both Gaussian-shaped, we can use the following equation to compute the size of the point-image:

$$\mathit{Point}\mathit{image}\mathit{size}(mm)=2\sqrt{M[{\langle {\sigma }_W^2\rangle }_i+{\sigma }_{\mathit{Scatter}}^2]}.$$ Eq. 3

where M is the cortical magnification from Eq. 1 and σ_Scatter is the average of the numerator in Eq. 2. The point-image size is scaled to be 2σ of the Gaussian model.

To compare retinotopy with the orientation map, we first computed the following between each pair of cells, i and j:

$$\mathit{Receptive}\mathit{field}\mathit{independence}=\frac{\sqrt{{(X_i-X_j)}^2+{(Y_i-Y_j)}^2}}{{\sigma }_{W,i}+{\sigma }_{W,j}}$$ Eq. 4

where the numerator is the retinotopic distance between RF peaks, based on the 2D Gaussian fits. The denominator is the sum of the RF widths, based on the 1D Gaussian fits at the optimal orientation. This was compared against the absolute difference in orientation preference ([0° 90°]) between the cell pairs (Fig. 4E).