Effects of Resolution and Registration Algorithm on the Accuracy of EPI vNavs for Real Time Head Motion Correction in MRI

Abstract

Low-resolution, EPI-based Volumetric Navigators (vNavs) have been used as a prospective motion-correction system in a variety of MRI neuroimaging pulse sequences. The use of low-resolution volumes represents a trade-off between motion tracking accuracy and acquisition time. However, this means that registration must be accurate on the order of 0.2 voxels or less to be effective for motion correction. While vNavs have shown promising results in clinical and research use, the choice of navigator and registration algorithm have not previously been systematically evaluated. In this work we experimentally evaluate the accuracy of vNavs, and possible design choices for future improvements to the system, using real human data. We acquired navigator volumes at three isotropic resolutions (6.4 mm, 8 mm, and 10 mm) with known rotations and translations. The vNavs were then rigidly registered using trilinear, tricubic, and cubic B-spline interpolation. We demonstrate a novel refactoring of the cubic B-spline algorithm that stores pre-computed coefficients to reduce the per-interpolation time to be identical to tricubic interpolation. Our results show that increasing vNav resolution improves registration accuracy, and that cubic B-splines provide the highest registration accuracy at all vNav resolutions. Our results also suggest that the time required by vNavs may be reduced by imaging at 10 mm resolution, without substantial cost in registration accuracy.

1. Introduction

Prospective motion detection and correction during an MRI scan has been shown to allow the acquisition of clinically useful images, even with substantial subject movement [7, 15]. While many methods have been developed to reduce the artifacts caused by motion during MRI scanning, Volumetric Navigators (vNavs) use the MRI scanner to track subject motion, requiring no additional equipment or setup be added to the scanner or workflow to enable motion correction [4, 12]. vNavs are low-resolution, whole-head volumes, acquired rapidly (~ 300 ms), and interspersed over the several minutes of a longer neuroimaging sequence. Head motion information is recovered from these volumes via registration, and the resulting estimates of head position are used to update the MRI scanner’s imaging coordinates, following the subject’s head to compensate. vNavs are used in both clinical and neuroscientific studies to measure and correct motion.

While vNavs can be acquired frequently, they cost both acquisition and processing time which must be found in the MRI sequence being corrected (e.g. during pre-existing dead-times). The effectiveness of the vNavs system relies on the accuracy of the volume registrations, which can be affected both by the choice of vNav resolution, and the interpolation method used in the registration cost function. The lowest-resolution navigator that provides acceptable motion tracking would be preferred in practice due to it having the shortest duration. Previous work with vNavs [4, 12] has mostly used 8 mm isotropic resolution volumes, and relied on the PACE algorithm [10] for image registration on the scanner. However, there has been no systematic evaluation of the choice of resolution or registration algorithm.

In this work we address this gap, evaluating the registration accuracy of different interpolation methods at various resolutions of vNavs. Three interpolation methods are implemented and tested on the volumetric data: trilinear, tricubic [6], and cubic B-spline interpolation [14, 11], and a Gauss-Newton search algorithm was implemented to perform rigid registration using the 2-norm cost function. We have acquired data in a human volunteer at three feasible vNav resolutions: 6.4 mm, 8 mm, and 10 mm. Motions detected from these low-resolution vNavs need to be accurate enough for correcting high resolution MR imaging with voxels on the order of 1 mm. Comparing this with the resolutions of our vNavs, we need registration accuracy on the order of $\frac{1}{10}$ of a vNav voxel.

2. Methods

2.1. Data Acquisition

Imaging was performed on a 3 T TIM Trio (Siemens Healthcare, Erlangen, Germany) with all data acquired using the body coil to reduce spatial variations in signal intensity. One human volunteer, having given informed consent, was scanned with a custom pulse sequence that acquires a series of vNavs. Data was acquired at three isotropic resolutions: 6.4 mm, 8 mm, and 10 mm (acquisition parameters are shown in Table 1). To ensure the subject remained as still as possible during the scan, the acquisitions were broken into ~ 30 s sets, during which the volunteer was instructed to hold his breath to minimize respiratory motion. Each set consisted of a volume at iso-center and on-axis, followed by volumes with a range of rotations from either 0.5° to 2.5° or 3° to 5° at 0.5° increments, and at each rotation a series of 5 translations from 1 mm to 5 mm at 1 mm increments. Rotations were performed around x, y, and z axes, with z translations, and additional rotations around the oblique x/y, x/z, and y/z axes with x/y translations. Volumes within each set are registered to the first volume of the set. A total of 432 volumes per resolution were acquired, from which 420 pairs (one reference and one moved volume) can be extracted for registration.

Table 1.

Sequence parameters for vNavs

	6.4 mm	8 mm	10 mm
TR	15 ms	11 ms	10 ms
TE	6.7 ms	5.0 ms	4.1 ms
FA	3°	3°	3°
BW	4310 Hz/Px	4596 Hz/Px	4578 Hz/Px
FOV	256 mm	256 mm	260 mm
Total Scan Time	600 ms	352 ms	260 ms

Our previous experiments have shown that larger rotations/translations are easy to detect with any choice of resolution or interpolation method because there are enough change in the volume. We chose to consider small rotations/translations only on the assumption that gross registration can be performed by a variety of methods. We instead are interested in the accuracy of registration near the ground truth.

2.2. Masking

When an image is rotated, the higher frequency components in the corners of the Fourier domain are aliased into lower-frequency regions. Applying a circular mask to filter out higher frequency components can reduce this effect [1]. In our work, masking was performed in both the Fourier and spatial domains to remove corners in the cubic volumes that cannot be extrapolated during rotation operations. The volumes were preprocessed before registration by applying a smoothed spherical mask in the Fourier domain. The mask was defined using the window function

$$m\left(r^{\prime }\right)=\{\begin{array}{cc}1\hfill & r^{\prime }<\frac{3}{4}\hfill \\ w_{\text{cos}}(\frac{8}{3}{r}^{\prime }-2)\hfill & \frac{3}{4}\le r^{\prime }\le 1,\hfill \\ 0\hfill & r^{\prime }>1\hfill \end{array}\phantom{\}}$$ (1)

where r′ = r/R, r is the radius from the image center, R is the radius of the volume, and w_cos is the cosine window function, defined as

$$w_{\text{cos}}\left(t\right)=\{\begin{array}{cc}\text{cos}\left(\pi t\right)\hfill & -\frac{1}{2}\le t\le \frac{1}{2}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}.$$ (2)

The same mask was applied again in the spatial domain, after the volumes were interpolated. Figure 1 shows sample slices prior to and after masking in three different resolutions.

Figure 1.

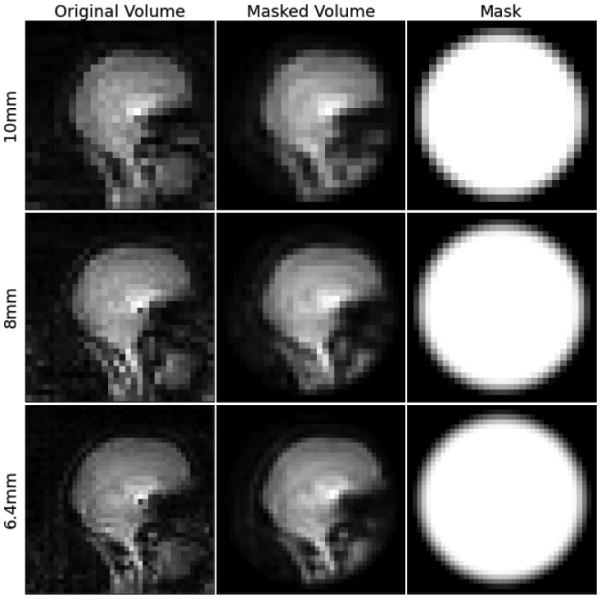
Original and masked slices from vNavs, and the masks used at different resolutions

2.3. Registration

2.3.1 Cost function

To perform prospective motion correction, navigator volumes acquired throughout the longer MRI scan would be registered to the first volume of the sequence, referred to as the reference volume V_ref : ${\mathbb{ℝ}}^3\to \mathbb{ℝ}$. Given a new moving volume V_mov : ${\mathbb{ℝ}}^3\to \mathbb{ℝ}$, we can describe our registration as minimizing the error function

$$ϵ=\sum _i{({\mathbf{v}}_{\text{ref}}\left({\mathbf{x}}_{\mathbf{i}}\right)-{\mathbf{V}}_{\text{mov}}({\mathbf{x}}_i+{\mathbf{d}}_i\left({\mathbf{P}}^{-1}\right)))}^2,$$ (3)

where v_ref is the vector that represents the reference volume sampled at Cartesian grid points. V_mov(x_i + d_i(P⁻¹)) is the function describing the moving volume evaluated at an unmeasured point x_i + d_i(P⁻¹), and x_i = (x_i, y_i, z_i) is the i^th grid point of the volume. d_i(P⁻¹) is the estimated displacement of x_i from V_mov to V_ref given the set of transformation parameters P⁻¹.

Our goal is real time registration, with total run-times on the order of tens of milliseconds. Given that we expect our volumes to have identical contrast and our noise variation to be negligible (due to the large voxels being used), we have chosen to use the 2-norm for our cost function.

We note that (3) requires resampling every incoming volume during the registration step, which can be computationally expensive. Registering the reference volume to the incoming volumes produces the opposite transformation, but only the reference volume needs to be resampled every time [10]. This changes our error function to,

$$ϵ=\sum _i{\left({\mathbf{V}}_{\text{ref}}({\mathbf{x}}_i+{\mathbf{d}}_i\left(\mathbf{P}\right))-{\mathbf{v}}_{\text{mov}}\left({\mathbf{x}}_i\right)\right)}^2,$$ (4)

where P denotes the parameters for the inverse transformation of P⁻¹ and v_mov is the vector that represents the moving volume sampled at Cartesian grid points. With (4), we can register the reference volume to incoming volumes instead and apply the opposite transformation for motion correction, to reduce computation.

2.3.2 Interpolators

Voxels located on a Cartesian grid are measured by the scanner, but to evaluate (4) we also need to evaluate the reference volume at points that have not been measured. We approximate the values that would have been measured off-grid using interpolators which have the linear form

$${\mathbf{V}}_{\text{ref}}({\mathbf{x}}_i+{\mathbf{d}}_i\left(\mathbf{P}\right))\approx \mathbf{I}({\mathbf{x}}_i+{\mathbf{d}}_i\left(\mathbf{P}\right),{\mathbf{v}}_{\text{ref}}),$$ (5)

where I(x_i + d_i(P), v_ref) is an interpolation operator that takes v_ref as input to estimate values of the reference volume at transformed point x_i + d_i(P). The choice of interpolator can significantly affect registration accuracy. Unsmooth cost functions, which can result from interpolation artifacts, can cause the minimization to be trapped in local minima [1]. We have evaluated the accuracy of three interpolators: trilinear, tricubic [6], and cubic B-spline [14, 11].

Trilinear interpolation approximates the value of a volume V at an unknown point x = (x, y, z) (with coordinates expressed in units of voxels) using the eight grid points around (x, y, z) from v, which is sampled on Cartesian grid points. The algorithm first finds the nearest “base” grid point x_ = (x_, y_, z_), whose indices are the floor of (x, y, z). From the “base” grid point, the relative off-set Δp = (Δp_x, Δp_y, Δp_z) = (x − x_, y − y_, z − z_) between the two points is computed. Since voxels are isotropic in our data, the interpolation equation is then

$$\begin{array}{cc}\hfill & {\mathbf{I}}_{\text{trilinear}}(\mathbf{x},\mathbf{v})\hfill \\ \hfill & =\sum _{i=0}^1\sum _{j=0}^1\sum _{k=0}^1[\mathbf{v}(x\_+i,y\_+j,z\_+k)\times \hfill \\ \hfill & \mid 1-i-\Delta p_x\mid \mid 1-j-\Delta p_y\mid \mid 1-k-\Delta p_z\mid ],\hfill \end{array}$$ (6)

Tricubic interpolation can be written in the form

$$\begin{array}{cc}\hfill & {\mathbf{I}}_{\text{tricubic}}(\mathbf{x},\mathbf{v})\hfill \\ \hfill & =\sum _{i=0}^3\sum _{j=0}^3\sum _{k=0}^3{a}_{ijk}\left(\mathbf{x}\_\right){(\Delta p_x)}^i{(\Delta p_y)}^j{(\Delta p_z)}^k,\hfill \end{array}$$ (7)

where a_ijk (x_) are the 64 coefficients of tricubic interpolation at the “base” grid point. The choice of a_ijk is generally defined by imposing continuity constraints on the interpolated function at the grid points, and for which we have followed a derivation by Lekien et al. [6]

First, we note that if we define a 64-vector a_tricubic(x_) that contains all the a_ijk (x_, y_, z_) and similarly a 64-vector k(Δp) that contains all the powers of (Δp_x)ⁱ(Δp_y)^j(Δp_z)^k that appear in (7), we can rewrite our interpolation equation as

$${\mathbf{I}}_{\text{tricubic}}(\mathbf{x},\mathbf{v})={\mathbf{a}}_{\text{tricubic}}{\left(\mathbf{x}\_\right)}^T\mathbf{k}(\Delta \mathbf{p}).$$ (8)

Lekien et al. showed that a_tricubic(x_) can be computed as a linear combination of values from the point x_ and the the additional 7 grid points that can be reached by adding 1 to each of its indices. The values needed at each point are the image, its three first derivatives, three second cross derivatives, and one third cross derivative; we have used central finite differences to compute the derivatives. These source values can be put in a 64-vector b_tricubic(x_), which can then by multiplied by a fixed matrix B_tricubic giving [6]

$${\mathbf{a}}_{\text{tricubic}}\left(\mathbf{x}\_\right)={\mathbf{B}}_{\text{tricubic}}{\mathbf{b}}_{\text{tricubic}}\left(\mathbf{x}\_\right).$$ (9)

From an efficiency perspective, Lekien et al. observed that, if many sample points with the same “base” grid point are going to be interpolated, a_tricubic(x_) is heavily reused. These vectors can then be precomputed and saved for every point of the volume [6]. Using the reversed order of registration described in (4), the reference volume needs to be resampled many times during the registration process, but doesn’t change as each new moving volume arrives. Therefore, the tricubic coefficients can be precomputed and saved for the reference volume, reducing registration time at the cost of a 64-fold increase in the memory required to store the reference volume.

Cubic B-spline interpolation is an example of a generalized interpolator, as defined by Unser et al. [13] These methods are “generalized” in that they first compute a volume of coefficients from the input image volume, and then perform a linear operation on the coefficients, with the resulting output being an interpolation of the original input volume [11]. They have shown that cubic B-spline, among many other families of interpolators, are an example of this generalized formulation and demonstrated efficient algorithms for the calculation of the coefficient volumes in the cubic B-spline case [14].

Unser et al. introduced an efficient two-step procedure for computing coefficient volumes by first computing an intermediate volume, c⁺, and then from this computing the desired coefficients, c [14]. However, this algorithm assumed mirror boundaries, and we have assumed circular boundaries in all our algorithms (in part, because circular wrap-around is expected to occur in MRI scans) giving the following algorithm (applied first along the x, then y, and finally z axes, with each of these three stages taking as input the previous step’s the output). With z₀ = $-2+\sqrt{3}$, compute g_i from f_i (the signal, of length n) using the recursion

$$\begin{array}{cc}\hfill g_0& =6f_0\hfill \\ \hfill g_i& =z_0{g}_{i-1}+6f_i(i\ne 0,i\ne n-1)\hfill \\ \hfill g_{n-1}& =\frac{z_0{g}_{n-2}+6f_{n-1}}{1-z_0^n}.\hfill \end{array}$$ (10)

Then compute c⁺ from g using

$$\begin{array}{cc}\hfill c_{n-1}^{+}& =g_{n-1}\hfill \\ \hfill c_i^{+}& =g_i+z_0^{i+1}{g}_{n-1}(i\ne n-1).\hfill \end{array}$$ (11)

Now, we can compute h_i from the $c_i^{+}$ using the backwards recursion

$$h_{n-1}=-z_0{c}_{n-1}^{+}$$ (12)

$$h_i=z_0(h_{i+1}-c_i^{+})(i\ne 0,i\ne n-1)$$ (13)

$$h_0=\frac{z_0(h_1+c_0^{+})}{1-z_0^n}.$$ (14)

Finally, from h we can compute c using

$$c_0=h_0$$ (15)

$$c_i=h_i-z_0^{n-i}{h}_1(i\ne 0).$$ (16)

After computing the coefficient volume, we interpolate a point in 3D using the 64 surrounding values in the coefficient volume via the equation

$$\begin{array}{cc}\hfill & {\mathbf{I}}_{\text{B-spline}}(\mathbf{x},\mathbf{v})=\hfill \\ \hfill & \sum _{i=-1}^2\sum _{j=-1}^2\sum _{k=-1}^2\beta (\Delta p_x-i,\Delta p_y-j,\Delta p_z-k)\hfill \\ \hfill & \mathbf{c}(x\_+i,y\_+j,z\_+k),\hfill \end{array}$$ (17)

where β(.) is the 3D cubic B-spline interpolator kernel, which, being separable, can be written as the product of three, 1D cubic B-spline interpolator kernels, as defined in [11]

$$\beta \left(x\right)=\{\begin{array}{cc}\frac{2}{3}-\frac{1}{2}\mid x{\mid }^2(2-\mid x\mid ),\hfill & 0\le \mid x\mid <1\hfill \\ \frac{1}{6}{(2-\mid x\mid )}^3,\hfill & 1\le \mid x\mid <2.\hfill \\ 0,\hfill & 2\le \mid x\mid \hfill \end{array}\phantom{\}}$$ (18)

Equation (17) is structurally very similar to (7), in that, with some rearrangement, it can be written as the inner product of a 64-vector of coefficients, a_B-spline(x_) and the 64-vector of powers of Δp_x, Δp_y, and Δp_z, which we have previously called k(Δp):

$${\mathbf{I}}_{\text{B-spline}}\left(\mathbf{x}\right)={\mathbf{a}}_{\text{B-spline}}{\left(\mathbf{x}\_\right)}^T\mathbf{k}(\Delta \mathbf{p}).$$ (19)

Mirroring the derivation for tricubic interpolation, we can combine the 64 values of c that are used in interpolation from “base” point x_ into a vector b_B-spline, and, from the structure of (17), define a fixed matrix B_B-spline such that

$${\mathbf{a}}_{\text{B-spline}}\left(\mathbf{x}\right)={\mathbf{B}}_{\text{B-spline}}{\mathbf{b}}_{\text{B-spline}}\left(\mathbf{x}\_\right).$$ (20)

We can thus use the same trade-off of memory for efficiency in repeated interpolations as demonstrated in [6]. As in tricubic interpolation, a_B-spline(x_) can be precomputed and saved for the reference volume. Given the “base” grid point and the relative offset, evaluation of I_B-spline(x) consists of computing k(Δp), which takes 62 operations, and performing a dot product with the appropriate precomputed vector, requiring 127 operations. Thus a total of 189 floating point operations are required to interpolate at an unknown point. A naive implementation of the algorithm proposed by Unser et al. requires at least 10 floating point operations at each of the 64 neighboring point to evaluate β(x) and multiply it with the coefficients. Hence our implementation is at least three times faster than the naive implementation.

2.3.3 Minimization

Given the time constraints of real time motion correction, we have opted to use a Gauss-Newton minimization algorithm, which requires only the first derivatives of the residual in our cost function. Formally, the Gauss-Newton algorithm descends towards the minimum of the cost function (4) with respect to the set of six rigid transformation parameters P through an iterative process.

$${\mathbf{P}}^{s+1}={\mathbf{P}}^s-{\left({{\mathbf{J}}_{\mathbf{r}}}^{\text{T}}{\mathbf{J}}_{\mathbf{r}}\right)}^{-1}{{\mathbf{J}}_{\mathbf{r}}}^{\text{T}}\mathbf{r}\left({\mathbf{P}}^s\right),$$ (21)

where r(P^s) is the residual between the moving volume and the reference volume interpolated with parameters P^s and J_r is the Jacobian with respect to the transformation parameters. Residual r(P) is defined at all grid points i via,

$$\begin{array}{cc}\hfill r_i\left(\mathbf{P}\right)& ={\mathbf{V}}_{\text{ref}}({\mathbf{x}}_i+{\mathbf{d}}_i\left(\mathbf{P}\right))-{\mathbf{v}}_{\text{mov}}\left({\mathbf{x}}_i\right)\hfill \\ \hfill & \approx \mathbf{I}({\mathbf{x}}_i+{\mathbf{d}}_i\left(\mathbf{P}\right),{\mathbf{v}}_{\text{ref}})-{\mathbf{v}}_{\text{mov}}\left({\mathbf{x}}_i\right).\hfill \end{array}$$ (22)

We approximate the Jacobian of the residual using a Taylor series approximation of the residual evaluated at the (unknown) true value of the parameters P₀ as follows

$$\begin{array}{cc}\hfill {\left({\mathbf{J}}_{\mathbf{r}}\right)}_i& ={\nabla }_{\mathbf{P}}{r}_i({\mathbf{P}}_0+\mathbf{P})\hfill \\ \hfill & \approx {\nabla }_{\mathbf{P}}{\mathbf{V}}_{\text{ref}}({\mathbf{x}}_i+{\mathbf{d}}_i\left({\mathbf{P}}_0\right)+{\mathbf{d}}_i\left(\mathbf{P}\right))\hfill \\ \hfill & \approx {\nabla }_{\mathbf{P}}[{\mathbf{V}}_{\text{ref}}({\mathbf{x}}_i+{\mathbf{d}}_i\left({\mathbf{P}}_0\right))\hfill \\ \hfill & +{\nabla }_{{\mathbf{x}}_i}{\mathbf{V}}_{\text{ref}}({\mathbf{x}}_i+{\mathbf{d}}_i\left({\mathbf{P}}_0\right)){\mathbf{d}}_i\left(\mathbf{P}\right)]\hfill \\ \hfill & ={\nabla }_{{\mathbf{x}}_i}{\mathbf{V}}_{\text{ref}}({\mathbf{x}}_i+{\mathbf{d}}_i\left({\mathbf{P}}_0\right)){\nabla }_{\mathbf{P}}{\mathbf{d}}_i\left(\mathbf{P}\right)\hfill \\ \hfill & ={\nabla }_{{\mathbf{x}}_i}{\mathbf{V}}_{\text{mov}}\left({\mathbf{x}}_i\right){\nabla }_{\mathbf{P}}{\mathbf{d}}_i\left(\mathbf{P}\right)\hfill \\ \hfill & \approx {\nabla }_{{\mathbf{x}}_i}{\mathbf{V}}_{\text{mov}}\left({\mathbf{x}}_i\right){\nabla }_{\mathbf{P}}{\mathbf{d}}_i\left(\mathbf{P}\right)\hfill \end{array}$$ (23)

where we have used the fact that, by definition, V_ref(x_i + d_i(P₀)) = V_mov(x_i) and used ∇_xi v_mov(x_i) to denote the discrete approximation to the partial derivatives at voxel i with respect to the three coordinate axes (we used central differences in our implementation).

The rigid transformation parameter P is stored as a 6-vector where the first three elements express translations along the three coordinate axes and the next three elements forms a vector that points along the axis of rotation whose magnitude is the angle of rotation in radians [9]. With such parametrization, we can use the fact that small rotations are effectively translations to approximate ∇_Pd_i(P) with the the linear relationship

$$\begin{array}{cc}\hfill {\nabla }_{\mathbf{P}}{\mathbf{d}}_i\left(\mathbf{P}\right)& \approx {\nabla }_{\mathbf{P}}{\mathbf{M}}_i\mathbf{P}\hfill \\ \hfill & ={\mathbf{M}}_i,\hfill \end{array}$$ (24)

where

$${\mathbf{M}}_i=\left[\begin{array}{cccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill z_i\hfill & \hfill -y_i\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill -z_i\hfill & \hfill 0\hfill & \hfill x_i\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill y_i\hfill & \hfill -x_i\hfill & \hfill 0\hfill \end{array}\right].$$ (25)

Substituting this approximation back into equation (23) gives us,

$${\left({\mathbf{J}}_{\mathbf{r}}\right)}_i\approx {\nabla }_{{\mathbf{x}}_i}{\mathbf{v}}_{\text{mov}}\left({\mathbf{x}}_{\mathbf{i}}\right){\mathbf{M}}_i.$$ (26)

Including all of our approximations, the steps defined in equation (21) can sometimes increase the residual error. To address this, we use a scaling factor to shrink our update ΔP; the factor starts at 1.0 and whenever a step increases error we undo the update to P and multiply the scaling factor by 0.25. The minimization is terminated when either the absolute difference between P^s and P^s−1 becomes negligible or a maximum number of iterations is reached. In our implementation, the former criterion is specified such that iteration stops when the every element of |P^s − P^s−1| is less than 10⁻⁵. The maximum number of iteration can be set according to the time constraint of real time motion correction. In our implementation for experimental results, this stopping criterion is never reached. Since we are registering reference volume to source volume, when the iterative process ends, P⁻¹ gives the desired transformation from the source volume to the reference volume.

2.4. Quantifying Registration Accuracy

Registration accuracy can be measured by comparing the result from Gauss-Newton algorithm and the “ground truth” transformation that was applied to the acquisition. Multiplying the inverse of the estimated rigid transform by the known true rigid transform results in a rigid transformation describing the error. The six parameters of this rigid transformation consist of three values describing translations, and three describing rotations, hence the error transformation can be measured separately for translations and rotations. Let R denote the rotation matrix of the difference in rotation between the approximated transformation and “ground truth”, and t be the difference in translation between the two (in mm). The natural measure of translation error is simply the 2-norm

$$E_{\text{trans}}=\sqrt{{\mathbf{t}}^T\mathbf{t}}.$$ (27)

The error in rotation can be summarized by the magnitude of its angle in degrees, which can be derived from R via,

$$E_{\text{rot}}=\text{arccos}\left(\frac{\mathbf{Tr}\left(\mathbf{R}\right)-1}{2}\right)$$ (28)

As a single summary metric, we have chosen to use the RMS displacement that the error transformation would produce in a sphere that is centered at the middle of the reference volume. We are using the assumption, as in Maurer et al., that the head is a sphere of radius 100 mm [8]. The target registration error for volume defined in [8] is a discrete form of the RMS measure derived by Jenkinson [5] as,

$$E_{\text{RMS}}=\sqrt{\frac{1}{5}{r}^2\mathrm{Tr}[{(\mathbf{R}-\mathbf{I})}^T(\mathbf{R}-\mathbf{I})+{\mathbf{t}}^T\mathbf{t}]}$$ (29)

giving an error displacement in mm, where r is the radius (in mm) of the sphere over which we average. In our comparisons, we have set r = 100 mm to represent an approximate radius for a human head. Note that this naturally defines a measure of rotation error, by taking just the first term in (29), giving the RMS translation inside the sphere due to error in rotation

$$t_{\text{rot-RMS}}=\sqrt{\frac{1}{5}{r}^2\mathrm{Tr}\left[{(\mathbf{R}-\mathbf{I})}^T(\mathbf{R}-\mathbf{I})\right]}$$ (30)

In addition to the average error, we are also interested in the worst-case error in a sphere of the same size. The maximum translation on the sphere imposed by the rotation error has magnitude (in mm)

$$t_{\text{rot-max}}=r\sqrt{3-\text{Tr}\left(\mathbf{R}\right)}.$$ (31)

Combining this with the displacement from translations gives the maximum displacement (in mm) in the sphere,

$$E_{\text{max}}=\sqrt{t_{\text{rot-max}}^2+2t_{\text{rot-max}}\mid \mathbf{t}-\left({\mathbf{t}}^T{\mathbf{u}}_{\mathbf{R}}\right){\mathbf{u}}_{\mathbf{R}}{\mid }_2+{\mathbf{t}}^T\mathbf{t}},$$ (32)

where u_R is a unit vector that represents the axis of rotation in angle-axis representation, which can be obtained by normalizing the last three elements of the six rigid transformation parameters.

3. Results

In all of the data we processed, the Gauss-Newton algorithm reached the stopping criterion roughly in 10 iterations and all produced plausible estimation of rigid motion.

Rotation error and translation error, from equations (28) and (27) respectively, are plotted in Figure (2). Cubic B-splines performed marginally better than tricubic, and significantly better than trilinear, for translations. However, as expected, trilinear interpolation suffers significantly in estimating rotations.

Figure 2.

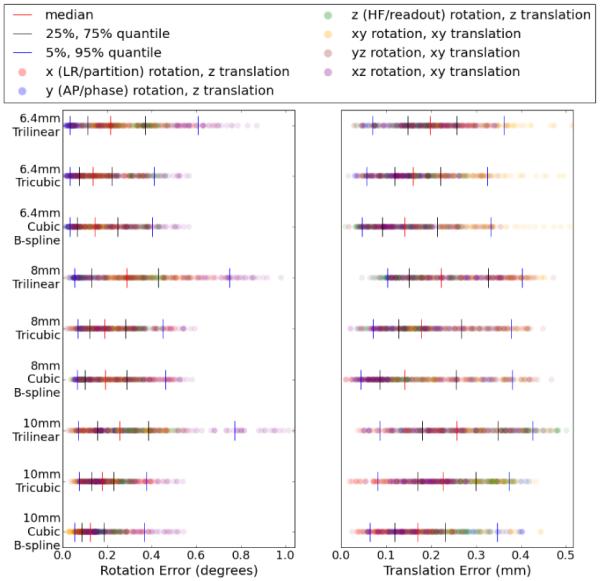
Rotation (left, degrees) and translation (right, mm) errors with cubic B-spline, tricubic and trilinear interpolation, with each row representing a separate algorithm/resolution combination. Each of the 420 results is plotted as a dot in each row, colored based on the ground truth axis of rotation. Quantiles are displayed with vertical lines.

Figure (3) shows the RMS displacement, defined in (29), from these registrations. The quantile values of the RMS displacement are listed in Table 2. At all resolutions, we find that cubic B-spline interpolation performs the best, followed by tricubic interpolation, and then trilinear interpolation. However, the results across resolutions are more mixed. With tricubic interpolation, the median registration accuracy is similar with 8 mm and 10 mm resolution, the variability in accuracy is smaller with 10 mm, the lower resolution. For cubic B-spline interpolation, the registration accuracy is reversed in that 10 mm resolution had the smallest RMS displacement in most quantiles.

Figure 3.

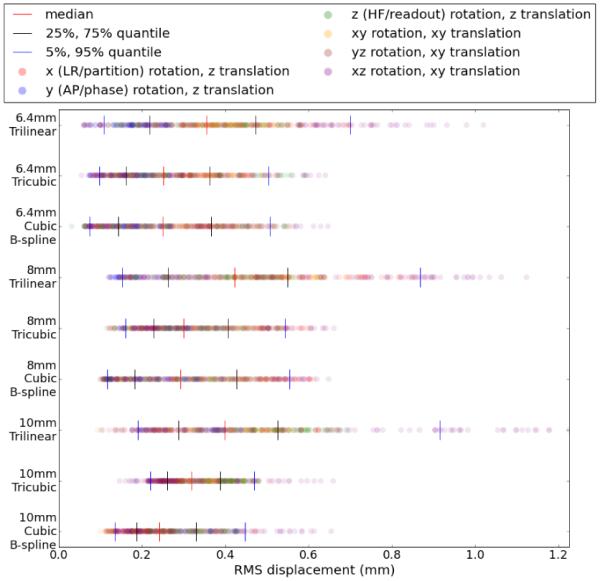
RMS error displacement from cubic B-spline, tricubic and trilinear interpolation, with each row representing a separate algorithm/resolution combination. Each of the 420 results is plotted as a dot in each row, colored based on the ground truth axis of rotation. Quantiles are displayed with vertical lines.

Table 2.

Quantiles of RMS displacement and maximum displacement (in mm) computed with trilinear, tricubic and cubic B-spline interpolations across three different resolutions. These values are depicted with vertical bars in Figures (3) and (4).

quantile	resolution (mm)	trilinear		tricubic		cubic B-spline
		RMS	Max	RMS	Max	RMS	Max
5%	6.4 8 10	0.11 0.15 0.19	0.16 0.24 0.31	0.10 0.16 0.22	0.17 0.25 0.34	0.07 0.12 0.13	0.13 0.19 0.22
25%	6.4 8 10	0.22 0.26 0.29	0.34 0.42 0.47	0.16 0.23 0.26	0.25 0.38 0.43	0.14 0.18 0.19	0.22 0.31 0.31
median	6.4 8 10	0.35 0.42 0.40	0.61 0.76 0.69	0.25 0.30 0.32	0.40 0.49 0.51	0.25 0.29 0.24	0.41 0.49 0.38
75%	6.4 8 10	0.47 0.55 0.53	0.82 1.00 0.94	0.36 0.41 0.39	0.61 0.71 0.64	0.37 0.43 0.33	0.63 0.76 0.54
95%	6.4 8 10	0.7 0.87 0.91	1.27 1.56 1.67	0.5 0.54 0.47	0.90 0.96 0.83	0.51 0.55 0.45	0.89 0.98 0.81

Figure (4) displays the maximum displacement of error transformation. The quantile values of the maximum displacement are also listed in Table 2. The trends in accuracy with resolution and algorithm are the same with this error metric as in Figure (3).

Figure 4.

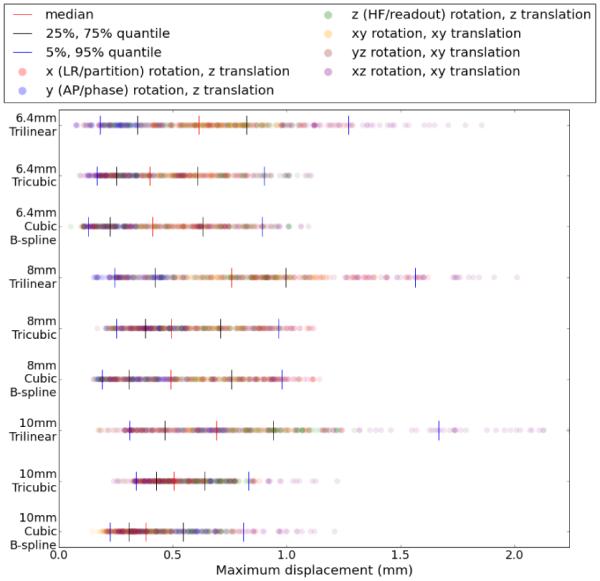
Maximum error displacement from cubic B-spline, tricubic and trilinear interpolation, with each row representing a separate algorithm/resolution combination. Each of the 420 results is plotted as a dot in each row, colored based on the ground truth axis of rotation. Quantiles are displayed with vertical lines.

To better understand these effects, we examined the contribution of rotations and translations to the error transformations separately, to see whether one is dominating the other. Figure (2) already shows the effect of translations, and Figure (5) shows maximum and RMS displacements due to just the rotation component of the error, derived from equations (31) and (30) respectively. Comparing Figure (2) and Figure (5), it can be observed that the relative scale of the RMS displacements in mm due to rotation and translation error are roughly the same, where as the scale of maximum displacements from rotation error is slightly larger than the translation error.

Figure 5.

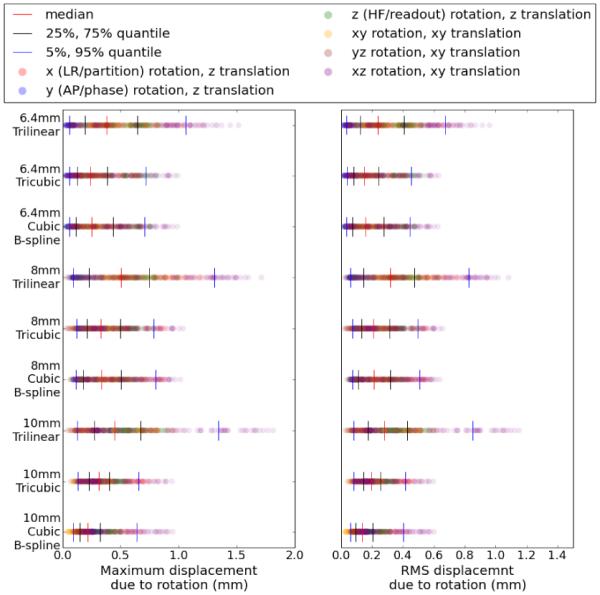
Maximum (left) and RMS (right) displacement from rotation error for cubic B-spline, tricubic, and trilinear interpolation, with each row representing a separate algorithm/resolution combination. Each of the 420 results is plotted as a dot in each row, colored based on the ground truth axis of rotation. Quantiles are displayed with vertical lines.

We tested improvements across different resolutions and interpolation methods using the Wilcoxon signed-rank test on the RMS errors of the registrations. The test was performed on each pair of resolutions or interpolation methods, and the test statistic from all 420 registrations in each condition was converted to a z-score. These z-scores from the test are summarized in Tables (3) and (4).

Table 3.

Wilcoxon signed-rank test for comparing registration accuracy across interpolation methods. A negative score indicates that there is an improvement in the pair from the first interpolation method to the second, and a positive score indicates the opposite. Bolded values in the table are z-scores that are not significant for a one-sided difference at p < 0.01.

	6.4 mm	8 mm	10 mm
Trilinear to Tricubic	−15.52	−12.84	−12.34
Trilinear to Cubic B-spline	−15.55	−15.93	−16.93
Tricubic to Cubic B-spline	− 2.61	−5.68	−15.63

Table 4.

Wilcoxon signed-rank test for comparing registration accuracy across resolutions. A negative score indicates that there is an improvement in the pair from the first resolution to the second, and a positive score indicates the opposite. Bolded values in the table are z-scores that are not significant for a one-sided difference at p < 0.01.

	10 to 8 mm	8 to 6.4 mm	10 to 6.4 mm
Trilinear	0.49	−11.62	−7.74
Tricubic	−3.09	−12.11	−10.79
Cubic B-spline	5.54	−11.29	− 0.71

These results support the observation that both tricubic and cubic B-spline interpolation outperforms trilinear interpolation, and cubic B-spline interpolation produces more accurate registration than tricubic interpolation at all resolutions. The results for comparison across resolutions are perhaps counter-intuitive; 10 mm resolution showed higher accuracy with both trilinear and cubic B-spline interpolation than 8 mm resolutions. However, there is an improvement in registration accuracy from 6.4 mm resolution to both 8 mm and 10 mm resolutions.

4. Discussion

Our accuracy goal was 1 mm error, based on the target application of real time MRI motion correction. Our results show that registration at all three vNav resolutions achieves this goal when using cubic B-spline interpolation or tricubic interpolation. In particular, the registration accuracy with cubic B-spline interpolation at 10 mm resolution is acceptable, which can be helpful in real time MRI motion correction since it is significantly faster to acquire and register this data compared to the 8 mm navigators currently being used in practice. We are working to acquire more data in order to explore the counter-intuitive result that 10 mm resolution were of higher accuracy than 8 mm resolution. There is also measurable improvement in accuracy from using 6.4 mm that may be worth the additional cost in acquisition and registration time in certain MRI applications, e.g., single-voxel spectroscopy where there is more available dead-time [4].

Our results also indicate that, at all resolutions, cubic B-splines provide more accurate results than either trilinear or tricubic interpolation. This is consistent with the literature, showing fewer artifacts in cubic B-spline interpolation compared to the other two algorithms [11]. We have demonstrated that, by paying a cost in memory, cubic B-spline interpolation can be made as computationally efficient as tricubic interpolation in our application.

Interestingly, we observed that registration accuracy decreased with rotations involving the head foot (HF) axis. This may be due to our scanning protocol’s axes (HF/readout/z, AP/phase/y, LR/partition/x), where rotations around the HF and LR axes cause the phase-encoded axis to rotate. This will, in turn, cause the susceptibility distortions around the sinuses to shift direction, potentially influencing the accuracy of our results, as noted in previous work registering higher-resolution EPI volumes [2]. Figure 6 shows an axial slice of the difference between a volume with no rotation and known true 5° rotations around each imaging axis. Comparing rotation around HF with that around AP, we see the sinus much more prominently in the HF rotation. Further work is needed to verify whether this hypothesis is correct. If so, it may be possible to mask out these regions, since they are localized to the sinuses and other internal air/tissue interfaces.

Figure 6.

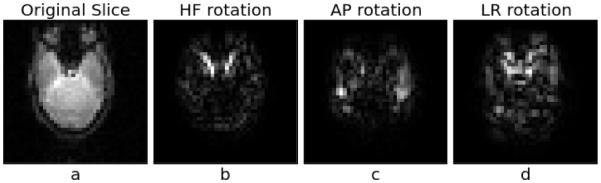
(a) Sample sagittal slice in the HF direction at 6.4 mm resolution, with mask applied in the Fourier domain only. (b)-(d) Difference between a volume with no rotation and volumes acquired with 5° rotations around the HF, AP and LR axes respectively, masked in both Fourier and image domains.

5. Conclusion

We have evaluated the accuracy of vNavs for tracking the human head using data with known ground-truth rigid transformations. This application demands accurate sub-voxel registration be performed as efficiently as possible on the vNav data as it arrives. We have explored choices of both vNav resolution, and derived and evaluated three efficient registration algorithms, to understand the trade-offs between acquisition and registration time and accuracy of motion tracking.

We demonstrated registration algorithms that perform accurate sub-voxel volume registration on vNavs. Median tracking errors from 6.4 mm, 8 mm and 10 mm vNavs using either cubic b-spline or tricubic interpolation achieved our goal of 1 mm. Our results show that improving vNav resolution provides measurable improvement in registration accuracy at the cost of acquisition time. Our algorithmic comparison shows that cubic B-spline interpolation provides the best results at all vNav resolutions, in particular cubic B-spline interpolation can achieve high accuracy, even at 10 mm resolution.

We have also presented a refactoring of the cubic B-splines interpolation algorithm that reduces the perinterpolation time by storing pre-computed interpolation coefficients. This makes the computational cost of cubic B-spline interpolation the same as tricubic interpolation in our application.

We identified distortions in our MRI data due to field inhomogeneity as a potential limitation to our current method and plan to acquire further data to explore masking strategies to mitigate their effects.

All image processing and analysis algorithms were implemented in Python. However, our eventual goal is to develop a new registration algorithm for use on-scanner with vNavs. In the derivations of the algorithms explored in this work, we have focused on the time-efficiency of our algorithms, with the goal that the remaining speed-up in the on-scanner implementation will come from low-level memory management, etc. in C++ and the potential for parallelizing work, not fundamentally different algorithms. Our initial prototype, single-threaded C++ implementation, using the Eigen [3] library, has an average registration time of 25 ms for an 8 mm vNav volume. Future work will involve parallelization of the algorithm and further optimization, along with integration to the scanner environment.

Although PACE is currently implemented on the scanner, the full algorithm is not publicly available. Additionally, the on-scanner implementation cannot be used with all of the resolutions we are evaluating. For these reasons, we have not compared our results directly with PACE. However, a comparison of the current vNav+PACE system with any new navigator/registration combination will be important once the new system is implemented on the scanner.